
Geometry
Area of a triangle:
The area of a triangle can be found with the following formula:
or
Area Review
b
2
h
b
1
bhA
2
1
2
bh
A
You can see why this works with the following diagrams:
b
h
b
h
Solve: Find the area of each triangle.
1. 2. 3.
4in
5in
13in
11in
15in
12in
9in
19in
21in
15in
14in
Area of a trapezoid:
The area of a triangle can be found with the following formula:
or
)(
2
1
21
bbhA
2
)(
21
bbh
A
Solve: Find the area of each trapezoid.
1. 2. 3.
3in
10in
10in
12in
9in
8in
6in
12in
10in
17in
9in
17in
15in
14in

Geometry
Area of a circle:
The area of a circle can be found with the following formula:
Circumference of a circle looks similar: or
Area Review
Area and circumference of a circle:
Find the area and circumference of each:
1. 2. 3.
rC
2
dC
6in
2
rA
15in
32in
Combinations:
Find the area and perimeter of each:
1. 2. 3.
5in
5in
10in
10in
14.1in
15in
15in
Review:
Find the area and perimeter/circumference of each:
1. 2. 3.
16in
12in
20in
25in
20in
10in
25in
9in
Geometry
11in
11in
Name________________________ Period _____
Find the area of each: For #7-12 find the circumference/perimeter.
ROUND TO THE TENTH WHERE APPLICABLE.
1. 2. 3.
1. _______ 2. _______ 3. _______
Area Practice
4. 5. 6.
4. _______ 5. _______ 6. _______
7. 8. 9.
7. A:_____ C: _____ 8. A: _____ C: _____ 9. A:_____ C: _____
5in
6in
14in
11in
15in
13in
14in
12in
25in
24in
7in
4in
11in
11in
13in
10in
4in
3in
6in
5in
7in
12.5in
10in
11in
10. 11. 12.
10. A: _____ P: _____ 11. A: _____ P:_____ 12. A: _____ P: _____
18n
30in
4in
6in
7in
8in
8in
11.3in

Geometry
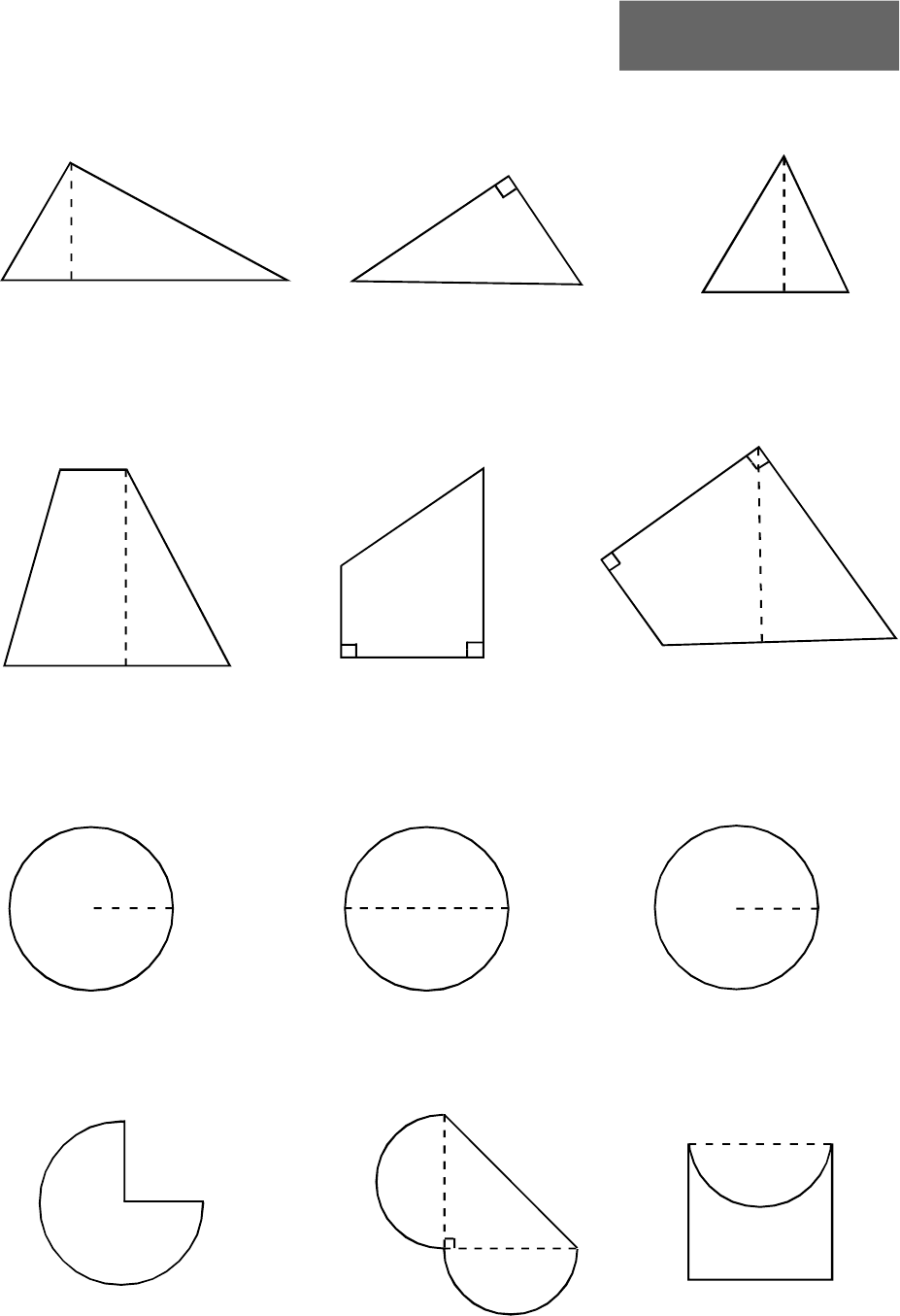
Area of Regular Polygons
What formula could be used to determine
the area (A) of a regular polygon given the:
Number of sides: n
Side length: s
Apothem (inradius): a
This is easiest to think about as
finding the area of n triangles with
base s and height a.
The area of the pentagon to the right is:
a
s
How can this formula be simplified given the perimeter P of the polygon?
Find the area of each regular polygon below: Round to the tenth.
1. A nonagon (9 sides) whose side length is 12cm and whose
apothem is 16.5cm?
_____________
2. A hexagon whose sides measure 6 inches and whose apothem
is 5.2 inches.
_____________
3. An octagon whose sides measure 61 inches and whose apothem
is 74 inches.
_____________
4. A heptagon whose apothem measure 10.25 inches and whose
sides are 10 inches long.
_____________
5. A polygon whose perimeter is 60 inches and whose apothem is 8.5 in?
_____________
14cm
10cm
Name________________________ Period _____
asnA
2
1
2
35051410
2
1
cmA

Geometry
Area of Regular Polygons
Name________________________ Period _____
Determine the area of each figure below:
6. 7.
6. ______ 7. ______
5 cm
3.4 cm
6 cm
4 cm
What is the perimeter of each figure below?
(round to the tenth)
8. Area = 585cm
2
9. Area = 364 in
2
8. ______ 9. ______
13 cm
10.4 in
What is the apothem of each regular polygon below?
(round to the tenth)
10. Area = 121 cm
2
11. Area = 1075 ft
2
10. ______ 11. ______
5 cm
25 feet
Geometry
Area of Regular Polygons
Name________________________ Period _____
Determine the area of each regular polygon below:
1. 2.
1. ______ 2. ___ _ _ _
5 cm
3.4 cm
9 cm
6 cm
3. 4.
3. ______ 4. ______
45cm
4.2 in
Given the area, what is the side length of each figure below?
(round to the tenth)
5. Area = 120.7in
2
6. Area = 58in
2
5. ______ 6. ______
13 ft
8.5 ft
6cm
52cm

Geometry
Determine the area of each shaded area below: (to the tenth)
(all polygons shown are regular)
7. 8.
7. ______ 8. ______
Polygon Area:
9. Find the area of the shaded region below:
Round to the tenth.
9. _______
6 cm
14 feet
8.2m
8m
2.2cm
2.2cm
17 feet
10. Challenge: Find the area of the shaded region below:
Round to the tenth.
10. _______
12ft

Geometry
Name________________________ Period _____
Surface Area is the sum of the areas of all faces which enclose a solid.
You should alreay be able to find the surface area of basic solids like those below:
Surface Area
Prisms have identical bases connected by parallelograms (generally rectangles).
To find the surface area of a prism, simply add the area of the bases to the area of
the lateral faces (sides).
Example:
5ft
10ft
4ft
9in
20in
Be methodical!
Two ends: 4 x 5 x 2 = 40ft
2
Front and back: 10 x 5 x 2 = 100ft
2
Top and bottom: 10 x 4 x 2 = 80ft
2
Surface area = 40 + 100 + 80 = 220ft
2
Top and bottom = 2(3.14 x 9
2
) = 508.68in
2
(remember the formula for area of a circle is
Rectangular ‘wrap’ = 2 x 3.14 x 9 x 20 = 1130.4in
2
(remember the formula for area of a the ‘wrap’ is
Total surface area: 1639.08in
2
.
2
r
hr)2(
(pentagon is regular)
10cm
8cm
7cm
Be methodical!
The pentagons are regular:
Each pentagon:
A = 1/2 x 7 x 10 x 5 = 175cm
2
times 2 = 350 cm
2
Five lateral faces:
A = 8 x 10 = 80 cm
2
times 5 = 400 cm
2
Total surface area =
350 + 400 = 750cm
2
Review practice:
1. What is the surface area of a 3-inch tall cylinder with a 7-inch radius?
____________
2. What is the surface area of a 9-foot tall prism whose bases are regular hexagons.
Each hexagon has 12-foot sides and a 10-foot apothem.
____________

Geometry
Name________________________ Period _____
Determine the surface area of each solid below:
Round all answers to the hundredth.
Work on a separate sheet.
3. A = _______ 4. A = ______ 5. A = _____
6. A = _______ 7. A = _______
Circle radius: 12ft
Pentagon sides: 3ft
Pentagon apothem: 2ft
8. A = _______ 9. A = _______
Surface Area
10in
7in
3ft
15ft
3ft
10in
9in
3m
20m
10ft
3ft
3ft
circle diameter = 2ft
100cm
30cm
31cm
octagon apothem = 12 inches
3ft
Geometry
30cm
16cm
16.5 cm
12m
9m
15ft
10ft
8ft
cylinder diameter = 18ft
10m
6m
10m
diameter = 4ft
Find the surface area of each:
There are 5 surfaces.
There are 9 surfaces.
There are 7 surfaces.
There are 7 surfaces.
Surface Area:
Geometry
The formula used to find the volume of a prism or cylinder:
Where B is the area of the base and h is the height.
This applies whether the figure is right or oblique (Oblique means slanted. Height is
measured along the altitude).
Prism/Cylinder Volume
100cm
30cm
31cm
7m
6m
BhV
Practice:
Find the volume of each solid. Round to the tenth.
1. 2.
1. ______ 2. ______
3. 4.
3. ______ 4. ______
5. 6.
5. ______ 6. ______
10cm
8cm
5m
13m
7m
12m
6ft
6ft
6ft
circle diameter = 4ft
(pentagon is regular)
10cm
7cm
6cm
Name________________________ Period _____
Geometry
The formula used to find the volume of a pyramid or cone:
Where B is the area of the base and h is the height.
This applies whether the figure is right or oblique (height is measured along the
altitude).
Pyramid/Cone Volume
BhV
3
1
Practice:
Find the volume of each solid.
7. (square-based pyramid) 8. (triangle-based pyramid)
7. ______ 8. ______
12ft
6ft
10ft
10ft
9. 10.
9. ______ 10. ______
4in
6in
5in
3in
8ft
8ft
5in
5in
6in
15in
10in
8in
Name________________________ Period _____
Geometry
Determine the volume of each solid below:
Round all answers to the hundredth.
Work on a separate sheet.
1.V = _______ 2. V = ______ 3. V = _____
4. V = _______ 5. V = _______
6. V = _______ 7. V = _______
6ft
3ft
5ft
5ft
15ft
6ft
5ft
cylinder diameter = 10ft
Name________________________ Period _____
Volume Practice
10in
10in
6in
4in
3in
4ft
15ft
4ft
17m
8m
15m
8in
6in
5in
10in

Geometry
Determine the area of each: Round to the tenth.
1. 2. 3.
Review
8in
6in
10in
50in
40in
20in
50in
6in
Determine the area of each: Round to the tenth.
1. 2. 3.
5cm
3.4cm
9cm
21in
8cm
20in
Determine the surface area of each: Round to the tenth.
1. 2. 3.
7in
11in
7cm
10cm
11cm
10ft
8ft
5ft
cylinder diameter = 12ft
Determine the volume of each: Round to the tenth.
1. 2. 3.
30m
18m
24m
12in
9in
8in
15in
17in
10m
6m
10m
diameter = 4m
Geometry
Name________________________ Period _____
Determine the surface area and volume for each:
1. A = _______ 2. A = ______ 3. A = _______
V = _______ V = ______ V = _______
4. A = _______ 5. A = _______
V = _______ V = _______
6. A = _______ 7. V = _______
V = _______ (no surface area on this one)
Surface Area and Volume
11in
6in
6in
8in
10in
7in
9in
3in
5in
5in
4in
4in
9in
Small Circle Radius: 4in
Large Circle Radius: 8in
7cm
10cm
11cm
3in
8in
4in
6in
5in
3in
(cylinder with a cone-shaped hole)

Geometry
Determine the surface area and volume for each:
1. A = _______ 2. A = ______ 3. A = _______
V = _______ V = ______ V = _______
Name________________________ Period _____
Surface Area and Volume
5in
12in
13in
7in
17in
5in
10in
10in
8in
8in
10m
6m
10m
diameter = 4ft
Determine the surface area and volume for each:
1. A = _______ 2. A = ______ 3. A = _______
V = _______ V = ______ V = _______
Name________________________ Period _____
Surface Area and Volume
5in
12in
13in
7in
17in
5in
10in
10in
8in
8in
10m
6m
10m
diameter = 4ft

Geometry
Changing the dimensions of an object effects the area and vol-
ume. Here are some easy examples:
Ex: A square is enlarged so that the length of each side is doubled. If
the area of the original square was 7 square inches, what will be the area
of the enlarged square?
Changing Dimensions
Ex: A cube has one-inch edges. How many times larger is the volume of
a cube with edges that are three times longer?
2x2=4 times bigger.
If you increase the dimensions of an object, the volume in-
creases by the product of those increases.
Example:
The volume of a rectangular prism is 10in
3
. You double the length, width,
and height. What will the new volume be?
Practice:
1. The area of a reactangle is 15cm
2
. If you triple the length and double
the width, what will the area of the new rectangle be?
2. A cube has a volume of 2cm
3
. Will a cube that has 8 times more vol-
ume be twice as tall, three times as tall, 4 times as tall, or 8 times as tall?
3. What happens to the area of a circle when you triple its radius?
3x3x3=27 times bigger.

Geometry
Practice:
Solve each.
1. A rectangular prism is 3x4x5 inches. How many times greater is the
volume of a 6x8x15 rectangular prism? (If you are not sure, find each
volume and divide).
2. When the sides of a triangle are 6 inches long, the area of the triangle
is about 15.6 square inches. What would be the area of an equilateral
triangle whose sides are 2 inches long? (round to the tenth)
3. A large circle has 81 times the area of a small circle. If the radius of
the large circle is 45 inches, what is the radius of the small circle?
Changing Dimensions
Practice:
Solve each.
1. The radius and height of a cone are tripled. What effect does this
have on the cone’s volume?
2. The radius of a cylinder is doubled, but the height is not changed. If
the original cylinder had a volume of 4cm
3
, what is the volume of the new
cylinder?
3. A cylinder and a cone have the same base and equal volumes. If the
cylinder is 15 inches tall, how tall is the cone?
Practice:
Solve each.
1. The length and width of a rectangular pyramid are tripled, and the
height is doubled. How many times larger is the new pyramid than the
original?
2. The dimensions of a cube are increased by 50% (1.5 times). If the
original cube had a volume of 16in
3
, what is the volume of the new cube?
3. You have a square sheet of construction paper. You want a sheet that
has twice the area. How many times wider will the new sheet be?
Geometry
Complete the following area problems:
1. 2. 3.
4. 5. 6.
Changing Dimensions
3in
4in
5in
6in
8in
10in
18in
24in
30in
3in
5in
6in
5in
6in
15in
7. 8. 9.
3in
6in
30in
Complete the following area problems:
10. What happens to the area of a square when you:
a. Double the sides. b. Triple the sides. c. Halve the sides.
_____________________ __________________ _________________
11. What happens to the volume of a cylinder when you:
a. Double the radius only. b. Triple the height only.
_____________________ __________________
c. Double the radius and triple the height.
_____________________
12. A rectangle has an area of 12cm
2
. What will the area be if you:
a. Triple all sides. b. Multiply all sides by 1.5.
_____________________ _____________________
Leave answers below in terms of Pi.
Name________________________ Period _____

Geometry
Practice:
Solve each.
13. A rectangular prism is 2x4x7 inches. How many times greater is the volume of a
6x8x7 rectangular prism? (If you are not sure, find each volume and divide).
14. When the sides of a pentagon are 6 inches long, the area of the pentagon is about
63 square inches. What would the area of a pentagon whose sides are 2 inches long?
15. A large circle has 36 times the area of a small circle. If the radius of the large
circle is 24 inches, what is the radius of the small circle?
Changing Dimensions
16. The radius and height of a cylinder are tripled. What effect does this have on the
volume?
17. The radius of a cylinder is doubled, and the height is multiplied by 5. If the origi-
nal cylinder had a volume of 10cm
3
, what is the volume of the new cylinder?
18. A right triangle has an area of 6in
2
. If all the dimensions are multiplied by 4, what
will the area of the new triangle be?
19. The length and width of a rectangular pyramid are doubled, and the height is
tripled. How many times larger is the new pyramid than the original?
20. The dimensions of a cube are increased so that they are 2.5 times longer. If the
original cube had a volume of 8in
3
, what is the volume of the new cube?
Name________________________ Period _____

Geometry
Practice:
Solve each.
1. The area of a circle is 30in
2
. If you triple the circle’s radius, what will its new area be?
2. When a hexagon has 2-inch sides, its area is about 10.4in
2
. What will be the approximate
area of a hexagon whose sides are 10 inches long??
3. A rectangular prism has a volume of 17cm
2
. If you double the length and width, but leave
the height unchanged, what will be the volume of the new prism?
4. If you want to double the area of a square, by what percent should you increase the length
of its sides.
hint: Try using a 10-inch square, double its area, and find the length of the sides of the new
square.
5. The volume of the regular dodecahedron below with an edge length of 4-inches is about
490 in
3
. What would be the volume of a regular dodecahedron whose edges are a foot long?
6. The volume of a cone is 3in
3
. What would be the volume after each modification below?
(each part refers to the original figure).
a. Double the radius only. ________________
b. Triple the height only. ________________
c. Double the height and triple the radius. _______________
d. Increase the height and radius by 50%. _______________
7. If you want to double the volume of a cube, by what percent should you increase the
edge length?
a.20% b.23% c.26% d.30% e.40%
Changing Dimensions
Name________________________ Period _____

Geometry
Name________________________ Period _____
Determine the area of each figure below.
Round to the tenth. Figures not to scale.
1. 2.
1. _________ 2. _________
Area and Volume Practice Test
3. 4.
3. _________ 4. _________
12in
13in
5in
9in
4in
5in
5in
3in
11cm
6in
7in
12m
9m
Determine the volume for each figure below:
(figures not to scale, round to the tenth)
5. Volume = _______ 6. Volume = _______
17m
8m
15m

Geometry
Name________________________ Period _____
Determine the surface area for each figure below:
(figures not to scale, round to the tenth)
7. Surface Area = _______ 8. Surface Area = ______
Area and Volume Practice Test
Solve each problem involving changing dimensions:
9. A rectangular prism has a volume of 5cm
3
. If you triple the length, width, and
height, what will the volume of the enlarged prism be?
9. __________
10. When the radius of a circle is multipled by 4, the area of the new circle is 40 in
3
.
What was the area of the original circle?
10. __________
11. The volume of a rectangular pyramid is 7m
3
. What is the volume of a pyramid
that is twice as tall, three times as long, and four times as wide?
11. __________
12. A cube has edges that are 6 centimeters long. How many times greater is the
volume of a cube with 9 centimeter sides?
12. __________
Pledge and sign:
12m
7m
12m
diameter = 5ft
17in
7in
13in
13in
9in
12in
