Student Solutions Manual for Elementary Differential Equations and

University of South Florida University of South Florida

Digital Commons @ University of Digital Commons @ University of

South Florida South Florida

Textbooks Collection Tampa Library

12-2013

Student Solutions Manual for Elementary Differential Equations Student Solutions Manual for Elementary Differential Equations

and Elementary Differential Equations with Boundary Value and Elementary Differential Equations with Boundary Value

Problems Problems

William F. Trench

Trinity University

, wtrench@trinity.edu

Follow this and additional works at: https://digitalcommons.usf.edu/oa_textbooks

Part of the Mathematics Commons, and the Ordinary Differential Equations and Applied Dynamics

Commons

Recommended Citation Recommended Citation

Trench, William F., "Student Solutions Manual for Elementary Differential Equations and Elementary

Differential Equations with Boundary Value Problems" (2013).

Textbooks Collection

. 7.

https://digitalcommons.usf.edu/oa_textbooks/7

This Book is brought to you for free and open access by the Tampa Library at Digital Commons @ University of

South Florida. It has been accepted for inclusion in Textbooks Collection by an authorized administrator of Digital

Commons @ University of South Florida. For more information, please contact [email protected].

STUDENT SOLUTIONS MANUAL FOR

ELEMENTARY

DIFFEREN TIAL EQUATIONS

AND

ELEMENTARY

DIFFEREN TIAL EQUATIONS

WITH BOUNDARY VALUE

PROBLEMS

William F. Trench

Andrew G. Cowles Disting uished Professor Emeritus

Department of Ma thematics

Trinity University

San Anto nio, Texas, USA

wtrench@trinity.edu

This book has been judged to meet the evaluation criteria set by the Edi-

torial Board of the American Insti tute of Mathematics in connection with

the Institute’s Open Textboo k Init iative. It may b e copied, modiﬁed, re-

distributed, translated, a nd built upo n subject to the Creative Commons

Attributi on-NonCommercial-ShareAlike 3.0 Unported License.

This book was published previously by Brooks/Cole Thomson Learning

Reproduct ion is permitted for any valid noncommercial educational, mathematical, or scientiﬁc purpose.

However, charges for proﬁt beyond reasonabl e printing costs are p rohibited.

TO BEVERLY

Contents

Chapter 1 Introduction 1

1.2 First Order Equations 1

Chapter 2 First Order Equations 5

2.1 Linear First Order Equations 5

2.2 Separable Equations 8

2.3 Existence and Uniqueness of Solutions of Nonlinear Equati ons 11

2.4 Transformation of Nonlinear Equations into Separable Equat ions 13

2.5 Exact Equations 17

2.6 Integrating Factors 21

Chapter 3 Numerical Methods 25

3.1 Euler’s Method 25

3.2 The Improved Euler Method and Related Methods 29

ii

Contents

3.3 The Runge-Kutta Method 34

Chapter 4 Applications of First Order Equations 39

4.1 Growth and Decay 39

4.2 Cooling and Mixing 40

4.3 Elementary Mechanics 43

4.4 Autonomous Second Order Equations 45

4.5 Applications to Curves 46

Chapter 5 Linear Second Order Equations 51

5.1 Homogeneous Linear Equations 51

5.2 Constant Coefﬁcient Homogeneous Equations 55

5.3 Nonhomgeneous Linear Equations 58

5.4 The Method of Undetermined Coefﬁcients I 60

5.5 The Method of Undetermined Coefﬁcients II 64

5.6 Reduction of Order 75

5.7 Varia tion of Parameters 79

Chapter 6 Applcations of Linear Second Order Equations 85

6.1 Spring Problems I 85

6.2 Spring Problems II 87

6.3 The RLC Circuit 89

6.4 Motion Under a Central Force 90

Chapter 7 Series Solutions of Linear Second Order Equations 108

7.1 Review of Power Series 91

7.2 Series Solutions Near an Ordinary Point I 93

7.3 Series Solutions Near an Ordinary Point II 96

7.4 Regular Singular Points; Eul er Equations 102

7.5 The Method of Frobenius I 103

7.6 The Method of Frobenius II 108

7.7 The Method of Frobenius III 118

Chapter 8 Laplace Transforms 125

8.1 Introduction to the Laplace Transform 125

8.2 The Inverse Laplace Transform 127

8.3 Solution of Initial Value Problems 134

8.4 The Unit Step Function 140

8.5 Constant Coefﬁcient Equations with Piecewise Continuous Forcing

Functions 143

8.6 Convolution 152

Contents

iii

8.7 Constant Cofﬁcient Equations with Impulses 55

Chapter 9 Linear Higher Order E quations 159

9.1 Introduction to Linear Hi gher Order Equations 159

9.2 Hig her Order Constant Coefﬁcient Homogeneous Equations 171

9.3 Undetermined Coefﬁcients for Higher Order Equations 175

9.4 Varia tion of Parameters for Higher Order Equations 181

Chapter 10 Linear Systems of Differential Equations 221

10.1 Introduction to Systems of Di fferential Equations 191

10.2 Linear Systems of Differential Equations 192

10.3 Basic Theory of Homogeneous Linear Systems 193

10.4 Constant Coefﬁcient Homogeneous Systems I 194

10.5 Constant Coefﬁcient Homogeneous Systems II 201

10.6 Constant Coefﬁcient Homogeneous Systems II 245

10.7 Vari ation of Parameters for Nonhomogeneous Linear Systems 218

Chapter 221

11.1 Eigenvalue Problems for y

00

C y D 0 221

11.2 Fourier Expansions I 223

11.3 Fourier Expansions II 229

Chapter 12 Fourier Solutions of Parti al Differential Equations 239

12.1 The Heat Equation 239

12.2 The Wave Equation 247

12.3 Laplace’s Equation in Rectangular Coordinates 260

12.4 Laplace’s Equation in Polar Coo rdinates 270

Chapter 13 B oundary Value Problems for Second Order Ordinary Differential Equations 273

13.1 Two-Point Boundary Value Problems 273

13.2 Sturm-Liouville Problems 279

CHAPTER 1

Introduction

1.2 BASIC CONCEPTS

1.2.2. ( a) If y D ce

2x

, then y

0

D 2ce

2x

D 2y.

(b) If y D

x

2

3

C

c

x

, then y

0

D

2x

3



c

x

2

, so xy

0

C y D

2x

2

3



c

x

C

x

2

3

C

c

x

D x

2

.

(c) If

y D

1

2

C ce

x

2

; then y

0

D 2xce

x

2

and

y

0

C 2xy D 2xce

x

2

C 2x



1

2

C ce

x

2



D 2xce

x

2

C x C 2cxe

x

2

D x:

(d) If

y D

1 C ce

x

2

=2

1  ce

x

2

=2

then

y

0

D

.1  ce

x

2

=2

/.cxe

x

2

=2

/  .1 C ce

x

2

=2

/cxe

x

2

=2

.1  cxe

x

2

=2

/

2

D

2cxe

x

2

=2

.1  ce

x

2

=2

/

2

and

y

2

 1 D

1 C ce

x

2

=2

1  ce

x

2

=2

!

2

 1

D

.1 C ce

x

2

=2

/

2

 .1  ce

x

2

=2

/

2

.1  ce

x

2

=2

/

2

D

4ce

x

2

=2

.1  ce

x

2

=2

/

2

;

1

2 Chapter 1

Basic Concepts

so

2y

0

C x.y

2

 1/ D

4cx C4cx

.1  ce

x

2

=2

/

2

D 0:

(e) If y D tan



x

3

C c



, then y

0

D x

2

sec

2



x

3

C c



D x

2



1 C tan

2



x

3

3 C c



D x

2

.1 C y

2

/.

(f) If

y D .c

1

C c

2

x/e

x

C sin x C x

2

; then

y

0

D .c

1

C 2c

2

x/e

x

C cos x C 2x;

y

0

D .c

1

C 3c

2

x/e

x

 sin x C 2;

and y

00

 2y

0

C y D c

1

e

x

.1  2 C 1/ C c

2

xe

x

.3  4 C 1/

sin x  2 cos x C sin x C 2  4x C x

2

D 2 cos x C x

2

 4x C 2:

(g) If y D c

1

e

x

Cc

2

x C

2

x

, then y

0

D c

1

e

x

Cc

2



2

x

2

and y

00

D c

1

e

x

C

4

x

3

, so .1x/y

00

Cxy

0

y D

c

1

.1  x C x  1/ C c

2

.x  x/ C

4.1  x/

x

3



2

x



2

x

D

4.1  x  x

2

/

x

3

(h) If y D

c

1

sin x C c

2

cos x

x

1=2

C 4x C 8 then y

0

D

c

1

cos x c

2

sin x

x

1=2



c

1

sin x C c

2

cos x

2x

3=2

C 4 and

y

00

D 

c

1

sin x C c

2

cos x

x

1=2



c

1

sin x  c

2

cos x

x

3=2

C

3

4

c

1

sin x C c

2

cos x

x

5=2

, so x

2

y

00

Cxy

0

C



x

2



1

4



y D

c

1



x

3=2

sin x  x

1=2

cos x C

3

4

x

1=2

sin x C x

1=2

cos x

1

2

x

1=2

sin x C x

3=2

sin x 

1

4

x

1=2

sin x



C c

2



x

3=2

cos x C x

1=2

sin x C

3

4

x

1=2

cos x

x

1=2

sin x 

1

2

x

1=2

cos x C x

3=2

cos x 

1

4

x

1=2

cos x



C4x C



x

2



1

4



.4x C8/ D 4x

3

C8x

2

C

3x  2.

1.2.4. ( a) If y

0

D xe

x

, then y D xe

x

C

R

e

x

dx C c D .1  x/e

x

C c, and y.0/ D 1 ) 1 D 1 C c,

so c D 0 and y D .1  x/e

x

.

(b) If y

0

D x sin x

2

, then y D 

1

2

cos x

2

C c; y



r



2



D 1 ) 1 D 0 C c, so c D 1 and

y D 1 

1

2

cos x

2

.

(c) Write y

0

D tan x D

sin x

cos x

D 

1

cos x

d

dx

.cos x/. Integrating this yields y D ln jcos xj C c;

y.=4/ D 3 ) 3 D ln .cos.=4// C c, or 3 D ln

p

2 C c, so c D 3  l n

p

2, so y D ln.jcos xj/ C

3  ln

p

2 D 3  ln.

p

2jcos xj/.

(d) If y

00

D x

4

, then y

0

D

x

5

C c

1

; y

0

.2/ D 1 )

32

5

C c

1

D 1 ) c

1

D 

37

15

, so y

0

D

x

5



37

15

. Therefore, y D

x

6

30



37

15

.x  2/ C c

2

; y.2/ D 1 )

64

30

C c

2

D 1 ) c

2

D 

47

15

, so

y D 

47

15



37

5

.x  2/ C

x

6

30

.

(e) (A)

R

xe

2x

dx D

xe

2x

2



1

2

Z

e

2x

dx D

xe

2x

2



e

2x

4

. Therefore, y

0

D

xe

2x

2



e

2x

4

C c

1

;

y

0

.0/ D 1 ) 

1

4

C c

1

D

5

4

) c

1

D

5

4

, so y

0

D

xe

2x

2



e

2x

4

C

5

4

; Usi ng (A) again, y D

xe

2x

4



e

2x

8



e

2x

8

C

5

4

x C c

2

D

xe

2x

4



e

2x

4

C

5

4

x C c

2

; y.0/ D 7 ) 

1

4

C c

2

D 7 ) c

2

D

29

4

, so

y D

xe

2x

4



e

2x

4

C

5

4

x C

29

4

.

(f) (A)

R

x sin x dx D x cos x C

R

cos x dx D x cos x C sin x and (B)

R

x cos x dx D x sin x 

R

sin x dx D x sin x Ccos x. If y

00

D x sin x, then (A ) implies that y

0

D x cos x sin x Cc

1

; y

0

.0/ D

3 ) c D 3, so y

0

D x cos x sin x 3. Now (B) implies that y D x sin x Ccos x Ccos x 3x Cc

2

D

x sin x C 2 cos x  3x C c

2

; y.0/ D 1 ) 2 C c

2

D 1 ) c

2

D 1, so y D x sin x C 2 cos x  3x  1.

Section 1.2

Basic Concepts

3

(g) If y

000

D x

2

e

x

, then y

00

D

R

x

2

e

x

dx D x

2

e

x

 2

R

xe

x

dx D x

2

e

x

 2xe

x

C 2e

x

C c

1

;

y

00

.0/ D 3 ) 2 Cc

1

D 3 ) c

1

D 1, so ( A ) y

00

D .x

2

2x C2/e

x

C1. Si nce

R

.x

2

2x C2/e

x

dx D

.x

2

 2x C 2/e

x



R

.2x  2/e

x

dx D .x

2

 2x C 2/e

x

 .2x  2/e

x

C 2e

x

D .x

2

 4x C 6/e

x

,

(A) implies that y

0

D .x

2

 4x C 6/e

x

C x C c

2

; y

0

.0/ D 2 ) 6 C c

2

D 2 ) c

2

D 8, so ( B)

y

0

D .x

2

4x C6/e

x

Cx 8; Since

R

.x

2

4x C6/e

x

dx D .x

2

4x C6/e

x



R

.2x 4/e

x

dx D .x

2



4xC6/e

x

.2x 4/e

x

C2e

x

D .x

2

6xC12/e

x

, (B) implies that y D .x

2

6xC12/e

x

C

x

2

8xCc

3

;

y.0/ D 1 ) 12 C c

3

D 1 ) c

3

D 11, so y D .x

2

 6x C12/e

x

C

x

2

 8x  11.

(h) If y

000

D 2 C sin 2x, then y

00

D 2x 

cos 2x

2

C c

1

; y

00

.0/ D 3 ) 

1

2

C c

1

D 3 ) c

1

D

7

2

,

so y

00

D 2x 

cos 2x

2

C

7

2

. Then y

0

D x

2



sin 2x

4

C

7

2

x C c

2

; y

0

.0/ D 6 ) c

2

D 6, so

y

0

D x

2



sin 2x

4

C

7

2

x6. Then y D

x

3

C

cos 2x

8

C

7

4

x

2

6xCc

3

; y.0/ D 1 )

1

8

Cc

3

D 1 ) c

3

D

7

8

,

so y D

x

3

C

cos 2x

8

C

7

4

x

2

 6x C

7

8

.

(i) If y

000

D 2x C1, then y

00

D x

2

Cx Cc

1

; y

00

.2/ D 7 ) 6 Cc

1

D 7 ) c

1

D 1; so y

00

D x

2

Cx C1.

Then y

0

D

x

3

C

x

2

C.x 2/ Cc

2

; y

0

.2/ D 4 )

14

3

Cc

2

D 4 ) c

2

D 

26

3

, so y

0

D

x

3

C

x

2

C

.x 2/ 

26

3

. Then y D

x

4

12

C

x

3

6

C

1

2

.x 2/

2



26

3

.x 2/Cc

3

; y.2/ D 1 )

8

3

Cc

3

D 1 ) c

3

D 

5

3

,

so y D

x

4

12

C

x

3

6

C

1

2

.x  2/

2



26

3

.x  2/ 

5

3

.

1.2.6. (a) If y D x

2

.1 Cln x/, then y.e/ D e

2

.1 Cln e/ D 2e

2

; y

0

D 2x.1 Cln x/ Cx D 3x C2x ln x,

so y

0

.e/ D 3e C 2e ln e D 5e; (A) y

00

D 3 C 2 C 2 ln x D 5 C 2 ln x. Now, 3xy

0

 4y D 3x.3x C

2x ln x/  4x

2

.1 C ln x/ D 5x

2

C 2x

2

ln x D x

2

y

00

, from (A).

(b) If y D

x

2

3

C x  1, t hen y.1/ D

1

3

C 1  1 D

1

3

; y

0

D

2

3

x C 1, so y

0

.1/ D

2

3

C 1 D

5

3

; (A)

y

00

D

2

3

. Now x

2

 xy

0

C y C 1 D x

2

 x



2

3

x C 1



C

x

2

3

C x  1 C 1 D

2

3

x

2

D x

2

y

00

, from (A).

(c) If y D .1 C x

2

/

1=2

, then y.0/ D .1 C 0

2

/

1=2

D 1; y

0

D x.1 C x

2

/

3=2

, so y

0

.0/ D 0; (A)

y

00

D .2x

2

1/.1Cx

2

/

5=2

. Now, .x

2

1/y x.x

2

C1/y

0

D .x

2

1/.1Cx

2

/

1=2

x.x

2

C1/.x/.1C

x

2

/

3=2

D .2x

2

 1/.1 C x

2

/

1=2

D y

00

.1 C x

2

/

2

from (A), so y

00

D

.x

2

 1/y  x.x

2

C 1/y

0

.x

2

C 1/

2

.

(d) If y D

x

2

1  x

, then y.1=2/ D

1=4

1  1=2

D

1

2

; y

0

D 

x.x  2/

.1  x/

2

, so y

0

.1=2/ D

.1=2/.3=2/

.1  1=2/

2

D 3;

(A) y

00

D

2

.1  x/

3

. Now, (B ) x Cy D x C

x

2

1  x

D

x

1  x

and (C) xy

0

y D 

x

2

.x  2/

.1  x/

2



x

2

1  x

D

x

2

.1  x/

2

. From (B) and (C), .x C y/.xy

0

 y/ D

x

3

.1  x/

3

D

x

3

2

y

00

, so y

00

D

2.x C y/.xy

0

 y/

x

3

.

1.2.8. (a) y D .x  c/

a

is deﬁned and x  c D y

1=a

on .c; 1/; moreover, y

0

D a.x  c/

a1

D

a



y

1=a



a1

D ay

.a1/=a

.

(b) if a > 1 or a < 0, then y  0 is a solution of (B) on .1; 1/.

1.2.10. (a) Since y

0

D c we must show that the right side of (B) reduces to c for all values of x in some

4 Chapter 1

Basic Concepts

inter val. If y D c

2

C cx C 2c C 1,

x

2

C 4x C 4y D x

2

C 4x C 4c

2

C 4cx C 8c C 4

D x

2

C 4.1 C c/x C 4.c

2

C 2c C 1/

D x

2

C 4.1 C c/ C 2.c C 1/

2

D .x C 2c C 2/

2

:

Therefore,

p

x

2

C 4x C 4y D x C 2c C 2 and the right side of (B) reduces to c if x > 2c  2.

(b) If y

1

D 

x.x C 4/

4

, then y

0

1

D 

x C 2

2

and x

2

C 4x C 4y D 0 fo r all x. Therefore, y

1

satisﬁes

(A) on .1; 1/.

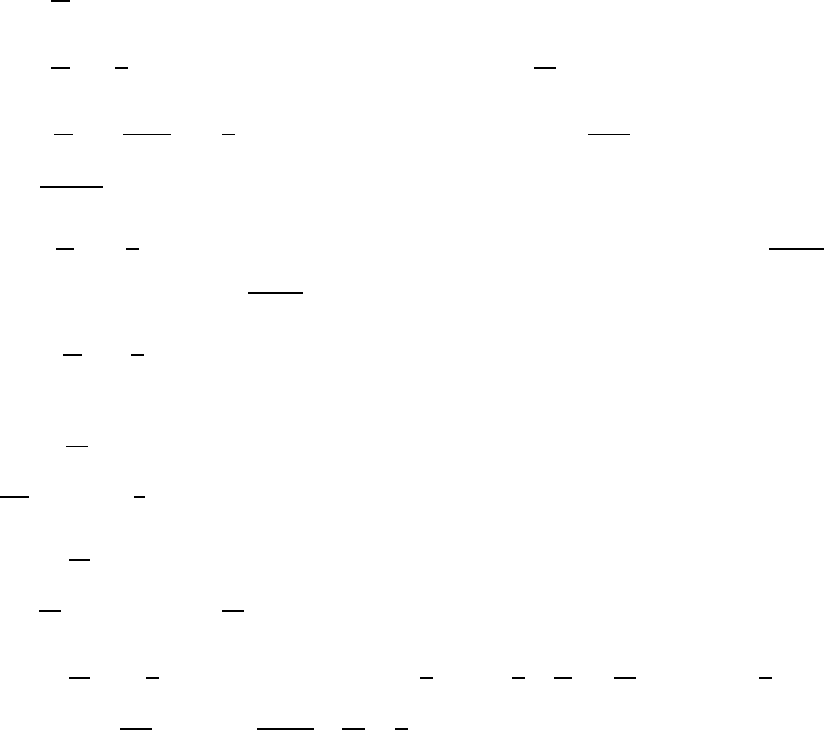
CHAPTER 2

First Order Equations

2.1 LINEAR FIRST ORDER EQUATIONS

2.1.2.

y

0

y

D 3x

2

; jln jyj D x

3

C k; y D ce

x

3

. y D ce

.ln x/

2

=2

.

2.1.4.

y

0

y

D 

3

x

; ln jyj D 3 ln jxj C k D ln jxj

3

C k; y D

c

x

3

.

2.1.6.

y

0

y

D 

1 C x

x

D 

1

x

 1; jln jyj D ln jxj  x C k; y D

ce

x

x

; y.1/ D 1 ) c D e;

y D

e

.x1/

x

.

2.1.8.

y

0

y

D 

1

x

 cot x; jln jyj D ln jxj  ln jsin xj C k D ln jx sin xj C k; y D

c

x sin x

;

y.=2/ D 2 ) c D  ; y D



x sin x

.

2.1.10.

y

0

y

D 

k

x

; jln jyj D k ln jxj C k

1

D ln jx

k

j C k

1

; y D cjxj

k

; y.1/ D 3 ) c D 3;

y D 3x

k

.

2.1.12.

y

0

1

y

1

D 3; ln jy

1

j D 3x; y

1

D e

3x

; y D ue

3x

; u

0

e

3x

D 1; u

0

D e

3x

; u D

e

3x

3

Cc; y D

1

3

C ce

3x

.

2.1.14.

y

0

1

y

1

D 2x; ln jy

1

j D x

2

; y

1

D e

x

2

; y D ue

x

2

; u

0

e

x

2

D xe

x

2

; u

0

D x;

u D

x

2

C c; y D e

x

2



x

2

C c



.

2.1.16.

y

0

1

y

1

D 

1

x

; ln jy

1

j D ln jxj; y

1

D

1

x

; y D

u

x

;

u

0

x

D

7

x

2

C 3; u

0

D

7

x

C 3x;

u D 7 ln jxj C

3x

2

C c; y D

7 ln jxj

x

C

3x

2

C

c

x

.

5

6 Chapter 2

First Order Equatio ns

2.1.18.

y

0

1

y

1

D 

1

x

 2x; ln jy

1

j D ln jxj  x

2

; y

1

D

e

x

2

x

; y D

ue

x

2

x

;

u

0

e

x

2

x

D x

2

e

x

2

;

u

0

D x

3

; u D

x

4

C c; y D e

x

2



x

3

4

C

c

x



.

2.1.20.

y

0

1

y

1

D tan x; ln jy

1

j D ln jcos xj; y

1

D cos x; y D u cos x; u

0

cos x D cos x; u

0

D 1;

u D x C c; y D .x C c/ cos x.

2.1.22.

y

0

1

y

1

D

4x  3

.x  2/.x  1/

D

5

x 2



1

x 1

; ln jy

1

j D 5 ln jx  2j  ln jx  1j D ln

ˇ

.x  2/

5

x  1

ˇ

;

y

1

D

.x  2/

5

x 1

; y D

u.x  2/

5

x 1

;

u

0

.x  2/

5

x  1

D

.x  2/

2

x  1

; u

0

D

1

.x  2/

3

; u D 

1

2

1

.x  2/

2

C

c; y D 

1

2

.x  2/

3

.x  1/

C c

.x  2/

5

.x  1/

.

2.1.24.

y

0

1

y

1

D 

3

x

; ln jy

1

j D 3 ln jxj D ln jxj

3

; y

1

D

1

x

3

; y D

u

x

3

;

u

0

x

3

D

e

x

2

; u

0

D xe

x

;

u D xe

x

 e

x

C c; y D

e

x

2



e

x

3

C

c

x

3

.

2.1.26.

y

0

1

y

1

D 

4x

1 C x

2

; ln jy

1

j D 2 ln.1 C x

2

/ D ln.1 C x

2

/

2

; y

1

D

1

.1 C x

2

/

2

; y D

u

.1 C x

2

/

2

;

u

0

.1 C x

2

/

2

D

2

.1 C x

2

/

2

; u

0

D 2; u D 2x C c; y D

2x C c

.1 C x

2

/

2

; y.0/ D 1 )

c D 1; y D

2x C 1

.1 C x

2

/

2

.

2.1.28.

y

0

1

y

1

D cot x; ln jy

1

j D ln jsin xj; y

1

D

1

sin x

; y D

u

sin x

;

u

0

sin x

D cos x; u

0

D

sin x cos x; u D

sin

2

x

2

Cc; y D

sin x

2

Cc csc x; y.=2/ D 1 ) c D

1

2

; y D

1

2

.sin x C csc x/.

2.1.30.

y

0

1

y

1

D 

3

x 1

; ln jy

1

j D 3 ln jx  1j D ln jx  1j

3

; y

1

D

1

.x  1/

3

; y D

u

.x  1/

3

;

u

0

.x  1/

3

D

1

.x  1/

4

C

sin x

.x  1/

3

; u

0

D

1

x  1

C sin x; u D ln jx  1j  cos x C c; y D

ln jx  1j  cos x C c

.x  1/

3

; y.0/ D 1 ) c D 0; y D

ln jx  1j  cos x

.x  1/

3

.

2.1.32.

y

0

1

y

1

D 

2

x

; ln jy

1

j D 2 ln jxj D ln.x

2

/; y

1

D x

2

; y D ux

2

; u

0

x

2

D x; u

0

D 

1

x

;

u D ln jxjC c; y D x

2

.c  ln jxj /; y.1/ D 1 ) c D 1; y D x

2

.1  ln x/.

2.1.34.

y

0

1

y

1

D 

3

x 1

; ln jy

1

j D 3 ln jx  1j D ln jx  1j

3

; y

1

D

1

.x  1/

3

; y D

u

.x  1/

3

;

u

0

.x  1/

3

D

1 C .x  1/ sec

2

x

.x  1/

4

; u

0

D

1

x 1

Csec

2

x; u D ln jx1jCtan xCc; y D

ln jx  1j C tan x Cc

.x  1/

3

;

y.0/ D 1 ) c D 1; y D

ln jx  1j C tan x C 1

.x  1/

3

.

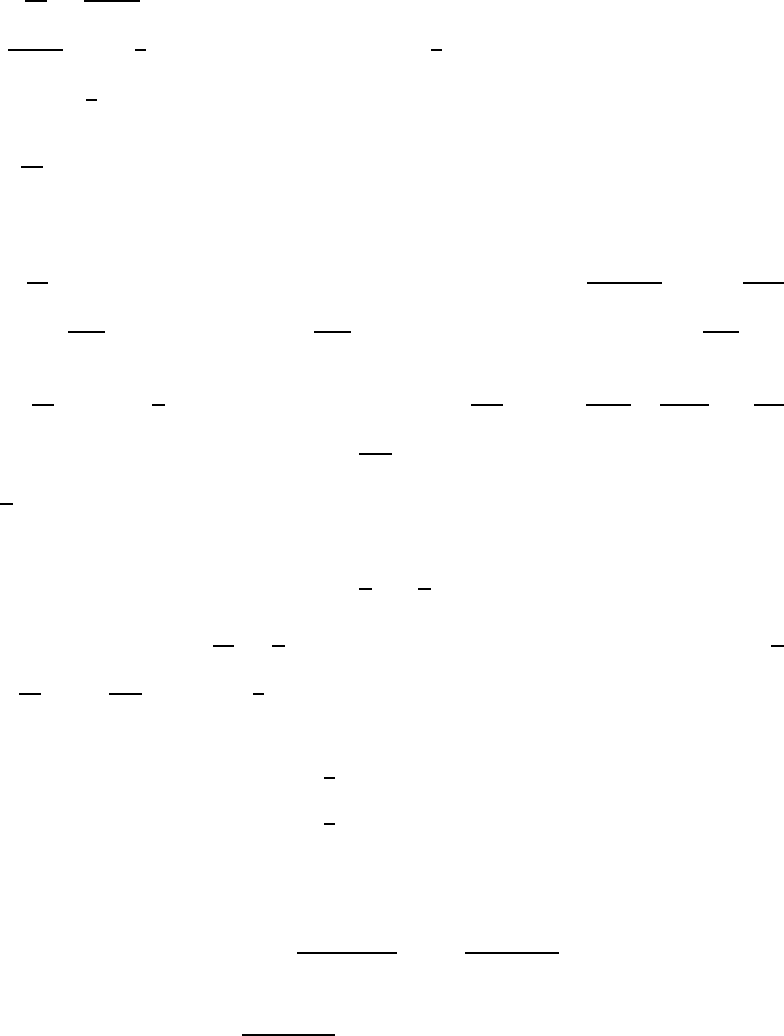
Section 2.1

Linear First Order Equations

7

2.1.36.

y

0

1

y

1

D

2x

x

2

 1

; ln jy

1

j D ln j x

2

 1j; y

1

D x

2

 1; y D u.x

2

 1/; u

0

.x

2

 1/ D x;

u

0

D

x

2

 1

; u D

1

2

ln jx

2

 1j C c; y D .x

2

 1/



1

2

ln jx

2

 1j C c



; y.0/ D 4 ) c D 4;

y D .x

2

 1/



1

2

ln jx

2

 1j  4



.

2.1.38.

y

0

1

y

1

D 2x; ln jy

1

j D x

2

; y

1

D e

x

2

; y D ue

x

2

; u

0

e

x

2

D x

2

; u

0

D x

2

e

x

2

; u D

cC

Z

x

0

t

2

e

t

2

dt; y D e

x

2



c C

Z

x

0

t

2

e

t

2

dt



; y.0/ D 3 ) c D 3; y D e

x

2



3 C

Z

x

0

t

2

e

t

2

dt



.

2.1.40.

y

0

1

y

1

D 1; ln jy

1

j D x; y

1

D e

x

; y D ue

x

; u

0

e

x

D

e

x

tan x

x

; u

0

D

tan x

x

;

u D c C

Z

x

1

tan t

t

dt; y D e

x



c C

Z

x

1

tan t

t

dt



; y.1/ D 0 ) c D 0; y D e

x

Z

x

1

tan t

t

dt.

2.1.42.

y

0

1

y

1

D 1 

1

x

; ln jy

1

j D x  ln jxj; y

1

D

e

x

x

; y D

ue

x

x

;

u

0

e

x

x

D

e

x

2

x

;

u

0

D e

x

e

x

2

; u D c C

Z

x

1

e

t

e

t

2

dt; y D

e

x

x



c C

Z

x

1

e

t

e

t

2

dt



; y.1/ D 2 ) c D 2e;

y D

1

x



2e

.x1/

C e

x

Z

x

1

e

t

e

t

2

dt



.

2.1.44. (b) Eqn. (A) is equivalent to

y

0



2

x

D 

1

x

.B/

on .1; 0/ and .0; 1/. Here

y

0

1

y

1

D

2

x

; ln jy

1

j D 2 ln jxj; y

1

D x

2

; y D ux

2

; u

0

x

2

D 

1

x

;

u

0

D 

1

x

3

; u D

1

2x

2

C c, so y D

1

2

C cx

2

is the general solution of (A) on .1; 0/ and .0; 1/.

(c) From the proof of (b), any so lution of (A) must be of the form

y D

8

ˆ

<

ˆ

:

1

2

C c

1

x

2

; x  0;

1

2

C c

2

x

2

; x < 0;

.C/

for x ¤ 0, and any function of the form (C) satisﬁes (A) for x ¤ 0. To complete the proof we must show

that any fu nction of the form (C) is differentiable and satisﬁes (A) at x D 0. By deﬁnition,

y

0

.0/ D lim

x!0

y.x/  y.0/

x 0

D lim

x!0

y.x/  1=2

x

if the limit exists. Bu t

y.x/  1=2

x

D



c

1

x; x > 0

c

2

x; x < 0;

so y

0

.0/ D 0. Si nce 0y

0

.0/  2y.0/ D 0  0  2.1=2/ D 1, any function of the form (C) satisﬁes (A) at

x D 0.

(d) From (b) any solution y of (A) on .1; 1/ is of the form (C), so y.0/ D 1=2.

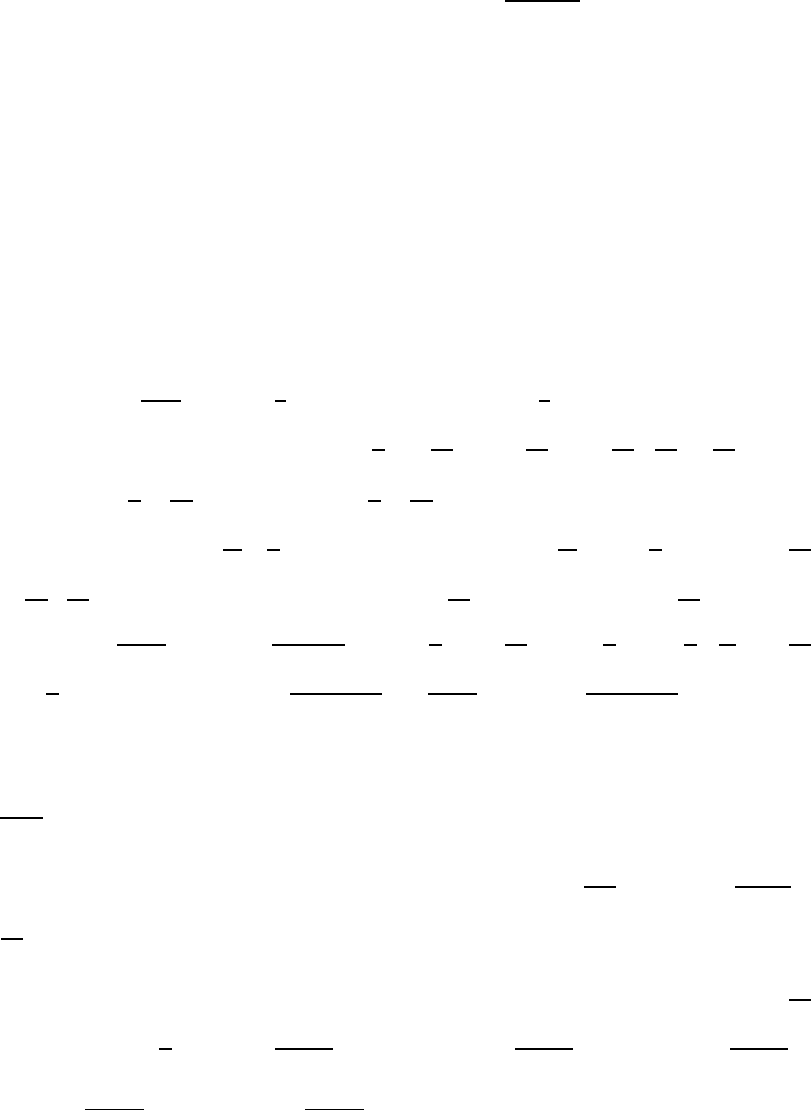
8 Chapter 2

First Order Equatio ns

(e) If x

0

> 0, then every function of the form ( C) with c

1

D

y

0

 1=2

x

2

0

and c

2

arbitrary is a solution

of the initial value problem on .1; 1/. Since these functions are all i dentical on .0; 1/, this does not

contradict Theorem 2.1.1, which implies that (B) (so (A)) has exactly one solution o n .0; 1/ such that

y.x

0

/ D y

0

. A similar argument applies if x

0

< 0.

2.1.46. (a) Let y D c

1

y

1

C c

2

y

2

. Then

y

0

C p.x/y D .c

1

y

1

C c

2

y

2

/

0

Cp.x/.c

1

y

1

C c

2

y

2

/

D c

1

y

0

1

C c

2

y

0

2

C c

1

p.x/y

1

C c

2

p.x/y

2

D c

1

.y

0

1

C p.x/y

1

/ C c

2

.y

2

C p.x/y

2

/ D c

1

f

1

.x/ C c

2

f

2

.x/:

(b) Let f

1

D f

2

D f and c

1

D c

2

D 1.

(c) Let f

1

D f , f

2

D 0, and c

1

D c

2

D 1.

2.1.48. (a) If ´ D tan y, then ´

0

D .sec

2

y/y

0

, so ´

0

 3´ D 1; ´

1

D e

3x

; ´ D ue

3x

; u

0

e

3x

D 1;

u

0

D e

3x

; u D

e

3x

3

C c; ´ D

1

3

C ce

3x

D tan y; y D tan

1



1

3

C ce

3x



.

(b) If ´ D e

y

2

, then ´

0

D 2yy

0

e

y

2

, so ´

0

C

2

x

´ D

1

x

2

; ´

1

D

1

x

2

; ´ D

u

x

2

;

u

0

x

2

D

1

x

2

; u

0

D 1;

u D x C c; ´ D

1

x

C

c

x

2

D e

y

2

; y D ˙



ln



1

x

C

c

x

2



1=2

.

(c) Rewrite the equation as

y

0

y

C

2

x

ln y D 4x. If ´ D ln y, then ´

0

D

y

0

y

, so ´

0

C

2

x

´ D 4x; ´

1

D

1

x

2

;

´ D

u

x

2

;

u

0

x

2

D 4x; u

0

D 4x

3

; u D x

4

C c; ´ D x

2

C

c

x

2

D ln y; y D exp



x

2

C

c

x

2



.

(d) If ´ D 

1

1 C y

, t hen ´

0

D

y

0

.1 C y/

2

, so ´

0

C

1

x

´ D 

3

x

2

; ´

1

D

1

x

; ´ D

u

x

;

u

0

x

D 

3

x

2

;

u

0

D 

3

x

; u D 3 ln jxj  c; ´ D 

3 ln jxj C c

x

D 

1

1 C y

; y D 1 C

x

3 ln jxj C c

.

2.2 SEPARABLE EQUATIONS

2.2.2. By inspection, y  k (k D integer ) is a con stant solution. Separate variables to ﬁnd others:



cos y

sin y



y

0

D sin x; ln .jsin yj/ D cos x C c.

2.2.4. y  0 is a constant solut ion. Separate variables to ﬁn d others:



ln y

y



y

0

D x

2

;

.ln y/

2

D



x

3

C c.

2.2.6. y  1 and y  1 are constant solu tions. For others, separate variables: .y

2

 1/

3=2

yy

0

D

1

x

2

;

.y

2

 1/

1=2

D 

1

x

 c D 



1 C cx

x



; .y

2

 1/

1=2

D



x

1 C cx



; .y

2

 1/ D



x

1 C cx



2

;

y

2

D 1 C



x

1 C cx



2

; y D ˙

1 C



x

1 Ccx



2

!

1=2

.

Section 2.2

Separable Equations

9

2.2.8. By inspection, y  0 is a con stant solution. Separate variables to ﬁnd others:

y

0

y

D 

x

1 C x

2

;

ln jyj D 

1

2

ln.1 C x

2

/ C k; y D

c

p

1 C x

2

, which includes the constant solution y  0.

2.2.10. .y1/

2

y

0

D 2xC3;

.y  1/

3

D x

2

C3xCc; .y1/

3

D 3x

2

C9xCc; y D 1 C



3x

2

C 9x C c/

1=3

.

2.2.12.

y

0

y.y C 1/

D x;



1

y



1

y C 1



y

0

D x; ln

ˇ

y

y C 1

ˇ

D 

x

2

C k;

y

y C 1

D ce

x

2

=2

; y.2/ D

1 ) c D

e

2

; y D .y C 1/ce

x

2

=2

; y.1  ce

x

2

=2

/ D ce

x

2

=2

; y D

ce

x

2

=2

1  ce

x

2

=2

; setting c D

e

2

yields y D

e

.x

2

4/=2

2  e

.x

2

4/=2

.

2.2.14.

y

0

.y C 1/.y  1/.y  2/

D 

1

x C 1

;



1

6

1

y C 1



1

2

1

y  1

C

1

3

1

y  2



y

0

D 

1

x C 1

;



1

y C 1



3

y  1

C

2

y  2



y

0

D



6

x C 1

; ln j y C 1j  3 ln jy  1j C 2 ln jy  2j D 6 ln jx C 1j C k;

.y C 1/.y  2/

2

.y  1/

3

D

c

.x C 1/

6

;

y.1/ D 0 ) c D 256;

.y C 1/.y  2/

2

.y  1/

3

D 

256

.x C 1/

6

.

2.2.16.

y

0

y.1 C y

2

/

D 2x;



1

y



y

2

C 1



y

0

D 2x; ln

jyj

p

y

2

C 1

!

D x

2

C k;

y

p

y

2

C1

D ce

x

2

;

y.0/ D 1 ) c D

1

p

2

;

y

p

y

2

C 1

D

e

x

2

p

2

; 2y

2

D .y

2

C1/e

x

2

; y

2

.2e

x

2

/ D e

2x

2

; y D

1

p

2e

2x

2

 1

.

2.2.18.

y

0

.y  1/.y  2/

D 2x;



1

y  2



1

y  1



y

0

D 2x; ln

ˇ

y  2

y  1

ˇ

D x

2

C k;

y  2

y  1

D ce

x

2

;

y.0/ D 3 ) c D

1

2

;

y  2

y  1

D

e

x

2

; y2 D

e

x

2

.y1/; y

1 

e

x

2

!

D 2

e

x

2

; y D

4  e

x

2

2  e

x

2

.

The in terval of validity is .1; 1/.

2.2.20.

y

0

y.y  2/

D 1;

1

2



1

y  2



1

y



y

0

D 1;



1

y  2



1

y



y

0

D 2; ln

ˇ

y  2

y

ˇ

D 2x C k;

y  2

y

D ce

2x

; y.0/ D 1 ) c D 1;

y  2

y

D e

2x

; y  2 D ye

2x

; y.1 C e

2x

/ D 2;

y D

2

1 C e

2x

. The interval o f validity is .1; 1/.

2.2.22. y  2 is a constant solution of the differential equation, and it satisﬁes the initial condition.

Therefore, y  2 is a solution of the initial value problem. The interval of validity is .1; 1/.

2.2.24.

y

0

1 C y

2

D

1

1 C x

2

; tan

1

y D tan

1

x C k; y D tan.tan

1

x C k/. Now use the ident ity

tan.A C B/ D

tan A C tan B

1  t an A tan B

with A D tan

1

x and B D tan

1

c to rewrite y as y D

x C c

1  cx

, where

c D tan k.

10 Chapter 2

First Order Equations

2.2.26. .sin y/y

0

D cos x; cos y D sin x C c; y./ D



2

) c D 0, so (A) cos y D sin x. To obtain

y explicity we note that sin x D cos.x C=2/, so (A) can be rewritten as cos y D cos.x C=2/. Thi s

equation holds if an only if one of the following condi tions holds for some integer k:

(B) y D x C



2

C 2k Imbox.C / y D x 



2

C 2k:

Among these choices the only way to satisfy the initial condition is to let k D 1 in (C), so y D x C

3

2

:

2.2.28. Rewrite the equation as P

0

D a˛P .P  1=˛/. By inspection, P  0 and P  1=˛ are

constant solution s. Separate variables to ﬁnd others:

P

0

P.P  1=˛/

D a˛;



1

P  1=˛



1

P



P

0

D a;

ln

ˇ

P  1=˛

P

ˇ

D at C k; (A)

P  1=˛

P

D ce

˛t

; P .1  ce

˛t

/ D 1=˛; (B) P D

1

˛.1  ce

˛t

/

.

From (A), P.0/ D P

0

) c D

P

0

 1=˛

P

0

. Substituting this into (B) yields P D

P

0

˛P

0

C .1  ˛P

0

/e

at

.

From this lim

t!1

P.t/ D 1=˛.

2.2.30. If q D rS the equation for I reduces to I

0

D rI

2

, so

I

0

I

2

D r ; 

1

I

D r t 

1

I

0

; so

I D

I

0

1 C rI

0

t

and lim

t!1

I.t/ D 0. If q ¤ rS, then rew rite the equation for I as I

0

D rI.I  ˛/

with ˛ D S 

q

r

. Separating variables yields

I

0

I.I  ˛/

D r ;



1

I  ˛



1

I



I

0

D r ˛; ln

ˇ

I  ˛

I

ˇ

D

r˛t C k; (A)

I  ˛

I

D ce

r˛t

; I.1  ce

r˛t

/ D ˛; (B) I D

˛

1  ce

r˛t

. From (A), I.0/ D I

0

)

c D

I

0

 ˛

I

0

. Substituting thi s into (B) yields I D

˛I

0

I

0

C .˛  I

0

/e

r˛t

. If q < rS, then ˛ > 0 and

lim

t!1

I.t/ D ˛ D S 

q

r

. If q > rS, then ˛ < 0 and lim

t!1

I.t/ D 0.

2.2.34. The given equation is separable if f D ap, where a is a constant. In this case the equation is

y

0

C p.x/y D ap.x/: .A/

Let P be an antiderivative o f p; that is, P

0

D p.

SOLUTION BY SEPARATION OF VARIABL ES. y

0

D p.x/.y  a/;

y

0

y  a

D p.x/; ln jy  aj D

P.x/ C k; y  a D ce

P.x/

; y D a C ce

P.x/

.

SOLUTION BY VARIATION OF PARAMETERS. y

1

D e

P.x/

is a solution of the complementary

equation, so solutions of (A) are of t he form y D ue

P.x/

where u

0

e

P.x/

D ap.x/. Hence, u

0

D

ap.x/e

P.x/

; u D ae

P.x/

C c; y D a C ce

P.x/

.

2.2.36. R ewrite the given equation as (A) y

0



2

x

y D

x

5

y C x

2

. y

1

D x

2

is a solution of y

0



2

x

y D 0.

Look for so lutions of (A) of the form y D ux

2

. Then u

0

x

2

D

x

5

.u C 1/x

2

D

x

3

u C 1

; u

0

D

x

u C 1

;

.u C 1/u

0

D x;

.1 C u/

2

D

x

2

C

c

2

; u D 1 ˙

p

x

2

C c; y D x

2



1 ˙

p

x

2

C c



.

Section 2.3

Existence and Uniqueness of Solutions of Nonlinear Equation s

11

2.2.38. y

1

D e

2x

is a solution of y

0

 2y D 0. Look for solutions of the nonlinear equation of t he

form y D ue

2x

. Then u

0

e

2x

D

xe

2x

1  u

; u

0

D

x

1  u

; .1  u/u

0

D x; 

.1  u/

2

D

1

2

.x

2

 c/;

u D 1 ˙

p

c  x

2

; y D e

2x



1 ˙

p

c  x

2



.

2.3 EXISTENCE AND UNIQUENESS OF SOLUTIONS OF NONLINEAR EQUATIONS

2.3.2. f .x; y/ D

e

x

Cy

x

2

C y

2

and f

y

.x; y/ D

1

x

2

C y

2



2y.e

x

C y/

.x

2

C y

2

/

2

are both continuous at all .x; y/ ¤

.0; 0/. Hence, Theorem 2.3.1 implies that if .x

0

; y

0

/ ¤ .0; 0/, then the initial value problem h as a a

unique solution on some open interval containing x

0

. Theorem 2.3.1 does no t apply if .x

0

; y

0

/ D .0; 0/.

2.3.4. f .x; y/ D

x

2

Cy

2

ln xy

and f

y

.x; y/ D

2y

ln xy



x

2

C y

2

x.ln xy/

2

are bo th continuous at all .x; y/ such

that xy > 0 and xy ¤ 1. Hence, Theorem 2.3.1 implies that if x

0

y

0

> 0 and x

0

y

0

¤ 1, then the initial

value problem has unique solution on an open interval containing x

0

. Theorem 2.3.1 does not appl y if

x

0

y

0

 0 or x

0

y

0

D 1.

2.3.6. f .x; y/ D 2xy and f

y

.x; y/ D 2x are both continuous at all .x; y/. Hence, Theorem 2.3.1

implies that if .x

0

; y

0

/ is arbitrary, then t he initial value problem has a unique solution on some open

inter val contai ning x

0

.

2.3.8. f .x; y/ D

2x C 3y

x  4y

and f

y

.x; y/ D

3

x 4y

C 4

2x C 3y

.x  4y/

2

are both continuous at all .x; y/ such

that x ¤ 4y. Hence, Theorem 2.3.1 impli es that if x

0

¤ 4y

0

, then the ini tial value problem has a unique

solution on some open interval containing x

0

. Theorem 2.3.1 does not apply if x

0

D 4y

0

.

2.3.10. f .x; y/ D x.y

2

1/

2=3

is continuous at all .x; y/, but f

y

.x; y/ D

4

3

xy.y

2

1/

1=3

is continuous

at .x; y/ if and only if y ¤ ˙1. Hence, Theorem 2.3.1 implies that if y

0

¤ ˙1, t hen the initial value

problem has a unique solution on some o pen interval containing x

0

, while if y

0

D ˙1, then the initial

value prob lem has at least one so lution (possibly not unique on any open inter val containing x

0

).

2.3.12. f .x; y/ D .x C y/

1=2

and f

y

.x; y/ D

1

2.x C y/

1=2

are b oth continuous at all .x; y/ such th at

x Cy > 0 Hence, Theorem 2.3.1 implies that if x

0

Cy

0

> 0, then the initial value problem has a uniq ue

solution on some open interval containing x

0

. Theorem 2.3.1 does not apply if x

0

C y

0

 0.

2.3.14. To apply Theorem 2.3.1, rewrite the given initial value problem as (A) y

0

D f .x; y/; y.x

0

/ D y

0

,

where f .x; y/ D p.x/y C q.x/ and f

y

.x; y/ D p.x/. If p and f are continuous on some open

inter val .a; b/ containing x

0

, then f and f

y

are continuous on some open rectangle containing .x

0

; y

0

/,

so Theorem 2.3.1 implies that (A) has a un ique sol ution on so m e open i nterval containing x

0

. The

conclusion of Theorem 2.1.2 i s more speciﬁc: the solut ion of (A ) exists and is unique on .a; b/. For

example, in the extreme case where .a; b/ D .1; 1/, Theorem 2.3.1 stil l implies only existence and

uniqueness on some open interval contain ing x

0

, while Theorem 2.1.2 implies that the solu tion exists and

is unique on .1; 1/.

2.3.16. First ﬁnd solutions of (A) y

0

D y

2=5

. Obviously y  0 is a so lution. If y 6 0, then we

can separate variables on any open interval wh ere y has no zeros: y

2=5

y

0

D 1;

5

3

y

3=5

D x C c;

y D



3

5

.x C c/

5=3



. (Note that this solution is also deﬁned at x D c, even though y.c/ D 0.

12 Chapter 2

First Order Equations

To satisfy the initial condition, let c D 1. Thus, y D



3

5

.x C 1/

5=3



is a solution of the initial value

problem on .1; 1/; moreover, since f .x; y/ D y

2=5

and f

y

.x; y/ D

2

5

y

3=5

are both continuous at

all .x; y/ such that y ¤ 0, this is the only solution on .5=3; 1/, by an argument similar to that given in

Example 2.3.7, the function

y D

(

0; 1 < x  

5

3



3

5

x C 1



5=3

; 

5

3

< x < 1

(To see that y satisﬁes y

0

D y

2=5

at x D 

5

3

use an argument similar to that of Discussion 2 .3.15-2) For

every a 

5

3

, the following function is also a solution :

y D

8

ˆ

<

ˆ

:



3

5

.x C a/



5=3

; 1 < x < a;

0; a  x  

5

3



3

5

x C 1



5=3

; 

5

3

< x < 1:

2.3.18. Obviously, y

1

 1 is a solution. From Discussion 2.3.18 (taking c D 0 in the two famili es of

solutions) yields y

2

D 1 C jxj

3

and y

3

D 1  jxj

3

. Other solutions are y

4

D 1 C x

3

, y

5

D 1  x

3

,

y

6

D



1 C x

3

; x  0;

1; x < 0

I y

7

D



1  x

3

; x  0;

1; x < 0

I

y

8

D



1; x  0;

1 Cx

3

; x < 0

I y

9

D



1; x  0;

1  x

3

; x < 0

It is straightforward to verify that all these functions satisfy y

0

D 3x.y1/

1=3

for all x ¤ 0. Moreover,

y

0

i

.0/ D lim

x!0

y

i

.x/  1

x

D 0 for 1  i  9, which implies that they also satisfy t he equation at x D 0.

2.3.20. Let y be any sol ution of (A) y

0

D 3x.y  1/

1=3

; y.3/ D 7. By continuity, there is some open

inter val I containing x

0

D 3 on which y.x/ < 1. From Discussion 2.3.18, y D 1 C .x

2

C c/

3=2

on I ;

y.3/ D 7 ) c D 5; (B) y D 1  .x

2

 5/

3=2

. It now follows that every solution of (A) sati sﬁes

y.x/ < 1 and is given by (B) on .

p

5; 1/; that is, (B) is the unique solution of (A) on .

p

5; 1/. This

solution can be extended uniquely to .0; 1/ as

y D



1; 0 < x 

p

5;

1  .x

2

 5/

3=2

;

p

5 < x < 1

It can be extended to .1; 1/ in inﬁnitely many ways. Thus,

y D



1; 1 < x 

p

5;

1  .x

2

 5/

3=2

;

p

5 < x < 1

is a solution of the initial value problem on .1; 1/. Mor oever, if ˛  0, then

y D

8

<

:

1 C .x

2

 ˛

2

/

3=2

; 1 < x < ˛;

1; ˛  x 

p

5;

1  .x

2

 5/

3=2

;

p

5 < x < 1;

Section 2.4

Transfo rmation of Non linear Equations into Separable Equation s

13

and

y D

8

<

:

1  .x

2

 ˛

2

/

3=2

; 1 < x < ˛;

1; ˛  x 

p

5;

1  .x

2

 5/

3=2

;

p

5 < x < 1;

are also solutions of the initial value problem on .1; 1/.

2.4 TRANSFORMATION OF NONL INEAR EQUATIONS INTO SEPARABLE EQUATIONS

2.4.2. Rewrite as y

0



2

7x

y D 

x

7y

6

. Then

y

0

1

y

1

D

2

7x

; ln jy

1

j D

2

7

ln jxj D ln jxj

2=7

; y

1

D x

2=7

;

y D ux

2=7

; u

0

x

2=7

D 

1

7u

6

x

5=7

; u

6

u

0

D 

1

7x

;

u

7

D 

1

7

ln jxj C

c

7

; u D .c  l n jxj /

1=7

;

y D x

2=7

.c  ln jxj/

1=7

.

2.4.4. Rewrite as y

0

C

2x

1 C x

2

y D

1

.1 C x

2

/

2

y

. Then

y

0

1

y

1

D 

2x

1 C x

2

; ln jy

1

j D ln.1 C x

2

/;

y

1

D

1

1 C x

2

; y D

u

1 C x

2

;

u

0

1 C x

2

D

1

u.1 C x

2

/

; u

0

u D 1;

u

2

D x C

c

2

; u D ˙

p

2x C c;

y D ˙

p

2x C c

1 C x

2

.

2.4.6.

y

0

1

y

1

D

1

3



1

x

C 1



; ln jy

1

j D

1

3

.ln jxj C x/; y

1

D x

1=3

e

x=3

; y D ux

1=3

e

x=3

; u

0

x

1=3

e

x=3

D

x

4=3

e

4x=3

u

4

;

u

0

u

4

D xe

x

; 

1

3u

3

D .x1/e

x



c

3

; u D

1

Œ3.1  x/e

x

C c

1=3

; y D



x

3.1  x/ C ce

x



1=3

.

2.4.8.

y

0

1

y

1

D x; ln jy

1

j D

x

2

; y

1

D e

x

2

=2

; y D ue

x

2

=2

; u

0

e

x

2

=2

D xu

3=2

e

3x

2

=4

;

u

0

u

3=2

D xe

x

2

=4

;

(A) 

2

u

1=2

D 2e

x

2

=4

C 2c; u

1=2

D 

1

c C e

x

2

=4

; u

D

1

.c C e

x

2

=4

/

2

; y D

1

.1 C ce

x

2

=4

/

2

. Because

of (A) we must choose c so that y.1/ D 4 and 1 C ce

1=4

< 0. This implies that c D 3e

1=4

;

y D



1 

3

2

e

.x

2

1/=4



2

.

2.4.10.

y

0

1

y

1

D 2; ln jy

1

j D 2x; y

1

D e

2x

; y D ue

2x

; u

0

e

2x

D 2u

1=2

e

x

; u

1=2

u

0

D 2e

x

;

2u

1=2

D 2e

x

C 2c; u

1=2

D c  e

x

> 0; y.0/ D 1 ) u.0/ D 1 ) c D 2; u D .2  e

x

/

2

;

y D .2e

x

 1/

2

.

2.4.12. Rewrite as y

0

C

2

x

y D

y

3

x

2

. Then

y

0

1

y

1

D 

2

x

; ln jy

1

j D 2 ln jxj D l n x

2

; y

1

D

1

x

2

;

y D

u

x

2

;

u

0

x

2

D

u

3

x

8

;

u

0

u

3

D

1

x

6

; 

1

2u

2

D 

1

5x

5

C c; y.1/ D

1

p

2

) u.1/ D

1

p

2

) c D 

4

5

;

u D



5x

5

2.1 C 4x

5

/



1=2

; y D



5x

2.1 C4x

5

/



1=2

.

2.4.14. P D ue

at

; u

0

e

at

D a˛u

2

e

2at

;

u

0

u

2

D a˛e

at

; 

1

u

D a

Z

t

0

˛./e

a

d  

1

P

0

; P D

P

0

e

at

1 C aP

0

R

t

0

˛./e

a

d 

, which can also be written as P D

P

0

e

at

C aP

0

e

at

R

t

0

˛./e

a

d 

. Therefore,

14 Chapter 2

First Order Equations

lim

t!1

P.t/ D

8

<

:

1 if L D 0;

0 if L D 1;

1=aL if 0 < L < 1:

2.4.16. y D ux; u

0

x C u D u

2

C 2u; (A) u

0

x D u.u C 1/. Since u  0 and u  1 are constant

solutions of (A), y  0 and y D x are solutions of the given equat ion. The nonconstant solutions

of (A) sati sf y D

u

0

u.u C1/

D

1

x

;



1

u



1

u C 1



u

0

D

1

x

; ln

ˇ

u

u C 1

ˇ

D ln jxj C k;

u

u C 1

D cx;

u D .u C 1/cx; u.1  cx/ D cx; u D

cx

1  cx

; y D

cx

2

1  cx

.

2.4.18. y D ux; u

0

x C u D u C sec; u

0

x D sec u; .cos u/u

0

D

1

x

; sin u D ln jxj C c; u D

sin

1

.ln jxj C c/; y D x sin

1

.ln jxj C c/.

2.4.20. R ewrite the given equation as y

0

D

x

2

C 2y

2

xy

; y D ux; u

0

x C u D

1

u

C 2u; u

0

x D

1 C u

2

u

;

uu

0

1 C u

2

D

1

x

;

1

2

ln.1Cu

2

/ D ln jxjCk; ln



1 C

y

2

x

2



D ln x

2

C2k; 1 C

y

2

x

2

D cx

2

; x

2

Cy

2

D cx

4

;

y D ˙x

p

cx

2

 1.

2.4.22. y D ux; u

0

x C u D u C u

2

; u

0

x D u

2

;

u

0

u

2

D

1

x

; 

1

u

D ln jxj C c; y.1/ D 2 ) u.1/ D

2 ) c D

1

2

; u D 

2

2 ln j xj C 1

; y D 

2x

2 ln jxj C 1

.

2.4.24. Rewrite the given equation as y

0

D 

x

2

C y

2

xy

; y D ux; u

0

x Cu D 

1

u

u; u

0

x D 

1 C 2u

2

u

;



uu

0

1 C 2u

2

D

1

x

; 

1

4

ln.1 C 2u

2

/ D ln jxj C k; x

4

.1 C 2u

2

/ D c; y.1/ D 2 ) u.1/ D 2 ) c D 9;

x

4

.1 C 2u

2

/ D 9; u

2

D

9  x

4

2x

4

; u D

1

x

2



9  x

4

2



1=2

; y D

1

x



9  x

4

2



1=2

.

2.4.26. Rewr ite the given equation as y

0

D 2 C

y

2

x

2

C 4

y

x

; y D ux; u

0

x C u D 2 C u

2

C 4u;

u

0

x D u

2

C3u C2 D .uC1/.uC2/;

u

0

.u C 1/.u C 2/

D

1

x

;



1

u C 1



1

u C 2



u

0

D

1

x

; ln

ˇ

u C 1

u C 2

ˇ

D

ln jxj C k;

u C 1

u C 2

D cx; y.1/ D 1 ) u.1/ D 1 ) c D

2

3

;

u C 1

u C 2

D

2

3

x; u C 1 D

2

3

x.u C 2/;

u



1 

2

3

x



D 1 C

4

3

x; u D 

4x  3

2x  3

; y D 

x.4x  3/

2x  3

.

2.4.28. y D ux; u

0

xCu D

1 C u

1  u

; u

0

x D

1 C u

2

1  u

;

.1  u/u

0

1 C u

2

D

1

x

; tan

1

u

1

2

ln.1Cu

2

/ D ln jxjCc;

tan

1

y

x



1

2

ln



1 C

y

2

x

2



D ln jxj C c; tan

1

y

x



1

2

ln.x

2

C y

2

/ D c.

2.4.30. y D ux; u

0

x C u D

u

3

C 2u

2

C u C 1

.u C 1/

2

D

u.u C 1/

2

C 1

.u C 1/

2

D u C

1

.u C 1/

2

; u

0

x D

1

.u C 1/

2

;

.u C 1/

2

u

0

D

1

x

;

.u C 1/

3

D ln jxj C c; .u C 1/

3

D 3.ln jxj C c/;



y

x

C 1



3

D 3.ln jxj C c/;

.y C x/

3

D 3x

3

.ln jxj C c/.

Section 2.4

Transfo rmation of Non linear Equations into Separable Equation s

15

2.4.32. y D ux; u

0

x Cu D

u

u  2

; ( A) u

0

x D

u.u  3/

2  u

; Since u  0 and u  3 are constant solutions

of (A), y  0 and y D 3x are solutions o f the given equation. The nonconstant solutions of (A) satisfy

.2  u/u

0

u.u  3/

D

1

x

;



1

u  3

C

2

u



u

0

D 

3

x

; ln ju  3j C 2 ln juj D 3 ln jxj C k; u

2

.u  3/ D

c

x

3

;

y

2

.y  3x/ D c.

2.4.34. y D ux; u

0

x C u D

1 C u C 3u

3

1 C 3u

2

D u C

1

1 C 3u

2

; .1 C 3u

2

/u

0

D

1

x

; u C u

3

D ln jxj C c;

y

x

C

y

3

x

3

D ln jxjC c.

2.4.36. Rewrite the given equation as y

0

D

x

2

 xy C y

2

xy

; y D ux; u

0

xCu D

1

u

1Cu; u

0

x D

1  u

u

;

uu

0

u  1

D 

1

x

;



1 C

1

u  1



u

0

D 

1

x

; uCln ju1j D ln jxjCk; e

u

.u1/ D

c

x

; e

y=x

.y x/ D c.

2.4.38. y D ux; u

0

x Cu D 1 C

1

u

Cu; (A) u

0

x D

u C 1

u

. Since (A ) has the constant solution u D 1;

y D x is a solution of the given equation. The no nconstant solutions of (A) satisfy

uu

0

u C 1

D

1

x

;



1 

1

u C 1



u

0

D

1

x

; u ln ju C1j D ln jxjCc;

y

x

ln

ˇ

y

x

 1

ˇ

D ln jxjCc; y x ln jy xj D cy.

2.4.40. If x D X  X

0

and y D Y  Y

0

, then

dy

dx

D

d Y

dx

D

d Y

dX

dx

D

d Y

dX

, so y D y.x/ satisﬁes the

given equation if and on ly if Y D Y .X/ satisﬁes

d Y

dX

D

a.X  X

0

/ C b.Y  Y

0

/ C ˛

c.X  X

0

/ C d.Y  Y

0

/ C ˇ

;

which reduces t o the nonlinear homogeneous equat ion

d Y

dX

D

aX C bY

cX C d Y

if and only if

aX

0

C bY

0

D ˛

cX

0

C d Y

0

D ˇ:

.B/

We will now show that if ad  bc ¤ 0, then it is possible (for any choice of ˛ and ˇ) to solve (B).

Multiplying the ﬁrst equation i n (B) by d and the second by b yields

daX

0

C dbY

0

D d˛

bcX

0

C bd Y

0

D bˇ:

Subtr acti ng the second of these equations from the ﬁrst yields .ad bc/X

0

D ˛d ˇb. Since ad bc ¤

0, this implies that X

0

D

˛d  ˇb

ad  bc

. Multiplying the ﬁrst equation in (B) by c and t he second by a yields

caX

0

C cbY

0

D c˛

acX

0

C adY

0

D aˇ:

16 Chapter 2

First Order Equations

Subtr acti ng the ﬁrst of t hese equation from the second yields .ad bc/Y

0

D ˛c ˇa. Since ad bc ¤ 0

this impl ies that Y

0

D

˛c  ˇa

ad  bc

.

2.4.42. For th e given equation, (B) of Exer ci se 2.4.40 is

2X

0

C Y

0

D 1

X

0

C 2Y

0

D 4:

Solving this pair of equati ons yields X

0

D 2 and Y

0

D 3. The transformed differential equation is

d Y

dX

D

2X C Y

X C 2Y

: .A/

Let Y D uX; u

0

X C U D

2 Cu

1 C 2u

; (B) u

0

X D 

2.u  1/.u C 1/

2u C1

. Since u  1 and u  1

satisfy ( B), Y D X and Y D X are solutions of (A). Since X D x C 2 and Y D y  3, it follows

that y D x C 5 and y D x C 1 are solutions of the given equation. The nonconstant solutions

of (B) satisfy

.2u C1/u

0

.u  1/.u C 1/

D 

2

X

;



1

u C 1

C

3

u  1



u

0

D 

4

X

; ln ju C 1j C 3 ln ju  1j D

4 ln jXj C k; .u C 1/.u  1/

3

D

c

X

4

; .Y C X/.Y  X/

3

D c; Setting X D x C 2 and Y D y  3

yields .y C x 1/.y  x  5/

3

D c.

2.4.44. Rewrite the given equation as y

0

D

y

3

Cx

3xy

2

; y D ux

1=3

; u

0

x

1=3

C

1

3x

2=3

u D

u

3

C 1

3u

2

x

2=3

;

u

0

x

1=3

D

1

3x

2=3

u

2

; u

2

u

0

D

1

3x

;

u

3

D

1

3

.ln jxj Cc/; u D .ln jxj C c/

1=3

; y D x

1=3

.ln jxj C c/

1=3

.

2.4.46. Rewrite the given equation as y

0

D

2.y

2

C x

2

y  x

4

/

x

3

; y D ux

2

; u

0

x

2

C 2xu D 2x.u

2

C

u  1/; (A) u

0

x

2

D 2x.u

2

 1/. Since u  1 and u  1 are constant solutions of (A ), y D x

2

and y D x

2

are solutions of the given equation. The nonconstant solutions of (A) satisfy

u

0

u

2

 1

D

2

x

;



1

u  1



1

u C 1



u

0

D

4

x

; ln

ˇ

u  1

u C 1

ˇ

D 4 ln jxj C k;

u  1

u C 1

D cx

4

; .u  1/ D .u C 1/cx

4

;

u.1  cx

4

/ D 1 C cx

4

; u D

1 C cx

4

1  cx

4

; y D

x

2

.1 C cx

4

/

1  cx

4

.

2.4.48. y D u tan x; u

0

tan x C u sec

2

x D .u

2

Cu C 1/ sec

2

x; u

0

tan x D .u

2

C1/ sec

2

x;

u

0

u

2

C 1

D

sec

2

x cot x D cot x Ctan x; tan

1

u D ln jsin xjln jcos xjCc D ln jtan xjCc; u D tan.ln jtan xjC

c/; y D tan x tan.ln jtan xj C c/.

2.4.50. Rewrite the given equati on as y

0

D

.y C

p

x/

2

2x.y C 2

p

x/

; y D ux

1=2

; u

0

x

1=2

C

1

2

p

x

u D

.u C 1/

2

p

x .u C 2/

;

u

0

x

1=2

D

1

2

p

x .u C 2/

; .u C 2/u

0

D

1

2x

;

.u C 2/

2

D

1

2

.ln jxj C c/; .u C 2/

2

D ln jxj C c;

u D 2 ˙

p

ln jxj C c; y D x

1=2

.2 ˙

p

ln jxj C c/.

2.4.52. y

1

D

1

x

2

is a solution of y

0

C

2

x

y D 0. Let y D

u

x

2

; th en

u

0

x

2

D

3x

2

.u

2

=x

4

/ C 6x.u=x

2

/ C 2

x

2

.2x.u=x

2

/ C 3/

D

3.u=x/

2

C 6.u=x/ C 2

x

2

.2.u=x/ C 3/

;

Section 2.5

Exact Equations

17

so (A) u

0

D

3.u=x/

2

C 6.u=x/ C 2

2.u=x/ C 3

. Since (A) is a ho mogeneous nonlinear equation, we now substitute

u D vx into (A). This yields v

0

x Cv D

3v

2

C 6v C 2

2v C 3

; v

0

x D

.v C 1/.v C 2/

2v C3

;

.2v C 3/v

0

.v C 1/.v C 2/

D

1

x

;



1

v C 1

C

1

v C 2



v

0

D

1

x

; ln j.v C 1/.v C 2/j D ln jxj C k; (B) .v C 1/.v C 2/ D cx. Since

y.2/ D 2 ) u.2/ D 8 ) v.2/ D 4, (B) implies that c D 15. .v C 1/.v C 2/ D 15x; v

2

C 3v C

2  15x D 0. From the quadratic formula, v D

3 C

p

1 C 60x

2

; u D vx D

x.3 C

p

1 C 60x/

2

;

y D

u

x

2

D

3 C

p

1 C 60x

2x

.

2.4.54. Differentiating (A) y

1

.x/ D

y.ax/

a

yields (B) y

0

1

.x/ D

1

a

y

0

.ax/  a D y

0

.ax/. Since y

0

.x/ D

q.y.x/=x/ on some interval I , (C) y

0

.ax/ D q.y.ax/=ax/ on some interval J . Substituting (A) and (B)

into (C) yields y

0

1

.x/ D q.y

1

.x/=x/ on J .

2.4.56. If y D ´ C 1, th en ´

0

C ´ D x´

2

; ´ D ue

x

; u

0

e

x

D xu

2

e

2x

;

u

0

u

2

D xe

x

; 

1

u

D

e

x

.x C 1/  c; u D

1

e

x

.x C1/ C c

; ´ D

1

x C 1 C ce

x

; y D 1 C

1

x C 1 C ce

x

.

2.4.58. If y D ´ C 1, th en ´

0

C

2

x

´ D ´

2

; ´

1

D

1

x

2

; ´ D

u

x

2

;

u

0

x

2

D

u

2

x

4

;

u

0

u

2

D

1

x

2

; 

1

u

D



1

x

C c D 

1  cx

x

; u D 

x

1  cx

; ´ D 

1

x.1  cx/

; y D 1 

1

x.1  cx/

.

2.5 EXACT EQUATIONS

2.5.2. M.x; y/ D 3y cos x C 4xe

x

C 2x

2

e

x

; N.x; y/ D 3 sin x C 3; M

y

.x; y/ D 3 cos x D N

x

.x; y/,

so t he equation is exact. We must ﬁnd F such that (A) F

x

.x; y/ D 3y cos x C 4xe

x

C 2x

2

e

x

and (B )

F

y

.x; y/ D 3 sin x C 3. Integrating (B) with respect to y yields (C) F .x; y/ D 3y sin x C 3y C .x/.

Differentiatin g (C) with respect to x yields (D) F

x

.x; y/ D 3y cos x C

0

.x/. Comparing (D) with

(A) shows that (E)

0

.x/ D 4xe

x

C 2x

2

e

x

. Integration by parts yields

Z

xe

x

dx D xe

x

 e

x

and

Z

x

2

e

x

dx D x

2

e

x

2xe

x

C2e

x

. Substi tuting from the last two equations into (E) yields .x/ D 2x

2

e

x

.

Substituting this into (C) yi el ds F .x; y/ D 3y sin x C3y C2x

2

e

x

. Therefore, 3y sin x C3y C2x

2

e

x

D c.

2.5.4. M.x; y/ D 2x  2y

2

; N.x; y/ D 12y

2

 4xy; M

y

.x; y/ D 4y D N

x

.x; y/, so the equation

is exact. We must ﬁnd F such that (A) F

x

.x; y/ D 2x  2y

2

and (B) F

y

.x; y/ D 12y

2

 4xy.

Integrating (A ) wit h respect to x yields (C) F .x; y/ D x

2

 2xy

2

C .y/. Differentiating (C) wi th

respect to y yields (D) F

y

.x; y/ D 4xy C 

0

.y/. Comparing (D) with (B) shows that 

0

.y/ D 12y

2

,

so we t ake .y/ D 4y

3

. Substituting this into (C) yields F .x; y/ D x

2

 2xy

2

C 4y

3

. Therefore,

x

2

 2xy

2

C4y

3

D c.

2.5.6. M.x; y/ D 4x C 7y; N.x; y/ D 3x C 4y; M

y

.x; y/ D 7 ¤ 3 D N

x

.x; y/, so the equation i s

not exact.

2.5.8. M.x; y/ D 2x C y; N.x; y/ D 2y C 2x; M

y

.x; y/ D 1 ¤ 2 D N

x

.x; y/, so the equation is not

exact.

18 Chapter 2

First Order Equations

2.5.10. M.x; y/ D 2x

2

C 8xy C y

2

; N.x; y/ D 2x

2

C

xy

3

; M

y

.x; y/ D 8x C 2y ¤ 4x C

y

3

D

N

x

.x; y/, so the equation is not exact.

2.5.12. M.x; y/ D y sin xyCxy

2

cos xy; N.x; y/ D x sin xyCxy

2

cos xy; M

y

.x; y/ D 3xy cos xyC

.1  x

2

y

2

/ sin xy ¤ .xy C y

2

/ cos xy C .1  xy

3

/ sin xy D N

x

.x; y/, so the equation is not exact.

2.5.14. M.x; y/ D e

x

.x

2

y

2

C 2xy

2

/ C 6x; N.x; y/ D 2x

2

ye

x

C 2; M

y

.x; y/ D 2xye

x

.x C 2/ D

N

x

.x; y/, so the equation is exact. We must ﬁnd F such that (A) F

x

.x; y/ D e

x

.x

2

y

2

C2xy

2

/C6x and

(B) F

y

.x; y/ D 2x

2

ye

x

C2. In tegrating (B) with respect to y yields (C) F .x; y/ D x

2

y

2

e

x

C2yC .x/.

Differentiatin g (C) with respect to x yields (D) F

x

.x; y/ D e

x

.x

2

y

2

C 2xy

2

/ C

0

.x/. Comparing (D)

with (A) shows that

0

.x/ D 6x, so we take .x/ D 3x

2

. Substituting thi s in to (C) yields F .x; y/ D

x

2

y

2

e

x

C 2y C 3x

2

. Therefore, x

2

y

2

e

x

C 2y C 3x

2

D c.

2.5.16. M.x; y/ D e

xy

.x

4

y C4x

3

/ C3y; N.x; y/ D x

5

e

xy

C3x; M

y

.x; y/ D x

4

e

xy

.xy C5/ C3 D

N

x

.x; y/, so th e equati on is exact. We must ﬁnd F such that (A) F

x

.x; y/ D e

xy

.x

4

y C 4x

3

/ C3y and

(B) F

y

.x; y/ D x

5

e

xy

C3x. Integrating (B) with resp ect to y yields (C) F .x; y/ D x

4

e

xy

C3xy C .x/.

Differentiatin g (C) with resp ect to x yields (D) F

x

.x; y/ D e

xy

.x

4

y C 4x

3

/ C 3y C

0

.x/. Comparing

(D) with (A) shows that

0

.x/ D 0, so we take .x/ D 0. Substituting this into (C) yields F .x; y/ D

x

4

e

xy

C 3xy. Therefore, x

4

e

xy

C 3xy D c.

2.5.18. M.x; y/ D 4x

3

y

2

 6x

2

y  2x  3; N.x; y/ D 2x

4

y  2x

3

; M

y

.x; y/ D 8x

3

y  6x

2

D

N

x

.x; y/, so the equation i s exact. We must ﬁnd F such th at (A) F

x

.x; y/ D 4x

3

y

2

 6x

2

y  2x  3

and (B) F

y

.x; y/ D 2x

4

y 2x

3

. Integrating (A) with respect to x yi elds (C) F.x; y/ D x

4

y

2

2x

3

y 

x

2

 3x C .y/. Differentiating (C) with respect to y yields (D) F

y

.x; y/ D 2x

4

y  2x

3

C 

0

.y/.

Comparing (D) wit h (B) shows that 

0

.y/ D 0, so we take .y/ D 0. Substituting this into (C) yields

F .x; y/ D x

4

y

2

2x

3

y x

2

3x. Therefore, x

4

y

2

2x

3

y x

2

3x D c. Since y.1/ D 3 ) c D 1,

x

4

y

2

 2x

3

y  x

2

 3x C 1 D 0 is an impl icit solution of the initial value prob lem. Solving this for y

by means of the quadratic formula yields y D

x C

p

2x

2

C 3x  1

x

2

.

2.5.20. M.x; y/ D .y

3

 1/e

x

; N.x; y/ D 3y

2

.e

x

C 1/; M

y

.x; y/ D 3y

2

e

x

D N

x

.x; y/, so the

equation is exact. We must ﬁnd F such that (A) F

x

.x; y/ D .y

3

1/e

x

and (B) F

y

.x; y/ D 3y

2

.e

x

C1/.

Integrating (A) with respect to x yields (C) F .x; y/ D .y

3

1/e

x

C.y/. Differentiating (C) with respect

to y yields (D) F

y

.x; y/ D 3y

2

e

x

C

0

.y/. Comparing (D) with (B) shows that 

0

.y/ D 3y

2

, so we take

.y/ D y

3

. Substituting this into (C) yields F.x; y/ D .y

3

1/e

x

Cy

3

. Therefore, .y

3

1/e

x

Cy

3

D c.

Since y.0/ D 0 ) c D 1, .y

3

 1/e

x

C y

3

D 1 is an implicit solution of the initial value problem.

Therefore, y

3

.e

x

C 1/ D e

x

 1, so y D



e

x

 1

e

x

C 1



1=3

.

2.5.22. M.x; y/ D .2x 1/.y 1/; N.x; y/ D .x C2/.x 3/; M

y

.x; y/ D 2x 1 D N

x

.x; y/, so the

equation is exact. We must ﬁnd F such that (A) F

x

.x; y/ D .2x  1/.y  1/ and ( B) F

y

.x; y/ D .x C

2/.x 3/. Integrating (A) with respect to x yields (C) F.x; y/ D .x

2

x/.y 1/C.y/. D ifferentiating

(C) with respect to y yields (D) F

y

.x; y/ D x

2

 x C 

0

.y/. Comparing (D) with (B) shows that



0

.y/ D 6, so we take .y/ D 6y. Substituting this into (C) yields F.x; y/ D .x

2

x/.y 1/ 6y.

Therefore, .x

2

x/.y 1/6y D c. Since y.1/ D 1 ) c D 6, .x

2

x/.y 1/6y D 6 is an implicit

solution of the initial value problem. Therefore, .x

2

 x  6/y D x

2

 x C 6, so y D

x

2

 x C 6

.x  3/.x C 2/

.

2.5.24. M.x; y/ D e

x

.x

4

y

2

C4x

3

y

2

C1/; N.x; y/ D 2x

4

ye

x

C2y; M

y

.x; y/ D 2x

3

ye

x

.x C 4/ D

N

x

.x; y/, so the equation is exact. We must ﬁnd F such that (A) F

x

.x; y/ D e

x

.x

4

y

2

C 4x

3

y

2

C 1/

Section 2.5

Exact Equations

19

and (B) F

y

.x; y/ D 2x

4

ye

x

C 2y. Integrating (B) with respect to y yields (C) F .x; y/ D x

4

y

2

e

x

C

y

2

C .x/. Differentiating (C) with respect to x yields (D) F

x

.x; y/ D e

x

y

2

.x

4

C 4x

3

/ C

0

.x/.

Comparing (D) with (A) shows that

0

.x/ D e

x

, so we take .x/ D e

x

. Substi tuting this into (C) y ields

F .x; y/ D .x

4

y

2

C 1/e

x

C y

2

. Therefore, .x

4

y

2

C 1/e

x

C y

2

D c.

2.5.28. M.x; y/ D x

2

C y

2

; N.x; y/ D 2xy; M

y

.x; y/ D 2y D N

x

.x; y/, so the equation is exact.

We must ﬁnd F such that (A) F

x

.x; y/ D x

2

C y

2

and (B) F

y

.x; y/ D 2xy. Integrating (A) with

respect to x yields (C) F .x; y/ D

x

3

C xy

2

C .y/. Differentiating (C) with respect to y yields (D)

F

y

.x; y/ D 2xy C 

0

.y/. Comparing (D) with (B ) shows that 

0

.y/ D 0, so we take .y/ D 0.

Substituting this into (C) yields F .x; y/ D

x

3

C xy

2

. Therefore,

x

3

C xy

2

D c.

2.5.30. (a) Exactness requires th at N

x

.x; y/ D M

y

.x; y/ D

@

@y

.x

3

y

2

C2xy C3y

2

/ D 2x

3

y C2x C6y.

Hence, N.x; y/ D

x

4

y

4

C x

2

C 6xy C g.x/, where g is differentiable.

(b) Exactness requires that N

x

.x; y/ D M

y

.x; y/ D

@

@y

.ln xy C 2y sin x/ D

1

y

C 2 sin x. Hence,

N.x; y/ D

x

y

 2 cos x C g.x/, where g is differentiable.

(c) Exactness requires that N

x

.x; y/ D M

y

.x; y/ D

@

@y

.x sin x C y sin y/ D y cos y C si n y. Hence,

N.x; y/ D x.y cos y C sin y/ C g.x/, wh ere g is differentiable.

2.5.32. The assumptions imply that

@M

1

@y

D

@N

1

@x

and

@M

2

@y

D

@N

2

@x

. Therefore,

@

@y

.M

1

C M

2

/ D

@M

1

@y

C

@M

2

@y

D

@N

1

@x

C

@N

2

@x

D

@

@x

.N

1

CN

2

/, which implies that .M

1

CM

2

/ dx C.N

1

CN

2

/ dy D 0

is exact on R.

2.5.34. Here M.x; y/ D Ax

2

CBxy CCy

2

and N.x; y/ D Dx

2

CExy CFy

2

. Since M

y

D Bx C2Cy

and N

x

D 2Dx C Ey, the equation is exact if and only if B D 2D and E D 2C .

2.5.36. Differentiating(A) F .x; y/ D

Z

y

0

N.x

0

; s/ dsC

Z

x

0

M.t; y/ dt with respect to x yields F

x

.x; y/ D

M.x; y/, since t he ﬁrst integral in (A) is independent of x and M.t; y/ is a continuous function of t for

each ﬁxed y. Differentiating (A) with respect to y and using the assumption that M

y

D N

x

yields

F

y

.x; y/ D N.x

0

; y/ C

Z

x

0

@M

@y

.t; y/ dt D N.x

0

; y/ C

Z

x

0

@N

@x

.t; y/ dt D N.x

0

; y/ C N.x; y/ 

N.x

0

; y/ D N.x; y/.

2.5.38. y

1

D

1

x

2

is a solution of y

0

C

2

x

y D 0. Let y D

u

x

2

; th en

u

0

x

2

D 

2x.u=x

2

/

.x

2

C 2x

2

.u=x

2

/ C 1/

D 

2xu

x

2

.x

2

C 2u C 1/

;

so u

0

D 

2xu

x

2

C 2u C1

, which can be rewritten as (A) 2xu dx C .x

2

C 2u C 1/ du D 0. Since

@

@u

.2xu/ D

@

@x

.x

2

C2uC1/ D 2x, (A) is exact. To solve (A) we must ﬁnd F such that (A) F

x

.x; u/ D

20 Chapter 2

First Order Equations

2xu and (B) F

u

.x; u/ D x

2

C2uC1. Integrating (A) with respect to x yields (C) F.x; u/ D x

2

uC.u/.

Differentiatin g (C) with respect to u yields (D) F

u

.x; u/ D x

2

C 

0

.u/. Co mparing (D ) with (B) shows

that 

0

.u/ D 2u C 1, so we take .u/ D u

2

C u. Substitut ing this into (C) yields F.x; u/ D x

2

u C

u

2

C u D u.x

2

C u C 1/. Therefore, u.x

2

C u C 1/ D c. Since y.1/ D 2 ) u.1/ D 2; c D 0.

Therefore, u.x

2

C u C 1/ D 0. Since u  0 does not satisfy u.1/ D 2, it follows that u D x

2

 1

and y D 1 

1

x

2

.

2.5.40. y

1

D e

x

2

is a solution of y

0

C2xy D 0. Let y D ue

x

2

; then u

0

e

x

2

D e

x

2



3x C 2u

2x C 3u



, so

u

0

D 

3x C 2u

2x C 3u

, which can be rewritt en as (A) .3x C2u/ dx C.2xC3u/ du D 0. Since

@

@u

.3x C2u/ D

@

@x

.2x C 3u/ D 2, (A) is exact. To solve (A) we must ﬁnd F such t hat (A) F

x

.x; u/ D 3x C 2u and

(B) F

u

.x; u/ D 2x C 3u. Integrating (A) with respect to x yields (C) F .x; u/ D

3x

2

C 2xu C .u/.

Differentiatin g (C) with respect to u yields (D) F

u

.x; u/ D 2x C 

0

.u/. Co mparing (D) with (B) shows

that 

0

.u/ D 3u, so we take .u/ D

3u

2

. Substituting this into (C) yi el ds F .x; u/ D

3x

2

C 2xu C

3u

2

. Therefore,

3x

2

C 2xu C

3u

2

D c. Since y.0/ D 1 ) u.0/ D 1; c D

3

2

. Therefore,

3x

2

C4xu C3u

2

D 3 is an implicit solution of the initial value problem. Rewriting this as 3u

2

C4xu C

.3x

2

3/ D 0 and solving for u by means of the quadratic formula yields u D 

2x C

p

9  5x

2

3

!

, so

y D e

x

2

2x C

p

9  5x

2

3

!

.

2.5.42. Since M dx C N dy D 0 is exact, (A) M

y

D N

x

. Since N dx C M dy D 0 is exact, (B)

M

x

D N

y

. Differentiating (A) with respect to y and (B) with respect to x yields (C) M

yy

D N

xy

and

(D) M

xx

D N

yx

. Since N

xy

D N

yx

, adding (C) and (D) yields M

xx

C M

yy

D 0. Differentiating

(A) with respect to x and (B) with respect to y yields (E) M

yx

D N

xx

and (F) M

xy

D N

yy

. Since

M

xy

D M

yx

, subtracting (F) from (E) yields N

xx

C N

yy

D 0.

2.5.44. (a) If F .x; y/ D x

2

 y

2

, then F

x

.x; y/ D 2x, F

y

.x; y/ D 2y, F

xx

.x; y/ D 2, and

F

yy

.x; y/ D 2. Therefore, F

xx

C F

yy

D 0, and G must satisfy (A) G

x

.x; y/ D 2y and (B)

G

y

.x; y/ D 2x. Integrati ng (A) with respect to x yields (C) G.x; y/ D 2xy C .y/. Differentiating (C)

with respect to y yields (D) G

y

.x; y/ D 2x C 

0

.y/. Comparing (D) with (B) shows that 

0

.y/ D 0, so

we take .y/ D c. Substituting this into (C) yields G.x; y/ D 2xy C c.

(b) If F .x; y/ D e

x

cos y, then F

x

.x; y/ D e

x

cos y, F

y

.x; y/ D e

x

sin y, F

xx

.x; y/ D e

x

cos y,

and F

yy

.x; y/ D e

x

cos y. Therefore, F

xx

C F

yy

D 0, and G must satisfy (A) G

x

.x; y/ D e

x

sin y

and (B ) G

y

.x; y/ D e

x

cos y. Integrating (A) with respect to x yields (C) G.x; y/ D e

x

sin y C .y/.

Differentiatin g (C) with respect to y yields (D) G

y

.x; y/ D e

x

cos y C 

0

.y/. Comparing (D) with (B)

shows that 

0

.y/ D 0, so we take .y/ D c. Substi tuting this into (C) yields G.x; y/ D e

x

sin y C c.

(c) If F .x; y/ D x

3

 3xy

2

, then F

x

.x; y/ D 3x

2

 3y

2

, F

y

.x; y/ D 6xy, F

xx

.x; y/ D 6x,

and F

yy

.x; y/ D 6x. Therefore, F

xx

C F

yy

D 0, and G must satisfy (A) G

x

.x; y/ D 6xy and

(B) G

y

.x; y/ D 3x

2

 3y

2

. Integrat ing (A) with respect to x yields (C) G.x; y/ D 3x

2

y C .y/.

Differentiatin g (C) with respect to y yields (D) G

y

.x; y/ D 3x

2

C 

0

.y/. Comparing (D) with (B)

shows that 

0

.y/ D 3y

2

, so we take .y/ D y

3

C c. Substituting this into (C) yields G.x; y/ D

3x

2

y  y

3

C c.

(d) If F .x; y/ D cos x cosh y, then F

x

.x; y/ D sin x cosh y, F

y

.x; y/ D cos x sinh y, F

xx

.x; y/ D

Section 2.6

Exact Equations

21

cos x cosh y, and F

yy

.x; y/ D cos x cosh y. Therefore, F

xx

C F

yy

D 0, and G must satisfy (A)

G

x

.x; y/ D cos x sinh y and (B ) G

y

.x; y/ D sin x cosh y. Integrat ing ( A ) with respect to x yields

(C) G.x; y/ D sin x sinh y C .y/. Differentiating (C) with respect to y yields (D) G

y

.x; y/ D

sin x cosh y C

0

.y/. Comparing (D) with (B) shows that 

0

.y/ D 0, so we take .y/ D c. Substituting

this into (C) yields G.x; y/ D sin x sinh y C c.

(e) If F .x; y/ D sin x cosh y, then F

x

.x; y/ D cos x cosh y, F

y

.x; y/ D sin x sinh y, F

xx

.x; y/ D

sin x cosh y, and F

yy

.x; y/ D sin x cosh y. Therefore, F

xx

C F

yy

D 0, and G must satisfy (A)

G

x

.x; y/ D sin x sinh y and (B) G

y

.x; y/ D cos x cosh y. Integrating (A) with respect to x yields

(C) G.x; y/ D cos x sinh y C .y/. Differentiatin g (C) with respect to y yields (D) G

y

.x; y/ D

cos x cosh y C 

0

.y/. Comparing (D) with (B) shows that 

0

.y/ D 0, so we take .y/ D c. Substi-

tuting this into (C) yields G.x; y/ D cos x sinh y C c.

2.6 INTEGRATING FACTORS

2.6.2. (a) and (b). To show that .x; y/ D

1

.x  y/

2

is an integrating factor for (A) and th at (B) is exact,

it sufﬁces to observe that

@

@x



xy

x y



D 

y

2

.x  y/

2

and

@

@y



xy

x  y



D

x

2

.x  y/

2

. By Theorem 2.5.1

this also sh ows that (C) is an implicit solution of (B). Since .x; y/ is never zero, any solution of (B) is

a sol ution of (A).

(c) If we interpret (A) as y

2

C x

2

y

0

D 0, then substituting y D x yields x

2

C x

2

 1 D 0.

(NOTE: In Exercises 2.6.3–2.6.23, the given equation is multiplied by an integrating factor to produce

an exact equation, and an implicit solution is found for th e latter. For a complete analy sis of the relation-

ship between the sets of solutions of the two equations it is necessary to check for additional solutions of

the given equation “along which" the integrating factor is undeﬁned, or for solutions of the exact equation

“along whi ch" the integrating factor vanishes. In the inter ests of brevity we omit these tedious details

except in cases where th ere actually is a difference between the sets of sol utions of the two equations.)

2.6.4. M.x; y/ D 3x

2

y; N.x; y/ D 2x

3

; M

y

.x; y/  N

x

.x; y/ D 3x

2

 6x

2

D 3x

2

; p.x/ D

M

y

.x; y/  N

x

.x; y/

N.x; y/

D 

3x

2

2x

3

D 

3

2x

;

R

p.x/ dx D 

3

2

ln jxj; .x/ D P .x/ D x

3=2

; th ere-

fore 3x

1=2

y dx C 2x

3=2

dy D 0 is exact. We must ﬁnd F su ch that (A) F

x

.x; y/ D 3x

1=2

y and (B)

F

y

.x; y/ D 2x

3=2

. Integrating (A) with respect to x yields (C) F .x; y/ D 2x

3=2

y C .y/. Differenti-

ating (C) with respect to y y ields (D) F

y

.x; y/ D 2x

3=2

C 

0

.y/. Comparing (D) with (B) shows that



0

.y/ D 0, so we take .y/ D 0. Substituting th is into (C) yields F.x; y/ D 2x

3=2

y, so x

3=2

y D c.

2.6.6. M.x; y/ D 5xy C2y C5; N.x; y/ D 2x; M

y

.x; y/ N

x

.x; y/ D .5x C2/ 2 D 5x; p.x/ D

M

y

.x; y/  N

x

.x; y/

N.x; y/

D

5x

2x

D

5

2

;

R

p.x/ dx D

5x

2

; .x/ D P .x/ D e

5x=2

; therefore e

5x=2

.5xy C

2y C 5/ dx C2xe

5x=2

dy D 0 is exact . We must ﬁnd F such that (A) F

x

.x; y/ D e

5x=2

.5xy C 2y C5/

and (B) F

y

.x; y/ D 2xe

5x=2

. I ntegrating (B) with resp ect to y yields ( C) F .x; y/ D 2xye

5x=2

C .x/.

Differentiatin g (C) with respect to x yields (D) F

x

.x; y/ D 5xye

5x=2

C 2ye

5x=2

C

0

.x/. C omparing

(D) with (A) shows that

0

.x/ D 5e

5x=2

, so we take .x/ D 2e

5x=2

. Substituting this into (C) yields

F .x; y/ D 2e

5x=2

.xy C 1/, so e

5x=2

.xy C 1/ D c.

2.6.8. M.x; y/ D 27xy

2

C 8y

3

; N.x; y/ D 18x

2

y C 12xy

2

; M

y

.x; y/  N

x

.x; y/ D .54xy C

24y

2

/  .36xy C 12y

2

/ D 18xy C 12y

2

; p.x/ D

M

y

.x; y/  N

x

.x; y/

N.x; y/

D

18xy C12y

2

18x

2

y C12y

2

x

D

1

x

;

R

p.x/ dx D ln jxj; .x/ D P .x/ D x; therefore .27x

2

y

2

C8xy

3

/ dx C.18x

3

y C12x

2

y

2

/ dy D 0 is

exact. We must ﬁnd F such that (A) F

x

.x; y/ D 27x

2

y

2

C8xy

3

and (B) F

y

.x; y/ D 18x

3

y C12x

2

y

2

.

Integrating (A) with respect to x yields (C) F .x; y/ D 9x

3

y

2

C 4x

2

y

3

C .y/. Differentiating (C)

22 Chapter 2

Integrating Factors

with respect to y yields (D) F

y

.x; y/ D 18x

3

y C 12x

2

y

2

C 

0

.y/. Comparing (D) wi th (B) shows

that 

0

.y/ D 0, so w e take .y/ D 0. Substituting this into (C) yields F.x; y/ D 9x

3

y

2

C 4x

2

y

3

, so

x

2

y

2

.9x C 4y/ D c.

2.6.10. M.x; y/ D y

2

; N.x; y/ D



xy

2

C 3xy C

1

y



; M

y

.x; y/  N

x

.x; y/ D 2y  .y

2

C 3y/ D

y.y C 1/; q.y/ D

N

x

.x; y/  M

y

.x; y/

M.x; y/

D

y.y C 1/

y

2

D 1 C

1

y

;

R

q.y/ dy D y ln jyj; .y/ D

Q.y/ D ye

y

; ther efore y

3

e

y

dx C e

y

.xy

3

C 3xy

2

C 1/ dy D 0 is exact. We must ﬁnd F such that

(A) F

x

.x; y/ D y

3

e

y

and (B) F

y

.x; y/ D e

y

.xy

3

C 3xy

2

C 1/. Integrating (A) with respect to x

yields (C) F .x; y/ D xy

3

e

y

C .y/. Differentiating (C) with respect to y yields (D) F

y

.x; y/ D

xy

3

e

y

C 3xy

2

e

y

C 

0

.y/. Comparing (D) with (B) shows that 

0

.y/ D e

y

, so we take .y/ D e

y

.

Substituting this into (C) yields F .x; y/ D xy

3

e

y

C e

y

, so e

y

.xy

3

C 1/ D c.

2.6.12. M.x; y/ D x

2

y C4xy C2y; N.x; y/ D x

2

Cx; M

y

.x; y/N

x

.x; y/ D .x

2

C4x C2/.2x C

1/ D x

2

C 2x C 1 D .x C 1/

2

; p.x/ D

M

y

.x; y/  N

x

.x; y/

N.x; y/

D

.x C 1/

2

x.x C 1/

D 1 C

1

x

;

R

p.x/ dx D

x Cln jxj; .x/ D P .x/ D xe

x

; th erefore e

x

.x

3

y C4x

2

y C2xy/ dx C e

x

.x

3

Cx

2

/ dy D 0 is exact.

We must ﬁnd F such that (A) F

x

.x; y/ D e

x

.x

3

y C 4x

2

y C 2xy/ and (B) F

y

.x; y/ D e

x

.x

3

C x

2

/.

Integrating (B) with respect to y y ields (C) F .x; y/ D y.x

3

C x

2

/e

x

C .x/. Di fferentiating (C) with

respect to x yields (D) F

x

.x; y/ D e

x

.x

3

y C 4x

2

y C 2xy/ C

0

.x/. Comparing (D) with (A) shows

that

0

.x/ D 0, so we take .x/ D 0. Substituting this into (C) yield s F.x; y/ D y.x

3

C x

2

/e

x

D

x

2

y.x C 1/e

x

, so x

2

y.x C1/e

x

D c.

2.6.14. M.x; y/ D cos x cos y; N.x; y/ D sin x cos y  sin x sin y C y; M

y

.x; y/  N

x

.x; y/ D

cos x sin y.cos x cos ycos x sin y/ D cos x cos y; q.y/ D

N

x

.x; y/  M

y

.x; y/

M.x; y/

D

cos x cos y

D

1;

R

q.y/ dy D 1; .y/ D Q.y/ D e

y

; therefore e

y

cos x cos y dx C e

y

.sin x cos y  sin x sin y C

y/ dy D 0 is exact. We must ﬁnd F such that ( A) F

x

.x; y/ D e

y

cos x cos y and (B) F

y

.x; y/ D

e

y

.sin x cos y sin x sin y Cy/. Integrat ing (A) with respect to x yields (C) F .x; y/ D e

y

sin x cos y C

.y/. Differentiating (C) with r espect to y yields (D) F

y

.x; y/ D e

y

.sin x cos y  sin x sin y/ C 

0

.y/.

Comparing (D) wi th (B) shows that 

0

.y/ D ye

y

, so we take .y/ D e

y

.y  1/. Substituting this into

(C) yields F .x; y/ D e

y

.sin x cos y C y  1/, so e

y

.sin x cos y C y 1/ D c.

2.6.16. M.x; y/ D y sin y; N.x; y/ D x.sin y y cos y/; M

y

.x; y/ N

x

.x; y/ D .y cos y Csin y/ 

.sin y  y cos y/ D 2y cos y; q.y/ D

N

x

.x; y/  M

y

.x; y/

N.x; y/

D 

2 cos y

sin y

;

R

q.y/ dy D 2 ln jsin yj;

.y/ D Q.y/ D

1

sin

2

y

; therefore



y

sin y



dx C x



1

sin y



y cos y

sin

2

y



dy D 0 i s exact. We must

ﬁnd F such that (A) F

x

.x; y/ D

y

sin y

and (B) F

y

.x; y/ D x



1

sin y



y cos y

sin

2

y



. Integrating (A)

with respect to x yi el ds (C) F .x; y/ D

xy

sin y

C .y/. Differentiating (C) with respect to y yields (D)

F

y

.x; y/ D x



1

sin y



y cos y

sin

2

y



C 

0

.y/. Comparing (D) with (B) shows that 

0

.y/ D 0, so we take

.y/ D 0. Substituting this into (C) yields F .x; y/ D

xy

sin y

, so

xy

sin y

D c. In addition, the given

equation has the constant solutions y D k, where k is an integer.

2.6.18. M.x; y/ D ˛y C xy; N.x; y/ D ˇx C ıxy; M

y

.x; y/  N

x

.x; y/ D .˛ C x/  .ˇ C ıy/;

and p.x/N.x; y/  q.y/M.x; y/ D p.x/x.ˇ C ıy/  q.y/y.˛ C x/. so ex actness requires that

Section 2.6

Exact Equations

23

.˛ C x/  .ˇ C ıy/ D p.x/x.ˇ C ıy/  q.y/y.˛ C x/, which holds if p.x/x D 1 and q.y/y D

1. Thus p.x/ D 

1

x

; q.y/ D 

1

y

;

R

p.x/ dx D ln jxj;

R

q.y/ dy D ln jyj; P .x/ D

1

x

;

Q.y/ D

1

y

; .x; y/ D

1

xy

. Therefore,



˛

x

C 



dx C



ˇ

y

C ı



dy D 0 is exact. We must ﬁnd F

such that (A) F

x

.x; y/ D

˛

x

C  and ( B) F

y

.x; y/ D

ˇ

y

C ı. Integrating (A) wit h respect to x yields

(C) F .x; y/ D ˛ ln jxj C x C .y/. Differentiating (C) with respect to y yields (D) F

y

.x; y/ D 

0

.y/.

Comparing (D) with (B) shows that 

0

.y/ D

ˇ

y

C ı, so we take .y/ D ˇ ln jyj C ıy. Substituting this

into (C) yields F .x; y/ D ˛ ln jxjCx Cˇ ln jyjCıy, so jxj

˛

jyj

ˇ

e

x

e

ıy

D c. The given equation also

has t he solutions x  0 and y  0.

2.6.20. M.x; y/ D 2y; N.x; y/ D 3.x

2

C x

2

y

3

/; M

y

.x; y/  N

x

.x; y/ D 2  .6x C 6xy

3

/; and

p.x/N.x; y/  q.y/M.x; y/ D 3p.x/.x

2

C x

2

y

3

/  2q.y/y. so exactness r equires that (A) 2  6x 

6xy

3

D 3p.x/x.x C xy

3

/  2q.y/y. To o btain similar terms on the two sides of (A) we let p.x/x D a

and q.y/y D b where a and b are constants such that 2 6x 6xy

3

D 3a.x Cxy

3

/2b, which hol ds if

a D 2 and b D 1. Thus, p.x/ D 

2

x

; q.y/ D 

1

y

;

R

p.x/ dx D 2 ln jxj;

R

q.y/ dy D ln jyj;

P.x/ D

1

x

2

; Q.y/ D

1

y

; .x; y/ D

1

x

2

y

. Therefore,

2

x

2

dx C 3



1

y

C y

2



dy D 0 is exact. We must

ﬁnd F such that (B) F

x

.x; y/ D

2

x

2

and (C) F

y

.x; y/ D 3



1

y

C y

2



. Integrating (B) with respect to x

yields (D) F .x; y/ D 

2

x

C .y/. Differentiating (D) with respect to y yields (E) F

y

.x; y/ D 

0

.y/.

Comparing (E) with (C) shows that 

0

.y/ D 3



1

y

C y

2



, so we take .y/ D y

3

C3 ln jyj. Substituting

this into ( D) yields F .x; y/ D 

2

x

Cy

3

C3 ln jyj, so 

2

x

Cy

3

C3 ln jyj D c. The given equation also

has t he solutions x  0 and y  0.

2.6.22. M.x; y/ D x

4

y

4

; N.x; y/ D x

5

y

3

; M

y

.x; y/  N

x

.x; y/ D 4x

4

y

3

 5x

4

y

3

D x

4

y

3

;

and p.x/N.x; y/  q.y/M.x; y/ D p.x/x

5

y

3

 q.y/x

4

y

4

. so exactness requires that x

4

y

3

D

p.x/x

5

y

3

 q.y/x

4

y

4

, which is equivalent to p.x/x  q.y/y D 1. This holds if p.x/x D a and

q.y/y D a C 1 where a is an arbitrary real number. Thus, p.x/ D

a

x

; q.y/ D

a C 1

y

;

R

p.x/ dx D

a ln jxj;

R

q.y/ dy D .a C 1/ ln jyj; P.x/ D jxj

a

; Q.y/ D jyj

aC1

; .x; y/ D j x

a

jjyj

aC1

. Therefore,

jxj

a

jyj

aC1



x

4

y

4

dx C x

5

y

3

dy



D 0 is exact for any choice of a. For simplici ty we let a D 4, so (A)

is equivalent to y dx C x dy D 0. We must ﬁnd F such that (B) F

x

.x; y/ D y and (C) F

y

.x; y/ D x.

Integrating (B) with respect to x yields (D) F .x; y/ D xy C .y/. Differentiating (D) with respect to y

yields (E) F

y

.x; y/ D x C 

0

.y/. Comparing (E) with (C) shows that 

0

.y/ D 0, so we take .y/ D 0.

Substituting this into (D) yiel ds F.x; y/ D xy, so xy D c.

2.6.24. M.x; y/ D x

4

y

3

Cy; N.x; y/ D x

5

y

2

x; M

y

.x; y/ N

x

.x; y/ D .3x

4

y

2

C1/ .5x

4

y

2



1/ D 2x

4

y

2

C 2; p.x/ D

M

y

.x; y/  N

x

.x; y/

N.x; y/

D 

2x

4

y

2

 2

x

5

y

2

 x

D 

2

x

;

R

p.x/ dx D 2 ln jxj;

.x/ D P .x/ D

1

x

2

; therefore



x

2

y

3

C

y

x

2



dx C



x

3

y

2



1

x



dy D 0 is exact. We must ﬁnd

F such that (A) F

x

.x; y/ D



x

2

y

3

C

y

x

2



and (B) F

y

.x; y/ D



x

3

y

2



1

x



. Integrating (A) wit h

24 Chapter 2

Integrating Factors

respect to x yields (C) F .x; y/ D

x

3

y

3



y

x

C .y/. Differentiating (C) with respect to y yields (D)

F

y

.x; y/ D x

3

y

2



1

x

C 

0

.y/. Comparing (D) with (B) shows that 

0

.y/ D 0, so we take .y/ D 0.

Substituting this into (C) yields F .x; y/ D

x

3

y

3



y

x

, so

x

3

y

3



y

x

D c.

2.6.26. M.x; y/ D 12xy C 6y

3

; N.x; y/ D 9x

2

C 10xy

2

; M

y

.x; y/  N

x

.x; y/ D .12x C 18y

2

/ 

.18xC10y

2

/ D 6x C8y

2

; and p.x/N.x; y/q.y/M.x; y/ D p.x/x.9xC10y

2

/q.y/y.12xC6y

2

/,

so exactness requires that (A) 6x C8y

2

D p.x/x.9x C10y

2

/ q.y/y.12x C6y

2

/. To obtai n similar

terms on the two sides of (A) we let p.x/x D a and q.y/y D b where a and b are constants such that

6x C 8y

2

D a.9x C 10y

2

/  b.12x C 6y

2

/, which holds if 9a  12b D 6, 10a  6b D 8; that is,

a D b D 2. Thus p.x/ D

2

x

; q.y/ D

2

y

;

R

p.x/ dx D 2 ln jxj;

R

q.y/ dy D 2 lnjyj; P.x/ D x

2

;

Q.y/ D y

2

; .x; y/ D x

2

y

2

. Therefore, .12x

3

y

3

C 6x

2

y

5

/ dx C .9x

4

y

2

C 10x

3

y

4

/ dy D 0 is exact.

We must ﬁnd F such that (B) F

x

.x; y/ D 12x

3

y

3

C 6x

2

y

5

and (C) F

y

.x; y/ D 9x

4

y

2

C 10x

3

y

4

.

Integrating (B) with respect to x yields (D) F .x; y/ D 3x

4

y

3

C 2x

3

y

5

C .y/. Differentiating (D)

with respect t o y yields (E) F

y

.x; y/ D 9x

4

y

2

C 10x

3

y

4

C 

0

.y/. Comparing (E) with (C) shows that



0

.y/ D 0, so we take .y/ D 0. Substituting this into (D) yields F .x; y/ D 3x

4

y

3

C 2x

3

y

5

, so

x

3

y

3

.3x C 2y

2

/ D c.

2.6.28. M.x; y/ D ax

m

yCby

nC1

; N.x; y/ D cx

mC1

Cdxy

n

; M

y

.x; y/N

x

.x; y/ D



ax

mC1

C .n C 1/by

n





Œ.m C 1/cx

m

C dy

n

; p.x/N.x; y/  q.y/M.x; y/ D xp.x/.cx

m

C dy

n

/  yp.y/.ax

m

C by

n

/. Let

(A) xp.x/ D ˛ and (B) yp.y/ D ˇ, where ˛ and ˇ are to be chosen so that



ax

mC1

C .n C 1/by

n





Œ.m C 1/cx

m

C dy

n

 D ˛.cx

m

C dy

n

/  ˇ.ax

m

Cby

n

/, which will hol d if

c˛  aˇ D a  .m C 1/c D

df

A

d˛  bˇ D d C .n C 1/b D

df

B:

.C/

Since ad  bc ¤ 0 it can be veriﬁed that ˛ D

aB  bA

ad  bc

and ˇ D

cB  dA

ad  bc

satisfy (C). From (A) and

(B), p.x/ D

˛

x

and q.y/ D

ˇ

y

, so .x; y/ D x

˛

y

ˇ

is an integrating factor for the given equation.

2.6.30. (a) Since M.x; y/ D p.x/y  f .x/ and N.x; y/ D 1,

M

y

.x; y/  N

x

.x; y/

N.x; y/

D p.x/ and

Theorem 2.6.1 implies that .x/ ˙ e

R

p.x/ d x

is an integrating factor for (C).

(b) Mul tiplying (A) through  D ˙e

R

p.x/ d x

yields (D) .x/y

0

C 

0

.x/y D .x/f .x/, which is

equivalent to ..x/y/

0

D .x/f .x/. Integrating this yields .x/y D c C

Z

.x/f .x/ dx, so y D

1

.x/



c C

Z

.x/f .x/ dx



, which i s equivalent to (B) since y

1

D

1



is a nont riv ial solution of y

0

C

p.x/y D 0.

CHAPTER 3

Numerica l Methods

3.1 EULER’S METHOD

3.1.2. y

1

D 1:200000000; y

2

D 1:440415946; y

3

D 1:729880994

3.1.4. y

1

D 2:962500000; y

2

D 2:922635828; y

3

D 2:880205639

3.1.6.

x h D 0 :1 h D 0 :05 h D 0 :025 Exact

0.0 2.000000000 2.000000000 2.000000000 2.000000000

0.1 2.100000000 2.169990965 2.202114518 2.232642918

0.2 2.514277288 2.649377900 2.713011720 2.774352565

0.3 3.317872752 3.527672599 3.628465025 3.726686582

0.4 4.646592772 4.955798226 5.106379369 5.254226636

0.5 6.719737638 7.171467977 7.393322991 7.612186259

0.6 9.876155616 10.538384528 10.865186799 11.18847526 9

0.7 14.629 532397 15.605686107 16.088630652 16.567103199

0.8 21.751 925418 23.197328550 23.913328531 24.623248150

0.9 32.399 118931 34.545932627 35.610005377 36.665439956

1.0 48.298 147362 51.492825643 53.076673685 54.647937102

3.1.8.

x h D 0 :05 h D 0:025 h D 0:0125 Exact

1.00 2.000 000000 2.000000000 2.000000000 2.000000000

1.05 2.250 000000 2.259280190 2.264490570 2.270158103

1.10 2.536 734694 2.559724746 2.572794280 2.587150838

1.15 2.867 950854 2.910936426 2.935723355 2.963263785

1.20 3.253 613825 3.325627715 3.367843117 3.415384615

1.25 3.706 750613 3.820981064 3.889251900 3.967391304

1.30 4.244 700641 4.420781829 4.528471927 4.654198473

1.35 4.891 020001 5.158883503 5.327348558 5.528980892

1.40 5.678 467290 6.085075790 6.349785943 6.676923077

1.45 6.653 845988 7.275522641 7.698316221 8.243593315

1.50 7.886 170437 8.852463793 9.548039907 10.500000000

25

26 Chapter 3

Numerical Methods

3.1.10.

x h D 0:1 h D 0:05 h D 0:025 h D 0:1 h D 0:05 h D 0:025

1.0 1.0000 00000 1.000000000 1.000000000 0.0000 0.0000 0.0000

1.1 0.9200 00000 0.921898275 0.922822717 -0.0384 -0.0189 -0.0094

1.2 0.8474 69326 0.851018464 0.852746371 -0.0745 -0.0368 -0.0183

1.3 0.7817 79403 0.786770087 0.789197876 -0.1092 -0.0540 -0.0268

1.4 0.7224 53556 0.728682209 0.731709712 -0.1428 -0.0707 -0.0351

1.5 0.6690 37867 0.676299618 0.679827306 -0.1752 -0.0868 -0.0432

1.6 0.6210 54176 0.629148585 0.633080163 -0.2062 -0.1023 -0.0509

1.7 0.5780 00416 0.586740390 0.590986601 -0.2356 -0.1170 -0.0583

1.8 0.5393 70187 0.548588902 0.553070392 -0.2631 -0.1310 -0.0653

1.9 0.5046 74296 0.514228603 0.518877246 -0.2889 -0.1441 -0.0719

2.0 0.4734 56737 0.483227470 0.487986391 -0.3129 -0.1563 -0.0781

Approximate Solutions Residuals

3.1.12.

x h D 0:1 h D 0:05 h D 0:025 “Exact"

1.0 0.000000000 0.000000000 0.000000000 0.000000000

1.1 -0.100000000 -0.099875000 -0.099780455 -0.099664000

1.2 -0.199000000 -0.198243434 -0.197800853 -0.197315517

1.3 -0.294996246 -0.293129862 -0.292110713 -0.291036003

1.4 -0.386095345 -0.382748403 -0.380986158 -0.379168221

1.5 -0.470695388 -0.465664569 -0.463078857 -0.460450590

1.6 -0.547627491 -0.540901018 -0.537503081 -0.534085626

1.7 -0.616227665 -0.607969574 -0.603849795 -0.599737720

1.8 -0.676329533 -0.666833345 -0.662136956 -0.657473792

1.9 -0.728190908 -0.717819639 -0.712718751 -0.707670533

2.0 -0.772381768 -0.761510960 -0.756179726 -0.750912371

3.1.14.

Euler’s method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 2.000000000 2.000000000 2.000000000 2.000000000

2.1 2.420000000 2.440610764 2.451962006 2.464119569

2.2 2.922484288 2.972198224 2.999753046 3.029403212

2.3 3.524104434 3.614025082 3.664184099 3.718409925

2.4 4.244823572 4.389380160 4.470531822 4.558673929

2.5 5.108581185 5.326426396 5.449503467 5.583808754

2.6 6.144090526 6.459226591 6.638409411 6.834855438

2.7 7.385795229 7.828984275 8.082588076 8.361928926

2.8 8.875017001 9.485544888 9.837137672 10.226228709

2.9 10.661 332618 11.489211987 11.969020902 12.502494409

3.0 12.804 226135 13.912944662 14.559623055 15.282004826

Euler semilinear method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 2.000000000 2.000000000 2.000000000 2.000000000

2.1 2.467233571 2.465641081 2.464871435 2.464119569

2.2 3.036062650 3.032657307 3.031011316 3.029403212

2.3 3.729169725 3.723668026 3.721008466 3.718409925

2.4 4.574236356 4.566279470 4.562432696 4.558673929

2.5 5.605052990 5.594191643 5.588940276 5.583808754

2.6 6.862874116 6.848549921 6.841623814 6.834855438

2.7 8.398073101 8.379595572 8.370660695 8.361928926

2.8 10.272163096 10.248681420 10.237326199 10.226228709

2.9 12.560265110 12.530733531 12.516452106 12.502494409

3.0 15.354122287 15.317257705 15.299429421 15.282004826

Section 3.1

Euler’s Method

27

3.1.16.

Euler’s method

x h D 0:2 h D 0:1 h D 0:05 “Exact"

1.0 2.0000 00000 2.000000000 2.000000000 2.000000000

1.2 1.7682 94197 1.786514499 1.794412375 1.801636774

1.4 1.6030 28371 1.628427487 1.639678822 1.650102616

1.6 1.4745 80412 1.502563111 1.515157063 1.526935885

1.8 1.3683 49549 1.396853671 1.409839229 1.422074283

2.0 1.2764 24761 1.304504818 1.317421794 1.329664953

2.2 1.1942 47156 1.221490111 1.234122458 1.246155344

2.4 1.1190 88175 1.145348276 1.157607418 1.169334346

2.6 1.0492 84410 1.074553688 1.086419453 1.097812069

2.8 0.9838 21745 1.008162993 1.019652023 1.030719114

3.0 0.9220 94379 0.945604800 0.956752868 0.967523153

Euler semilinear method

x h D 0 :2 h D 0:1 h D 0:05 “E xact"

1.0 2.000000000 2.000000000 2.000000000 2.00000 0000

1.2 1.806911831 1.804304958 1.802978526 1.80163 6774

1.4 1.659738603 1.654968381 1.652547436 1.65010 2616

1.6 1.540257861 1.533652916 1.530308405 1.52693 5885

1.8 1.438532932 1.430361800 1.426232584 1.42207 4283

2.0 1.348782285 1.339279577 1.334486249 1.32966 4953

2.2 1.267497415 1.256876924 1.251528766 1.24615 5344

2.4 1.192497494 1.180958765 1.175157264 1.16933 4346

2.6 1.122416379 1.110147777 1.103988310 1.09781 2069

2.8 1.056405906 1.043585743 1.037158237 1.03071 9114

3.0 0.993954754 0.980751307 0.974140320 0.96752 3153

3.1.18.

Euler’s method

x h D 0:2 h D 0:1 h D 0:05 “Exact"

0.0 1.0000 00000 1.000000000 1.000000000 1.000000000

0.2 1.2000 00000 1.186557290 1.179206574 1.171515153

0.4 1.3335 43409 1.298441890 1.280865289 1.263370891

0.6 1.3713 40142 1.319698328 1.295082088 1.271251278

0.8 1.3263 67357 1.270160237 1.243958980 1.218901287

1.0 1.2330 56306 1.181845667 1.158064902 1.135362070

1.2 1.1223 59136 1.080477477 1.060871608 1.042062625

1.4 1.0131 00262 0.981124989 0.965917496 0.951192532

1.6 0.9140 00211 0.890759107 0.879460404 0.868381328

1.8 0.8278 48558 0.811673612 0.803582000 0.795518627

2.0 0.7545 72560 0.743869878 0.738303914 0.732638628

Euler semilinear method

x h D 0 :2 h D 0:1 h D 0:05 “E xact"

0.0 1.000000000 1.000000000 1.000000000 1.00000 0000

0.2 1.153846154 1.162906599 1.167266650 1.17151 5153

0.4 1.236969953 1.250608357 1.257097924 1.26337 0891

0.6 1.244188456 1.258241892 1.264875987 1.27125 1278

0.8 1.195155456 1.207524076 1.213335781 1.21890 1287

1.0 1.115731189 1.125966437 1.130768614 1.13536 2070

1.2 1.025938754 1.034336918 1.038283392 1.04206 2625

1.4 0.937645707 0.944681597 0.948002346 0.95119 2532

1.6 0.856581823 0.862684171 0.865583126 0.86838 1328

1.8 0.784832910 0.790331183 0.792963532 0.79551 8627

2.0 0.722610454 0.727742966 0.730220211 0.73263 8628

28 Chapter 3

Numerical Methods

3.1.20.

Euler’s method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

0.0 1.0000 00000 1.000000000 1.000000000 1.000000000

0.1 0.7000 00000 0.725841563 0.736671690 0.746418339

0.2 0.4983 30000 0.532982493 0.547988831 0.561742917

0.3 0.3562 72689 0.392592562 0.408724303 0.423724207

0.4 0.2545 55443 0.289040639 0.304708942 0.319467408

0.5 0.1814 40541 0.212387189 0.226758594 0.240464879

0.6 0.1289 53069 0.155687255 0.168375130 0.180626161

0.7 0.0913 93543 0.113851516 0.124744976 0.135394692

0.8 0.0646 13612 0.083076641 0.092230966 0.101293057

0.9 0.0455 85102 0.060505907 0.068068776 0.075650324

1.0 0.0321 05117 0.043997045 0.050159310 0.056415515

Euler semilinear method

x h D 0 :1 h D 0:05 h D 0:025 “Exact"

0.0 1.000000000 1.000000000 1.000000000 1.00000 0000

0.1 0.740818221 0.743784320 0.745143557 0.74641 8339

0.2 0.555889275 0.558989106 0.560410719 0.56174 2917

0.3 0.418936461 0.421482025 0.422642541 0.42372 4207

0.4 0.315890439 0.317804400 0.318668549 0.31946 7408

0.5 0.237908421 0.239287095 0.239902094 0.24046 4879

0.6 0.178842206 0.179812811 0.180239888 0.18062 6161

0.7 0.134165506 0.134840668 0.135133367 0.13539 4692

0.8 0.100450939 0.100918118 0.101117514 0.10129 3057

0.9 0.075073968 0.075396974 0.075532643 0.07565 0324

1.0 0.056020154 0.056243980 0.056336491 0.05641 5515

3.1.22.

Euler’s method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 1.0000 00000 1.000000000 1.000000000 1.000000000

2.1 1.0000 00000 1.005062500 1.007100815 1.008899988

2.2 1.0205 00000 1.026752091 1.029367367 1.031723469

2.3 1.0534 89840 1.059067423 1.061510137 1.063764243

2.4 1.0935 21685 1.097780573 1.099748225 1.101614730

2.5 1.1371 37554 1.140059654 1.141496651 1.142903776

2.6 1.1822 69005 1.184090031 1.185056276 1.186038851

2.7 1.2277 45005 1.228755801 1.229350441 1.229985178

2.8 1.2729 40309 1.273399187 1.273721920 1.274092525

2.9 1.3175 45833 1.317651554 1.317786528 1.317967533

3.0 1.3614 27907 1.361320824 1.361332589 1.361383810

Euler semilinear method

x h D 0 :1 h D 0:05 h D 0:025 “Exact"

2.0 1.000000000 1.000000000 1.000000000 1.00000 0000

2.1 0.982476904 0.996114142 1.002608435 1.00889 9988

2.2 0.988105346 1.010577663 1.021306044 1.03172 3469

2.3 1.009495813 1.037358814 1.050731634 1.06376 4243

2.4 1.041012955 1.071994816 1.086964414 1.10161 4730

2.5 1.078631301 1.111346365 1.127262285 1.14290 3776

2.6 1.119632590 1.153300133 1.169781376 1.18603 8851

2.7 1.162270287 1.196488725 1.213325613 1.22998 5178

2.8 1.205472927 1.240060456 1.257146091 1.27409 2525

2.9 1.248613584 1.283506001 1.300791772 1.31796 7533

3.0 1.291345518 1.326535737 1.344004102 1.36138 3810

Section 3.2

The Improved Euler Method and R el ated Methods

29

3.2 THE IMPROVED EULER METHOD AND RELATED METHODS

3.2.2. y

1

D 1:220207973; y

2

D 1:489578775 y

3

D 1:819337186

3.2.4. y

1

D 2:961317914; y

2

D 2:920132727; y

3

D 2:876213748.

3.2.6.

x h D 0 :1 h D 0 :05 h D 0 :025 Exact

0.0 2.000000000 2.000000000 2.000000000 2.000000000

0.1 2.257138644 2.238455342 2.234055168 2.232642918

0.2 2.826004666 2.786634110 2.777340360 2.774352565

0.3 3.812671926 3.747167263 3.731674025 3.726686582

0.4 5.387430580 5.285996803 5.261969043 5.254226636

0.5 7.813298361 7.660199197 7.623893064 7.612186259

0.6 11.489 337756 11.260349005 11.206005869 11.188475269

0.7 17.015 861211 16.674352914 16.593267820 16.567103199

0.8 25.292 140630 24.783149862 24.662262731 24.623248150

0.9 37.662 496723 36.903828191 36.723608928 36.665439956

1.0 56.134 480009 55.003390448 54.734674836 54.647937102

3.2.8.

x h D 0:05 h D 0:025 h D 0:0125 Exact

1.00 2.000000000 2.000000000 2.000000000 2.000000000

1.05 2.268367347 2.269670336 2.270030868 2.270158103

1.10 2.582607299 2.585911295 2.586827341 2.587150838

1.15 2.954510022 2.960870733 2.962638822 2.963263785

1.20 3.400161788 3.411212150 3.414293964 3.415384615

1.25 3.942097142 3.960434900 3.965570792 3.967391304

1.30 4.612879780 4.642784826 4.651206769 4.654198473

1.35 5.461348619 5.510188575 5.524044591 5.528980892

1.40 6.564150753 6.645334756 6.668600859 6.676923077

1.45 8.048579617 8.188335998 8.228972215 8.243593315

1.50 10.14 1969585 10.396770 409 10.472502111 10.500000000

3.2.10.

x h D 0:1 h D 0:05 h D 0:025 h D 0:1 h D 0:05 h D 0:025

1.0 1.0000 00000 1.000000000 1.000000000 0.00000 0.000000 0.000000

1.1 0.9237 34663 0.923730743 0.923730591 0.00004 0.000001 -0.000001

1.2 0.8544 75600 0.854449616 0.854444697 0.00035 0.000068 0.000015

1.3 0.7916 50344 0.791596016 0.791584634 0.00078 0.000167 0.000039

1.4 0.7347 85779 0.734703826 0.734686010 0.00125 0.000277 0.000065

1.5 0.6834 24095 0.683318666 0.683295308 0.00171 0.000384 0.000091

1.6 0.6370 97057 0.636973423 0.636945710 0.00213 0.000483 0.000115

1.7 0.5953 30359 0.595193634 0.595162740 0.00250 0.000572 0.000137

1.8 0.5576 58422 0.557513000 0.557479947 0.00283 0.000650 0.000156

1.9 0.5236 38939 0.523488343 0.523453958 0.00311 0.000718 0.000173

2.0 0.4928 62999 0.492709931 0.492674855 0.00335 0.000777 0.000187

Approximate Solutions Residuals

30 Chapter 3

Numerical Methods

3.2.12.

x h D 0:1 h D 0:05 h D 0:025 “Exact"

1.0 0.000000000 0.000000000 0.000000000 0.000000000

1.1 -0.099500000 -0.099623114 -0.099653809 -0.099664000

1.2 -0.196990313 -0.197235180 -0.197295585 -0.197315517

1.3 -0.290552949 -0.290917718 -0.291006784 -0.291036003

1.4 -0.378532718 -0.379013852 -0.379130237 -0.379168221

1.5 -0.459672297 -0.460262848 -0.460404546 -0.460450590

1.6 -0.533180153 -0.533868468 -0.534032512 -0.534085626

1.7 -0.598726853 -0.599496413 -0.599678824 -0.599737720

1.8 -0.656384109 -0.657214624 -0.657410640 -0.657473792

1.9 -0.706530934 -0.707400266 -0.707604759 -0.707670533

2.0 -0.749751364 -0.750637632 -0.750845571 -0.750912371

3.2.14.

Improved Euler method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 2.000000000 2.000000000 2.000000000 2.000000000

2.1 2.461242144 2.463344439 2.463918368 2.464119569

2.2 3.022367633 3.027507237 3.028911026 3.029403212

2.3 3.705511610 3.714932709 3.717507170 3.718409925

2.4 4.537659565 4.553006531 4.557202414 4.558673929

2.5 5.551716960 5.575150456 5.581560437 5.583808754

2.6 6.787813853 6.822158665 6.831558101 6.834855438

2.7 8.294896222 8.343829180 8.357227947 8.361928926

2.8 10.132 667135 10.200955596 10.219663917 10.226228709

2.9 12.373 954732 12.467758807 12.493470722 12.502494409

3.0 15.107 600968 15.234856000 15.269755072 15.282004826

Improved Euler semilinear method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 2.000000000 2.000000000 2.000000000 2.000000000

2.1 2.464261688 2.464155139 2.464128464 2.464119569

2.2 3.029706047 3.029479005 3.029422165 3.029403212

2.3 3.718897663 3.718531995 3.718440451 3.718409925

2.4 4.559377397 4.558849990 4.558717956 4.558673929

2.5 5.584766724 5.584048510 5.583868709 5.583808754

2.6 6.836116246 6.835170986 6.834934347 6.834855438

2.7 8.363552464 8.362335253 8.362030535 8.361928926

2.8 10.228288880 10.226744312 10.226357645 10.226228709

2.9 12.505082132 12.503142042 12.502656361 12.502494409

3.0 15.285231726 15.282812424 15.282206780 15.282004826

3.2.16.

Improved Euler method

x h D 0:2 h D 0:1 h D 0:05 “Exact"

1.0 2.0000 00000 2.000000000 2.000000000 2.000000000

1.2 1.8015 14185 1.801606135 1.801629115 1.801636774

1.4 1.6499 11580 1.650054870 1.650090680 1.650102616

1.6 1.5267 11768 1.526879870 1.526921882 1.526935885

1.8 1.4218 41570 1.422016119 1.422059743 1.422074283

2.0 1.3294 41172 1.329609020 1.329650971 1.329664953

2.2 1.2459 53205 1.246104819 1.246142713 1.246155344

2.4 1.1691 62994 1.169291515 1.169323639 1.169334346

2.6 1.0976 77870 1.097778523 1.097803683 1.097812069

2.8 1.0306 26179 1.030695880 1.030713305 1.030719114

3.0 0.9674 73721 0.967510790 0.967520062 0.967523153

Section 3.2

The Improved Euler Method and R el ated Methods

31

Improved Euler semilinear me thod

x h D 0 :2 h D 0:1 h D 0:05 “E xact"

1.0 2.000000000 2.000000000 2.000000000 2.00000 0000

1.2 1.801514185 1.801606135 1.801629115 1.80163 6774

1.4 1.649911580 1.650054870 1.650090680 1.65010 2616

1.6 1.526711768 1.526879870 1.526921882 1.52693 5885

1.8 1.421841570 1.422016119 1.422059743 1.42207 4283

2.0 1.329441172 1.329609020 1.329650971 1.32966 4953

2.2 1.245953205 1.246104819 1.246142713 1.24615 5344

2.4 1.169162994 1.169291515 1.169323639 1.16933 4346

2.6 1.097677870 1.097778523 1.097803683 1.09781 2069

2.8 1.030626179 1.030695880 1.030713305 1.03071 9114

3.0 0.967473721 0.967510790 0.967520062 0.96752 3153

3.2.18.

Improved Euler method

x h D 0:2 h D 0:1 h D 0:05 “Exact"

0.0 1.0000 00000 1.000000000 1.000000000 1.000000000

0.2 1.1667 71705 1.170394902 1.171244037 1.171515153

0.4 1.2558 35116 1.261642355 1.262958788 1.263370891

0.6 1.2635 17157 1.269528214 1.270846761 1.271251278

0.8 1.2125 51997 1.217531648 1.218585457 1.218901287

1.0 1.1308 12573 1.134420589 1.135150284 1.135362070

1.2 1.0391 04333 1.041487727 1.041938536 1.042062625

1.4 0.9494 40052 0.950888923 0.951132561 0.951192532

1.6 0.8674 75787 0.868263999 0.868364849 0.868381328

1.8 0.7951 83973 0.795523696 0.795530315 0.795518627

2.0 0.7326 79223 0.732721613 0.732667905 0.732638628

Improved Euler semilinear me thod

x h D 0 :2 h D 0:1 h D 0:05 “E xact"

0.0 1.000000000 1.000000000 1.000000000 1.00000 0000

0.2 1.170617859 1.171292452 1.171459576 1.17151 5153

0.4 1.261629934 1.262938347 1.263262919 1.26337 0891

0.6 1.269173253 1.270734290 1.271122186 1.27125 1278

0.8 1.216926014 1.218409355 1.218778420 1.21890 1287

1.0 1.133688235 1.134944960 1.135257876 1.13536 2070

1.2 1.040721691 1.041728386 1.041979126 1.04206 2625

1.4 0.950145706 0.950931597 0.951127345 0.95119 2532

1.6 0.867573431 0.868179975 0.868331028 0.86838 1328

1.8 0.794899034 0.795364245 0.795480063 0.79551 8627

2.0 0.732166678 0.732521078 0.732609267 0.73263 8628

3.2.20.

Improved Euler method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

0.0 1.0000 00000 1.000000000 1.000000000 1.000000000

0.1 0.7491 65000 0.747022742 0.746561141 0.746418339

0.2 0.5659 42699 0.562667885 0.561961242 0.561742917

0.3 0.4286 18351 0.424803657 0.423978964 0.423724207

0.4 0.3245 56426 0.320590918 0.319732571 0.319467408

0.5 0.2454 17735 0.241558658 0.240723019 0.240464879

0.6 0.1852 35654 0.181643813 0.180866303 0.180626161

0.7 0.1395 46094 0.136310496 0.135610749 0.135394692

0.8 0.1049 38506 0.102096319 0.101482503 0.101293057

0.9 0.0787 87731 0.076340645 0.075813072 0.075650324

1.0 0.0590 71894 0.056999028 0.056553023 0.056415515

32 Chapter 3

Numerical Methods

Improved Euler semilinear me thod

x h D 0 :1 h D 0:05 h D 0:025 “Exact"

0.0 1.000000000 1.000000000 1.000000000 1.00000 0000

0.1 0.745595127 0.746215164 0.746368056 0.74641 8339

0.2 0.560827568 0.561515647 0.561686492 0.56174 2917

0.3 0.422922083 0.423524585 0.423674586 0.42372 4207

0.4 0.318820339 0.319306259 0.319427337 0.31946 7408

0.5 0.239962317 0.240339716 0.240433757 0.24046 4879

0.6 0.180243441 0.180530866 0.180602470 0.18062 6161

0.7 0.135106416 0.135322934 0.135376855 0.13539 4692

0.8 0.101077312 0.101239368 0.101279714 0.10129 3057

0.9 0.075489492 0.075610310 0.075640381 0.07565 0324

1.0 0.056295914 0.056385765 0.056408124 0.05641 5515

3.2.22.

Improved Euler method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 1.0000 00000 1.000000000 1.000000000 1.000000000

2.1 1.0102 50000 1.009185754 1.008965733 1.008899988

2.2 1.0335 47273 1.032105322 1.031811002 1.031723469

2.3 1.0655 62151 1.064135919 1.063849094 1.063764243

2.4 1.1031 45347 1.101926450 1.101685553 1.101614730

2.5 1.1440 85693 1.143140125 1.142957158 1.142903776

2.6 1.1868 78796 1.186202854 1.186075600 1.186038851

2.7 1.2305 30804 1.230088035 1.230007943 1.229985178

2.8 1.2744 04357 1.274147657 1.274104430 1.274092525

2.9 1.3181 04153 1.317987551 1.317971490 1.317967533

3.0 1.3613 95309 1.361379259 1.361382239 1.361383810

Improved Euler semilinear me thod

x h D 0 :1 h D 0:05 h D 0:025 “Exact"

2.0 1.000000000 1.000000000 1.000000000 1.00000 0000

2.1 1.012802674 1.009822081 1.009124116 1.00889 9988

2.2 1.038431870 1.033307426 1.032108359 1.03172 3469

2.3 1.072484834 1.065821457 1.064263950 1.06376 4243

2.4 1.111794329 1.104013534 1.102197168 1.10161 4730

2.5 1.154168041 1.145554968 1.143547198 1.14290 3776

2.6 1.198140189 1.188883373 1.186728849 1.18603 8851

2.7 1.242762459 1.232984559 1.230712361 1.22998 5178

2.8 1.287441845 1.277221941 1.274850828 1.27409 2525

2.9 1.331821976 1.321210992 1.318753047 1.31796 7533

3.0 1.375699933 1.364730937 1.362193997 1.36138 3810

3.2.24.

x h D 0:1 h D 0:05 h D 0:025 Exact

1.0 1.0000 00000 1.000000000 1.000000000 1.000000000

1.1 1.1510 19287 1.153270661 1.153777957 1.153937085

1.2 1.2387 98618 1.241884421 1.242580821 1.242799540

1.3 1.2892 96258 1.292573128 1.293313355 1.293546032

1.4 1.3176 86801 1.320866599 1.321585242 1.321811247

1.5 1.3330 73855 1.336036248 1.336705820 1.336916440

1.6 1.3410 27170 1.343732006 1.344343232 1.344535503

1.7 1.3450 01345 1.347446389 1.347998652 1.348172348

1.8 1.3471 55352 1.349355473 1.349852082 1.350008229

1.9 1.3488 39325 1.350816158 1.351261995 1.351402121

2.0 1.3508 90736 1.352667599 1.353067951 1.353193719

Section 3.2

The Improved Euler Method and R el ated Methods

33

3.2.26.

x h D 0 :05 h D 0 :025 h D 0:0125 Exact

1.00 2.000000000 2.000000000 2.000000000 2.000000000

1.05 2.268496358 2.269703943 2.270043628 2.270158103

1.10 2.582897367 2.585985695 2.586855275 2.587150838

1.15 2.954995034 2.960992388 2.962683751 2.963263785

1.20 3.400872342 3.411384294 3.414355862 3.415384615

1.25 3.943047906 3.960651794 3.965644965 3.967391304

1.30 4.614039436 4.643018510 4.651277424 4.654198473

1.35 5.462568051 5.510357362 5.524069547 5.528980892

1.40 6.564985580 6.645224236 6.668472955 6.676923077

1.45 8.047824947 8.187384679 8.228413044 8.243593315

1.50 10.13 6329642 10.393419 681 10.470731411 10.500000000

3.2.28.

x h D 0:1 h D 0:05 h D 0:025 “Exact"

0.0 1.0000 00000 1.000000000 1.000000000 1.000000000

0.1 0.9841 42840 0.984133302 0.984130961 0.984130189

0.2 0.9650 66124 0.965044455 0.965039117 0.965037353

0.3 0.9426 48578 0.942611457 0.942602279 0.942599241

0.4 0.9167 05578 0.916648569 0.916634423 0.916629732

0.5 0.8869 70525 0.886887464 0.886866778 0.886859904

0.6 0.8530 66054 0.852948011 0.852918497 0.852908668

0.7 0.8144 58249 0.814291679 0.814249848 0.814235883

0.8 0.7703 80571 0.770143777 0.770083998 0.770063987

0.9 0.7196 99643 0.719355385 0.719267905 0.719238519

1.0 0.6606 58411 0.660136630 0.660002840 0.659957689

3.2.30.

x h D 0:1 h D 0:05 h D 0:025 “Exact"

1.0 0.000000000 0.000000000 0.000000000 0.000000000

1.1 -0.099666667 -0.099665005 -0.099664307 -0.099674132

1.2 -0.197322275 -0.197317894 -0.197316222 -0.197355914

1.3 -0.291033227 -0.291036361 -0.291036258 -0.291123993

1.4 -0.379131069 -0.379160444 -0.379166504 -0.379315647

1.5 -0.460350276 -0.460427667 -0.460445166 -0.460662347

1.6 -0.533897316 -0.534041581 -0.534075026 -0.534359685

1.7 -0.599446325 -0.599668984 -0.599721072 -0.600066382

1.8 -0.657076288 -0.657379719 -0.657450947 -0.657845646

1.9 -0.707175010 -0.707553135 -0.707641993 -0.708072516

2.0 -0.750335016 -0.750775571 -0.750879100 -0.751331499

3.2.32. (a) Let x

i

D a C ih, i D 0; 1; : : : ; n. If y is the solution of the initial value problem

y

0

D f .x/, y.a/ D 0, then y.b/ D

R

b

a

f .x/ dx. The improved Euler method yields y

iC1

D y

i

C

:5h .f .a C ih/ C f .a C .i C 1/h//, i D 0; 1; : : : ; n  1, where y

0

D a and y

n

is an approxi mation to

Z

b

a

f .x/ dx. But

y

n

D

n1

X

iD0

.y

iC1

 y

i

/ D :5h .f .a/ C f .b// C h

n1

X

iD1

f .a C ih/:

(c) The local truncation error is a multiple of y

000

. Qx

i

/ D f

00

. Qx

i

/, where x

i

< Qx

i

< x

iC1

. Therefore,

the quadrature formula is exact if f is a polynomial of degree < 2.

(d) Let E.f / D

Z

b

a

f .x/ dx  y

n

. Not e that E is linear. If f is a polynomial of degree 2, then

34 Chapter 3

Numerical Methods

f .x/ D f

0

.x/ C K.x  a/

2

where deg.f

0

/  1. Since E.f

0

/ D 0 from (c) and

E..x  a/

2

/ D

.b  a/

3



.b  a/

2

h

2

 h

3

n1

X

iD1

i

2

D h

3



n

3



n

2



n.n  1/.2n  1/

6



D 

nh

3

6

D 

.b  a/h

2

6

;

E.f / D 

K.b  a/h

2

6

; th erefore the error is pro portion al to h

2

.

3.3 THE RUNGE–KUTTA METHOD

3.3.2. y

1

D 1:221551366; y

2

D 1:492920208

3.3.4. y

1

D 2:961316248; y

2

D 2:920128958.

3.3.6.

x h D 0 :1 h D 0 :05 h D 0 :025 Exact

0.0 2.000000000 2.000000000 2.000000000 2.000000000

0.1 2.232752507 2.232649573 2.232643327 2.232642918

0.2 2.774582759 2.774366625 2.774353431 2.774352565

0.3 3.727068686 3.726710028 3.726688030 3.726686582

0.4 5.254817388 5.254263005 5.254228886 5.254226636

0.5 7.613077020 7.612241222 7.612189662 7.612186259

0.6 11.189 806778 11.188557546 11.188480365 11.188475269

0.7 16.569 088310 16.567225975 16.567110808 16.567103199

0.8 24.626 206255 24.623431201 24.623259496 24.623248150

0.9 36.669 848687 36.665712858 36.665456874 36.665439956

1.0 54.654 509699 54.648344019 54.647962328 54.647937102

3.3.8.

x h D 0:05 h D 0:025 h D 0:0125 Exact

1.00 2.000000000 2.000000000 2.000000000 2.000000000

1.05 2.270153785 2.270157806 2.270158083 2.270158103

1.10 2.587139846 2.587150083 2.587150789 2.587150838

1.15 2.963242415 2.963262317 2.963263689 2.963263785

1.20 3.415346864 3.415382020 3.415384445 3.415384615

1.25 3.967327077 3.967386886 3.967391015 3.967391304

1.30 4.654089950 4.654191000 4.654197983 4.654198473

1.35 5.528794615 5.528968045 5.528980049 5.528980892

1.40 6.676590929 6.676900116 6.676921569 6.676923077

1.45 8.242960669 8.243549415 8.243590428 8.243593315

1.50 10.49 8658198 10.499906 266 10.499993820 10.500000000

3.3.10.

x h D 0:1 h D 0:05 h D 0:025 h D 0:1 h D 0:05 h D 0:025

1.0 1.0000 00000 1.000000000 1.000000000 0.000000000 0.0000000000 0.00000000000

1.1 0.9237 30622 0.923730677 0.923730681 -0.000000608 -0.0000000389 -0.00000000245

1.2 0.8544 43253 0.854443324 0.854443328 -0.000000819 -0.0000000529 -0.00000000335

1.3 0.7915 81155 0.791581218 0.791581222 -0.000000753 -0.0000000495 -0.00000000316

1.4 0.7346 80497 0.734680538 0.734680541 -0.000000523 -0.0000000359 -0.00000000233

1.5 0.6832 88034 0.683288051 0.683288052 -0.000000224 -0.0000000178 -0.00000000122

1.6 0.6369 37046 0.636937040 0.636937040 0.000000079 0.0000000006 -0.00000000009

1.7 0.5951 53053 0.595153029 0.595153028 0.000000351 0.0000000171 0.00000000093

1.8 0.5574 69558 0.557469522 0.557469520 0.000000578 0.0000000309 0.00000000179

1.9 0.5234 43129 0.523443084 0.523443081 0.000000760 0.0000000421 0.00000000248

2.0 0.4926 63789 0.492663738 0.492663736 0.000000902 0.0000000508 0.00000000302

Approximate Solutions Residuals

Section 3.3

The Ru nge–Kutta Method

35

3.3.12.

x h D 0:1 h D 0:05 h D 0:025 “Exact"

1.0 0.000000000 0.000000000 0.000000000 0.000000000

1.1 -0.099663901 -0.099663994 -0.099664000 -0.099664000

1.2 -0.197315322 -0.197315504 -0.197315516 -0.197315517

1.3 -0.291035700 -0.291035983 -0.291036001 -0.291036003

1.4 -0.379167790 -0.379168194 -0.379168220 -0.379168221

1.5 -0.460450005 -0.460450552 -0.460450587 -0.460450590

1.6 -0.534084875 -0.534085579 -0.534085623 -0.534085626

1.7 -0.599736802 -0.599737663 -0.599737717 -0.599737720

1.8 -0.657472724 -0.657473726 -0.657473788 -0.657473792

1.9 -0.707669346 -0.707670460 -0.707670529 -0.707670533

2.0 -0.750911103 -0.750912294 -0.750912367 -0.750912371

3.3.14.

Runge–Kutta method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 2.000000000 2.000000000 2.000000000 2.000000000

2.1 2.464113907 2.464119185 2.464119544 2.464119569

2.2 3.029389360 3.029402271 3.029403150 3.029403212

2.3 3.718384519 3.718408199 3.718409812 3.718409925

2.4 4.558632516 4.558671116 4.558673746 4.558673929

2.5 5.583745479 5.583804456 5.583808474 5.583808754

2.6 6.834762639 6.834849135 6.834855028 6.834855438

2.7 8.361796619 8.361919939 8.361928340 8.361928926

2.8 10.226 043942 10.226216159 10.226227891 10.226228709

2.9 12.502 240429 12.502477158 12.502493285 12.502494409

3.0 15.281 660036 15.281981407 15.282003300 15.282004826

Runge–Kutta semilinear method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 2.000000000 2.000000000 2.000000000 2.000000000

2.1 2.464119623 2.464119573 2.464119570 2.464119569

2.2 3.029403325 3.029403219 3.029403212 3.029403212

2.3 3.718410105 3.718409936 3.718409925 3.718409925

2.4 4.558674188 4.558673945 4.558673930 4.558673929

2.5 5.583809105 5.583808776 5.583808755 5.583808754

2.6 6.834855899 6.834855467 6.834855440 6.834855438

2.7 8.361929516 8.361928963 8.361928928 8.361928926

2.8 10.226229456 10.226228756 10.226228712 10.226228709

2.9 12.502495345 12.502494468 12.502494413 12.502494409

3.0 15.282005990 15.282004899 15.282004831 15.282004826

3.3.16.

Runge–Kutta method

x h D 0:2 h D 0:1 h D 0:05 “Exact"

1.0 2.0000 00000 2.000000000 2.000000000 2.000000000

1.2 1.8016 36785 1.801636775 1.801636774 1.801636774

1.4 1.6501 02633 1.650102617 1.650102616 1.650102616

1.6 1.5269 35904 1.526935886 1.526935885 1.526935885

1.8 1.4220 74302 1.422074284 1.422074283 1.422074283

2.0 1.3296 64970 1.329664954 1.329664953 1.329664953

2.2 1.2461 55357 1.246155345 1.246155344 1.246155344

2.4 1.1693 34355 1.169334347 1.169334346 1.169334346

2.6 1.0978 12074 1.097812070 1.097812069 1.097812069

2.8 1.0307 19113 1.030719114 1.030719114 1.030719114

3.0 0.9675 23147 0.967523152 0.967523153 0.967523153

36 Chapter 3

Numerical Methods

Runge–Kutta semilinear method

x h D 0 :2 h D 0:1 h D 0:05 “E xact"

1.0 2.000000000 2.000000000 2.000000000 2.00000 0000

1.2 1.801636785 1.801636775 1.801636774 1.80163 6774

1.4 1.650102633 1.650102617 1.650102616 1.65010 2616

1.6 1.526935904 1.526935886 1.526935885 1.52693 5885

1.8 1.422074302 1.422074284 1.422074283 1.42207 4283

2.0 1.329664970 1.329664954 1.329664953 1.32966 4953

2.2 1.246155357 1.246155345 1.246155344 1.24615 5344

2.4 1.169334355 1.169334347 1.169334346 1.16933 4346

2.6 1.097812074 1.097812070 1.097812069 1.09781 2069

2.8 1.030719113 1.030719114 1.030719114 1.03071 9114

3.0 0.967523147 0.967523152 0.967523153 0.96752 3153

3.3.18.

Runge–Kutta method

x h D 0:2 h D 0:1 h D 0:05 “Exact"

0.0 1.0000 00000 1.000000000 1.000000000 1.000000000

0.2 1.1715 15610 1.171515156 1.171515152 1.171515153

0.4 1.2633 65845 1.263370556 1.263370869 1.263370891

0.6 1.2712 38957 1.271250529 1.271251232 1.271251278

0.8 1.2188 85528 1.218900353 1.218901230 1.218901287

1.0 1.1353 46772 1.135361174 1.135362016 1.135362070

1.2 1.0420 49558 1.042061864 1.042062579 1.042062625

1.4 0.9511 81964 0.951191920 0.951192495 0.951192532

1.6 0.8683 72923 0.868380842 0.868381298 0.868381328

1.8 0.7955 11927 0.795518241 0.795518603 0.795518627

2.0 0.7326 33229 0.732638318 0.732638609 0.732638628

Runge–Kutta semilinear method

x h D 0 :2 h D 0:1 h D 0:05 “E xact"

0.0 1.000000000 1.000000000 1.000000000 1.00000 0000

0.2 1.171517316 1.171515284 1.171515161 1.17151 5153

0.4 1.263374485 1.263371110 1.263370904 1.26337 0891

0.6 1.271254636 1.271251485 1.271251291 1.27125 1278

0.8 1.218903802 1.218901442 1.218901297 1.21890 1287

1.0 1.135363869 1.135362181 1.135362077 1.13536 2070

1.2 1.042063952 1.042062706 1.042062630 1.04206 2625

1.4 0.951193560 0.951192595 0.951192536 0.95119 2532

1.6 0.868382157 0.868381378 0.868381331 0.86838 1328

1.8 0.795519315 0.795518669 0.795518629 0.79551 8627

2.0 0.732639212 0.732638663 0.732638630 0.73263 8628

3.3.20.

Runge–Kutta method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

0.0 1.0000 00000 1.000000000 1.000000000 1.000000000

0.1 0.7464 30962 0.746418992 0.746418376 0.746418339

0.2 0.5617 61987 0.561743921 0.561742975 0.561742917

0.3 0.4237 46057 0.423725371 0.423724274 0.423724207

0.4 0.3194 89811 0.319468612 0.319467478 0.319467408

0.5 0.2404 86460 0.240466046 0.240464947 0.240464879

0.6 0.1806 46105 0.180627244 0.180626225 0.180626161

0.7 0.1354 12569 0.135395665 0.135394749 0.135394692

0.8 0.1013 08709 0.101293911 0.101293107 0.101293057

0.9 0.0756 63769 0.075651059 0.075650367 0.075650324

1.0 0.0564 26886 0.056416137 0.056415552 0.056415515

Section 3.3

The Ru nge–Kutta Method

37

Runge–Kutta semilinear method

x h D 0 :1 h D 0:05 h D 0:025 “Exact"

0.0 1.000000000 1.000000000 1.000000000 1.00000 0000

0.1 0.746416306 0.746418217 0.746418332 0.74641 8339

0.2 0.561740647 0.561742780 0.561742908 0.56174 2917

0.3 0.423722193 0.423724084 0.423724199 0.42372 4207

0.4 0.319465760 0.319467308 0.319467402 0.31946 7408

0.5 0.240463579 0.240464800 0.240464874 0.24046 4879

0.6 0.180625156 0.180626100 0.180626158 0.18062 6161

0.7 0.135393924 0.135394645 0.135394689 0.13539 4692

0.8 0.101292474 0.101293021 0.101293055 0.10129 3057

0.9 0.075649884 0.075650297 0.075650322 0.07565 0324

1.0 0.056415185 0.056415495 0.056415514 0.05641 5515

3.3.22.

Runge–Kutta method

x h D 0:1 h D 0:05 h D 0:025 “Exact"

2.0 1.0000 00000 1.000000000 1.000000000 1.000000000

2.1 1.0089 12398 1.008900636 1.008900025 1.008899988

2.2 1.0317 40789 1.031724368 1.031723520 1.031723469

2.3 1.0637 81819 1.063765150 1.063764295 1.063764243

2.4 1.1016 30085 1.101615517 1.101614774 1.101614730

2.5 1.1429 15917 1.142904393 1.142903811 1.142903776

2.6 1.1860 47678 1.186039295 1.186038876 1.186038851

2.7 1.2299 91054 1.229985469 1.229985194 1.229985178

2.8 1.2740 95992 1.274092692 1.274092535 1.274092525

2.9 1.3179 69153 1.317967605 1.317967537 1.317967533

3.0 1.3613 84082 1.361383812 1.361383809 1.361383810

Runge–Kutta semilinear method

x h D 0 :1 h D 0:05 h D 0:025 “Exact"

2.0 1.000000000 1.000000000 1.000000000 1.00000 0000

2.1 1.008913934 1.008900843 1.008900041 1.00889 9988

2.2 1.031748526 1.031725001 1.031723564 1.03172 3469

2.3 1.063798300 1.063766321 1.063764371 1.06376 4243

2.4 1.101656264 1.101617259 1.101614886 1.10161 4730

2.5 1.142951721 1.142906691 1.142903955 1.14290 3776

2.6 1.186092475 1.186042105 1.186039051 1.18603 8851

2.7 1.230043983 1.229988742 1.229985397 1.22998 5178

2.8 1.274156172 1.274096377 1.274092762 1.27409 2525

2.9 1.318035787 1.317971658 1.317967787 1.31796 7533

3.0 1.361456502 1.361388196 1.361384079 1.36138 3810

3.3.24.

x h D :1 h D :0 5 h D :025 Exact

1.00 0.142854841 0.142857001 0.142857134 0.142857143

1.10 0.053340745 0.053341989 0.053342066 0.053342071

1.20 -0.046154629 -0.046153 895 -0.046 153849 -0.046153846

1.30 -0.153363206 -0.153362 764 -0.153 362736 -0.153362734

1.40 -0.266397049 -0.266396 779 -0.266 396762 -0.266396761

1.50 -0.383721107 -0.383720 941 -0.383 720931 -0.383720930

1.60 -0.504109696 -0.504109 596 -0.504 109589 -0.504109589

1.70 -0.626598326 -0.626598 268 -0.626 598264 -0.626598264

1.80 -0.750437351 -0.750437 320 -0.750 437318 -0.750437318

1.90 -0.875050587 -0.875050 574 -0.875 050573 -0.875050573

2.00 -1.000000000 -1.000000 000 -1.000 000000 -1.000000000

38 Chapter 3

Numerical Methods

3.3.26.

x h D :1 h D :0 5 h D :025 Exact

0.50 -8.954103230 -8.954063 245 -8.954 060698 -8.954060528

0.60 -5.059648314 -5.059633 293 -5.059 632341 -5.059632277

0.70 -2.516755942 -2.516749 850 -2.516 749465 -2.516749439

0.80 -0.752508672 -0.752506 238 -0.752 506084 -0.752506074

0.90 0.530528482 0.530529270 0.530529319 0.530529323

1.00 1.500000000 1.500000000 1.500000000 1.500000000

1.10 2.256519743 2.256519352 2.256519328 2.256519326

1.20 2.863543039 2.863542454 2.863542417 2.863542415

1.30 3.362731379 3.362730700 3.362730658 3.362730655

1.40 3.782361948 3.782361231 3.782361186 3.782361183

1.50 4.142171279 4.142170553 4.142170508 4.142170505

3.3.28. (a) Let x

i

D a C ih, i D 0; 1; : : : ; n. If y is the solution of the initial value problem

y

0

D f .x/, y.a/ D 0, then y.b/ D

R

b

a

f .x/ dx. The Runge-Kutta method y ields y

iC1

D y

i

C

h

6

.f .a C ih/ C 4f .a C .2i C 1/h=2/ Cf .a C .i C 1/h//, i D 0; 1; : : : ; n  1, where y

0

D a and y

n

is an approximation to

Z

b

a

f .x/ dx. But

y

n

D

n1

X

iD0

.y

iC1

 y

i

/ D

h

6

.f .a/ C f .b// C

h

3

n1

X

iD1

f .a C ih/ C

2h

3

n

X

iD1

f .a C .2i  1/h=2/ :

(c) The local truncation error is a multiple of y

.5/

. Qx

i

/ D f

.4/

. Qx

i

/, where x

i

< Qx

i

< x

iC1

. Therefore,

the quadrature formula is exact if f is a polynomial of degree < 4.

(d) Let E.f / D

Z

b

a

f .x/ dx  y

n

. Note that E is linear. If f is a polynomial of degree 4, then

f .x/ D f

0

.x/ C K.x  a/

4

where deg.f

0

/  3 and K is constant. Since E.f

0

/ D 0 from (c) and

E..x  a/

4

/ D

.b  a/

5



.b  a/

4

h

6



h

5

3

n1

X

iD1

i

4



2h

5

3

n

X

iD1

.i  1=2/

4

D h

5



n

5



n

4

6





n

5

15



n

4

6

C

n

3

9



n

90







2n

5

15



n

3

9

C

7n

360



D 

nh

5

120

D 

.b  a/h

4

120

;

E.f / D 

.b  a/h

4

120

; thus, the error is proportional to h

4

.

CHAPTER 4

Applications of First Order Equations

4.1 GROWTH AND DECAY

4.1.2. k D ln 2 and  D 2 ) k D

ln 2

2

; Q.t/ D Q

0

e

t ln 2=2

; if Q.T / D

Q

0

10

, then

Q

0

10

D

Q

0

e

T ln 2=2

; ln 10 D

T ln 2

2

; T D

2 ln 10

ln 2

days.

4.1.4. Let t

1

be the elapsed time since the tree died. Since p.t/ D e

.t ln 2/

, it follows that p

1

D

p

0

e

.t

1

ln 2/=

, so ln



p

1

p

0



D 

t

1



ln 2 and t

1

D 

ln.p

0

=p

1

/

ln 2

.

4.1.6. Q D Q

0

e

kt

; Q

1

D Q

0

e

kt

1

; Q

2

D Q

0

e

kt

2

;

Q

2

Q

1

D e

k.t

2

t

1

/

; ln



Q

1

Q

2



D k.t

2

 t

1

/;

k D

1

t

2

 t

1

ln



Q

1

Q

2



.

4.1.8. Q

0

D :06Q; Q.0/ D Q

0

; Q D Q

0

e

:06t

. We must ﬁnd  such that Q./ D 2Q

0

; that is,

Q

0

e

:06

D 2Q

0

, so :06 D ln 2 and  D

ln 2

:06

D

50 ln2

3

yr.

4.1.10. (a) If T is the time to triple the value, then Q.T / D Q

0

e

:05T

D 3Q

0

, so e

:05T

D 3. Therefore,

:05T D ln 3 and T D 20 ln 3.

(b) If Q.10/ D 100000, then Q

0

e

:5

D 100000, so Q

0

D 100000e

:5

4.1.12. Q

0

D 

Q

2

; Q.0/ D 50;

Q

0

Q

2

D 

1

2

; 

1

Q

D 

t

2

C c; Q.0/ D 50 ) c D 

1

50

;

1

Q

D

t

2

C

1

50

D

1 C 25t

50

; Q D

50

1 C 25t

. Now Q.T / D 25 ) 1 C25T D 2 ) 25T D 1 ) T D

1

25

years.

4.1.14. Since  D 1500, k D

ln 2

1500

; hence Q D Q

0

e

.t ln 2/=1500

. If Q.t

1

/ D

3Q

0

4

, then e

.t

1

ln 2/=1500

D

3

4

; t

1

ln 2

1500

D ln



3

4



D ln



4

3



; t

1

D 1500

ln



4

3



ln 2

. Finally, Q.2000/ D Q

0

e



4

3

ln 2

D 2

4=3

Q

0

.

39

40 Chapter 4

Applications of First Order Equations

4.1.16. (A) S

0

D 1 

S

10

; S.0/ D 20. Rewrite the differential equation in (A) as (B) S

0

C

S

10

D 1. Since

S

1

D e

t=10

is a solution of the complementary equation, the so lutions of (B) are given by S D ue

t=10

,

where u

0

e

t=10

D 1. Therefore, u

0

D e

t=10

; u D 10e

t=10

C c; S D 10 C ce

t=10

. Now S.0/ D 20 )

c D 10, so S D 10 C 10e

t=10

and lim

t!1

S.t/ D 10 g.

4.1.18. (A) V

0

D 750 C

V

20

; V .0/ D 25000. Rewrite the differential equatio n in (A) as (B) V

0



V

20

D 750. Since V

1

D e

t=20

is a solution of the complementary equation, the solutions of (B) are

given by V D ue

t=20

, wher e u

0

e

t=20

D 750. Therefore, u

0

D 750e

t=20

; u D 15000e

t=20

C c;

V D 15000 C ce

t=20

; V .0/ D 25000 ) c D 10000. Therefore, V D 15000 C10000e

t=20

.

4.1.20. p

0

D

p

2



p

2

8

D 

1

8

p.p4/;

p

0

p.p  4/

D 

1

8

;

1

4



1

p  4



1

p



p

0

D 

1

8

;



1

p  4



1

p



p

0

D



1

2

;

ˇ

p  4

p



D 

t

2

C k;

p  4

p

D ce

t=2

; p.0/ D 100 ) c D

24

25

;

p  4

p

D

24

25

e

t=2

; p  4 D

24

25

pe

t=2

; p



1 

24

25

e

t=2



D 4; p D

4

1 

24

25

e

t=2

D

100

24  24e

t=2

.

4.1.22. (a)P

0

D rP  12M .

(b) P D ue

rt

; u

0

e

rt

D 12M ; u

0

D 12Me

rt

; u D

12M

r

e

rt

C c; P D

12M

r

C ce

rt

; P .0/ D

P

0

) c D P

0



12M

r

; P D

12M

r

.1  e

rt

/ C P

0

e

rt

.

(c) Since P .N / D 0, the answer to (b) implies that M D

rP

0

12.1 e

rN

/

4.1.24. The researcher’s salary is the solution of the initial value problem S

0

D aS; S.0/ D S

0

.

Therefore, S D S

0

e

at

. If P D P .t/ is the value of the trust fund, then P

0

D S

0

e

at

C rP , or

P

0

 rP D S

0

e

at

. Therefore, (A) P D ue

rt

, wher e u

0

e

rt

D S

0

e

at

, so (B) u

0

D S

0

e

.ar/t

. If

a ¤ r , then (B) implies that u D

S

0

r  a

e

.ar/t

C c, so (A) implies that P D

S

0

r  a

e

at

C ce

rt

. Now

P.0/ D P

0

) c D P

0



S

0

r  a

; therefore P D

S

0

r  a

e

at

C



P

0



S

0

r  a



e

rt

. We must choose

P

0

so th at P .T / D 0; that is, P D

S

0

r  a

e

aT

C



P

0



S

0

r  a



e

rT

D 0. Solving this for P

0

yields

P

0

D

S

0

.1  e

.ar/T

/

r  a

. If a D r, then (B) becomes u

0

D S

0

, so u D S

0

t C c and (A) implies th at

P D .S

0

t C c/e

rt

. Now P .0/ D P

0

) c D P

0

; th erefore P D .S

0

t C P

0

/e

rt

. To make P .T / D 0

we must take P

0

D S

0

T .

4.1.26. Q

0

D

at

1 C btQ

2

 kQ; lim

t!1

Q.t/ D .a=bk/

1=3

.

4.2 COOLING AND MIXING

4.2.2. Since T

0

D 100 and T

M

D 10, T D 10 C 110e

kt

. Now T .1/ D 80 ) 80 D 10 C110e

k

,

so e

k

D

9

11

and k D ln

11

9

. Therefore, T D 10 C 110e

t ln

11

9

.

4.2.4. Let T be the thermometer reading. Since T

0

D 212 and T

M

D 70, T D 70 C 142e

kt

. N ow

T .2/ D 125 ) 125 D 70 C 142e

2k

, so e

2k

D

55

142

and k D

1

2

ln

142

55

. Therefore, (A) T D

Section 4.2

Cooling and Mixing

41

70 C 142e



t

2

ln

142

55

.

(a) T .2/ D 70 C 142e

2ln

142

55

D 70 C 142



55

142



2

 91:30

ı

F.

(b) Let  be the time when T ./ D 72, so 72 D 70 C 142e





2

ln

142

55

, or e





2

ln

142

55

D

1

71

. Therefore,

 D 2

ln 71

ln

142

55

 8:99 min.

(c) Since (A) implies that T > 70 for all t > 0, the thermometer will never read 69

ı

F.

4.2.6. Since T

M

D 20, T D 20 C .T

0

 20/e

kt

. Now T

0

 5 D 20 C .T

0

 20/e

4k

and T

0

 7 D

20 C.T

0

20/e

8k

. Therefore,

T

0

 25

T

0

 20

D e

4k

and



T

0

 27

T

0

 20



D e

8k

, so

T

0

 27

T

0

 20

D



T

0

 25

T

0

 20



2

,

which implies that .T

0

 20/.T

0

 27/ D .T

0

 25/

2

, or T

2

0

 47T

0

C 540 D T

2

0

 50T

0

C 625; hence

3T

0

D 85 and T

0

D .85=3/

ı

C .

4.2.8. Q

0

D 3 

3

40

Q; Q.0/ D 0. Rewrite the differential equation as (A) Q

0

C

3

40

Q D 3. Since

Q

1

D e

3t=40

is a solution of the complementary equation, the solutions of (A) are given by Q D

ue

3t=40

where u

0

e

3t=40

D 3. Therefore,u

0

D 3e

3t=40

, u D 40e

3t=40

C c, and Q D 40 C ce

3t=40

.

Now Q.0/ D 0 ) c D 40, so Q D 40.1  e

3t=40

/.

4.2.10. Q

0

D

3

2



Q

20

; Q.0/ D 10. Rewrite the differential equation as (A) Q

0

C

Q

20

D

3

2

. Since

Q

1

D e

t=20

is a solution of the complementary equation, the solutio ns o f (A) are given by Q D ue

t=20

where u

0

e

t=20

D

3

2

. Therefore,u

0

D

3

2

e

t=20

, u D 30e

t=20

C c, and Q D 30 C ce

t=20

. Now

Q.0/ D 10 ) c D 20, so Q D 30  20e

t=20

and K D

Q

100

D :3  :2e

t=20

.

4.2.12. Q

0

D 10 

Q

5

, or (A) Q

0

C

Q

5

D 10. Since Q

1

D e

t=5

is a solution of the complementary

equation, the solutions of (A) are given by Q D ue

t=5

where u

0

e

t=5

D 10. Therefore,u

0

D 10e

t=5

,

u D 50e

t=10

C c, and Q D 50 C ce

t=5

. Since lim

t!1

Q.t/ D 50, the mininum capacity is 50 gallons.

4.2.14. Since there are 2t C 600 gallons of mixture in the tank at time t and mixture is bein g drained

at 4 gallons/min, Q

0

D 3 

2

t C 300

Q; Q.0/ D 40. Rewrite the di fferential equation as (A) Q

0

C

2

t C 300

Q D 3. Since Q

1

D

1

.t C 300/

2

is a solution of the complementary equation, the solutions

of (A) are given b y Q D

u

.t C 300/

2

where

u

0

.t C 300/

2

D 3. Therefore, u

0

D 3.t C 300/

2

, u D

.t C 300/

3

C c, and Q D t C 300 C

c

.t C 300/

2

. Now Q.0/ D 40 ) c D 234  10

5

, so Q D

t C 300 

234  10

5

.t C 300/

2

; 0  t  300.

4.2.16. (a ) S

0

D k

m

.S  T

m

/; S.0/ D 0, so (A) S D T

m

C .S

0

 T

m

/e

k

m

t

. T

0

D k.T  S/ D

k



T  T

m

 .S

0

 T

m

/e

k

m

t



, from (A). Therefore,T

0

CkT D kT

m

Ck.S

0

T

m

/e

k

m

t

; T D ue

kt

;

(B) u

0

D kT

m

e

kt

C k.S

0

 T

m

/e

.kk

m

/t

; u D T

m

e

kt

C

k

k  k

m

.S

0

 T

m

/e

.kk

m

/t

Cc; T .0/ D T

0

)

c D T

0

T

m



k

k  k

m

.S

0

T

m

/; u D T

m

e

kt

C

k

k  k

m

.S

0

T

m

/e

.kk

m

/t

CT

0

T

m



k

k  k

m

.S

0

T

m

/;

42 Chapter 4

Applications of First Order Equations

T D T

m

C .T

0

 T

m

/e

kt

C

k.S

0

 T

m

/

.k  k

m

/



e

k

m

t

 e

kt



.

(b) If k D k

m

(B) becomes (B) u

0

D kT

m

e

kt

Ck.S

0

T

m

/; u D T

m

e

kt

Ck.S

0

T

m

/t C c; T .0/ D

T

0

) c D T

0

T

m

; u D T

m

e

kt

Ck.S

0

T

m

/t C.T

0

T

m

/; T D T

m

Ck.S

0

T

m

/te

kt

C.T

0

T

m

/e

kt

.

(c) lim

t!1

T .t/ D lim

t!1

S.t/ D T

m

in either case.

4.2.18. V

0

D aV  bV

2

D bV .V  b=a/;

V

0

V .V  a=b/

D b;



1

V  a=b



1

V



V

0

D a;

ln

ˇ

V  a=b

V

ˇ

D at C k; (A)

V  a=b

V

D ce

at

; (B) V D

a

b

1

1  ce

at

. Since V .0/ D V

0

, (A)

) c D

V

0

 a=b

V

0

. Substituting this into (B) yi el ds V D

a

b

V

0

V

0

 .V

0

 a=b/ e

at

so l im

t!1

V .t/ D

a=b

4.2.20. If Q

n

.t/ is the number of pounds of salt in T

n

at time t, then Q

0

nC1

C

r

W

Q

nC1

D rc

n

.t/; n D

0; 1; : : : , wher e c

0

.t/  c. Therefore,Q

nC1

D u

nC1

e

rt=w

; (A) u

0

nC1

D re

rt=W

c

n

.t/. In particular,

with n D 0, u

1

D cW.e

rt=W

 1/, so Q

1

D cW.1  e

rt=W

/ and c

1

D c.1  e

rt=W

/. We will shown

by induction that c

n

D c

0

@

1  e

rt=W

n1

X

j D0

1

j Š



rt

W



j

1

A

. This is true for n D 1; if it is true for a given n,

then, from (A),

u

0

nC1

D c re

rt=W

0

@

1  e

rt=W

n1

X

j D0

1

j Š



rt

W



j

1

A

D cr e

rt=W

 cr

n1

X

j D0

1

j Š



rt

W



j

;

so (since Q

nC1

.0/ D 0),

u

nC1

D cW.e

rt=W

 1/  c

n1

X

j D0

1

.j C 1/Š

r

j C1

W

j

t

j C1

:

Therefore,

c

nC1

D

1

W

u

nC1

e

rt=W

D c

0

@

1  e

rt=W

n

X

j D0

1

j Š



rt

W



j

1

A

;

which completes the induct ion. From this, lim

t!1

c

n

.t/ D c.

4.2.22. Since the incoming solution cont ai ns 1/2 lb of salt per gallo n and there are always 600 gal-

lons i n the tank, we conclude in tuitively that lim

t!1

Q.t/ D 300. To verify this rigorously, note

that Q

1

.t/ D exp





1

150

Z

t

0

a./ d 



is a solution of the complementary equation, (A) Q

1

.0/ D 1,

and (B) lim

t!1

Q

1

.t/ D 0 (since lim

t!1

a.t/ D 1). Therefore,Q D Q

1

u; Q

1

u

0

D 2; u

0

D

2

Q

1

; u D Q

0

C 2

Z

t

0

d 

Q

1

./

(see (A)), and Q.t/ D Q

0

Q

1

.t/ C 2Q

1

.t/

Z

t

0

d 

Q

1

./

. From (B),

lim

t!1

Q.t/ D 2 li m

t!1

Q

1

.t/

Z

t

0

d 

Q

1

./

, a 0  1 indeterminate form. By L’Hospital’s rule, lim

t!1

Q.t/ D

2 lim

t!1

1

Q

1

.t/



Q

0

1

.t/

Q

2

1

.t/



D 2 lim

t!1

Q

1

.t/

Q

0

1

.t/

D 300.

vspace*10pt

Section 4.3

Elementary Mechanics

43

4.3 ELEMENTARY MECHANICS

4.3.2. The ﬁreﬁghter’s mass is m D

192

32

D 6 sl, so 6v

0

D 192  kv, or (A) v

0

C

k

6

v D 32.

Since v

1

D e

kt= 6

is a solution of the complementary equat ion, the solutions of (A) are v D ue

kt= 6

where u

0

e

kt= 6

D 32. Therefore,u

0

D 32e

kt=6

; u D 

192

k

e

kt=6

C c; v D 

192

k

C ce

kt= 6

. Now

v.0/ D 0 ) c D

192

k

. Therefore,v D 

192

k

.1  e

kt= 6

/ and lim

t!1

v.t/ D 

192

k

D 16 ft/s, so

k D 12 lb-s/ft and v D 16.1  e

2t

/.

4.3.3. m D

64000

32

D 2000, so 2000v

0

D 500002000v, or (A) v

0

Cv D 25. Since v

1

D e

t

is a solution

of the complementary equation, the solutions of (A) are v D ue

t

where u

0

e

t

D 25. Therefore,u

0

D

25e

t

; u D 25e

t

C c; v D 25 C ce

t

. Now v.0/ D 0 ) c D 25. Therefore,v D 25.1  e

t

/ and

lim

t!1

v.t/ D 25 ft/s.

4.3.4. 20v

0

D 10 

1

2

v, or (A) v

0

C

1

20

v D

1

2

. Since v

1

D e

t=40

is a solution of the compl ementary

equation, the solut ions of (A) are v D ue

t=40

where u

0

e

t=40

D

1

2

. Therefore,u

0

D

e

t=40

2

; u D

20e

t=40

C c; v D 20 C ce

t=40

. Now v.0/ D 7 ) c D 27. Therefore,v D 20  27e

t=40

.

4.3.6. m D

3200

32

D 100 sl. The component of the gravitational force in the dir ection of motion is

3200 cos.=3/ D 1600 lb. Therefore, 100v

0

D 1600Cv

2

. Separating variables yields

v

0

.v  40/.v C 40/

D

1

100

, or



1

v  40



1

v C 40



D

4

5

. Therefore, ln

ˇ

v  40

v C 40

ˇ

D

4t

5

Ck and

v  40

v C 40

D ce

4t=5

. Now v.0/ D

64 ) c D

13

3

; th erefore

v  40

v C 40

D

13e

4t=5

3

, so v D

40.3 C 13e

4t=5

/

3  13e

4t=5

, o r v D 

40.13 C 3e

4t=5

/

13  3e

4t=5

.

4.3.8. Fr om Example 4.3.1, (A) v D 

mg

k

C



v

0

C

mg

k



e

kt=m

. Integrat ing this yields (B) y D



mgt

k



m

k



v

0

C

mg

k



e

kt=m

C c. N ow y.0/ D y

0

) c D y

0

C

m

k



v

0

C

mg

k



. Substituting this

into (B) yields

y D 

mgt

k



m

k



v

0

C

mg

k



e

kt=m

C y

0

C

m

k



v

0

C

mg

k



D y

0

C

m

k



v

0

 gt C

mg

k





v

0

C

mg

k



e

kt=m



D y

0

C

m

k

.v

0

 v  gt/

where the last equality follows from (A).

4.3.10. m D

256

32

D 8 sl. Since the resisting force is 1 lb when jvj D 4 ft/s, k D

1

16

. Therefore,

8v

0

D 256 C

1

16

v

2

D

1

16



v

2

 .64/

2



. Separating variables yields

v

0

.v  64/.v C 64/

D

1

128

, or



1

v  64



1

v C 64



v

0

D 1. Therefore,ln

ˇ

v  64

v C 64

ˇ

D t C k and

v  64

v C 64

D ce

t

. Now v.0/ D 0 ) c D

1; therefore

v  64

v C 64

D e

t

, so v D

64.1  e

t

/

1 C e

t

, or v D 

64.1 e

t

/

1 C e

t

. Therefore, lim

t!1

v.t/ D

64.

44 Chapter 4

Applications of First Order Equations

4.3.12. (a) mv

0

D mg  kv

2

D mg.1 C 

2

v

2

/, where  D

s

k

mg

. Therefore,(A)

v

0

1 C 

2

v

2

D g.

With the substitution u D  v,

Z

dv

1 C 

2

v

2

D

1



Z

du

1 C u

2

D

1



tan

1

u D

1



tan

1

.v/. There-

fore,

1



tan

1

.v/ D gt C c. Now v.0/ D v

0

) c D

1



tan

1

.v

0

/, so

1



tan

1

.v/ D gt C

1



tan

1

.v

0

/. Since v.T / D 0, it follows that T D

1

g

tan

1

v

0

D

r

m

kg

tan

1

v

0

s

k

mg

!

.

(b) Replacing t by t  T and setting v

0

D 0in the answer to the previou s exercise yields v D



r

mg

k

1  e

2

q

gk

m

.tT /

1 C e

2

q

gk

m

.tT /

.

4.3.14. (a) mv

0

D mg Cf .jvj/; since s D jvj D v, (A) ms

0

D mg  f .s/.

(b) Since f is incr easing and lim

t!1

f .s/  mg, mg  f .s/ > 0 for all s. This and (A) impl y that s

is an increasing function of t , so either (B) lim

t!1

s.t/ D 1 or (C ) lim

t!1

s.t/ D s < 1. However,

(A) and (C) imply that s

0

.t/ > K D g  f .s/=m for all t > 0. Consequently, s.t/ > s

0

C Kt for all

t > 0, which contradicts (C) becau se K > 0.

(c) There is a u nique positive number s

T

such that f .s

T

/ D mg, and s  s

T

is a constant solution of

(A). Now sup pose that s.0/ < s

T

. Then Theorem 2.3.1 implies that (D) s.t/ < s

T

for all t > 0, so (A)

implies that s is strictly increasing. This and (D) imply that lim

t!1

s.t/ D s  s

T

. If s < s

T

then (A)

implies that s

0

.t/ > K D g  f .s/=m. Consequently, s.t/ > s.0/ CKt, which contr adicts (D) because

K > 0. Therefore, s.0/ < s

T

) lim

t!1

s.t/ D s

T

. A similar proof with inequlities reversed shows

that s.0/ > s

T

) lim

t!1

s.t/ D s

T

.

4.3.16. (a) (A) mv

0

D mg C k

p

jvj; since th e magnitude of the resistance is 64 lb when v D 16 ft/s,

4k D 64, so k D 16 lb s

1=2

=ft

1=2

. Since m D 2 and g D 32, (A) becomes 2v

0

D 64 C 16

p

jvj, or

v

0

D 32 C 8

p

jvj.

(b) From Exercise 4.3.14(c), v

T

is the negative number such that 32 C8

p

jv

T

j D 0; thus, v

T

D 16

ft/s.

4.3.18. With h D 0, v

e

D

p

2gR, where R is the radius of th e moo n and g is the acceleration due to

gravity at the moon’s surface. With length in miles, g D

5:31

5280

mi/s

2

, so v

e

D

r

2  5:31  1080

5280

 1:47

miles/s.

4.3.20. Suppose that there is a number y

m

such that y.t/  y

m

for all t  0 and let ˛ D

gR

2

.y

m

C R/

2

.

Then

d

2

y

dt

2

 ˛ for all t  0. Integrating this inequality from t D 0 to t D T > 0 yields v.T /  v

0



˛T , or v.T /  v

0

 ˛T , so v.T / < 0 for T >

v

0

˛

. This implies that the vehicle must eventually fall

back to Earth, which contradicts the assumption that it conti nues to climb forever.

4.4 AUTONOMOUS SECOND ORDER EQUATIONS

4.4.1. y D 0 is a stable equilibriu m. The phase plane equivalent is v

dv

dy

Cy

3

D 0, so t he trajectories are

v

2

C

y

4

D c.

Section 4.4

Autonomous Second Order Equations

45

4.4.2. y D 0 is an unstable equilibrium. The phase plane equivalent is v

dv

dy

Cy

2

D 0, so the trajectories

are v

2

C

2y

3

D c.

4.4.4. y D 0 is a stabl e equilibriu m. The phase plane equivalent is v

dv

dy

C ye

y

D 0, so the trajectories

are v

2

 e

y

.y C 1/ D c.

4.4.6. p.y/ D y

3

 4y D .y C 2/y.y  2/, so the equilibria are 2; 0; 2. Since

y.y  2/.y C 2/ < 0 if y < 2 or 0 < y < 2;

> 0 if  2 < y < 0 or y > 2;

0 is unstabl e and 2; 2 are stable. The phase plane equivalent i s v

dv

dy

C y

3

 4y D 0, so the traject ories

are 2v

2

C y

4

 8y

2

D c. Setti ng .y; v/ D .0; 0/ yiel ds c D 0, so the equation of the separatrix is

2v

2

 y

4

C 8y

2

D 0.

4.4.8. p.y/ D y.y  2/.y  1/.y C 2/, so the equilibria are 2; 0; 1; 2. Since

y.y  2/.y  1/.y C 2/ > 0 if y < 2 or 0 < y < 1 or y > 2;

< 0 if  2 < y < 0 or 1 < y < 2;

0; 2 are stable and 2; 1 are unstable. The phase plane equivalent is v

dv

dy

Cy.y2/.y1/.yC2/ D 0, so

the trajectories are 30v

2

Cy

2

.12y

3

15y

2

80yC120/ D c. Setting .y; v/ D .2; 0/ and .y; v/ D .1; 0/

yields c D 496 and c D 37 respectively, so the equations of the separatrices are 30v

2

Cy

2

.12y

3

15y

2



80y C 120/ D 496 and 30v

2

C y

2

.12y

3

 15y

2

 80y C 120/ D 37.

4.4.10. p.y/ D y

3

 ay. If a  0, then p.0/ D 0, p.y/ > 0 if y > 0, and p.y/ < 0 if y < 0, so 0 is

stable. If a > 0, then

y

3

 ay D y.y 

p

a/.y C

p

a/ > 0 if 

p

a < y < 0 or y >

p

a;

< 0 if y < 

p

a or 0 < y <

p

a;

so 

p

a and

p

a are stable and 0 is unstable. We say that a D 0 is a critical value because it separates

the two cases.

4.4.12. p.y/ D y  ay

3

. If a  0, then p.0/ D 0, p.y/ > 0 if y > 0, and p.y/ < 0 if y < 0, so 0 is

stable. If a > 0, then

y  ay

3

D ay.y  1=

p

a/.y C 1=

p

a/ > 0 if y < 1=

p

a < y < 0 o r 0 < y < 1=

p

a

< 0 if  1=

p

a < y < 0 or y > 1=

p

a;

so 

p

a and

p

a are u nstable and 0 is stable. We say that a D 0 is a critical value becau se it separates

the two cases.

4.4.24. (a) Since v

0

D p.y/  k and v.0/ D 0, v  kt and theref ore y  y

0

C kt

2

=2 for 0  t < T .

(b) Let 0 <  < . Supp ose that y is the solution of the initial value problem (A) y

00

C p.y/ D

0; y.0/ D y

0

; y

0

.0/ D 0, where y < y

0

< y C . Now let Y D y  y and P .Y / D p.Y C

y/. Then P.0/ D 0 and P .Y / < 0 if 0 < Y   . Morover, Y is the solution of Y

00

C p.Y / D

46 Chapter 4

Applications of First Order Equations

0; Y.0/ D Y

0

; Y

00

.0/ D 0, where Y

0

D y

0

 y, so 0 < Y

0

< . From (a), Y.t/   for some t > 0.

Therefore,y.t/ > y C  for some t > 0, so y is an unstable equilibrium of y

00

C p.y/ D 0.

4.5 APPLICATIONS TO CURVES

4.5.2. Differentiating (A) e

xy

D cy yields (B) .xy

0

C y/e

xy

D cy

0

. From (A), c D

e

xy

y

. Substituting

this into (B) and cancelling e

xy

yields xy

0

C y D

y

0

y

, so y

0

D 

y

2

.xy  1/

.

4.5.4. Solving y D x

1=2

Ccx for c yields c D

y

x

x

1=2

, and differen tiating yields 0 D

y

0

x



y

x

2

C

x

3=2

2

,

or xy

0

 y D 

x

1=2

2

.

4.5.6. Rewrit ing y D x

3

C

c

x

as xy D x

4

C c and differentiating yields xy

0

Cy D 4x

3

.

4.5.8. Rewriting y D e

x

C c.1 C x

2

/ as

y

1 C x

2

D

e

x

1 C x

2

C c and differentiating yields

y

0

1 Cx

2



2xy

.1 C x

2

/

2

D

e

x

1 C x

2



2xe

x

.1 C x

2

/

2

, so .1 Cx

2

/y

0

 2xy D .1  x/

2

e

x

.

4.5.10. If ( A ) y D f C cg, then (B) y

0

D f

0

C cg

0

. Mutiplying (A) by g

0

and (B) by g yields (C)

yg

0

D fg

0

Ccgg

0

and (D) y

0

g D f

0

gCcg

0

g, and subtracting (C) from (D) yi elds y

0

gyg

0

D f

0

gfg

0

.

4.5.12. Let .x

0

; y

0

/ be the center and r be the radius of a circle in the family. Since .1; 0/ and .1; 0/ are

on the circle, .x

0

C 1/

2

C y

2

0

D .x

0

 1/

2

C y

2

0

, which implies that x

0

D 0. Therefore,the equation of

the circle is (A) x

2

C .y  y

0

/

2

D r

2

. Since .1; 0/ is on the circle, r

2

D 1 C y

2

0

. Substituting this int o

(A) shows that the equation of the circle is x

2

Cy

2

2yy

0

D 1, so 2y

0

D

x

2

C y

2

 1

y

. Differentiating

y.2x C 2yy

0

/  y

0

.x

2

C y

2

 1/ D 0, so y

0

.y

2

 x

2

C 1/ C2xy D 0.

4.5.14. From Example 4.5.6 the equation of the line tangent to t he parabola at .x

0

; x

2

0

/ is (A) y D

x

2

0

C2x

0

x.

(a) From (A), .x; y/ D .5; 9/ is on the tangent line t hrough .x

0

; x

2

0

/ if and only if 9 D x

2

0

C 10x

0

,

or x

2

0

 10x

0

C 9 D .x

0

 1/.x

0

 9/ D 0. Letting x

0

D 1 in (A ) yields the line y D 1 C 2x, tangent

to t he parabola at .x

0

; x

2

0

/ D .1; 1/. Letting x

0

D 9 in ( A) yields the line y D 81 C18x, t angen t to the

parabola at .x

0

; x

2

0

/ D .9; 81/.

(b) From (A), .x; y/ D .6; 11/ is on the tangent line thro ugh .x

0

; x

2

0

/ if and only if 11 D x

2

0

C12x

0

,

or x

2

0

12x

0

C11 D .x

0

1/.x

0

11/ D 0. Letti ng x

0

D 1 in (A) yields the line y D 1 C2x, tangent

to the parabola at .x

0

; x

2

0

/ D .1; 1/. Letti ng x

0

D 11 in (A) yields the line y D 121 C 22x, tangent to

the parabola at .x

0

; x

2

0

/ D .11; 21/.

(c) From (A), .x; y/ D .6; 20/ is on the tangent line thro ugh .x

0

; x

2

0

/ if and only if 20 D x

2

0

12x

0

,

or x

2

0

C 12x

0

C 20 D .x

0

C 2/.x

0

C 10/ D 0. Letting x

0

D 2 in (A) yields the line y D 4  4x,

tangent to t he parabola at .x

0

; x

2

0

/ D .2; 4/. Lett ing x

0

D 10 in (A) yields the line y D 100 20x,

tangent to t he parabola at .x

0

; x

2

0

/ D .10; 100/.

(d) From (A), .x; y/ D .3; 5/ is on the tangent l ine through .x

0

; x

2

0

/ if and only if 5 D x

2

0

 6x

0

,

or x

2

0

C6x

0

C5 D .x

0

C1/.x

0

C5/ D 0. Letting x

0

D 1 in (A) yield s the line y D 1 2x, tangent

to t he parabola at .x

0

; x

2

0

/ D .1; 1/. Letting x

0

D 5 in (A) yield s the line y D 25  10x, tang ent to

the parabola at .x

0

; x

2

0

/ D .5; 25/.

Section 4.5

Applications to Curves

47

4.5.15. (a) If .x

0

; y

0

/ is any po int on the circle such that x

0

¤ ˙1 (and therefore y

0

¤ 0), then

differentiating (A) yields 2x

0

C 2y

0

y

0

D 0, so y

0

D 

x

0

y

0

. Therefore,the equation of the tangent line is

y D y

0



x

0

y

0

.x  x

0

/. Since x

2

0

C y

2

0

D 1, this is equivalent to (B).

(b) Since y

0

D 

x

0

y

0

on the tangent line, we can rewrite (B) as y xy

0

D

1

y

0

. Hence (F)

1

.y  xy

0

/

2

D

y

2

0

and (G) x

2

0

D 1  y

2

0

D

.y  xy

0

/

2

 1

.y  xy

0

/

2

. Since .y

0

/

2

D

x

2

0

y

2

0

, (F) and (G) imply that .y

0

/

2

D

.y  xy

0

/

2

 1, which implies (C).

(c) Using t he quadratic for mula to solve (C) for y

0

yields

y

0

D

xy ˙

p

x

2

C y

2

 1

x

2

 1

.H/

if .x; y/ is on a tangent line with slope y

0

. If y D

1  x

0

x

y

0

, then x

2

Cy

2

1 D x

2

C



1  x

0

x

y

0



2

1 D



x  x

0

y

0



2

(since x

2

0

C y

2

0

D 1). Since y

0

D 

x

0

y

0

, this implies that (H) i s equivalent to 

x

0

y

0

D

1

x

2

 1



x.1  x

0

x/

y

0

˙

ˇ

x x

0

y

0

ˇ



, which holds if and only if we choose the “˙" so that ˙

ˇ

x x

0

y

0

ˇ

D





x  x

0

y

0



. Therefore,we must choose ˙ D  if

x x

0

y

0

> 0, so (H) reduces to (D), or ˙ D C if

x  x

0

y

0

< 0, so (H) reduces to (E).

(d) Differentiating (A) yields 2x C 2yy

0

D 0, so y

0

D 

x

y

on either semicircle. Sin ce (D) and (E)

both reduce to y

0

D

xy

1  x

2

D 

x

y

(since x

2

C y

2

D 1) on both semicircles, the conclusio n fol lows.

(e) From (D) and (E) the slopes of tangent lines from (5,5) tangent to the circle are y

0

D

25 ˙

p

49

24

D

3

4

;

4

3

. Therefore, tangent lines are y D 5 C

3

4

.x  5/ D

1 C 3x=5

4=5

and y D 5 C

4

3

.x  5/ D

1  4x=5

3=5

,

which intersect the circle at .3=5; 4=5/ .4=5; 3=5/, respectively. (See (B)).

4.5.16. (a) If .x

0

; y

0

/ is any point on the parabola such that x

0

> 0 (and therefore y

0

¤ 0), then

differentiating (A) yield s 1 D 2y

0

y

0

, so y

0

D

1

2y

0

. Therefore,the equation of the tangent line is y D

y

0

C

1

2y

0

.x  x

0

/. Since x

0

D y

2

0

, this is equivalent to (B).

(b) Since y

0

D

1

2y

0

on the tangent line, we can rewrite (B) as

y

0

2

D y xy

0

. Substi tuting this into (B)

yields y D .y  xy

0

/ C

x

4.y  xy

0

/

, which impli es (C).

(c) Using t he quadratic for mula to solve (C) for y

0

yields

y

0

D

y ˙

p

y

2

 x

2x

.F/

if .x; y/ is on a tangent line with slope y

0

. If y D

y

0

2

C

x

2y

0

, then y

2

 x D

1

4



y

0



x

y

0



2

so (F)

48 Chapter 4

Applications of First Order Equations

is equivalent to

1

2y

0

D

y

0

C

x

y

0

˙

ˇ

y

0



x

y

0

ˇ

4x

which holds if and only if we choose the “˙" so th at

˙

ˇ

y

0



x

y

0

ˇ

D 



y

0



x

y

0



. Therefore,we must choose ˙ D C if x > y

2

0

D x

0

, so (F) reduces to (D),

or ˙ D  if x < y

2

0

D x

0

, so (F) reduces to (E).

(d) Differentiating (A) yields 1 D 2yy

0

, so y

0

D

1

2y

on either half of the parabola. Since (D) and (E)

both reduce to this if x D y

2

, the conclusion fo llows.

4.5.18. The equation of the line tangent to the curve at .x

0

; y.x

0

// is y D y.x

0

/ C y

0

.x

0

/.x  x

0

/.

Since y.x

0

=2/ D 0, y.x

0

/ 

y

0

.x

0

/x

0

2

D 0. Since x

0

is arbitrary, i t follows that y

0

D

2y

x

, so

y

0

y

D

2

x

,

ln jyj D 2 ln jxjC k, and y D cx

2

. Since .1; 2/ is on the curve, c D 2. Therefore,y D 2x

2

.

4.5.20. The equation of the line tangent to the curve at .x

0

; y.x

0

// is y D y.x

0

/ C y

0

.x

0

/.x  x

0

/.

Since .x

1

; y

1

/ is on the line, y.x

0

/ C y

0

.x

0

/.x

1

 x

0

/ D y

1

. Since x

0

is arbitrary, it follows that

y C y

0

.x

1

 x/ D y

1

, so

y

0

y  y

1

D

1

x x

1

, ln jy  y

1

j D ln jx x

1

j C k, and y  y

1

D c.x  x

1

/.

4.5.22. The equation of the line tangent to the curve at .x

0

; y.x

0

// is y D y.x

0

/ Cy

0

.x

0

/.x x

0

/. Since

y.0/ D x

0

, x

0

D y.x

0

/y

0

.x

0

/x

0

. Since x

0

is arbitrary, it follows that x D yxy

0

, so (A) y

0



y

x

D 1.

The solutions of (A) are of the form y D ux, wh ere u

0

x D 1, so u

0

D 

1

x

. Therefore,u D ln jxjCc

and y D x ln jxj C cx.

4.5.24. The equation of the line normal to the curve at .x

0

; y

0

/ is y D y.x

0

/ 

x x

0

y

0

.x

0

/

. Sin ce y.0/ D

2y.x

0

/, y.x

0

/ C

x

0

y

0

.x

0

/

D 2y.x

0

/. Since x

0

is arbitrary, it follows that y

0

y D x, so (A)

y

2

D

x

2

C

c

2

and y

2

D x

2

C c. Now y.2/ D 1 $ c D 3. Therefore,y D

p

x

2

 3.

4.5.26. Differentiating the given equation yields 2x C 4y C 4xy

0

C 2yy

0

D 0, so y

0

D 

x C 2y

2x C y

is a differential equatio n for the given family, and (A) y

0

D

2x C y

x C 2y

is a differential equatio n for the

orthogonal traj ectories. Substituting y D ux in (A) yields u

0

x Cu D

2 C u

1 C 2u

, so u

0

x D 

2.u

2

 1/

1 C 2u

and

1 C 2u

.u  1/.u C 1/

u

0

D 

2

x

, or



3

u  1

C

1

u C 1



u

0

D 

4

x

. Therefore, 3 ln ju1jCln juC1j D 4 l n jxjC

K, so .u1/

3

.uC1/ D

k

x

4

. Substituting u D

y

x

yields the orthogonal trajectories .y x/

3

.y Cx/ D k.

4.5.28. Differentiating yield s ye

x

2

.1C2x

2

/Cxe

x

2

y

0

D 0, so y

0

D

y.1 C 2x

2

/

x

is a differential equation

for the given family. Theref ore,(A) y

0

D 

x

y.1 C 2x

2

/

is a differential equation for t he o rthogonal

trajectories. From (A), yy

0

D 

x

1 C 2x

2

, so

y

2

D 

1

4

ln.1 C2x

2

/ C

k

2

, and the orthogonal trajectories

are given by y

2

D 

1

2

ln.1 C 2x

2

/ C k.

Section 4.5

Applications to Curves

49

4.5.30. Differentiating (A) y D 1 C cx

2

yields (B) y

0

D 2cx. From (C), c D

y  1

x

2

. Substituting this

into (B) yields the differential equation y

0

D

2.y  1/

x

for the given family of parabolas. Therefore,y

0

D



x

2.y  1/

is a differential equation for the orthogonal trajectori es. Separating variables yields 2.y 

1/y

0

D x, so .y 1/

2

D 

x

2

Ck. Now y.1/ D 3 $ k D

9

2

, so .y 1/

2

D 

x

2

C

9

2

. Therefore,(D)

y D 1 C

r

9  x

2

. This curve interesects the parab ola (A) if and only if the equation (C) cx

2

D

r

9  x

2

has a solution x

2

in .0; 9/. Therefore,c > 0 is a necessaary condition fo r intersection. We will

show that it is also sufﬁcient. Squaring both sid es of (C) and simplifying yields 2c

2

x

4

Cx

2

9 D 0. Using

the quadratic formula to solve this for x

2

yields x

2

D

1 C

p

1 C 72c

2

4c

2

. The condit ion x

2

< 9 holds if

and only if 1C

p

1 C 72c

2

< 36c

4

, which is equivalent to 1C72c

2

< .1C36c

2

/

2

D 1C72c

2

C1296c

4

,

which holds for all c > 0.

4.5.32. The angles  and 

1

from the x-axis to the tangents to C and C

1

satisfy tan  D f .x

0

; y

0

/ and

tan 

1

D

f .x

0

; y

0

/ C tan ˛

1  f .x

0

; y

0

/ tan ˛

D

tan  C tan ˛

1  t an  tan ˛

D tan. C˛/. Therefore, assuming  and 

1

are both in

Œ0; 2/, 

1

D  C ˛.

4.5.34. Circles centered at the ori gin are given by x

2

C y

2

D r

2

. Differentiating yields 2x C 2yy

0

D 0,

so y

0

D 

x

y

is a differential equation for the given fami ly, and y

0

D

.x=y/ C tan ˛

1 C .x=y/ tan ˛

is a differential

equation for the desired famil y. Substituting y D ux yields u

0

x Cu D

1=u C tan ˛

1 C .1=u/ tan ˛

D

1 C u tan ˛

u C tan ˛

.

Therefore,u

0

x D 

1 C u

2

u C tan ˛

,

u C tan ˛

1 C u

2

u

0

D 

1

x

and

1

2

ln.1 C u

2

/ C tan ˛ tan

1

u D ln jxj C k.

Substituting u D

y

x

yields

1

2

ln.x

2

C y

2

/ C .tan ˛/ tan

1

y

x

D k.

CHAPTER 5

Linear Second Order Equations

5.1 HOMOGENEOUS LINEAR E QUATIONS

5.1.2. (a) If y

1

D e

x

cos x, then y

0

1

D e

x

.cos x  sin x/ and y

00

1

D e

x

.cos x  sin x  sin x  cos x/ D

2e

x

sin x, so y

00

1

 2y

0

1

C2y

1

D e

x

.2 sin x  2 cos x C 2 sin x C 2 cos x/ D 0. If y

2

D e

x

sin x, then

y

0

2

D e

x

.sin x Ccos x/ and y

00

2

D e

x

.sin x C cos x C cos x  sin x/ D 2e

x

cos x, so y

00

2

 2y

0

2

C2y

2

D

e

x

.2 cos x  2 sin x  2 cos x C 2 sin x/ D 0.

(b) If (B) y D e

x

.c

1

cos x C c

2

sin x/, then

y

0

D e

x

.c

1

.cos x  sin x/ Cc

2

.sin x C cos x// .C/

and

y

00

D c

1

e

x

.cos x  sin x  sin x  cos x/

Cc

2

e

x

.sin x C cos x C cos x  si n x/

D 2e

x

.c

1

sin x C c

2

cos x/;

so

y

00

 2y

0

C 2y D c

1

e

x

.2 sin x  2 cos x C 2 sin x C 2 cos x/

Cc

2

e

x

.2 cos x 2 sin x  2 cos x C2 sin x/ D 0:

(c) We must choose c

1

and c

2

in (B) so that y.0/ D 3 and y

0

.0/ D 2. Setting x D 0 in (B) and (C)

shows that c

1

D 3 and c

1

C c

2

D 2, so c

2

D 5. Therefore, y D e

x

.3 cos x  5 sin x/.

(d) We must choose c

1

and c

2

in (B) so that y.0/ D k

0

and y

0

.0/ D k

1

. Setting x D 0 in (B) and (C)

shows that c

1

D k

0

and c

1

Cc

2

D k

1

, so c

2

D k

1

k

0

. Therefore, y D e

x

.k

0

cos x C .k

1

 k

0

/ sin x/.

5.1.4. ( a) If y

1

D

1

x  1

, then y

0

1

D 

1

.x  1/

2

and y

00

1

D

2

.x  1/

3

, so

.x

2

 1/y

00

1

C 4xy

0

1

C2y

1

D

2.x

2

 1/

.x  1/

3



4x

.x  1/

2

C

2

x 1

D

2.x C 1/  4x C 2.x  1/

.x  1/

2

D 0:

Similar manipulations show that .x

2

 1/y

00

2

C 4xy

0

2

C 2y

2

D 0. The general solution on each of the

inter vals .1; 1/, .1; 1/, and .1; 1/ is (B) y D

c

1

x  1

C

c

2

x C 1

.

51

52 Chapter 5

Linear Second Order Equations

(b) Differentiating (B) yields (C) y

0

D 

c

1

.x  1/

2



c

2

.x C 1/

2

. We must choose c

1

and c

2

in (B) so

that y.0/ D 5 and y

0

.0/ D 1. Setting x D 0 in (B) and (C) shows that c

1

C c

2

D 5; c

1

 c

2

D 1.

Therefore,c

1

D 2 and c

2

D 3, so y D

2

x 1



3

x C 1

on .1; 1/.

(d) The Wronskian of fy

1

; y

2

g is

W.x/ D

ˇ

1

x  1

1

x C 1



1

.x  1/

2



1

.x C 1/

2

ˇ

D

2

.x

2

 1/

2

; .D/

so W .0/ D 2. Since p.x/ D

4x

x

2

 1

, so

Z

x

0

p.t/ dt D

Z

x

0

4t

t

2

 1

dt D ln.x

2

 1/

2

, Abel’s f ormula

implies that W .x/ D W .0/e

ln.x

2

1/

2

D

2

.x

2

 1/

2

, consistent with (D).

5.1.6. From Abel’s formula, W.x/ D W./e

3

R

x



.t

2

C1/ d t

D 0  e

3

R

x



.t

2

C1/ d t

D 0.

5.1.8. p.x/ D

1

x

; therefore

Z

x

1

p.t/ dt D

Z

x

1

dt

t

D ln x, so Abel’s formula yields W .x/ D W .1/e

ln x

D

1

x

.

5.1.10. p.x/ D 2; P .x/ D 2x; y

2

D uy

1

D ue

3x

; u

0

D

Ke

P.x/

y

2

1

.x/

D

Ke

2x

e

6x

D Ke

4x

;

u D 

K

4

e

4x

. Choose K D 4; then y

2

D e

4x

e

3x

D e

x

.

5.1.12. p.x/ D 2a; P.x/ D 2ax; y

2

D uy

1

D ue

ax

; u

0

D

Ke

P.x/

y

2

1

.x/

D

Ke

2ax

e

2ax

D K; u D Kx.

Choo se K D 1; then y

2

D xe

ax

.

5.1.14. p.x/ D 

1

x

; P .x/ D ln x; y

2

D uy

1

D ux; u

0

D

Ke

P.x/

y

2

1

.x/

D

Kx

x

2

D

K

x

; u D K ln x.

Choo se K D 1; then y

2

D x ln x.

5.1.16. p.x/ D 

1

x

; P .x/ D ln jxj; y

2

D uy

1

D ux

1=2

e

2x

; u

0

D

Ke

P.x/

y

2

1

.x/

D

Kx

xe

4x

D e

4x

;

u D 

Ke

4x

4

. Choose K D 4; then y

2

D e

4x

.x

1=2

e

2x

/ D x

1=2

e

2x

.

5.1.18. p.x/ D 

2

x

; P .x/ D 2 l n jxj ; y

2

D uy

1

D ux cos x; u

0

D

Ke

P.x/

y

2

1

.x/

D

Kx

2

x

2

cos

2

x

D

K sec

2

x; u D K tan x. Choose K D 1; then y

2

D tan x.x cos x/ D x sin x.

5.1.20. p.x/ D 

3x C 2

3x  1

D 1 

3

3x  1

; P .x/ D x  ln j3x  1j; y

2

D uy

1

D ue

2x

;

u

0

D

Ke

P.x/

y

2

1

.x/

D

K.3x  1/e

x

e

4x

D K.3x  1/e

3x

; u D Kxe

3x

. Choose K D 1; then

y

2

D xe

3x

e

2x

D xe

x

.

Section 5.1

Homogeneous Linear Equations

53

5.1.22. p.x/ D 

2.2x

2

 1/

x.2x C1/

D 2 

2

2x C 1

C

2

x

; P .x/ D 2x  ln j2x C 1j C 2 ln jxj; y

2

D

uy

1

D

u

x

; u

0

D

Ke

P.x/

y

2

1

.x/

D

K.2x C 1/e

2x

x

2

x

2

D K.2x C 1/e

2x

; u D Kxe

2x

. Choose K D 1; then

y

2

D

xe

2x

x

D e

2x

.

5.1.24. Suppose that y  0 on .a; b/. Then y

0

 0 and y

00

 0 on .a; b/, so y is a solu tion of (A)

y

00

Cp.x/y

0

Cq.x/y D 0; y.x

0

/ D 0; y

0

.x

0

/ D 0 on .a; b/. Since Theorem 5.1.1 implies that (A) has

only one so lution on .a; b/, the conclusion follows.

5.1.26. If f´

1

; ´

2

g is a fundamental set of solutions of (A) on .a; b/, then every solution y of (A) on .a; b/

is a li near combination of f ´

1

; ´

2

g; that is, y D c

1

´

1

C c

2

´

2

D c

1

.˛y

1

C ˇy

2

/ C c

2

.y

1

C ıy

2

/ D

.c

1

˛ C c

2

/y

1

C .c

1

ˇ C c

2

ı/y

2

, which shows that every solution of ( A ) on .a; b/ can be written as a

linear combinat ion of fy

1

; y

2

g. Therefore,fy

1

; y

2

g is a fundamental set of solutions of (A) on .a; b/.

5.1.28. The Wronsk ian of f y

1

; y

2

g is

W D

ˇ

y

1

y

2

y

0

1

y

0

2

ˇ

D

ˇ

y

1

ky

1

y

0

1

ky

0

1

ˇ

D k.y

1

y

0

1

 y

0

1

y

1

/ D 0:

nor y

2

can be a solution of y

00

C p.x/y

0

C q.x/y D 0 on .a; b/.

5.1.30. W .x

0

/ D



y

1

.x

0

/y

0

2

.x

0

/  y

0

1

.x

0

/y

2

.x

0

/



D 0 if either y

1

.x

0

/ D y

2

.x

0

/ D 0 or y

0

1

.x

0

/ D

y

0

2

.x

0

/ D 0, and Theorem 5.1.6 implies that fy

1

; y

2

g is linearly dependent on .a; b/.

5.1.32. Let x

0

be an arbitrar y point in .a; b/. By the motivating argument preceding Theorem 5.1.4, (B)

W.x

0

/ D y

1

.x

0

/y

0

2

.x

0

/  y

0

1

.x

0

/y

2

.x

0

/ ¤ 0. Now let y be th e solution of y

00

C p.x/y

0

C q.x/y D

0; y.x

0

/ D y

1

.x

0

/; y

0

.x

0

/ D y

0

1

.x

0

/. By assumption, y is a linear combination of fy

1

; y

2

g on .a; b/;

that is, y D c

1

y

1

C c

2

y

2

, where

c

1

y

1

.x

0

/ C c

2

y

2

.x

0

/ D y

1

.x

0

/

c

1

y

0

1

.x

0

/ C c

2

y

0

2

.x

0

/ D y

0

1

.x

0

/:

Solving this system by Cramers’ rule yiel ds

c

1

D

1

W.x

0

/

ˇ

y

1

.x

0

/ y

2

.x

0

/

y

0

1

.x

0

/ y

0

2

.x

0

/

ˇ

D 1 and c

2

D

1

W.x

0

/

ˇ

y

1

.x

0

/ y

1

.x

0

/

y

0

1

.x

0

/ y

1

.x

0

/

ˇ

D 0:

Therefore,y D y

1

, which shows that y

1

is a solution of (A). A similar argument shows that y

2

is a

solution of (A).

5.1.34. Expanding the determinant by cofactors of its ﬁr st column shows that the ﬁrst equation in the

exercise can be written as

y

W

ˇ

y

0

1

y

0

2

y

00

1

y

00

2

ˇ



y

0

W

ˇ

y

1

y

2

y

00

1

y

00

2

ˇ

C

y

00

W

ˇ

y

1

y

2

y

0

1

y

0

2

ˇ

D 0;

which is of the form (A) with

p D 

1

W

ˇ

y

1

y

2

y

00

1

y

00

2

ˇ

and q D

1

W

ˇ

y

0

1

y

0

2

y

00

1

y

00

2

ˇ

:

54 Chapter 5

Linear Second Order Equations

5.1.36. Theorem 5.1.6 implies that th at there are constants c

1

and c

2

such that (B) y D c

1

y

1

C c

2

y

2

on

.a; b/. To see that c

1

and c

2

are unique, assume that (B) holds, and let x

0

be a point in .a; b/. Then (C)

y

0

D c

1

y

0

1

C c

2

y

0

2

. Setting x D x

0

in (B) and (C) yields

c

1

y

1

.x

0

/ C c

2

y

2

.x

0

/ D y.x

0

/

c

1

y

0

1

.x

0

/ C c

2

y

0

2

.x

0

/ D y

0

.x

0

/:

Since Theorem 5 .1.6 implies t hat y

1

.x

0

/y

0

2

.x

0

/  y

0

1

.x

0

/y

2

.x

0

/ ¤ 0, the argument preceding Theo-

rem 5.1.4 implies that c

1

and c

2

are given uniquely by

c

1

D

y

0

2

.x

0

/y.x

0

/  y

2

.x

0

/y

0

.x

0

/

y

1

.x

0

/y

0

2

.x

0

/  y

0

1

.x

0

/y

2

.x

0

/

c

2

D

y

1

.x

0

/y

0

.x

0

/  y

0

1

.x

0

/y.x

0

/

y

1

.x

0

/y

0

2

.x

0

/  y

0

1

.x

0

/y

2

.x

0

/

:

5.1.38. The general solution of y

00

D 0 is y D c

1

C c

2

x, so y

0

D c

2

. Imposing the stated initial

conditions on y

1

D c

1

C c

2

x yields c

1

C c

2

x

0

D 1 and c

2

D 0; therefore c

1

D 1, so y

1

D 1. Imposing

the stated initial conditions on y

2

D c

1

C c

2

x yields c

1

C c

2

x

0

D 0 and c

2

D 1; theref ore c

1

D x

0

, so

y

2

D x  x

0

. The solution of the general initial value problem is y D k

0

C k

1

.x  x

0

/.

5.1.40. Let y

1

D a

1

cos !x C a

2

sin !x and y

2

D b

1

cos !x C b

2

sin !x. Then

a

1

cos !x

0

C a

2

sin !x

0

D 1

!.a

1

sin !x

0

C a

2

cos !x

0

/ D 0

and

b

1

cos !x

0

C b

2

sin !x

0

D 0

!.b

1

sin !x

0

C b

2

cos !x

0

/ D 1:

Solving these systems yields a

1

D cos !x

0

, a

2

D sin !x

0

, b

1

D 

sin !x

0

!

, and b

2

D

cos !x

0

!

.

Therefore, y

1

D cos !x

0

cos !x C sin !x

0

sin !x D cos !.x  x

0

/ and y

2

D

1

!

.sin !x

0

cos !x C

cos !x

0

sin !x/ D

1

!

sin !.xx

0

/. The solution of the gener al initial value problem is y D k

0

cos !.x

x

0

/ C

k

1

!

sin !.x  x

0

/.

5.1.42. (a) If y

1

D x

2

, then y

0

1

D 2x and y

00

1

D 2, so x

2

y

00

1

4xy

0

1

C6y

1

D x

2

.2/ 4x.2x/ C6x

2

D 0

for x in .1; 1/. If y

2

D x

3

, t hen y

0

2

D 3x

2

and y

00

2

D 6x, so x

2

y

00

2

 4xy

0

2

C 6y

2

D x

2

.6x/ 

4x.3x

2

/ C 6x

3

D 0 for x in .1; 1/. If x ¤ 0, then y

2

.x/=y

1

.x/ D x, which is nonconstant on

.1; 0/ and .0; 1/, so Theorem 5.1.6 implies that fy

1

; y

2

g is a fundamental set of solu tions of (A) on

each of these intervals.

(b) Theorem 5.1.6 and (a) imply that y satisﬁes (A) on .1; 0/ and on .0; 1/ if and only if y D



a

1

x

2

C a

2

x

3

; x > 0;

b

1

x

2

C b

2

x

3

; x < 0:

Since y.0/ D 0 we can complete t he proof that y is a solution of (A) on

.1; 1/ by showing that y

0

.0/ and y

00

.0/ both exist if and only if a

1

D b

1

. Since

y.x/  y.0/

x  0

D



a

1

x C a

2

x

2

; if x > 0;

b

1

x C b

2

x

2

; if x < 0;

it follows that y

0

.0/ D lim

x!0

y.x/  y.0/

x 0

D 0. Therefore, y

0

D



2a

1

x C 3a

2

x

2

; x  0;

2b

1

x C 3b

2

x

2

; x < 0:

Since

y

0

.x/  y

0

.0/

x 0

D



2a

1

C 3a

2

x; if x > 0;

2b

1

C 3b

2

x; if x < 0;

it follows that y

00

.0/ D lim

x!0

y

0

.x/  y

0

.0/

x  0

exists if and

Section 5.2

Constant Coefﬁcient Homogeneous Equations

55

only if a

1

D b

1

. By renaming a

1

D b

1

D c

1

, a

2

D c

2

, and b

2

D c

3

we see that y is a solution of (A) on

.1; 1/ if and on ly if y D



c

1

x

2

C c

2

x

3

; x  0;

c

1

x

2

C c

3

x

3

; x < 0:

(c) We have sh own that y.0/ D y

0

.0/ D 0 for any choice of c

1

and c

2

in (C). Therefore,the given

initial value problem has a solution if and only if k

0

D k

1

D 0, in wh ich case every function of the form

(C) i s a solution.

(d) If x

0

> 0, then c

1

and c

2

in (C) are uniquely d et ermined by k

0

and k

1

, but c

3

can be chosen

arbitrarily. Therefore,(B) has a unique solution on .0; 1/, but inﬁnitely many solutions on .1; 1/. If

x

0

< 0, then c

1

and c

3

in (C) are uniquely determined by k

0

and k

1

, but c

2

can be chosen arbitrarily.

Therefore,(B) has a unique solution on .1; 0/, but inﬁnitely many solutions on .1; 1/.

5.1.44. (a) If y

1

D x

3

, then y

0

1

D 3x

2

and y

00

1

D 6x, so x

2

y

00

1

 6xy

0

1

C 12y

1

D x

2

.6x/  6x.3x

2

/ C

12x

3

D 0 for x in .1; 1/. If y

2

D x

4

, then y

0

2

D 4x

3

and y

00

2

D 12x

2

, so x

2

y

00

2

 6xy

0

2

C 12y

2

D

x

2

.12x

2

/  6x.4x

3

/ C 12x

4

D 0 f or x in .1; 1/. If x ¤ 0, then y

2

.x/=y

1

.x/ D x, which is

nonconstant on .1; 0/ and .0; 1/, so Theorem 5.1.6 implies that fy

1

; y

2

g is a fundamental set of

solutions of (A) on each of these intervals.

(b) Theorem 5.1.2 and (a) imply that y satisﬁes (A ) on .1; 0/ and on .0; 1/ if and only if (C)

y D



a

1

x

3

C a

2

x

4

; x > 0;

b

1

x

3

C b

2

x

4

; x < 0:

Since y.0/ D 0 we can complete the proof that y is a solution of

(A) on .1; 1/ by showing that y

0

.0/ and y

00

.0/ both exist for any choice of a

1

, a

2

, b

1

, and b

2

.

Since

y.x/  y.0/

x  0

D



a

1

x

2

C a

2

x

3

; if x > 0;

b

1

x

2

C b

2

x

3

; if x < 0;

it follows that y

0

.0/ D lim

x!0

y.x/  y.0/

x 0

D 0.

Therefore, y

0

D



3a

1

x

2

C 4a

2

x

3

; x  0;

3b

1

x

2

C 4b

2

x

3

; x < 0:

Since

y

0

.x/  y

0

.0/

x 0

D



3a

1

x C 4a

2

x

2

; if x > 0;

3b

1

x C 4b

2

x

2

; if x < 0;

it follows that y

00

.0/ D lim

x!0

y

0

.x/  y

0

.0/

x 0

D 0. Therefore,(B) is a solution of (A) on .1; 1/.

(c) We have shown that y.0/ D y

0

.0/ D 0 for any choice of a

1

, a

2

, b

1

, and b

2

in (B). Therefore,the

given initial value problem has a solution if and on ly if k

0

D k

1

D 0, in which case every function of the

form (B) is a solution.

(d) If x

0

> 0, then a

1

and a

2

in (B) are uniquely determined by k

0

and k

1

, but b

1

and b

2

can be chosen

arbitrarily. Therefore,(C) has a unique so lution on .0; 1/, but inﬁnitely many so lutions on .1; 1/.

If x

0

< 0, th en b

1

and b

2

in (B) are uniquely determin ed by k

0

and k

1

, but a

1

and a

2

can be chosen

arbitrarily. Therefore,(C) has a unique solution on .1; 0/, but inﬁnitely many solutions on .1; 1/.

5.2 CONSTANT COEFFICIENT HOMOGENEOUS EQUATIONS

5.2.2. p.r/ D r

2

 4r C 5 D .r  2/

2

C1; y D e

2x

.c

1

cos x C c

2

sin x/.

5.2.4. p.r/ D r

2

 4r C 4 D .r  2/

2

; y D e

2x

.c

1

C c

2

x/.

5.2.6. p.r/ D r

2

C 6r C 10 D .r C 3/

2

C 1; y D e

3x

.c

1

cos x C c

2

sin x/.

5.2.8. p.r/ D r

2

C r D r.r C 1/; y D c

1

C c

2

e

x

.

5.2.10. p.r/ D r

2

C 6r C 13y D .r C 3/

2

C 4; y D e

3x

.c

1

cos 2x C c

2

sin 2x/.

5.2.12. p.r/ D 10r

2

 3r  1 D .2r  1/.5r C 1/ D 10.r  1=2/.r C 1=5/; y D c

1

e

x=5

Cc

2

e

x=2

.

5.2.14. p.r/ D 6r

2

 r  1 D .2r  1/.3r C 1/ D 6.r  1=2/.r C 1=3/; y D c

1

e

x=3

C c

2

e

x=2

;

y

0

D 

c

1

3

e

x=3

C

c

2

e

x=2

; y.0/ D 10 ) c

1

Cc

2

D 10; y

0

.0/ D 0 ) 

c

1

3

C

c

2

D 0; c

1

D 6; c

2

D 4;

y D 4e

x=2

C 6e

x=3

.

56 Chapter 5

Linear Second Order Equations

5.2.16. p.r/ D 4r

2

 4r  3 D .2r  3/.2r C 1/ D 4.r  3=2/.r C 1=2/; y D c

1

e

x=2

C c

2

e

3x=2

;

y

0

D 

c

1

2

e

x=2

C

3c

2

e

3x=2

; y.0/ D

13

12

) c

1

C c

2

D

13

12

; y

0

.0/ D

23

24

) 

c

1

2

C

3c

2

D

23

24

;

c

1

D

1

3

; c

2

D

3

4

; y D

e

x=2

3

C

3e

3x=2

4

.

5.2.18. p.r/ D r

2

C 7r C 12 D .r C 3/.r C 4/; y D c

1

e

4x

C c

2

e

3x

; y

0

D 4c

1

e

4x

 3c

2

e

3x

;

y.0/ D 1 ) c

1

C c

2

D 1; y

0

.0/ D 0 ) 4c

1

 3c

2

D 0; c

1

D 3, c

2

D 4; y D 3e

4x

 4e

3x

.

5.2.20. p.r/ D 36r

2

 12r C 1 D .6r  1/

2

D 36.r  1=6/

2

; y D e

x=6

.c

1

C c

2

x/; y

0

D

e

x=6

6

.c

1

C

c

2

x/ C c

2

e

x=6

; y.0/ D 3 ) c

1

D 3; y

0

.0/ D

5

2

)

c

1

6

C c

2

D

5

2

) c

2

D 2; y D e

x=6

.3 C 2x/.

5.2.22. (a) From (A), ay

00

.x/ C by

0

.x/ C cy.x/ D 0 for all x. Replacing x by x  x

0

yields (C)

ay

00

.x  x

0

/ C by

0

.x  x

0

/ C cy.x  x

0

/ D 0. If ´.x/ D y.x  x

0

/, then the chain rule implies t hat

´

0

.x/ D y

0

.x  x

0

/ and ´

00

.x/ D y

00

.x  x

0

/, so (C) is equivalent to a´

00

C b´

0

C c´ D 0.

(b) If fy

1

; y

2

g is a fundamental set of solutions of (A) then Theorem 5.1.6 implies that y

2

=y

1

is

nonconstant. Therefore,

´

2

.x/

´

1

.x/

D

y

2

.x  x

0

/

y

1

.x  x

0

/

is also nonconstant, so Theorem 5.1.6 implies that f´

1

; ´

2

g

is a fundamental set of solutions of (A).

(c) Let p.r/ D ar

2

C br C c b e the characteristic polynomial of (A). Then:

 If p.r/ D 0 has distinct real roots r

1

and r

2

, then the general solution of (A) is

y D c

1

e

r

1

.xx

0

/

C c

2

e

r

2

.xx

0

/

:

 If p.r/ D 0 has a repeated root r

1

, then the general solution of (A) is

y D e

r

1

.xx

0

/

.c

1

C c

2

.x  x

0

//:

 If p.r/ D 0 has complex conjugate roots r

1

D  C i! and r

2

D   i! .where ! > 0/, then the

general solution of (A) is

y D e

.xx

0

/

.c

1

cos !.x  x

0

/ C c

2

sin !.x  x

0

//:

5.2.24. p.r/ D r

2

 6r  7 D .r  7/.r C 1/;

y D c

1

e

.x2/

C c

2

e

7.x2/

I

y

0

D c

1

e

.x2/

C 7c

2

e

7.x2/

I

y.2/ D 

1

3

) c

1

C c

2

D 

1

3

; y

0

.2/ D 5 ) c

1

C 7c

2

D 5; c

1

D

1

3

; c

2

D 

2

3

; y D

1

3

e

.x2/



2

3

e

7.x2/

.

5.2.26. p.r/ D 9r

2

C6r C 1 D .3r C 1/

2

D 9.r C 1=3/

2

;

y D e

.x2/=3

.c

1

C c

2

.x  2// I

y

0

D 

1

3

e

.x2/=3

.c

1

C c

2

.x  2// Cc

2

e

.x2/=3

I

Section 5.2

Constant Coefﬁcient Homogeneous Equations

57

y.2/ D 2 ) c

1

D 2; y

0

.2/ D 

14

3

) 

c

1

3

C c

2

D 

14

3

) c

2

D 4; y D e

.x2/=3

.2  4.x  2//.

5.2.28. p.r/ D r

2

C 3;

y D c

1

cos

p

3



x 



3



C c

2

sin

p

3



x 



3



I

y

0

D 

p

3c

1

sin

p

3



x 



3



C

p

3c

2

cos

p

3



x 



3



I

y.=3/ D 2 ) c

1

D 2; y

0

.=3/ D 1 ) c

2

D 

1

p

3

;

y D 2 cos

p

3



x 



3





1

p

3

sin

p

3



x 



3



:

5.2.30. y is a so lution of ay

00

C by

0

C cy D 0 if and only if

y D c

1

e

r

1

.xx

0

/

C e

r

2

.xx

0

/

y

0

D r

1

c

1

e

r

1

.xx

0

/

C r

2

e

r

2

.x  x

0

/:

Now y

1

.x

0

/ D k

0

and y

0

1

.x

0

/ D k

1

) c

1

C c

2

D k

0

; r

1

c

1

C r

2

c

2

D k

1

. Therefore,c

1

D

r

2

k

0

 k

1

r

2

 r

1

and c

2

D

k

1

 r

1

k

0

r

2

 r

1

. Substi tuting c

1

and c

2

into the above equations for y and y’ yields

y D

r

2

k

0

 k

1

r

2

 r

1

e

r

1

.xx

0

/

C

k

1

 r

1

k

0

r

2

 r

1

e

r

2

.xx

0

/

D

k

0

r

2

 r

1



r

2

e

r

1

.xx

0

/

 r

1

e

r

2

.xx

0

/



C

k

1

r

2

 r

1



e

r

2

.xx

0

/

 e

r

1

.xx

0

/



:

5.2.32. y is a solution of ay

00

C by

0

Ccy D 0 if and only if

y D e

.xx

0

/

.c

1

cos !.x  x

0

/ C c

2

sin !.x  x

0

// (A)

and

y

0

D e

.xx

0

/

.c

1

cos !.x  x

0

/ C c

2

sin !.x  x

0

//

C!e

.xx

0

/

.c

1

sin !.x  x

0

/ C c

2

cos !.x  x

0

// :

Now y

1

.x

0

/ D k

0

) c

1

D k

0

and y

0

1

.x

0

/ D k

1

) c

1

C !c

2

D k

1

, so c

2

D

k

1

 k

0

!

. Substituting

c

1

and c

2

into (A) yields

y D e

.xx

0

/



k

0

cos !.x  x

0

/ C



k

1

 k

0

!



sin !.x  x

0

/



:

5.2.34. (b)

e

i

1

e

i

2

D .cos 

1

C i sin 

1

/.cos 

2

Ci sin 

2

/

D .cos 

1

cos 

2

 sin 

1

sin 

2

/ C i.sin 

1

cos 

2

C cos 

1

sin 

2

/

D cos.

1

C 

2

/ C i sin.

1

C 

2

/ D e

i.

1

C

2

/

:

58 Chapter 5

Linear Second Order Equations

(c)

e

´

1

C´

2

D e

.˛

1

Ciˇ

1

/C.˛

2

Ciˇ

2

/

D e

.˛

1

C˛

2

/Ci.ˇ

1

Cˇ

2

/

D e

.˛

1

C˛

2

/

e

i.ˇ

1

Cˇ

2

/

(from (F) wi th ˛ D ˛

1

C ˛

2

and ˇ D ˇ

1

C ˇ

2

)

D e

˛

1

e

˛

2

e

i.ˇ

1

Cˇ

2

/

(property of the real–valued exponential function)

D e

˛

1

e

˛

2

e

iˇ

1

e

iˇ

2

(from (b))

D e

˛

1

e

iˇ

1

e

˛

2

e

iˇ

2

D e

˛

1

Ciˇ

1

e

˛

2

Ciˇ

2

D e

´

1

e

´

2

:

(d) The real and imaginary parts of ´

1

D e

.Ci!/x

are u

1

D e

x

cos !x and v

1

D e

x

sin !x, which

are both solutions of ay

00

C by

0

C cy D 0, by Theorem 5.2.1(c). Similarly, the real and imaginary parts

of ´

2

D e

.i!/x

are u

2

D e

x

cos.!x/ D e

x

cos !x and v

1

D e

x

sin.!x/ D e

x

sin !x, which

are both solutions of ay

00

C by

0

C cy D 0, by Theorem 5.2.1,(c).

5.3 NONHOMOGENEOUS LINEAR EQUATIONS

5.3.2. The characteristic po lynomial of the complementary equation is p.r/ D r

2

4r C5 D .r 2/

2

C1,

so fe

2x

cos x; e

2x

sin xg is a fund amental set of solution s for the complementary equ at ion. Let y

p

D

A CBx; then y

00

p

4y

0

p

C5y

p

D 4B C5.A CBx/ D 1 C5x. Therefore,5B D 5; 4B C5A D 1, so

B D 1, A D 1. Therefore,y

p

D 1 C x is a particular solution and y D 1 Cx C e

2x

.c

1

cos x C c

2

sin x/

is the general solution.

5.3.4. The characteristic polynomial of the complementary equation is p.r/ D r

2

4r C4 D .r 2/

2

, so

fe

2x

; xe

2x

g is a fundamental set of solutions for the complementary equation. Let y

p

D A CBx CCx

2

;

then y

00

p

4y

0

p

C4y

p

D 2C 4.B C2Cx/ C4.A CBx CCx

2

/ D .2C 4B C4A/ C.8C C4B/x C

4Cx

2

D 2 C 8x  4x

2

. Therefore,4C D 4; 8C C 4B D 8; 2C  4B C 4A D 2, so C D 1,

B D 0, and A D 1. Therefore,y

p

D 1  x

2

is a particular solution and y D 1  x

2

C e

2x

.c

1

C c

2

x/ is

the general solution.

5.3.6. The characteristic polynomial of the complementary equation is p.r/ D r

2

C 6r C 10 D .r C

3/

2

C 1, so fe

3x

cos x; e

3x

sin xg i s a fundamental set of solutions for the complementary equation.

Let y

p

D A C Bx; then y

00

p

C 6y

0

p

C 10y

p

D 6B C 10.A C Bx/ D 22 C 20x. Therefore,10B D

20; 6B C 10A D 22, so B D 2, A D 1. Therefore,y

p

D 1 C 2x is a particular solution and (A)

y D 1 C2x Ce

3x

.c

1

cos x Cc

2

sin x/ is the general solution. Now y.0/ D 2 ) 2 D 1 Cc

1

) c

1

D 1.

Differentiatin g (A) yields y

0

D 2 3e

3x

.c

1

cos x Cc

2

sin x/ C e

3x

.c

1

sin x Cc

2

cos x/, so y

0

.0/ D

2 ) 2 D 2 3c

1

C c

2

) c

2

D 1. y D 1 C 2x C e

3x

.cos x  sin x/ is the solution of the initial

value prob lem.

5.3.8. If y

p

D

A

x

, then x

2

y

00

p

C 7xy

0

p

C 8y

p

D A



x

2



2

x

3



C 7x



1

x

2



C



8

x



D

3A

x

D

6

x

if

A D 2. Therefore,y

p

D

2

x

is a particular solution.

5.3.10. If y

p

D Ax

3

, then x

2

y

00

p

 xy

0

p

C y

p

D A



x

2

.6x/  x.3x

2

/ C x

3



D 4Ax

3

D 2x

3

if A D

1

2

.

Therefore,y

p

D

x

3

2

is a particular solution.

5.3.12. If y

p

D Ax

1=3

, then x

2

y

00

p

C xy

0

p

C y

p

D A

x

2

2x

5=3

9

!

C x

x

2=3

3

!

C x

1=3

!

D

10A

9

x

1=3

D 10x

1=3

if A D 9. Therefore,y

p

D 9x

1=3

is a particular solution.

Section 5.3

Nonhomogeneous Linear Equations

59

5.3.14. If y

p

D

A

x

3

, then x

2

y

00

p

C 3xy

0

p

 3y

p

D A



x

2



12

x

5



C 3x



3

x

4



C

3

x

3



D 0. Therefore,y

p

is not a solution of the given equat ion for any choice of A.

5.3.16. The characteristic p olynomial of the complementary equation is p.r/ D r

2

C5r 6 D .r C6/.r 

1/, so fe

6x

; e

x

g is a fund amental set of so lutions fo r the complementary equation. Let y

p

D Ae

3x

; then

y

00

p

C5y

0

p

6y

p

D p.3/Ae

3x

D 18Ae

3x

D 6e

3x

if A D

1

3

. Therefore,y

p

D

e

3x

3

is a particular solution

and y D

e

3x

3

C c

1

e

6x

C c

2

e

x

is the general solution.

5.3.18. The characteristic polynomial of the complementary equatio n is p.r / D r

2

C8r C7 D .r C1/.r C

7/, so fe

7x

; e

x

g is a fundamental set of solutions for the complementary equation. Let y

p

D Ae

2x

;

then y

00

p

C 8y

0

p

C 7y

p

D p.2/Ae

2x

D 5Ae

2x

D 10e

2x

if A D 2. Therefore,y

p

D 2e

2x

is

a particular solution and (A) y D 2e

2x

Cc

1

e

7x

Cc

2

e

x

is the general solution. Differentiating (A)

yields y

0

D 4e

2x

 7c

1

e

7x

 c

2

e

x

. Now y.0/ D 2 ) 2 D 2 C c

1

C c

2

and y

0

.0/ D 10 )

10 D 4  7c

1

 c

2

. Therefore,c

1

D 1 and c

2

D 1, so y D 2e

2x

 e

7x

Ce

x

is the solution of the

initial value problem.

5.3.20. The characteristic polynomial of the complementary equatio n is p.r/ D r

2

C 2r C 10 D .r C

1/

2

C 9, so fe

x

cos 3x; e

x

sin 3xg is a fundamental set of solutions for the complementary equation.

If y

p

D Ae

x=2

, then y

00

p

C 2y

0

p

C 10y

p

D p.1=2/Ae

x=2

D

45

4

Ae

x=2

D e

x=2

if A D

4

45

. Therefore,

y

p

D

4

45

e

x=2

is a particular sol ution and y D

4

45

e

x=2

Ce

x

.c

1

cos 3xCc

2

sin 3x/ is the general solution.

5.3.22. The characteristic polynomial of the complementary equation is p.r/ D r

2

 7r C 12 D .r 

4/.r 3/. If y

p

D Ae

4x

, then y

00

p

7y

0

p

C12y

p

D p.4/Ae

4x

D 0 e

4x

D 0, so y

00

p

7y

0

p

C12y

p

¤ 5e

4x

for any choice of A.

5.3.24. The characteristic polynomial of the complementary equation is p.r/ D r

2

8r C16 D .r 4/

2

,

so fe

4x

; xe

4x

g is a fundamental set of solu tions for the complementary equation. If y

p

D A cos x C

B sin x, then y

00

p

8y

0

p

C16y

p

D .A cos xCB sin x/8.A si n xCB cos x/C16.A cos x CB sin x/ D

.15A 8B/ cos x C.8A C15B/ sin x, so 15A 8B D 23; 8A C15B D 7, which implies that A D 1

and B D 1. Hence y

p

D cos x  sin x and y D cos x  sin x C e

4x

.c

1

C c

2

x/ is the general solution.

5.3.26. The characteristic polynomial of the complementary equation is p.r/ D r

2

2r C3 D .r 1/

2

C2,

so fe

x

cos

p

2x; e

x

sin

p

2xg is a fundamental set of solutions f or the complementary equation. If y

p

D

A cos 3x C B sin 3x, then y

00

p

 2y

0

p

C 3y

p

D 9.A cos 3x C B sin 3x/  6.A sin 3x C B cos 3x/ C

3.A cos 3x CB sin 3x/ D .6A C6B/ cos 3x C.6A 6B/ sin 3x, so 6A 6B D 6; 6A 6B D 6,

which implies that A D 1 and B D 0. Hence y

p

D cos 3x is a particular solution and y D cos 3x C

e

x

.c

1

cos

p

2x Cc

2

sin

p

2x/ is the general solution.

5.3.28. The characteristic po lynomial of the complementary equation is p.r/ D r

2

C 7r C 12 D .r C

3/.r C 4/, so fe

4x

; e

3x

g is a fundamental set o f solutions for the complementary equation. If y

p

D

A cos 2x CB sin 2x, then y

00

p

C7y

0

p

C12y

p

D 4.A cos 2x CB sin 2x/ C14.A si n 2x CB cos 2x/ C

12.A cos x CB si n x/ D .8AC14B/ cos 2x C.8B 14a/ sin2x, so 8AC14B D 2; 14AC8B D 36,

which implies that A D 2 and B D 1. Hence y

p

D 2 cos 2x C sin 2x is a part icular solution and

(A) y D 2 cos 2x C sin 2x C c

1

e

4x

C c

2

e

3x

is the general solution. Differentiating (A) yields

y

0

D 2 sin 2x C 2 cos 2x  4c

1

e

4x

 3c

2

e

3x

. Now y.0/ D 3 ) 3 D 2 C c

1

C c

2

and y

0

.0/ D

3 ) 3 D 2  4c

1

 3c

2

. Therefore, c

1

D 2 and c

2

D 3, so y D 2 cos 2x C sin 2x C 2e

4x

 3e

3x

is the solution of the initial value problem.

60 Chapter 5

Linear Second Order Equations I

5.3.30. fcos !

0

x; sin!

0

xg is a fundamental set of solutions of the complementary equation. If y

p

D

A cos !x C B sin !x, then y

00

p

C !

2

0

y

p

D !

2

.A cos !x C B sin !x/ C !

2

0

.A cos !x C B sin !x/ D

.!

2

0

 !

2

/.A cos !x C B sin !x/ D M cos !x C N sin !x if A D

M

!

2

0

 !

2

and B D

N

!

2

0

 !

2

.

Therefore,

y

p

D

1

!

2

0

 !

2

.M cos !x C N sin !x/

is a particular solution of t he given equation and

y D

1

!

2

0

 !

2

.M cos !x C N sin !x/ C c

1

cos !

0

x Cc

2

sin !

0

x

is the general solution.

5.3.32. If y

p

D A cos !x C B sin !x, then ay

00

p

C by

0

p

C cy

p

D a!

2

.A cos !x C B sin !x/ C

b!.A sin !xCB cos !x/Cc.A cos !xCB sin !x/ D



.c  a!

2

/A C b!B



cos !xC



b!A C .c  a!

2

/B



sin !x.

Therefore, y

p

is a solution of (A) if and only if the set of equations (B) .c  a!

2

/A C b!B D

M; b!A C .c  a!

2

/B D N has a solution. If .c  a!

2

/

2

C .b!/

2

¤ 0, then (B) has the so-

lution A D

.c  a!

2

/M  b!N

.c  a!

2

/

2

C .b!/

2

, B D

.c  a!

2

/N C b!M

.c  a!

2

/

2

C .b!/

2

, and y

p

D A cos !x C B sin !x is a

solution of (A). If .c a!

2

/

2

C.b!/

2

D 0 (which is true if and only if the left side of (A) is of the form

a.y

00

C!

2

y/, then the coefﬁcients of A and B in (B) are all zero, so (B) does not have a solution, so (A)

does n ot have a solution of the form y

p

D A cos !x C B sin !x.

5.3.34. From Exercises 5.3.2 and 5.3.17, y

p

1

D 1 C x and y

p

2

D e

2x

are particular solutions of

y

00

4y

0

C5y D 1C5x and y

00

4y

0

C5y D e

2x

respectively, and fe

2x

cos x; e

2x

sin xgis a fundamental

set of solutions of the complementary equation. Therefore,y

p

D y

p

1

Cy

p

2

D 1 Cx Ce

2x

is a particular

solution of the given equation, and y D 1 C x C e

2x

.1 C c

1

cos x C c

2

sin x/ is the general solution.

5.3.36. From Exercises 5.3.4 and 5.3.19, y

p

1

D 1  x

2

and y

p

2

D e

x

are particular solutions of

y

00

 4y

0

C 4y D 2 C8x  4x

2

and y

00

 4y

0

C4y D e

x

respectively, and fe

2x

; xe

2x

g is a fundamental

set of solutions of the complementary equation. Therefore,y

p

D y

p

1

Cy

p

2

D 1 x

2

Ce

x

is a particular

solution of the given equation, and y D 1  x

2

C e

x

C e

2x

.c

1

C c

2

x/ is the general solution.

5.3.38. From Exercises 5.3.6 and 5.3.21, y

p

1

D 1 C 2x and y

p

2

D e

3x

are particular solutions of

y

00

C6y

0

C10y D 22 C20x and y

00

C6y

0

C10y D e

3x

respectively, and fe

3x

cos x; e

3x

sin xg is a

fundamental set of solutions of the complementary equation. Therefore,y

p

D y

p

1

Cy

p

2

D 1C2x Ce

3x

is a parti cular solution of the given equatio n, and y D 1 C 2x C e

3x

.1 C c

1

cos x C c

2

sin x/ is the

general solution.

5.3.40. Letting c

1

D c

2

D 0 shows that ( A) y

00

p

C p.x/y

0

p

C q.x/y

p

D f . Letting c

1

D 1 and c

2

D 0

shows that (B) .y

1

C y

p

/

00

C p.x/.y

1

C y

p

/

0

C q.x/.y

1

C y

p

/ D f . Now subtract (A) from (B) to see

that y

00

1

C p.x/y

0

1

C q.x/y

1

D 0. Letting c

1

D 0 and c

2

D 1 shows that (C) .y

2

C y

p

/

00

C p.x/.y

2

C

y

p

/

0

Cq.x/.y

2

C y

p

/ D f . Now subtract (A) from (C) to see that y

00

2

C p.x/y

0

2

C q.x/y

2

D 0.

5.4 THE METHOD OF UNDETERMINED C OEFFICIENTS I

5.4.2. If y D ue

3x

, then y

00

6y

0

C5y D e

3x

Œ.u

00

 6u

0

C 9u/  6.u

0

 3u/ C 5u D e

3x

.358x/,

so u

00

12u

0

C32u D 358x and u

p

D ACBx, where 12BC32.ACBx/ D 358x. Therefore,32B D

8, 32A 12B D 35, so B D 

1

4

, A D 1, and u

p

D 1 

x

4

. Therefore, y

p

D e

3x



1 

x

4



.

Section 5.4

The Method of Undetermined Coefﬁcients I

61

5.4.4. I f y D ue

2x

, then y

00

C 2y

0

Cy D e

2x

Œ.u

00

C4u

0

C 4u/ C 2.u

0

C2u/ C u D e

2x

.7  15x C

9x

2

/ so u

00

C 6u

0

C 9u D 7  15x C 9x

2

and u

p

D A C Bx C Cx

2

, where 2C C 6.B C 2Cx/ C

9.A C Bx C Cx

2

/ D 7  15x C 9x

2

. Therefore,9C D 9, 9B C 12C D 15, 9A C 6B C 2C D 7,

so C D 1, B D 3, A D 1, and u

p

D 1  3x C x

2

. Therefore,y

p

D e

2x

.1  3x C x

2

/.

5.4.6. If y D ue

x

, then y

00

 y

0

 2y D e

x

Œ.u

00

C 2u

0

C u/  .u

0

Cu/  2u D e

x

.9 C 2x  4x

2

/ so

u

00

Cu

0

2u D 9 C2x 4x

2

, and u

p

D A CBx CCx

2

, where 2C C.B C2Cx/ 2.A CBx CCx

2

/ D

9 C2x 4x

2

. Therefore,2C D 4, 2B C2C D 2, 2A CB C2C D 9, so C D 2, B D 1, A D 2,

and u

p

D 2 C x C 2x

2

. Therefore, y

p

D e

x

.2 C x C 2x

2

/.

5.4.8. If y D ue

x

, t hen y

00

 3y

0

C 2y D e

x

Œ.u

00

C 2u

0

C u/  3.u

0

C u/ C 2u D e

x

.3  4x/, so

u

00

 u

0

D 3  4x and u

p

D Ax C Bx

2

, where 2B  .A C 2Bx/ D 3  4x. Therefore,2B D 4,

A C 2B D 3, so B D 2, A D 1, and u

p

D x.1 C 2x/. Therefore,y

p

D xe

x

.1 C 2x/.

5.4.10. If y D ue

2x

, then 2y

00

 3y

0

 2y D e

2x

Œ2.u

00

C 4u

0

C 4u/  3.u

0

C 2u/  2u D e

2x

.6 C

10x/, so 2u

00

C 5u

0

D 6 C 10x and u

p

D Ax C Bx

2

, wher e 2.2B/ C 5.A C 2Bx/ D 6 C 10x.

Therefore,10B D 10, 5A C 4B D 6, so B D 1, A D 2, and u

p

D x.2 C x/. Therefore,y

p

D

xe

2x

.2 C x/.

5.4.12. If y D ue

x

, then y

00

 2y

0

C y D e

x

Œ.u

00

C 2u

0

C u/  2.u

0

C u/ C u D e

x

.1  6x/, so

u

00

D 16x Integrating twice and taking the constants of integration to be zero yields u

p

D x

2



1

2

 x



.

Therefore, y

p

D x

2

e

x



1

2

 x



.

5.4.14. If y D ue

x=3

, then 9y

00

C 6y

0

C y D e

x=3



9



u

00



2u

0

3

C

u

9



C 6



u

0



u

3



C u



D

e

x=3

.2  4x C 4x

2

/, so 9u

00

D 2  4x C 4x

2

, or u

00

D

1

9

.2  4x C 4x

2

/. Integrating twice

and taking the constants of integration to be zero yields u

p

D

x

2

27

.3  2x C x

2

/. Therefore, y

p

D

x

2

e

x=3

27

.3  2x C x

2

/.

5.4.16. If y D ue

x

, then y

00

 6y

0

C 8y D e

x

Œ.u

00

C 2u

0

C u/  6.u

0

C u/ C 8u D e

x

.11  6x/, so

u

00

4u

0

C3u D 11 6x and u

p

D ACBx, where 4B C3.A CBx/ D 11 6x. Therefore,3B D 6,

3A  4B D 11, so B D 2, A D 1 and u

p

D 1  2x. Therefore,y

p

D e

x

.1  2x/. The characteristic

polynomial of the complementary equation is p.r/ D r

2

 6r C 8 D .r  2/.r  4/, so fe

2x

; e

4x

g is a

fundamental set of solutions of the complementary equati on. Therefore, y D e

x

.12x/Cc

1

e

2x

Cc

2

e

4x

is the general solution of the nonhomogeneous equation.

5.4.18. If y D ue

x

, then y

00

C 2y

0

 3y D e

x

Œ.u

00

C 2u

0

C u/ C 2.u

0

C u/  3u D 16xe

x

, so

u

00

C 4u

0

D 16x and u

p

D Ax C Bx

2

, where 2B C 4.A C 2Bx/ D 16x. Therefore,8B D 16,

4AC2B D 0, so B D 2, A D 1, and u

p

D x.12x/. Therefore,y

p

D xe

x

.12x/. The characteristic

polynomial of the complementary equation is p.r/ D r

2

C 2r  3 D .r C 3/.r  1/, so fe

x

; e

3x

g is a

fundamental set of sol utions of the complementary equation. Therefore, y D xe

x

.12x/Cc

1

e

x

Cc

2

e

3x

is the general solution of the nonhomogeneous equation.

5.4.20. If y D ue

2x

, then y

00

4y

0

5y D e

2x

Œ.u

00

C 4u

0

C 4u/  4.u

0

C 2u/  5u D 9e

2x

.1Cx/, so

u

00

9u D 9 C9x and u

p

D A CBx, where 9.A CBx/ D 9 C9x. Therefore,9B D 9, 9A D 9,

so B D 1, A D 1, and u

p

D 1  x. Therefore,y

p

D e

2x

.1 C x/. The characteristic polynomial

of th e complementary equation is p.r/ D r

2

 4r 5 D .r  5/.r C 1/, so fe

x

; e

5x

g is a fundamental

62 Chapter 5

Linear Second Order Equations I

set of solutions o f the complementary equation. Therefore,(A) y D e

2x

.1 C x/ C c

1

e

x

C c

2

e

5x

is

the general solution of the nonhomogeneous equation. Differentiating (A) yields y

0

D 2e

2x

.1 C x/ 

e

2x

 c

1

e

x

C 5c

2

e

5x

. Now y.0/ D 0; y

0

.0/ D 10 ) 0 D 1 C c

1

C c

2

; 10 D 3  c

1

C 5c

2

, so

c

1

D 2, c

2

D 1. Therefore,y D e

2x

.1 C x/ C2e

x

e

5x

is the solution of the initial value problem.

5.4.22. If y D ue

x

, then y

00

C4y

0

C3y D e

x

Œ.u

00

 2u

0

C u/ C 4.u

0

 u/ C 3u D e

x

.2C8x/, so

u

00

C2u

0

D 2 8x and u

p

D Ax CBx

2

, where 2B C 2.A C2Bx/ D 2 8x. Therefore,4B D 8,

2A C 2B D 2, so B D 2, A D 1, and u

p

D x.1  2x/. Therefore,y

p

D xe

x

.1  2x/. The

characteristic polynomial of the complementary equation is p.r/ D r

2

C 4r C 3 D .r C 3/.r C 1/,

so fe

x

; e

3x

g is a fundamental set of solutions of the complementary equation. Therefore,(A) y D

xe

x

.12x/Cc

1

e

x

Cc

2

e

3x

is the general solu tion of the nonhomogeneous equation. Differentiating

(A) yields y

0

D xe

x

.1  2x/ Ce

x

.1  4x/  c

1

e

x

 3c

2

e

3x

. Now y.0/ D 1; y

0

.0/ D 2 ) 1 D

c

1

Cc

2

; 2 D 1 c

1

3c

2

, so c

1

D 2, c

2

D 1. Therefore,y D e

x

.2 Cx 2x

2

/ e

3x

is the solution

of th e initial value problem.

5.4.24. We must ﬁnd part icular sol utions y

p

1

and y

p

2

of (A) y

00

C y

0

C y D xe

x

and (B) y

00

C

y

0

C y D e

x

.1 C 2x/, respectively. To ﬁnd a particular solution of (A) we write y D ue

x

. Then

y

00

C y

0

C y D e

x

Œ.u

00

C 2u

0

C u/ C .u

0

C u/ C u D xe

x

so u

00

C 3u

0

C 3u D x and u

p

D A C Bx,

where 3B C 3.A C Bx/ D x. Therefore,3B D 1, 3A C 3B D 0, so B D

1

3

, A D 

1

3

, and u

p

D



1

3

.1  x/, so y

p

1

D 

e

x

3

.1  x/. To ﬁn d a particular so lution of (B) we write y D ue

x

. Then

y

00

C y

0

C y D e

x

Œ.u

00

 2u

0

C u/ C .u

0

 u/ Cu D e

x

.1 C 2x/, so u

00

 u

0

C u D 1 C 2x and

u

p

D A C Bx, where B C .A C Bx/ D 1 C 2x. Therefore, B D 2, A  B D 1, so A D 3, and

u

p

D 2 C 3x, so y

p

2

D e

x

.3 C 2x/. Now y

p

D y

p

1

C y

p

2

D 

e

x

3

.1  x/ C e

x

.3 C 2x/.

5.4.26. We must ﬁnd particular so lutions y

p

1

and y

p

2

of (A) y

00

 8y

0

C 16y D 6xe

4x

and (B ) y

00



8y

0

C16y D 2 C16x C16x

2

, respectively. To ﬁnd a particular solu tion of (A) we write y D ue

4x

. Then

y

00

 8y

0

C 16y D e

x

Œ.u

00

C 8u

0

C 16u/  8.u

0

C 4u/ C 16u D 6xe

4x

, so u

00

D 6x, u

p

D x

3

. and

y

p

1

D x

3

e

4x

. To ﬁnd a particular solution of (B) we write y

p

D ACBxCCx

2

. Then y

00

p

8y

0

p

C16y

p

D

2C 8.B C2Cx/C16.ACBxCCx

2

/ D .16A8B C2C /C.16B 16C /xC16Cx

2

D 2C16xC16x

2

if 16C D 16, 16B  16C D 16, 16A  8B C 2C D 2. Therefore,C D 1, B D 2, A D 1, and

y

p

2

D 1 C 2x C x

2

. Now y

p

D y

p

1

C y

p

2

D x

3

e

4x

C 1 C 2x C x

2

.

5.4.28. We must ﬁnd particular solutions y

p

1

and y

p

2

of (A) y

00

 2y

0

C 2y D e

x

.1 C x/ and (B)

y

00

2y

0

C2y D e

x

.2 8x C5x

2

/, respectively. To ﬁnd a particular solution of (A) we wr ite y D ue

x

.

Then y

00

 2y

0

C 2y D e

x

Œ.u

00

C 2u

0

C u/  2.u

0

C u/ C 2u D e

x

.1 C x/, so u

00

C u D 1 C x and

u

p

D 1 C x, so y

p

1

D e

x

.1 C x/. To ﬁnd a particular solution of (B) we write y D ue

x

. Then

y

00

 2y

0

C 2y D e

x

Œ.u

00

 2u

0

C u/  2.u

0

 u/ C 2u D e

x

.2  8x C 5x

2

/, so u

00

 4u

0

C 5u D

2 8x C5x

2

and u

p

D A CBx CCx

2

, where 2C 4.B C2Cx/ C5.A CBx CCx

2

/ D 2 8x C5x

2

.

Therefore,5C D 5, 5B  8C D 8, 5A  4B C 2C D 2, so C D 1, B D 0, A D 0, and u

p

D x

2

.

Therefore,y

p

2

D x

2

e

x

. Now y

p

D y

p

1

C y

p

2

D e

x

.1 C x/ C x

2

e

x

.

5.4.30. (a) If y D ue

˛x

, t hen ay

00

C by

0

C cy D e

˛x



a.u

00

C 2˛u

0

C ˛

2

u/ C b.u

0

C ˛u/ C cu



D

e

˛x



au

00

C .2a˛ C b//u

0

C .a˛

2

C b˛ Cc/u



D e

˛x

.au

00

Cp

0

.˛/u

0

Cp.˛/u/. Therefore,ay

00

Cby

0

C

cy D e

˛x

G.x/ if and only if au

00

C p

0

.˛/u

0

C p.˛/u D G.x/.

(b) Substituting u

p

D A C Bx C Cx

2

C Dx

3

into (B) yields

a.2C C 6Dx/ C p

0

.˛/.B C2Cx C 3Dx

2

/ C p.˛/.A C Bx C Cx

2

C Dx

3

/

D Œp.˛/A C p

0

.˛/B C 2aC  C Œp.˛/B C 2p

0

.˛/C C 6aDx

CŒp.˛/C C 3p

0

.˛/Dx

2

C p.˛/Dx

3

D g

0

Cg

1

x C g

2

x

2

C g

3

x

3

Section 5.4

The Method of Undetermined Coefﬁcients I

63

if

p.˛/D D g

3

p.˛/C C 3p

0

.˛/D D g

2

p.˛/B C2p

0

.˛/C C 6aD D g

1

p.˛/A C p

0

.˛/B C 2aC D g

0

:

.C/

Since e

˛x

is n ot a solution of the complementary equation, p.˛/ ¤ 0. Therefore,the triangular syst em

(C) can be solved successively for D, C , B and A.

(c) Since e

˛x

is a solution of the complementary equation while xe

˛x

is not, p.˛/ D 0 and p

0

.˛/ ¤ 0.

Therefore, ( B) reduces to (D) au

00

Cp

0

.˛/u D G.x/. Substituting u

p

D Ax CBx

2

CCx

3

CDx

4

into

(D) yields

a.2B C 6Cx C 12Dx

2

/ C p

0

.˛/.A C 2Bx C 3Cx

2

C 4Dx

3

/

D .p

0

.˛/A C 2aB/ C .2p

0

.˛/B C 6aC /x C .3p

0

.˛/C C 12aD/x

2

C4p

0

.˛/Dx

3

D g

0

C g

1

x C g

2

x

2

C g

3

x

3

if

4p

0

.˛/D D g

3

3p

0

.˛/C C 12aD D g

2

2p

0

.˛/B C 6aC D g

1

p

0

.˛/A C 2aB D g

0

:

Since p

0

.˛/ ¤ 0 this triangular system can be solved successively for D, C , B and A.

(d) Since e

˛x

and xe

˛x

are solu tions of t he complementary equation, p.˛/ D 0 and p

0

.˛/ D 0.

Therefore, (B) reduces to (D) au

00

D G.x/, so u

00

D

G.x/

a

. Integrating this twice and taking the

constants of integr at ion yields the particular solution u

p

D x

2



g

0

2

C

g

1

6

x C

g

2

12

x

2

C

g

3

20

x

3



.

5.4.32. If y

p

D Axe

4x

, then y

00

p

7y

0

p

C12y

p

D Œ.8 C16x/ 7.1 C4x/ C12xAe

4x

D Ae

4x

D 5e

4x

if A D 1, so y

p

D 5xe

4x

.

5.4.34. If y

p

D e

3x

.A C Bx C Cx

2

/, then

y

00

p

 3y

0

p

C 2y

p

D e

3x

Œ.9A C6B C 2C / C .9B C 12C /x C 9Cx

2



3e

3x

Œ.3A C B/ C .3B C 2C /x C 3Cx

2



C2e

3x

.A C Bx C Cx

2

/

D e

3x

Œ.2A C 3B C 2C / C .2B C 6C /x C 2Cx

2



D e

3x

.1 C 2x C x

2

/

if 2C D 1; 2B C 6C D 2; 2A C 3B C 2C D 1. Therefore,C D

1

2

, B D 

1

2

, A D 

1

4

, and

y

p

D 

e

3x

4

.1 C 2x  2x

2

/.

5.4.36. If y

p

D e

x=2

.Ax

2

C Bx

3

C Cx

4

/, then

4y

00

p

C 4y

0

p

C y

p

D e

x=2

Œ8A  .8A  24B/x C .A  12B C 48C /x

2



Ce

x=2

Œ.B  16C /x

3

C Cx

4



Ce

x=2

Œ8Ax  .2A  12B/x

2

 .2B  16C /x

3

 2Cx

4



Ce

x=2

.Ax

2

C Bx

3

C Cx

4

/

D e

x=2

.8A C 24Bx C 48Cx

2

/ D e

x=2

.8 C 48x C 144x

2

/

64 Chapter 5

Linear Second Order Equations

if 48C D 144, 24B D 48, and 8A D 8. Therefore,C D 3, B D 2, A D 1, and y

p

D x

2

e

x=2

.1 C

2x C 3x

2

/.

5.4.38. If y D

R

e

˛x

P.x/ dx, then y

0

D e

˛x

P.x/. Let y D ue

˛x

; then .u

0

C˛u/e

˛x

D e

˛x

P.x/, which

implies (A). We must show that i t is possible to choose A

0

; : : : ; A

k

so that (B) .A

0

CA

1

x CA

k

x

k

/

0

C

˛.A

0

C A

1

x C A

k

x

k

/ D p

0

C p

1

x C  C p

k

x

k

. By equating the coefﬁcients of x

k

; x

k1

; : : : ; 1

(in that order) on the two sides of (B), we see that (B) holds if and onl y if ˛A

k

D p

k

and .k  j C

1/A

kj C1

C˛A

k

D p

kj

; 1  j  k.

5.4.40. If y D

R

x

k

e

˛x

dx, then y

0

D x

k

e

˛x

. Let y D ue

˛x

; then .u

0

C ˛u/e

˛x

D x

k

e

˛x

, so

u

0

C ˛u D x

k

. This equation has a particular solution u

p

D A

0

C A

1

x C A

k

x

k

, where (A) .A

0

C

A

1

x  C A

k

x

k

/

0

C ˛.A

0

C A

1

x  C A

k

x

k

/ D x

k

. By equating the coefﬁcients of x

k

; x

k1

; : : : ; 1

on the two sides of (A), we see th at (A) holds if and only if ˛A

k

D 1 and .k  j C 1/A

kj C1

C

˛A

k

 j D 0; 1  j  k. Therefore, A

k

D

1

˛

, A

k1

D 

k

˛

2

, A

k2

D

k.k  1/

˛

3

, and, in general,

A

kj

D .1/

j

k.k  1/ .k  j C 1/

˛

j C1

D

.1/

j

kŠ

˛

j C1

.k  j /Š

; 1  j  k. By introducing the index

r D k  j we can rewrite this as A

r

D

.1/

kr

kŠ

˛

krC1

rŠ

; 0  r  k. Therefore, u

p

D

.1/

k

kŠ

˛

kC1

k

X

rD0

.˛x/

r

rŠ

and y D

.1/

k

kŠe

˛x

˛

kC1

k

X

rD0

.˛x/

r

rŠ

C c.

5.5 THE METHOD OF UNDETERMINED C OEFFICIENTS II

5.5.2. Let

y

p

D .A

0

C A

1

x/ cos x C .B

0

C B

1

x/ sin xI then

y

0

p

D .A

1

C B

0

C B

1

x/ cos x C .B

1

 A

0

 A

1

x/ sin x

y

00

p

D .2B

1

 A

0

 A

1

x/ cos x  .2A

1

C B

0

CB

1

x/ sin x; so

y

00

p

C 3y

0

p

C y

p

D .3A

1

C 3B

0

C2B

1

C 3B

1

x/ cos x

C.3B

1

 3A

0

 2A

1

 3A

1

x/ sin x

D .2  6x/ cos x  9 sin x

if 3B

1

D 6, 3A

1

D 0, 3B

0

C 3A

1

C 2B

1

D 2, 3A

0

C 3B

1

C 2A

1

D 9. Therefore,A

1

D 0,

B

1

D 2, A

0

D 1, B

0

D 2, and y

p

D cos x C .2  2x/ sin x.

5.5.4. Let y D ue

2x

. Then

y

00

C 3y

0

 2y D e

2x



.u

00

C 4u

0

C 4u/ C 3.u

0

C 2u/  2u



D e

2x

.u

00

C 7u

0

C 8u/ D e

2x

.5 cos 2x C 9 sin 2x/

if u

00

C 7u

0

C 8u D 5 cos 2x  9 sin 2x. Now let u

p

D A cos 2x C B sin 2x. Then

u

00

p

C 7u

0

p

C8u

p

D 4.A co s 2x C B sin 2x/ C 14.A sin 2x C B cos 2x/

C8.A cos 2x C B sin 2x/

D .4A C 14B/ cos 2x  .14A  4B/ sin 2x

D 5 cos 2x  9 sin 2x

Section 5.5

The Method of Undetermined Coefﬁcients II

65

if 4A C 14B D 5, 14A C 4B D 9. Therefore,A D

1

2

, B D 

1

2

,

u

p

D

1

2

.cos 2x  sin 2x/; and y

p

D

e

2x

2

.cos 2x  sin 2x/:

5.5.6. Let y D ue

2x

. Then

y

00

C 3y

0

 2y D e

2x



.u

00

 4u

0

C 4u/ C 3.u

0

 2u/  2u



D e

2x

.u

00

 u

0

 4u/

D e

2x

Œ.4 C 20x/ cos 3x C .26  32x/ sin 3x

if u

00

 u

0

 4u D .4 C20x/ cos 3x C .26  32x/ sin 3x. Let

u

p

D .A

0

C A

1

x/ cos 3x C .B

0

CB

1

x/ sin 3xI then

u

0

p

D .A

1

C 3B

0

C 3B

1

x/ cos 3x C .B

1

 3A

0

 3A

1

x/ sin 3x

u

00

p

D .6B

1

 9A

0

 9A

1

x/ cos 3x  .2A

1

C 9B

0

C 9B

1

x/ sin 3x; so

u

00

p

 u

0

p

 4u

p

D Œ13A

0

C A

1

C 3B

0

 6B

1

C .13A

1

C 3B

1

/x cos 3x

Œ13B

0

C B

1

 3A

0

C 6A

1

C .13B

1

 3A

1

/x sin 3x

D .4 C 20x/ cos 3x C .26  32x/ sin 3x if

13A

1

 3B

1

D 20

3A

1

 13B

1

D 32

and

13A

0

 3B

0

 A

1

C 6B

1

D 4

3A

0

 13B

0

 6A

1

 B

1

D 26:

From the ﬁrst two equations, A

1

D 2, B

1

D 2. Substituti ng these in the last two equations yields

13A

0

 3B

0

D 10, 3A

0

 13B

0

D 16. Solv ing this pair yields A

0

D 1, B

0

D 1. Therefore,

u

p

D .1  2x/.cos 3x  sin 3x/ and y

p

D e

2x

.1  2x/.cos 3x  sin 3x/:

5.5.8. Let

y

p

D .A

0

x C A

1

x

2

/ cos x C .B

0

x CB

1

x

2

/ sin xI then

y

0

p

D



A

0

C .2A

1

C B

0

/x CB

1

x

2



cos x C



B

0

C .2B

1

 A

0

/x  B

1

x

2



sin x

y

00

p

D



2A

1

C 2B

0

 .A

0

 4B

1

/x  A

1

x

2



cos x

C



2B

1

 2A

0

 .B

0

C 4A

1

/x  B

1

x

2



sin x; so

y

00

p

C y

p

D .2A

1

C 2B

0

C 4B

1

x/ cos x C .2B

1

 2A

0

 4A

1

x/ sin x

D .4 C 8x/ cos x C .8  4x/ sin x

if 4B

1

D 8, 4A

1

D 4, 2B

0

C 2A

1

D 4, 2A

0

C 2B

1

D 8. Therefore, A

1

D 1, B

1

D 2, A

0

D 2,

B

0

D 3, and y

p

D x Œ.2  x/ cos x C .3  2x/ sin x.

5.5.10. Let y D ue

x

. Then

y

00

C 2y

0

C 2y D e

x



.u

00

 2u

0

C u/ C 2.u

0

 u/ C 2u



D e

x

.u

00

Cu/ D e

x

.8 cos x  6 sin x/

66 Chapter 5

Linear Second Order Equations

if u

00

C u D 8 cos x  6 sin x. Now let

u

p

D Ax cos x C Bx sin xI then

u

0

p

D .A C Bx/ cos x C .B  Ax/ sin x

u

00

p

D .2B  Ax/ cos x  .2A C Bx/ sin x; so

u

00

p

C u

p

D 2B cos x  2A sin x D 8 co s x  6 sin x

if 2B D 8, 2A D 6. Therefore,A D 3, B D 4, u

p

D x.3 cos x C 4 sin x/, and y

p

D xe

x

.3 cos x C

4 sin x/.

5.5.12. Let

y

p

D .A

0

CA

1

x C A

2

x

2

/ cos x C .B

0

CB

1

x C B

2

x

2

/ sin xI then

y

0

p

D



A

1

C B

0

C .2A

2

C B

1

/x C B

2

x

2



cos x

C



B

1

 A

0

C .2B

2

 A

1

/x  A

2

x

2



sin x;

y

00

p

D



A

0

C 2A

2

C 2B

1

 .A

1

 4B

2

/x  A

2

x

2



cos x

C



B

0

C 2B

2

 2A

1

 .B

1

C 4A

2

/x  B

2

x

2



sin x; so

y

00

p

C 2y

0

p

C y

p

D 2



A

1

C A

2

C B

0

C B

1

C.2A

2

C B

1

C 2B

2

/x C B

2

x

2



cos x

C2



B

1

C B

2

 A

0

 A

1

C .2B

2

 A

1

 2A

2

/x  A

2

x

2



sin x

D 8x

2

cos x 4x sin x if

(i)

2B

2

D 8

2A

2

D 0

; (ii)

2B

1

C 4A

2

C 4B

2

D 0

2A

1

 4A

2

C 4B

2

D 4

;

(iii)

2B

0

C 2A

1

C 2B

1

C 2A

2

D 0

2A

0

 2A

1

C 2B

1

C 2B

2

D 0

:

From (i), A

2

D 0, B

2

D 4. Substituting these int o (ii) and solving for A

1

and B

1

yields A

1

D 10,

B

1

D 8. Substituting the known coefﬁcient s into (iii) and solving for A

0

and B

0

yields A

0

D 14,

B

0

D 2. Therefore,y

p

D .14  10x/ cos x  .2 C 8x  4x

2

/ sin x.

5.5.14. Let

y

p

D .A

0

C A

1

x C A

2

x

2

/ cos 2x C .B

0

CB

1

x C B

2

x

2

/ sin 2xI then

y

0

p

D



A

1

C 2B

0

C .2A

2

C 2B

1

/x C 2B

2

x

2



cos 2x

C



B

1

 2A

0

C .2B

2

 2A

1

/x  2A

2

x

2



sin 2x

y

00

p

D



4A

0

C 2A

2

C 4B

1

 .4A

1

 8B

2

/x  4A

2

x

2



cos 2x

C



4B

0

 2B

2

 4A

1

 .4B

1

C8A

2

/x  4B

2

x

2



sin 2x; so

y

00

p

C3y

0

p

C 2y

p

D Œ2A

0

C 3A

1

C 4A

2

C 6B

0

C 4B

1

.2A

1

 6A

2

 6B

1

 8B

2

/x  .2A

2

 6B

2

/x

2



cos 2x

CŒ2B

0

C 3B

1

C 4B

2

 6A

0

 4A

1

.2B

1

 6B

2

C 6A

1

C 8A

2

/x  .2B

2

C 6A

2

/x

2



sin 2x

D .1  x 4x

2

/ cos 2x .1 C 7x C 2x

2

/ sin 2x if

Section 5.5

The Method of Undetermined Coefﬁcients II

67

(i)

2A

2

C 6B

2

D 4

6A

2

 2B

2

D 2

; (ii)

2A

1

C 6B

1

C 6A

2

C 8B

2

D 1

6A

1

 2B

1

 8A

2

C 6B

2

D 7

;

(iii)

2A

0

C 6B

0

C 3A

1

C 4B

1

C 2A

2

D 1

6A

0

 2B

0

 4A

0

C 3B

1

C 2B

2

D 1

:

From (i), A

2

D

1

2

, B

2

D 

1

2

. Substituting these int o (ii) and solving for A

1

and B

1

yields A

1

D 0,

B

1

D 0. Substituting the known coefﬁcients into (iii) and solving for A

0

and B

0

yields A

0

D 0, B

0

D 0.

Therefore, y

p

D

x

2

.cos 2x  sin 2x/.

5.5.16. Let y D ue

x

. Then

y

00

 2y

0

C y D e

x



.u

00

C 2u

0

C u/  2.u

0

C u/ C u



D e

x

u

00

D e

x



.3 C 4x  x

2

/ cos x C .3  4x  x

2

/ sin x



if u

00

D .3 C 4x  x

2

/ cos x  .3  4x  x

2

/ sin x. Now let

u

p

D .A

0

C A

1

x C A

2

x

2

/ cos x C .B

0

C B

1

x C B

2

x

2

/ sin xI then

u

0

p

D



A

1

C B

0

C .2A

2

C B

1

/x CB

2

x

2



cos x

C



B

1

 A

0

C .2B

2

 A

1

/x  A

2

x

2



sin x;

u

00

p

D



A

0

C 2A

2

C 2B

1

 .A

1

 4B

2

/x  A

2

x

2



cos x

C



B

0

C 2B

2

 2A

1

 .B

1

C 4A

2

/x  B

2

x

2



sin x

D .3 C 4x  x

2

/ cos x  .3  4x  x

2

/ sin x if

(i)

A

2

D 1

B

2

D 1

; (ii)

A

1

C 4B

2

D 4

B

1

 4A

2

D 4

;

(iii)

A

0

C 2B

1

C 2A

2

D 3

B

0

 2A

1

C 2B

2

D 3

:

From (i), A

2

D 1, B

2

D 1. Substituting these into (ii) and solving for A

1

and B

1

yields A

1

D 0,

B

1

D 0. Substituting the known coefﬁcients into (iii) and solving for A

0

and B

0

yields A

0

D 1, B

0

D 1.

Therefore,u

p

D .1  x

2

/.cos x C sin x/ and y

p

D e

x

.1  x

2

/.cos x C sin x/.

5.5.18. Let y D ue

x

. Then

y

00

C 2y

0

C y D e

x



.u

00

 2u

0

C u/ C 2.u

0

 u/ C u



D e

x

u

00

D e

x

Œ.5  2x/ cos x  .3 C 3x/ sin x

if u

00

D .5  2x/ cos x  .3 C 3x/ sin x. Let

u

p

D .A

0

C A

1

x/ cos x C .B

0

C B

1

x/ sin xI th en

u

0

p

D .A

1

C B

0

C B

1

x/ cos x C .B

1

 A

0

 A

1

x/ sin x

u

00

p

D .2B

1

 A

0

 A

1

x/ cos x  .2A

1

C B

0

C B

1

x/ sin x

D .5  2x/ cos x  .3 C 3x/ sin x

if A

1

D 2, B

1

D 3, A

0

C 2B

1

D 5, B

0

 2A

1

=-3. Therefore, A

1

D 2, B

1

D 3, A

0

D 1,

B

0

D 1, u

p

D e

x

Œ.1 C 2x/ cos x  .1  3x/ sin x, and y

p

D e

x

Œ.1 C 2x/ cos x  .1  3x/ sin x.

68 Chapter 5

Linear Second Order Equations

5.5.20. Let

y

p

D .A

0

x C A

1

x

2

C A

2

x

3

/ cos x C .B

0

x C B

1

x

2

C B

2

x

3

/ sin xI then

y

0

p

D



A

0

C .2A

1

C B

0

/x C .3A

2

C B

1

/x

2

C B

2

x

3



cos x

C



B

0

C .2B

1

 A

0

/x C .3B

2

 A

1

/x

2

 A

2

x

3



sin x

y

00

p

D



2A

1

C 2B

0

 .A

0

 6A

2

 4B

1

/x  .A

1

 6B

2

/x

2

 A

2

x

3



cos x

C



2B

1

 2A

0

 .B

0

C6B

2

C 4A

1

/x  .B

1

C 6A

2

/x

2

 B

2

x

3



sin x; so

y

00

p

C y

p

D



2A

1

C 2B

0

C .6A

2

C 4B

1

/x C 6B

2

x

2



cos x

C



2B

1

 2A

0

C .6B

2

 4A

1

/x  6A

2

x

2



sin x

D .2 C 2x/ cos x C .4 C6x

2

/ sin x if

(i)

6B

2

D 0

6A

2

D 6

; (ii)

4B

1

C 6A

2

D 2

4A

1

C 6B

2

D 0

; (iii)

2B

0

C 2A

1

D 2

2A

0

C 2B

1

D 4

:

From (i), A

2

D 1, B

2

D 0. Substituti ng these into (ii) and solv ing for A

1

and B

1

yields A

1

D 0,

B

1

D 2. Substituting the known coefﬁcients into (iii) and solving for A

0

and B

0

yields A

0

D 0, B

0

D 2.

Therefore,y

p

D x

3

cos x C .x C 2x

2

/ sin x.

5.5.22. Let y D ue

x

. Then

y

00

 7y

0

C 6y D e

x



.u

00

C 2u

0

C u/  7.u

0

C u/ C 6u



D e

x

.u

00

 5u

0

/ D e

x

.17 cos x  7 sin x/

if u

00

 5u

0

D 17 cos x C 7 sin x. Now let u

p

D A cos x C B sin x. Then

u

00

p

 5u

0

p

D .A cos x C B sin x/  5.A sin x C B cos x/

D .A  5B/ cos x  .B  5A/ si n x D 17 cos x C 7 sin x

if A  5B D 17, 5A  B D 7. Therefore,A D 2, B D 3, u

p

D 2 cos x C 3 sin x, and y

p

D

e

x

.2 cos x C 3 sin x/. The characteristic polynomial of the complementary equation is p.r/ D r

2



7r C 6 D .r  1/.r  6/, so fe

x

; e

6x

g is a fundamental set of solutions of th e complementary equation.

Therefore, (A) y D e

x

.2 cos x C3 sin x/ Cc

1

e

x

Cc

2

e

6x

is the general solution of the nonhomogeneous

equation. Differentiating (A) yields y

0

D e

x

.2 cos x C3 sin x/Ce

x

.2 sin x C3 cos x/Cc

1

e

x

C6c

2

e

6x

,

so y.0/ D 4; y

0

.0/ D 2 ) 4 D 2 C c

1

C c

2

; 2 D 2 C 3 C c

1

C 6c

2

) c

1

C c

2

D 2; c

1

C 6c

2

D 3,

so c

1

D 3, c

2

D 1, and y D e

x

.2 cos x C 3 sin x/ C 3e

x

 e

6x

.

5.5.24. Let y D ue

x

. Then

y

00

C 6y

0

C 10y D e

x



.u

00

C 2u

0

C u/ C 6.u

0

C u/ C 10u



D e

x

.u

00

C8u

0

C 17u/ D 40e

x

sin x

if u

00

C 8u

0

C 17u D 40 si n x. Let u

p

D A cos x C B sin x. Then

u

00

p

C 6u

0

p

C 17u

p

D .A cos x C B sin x/ C8.A sin x C B cos x/

C17.A cos x C B sin x/

D .16A C 8B/ cos x  .8A  16B/ sin x D 40 sin x

Section 5.5

The Method of Undetermined Coefﬁcients II

69

if 16A C 8B D 0, 8A C 16B D 40. Therefore,A D 1, B D 2, and y

p

D e

x

.cos x  2 si n x/.

The characteristic polynomial of t he complementary equation is p.r/ D r

2

C 6r C 10 D .r C 3/

2

C 1,

so fe

3x

cos x; e

3x

sin xg is a fundamental set of solutions of the complementary equat ion, and (A)

y D e

x

.cos x  2 sin x/ C e

3x

.c

1

cos x C c

2

sin x/ is the general solution of th e nonhomogeneous

equation. Therefore,y.0/ D 2 ) 2 D 1 C c

1

, so c

1

D 1. Differentiating (A) yields y

0

D e

x

.cos x 

2 sin x/e

x

.sin xC2 cos x/3e

3x

.c

1

cos xCc

2

sin x/Ce

3x

.c

1

sin x Cc

2

cos x/. Therefore,y

0

.0/ D

3 ) 3 D 1  2  3c

1

C c

2

, so c

2

D 1, and y D e

x

.cos x  2 sin x/ C e

3x

.cos x C sin x/.

5.5.26. Let y D ue

3x

. Then

y

00

 3y

0

C 2y D e

3x



.u

00

C 6u

0

C 9u/ 3.u

0

C 3u/ C 2u



D e

3x

.u

00

C 3u

0

C 2u/ D e

3x

Œ21 cos x  .11 C 10x/ sin x

if u

00

C 3u

0

C 2u D 21 cos x  .11 C 10x/ sin x. Now let

u

p

D .A

0

C A

1

x/ cos x C .B

0

C B

1

x/ sin xI then

u

0

p

D .A

1

C B

0

C B

1

x/ cos x C .B

1

 A

0

 A

1

x/ sin x

u

00

p

D .2B

1

 A

0

 A

1

x/ cos x  .2A

1

C B

0

C B

1

x/ sin x; so

u

00

C 3u

0

C 2u D ŒA

0

C 3A

1

C 3B

0

C 2B

1

C .A

1

C 3B

1

/x cos x

CŒB

0

C 3B

1

 3A

0

 2A

1

C .B

1

 3A

1

/x sin x

D 21 cos x  .11 C 10x/ sin x if

A

1

C 3B

1

D 0

3A

1

C B

1

D 10

and

A

0

C 3B

0

C 3A

1

C 2B

1

D 21

3A

0

C B

0

 2A

1

C3B

1

D 11

:

From the ﬁrst two equations A

1

D 3, B

1

D 1. Substit uting these in last two equations yields and

solving for A

0

and B

0

yields A

0

D 2, B

0

D 4. Therefore, u

p

D .2 C 3x/ cos x C .4  x/ sin x and

y

p

D e

3x

Œ.2 C 3x/ cos x C .4  x/ sin x. The characteristic polynomi al of the complementary equati on

is p.r/ D r

2

3r C2 D .r 1/.r 2/, so fe

x

; e

2x

gis a fundamental set of solutions of the complementary

equation, and (A ) y D e

3x

Œ.2 C 3x/ cos x C.4  x/ sin x Cc

1

e

x

Cc

2

e

2x

is the general solution of the

nonhomogeneous equation. Differentiating (A) yields

y

0

D 3e

3x

Œ.2 C 3x/ cos x C .4  x/ sin x

Ce

3x

Œ.7  x/ cos x  .3 C 3x/ sin x C c

1

e

x

C 2c

2

e

2x

:

Therefore,y.0/ D 0; y

0

.0/ D 6 ) 0 D 2 Cc

1

Cc

2

; 6 D 6 C7 Cc

1

C2c

2

, so c

1

Cc

2

D 2; c

1

C2c

2

D

7. Therefore, c

1

D 3, c

2

D 5, and y D e

3x

Œ.2 C 3x/ cos x C .4  x/ sin x C 3e

x

 5e

2x

.

5.5.28. We must ﬁnd parti cular solutions y

p

1

, y

p

2

, and y

p

3

of (A) y

00

C y D 4 cos x  2 sin x and (B)

y

00

Cy D xe

x

, and (C) y

00

Cy D e

x

, respectively. To ﬁnd a particular solution of (A) we write

y

p

1

D Ax cos x C Bx sin xI t hen

y

0

p

1

D .A C Bx/ cos x C .B  Ax/ sin x

y

00

p

1

D .2B  Ax/ cos x  .2A C Bx/ sin x; so

y

00

p

1

Cy

p

1

D 2B cos x 2A sin x D 4 cos x 2 sin x if 2B D 4, 2A D 2. Therefore, A D 1, B D 2,

and y

p

1

D x.cos x C 2 sin x/. To ﬁnd a particu lar solution of (B) we write y D ue

x

. Then

y

00

C y D e

x



.u

00

C 2u

0

Cu/ C u



D e

x

.u

00

C 2u

0

C 2u/ D xe

x

70 Chapter 5

Linear Second Order Equations

if u

00

C 2u

0

C 2u D x. Now u

p

D A C Bx, where 2B C 2.A C Bx/ D x. Therefore, 2B D 1,

2A C 2B D 0, so B D

1

2

, A D 

1

2

, u

p

D 

1

2

.1  x/, and y

p

2

D 

e

x

2

.1  x/. To ﬁnd a particular

solution of (C) we write y

p

3

D Ae

x

. Then y

00

p

3

C y

p

3

D 2Ae

x

D e

x

if 2A D 1, so A D

1

2

and

y

p

3

D

e

x

2

Now y

p

D y

p

1

C y

p

2

C y

p

3

D x.cos x C 2 sin x/ 

e

x

2

.1  x/ C

e

x

2

.

5.5.30. We must ﬁn d particular solution s y

p

1

, y

p

2

and y

p

3

of (A) y

00

 2y

0

C 2y D 4xe

x

cos x, (B)

y

00

 2y

0

C 2y D xe

x

, and (C) y

00

 2y

0

C 2y D 1 C x

2

, respectively. To ﬁnd a particular solution of

(A) we write y D ue

x

. Then y

00

2y

0

C2y D e

x

Œ.u

00

C 2u

0

C u/  2.u

0

C u/ C 2u D e

x

.u

00

Cu/ D

4xe

x

cos x if u

00

C u D 4x cos x. Now let

u

p

D .A

0

x C A

1

x

2

/ cos x C .B

0

x C B

1

x

2

/ sin xI then

u

0

p

D



A

0

C .2A

1

C B

0

/x C B

1

x

2



cos x C



B

0

C .2B

1

 A

0

/x  B

1

x

2



sin x

u

00

p

D



2A

1

C 2B

0

 .A

0

 4B

1

/x  A

1

x

2



cos x

C



2B

1

 2A

0

 .B

0

C4A

1

/x  B

1

x

2



sin x; so

u

00

p

C u

p

D .2A

1

C 2B

0

C4B

1

x/ cos x C .2B

1

 2A

0

 4A

1

x/ sin x

D 4x cos x

if 4B

1

D 4, 4A

1

D 0, 2B

0

C 2A

1

D 0, 2A

0

C 2B

1

D 0. Therefore, A

1

D 0, B

1

D 1, A

0

D 1,

B

0

D 0, u

p

D x.cos x C x sin x/, and y

p

1

D xe

x

.cos x C x sin x/. To ﬁnd a p articular solution of (B)

we write y D ue

x

. Then

y

00

 2y

0

C 2y D e

x



.u

00

 2u

0

C u/  2.u

0

 u/ C2u



D e

x

.u

00

 4u

0

C 5u/ D xe

x

if u

00

 4u

0

C 5u D x. Now u

p

D A C Bx where 4B C 5.A C Bx/ D x. Therefore, 5B D 1,

5A  4B D 0, B D

1

5

, A D

4

25

, u

p

D

1

25

.4 C 5x/, and y

p

2

D

e

x

25

.4 C 5x/. To ﬁnd a particular

solution of (C) we write y

p

3

D A C Bx C Cx

2

. Then

y

00

p

3

 2y

0

p

3

C 2y

p

3

D 2C  2.B C 2Cx/ C 2.A C Bx CCx

2

/

D .2A  2B C 2C / C .2B  4C /x C 2Cx

2

D 1 C x

2

if 2A2B C2C D 1, 2B 4C D 0, 2C D 1. Therefore,C D

1

2

, B D 1, A D 1, and y

p

3

D 1Cx C

x

2

.

Now y

p

D y

p

1

C y

p

2

C y

p

3

D xe

x

.cos x C x sin x/ C

e

x

25

.4 C 5x/ C 1 C x C

x

2

.

5.5.32. We must ﬁnd particular solutions y

p

1

and y

p

2

of (A) y

00

4y

0

C4y D 6e

2x

and (B) y

00

4y

0

C4y D

25 si n x, respectively. To ﬁnd a particular solution of (A), let y D ue

2x

. Then

y

00

 4y

0

C 4y D e

2x



.u

00

C 4u

0

C 4u/  4.u

0

C 2u/ C4u



D e

2x

u

00

D 6e

2x

if u

00

D 6. Integrating twice and taking the constant s of integration to be zero yields u

p

D 3x

2

, so

y

p

1

D 3x

2

e

2x

. To ﬁnd a particular solut ion of (B), let y

p

2

D A cos x C B sin x. Then

y

00

p

2

 4y

0

p

2

C 4y

p

2

D .A cos x C B sin x/  4.A sin x C B cos x/

C4.A cos x C B sin x/

D .3A  4B/ cos x C .4A C 3B/ sin x D 25 sin x

Section 5.5

The Method of Undetermined Coefﬁcients II

71

if 3A  4B D 0, 4A C 3B D 25. Therefore,A D 4, B D 3, and y

p

2

D 4 cos x C 3 sin x. Now

y

p

D y

p

1

C y

p

2

D 3x

2

e

2x

C 4 cos x C 3 sin x. The characteristic polynomial of the complementary

equation is p.r/ D r

2

 4r C 4 D .r  2/

2

, so fe

2x

; xe

2x

g is a fundamental set of solution s of the

complementary equation. Therefore,(C) y D 3x

2

e

2x

C4 cos x C 3 sin x Ce

2x

.c

1

C c

2

x/ is the general

solution of the nonhomogeneous equation. Now y.0/ D 5 ) 5 D 4 Cc

1

, so c

1

D 1. Differentiating (C)

yields y

0

D 6e

2x

.x Cx

2

/4 sin x C3 cos x C2e

2x

.c

1

Cc

2

x/Cc

2

e

2x

, so y

0

.0/ D 3 ) 3 D 3 C2 Cc

2

.

Therefore,c

2

D 2, and y D .1  2x C 3x

2

/e

2x

C 4 cos x C 3 sin x.

5.5.34. We must ﬁnd particular solutions y

p

1

and y

p

2

of (A) y

00

C 4y

0

C 4y D 2 cos 2x C 3 sin 2x

and (B) y

00

C 4y

0

C 4y D e

x

, respectively. To ﬁnd a particular solution of (A) we write y

p

1

D

A cos 2x C B sin 2x. Then

y

00

p

1

C 4y

0

p

1

C 4y

p

1

D 4.A co s 2x C B sin 2x/ C 8.A sin 2x C B cos 2x/

C4.A cos 2x C B sin 2x/ D 8A sin 2x C 8B cos 2x

D 2 cos 2x C 3 sin 2x

if 8B D 2, 8A D 3. Therefore,A D 

3

8

, B D

1

4

, and y

p

1

D 

3

8

cos 2x C

1

4

sin 2x. To ﬁnd a

particular solution of (B) we write y

p

2

D Ae

x

. Then y

00

p

2

C 4y

0

p

2

C 4y

p

2

D A.1  4 C 4/e

x

D

Ae

x

D e

x

if A D 1. Therefore,y

p

2

D e

x

. Now y

p

D y

p

1

C y

p

2

D 

3

8

cos 2x C

1

4

sin 2x C e

x

.

The characteristic polynomial o f the complementary equation is p.r/ D r

2

C 4r C 4 D .r  2/

2

,

so fe

2x

; xe

2x

g is a fundamen tal set of solutions of the complementary equ ation. Therefore,(C) y D



3

8

cos 2x C

1

4

sin 2x C e

x

Ce

2x

.c

1

Cc

2

x/ is the general solution of the nonhomogeneous equation.

Now y.0/ D 1 ) 1 D 

3

8

C 1 C c

1

, so c

1

D 

13

8

. Differentiating (C) yields y

0

D

3

4

sin 2x C

1

2

cos 2x e

x

2e

2x

.c

1

Cc

2

x/Cc

2

e

2x

, so y

0

.0/ D 2 ) 2 D

1

2

12c

1

Cc

2

. Therefore,c

2

D 

3

4

,

and y D 

3

8

cos 2x C

1

4

sin 2x C e

x



13

8

e

2x



3

4

xe

2x

.

5.5.36. (a), (b), and (c) require only routine manipulations. (d) The coefﬁcients o f sin !x in y

0

p

, y

00

p

,

ay

00

p

Cby

0

p

Ccy

p

, and y

00

p

C!

2

y

p

can be obtained by replacing A b y B and B by A in the corresponding

coefﬁcients of cos !x.

5.5.38. Let y D ue

x

. Then

ay

00

C by

0

C cy D e

x



a.u

00

C2u

0

C 

2

u/ C b.u

0

C u/ C cu



D e

x



au

00

C .2a C b/u

0

C .a

2

C b C c/u



D e

x



au

00

C p

0

./u

0

C p./u



D e

x

.P.x/ cos !x C Q.x/ sin !x/ if

(A) au

00

Cp

0

./u

0

Cp./uP .x/ cos !x CQ.x/ sin !x, where p.r/ D ar

C

br Cc is that characteristic

polynomial of the complementary equation (B) ay

00

C by

0

C cy D 0. If e

x

cos !x and e

x

sin !x are

not solutions of (B), then cos !x and sin !x are not solutions of the complementary equation f or (A).

Then Theorem 5.5.1 implies that (A) has a particular solution

u

p

D .A

0

C A

1

x C C A

k

x

k

/ cos !x C .B

0

CB

1

x C C B

k

x

k

/ sin !x;

and y

p

D u

p

e

x

is a particul ar solution of the stated form for the given equation. If e

x

cos !x and

e

x

sin !x are solutions of (B ), then cos !x and sin !x are sol utions of the compl ementary equation for

72 Chapter 5

Linear Second Order Equations

(A). Then Theorem 5.5.1 implies that (A) has a particular solution

u

p

D .A

0

x C A

1

x

2

C C A

k

x

kC1

/ cos !x C .B

0

x C B

1

x

2

C C B

k

x

kC1

/ sin !x;

and y

p

D u

p

e

x

is a particular solution of t he stated form for the given equation.

5.5.40. (a) Let y D

R

x

2

cos x dx; then y

0

D x

2

cos x Now let

y

p

D .A

0

CA

1

x C A

2

x

2

/ cos x C .B

0

CB

1

x C B

2

x

2

/ sin xI then

y

0

p

D



A

1

C B

0

C .2A

2

C B

1

/x C B

2

x

2



cos x

C



B

1

 A

0

C .2B

2

 A

1

/x  A

2

x

2



sin x D x

2

cos x if

(i)

B

2

D 1

A

2

D 0

; (ii)

B

1

C2A

2

D 0

A

1

C 2B

2

D 0

; (iii)

B

0

C A

1

D 0

A

0

C B

1

D 0

:

Solving these equations yields A

2

D 0, B

2

D 1, A

1

D 2, B

1

D 0, A

0

D 0, B

0

D 2. Therefore,y

p

D

2x cos x  .2  x

2

/ sin x and y D 2x cos x  .2  x

2

/ sin x C c.

(b) Let y D

R

x

2

e

x

cos x dx D ue

x

; th en y

0

D .u

0

C u/e

x

D x

2

e

x

cos x if u

0

C u D x

2

cos x. Now

let

u

p

D .A

0

C A

1

x C A

2

x

2

/ cos x C .B

0

C B

1

x C B

2

x

2

/ sin xI then

u

0

p

D



A

1

C B

0

C .2A

2

C B

1

/x CB

2

x

2



cos x

C



B

1

 A

0

C .2B

2

 A

1

/x  A

2

x

2



sin x; so

u

00

p

C u

p

D



A

0

CA

1

C B

0

C .A

1

C 2A

2

C B

1

/x C .A

2

C B

2

/x

2



cos x

C



B

0

C B

1

 A

0

C .B

1

C 2B

2

 A

1

/x C .B

2

 A

2

/x

2



sin x

D x

2

cos x if

(i)

A

2

C B

2

D 1

A

2

C B

2

D 0

; (ii)

A

1

C B

1

C 2A

2

D 0

A

1

C B

1

C 2B

2

D 0

;

(iii)

A

0

C B

0

C A

1

D 0

A

0

C B

0

C B

1

D 0

:

From (i), A

2

D

1

2

, B

2

D

1

2

. Substituting these into (ii ) and solving for A

1

and B

1

yields A

1

D 0,

B

1

D 1. Substituting these into (iii) and solving for A

0

and B

0

yields A

0

D 

1

2

, B

0

D

1

2

. Therefore,

u

p

D 

1

2



.1  x

2

/ cos x  .1  x/

2

sin x



and y D 

e

x

2



.1  x

2

/ cos x  .1  x/

2

sin x



.

(c) Let y D

R

xe

x

sin 2x dx D ue

x

; then y

0

D .u

0

 u/e

x

D xe

x

sin 2x if u

0

 u D x sin 2x.

Now let

u

p

D .A

0

C A

1

x/ cos 2x C .B

0

C B

1

x/ sin 2xI then

u

0

p

D Œ.A

1

C 2B

0

/ C 2B

1

x cos 2x C Œ.B

1

 2A

0

/  2A

1

x sin 2x; so

u

00

p

 u

p

D ŒA

0

C A

1

C 2B

0

 .A

1

 2B

1

/x cos 2x

CŒB

0

C B

1

 2A

0

 .B

1

C 2A

1

/x sin 2x D x sin 2x if

Section 5.5

The Method of Undetermined Coefﬁcients II

73

(i)

A

1

C 2B

1

D 0

2A

1

 B

1

D 1

; (ii)

 A

0

C 2B

0

CA

1

D 0

2A

0

 B

0

C B

1

D 0

:

From (i), A

1

D 

2

5

, B

1

D 

1

5

. Su bstituting these into (ii) and solving for A

0

and B

0

yields A

0

D 

4

25

,

B

0

D

3

25

. Therefore,

u

p

D 

1

25

Œ.4 C 10x/ cos 2x  .3  5x/ sin 2x C c and

y

p

D 

e

x

25

Œ.4 C 10x/ cos 2x  .3  5x/ sin 2x C c:

(d) Let y D

R

x

2

e

x

sin x dx D ue

x

; then y

0

D .u

0

 u/e

x

D x

2

e

x

sin x if u

0

 u D x

2

sin x.

Now let

u

p

D .A

0

C A

1

x C A

2

x

2

/ cos x C .B

0

C B

1

x C B

2

x

2

/ sin xI then

u

0

p

D



A

1

C B

0

C .2A

2

C B

1

/x CB

2

x

2



cos x

C



B

1

 A

0

C .2B

2

 A

1

/x  A

2

x

2



sin x; so

u

00

p

 u

p

D



A

0

C A

1

C B

0

 .A

1

 2A

2

 B

1

/x  .A

2

 B

2

/x

2



cos x

C



B

0

C B

1

 A

0

 .B

1

 2B

2

C A

1

/x  .B

2

C A

2

/x

2



sin x

D x

2

sin x i f

(i)

A

2

C B

2

D 0

A

2

 B

2

D 1

; (ii)

A

1

C B

1

C 2A

2

D 0

A

1

 B

1

C 2B

2

D 0

;

(iii)

A

0

C B

0

C A

1

D 0

A

0

 B

0

C B

1

D 0

:

From (i), A

2

D 

1

2

, B

2

D 

1

2

. Substituting these into (ii ) and solving for A

1

and B

1

yields A

1

D 1,

B

1

D 0. Substituting these into (iii) and solving for A

0

and B

0

yields A

0

D 

1

2

, B

0

D

1

2

. Therefore,

u

p

D 

e

x

2



.1 C x/

2

cos x  .1  x

2

/ sin x



and

y D 

e

x

2



.1 C x/

2

cos x  .1  x

2

/ sin x



C c:

(e) Let y D

R

x

3

e

x

sin x dx D ue

x

; th en y

0

D .u

0

Cu/e

x

D x

3

e

x

sin x i f u

0

Cu D x

3

sin x. Now let

u

p

D .A

0

C A

1

x C A

2

x

2

C A

3

x

3

/ cos x C .B

0

C B

1

x C B

2

x

2

C B

3

x

3

/ sin xI then

u

0

p

D



A

1

C B

0

C .2A

2

C B

1

/x C.3A

3

C B

2

/x

2

C B

3

x

3



cos x

C



B

1

 A

0

C .2B

2

 A

1

/x C .3B

3

 A

2

/x

2

 A

3

x

3



sin x; so

u

00

p

C u

p

D ŒA

0

C A

1

C B

0

C .A

1

C 2A

2

C B

1

/x

C.A

2

C 3A

3

C B

2

/x

2

C .A

3

C B

3

/x

3



cos x

CŒB

0

C B

1

 A

0

C .B

1

C 2B

2

 A

1

/x

C.B

2

C 3B

3

 A

2

/x

2

C .B

3

 A

3

/x

3



sin x D x

3

sin x if

74 Chapter 5

Linear Second Order Equations

(i)

A

3

C B

3

D 0

A

3

C B

3

D 1

; (ii)

A

2

C B

2

C 3A

3

D 0

A

2

C B

2

C 3B

3

D 0

;

(iii)

A

1

C B

1

C 2A

2

D 0

A

1

C B

1

C 2B

2

D 0

; (iv)

A

0

C B

0

C A

1

D 0

A

0

C B

0

C B

1

D 0

:

From (i), A

3

D 

1

2

, B

3

D

1

2

. Substitutin g these into (ii) and solving for A

2

and B

2

yields A

2

D

3

2

,

B

2

D 0. Substituting these into (iii) and solving for A

1

and B

1

yields A

1

D 

3

2

, B

1

D 

3

2

. Substi tuting

these i nto (iv) and solving for A

0

and B

0

yields A

0

D 0, B

0

D

3

2

. Therefore,

u

p

D 

1

2



x.3  3x C x

2

/ cos x  .3  3x C x

3

/ sin x



and

y D 

e

x

2



x.3  3x C x

2

/ cos x  .3  3x C x

3

/ sin x



C c:

(f) Let y D

R

e

x

Œx cos x  .1 C 3x/ sin x dx D ue

x

; then y

0

D .u

0

Cu/e

x

D e

x

Œx cos x  .1 C 3x/ sin x

if u

0

C u D x cos x  .1 C 3x/ sin x. Now let

u

p

D .A

0

C A

1

x/ cos x C .B

0

C B

1

x/ sin xI th en

u

0

p

D ŒA

1

C B

0

CB

1

x cos x C ŒB

1

 A

0

 A

1

x sin x; so

u

00

p

C u

p

D ŒA

0

C A

1

C B

0

C .A

1

C B

1

/x cos x

CŒB

0

C B

1

 A

0

C .B

1

 A

1

/x sin x

D x cos x  .1 C 3x/ sin x if

(i)

A

1

C B

1

D 1

A

1

C B

1

D 3

; (ii)

A

0

C B

0

C A

1

D 0

A

0

C B

0

C B

1

D 1

:

From (i) , A

1

D 2, B

1

D 1. Substi tuting these into (ii) and solving for A

0

and B

0

yields A

0

D 1, B

0

D

1. Therefore, u

p

D Œ.1  2x/ cos x C .1 C x/ sin x and y D e

x

Œ.1  2x/ cos x C .1 C x/ sin xC

c.

(g) Let y D

R

e

x



.1 C x

2

/ cos x C .1  x

2

/ sin x



dx D ue

x

; th en

y

0

D .u

0

 u/e

x

D e

x



.1 C x

2

/ cos x C .1  x

2

/ sin x



if u

0

 u D .1 C x

2

/ cos x C .1  x

2

/ sin x. Now let

u

p

D .A

0

C A

1

x C A

2

x

2

/ cos x C .B

0

C B

1

x C B

2

x

2

/ sin xI then

u

0

p

D



A

1

C B

0

C .2A

2

C B

1

/x CB

2

x

2



cos x

C



B

1

 A

0

C .2B

2

 A

1

/x  A

2

x

2



sin x; so

u

00

p

 u

p

D



A

0

C A

1

C B

0

 .A

1

 2A

2

 B

1

/x  .A

2

 B

2

/x

2



cos x

C



B

0

C B

1

 A

0

 .B

1

 2B

2

C A

1

/x  .B

2

C A

2

/x

2



sin x

D .1 C x

2

/ cos x C .1  x

2

/ sin x if

(i)

A

2

C B

2

D 1

A

2

 B

2

D 1

; (ii)

A

1

C B

1

C 2A

2

D 0

A

1

 B

1

C 2B

2

D 0

;

Section 5.6

Reduction of Order

75

(iii)

A

0

C B

0

C A

1

D 1

A

0

 B

0

C B

1

D 1

:

From (i), A

2

D 0, B

2

D 1. Substituting these into (ii) and so lving for A

1

and B

1

yields A

1

D 1,

B

1

D 1. Substituting these into (iii) and solving for A

0

and B

0

yields A

0

D 0, B

0

D 0. Therefore,u

p

D

x cos x C x.1 C x/ sin x and y D e

x

Œx cos x C x.1 C x/ sin x C c.

5.6 REDUCTION OF ORDER

(NOTE: The term uy

00

1

is indicated by “" in some of the following solutions, where y

00

1

is complicated.

Since this term always drops out of the differential equation for u, it is not necessary to include it.)

5.6.2. If y D ux, then y

0

D u

0

x C u and y

00

D u

00

x C 2u

0

, so x

2

y

00

C xy

0

 y D x

3

u

00

C 3x

2

u

0

D

4

x

2

if u

0

D ´, w here (A) ´

0

C

3

x

´ D

4

x

5

. Since

Z

3

x

dx D 3 ln jxj , ´

1

D

1

x

3

is a solution of the

complementary equation for (A). Therefore,the solutions of (A) are of th e form (B) ´ D

v

x

3

, where

v

0

x

3

D

4

x

5

, so v

0

D

4

x

2

. Hence, v D 

4

x

C C

1

; u

0

D ´ D 

4

x

4

C

1

x

3

(see (B)); u D

4

3x

3



C

1

2x

2

C C

2

;

y D ux D

4

3x

2



C

1

2x

C C

2

x, o r y D

4

3x

2

C c

1

x C

c

2

x

. As a byproduct, fx; 1=xg is a fundamental set

of solutions of the complementary equation.

5.6.4. If y D ue

2x

, t hen y

0

D .u

0

C 2u/e

2x

and y

00

D .u

00

C 4u

0

C 4u/e

2x

, so y

00

 3y

0

C 2y D

.u

00

C u

0

/e

2x

D

1

1 C e

x

if u

0

D ´, where (A) ´

0

C ´ D

e

2x

1 C e

x

. Since ´

1

D e

x

is a solution of

the complementary equation for (A), the solutions of (A) are of the form (B) ´ D ve

x

, where v

0

e

x

D

e

2x

1 C e

x

, so v

0

D

e

x

1 C e

x

. Hence, v D ln.1 C e

x

/ C C

1

; u

0

D ´ D e

x

ln.1 C e

x

/ C C

1

e

x

(see (B)); u D .1 Ce

x

/ ln.1 Ce

x

/ 1 e

x

C

1

e

x

CC

2

; y D ue

2x

D .e

2x

Ce

x

/ ln.1 Ce

x

/ 

.C

1

C 1/e

x

C .C

2

 1/e

2x

, or y D .e

2x

C e

x

/ ln.1 C e

x

/ C c

1

e

2x

C c

2

e

x

. As a byproduct, fe

2x

; e

x

g

is a fundamental set of solutions of the complementary equation.

5.6.6. If y D ux

1=2

e

x

, then y

0

D u

0

x

1=2

e

x

Cu

x

1=2

C

x

1=2

2

!

e

x

and y

00

D u

00

x

1=2

e

x

C2u

0

x

1=2

C

x

1=2

2

!

e

x

C

 so 4x

2

y

00

C .4x  8x

2

/y

0

C .4x

2

 4x  1/y D e

x

.4x

5=2

u

00

C 8x

3=2

u

0

/ D 4x

1=2

e

x

.1 C 4x/ if

u

0

D ´, where (A) ´

0

C

2

x

´ D

1 C 4x

x

2

. Since

Z

2

x

dx D 2 ln jxj, ´

1

D

2

x

2

is a solution of the

complementary equation for (A). Therefore,the solutions of (A) are of th e form (B) ´ D

v

x

2

, where

v

0

x

2

D

1 C 4x

x

2

, so v

0

D 1 C 4x. Hence, v D x C 2x

2

C C

1

; u

0

D ´ D

1

x

C 2 C

C

1

x

2

(see

(B)); u D ln x C 2x 

C

1

x

C C

2

; y D ux

1=2

e

x

D e

x

.2x

3=2

C x

1=2

ln x  C

1

x

1=2

C C

2

x

1=2

/, or

y D e

x

.2x

3=2

C x

1=2

ln x C c

1

x

1=2

C c

2

x

1=2

/. As a byproduct, fx

1=2

e

x

; x

1=2

e

x

g is a fundamental

set o f solutions of t he complementary equation.

5.6.8. If y D ue

x

2

, then y

0

D u

0

e

x

2

2xue

x

2

and y

00

D u

00

e

x

2

4xu

0

e

x

2

C, so y

00

C4xy

0

C

.4x

2

C 2/y D u

00

e

x

2

D 8e

x.xC2/

D 8e

x

2

e

2x

if u

00

D 8e

2x

. Therefore,u

0

D 4e

2x

C C

1

;

u D 2e

2x

CC

1

x CC

2

, and y D ue

x

2

D e

x

2

.2e

2x

CC

1

x CC

2

/, or y D e

x

2

.2e

2x

Cc

1

Cc

2

x/.

As a byproduct, fe

x

2

; xe

x

2

g is a fundamental set of solutions of the complementary equation.

76 Chapter 5

Linear Second Order Equations

5.6.10. If y D uxe

x

, then y

0

D u

0

xe

x

 ue

x

.x  1/ and y

00

D u

00

xe

x

 2u

0

e

x

.x  1/ C ,

so x

2

y

00

C 2x.x  1/y

0

C .x

2

 2x C 2/y D x

3

u

00

D x

3

e

2x

if u

00

D e

3x

. Therefore,u

0

D

e

3x

3

C C

1

;

u D

e

3x

9

CC

1

x CC

2

, and y D uxe

x

D

xe

2x

9

Cxe

x

.C

1

x CC

2

/, or y D

xe

2x

9

Cxe

x

.c

1

Cc

2

x/.

As a byproduct, fxe

x

; x

2

e

x

g is a fundamental set of solutions of the complementary equation .

5.6.12. If y D ue

x

, then y

0

D .u

0

C u/e

x

and y

00

D .u

00

C 2u

0

C u/e

x

, so .1  2x/y

00

C 2y

0

C

.2x  3/y D e

x

Œ.1  2x/u

00

C .4  4x/u

0

 D .1  4x C 4x

2

/e

x

if u

0

D ´, where (A) ´

0

C

4  4x

1  2x

´ D

1  2x. Since

Z

4  4x

1  2x

dx D

Z



2 C

2

1  2x



dx D 2x  ln j1  2xj, ´

1

D .1  2x/e

2x

is

a sol ution of the complementary equation for (A). Therefore,the solutions of (A) are of t he form (B)

´ D v.1  2x/e

2x

, where v

0

.1  2x/e

2x

D .1  2x/, so v

0

D e

2x

. Hence, v D

e

2x

2

C C

1

;

u

0

D ´ D



1

2

C C

1

e

2x



.1  2x/ (see (B)); u D 

.2x  1/

2

8

C C

1

xe

2x

C C

2

; y D ue

x

D



.2x  1/

2

e

x

8

CC

1

xe

x

CC

2

e

x

, o r y D 

.2x  1/

2

e

x

8

Cc

1

e

x

Cc

2

xe

x

. As a byproduct, fe

x

; xe

x

g

is a fundamental set of solutions of the complementary equation.

5.6.14. If y D ue

x

, then y

0

D .u

0

 u/e

x

and y

00

D .u

00

 2u

0

C u/e

x

, so 2xy

00

C .4x C

1/y

0

C .2x C 1/y D e

x

.2xu

00

C u

0

/ D 3x

1=2

e

x

if u

0

D ´, where (A) ´

0

C

1

2x

´ D

3

2

x

1=2

. Sin ce

Z

1

2x

dx D

1

2

ln jxj, ´

1

D x

1=2

is a solution o f the complementary equati on for (A). Therefore,the

solutions of (A) are o f the form (B) ´ D vx

1=2

, where v

0

x

1=2

D

3

2

x

1=2

, so v

0

D

3

2

. Hence,

v D

3x

2

C C

1

; u

0

D ´ D

3

2

x

1=2

C C

1

x

1=2

(see (B)); u D x

3=2

C 2C

1

x

1=2

C C

2

; y D ue

x

D

e

x

.x

3=2

C 2C

1

x

1=2

C C

2

/, or y D e

x

.x

3=2

C c

1

C c

2

x

1=2

/ As a byproduct, is a fe

x

; x

1=2

e

x

g

fundamental set of solutions of the complementary equation.

5.6.16. If y D ux

1=2

, then y

0

D u

0

x

1=2

C

u

2x

1=2

and y

00

D u

00

x

1=2

C

u

0

x

1=2

C  so 4x

2

y

00



4x.x C 1/y

0

C .2x C 3/y D 4x

5=2

.u

00

 u

0

/ D 4x

5=2

e

2x

if u

0

D ´, where (A) ´

0

 ´ D e

2x

. Since

´

1

D e

x

is a solution of the complementary equatio n for (A), the solutions of (A) are of the form (B)

´ D ve

x

, wher e v

0

e

x

D e

2x

, so v

0

D e

x

. H ence, v D e

x

C C

1

; u

0

D ´ D e

2x

C C

1

e

x

(see (B));

u D

e

2x

2

C C

1

e

x

C C

2

; y D ux

1=2

D x

1=2



e

2x

2

C C

1

e

x

C C

2



, or y D x

1=2



e

2x

2

C c

1

Cc

2

e

x



.

As a byproduct, fx

1=2

; x

1=2

e

x

g is a fundamental set of solutions of the complementary equation.

5.6.18. If y D ue

x

, then y

0

D .u

0

C u/e

x

and y

00

D .u

00

C 2u

0

C u/e

x

, so xy

00

C .2  2x/y

0

C

.x  2/y D e

x

.xu

00

C 2u

0

/ D 0 if

u

00

u

0

D 

2

x

; ln ju

0

j D 2 ln jxj C k; u

0

D

C

1

x

2

; u D 

C

1

x

C C

2

.

Therefore,y D ue

x

D e

x





C

1

x

C C

2



is the general solution, and fe

x

; e

x

=xg is a f undamental set of

solutions.

5.6.20. If y D u ln jxj, then y

0

D u

0

ln jxj C

u

x

and y

00

D u

00

ln jxj C

2u

0

x

, so x

2

.ln jxj/

2

y

00



.2x ln jxj/y

0

C .2 C ln jxj/y D x

2

.ln j xj/

3

u

00

D 0 if u

00

D 0; u

0

D C

1

; u D C

1

x C C

2

. Therefore,y D

u ln jxj D .C

1

x CC

2

/ ln jxj is the general solution, and fln jxj; x ln jxjg is a fundamental set of sol utions.

Section 5.6

Reduction of Order

77

5.6.22. If y D ue

x

, then y

0

D u

0

e

x

Cue

x

and y

00

D u

00

e

x

C2u

0

e

x

Cue

x

, so xy

00

.2xC2/y

0

C.xC2/y D

e

x

.xu

00

 2u

0

/ D 0 if

u

00

u

0

D

2

x

; ln ju

0

j D 2 ln jxj C k; u

0

D C

1

x

2

; u D

C

1

x

3

C C

2

. Therefore,

y D ue

x

D



C

1

x

3

C C

2



e

x

is the general solution, and fe

x

; x

3

e

x

g is a fundamental set of solutions.

5.6.24. If y D ux sin x, then y

0

D u

0

x sin x C u.x cos x C sin x/ and y

00

D u

00

x sin x C 2u

0

.x cos x C

sin x/C, so x

2

y

00

2xy

0

C.x

2

C2/y D .x

3

sin x/u

00

C2.x

3

cos x/u

0

D 0 if

u

00

u

0

D 

2 cos x

sin x

; ln ju

0

j D

2 ln jsin xjCk; u

0

D

C

1

sin

2

x

; u D C

1

cot x CC

2

. Therefore, y D ux sin x D x.C

1

cos x CC

2

sin x/

is the general solution, and fx sin x; x cos xg is a fun damental set of solutions.

5.6.26. If y D ux

1=2

, then y

0

D u

0

x

1=2

C

u

2x

1=2

and y

00

D u

00

x

1=2

C

u

0

x

1=2

C  so 4x

2

.sin x/y

00



4x.x cos x Csin x/y

0

C.2x cos x C3 sin x/y D 4x

5=2

.u

00

sin x u

0

cos x/ D 0 if

u

00

u

0

D

cos x

sin x

; ln ju

0

j D

ln jsin xj C k; u

0

D C

1

sin x; u D C

1

cos x C C

2

. Therefore,y D ux

1=2

D .C

1

cos x C C

2

/x

1=2

is

the general solution, and fx

1=2

; x

1=2

cos xg is a fundamental set of solutions.

5.6.28. If y D

u

x

, then y

0

D

u

0

x



u

x

2

and y

00

D

u

00

x



2u

0

x

2

C, so .2x C1/xy

00

2.2x

2

1/y

0

4.x C

1/y D .2x C 1/u

00

 .4x C 4/u

0

D 0 if

u

00

u

0

D

4x C 4

2x C 1

D 2 C

2

2x C 1

; ln ju

0

j D 2x C ln j2x C 1jCk;

u

0

D C

1

.2x C 1/e

2x

; u D C

1

xe

2x

C C

2

. Therefore,y D

u

x

D C

1

e

2x

C

2

x

is the general solution, and

f1=x; e

2x

g is a fundamental set of solutions.

5.6.30. If y D ue

2x

, then y

0

D .u

0

C 2u/e

2x

and y

00

D .u

00

C 4u

0

C 4u/e

2x

, so xy

00

 .4x C 1/y

0

C

.4x C 2/y D e

2x

.xu

00

 u

0

/ D 0 if

u

00

u

0

D

1

x

; ln ju

0

j D ln jxj C k; u

0

D C

1

x; u D

C

1

x

2

C C

2

.

Therefore, y D ue

2x

D e

2x



C

1

x

2

C C

2



is the general solution, and fe

2x

; x

2

e

2x

g is a fundamental

set o f solutions.

5.6.32. If y D ue

2x

, then y

0

D .u

0

C 2u/e

2x

and y

00

D .u

00

C 4u

0

C 4u/e

2x

, so .3x  1/y

00



.3x C 2/y

0

 .6x  8/y D e

2x

Œ.3x  1/u

00

C .9x  6/u

0

 D 0 if

u

00

u

0

D 

9x  6

3x  1

D 3 C

3

3x  1

.

Therefore,ln ju

0

j D 3x Clnj3x 1jCk, so u

0

D C

1

.3x 1/e

3x

, u D C

1

xe

3x

CC

2

. Therefore,the

general solution is y D ue

2x

D C

1

xe

x

C C

2

e

2x

, or (A) y D c

1

e

2x

C c

2

xe

x

. Now y.0/ D 2 )

c

1

D 2. Differentiating (A) yields y

0

D 2c

1

e

2x

Cc

2

.e

x

xe

x

/. Now y

0

.0/ D 3 ) 3 D 2c

1

Cc

2

, so

c

2

D 1 and y D 2e

2x

 xe

x

.

5.6.34. If y D ux, then y

0

D u

0

x Cu and y

00

D u

00

x C2u

0

, so x

2

y

00

C2xy

0

2y D x

3

u

00

C4x

2

u

0

D x

2

if

u

0

D ´, where (A) ´

0

C

4

x

´ D

1

x

. Since

Z

4

x

dx D 4 ln jxj, ´

1

D

1

x

4

is a solution of the complementary

equation for (A). Therefore,the solutions of (A) are of the form (B) ´ D

v

x

4

, where

v

0

x

4

D

1

x

, so v

0

D x

3

.

Hence, v D

x

4

CC

1

; u

0

D ´ D

1

4

C

1

x

4

(see (B) ); u D

x

4



C

1

3x

3

CC

2

. Therefore,the general solution is

y D ux D

x

2

4



C

1

3x

2

CC

2

x, or (C) y D

x

2

4

Cc

1

x C

c

2

x

2

. Differentiating (C) yields y

0

D

x

2

Cc

1

2

c

2

x

3

:

78 Chapter 5

Linear Second Order Equations

Now y.1/ D

5

4

; y

0

.1/ D

3

2

) c

1

C c

2

D 1; c

1

 2c

2

D 1, so c

1

D 1, c

2

D 0 and y D

x

2

4

Cx.

5.6.36. If y D uy

1

, then y

0

D u

0

y

1

Cuy

0

1

and y

00

D u

00

y

1

C2u

0

y

0

1

Cuy

00

1

, so y

00

Cp

1

.x/y

0

Cp

2

.x/y D

y

1

u

00

C .2y

0

1

C p

1

y

1

/u

0

D 0 if u is any fu nction such that (B)

u

00

u

0

D 2

y

0

1

y

1

 p

1

. If ln ju

0

.x/j D

2 ln jy

1

.x/j

Z

x

0

p

1

.t/ dt, then u satisﬁes (B); therefore, if (C) u

0

.x/ D

1

y

2

1

.x/

exp





Z

x

0

p

1

.s/ ds



,

then u satisﬁes (B). Since u.x/ D

Z

x

0

1

y

2

1

.t/

exp





Z

t

x

0

p

1

.s/ds



satisﬁes (C), y

2

D uy

1

is a solution

of (A) on .a; b/. Since

y

2

y

1

D u is noncon stant, Theorem 5.1.6 implies that fy

1

; y

2

g is a fundamental set

of solutions of (A) on .a; b/.

5.6.38. (a ) The associated linear equation is ( A ) ´

00

C k

2

´ D 0, with characteristic polynomial p.r/ D

r

2

Ck

2

. The general solution of (A) is ´ D c

1

cos kx Cc

2

sin kx. Since ´

0

D kc

1

sin kx Ckc

2

cos kx,

y D

´

0

´

D

kc

1

sin kx C kc

2

cos kx

c

1

cos kx C c

2

sin kx

.

(b) The associated linear equati on is (A) ´

00

 3´

0

C 2´ D 0, with characteristic polynomial p.r/ D

r

2

3r C2 D .r 1/.r 2/. The general solution of (A) is ´ D c

1

e

x

Cc

2

e

2x

. Since ´

0

D c

1

e

x

Cc

2

e

2x

,

y D

´

0

´

D

c

1

C 2c

2

e

x

c

1

C c

2

e

x

.

(c) The associated linear equation is (A) ´

00

C5´

0

6´ D 0, wit h characteristic polynomial p.r/ D r

2

C

5r 6 D .r C6/.r 1/. The general solution of (A) is ´ D c

1

e

6x

Cc

2

e

x

. Since ´

0

D 6c

1

e

6x

Cc

2

e

x

,

y D

´

0

´

D

6c

1

C c

2

e

7x

c

1

C c

2

e

7x

.

(d) The associated l inear equation is (A ) ´

00

C 8´

0

C 7´ D 0, with characteristic polynomial p.r/ D

r

2

C 8r C 7 D .r C 7/.r C 1/. The general solution of (A) is ´ D c

1

e

7x

C c

2

e

x

. Since ´

0

D

7c

1

e

7x

 2c

2

e

x

, y D

´

0

´

D 

7c

1

C c

2

e

6x

c

1

C c

2

e

6x

.

(e) The associated linear equation is (A) ´

00

C14´

0

C50´ D 0, with characteristic polynomial p.r / D

r

2

C 14r C 50 D .r C 7/

2

C 1. The general solution of (A) is ´ D e

7x

.c

1

cos x C c

2

sin x/. Since

´

0

D 7e

7x

.c

1

cos x Cc

2

sin x/ Ce

7x

.c

1

sin x Cc

2

cos x/ D .7c

1

c

2

/ cos x .c

1

C7c

2

/ sin x,

y D

´

0

´

D 

.7c

1

 c

2

/ cos x C .c

1

C 7c

2

/ sin x

c

1

cos x C c

2

sin x

.

(f) The given equation is equivalent to (A ) y

0

C y

2



1

6

y 

1

6

D 0. The associated li near equatio n is

(B) ´

00



1

6

´

0



1

6

´ D 0, with characteristic polynomial p.r/ D r

2



1

6

r 

1

6

D



r C

1

3



r 

1

2



.

The general solu tion of (B) is ´ D c

1

e

x=3

C c

2

e

x=2

. Since ´

0

D 

c

1

3

e

x=3

C

c

2

e

x=2

, y D

´

0

´

D

2c

1

C 3c

2

e

5x=6

6.c

1

C c

2

e

5x=6

/

.

(g) The given equation is equivalent to (A ) y

0

Cy

2



1

3

y C

1

36

D 0. The associated linear equation is

(B) ´

00



1

3

´

0

C

1

36

´ D 0, with characteristic polynomial p.r/ D r

2



1

3

r C

1

36

D



r 

1

6



2

. The general

solution of (B) is ´ D e

x=6

.c

1

C c

2

x/. Since ´

0

D

e

x=6

6

.c

1

C c

2

x/ C c

2

e

x=6

D

e

x=6

6

.c

1

C c

2

.x C 6//,

Section 5.7

Variation of Parameters

79

y D

´

0

´

D

c

1

C c

2

.x C 6/

6.c

1

C c

2

x/

.

5.6.40. (a) Suppose that ´ is a solution of (B) and let y D

´

0

r´

. Then (D )

´

00

r´

C



p.x/ 

r

0

.x/

r.x/



yCq.x/ D

0 and y

0

D

´

00

r´



1

r



´

0

´



2



r

0

´

0

r

2

´

D

´

00

r´

 ry

2



r

0

r

y, so

´

00

r´

D y

0

C ry

2

C

r

0

r

y. Therefore, (D)

implies th at y satisﬁes (A). Now suppose that y is a solution of (A) and let ´ be any function such that

´

0

D ry´. Then ´

00

D r

0

y´ C ry

0

´ C ry´

0

D

r

0

r

´

0

C .y

0

C ry

2

/r´ D

r

0

r

´

0

 .p.x/y C q.x//r´, so

´

00



r

0

r

´

0

C p.x/ry´ C q.x/r´ D 0, which implies that ´ satisﬁes (B), since ry´ D ´

0

.

(b) If f´

1

; ´

2

g is a fundamental set of solutions of (B) on .a; b/, then ´ D c

1

´

1

C c

2

´

2

is the general

solution of (B) on .a; b/. This and (a) imply that (C) is the general solution of ( A) on .a; b/.

5.7 VARIATION OF PAR AMETERS

5.7.2. ( A) y

p

D u

1

cos 2x C u

2

sin 2x;

u

0

1

cos 2x C u

0

2

sin 2x D 0 (B)

2u

0

1

sin 2x C 2u

0

2

cos 2x D sin 2x sec

2

x: (C)

Multiplying (B) by 2 sin 2x and (C) by cos 2x and adding the resulting equations yields 2u

0

2

D tan 2x,

so u

0

2

D

tan 2x

2

. Then (B) implies that u

0

1

D u

0

2

tan.2x/ D 

tan

2

2x

2

D

1  sec

2

2x

2

. Therefore,u

1

D

x

2



tan 2x

4

and u

2

D 

ln jcos 2xj

4

. Now (A) yields y

p

D 

sin 2x ln jcos 2xj

4

C

x cos 2x

2



sin 2x

4

.

Since sin 2x satisﬁes the complementary equation we redeﬁne y

p

D 

sin 2x ln jcos 2xj

4

C

x cos 2x

2

.

5.7.4. ( A) y

p

D u

1

e

x

cos x C u

2

e

x

sin x;

u

0

1

e

x

cos x C u

0

2

e

x

sin x D 0 (B)

u

0

1

.e

x

cos x e

x

sin x/ C u

0

2

.e

x

sin x C e

x

cos x/ D 3e

x

sec x: (C)

Subtr acti ng (B) from (C) and cancelling e

x

from the resulting equations yields

u

0

1

cos x C u

0

2

sin x D 0 (D)

u

0

1

sin x C u

0

2

cos x D 3 sec x: (E)

Multiplying (D) by sin x and (E) by cos x and adding th e results yields u

0

2

D 3. From (D), u

0

1

D

u

0

2

tan x D 3 tan x. Therefore u

1

D 3 ln jcos xj, u

2

D 3x. Now (A) yields y

p

D 3e

x

.cos x ln jcos xjC

x sin x/.

5.7.6. ( A) y

p

D u

1

e

x

C u

2

e

x

;

u

0

1

e

x

C u

0

2

e

x

D 0 (B)

u

0

1

e

x

 u

0

2

e

x

D

4e

x

1 C e

2x

: (C)

Adding (B) to (C) yields 2u

0

1

e

x

D

4e

x

1 C e

2x

, so u

0

1

D

2e

2x

1  e

2x

. From (B), u

0

2

D e

2x

u

0

1

D



2

1  e

2x

D

2e

2x

1  e

2x

. Using the substitution v D e

2x

we integrate u

0

1

to obtain u

1

D ln.1  e

2x

/.

80 Chapter 5

Linear Second Order Equations

Using the substitution v D e

2x

we i ntegrate u

0

2

to obtain u

1

D ln.1  e

2x

/. Now (A) yields y

p

D

e

x

ln.1  e

2x

/  e

x

ln.e

2x

 1/.

5.7.8. ( A) y

p

D u

1

e

x

C u

2

e

x

;

u

0

1

e

x

C u

0

2

e

x

D 0 (B)

u

0

1

e

x

C u

0

2



e

x



e

x

2



D

e

2x

x

: (C)

Subtr acti ng (B) from (C) yields 

u

0

2

e

x

2

D

e

2x

x

, so u

0

2

D xe

x

. From (B), u

0

1

D

u

0

2

x

D e

x

. Therefore

u

1

D e

x

, u

2

D xe

x

C e

x

. Now (A) yields y

p

D

e

2x

x

.

5.7.10. (A) y

p

D u

1

e

x

2

C u

2

xe

x

2

;

u

0

1

e

x

2

C u

0

2

xe

x

2

D 0 (B)

2xu

0

1

e

x

2

C u

0

2

.e

x

2

 2x

2

e

x

2

/ D 4e

x.xC2/

: (C)

Multiplying (B) by 2x and adding the result to (C ) yields u

0

2

e

x

2

D 4e

x.xC2/

, so u

0

2

D 4e

2x

. From

(B), u

0

1

D u

0

2

x D 4xe

2x

. Therefore u

1

D .2x C 1/e

2x

, u

2

D 2e

2x

. Now (A) yields y

p

D

e

x.xC2/

.

5.7.12. (A) y

p

D u

1

x C u

2

x

3

;

u

0

1

x C u

0

2

x

3

D 0 (B)

u

0

1

C 3u

0

2

x

2

D

2x

4

sin x

x

2

D 2x

2

sin x (C):

Multiplying (B) by

1

x

and subt racting the result from (C) yields 2x

2

u

0

2

D 2x

2

sin x, so u

0

2

D sin x. From

(B), u

0

1

D u

0

2

x

2

D x

2

sin x. Therefore u

1

D .x

2

2/ cos x 2x sin x, u

2

D cos x. Now (A) yields

y

p

D 2x

2

sin x  2x cos x.

5.7.14. (A) y

p

D u

1

cos

p

x Cu

2

sin

p

x;

u

0

1

cos

p

x C u

0

2

sin

p

x D 0 (B)

u

0

1

sin

p

x

2

p

x

C u

0

2

cos

p

x

2

p

x

D

sin

p

x

4x

(C):

Multiplying (B ) by

sin

p

x

2

p

x

and (C) by cos

p

x and adding the resulting equations yields

u

0

2

p

x

D

sin

p

x cos

p

x

4x

, so u

0

2

D

sin

p

x cos

p

x

2

p

x

. From (B), u

0

1

D u

0

2

tan

p

x D 

sin

2

p

x

2

p

x

. Therefore,

u

1

D

sin

p

x cos

p

x

2



p

x

2

, u

2

D

sin

2

p

x

2

. Now ( A ) yields y

p

D

sin

p

x

2



p

x cos

p

x

2

. Since

sin

p

x satisﬁes th e complementary equation we redeﬁne y

p

D 

p

x cos

p

x

2

.

Section 5.7

Variation of Parameters

81

5.7.16. (A) y

p

D u

1

x

a

C u

2

x

a

ln x;

u

0

1

x

a

C u

0

2

x

a

ln x D 0 (B)

au

0

1

x

a1

Cu

0

2

.ax

a1

ln x C x

a1

/ D

x

aC1

x

2

D x

a1

(C):

Multiplying (B) by

a

x

and su btracting th e result from (C) yields u

0

2

x

a1

D x

a1

, so u

0

2

D 1. From (B),

u

0

1

D u

0

2

ln x D ln x. Therefore, u

1

D x  ln x, u

2

D x. Now (A) yields y

p

D x

aC1

.

5.7.18. y

p

D u

1

e

x

2

C u

2

e

x

2

;

u

0

1

e

x

2

C u

0

2

e

x

2

D 0 (B)

2u

0

1

xe

x

2

 2u

0

2

xe

x

2

D

8x

5

x

D 8x

4

: (B)

Multiplying (B) by 2x and adding the result to (C) yields 4u

0

1

xe

x

2

D 8x

4

, so u

0

1

D 2x

3

e

x

2

. From (B),

u

0

2

D u

0

1

e

2x

2

D 2x

3

e

x

2

. Therefore u

1

D e

x

2

.x

2

C 1/, u

2

D e

x

2

.x

2

 1/. Now (A) yields

y

p

D 2x

2

.

5.7.20. (A) y

p

D u

1

p

xe

2x

C u

2

p

xe

2x

;

u

0

1

p

xe

2x

C u

0

2

p

xe

2x

D 0 (B)

u

0

1

e

2x



2

p

x C

1

2

p

x



 u

0

2

e

2x



2

p

x 

1

2

p

x



D

8x

5=2

4x

2

D 2

p

x (C):

Multiplying (B) by

1

2x

, subtracting the result from (C), and cancelling common factor s from the resulting

equations y ields

u

0

1

e

2x

C u

0

2

e

2x

D 0 (D)

u

0

1

e

2x

 u

0

2

e

2x

D 1: (E)

Adding (D) to (E) yields 2u

0

1

e

2x

D 1, so u

0

1

D

e

2x

2

. From (D), u

0

2

D u

0

1

e

4x

D 

e

2x

2

. Therefore,

u

1

D 

e

2x

4

, u

2

D 

e

2x

4

. Now (A) yields y

p

D 

p

x

2

.

5.7.22. (A)y

p

D u

1

xe

x

C u

2

xe

x

;

u

0

1

xe

x

C u

0

2

xe

x

D 0 (B)

u

0

1

.x C 1/e

x

 u

0

2

.x  1/e

x

D

3x

4

x

2

D 3x

2

(C):

Multiplying (B) by

1

x

, subtracting the resulting eq uation from (C), and cancelling common factors yields

u

0

1

e

x

C u

0

2

e

x

D 0 (D)

u

0

1

e

x

 u

0

2

e

x

D 3x: (E)

Adding (D) to (E) yi elds 2u

0

1

e

x

D 3x, so u

0

1

D

3xe

x

2

. From (D), u

0

2

D u

0

1

e

2x

D 

3xe

x

2

. Therefore

u

1

D 

3e

x

.x C 1/

2

, u

2

D 

3e

x

.x  1/

2

. Now (A) yields y

p

D 3x

2

.

82 Chapter 5

Linear Second Order Equations

5.7.24. (A) y

p

D

u

1

x

C u

2

x

3

;

u

0

1

x

C u

0

2

x

3

D 0 (B)



u

0

1

x

2

C 3u

0

2

x

2

D

x

3=2

x

2

D x

1=2

: (C)

Multiplying (B) by

1

x

and addi ng the resul t to (C) yields 4u

0

2

x

2

D x

1=2

, so u

0

2

D

x

5=2

4

. From (B),

u

0

1

D u

0

2

x

4

D 

x

3=2

4

. Therefore u

1

D 

x

5=2

10

, u

2

D 

x

3=2

6

. Now (A) yields y

p

D 

4x

3=2

15

.

5.7.26. (A) y

p

D u

1

x

2

e

x

C u

2

x

3

e

x

;

u

0

1

x

2

e

x

C u

0

2

x

3

e

x

D 0 (B)

u

0

1

.x

2

e

x

C 2xe

x

/ C u

0

2

.x

3

e

x

C 3x

2

e

x

/ D

2xe

x

2

D

2e

x

: (C)

Subtr acti ng (B) from (C) and cancelling common factors in the resulting equations yields

u

0

1

C u

0

2

x D 0 (D)

2u

0

1

x C 3u

0

2

x

2

D

2

x

: (E)

Multiplying (D) by 2x and subtracting the result from (E) yields x

2

u

0

2

D

2

x

, so u

0

2

D

2

x

3

. From (D),

u

0

1

D u

0

2

x D 

2

x

2

. Therefore u

1

D

2

x

, u

2

D 

1

x

2

. Now (A) yields y

p

D xe

x

.

5.7.28. (A) y

p

D u

1

x C u

2

e

x

;

u

0

1

x C u

0

2

e

x

D 0 (B)

u

0

1

C u

0

2

e

x

D

2.x  1/

2

e

x

x 1

D 2.x  1/e

x

: (C)

Subtr acti ng (B) fr om (C) yield s u

0

1

.1x/ D 2.x1/e

x

, so u

0

1

D 2e

x

. From (B), u

0

2

D u

0

1

xe

x

D 2x.

Therefore, u

1

D 2e

x

, u

2

D x

2

. Now (A) yields y

p

D xe

x

.x  2/.

5.7.30. (A) y

p

D u

1

e

2x

Cu

2

xe

x

;

u

0

1

e

2x

C u

0

2

xe

x

D 0 (B)

2u

0

1

e

2x

C u

0

2

.e

x

 xe

x

/ D

.3x  1/

2

e

2x

3x  1

D .3x  1/e

2x

: (C)

Multiplying (B) by 2 and subtracting th e result from (C) yields u

0

2

.1  3x/e

x

D .3x  1/e

2x

, so

u

0

2

D e

3x

. From (B), u

0

1

D u

0

2

xe

3x

D x. Therefore u

1

D

x

2

, u

2

D 

e

3x

3

. Now (A) yields

y

p

D

xe

2x

.3x  2/

3

. The general solution of the given equation is y D

xe

2x

.3x  2/

3

Cc

1

e

2x

Cc

2

xe

x

.

Differentiatin g this yields y

0

D

e

2x

.3x

2

C x  1/

3

C 2c

1

e

2x

C c

2

.1  x/e

x

. Now y.0/ D 1; y

0

.0/ D

2 ) c

1

D 1; 2 D 

1

3

C 2c

1

C c

2

, so c

2

D

1

3

, and y D

e

2x

.3x

2

 2x C 6/

6

C

xe

x

3

.

Section 5.7

Variation of Parameters

83

5.7.32. (A) y

p

D u

1

.x  1/e

x

Cu

2

.x  1/;

u

0

1

.x  1/e

x

C u

0

2

.x  1/ D 0 (B)

u

0

1

xe

x

C u

0

2

D

.x  1/

3

e

x

.x  1/

2

D .x  1/e

x

: (C)

From (B), u

0

1

D u

0

2

e

x

. Substi tuting this into (C) yields u

0

2

.x1/ D .x1/e

x

, so u

0

2

D e

x

, u

0

1

D 1.

Therefore u

1

D x, u

2

D e

x

. Now (A) yields y

p

D e

x

.x1/

2

. The general solution of the given equation

is y D .x 1/

2

e

x

Cc

1

.x 1/e

x

Cc

2

.x 1/. Differentiating this yields y

0

D .x

2

1/e

x

Cc

1

xe

x

Cc

2

.

Now y.0/ D 4; y

0

.0/ D 6 ) 4 D 1  c

1

 c

2

; 6 D 1 C c

2

, so c

1

D 2; c

2

D 5 and

y D .x

2

 1/e

x

 5.x  1/.

5.7.34. (A) y

p

D u

1

x C

u

2

x

2

;

u

0

1

x C

u

0

2

x

2

D 0 (B)

u

0

1



2u

0

2

x

3

D 

2x

2

x

2

D 2: (C)

Multiplying (B) by

2

x

and adding the result to (C) yields 3u

0

1

D 2, so u

0

1

D 

2

3

. From (B), u

0

2

D

u

0

1

x

3

D

2x

3

. Therefore u

1

D 

2x

3

, u

2

D

x

4

6

. N ow (A) yields y

p

D 

x

2

. The general solution

of the given equation is y D 

x

2

C c

1

x C

c

2

x

2

. Differentiating this yields y

0

D x C c

1



2c

2

x

3

. Now

y.1/ D 1; y

0

.1/ D 1 ) 1 D 

1

2

C c

1

C c

2

; 1 D 1 C c

1

 2c

2

, so c

1

D 1; c

2

D

1

2

, and

y D 

x

2

C x C

1

2x

2

.

5.7.36. Since y D y

p

 a

1

y

1

 a

2

y

2

,

P

0

.x/y

00

C P

1

.x/y

0

C P

2

.x/y D P

0

.x/.y

p

 a

1

y

1

 a

2

y

2

/

00

CP

1

.x/.y

p

 a

1

y

1

 a

2

y

2

/

0

CP

2

.x/.y

p

 a

1

y

1

 a

2

y

2

/

D .P

0

.x/y

00

p

C P

1

.x/y

0

p

C P

2

.x/y

p

/

a

1



P

0

.x/y

00

1

C P

1

.x/y

0

1

C P

2

.x/y

1



a

2



P

0

.x/y

00

2

C P

1

.x/y

0

2

C P

2

.x/y

2



D F .x/ a

1

 0  a

2

 0 D F .x/I

hence y is a particular solution of ( A ).

5.7.38. (a) y

p

D u

1

e

x

C u

2

e

x

is a solution of (A) o n .a; 1/ if u

0

1

e

x

C u

0

2

e

x

D 0 and u

0

1

e

x



u

0

2

e

x

D f .x/. Solving these two equations yields u

0

1

D

e

x

f

2

, u

0

2

D 

e

x

f

2

. The functions u

1

.x/ D

1

2

Z

x

0

e

t

f .t/ dt and u

2

.x/ D 

1

2

Z

x

0

e

t

f .t/ dt satisfy these conditions. Therefore,

y

p

.x/ D

e

x

2

Z

x

0

e

t

f .t/ dt 

e

x

2

Z

x

0

e

t

f .t/ dt

D

1

2

Z

x

0

f .t/



e

.xt /e

.xt/



dt D

Z

x

0

f .t/ sinh.x  t/ dt:

84 Chapter 5

Linear Second Order Equations

is a particular solution of y

00

 y D f .x/. Differentiating y

p

yields

y

0

p

.x/ D

e

x

2

Z

x

0

e

t

f .t/ dt C

e

x

2

e

x

C

e

x

2

Z

x

0

e

t

f .t/ dt 

e

x

2

e

x

D

e

x

2

Z

x

0

e

t

f .t/ dt C

e

x

2

Z

x

0

e

t

f .t/ dt

D

1

2

Z

x

0

f .t/



e

.xt /

Ce

.xt /



dt D

Z

x

0

f .t/ cosh.x  t/ dt:

Since y

p

.x

0

/ D y

0

p

.x

0

/ D 0, the solution of the initi al value problem is

y D y

p

C k

0

cosh x C k

1

sinh x

D k

0

cosh x C k

1

sinh x C

Z

x

0

sinh.x  t/f .t/ dt:

The derivative of the solution is

y

0

D y

0

p

C k

0

sinh x C k

1

cosh x

D k

0

sinh x C k

1

cosh x C

Z

x

0

cosh.x  t/f .t/ dt:

CHAPTER 6

Applications of Linear Second Order

Equations

6.1 SPRING PROBLEMS I

6.1.2. Since

k

m

D

g

l

D

32

:1

D 320 the equation of motion is (A) y

00

C 320y D 0. The general

solution of (A) is y D c

1

cos 8

p

5t C c

2

sin 8

p

5t, so y

0

D 8

p

5.c

1

sin 8

p

5t C c

2

cos 8

p

5t/. Now

y.0/ D 

1

4

) c

1

D 

1

4

and y

0

.0/ D 2 ) c

2

D 

1

4

p

5

, so y D 

1

4

cos 8

p

5t 

1

4

p

5

sin 8

p

5t ft.

6.1.4. Since

k

m

D

g

l

D

32

:5

D 64 the equation of motion is (A) y

00

C 64y D 0. The general solution

of (A) is y D c

1

cos 8t C c

2

sin 8t, so y

0

D 8.c

1

sin 8t C c

2

cos 8t/. Now y.0/ D

1

4

) c

1

D

1

4

and

y

0

.0/ D 

1

2

) c

2

D 

1

16

, so y D

1

4

cos 8t 

1

16

sin 8t ft; R D

p

17

16

ft; !

0

D 8 rad/s; T D =4 s;

  :245 rad  14:04

ı

.

6.1.6. Since k D

mg

l

D

.9:8/10

:7

D 140, the equation of motion of the 2 kg mass is (A) y

00

C 70y D

0. The general solution of (A) is y D c

1

cos

p

70t C c

2

sin

p

70t, so y

0

D

p

70.c

1

sin

p

70t C

c

2

cos

p

70t/. Now y.0/ D 

1

4

) c

1



1

4

Dand y

0

.0/ D 2 ) c

2

D

2

p

70

, so y D 

1

4

cos

p

70 t C

2

p

70

sin

p

70 t

m; R D

1

4

r

67

35

m; !

0

D

p

70 rad/s; T D 2=

p

70 s;   2:38 rad  136:28

ı

.

6.1.8. Since

k

m

D

g

l

D

32

1=2

D 64 the equation of motion is (A) y

00

C 64y D 0. The general solution

of (A) is y D c

1

cos 8t C c

2

sin 8t, so y

0

D 8.c

1

sin 8t C c

2

cos 8t/. Now y.0/ D

1

2

) c

1

D

1

2

and

y

0

.0/ D 3 ) c

2

D 

3

8

, so y D

1

2

cos 8t 

3

8

sin 8t ft.

6.1.10. m D

64

32

D 2, so the equation of motion is 2y

00

C 8y D 2 sin t, or (A) y

00

C 4y D sin t. Let

y

p

D A cos t C B sin t ; th en y

00

p

D A cos t  B sin t , so y

00

p

C 4y

p

D 3A cos t C 3B sin t D sin t if

3A D 0, 3B D 1. Therefore,A D 0, B D

1

3

, and y

p

D

1

3

sin t. The general solution of

85

86 Chapter 6

Applications of Linear Second Order Equations

(A) is (B) y D

1

3

sin t C c

1

cos 2t C c

2

sin 2t, so y.0/ D

1

2

) c

1

D

1

2

. Differen tiating (B) yields

y

0

D

1

3

cos t  2c

1

sin 2t C 2c

2

cos 2t, so y

0

.0/ D 2 ) 2 D

1

3

C 2c

2

, so c

2

D

5

6

. Therefore,

y D

1

3

sin t C

1

2

cos 2t C

5

6

sin 2t ft.

6.1.12. m D

4

32

D

1

8

and k D

mg

l

D 4, so the equation of motion is

1

8

y

00

C 4y D

1

4

sin 8t, or (A)

y

00

C32y D 2 sin 8t. Let y

p

D A cos 8t CB sin 8t; then y

00

p

D 64A cos t 64B sin 8t, so y

00

p

C32y

p

D

32A cos 8t  32B sin 8t D 2 sin 8t if 32A D 0, 32B D 2. Therefore,A D 0, B D 

1

16

, and

y

p

D 

1

16

sin 8t. The general solu tion of (A) is (B) y D 

1

16

sin 8t C c

1

cos 4

p

2t C c

2

sin 4

p

2t, so

y.0/ D

1

3

) c

1

D

1

3

. Differentiating ( B) yields y

0

D 

1

2

cos 8tC4

p

2.c

1

sin 4

p

2t Cc

2

cos 4

p

2t/, so

y

0

.0/ D 1 ) 1 D 

1

2

C4

p

2c

2

, so c

2

D 

1

8

p

2

. Therefore,y D 

1

16

sin 8t C

1

3

cos 4

p

2t 

1

8

p

2

sin 4

p

2t ft.

6.1.14. Since T D

2

!

0

D 2

r

m

k

the period i s prop ortional to the square root of the mass. Therefore,

doubling the mass mut iplies the period by

p

2; hence the period of the syst em with th e 20 gm mass is

T D 4

p

2 s.

6.1.16. m D

6

32

D

3

16

and k D

mg

l

D

6

1=3

D 18 so t he equation of motion is

3

16

y

00

C 18y D

4 sin !t  6 cos !t, or (A) y

00

C 96y D

64

3

sin !t  32 cos !t. The displacement will be un bounded if

! D

p

96 D 4

p

6, in which case (A) becomes (B) y

00

C 96y D

64

3

sin 4

p

6t  32 cos 4

p

6t. Let

y

p

D At cos 4

p

6t C Bt sin 4

p

6tI then

y

0

p

D .A C 4

p

6Bt/ cos 4

p

6t C .B  4

p

6At/ sin 4

p

6t

y

00

p

D .8

p

6B  96At/ cos 4

p

6t  .8

p

6A C 96Bt/ sin 4

p

6t; so

y

00

p

C 96y

p

D 8

p

6B cos 4

p

6t  8

p

6A sin 4

p

6t D

64

3

sin 4

p

6t  32 cos 4

p

6t

if 8

p

6B D 32, 8

p

6A D

64

3

. Therefore, A D 

8

3

p

6

, B D 

4

p

6

, and y

p

D 

t

p

6



8

3

cos 4

p

6t C4 sin 4

p

6t



.

The general solution of (B) i s

y D 

t

p

6



8

3

cos 4

p

6t C 4 sin 4

p

6t



C c

1

cos 4

p

6t C c

2

sin 4

p

6t; .C/

so y.0/ D 0 ) c

1

D 0. Differentiating (C) yields

y

0

D 



8

3

p

6

cos 4

p

6t C

4

p

6

sin 4

p

6t



 4t





8

3

sin 4

p

6t C 4 cos 4

p

6t



C4

p

6.c

1

sin 4

p

6t C c

2

cos

p

6t/;

so y

0

.0/ D 0 ) 0 D 

8

3

p

6

C 4

p

6c

2

, and c

2

D

1

9

. Therefore,

y D 

t

p

6



8

3

cos 4

p

6t C 4 sin 4

p

6t



C

1

9

sin 4

p

6t ft:

Section 6.2

Sprin g Problems II

87

6.1.18. The equation of motion is (A) y

00

C !

2

0

y D 0. The general solution of (A) is y D c

1

cos !

0

t C

c

2

sin !

0

t. Now y.0/ D y

0

) c

1

D y

0

. Since y

0

D !

0

.c

1

sin !

0

t C c

2

cos !

0

t/, y

0

.0/ D v

0

) c

2

D

v

0

!

0

. Therefore, y D y

0

cos !

0

t C

v

0

!

0

sin !

0

t;

R D

1

!

0

p

.!

0

y

0

/

2

C .v

0

/

2

I cos  D

y

0

!

0

p

.!

0

y

0

/

2

C .v

0

/

2

I sin  D

v

0

p

.!

0

y

0

/

2

C .v

0

/

2

:

Discussion 6.1.1 In Exercises 19, 20, and 21 we use the fact that in a spring–mass system w ith mass m

and spring constant k the period of th e motion is T D 2

r

m

k

. Therefore, if we have two systems with

masses m

1

and m

2

and spring const ants k

1

and k

2

, then the periods are related by

T

2

T

1

D

s

m

2

k

1

m

1

k

2

. We

will use this formula in the solutions of these exercises.

6.1.20. Let m

2

D 2m

1

. Since k

1

D k

2

,

T

2

T

1

D

s

2m

1

m

1

D

p

2, so T

2

D

p

2T

1

.

6.1.21. Suppose th at T

2

D 3T

1

. Since m

1

D m

2

,

s

k

1

k

2

D 3, k

1

D 9k

2

.

6.2 SPRING PROBLEMS II

6.2.2. Since k D

mg

l

D

16

3:2

D 5 the equation of motion is

1

2

y

00

Cy

0

C5y D 0, or (A) y

00

C2y

0

C10y D 0.

The characteristic p olynomial of (A) is p.r/ D r

2

C2rC10 D .rC1/

2

C9. Therefore,the general solution

of (A) is y D e

t

.c

1

cos 3t C c

2

sin 3t/, so y

0

D y C 3e

t

.c

1

sin 3t C c

2

cos 3t/. Now y.0/ D 3

and y

0

.0/ D 2 ) c

1

D 3 and 2 D 3 C 3c

2

, or c

2

D 

1

3

. Therefore,y D e

t



3 cos 3t C

1

3

sin 3t



ft. The time–varying amplitude is

p

82

3

e

t

ft.

6.2.4. Since k D

mg

l

D

96

3:2

D 30 the equation of motion is 3y

00

C 18y

0

C 30y D 0, or (A) y

00

C 6y

0

C

10y D 0. The characteristic polynomial of (A) is p.r/ D r

2

C 6r C 10 D .r C 3/

2

C 1. Therefore,the

general solution of (A) is y D e

3t

.c

1

cos t C c

2

sin t/, so y

0

D 3y C e

3t

.c

1

sin t C c

2

cos t/.

Now y.0/ D 

5

4

and y

0

.0/ D 12 ) c

1

D 

5

4

and 12 D

15

4

C c

2

, or c

2

D 

63

4

. Therefore,

y D 

e

3t

4

.5 cos t C 63 sin t/ ft.

6.2.6. Since k D

mg

l

D

8

:32

D 25 the equation of motio n is

1

4

y

00

C

3

2

y

0

C 25y D 0, or (A) y

00

C6y

0

C

100y D 0. The characteristic polynomial of (A) is p.r/ D r

2

C6r C100 D .r C3/

2

C91. Therefore,the

general solution of (A) is y D e

3t

.c

1

cos

p

91tCc

2

sin

p

91t/, so y

0

D 3yC

p

91e

3t

.c

1

sin

p

91t C

c

2

cos

p

91t/. Now y.0/ D

1

2

and y

0

.0/ D 4 ) c

1

D

1

2

and 4 D 

3

2

C

p

91c

2

, or c

2

D

11

2

p

91

.

Therefore,y D

1

2

e

3t



cos

p

91t C

11

p

91

sin

p

91t



ft.

6.2.8. Since k D

mg

l

D

20  980

5

D 3920 the equation of motion is 20y

00

C 400y

0

C 3920y D 0,

or (A) y

00

C 20y

0

C 196y D 0. The characteristic polynomial of (A) is p.r/ D r

2

C 20r C 196 D

88 Chapter 6

Applications of Linear Second Order Equations

.r C 10/

2

C 96. Therefore,the general solution of (A) is y D e

10t

.c

1

cos 4

p

6t C c

2

sin 4

p

6t/, so

y

0

D 10y C 4

p

6e

10t

.c

1

sin 4

p

6t C c

2

cos 4

p

6t/. Now y.0/ D 9 and y

0

.0/ D 0 ) c

1

D 9 and

0 D 90 C 4

p

6c

2

, or c

2

D

45

2

p

6

. Therefore, y D e

10t



9 cos 4

p

6t C

45

2

p

6

sin 4

p

6t



cm.

6.2.10. Since k D

mg

l

D

32

1

D 32 the equation of motion is (A) y

00

C 3y

0

C 32y D 0. The characteris-

tic polynomial of (A) is p.r / D r

2

C3rC32 D



r C

3

2



2

C

119

4

. Therefore,the general solution of (A) is

y D e

3t=2

c

1

cos

p

119

2

t C c

2

sin

p

119

2

t

!

, so y

0

D 

3

2

yC

p

119

2

e

3t=2

c

1

sin

p

119

2

t C c

2

cos

p

119

2

t

!

.

Now y.0/ D

1

2

and y

0

.0/ D 3 ) c

1

D

1

2

and 3 D 

3

4

C

p

119

2

c

2

, or c

2

D 

9

2

p

119

. Therefore,

y D e



3

2

t

1

2

cos

p

119

2

t 

9

2

p

119

sin

p

119

2

t

!

ft.

6.2.12. Since k D

mg

l

D

2

:32

D

25

4

the equation of motion is

1

16

y

00

C

1

8

y

0

C

25

4

y D 0, or (A)

y

00

C 2y

0

C 100y D 0. The characteristic polynomial of (A) is p.r/ D r

2

C 2r C 100 D .r C

1/

2

C 99. Therefore,the general solution of (A) is y D e

t

.c

1

cos 3

p

11t C c

2

sin 3

p

11t/, so y

0

D

y C 3

p

11e

t

.c

1

sin 3

p

11t C c

2

cos 3

p

11t/. Now y.0/ D 

1

3

and y

0

.0/ D 5 ) c

1

D 

1

3

and

5 D

1

3

C 3

p

11c

2

, or c

2

D

14

9

p

11

. Therefore,y D e

t





1

3

cos 3

p

11t C

14

9

p

11

sin 3

p

11t



ft.

6.2.14. Since k D

mg

l

D 32 the equation of motio n is (A) y

00

C 12y

0

C 32y D 0. The characteristic

polynomial of (A) is p.r/ D r

2

C 12r C 32 D .r C 8/.r C 4/. Therefore, th e general solution of (A) is

y D c

1

e

8t

Cc

2

e

4t

, so y

0

D 8c

1

e

8t

4c

2

e

4t

. Now y.0/ D 

2

3

and y

0

.0/ D 0 ) c

1

Cc

2

D

2

3

;-

8c

1

 4c

2

D 0, so c

1

D 

2

3

, c

2

D

4

3

, and y D 

2

3

.e

8t

 2e

4t

/.

6.2.16. Since k D

mg

l

D

100  980

98

D 100 the equation of motion is 100y

00

C 600y

0

C 1000y D 0, o r

(A) y

00

C6y

0

C10y D 0. The characteristic polynomial of (A) is p.r/ D r

2

C6r C10 D .r C3/

2

C1.

Therefore, the general solution of (A) is y D e

3t

.c

1

cos t C c

2

sin t/, so y

0

D 3y C e

t

.c

1

sin t C

c

2

cos t/. Now y.0/ D 10 and y

0

.0/ D 100 ) c

1

D 10 and 100 D 30 C c

2

, or c

2

D 70.

Therefore, y D e

3t

.10 cos t  70 sin t/ cm.

6.2.18. The equation of motion is (A) 2y

00

C4y

0

C20y D 3 cos 4t 5 sin 4t. The steady state component

of the solution of (A) is o f the form y

p

D A cos 4t CB sin 4t; therefore y

0

p

D 4A sin 4t C4B cos 4t and

y

00

p

D 16A cos 4t 16B sin 4t, so 2y

00

p

C4y

0

p

C20y

p

D .12A C16B/ cos 4t .16A C12B/ sin 4t D

3 cos 4t  5 sin 4t if 12A C 16B D 3, 16A  12B D 5; therefore A D

11

100

, B D

27

100

, and

y

p

D

11

100

cos 4t C

27

100

sin 4t cm.

6.2.20. Since k D

mg

l

D

9:8

:49

D 20 the equation of motio n is (A) y

00

C4y

0

C20y D 8 sin 2t  6 cos 2t.

The steady state component of the solution of (A) is of the form y

p

D A cos 2t C B sin 2t; therefore

Section 6.3

The RLC Circuit

89

y

0

p

D 2A sin 2t C 2B cos 2t and y

00

p

D 4A cos 2t  4B sin 2t, so y

00

p

C 4y

0

p

C 20y

p

D .16A C

8B/ cos 2t  .8A  16B/ sin 2t D 8 sin 2t  6 cos 2t if 16A C 8B D 6, 8A C 16B D 8; therefore

A D 

1

2

, B D

1

4

, and y D 

1

2

cos 2t C

1

4

sin 2t m.

6.2.22. If e

r

1

t

.c

1

C c

2

t/ D 0, t hen (A) c

1

C c

2

t D 0. If c

2

D 0, then c

1

¤ 0 (by assumption), so (A) is

impossib le. If c

1

¤ 0, then th e left side of (A) is strictly monotonic and therefore cannot have the same

value for two distinct values of t.

6.2.24. If y D e

ct=2m

.c

1

cos !

1

t C c

2

sin !

1

t/, then y

0

D 

c

2m

y C !

1

e

ct=2m

.c

1

sin !

1

t C

c

2

cos !

1

t/, so y.0/ D y

0

and y

0

.0/ D v

0

) c

1

D y

0

and v

0

D 

cy

0

2m

Cc

2

!

1

, so c

2

D

1

!

1



v

0

C

cy

0

2m

t



and y D e

ct=2m



y

0

cos !

1

t C

1

!

1



v

0

C

cy

0

2m



sin !

1

t



.

6.2.26. If y D e

r

1

t

.c

1

C c

2

t/, then y

0

D r

1

y C c

2

e

r

1

t

, so y.0/ D y

0

and y

0

.0/ D v

0

) c

1

D y

0

and

v

0

D r

1

y

0

C c

2

, so c

2

D v

0

 r

1

y

0

. Therefore, y D e

r

1

t

.y

0

C .v

0

 r

1

y

0

/t/.

6.3 THE RLC CIRCUIT

6.3.2.

1

20

Q

00

C 2Q

0

C 100Q D 0; Q

00

C 40Q

0

C 2000Q D 0; r

2

C 40r C 2000 D .r C 20/

2

C

1600 D 0; r D 20 ˙ 40i ; Q D e

20t

.2 cos 40t C c

2

sin 40t/ (since Q

0

D 2); I D Q

0

D

e

20t

..40c

2

 40/ cos 40t  .20c

2

C 80/ sin 40t/; I

0

D 2 ) 40c

2

 40 D 2 ) c

2

D

21

20

, so

20c

2

C 80 D 101; I D e

20t

.2 cos 40t  101 sin 40t/.

6.3.4.

1

10

Q

00

C 6Q

0

C 250Q D 0; Q

00

C 60Q

0

C 2500Q D 0; r

2

C 60r C 2500 D .r C 30/

2

C

1600 D 0; r D 30 ˙ 40i ; Q D e

30t

.3 cos 40t C c

2

sin 40t/ (since Q

0

D 3); I D Q

0

D

e

30t

..40c

2

 90/ cos 40t  .30c

2

C 120/ sin 40t/; I

0

D 10 ) 40c

2

 90 D 10 ) c

2

D 2, so

30c

2

 120 D 180; I D 10e

30t

.cos 40t C 18 sin 40t/.

6.3.6. Q

p

D A cos 10t C B sin 10t; Q

0

p

D 10B cos 10t  10A sin 10t; Q

00

p

D 100A cos 10t 

100B sin 10t;

1

10

Q

00

p

C 3Q

0

p

C 100Q

9

D .90A C 30B/ cos 10t  .30A  90B/ sin 10t D 5 cos 10t 

5 sin 10t, so 90A C 30B D 5, 30A C 90B D 5. Therefore, A D 1=15, B D 1=30, Q

p

D

cos 10t

15



sin 10t

30

, and I

p

D 

1

3

.cos 10t C 2 sin 10t/.

6.3.8. Q

p

D A cos 50t C B sin 50t; Q

0

p

D 50B cos 50t  50A sin 50t ; Q

00

p

D 2500A cos 50t 

2500B sin 50t;

1

10

Q

00

p

C2Q

0

p

C100Q

p

.150AC100B/ cos 50t .100AC150B/ sin50t D 3 cos 50t 

6 sin 50t, so 150A C 100B D 3, 100A C 1500B D 6. Therefore,A D 3=650, B D 12=325,

Q

p

D

3

650

.cos 50t C 8 sin 50t/, and I

p

D

3

13

.8 cos 50t  sin 50t/.

6.3.10. Q

p

D A cos 30t C B sin 30t; Q

0

p

D 30B cos 30t  30A sin 30t; Q

00

p

D 900A cos 30t 

900B sin 30t;

1

20

Q

00

p

C4Q

0

p

C125Q

p

D .80A C120B/ cos 30t .120A 80B/ sin 30t D 15 cos 30t 

30 si n 30t , so 80AC120B D 15, 120AC80B D 30, A D 3=13, B D 3=104, Q

p

D

3

104

.8 cos 30t

sin 30t/, and I

p

D 

45

52

.cos 30t C 8 sin 30t/.

90 Chapter 6

Applications of Linear Second Order Equations

6.3.12. Let  D .!/ be the amplitude of I

p

. From the solution of Exercise 6.3.11, Q

p

D A cos !t C

B cos !t , where A D

.1=C  L!

2

/U  R!V



, B D

R!U C .1=C  L!

2

/V



, and  D .1=C 

L!

2

/

2

CR

2

!

2

. Since I

p

D Q

0

p

D !.A si n !t CB cos !t/, i t follows that 

2

.!/ D !

2

.A

2

C B

2

/ D

U

2

C V

2

.!/

, with .!/ D



!

2

D .1=C!  L!/

2

C R

2

, which attains it mininmum value R

2

when

! D !

0

D

1

p

LC

. The maximum amplitude o f I

p

is .!/ D

p

U

2

C V

2

R

.

6.4 MOTION UNDER A CE N TRAL FORCE

6.4.2. Let h D r

2

0



0

; then  D

h

2

k

. Since r D



1 C e cos.  /

, it follows th at (A) e cos.  / D



r

 1. Differentiating this with respect to t y ields e sin.  /

0

D 

r

0

r

2

, so (B) e sin.  / D

r

0

h

, sin ce r

2



0

 h. Squaring and adding (A) and (B) and setting t D 0 in the result yields e D

"





r

0

 1



2

C



r

0

h



2

#

1=2

. I f e D 0, then 

0

is undeﬁned, but also irrelevant; if e ¤ 0, then set t D 0

in (A) and ( B) to see that  D 

0

 ˛, where   ˛ <  , cos ˛ D

1

e





r

0

 1



and sin ˛ D

r

0

eh

6.4.4. Recall that (A)

d

2

u

d



2

D 

1

mh

2

u

2

f .1=u/. Let u D

1

r

D

1

c

2

; then

d

2

u

d

2

D

6

c

4

D 6cu

2

.

6cu

2

C u D 

1

mh

2

u

2

f .1=u/, so f .1=u/ D mh

2

.6cu

4

C u

3

/ and f .r/ D mh

2



6c

r

4

C

1

r

3



.

6.4.6. ( a) With f .r / D 

mk

r

3

, Eqn. 6.4.11 becomes (A)

d

2

u

d

2

C



1 

k

h

2



u D 0. The initial condit ions

imply that u.

0

/ D

1

r

0

and

du

d

.

0

/ D 

r

0

h

(see Eqn. (6.4.)

(b) Let  D

ˇ

1 

k

h

2

ˇ

1=2

. (i) If h

2

< k, then (A) becomes

d

2

u

d

2

 

2

u D 0, and the solution

of the initial value problem for u is u D

1

r

0

cosh .  

0

/ 

r

0

h

sinh .  

0

/; therefore r D

r

0



cosh .  

0

/ 

r

0

r

0

h

sinh .  

0

/



1

. (ii) If h

2

D k, then (A) becomes

d

2

u

d

2

D 0, and the solu-

tion of the initial value problem for u is u D

1

r

0



r

0

h

.  

0

/; therefore r D r

0



1 

r

0

r

0

h

.  

0

/



1

.

(iii) If h

2

> k, then (A) becomes

d

2

u

d

2

C 

2

u D 0, and the solution of the initial value problem for u is

u D

1

r

0

cos .  

0

/ 

r

0

h

sin .  

0

/; therefore r D r

0



cos .  

0

/ 

r

0

r

0

h

sin .  

0

/



1

.

CHAPTER 7

Series Solutions of Linear Second

Equations

7.1 REVIEW OF POWER SERIES

7.1.2. From Theorem 7.1.3,

P

1

mD0

b

m

´

m

converges if j´j < 1=L and diverges if j´j > 1=L. Therefore,

P

1

mD0

b

m

.x  x

0

/

2

converges if jx  x

0

j < 1=

p

L and diverges if jx  x

0

j > 1=

p

L.

7.1.4. From Theorem 7.1.3,

P

1

mD0

b

m

´

m

converges if j´j < 1=L and diverges if j´j > 1=L. Therefore,

P

1

mD0

b

m

.x  x

0

/

km

converges if jx  x

0

j < 1=

k

p

L and diverges if jx  x

0

j > 1=

k

p

L.

7.1.12. .1 C 3x

2

/y

00

C 3x

2

y

0

 2y D

1

X

nD2

n.n  1/a

n

x

n2

C 3

1

X

nD2

n.n  1/a

n

x

n

C 3

1

X

nD1

na

n

x

nC1



2

1

X

nD0

a

n

x

n

D

1

X

nD0

.n C2/.n C1/a

nC2

x

n

C3

1

X

nD1

n.n 1/na

n

x

n

C3

1

X

nD1

.n 1/a

n1

x

n

2

1

X

nD0

a

n

x

n

D

2a

2

 2a

0

C

1

X

nD1

Œ.n C 2/.n C 1/a

nC2

C .3n.n  1/  2/a

n

C 3.n  1/a

n1

x

n

.

7.1.13. .1 C2x

2

/y

00

C.23x/y

0

C4y D

1

X

nD2

n.n1/a

n

x

n2

C2

1

X

nD2

n.n1/a

n

x

n

C2

1

X

nD1

na

n

x

n1



2

1

X

nD0

a

n

x

n

C4

1

X

nD0

a

n

x

n

D

1

X

nD0

.n C2/.n C1/a

nC2

x

n

C2

1

X

nD0

n.n 1/a

n

x

n

C2

1

X

nD0

.n C 1/a

nC1

x

n



3

1

X

nD0

a

n

x

n

C 4

1

X

nD0

a

n

x

n

1

X

nD0



.n C 2/.n C1/a

nC2

C 2.n C1/a

nC1

C .2n

2

 5n C 4/a

n



x

n

.

7.1.14. .1 C x

2

/y

00

C .2  x/y

0

C 3y D

1

X

nD2

n.n  1/a

n

x

n2

C

1

X

nD2

n.n  1/a

n

x

n

C 2

1

X

nD1

na

n

x

n1



1

X

nD1

na

n

x

n

C 3

1

X

nD0

a

n

x

n

D

1

X

nD0

.n C 2/.n C 1/a

nC2

x

n

C

1

X

nD0

n.n  1/a

n

x

n

C 2

1

X

nD0

.n C 1/a

nC1

x

n



1

X

nD0

na

n

x

n

C 3

1

X

nD0

a

n

x

n

D

1

X

nD0



.n C 2/.n C 1/a

nC2

C 2.n C 1/a

nC1

C .n

2

 2n C3/a

n



x

n

.

91

92 Chapter 7

Series Solutions of Linear Second Equati ons

7.1.16. Let t D xC1; then xy

00

C.4C2x/y

0

C.2Cx/y D .1Ct/y

00

C.2C2t/y

0

C.1Ct/y D 

1

X

nD2

n.n

1/a

n

t

n2

C

1

X

nD2

n.n 1/a

n

t

n1

C2

1

X

nD1

na

n

t

n1

C2

1

X

nD1

na

n

t

n

C

1

X

nD0

a

n

t

n

C

1

X

nD0

a

n

t

nC1

D 

1

X

nD0

.n C

2/.nC1/a

nC2

t

n

C

1

X

nD0

.nC1/na

nC1

t

n

C2

1

X

nD0

.nC1/a

nC1

t

n

C2

1

X

nD0

na

n

t

n

C

1

X

nD0

a

n

t

n

C

1

X

nD1

a

n1

t

n

D

.2a

2

C2a

1

Ca

0

/C

1

X

nD1

Œ.n C 2/.n C 1/a

nC2

C .n C 1/.n C 2/a

nC1

C .2n C 1/a

n

C a

n1

 .xC2/

n

.

7.1.20. y

0

.x/ D x

r

1

X

nD0

na

n

x

n1

C rx

r1

1

X

nD0

a

n

x

n

D

1

X

nD0

.n C r /x

nCr1

y

00

D

d

dx

y

0

.x/ D

d

dx

"

x

r1

1

X

nD0

.n C r /a

n

x

n

#

D x

r1

1

X

nD0

.n C r/na

n

x

n1

C.r  1/x

r2

1

X

nD0

.n C

r/a

n

x

n

D

1

X

nD0

.n C r /.n C r  1/a

n

x

nCr2

.

7.1.22. x

2

.1 C x/y

00

C x.1 C 2x/y

0

 .4 C 6x/y D .x

2

y

00

C xy

0

 4y/ C x.x

2

y

00

C 2xy

0

 6y/ D

1

X

nD0

Œ.n C r/.n C r  1/ C .n C r/ 4a

n

x

nCr

C

1

X

nD0

Œ.n C r/.n C r  1/ C2.n Cr/  6a

n

x

nCrC1

D

1

X

nD0

.n C r  2/.n C r C 2/a

n

x

nCr

C

1

X

nD0

.n C r C 3/.n C r  2/a

n

x

nCrC1

D

1

X

nD0

.n C r  2/.n C

r C 2/a

n

x

nCr

C

1

X

nD1

.n C r C2/.n C r  3/a

n1

x

nCr

D x

r

1

X

nD0

b

n

x

n

with b

0

D .r  2/.r C 2/a

0

and

b

n

D .n C r  2/.n C r C 2/a

n

C .n C r C 2/.n C r 3/a

n1

, n  1.

7.1.24. x

2

.1 C 3x/y

00

C x.2 C 12x C x

2

/y

0

C 2x.3 C x/y D .x

2

y

00

C 2xy

0

/ C x.3x

2

y

00

C 12xy

0

C

6y/ Cx

2

.xy

0

C2y/ D

1

X

nD0

Œ.n Cr/.n Cr 1/ C2.n Cr /a

n

x

nCr

C

1

X

nD0

Œ3.n Cr/.n Cr 1/ C12.n C

r/ C6a

n

x

nCrC1

C

1

X

nD0

Œ.nCr/C2a

n

x

nCrC2

D

1

X

nD0

.nCr /.n Cr C1/a

n

x

nCr

C3

1

X

nD0

.nCr C1/.n C

r C2/a

n

x

nCrC1

C

1

X

nD0

.n Cr C2/a

n

x

nCrC2

D

1

X

nD0

.n Cr/.n Cr C1/a

n

x

nCr

C3

1

X

nD1

.n Cr/.n Cr C

1/a

n1

x

nCr

C

1

X

nD2

.n C r /a

n2

x

nCr

D x

r

1

X

nD0

b

n

x

n

with b

0

D r .r C 1/a

0

, b

1

D .r C 1/.r C 2/a

1

C

3.r C 1/.r C 2/a

0

, b

n

D .n C r /.n C r C 1/a

n

C 3.n Cr/.n C r C 1/a

n1

C .n C r/a

n2

, n  2.

7.1.26. x

2

.2Cx

2

/y

00

C2x.5Cx

2

/y

0

C2.3x

2

/y D .2x

2

y

00

C10xy

0

C6y/Cx

2

.x

2

y

00

C2xy

0

2y/ D

1

X

nD0

Œ2.nCr/.n Cr 1/ C10.n Cr/ C6a

n

x

nCr

C

1

X

nD0

Œ.n Cr/.n Cr 1/ C2.n Cr / 2a

n

x

nCrC2

D

2

1

X

nD0

.n C r C1/.n C r C 3/a

n

x

nCr

C

1

X

nD0

.n C r  1/.n C r C 2/a

n

x

nCrC2

D 2

1

X

nD0

.n C r C 1/.n C

Section 7.2

Series Solutions Near an Ordinary Point I

93

r C 3/a

n

x

nCr

C

1

X

nD2

.n C r  3/.n C r/a

n2

x

nCr

D x

r

1

X

nD0

b

n

x

n

with b

0

D 2.r C 1/.r C 3/a

0

,

b

1

D 2.r C 2/.r C 4/a

1

b

n

D 2.n C r C 1/.n C r C 3/a

n

C .n C r  3/.n C r/a

n2

, n  2.

7.2 SERIES SOLUTIONS NEAR AN ORDINARY POINT I

7.2.2. p.n/ D n.n  1/ C 2n  2 D .n C 2/.n  1/; a

nC2

D 

n1

nC1

a

n

; a

2mC2

D 

2m  1

2m C 1

a

2m

, so

a

2m

D

.1/

m

2m  1

a

0

; a

2mC3

D 

m

m C 2

a

2mC1

D 0 if m  0; y D a

0

1

X

mD0

.1/

mC1

x

2m

2m  1

Ca

1

x.

7.2.4. p.n/ D n.n  1/  8n  12 D .n C 3/.n C 4/; a

nC2

D 

.nC3/.nC4/

.nC2/.nC1/

a

n

; a

2mC2

D



.m C 2/.2m C 3/

.m C 1/.2m C 1/

a

2m

, so a

2m

D .mC1/.2mC1/a

0

; a

2mC3

D

.m C 2/.2m C 5/

.m C 1/.2m C 3/

a

2mC1

so a

2mC1

D

.m C 1/.2m C 3/

3

a

1

; y D a

0

1

X

mD0

.m C 1/.2m C 1/x

2m

C

a

1

3

1

X

mD0

.m C 1/.2m C 3/x

2mC1

.

7.2.6. p.n/ D n.n1/C2nC

1

4

D

.2n C 1/

2

4

; a

nC2

D 

.2nC1/

2

4.nC2/.nC1/

a

n

; a

2mC2

D 

.4m C 1/

2

8.m C 1/.2m C1/

a

2m

,

so a

2m

D .1/

m

2

4

m1

Y

j D0

.4j C 1/

2

2j C 1

3

5

1

8

m

mŠ

a

0

; a

2mC3

D 

.4m C 3/

2

8.2m C 3/.m C 1/

a

2mC1

so a

2mC1

D

.1/

m

2

4

m1

Y

j D0

.4j C 3/

2

2j C 3

3

5

1

8

m

mŠ

a

1

; y D a

0

1

X

mD0

.1/

m

2

4

m1

Y

j D0

.4j C 1/

2

2j C 1

3

5

x

2m

8

m

mŠ

C a

1

X

mD0

.1/

m

2

4

m1

Y

j D0

.4j C 3/

2

2j C 3

3

5

x

2mC1

8

m

mŠ

7.2.8. p.n/ D n.n1/10nC28 D .n7/.n4/; a

nC2

D 

.n7/.n4/

.nC2/.nC1/

a

n

; a

2mC2

D 

2.2m  7/.m  2/

2.m C 1/.2m C 1/

a

2m

,

so a

2

D 14a

0

, a

4

D 

5

6

a

2

D

35

3

a

0

, a

2m

D 0 if m  3; a

2mC3

D 

.m  3/.2m  3/

.2m C 3/.m C 1/

a

2mC1

, so

a

3

D 3a

1

, a

5

D 

1

5

a

3

D

3

5

a

1

, a

7

D

1

21

a

5

D

1

35

a

1

;

y D a

0



1  14x

2

C

35

3

x

4



C a

1



x  3x

3

C

3

5

x

5

C

1

35

x

7



.

7.2.10. p.n/ D 2n C 3; a

nC2

D 

2n C 3

.n C 2/.n C 1/

a

n

; a

2mC2

D 

4m C3

2.m C 1/.2m C1/

a

2m

, so a

2m

D

2

4

m1

Y

j D0

4j C 3

2j C 1

3

5

.1/

m

2

m

mŠ

a

0

; a

2mC3

D 

4m C5

2.2m C 3/.m C 1/

a

2mC1

so a

2mC1

D

2

4

m1

Y

j D0

4j C 5

2j C 3

3

5

.1/

m

2

m

mŠ

a

1

;

y D a

0

1

X

mD0

.1/

m

2

4

m1

Y

j D0

4j C 3

2j C 1

3

5

x

2m

2

m

mŠ

C a

1

X

mD0

.1/

m

2

4

m1

Y

j D0

4j C 5

2j C 3

3

5

x

2mC1

2

m

mŠ

7.2.12. p.n/ D 2n.n 1/ 9n  6 D .n  6/.2n C1/; a

nC2

D 

.n  6/.2n C 1/

.n C 2/.n C 1/

a

n

; a

0

D y.0/ D 1;

a

1

D y

0

.0/ D 1.

7.2.13. p.n/ D 8n.n  1/ C 2 D 2.2n  1/

2

; a

nC2

D 

2.2n 1/

2

.n C 2/.n C 1/

a

n

; a

0

D y.0/ D 2; a

1

D

y

0

.0/ D 1.

94 Chapter 7

Series Solutions of Linear Second Order Equations

7.2.16. p.n/ D 1; a

nC2

D

1

.n C 2/.n C1/

a

n

; a

2mC2

D

1

.2m C 2/.2m C1/

a

2m

, so a

2m

D

1

.2m/Š

a

0

;

a

2mC3

D

1

.2m C 3/.2m C 1/

a

2mC1

, so a

2mC1

D

1

.2m C 1/Š

a

1

; y D a

0

1

X

mD0

.x  3/

2m

.2m/Š

C a

1

X

mD0

.x  3/

2mC1

.2m C 1/Š

.

7.2.18. Let t D x  1; then .1  2t

2

/y

00

 10ty

0

 6y D 0; p.n/ D 2n.n  1/  10n  6 D

2.n C 1/.n C 3/; a

nC2

D

2.n C 3/

n C 2

a

n

; a

2mC2

D

2m C 3

m C 1

a

2m

, so a

2m

D

1

mŠ

2

4

m1

Y

j D0

.2j C 3/

3

5

a

0

;

a

2mC3

D

4.m C 2/

2m C 3

a

2mC1

, so a

2mC1

D

4

m

.m C 1/Š

Q

m1

j D0

.2j C 3/

a

1

; y D a

0

1

X

mD0

2

4

m1

Y

j D0

.2j C 3/

3

5

.x  1/

2m

mŠ

C a

1

X

mD0

4

m

.m C 1/Š

Q

m1

j D0

.2j C 3/

.x  1/

2mC1

.

7.2.20. Let t D x C 1; then



1 C

3t

2

3



y

00



9t

2

y

0

C

3

2

y D 0; p.n/ D

3

2

n.n  1/ C

9

2

n C

3

2

D

3

2

.n C

1/

2

; a

nC2

D 

3.n C 1/

2.n C 2/

a

n

; a

2mC2

D 

3.2m C 1/

4.m C 1/

a

2m

, so a

2m

D .1/

m

2

4

m1

Y

j D0

.2j C 1/

3

5

3

m

4

m

mŠ

a

0

;

a

2mC3

D 

3.m C 1/

2m C 3

a

2mC1

, so a

2mC1

D .1/

m

3

m

mŠ

Q

m1

j D0

.2j C 3/

a

1

;

y D a

0

1

X

mD0

.1/

m

2

4

m1

Y

j D0

.2j C 1/

3

5

3

m

4

m

mŠ

.x C 1/

2m

C a

1

X

mD0

.1/

m

3

m

mŠ

Q

m1

j D0

.2j C 3/

.x C 1/

2mC1

.

7.2.22. p.n/ D n C 3; a

nC2

D 

n C 3

.n C 2/.n C 1/

a

n

; a

0

D y.3/ D 2; a

1

D y

0

.3/ D 3.

7.2.24. Let t D x  3; .1 C 4t

2

/y

00

C y D 0; p.n/ D .4n.n  1/ C 1 D 2n  1/

2

; a

nC2

D



.2n  1/

2

.n C 2/.n C 1/

a

n

; a

0

D y.3/ D 4; a

1

D y

0

.3/ D 6.

7.2.26. Let t D x C 1;



1 C

2t

2

3



y

00



20

3

ty

0

C 20y D 0; p.n/ D

2

3

n.n  1/ 

20

3

n C 20 D

2.n  6/.n  5/

3

; a

nC2

D 

2.n  6/.n  5/

3.n C 2/.n C1/

a

n

; a

0

D y.1/ D 3; a

1

D y

0

.1/ D 3.

7.2.28. From Theorem 7.2.2, a

nC2

D 

p.n/

.n C 2/.n C 1/

a

n

; a

2mC2

D 

p.2m/

.2m C 2/.2m C 1/

a

2m

, so

a

2m

D

2

4

m1

Y

j D0

p.2j /

3

5

.1/

m

.2m/Š

a

0

; a

2mC3

D 

p.2m C 1/

.2m C 3/.2m C2/

a

2m

, so a

2mC1

D

2

4

m1

Y

j D0

p.2j C 1/

3

5

.1/

m

.2m C 1/Š

a

1

.

7.2.30. (a) Here p.n/ D Œn.n  1/ C 2b n  ˛.˛ C 2b  1/ D .n  ˛/.n C ˛ C 2b  1/, so

Exercise 7.2.28 implies that y

1

and y

2

have the stated forms. If ˛ D 2k, then

y

1

D

1

X

mD0

2

4

m1

Y

j D0

.2j  2k/.2j C 2k C 2b  1/

3

5

x

2m

.2m/Š

.C/:

Section 7.2

Series Solutions Near an Ordinary Point I

95

If ˛ D 2k C 1, th en

y

2

D

1

X

mD0

2

4

m1

Y

j D0

.2j  2k/.2j C 2k C2b/

3

5

x

2mC1

.2m C 1/Š

: .D/

Since 2b is not a negative integer and

Q

m1

j D0

.2j  2k/ D 0 if m > k, y

1

in (C) and y

2

in (D) have the

stated properties. This implies the conclusions regarding P

n

.

(b) Multiplying (A) th rough by .1  x

2

/

b1

yields

Œ.1  x

2

/

b

P

0

n



0

D n.n C 2b  1/.1  x

2

/

b1

P

n

: .E/

(c) Therefore,

Œ.1  x

2

/

b

P

0

m



0

D m.m C 2b  1/.1  x

2

/

b1

P

m

: .F/

Subtr act P

n

times (F) from P

m

times (E) to obtain (B).

(d) Int egrating the left side of (B) by parts over Œ1; 1 yields zero, which implies the conclusion.

7.2.32. (a) Let Ly D .1 C˛x

3

/y

00

Cˇx

2

y

0

Cxy. If y D

1

X

nD0

a

n

x

n

, then Ly D

1

X

nD2

n.n 1/a

n

x

n2

C

1

X

nD0

p.n/a

n

x

nC1

D 2a

2

C

1

X

nD0

Œ.n C 3/.n C 2/a

nC3

C p.n/a

n

x

nC1

D 0 if and only if a

2

D 0 and

a

nC3

D 

p.n/

.n C 3/.n C 2/

a

n

for n  0.

7.2.34. p.r / D 2r.r  1/  10r  8 D 2.r C 2/

2

; (A)

m1

Y

j D0

p.3j /

3j C 2

D

m1

Y

j D0

.2/.3j C 2/

2

3j C 2

D

.1/

m

2

m

m1

Y

j D0

.3j C 2/; (B)

m1

Y

j D0

p.3j C 1/

3j C 4

D

m1

Y

j D0

.2/.3j C 3/

2

3j C 4

D

.1/

m

2

m

.mŠ/

2

Q

m1

j D0

.3j C 4/

. Su bstituting (A)

and (B) into the result of Exercise 7 .2.32(c) yields

y D a

0

1

X

mD0



2

3



m

2

4

m1

Y

j D0

.3j C 2/

3

5

x

3m

mŠ

C a

1

X

mD0

6

m

mŠ

Q

m1

j D0

.3j C 4/

x

3mC1

.

7.2.36. p.r/ D 2r.r  1/ C 6r C24 D 2.r  6/.r C 2/; (A)

m1

Y

j D0

p.3j /

3j C 2

D

m1

Y

j D0

.6/.j  2/.

(B)

m1

Y

j D0

p.3j C 1/

3j C 4

D

m1

Y

j D0

.6/.j C 1/.3j  5/

3j C 4

D .1/

m

6

m

m1

Y

j D0

3j  5

3j C 4

. Substituting (A) and

(B) i nto the result of Exercise 7.2.32(c) yields

y D a

0

.1  4x

3

C 4x

6

/ C a

1

X

mD0

2

m

2

4

m1

Y

j D0

3j  5

3j C 4

3

5

x

3mC1

.

7.2.38. (a) Let Ly D .1 C ˛x

kC2

/y

00

C ˇx

kC1

y

0

C x

k

y. If y D

1

X

nD0

a

n

x

n

, then Ly D

1

X

nD2

n.n 

1/a

n

x

n2

C

1

X

nD0

p.n/a

n

x

nCk

D

1

X

nDk

.n C k C 2/.n C k  1/a

nCkC2

x

nCk

C

1

X

nD0

Œ.n C k C 2/.n C

96 Chapter 7

Series Solutions of Linear Second Order Equations

k C 1/a

nCkC2

C p.n/a

n

x

nCk

D 0 if and only if a

k

D 0 for 2  n  k C 1 and (A) a

nCkC1

D



p.n/

.n C k C 2/.n C k C 1/

a

n

for n  0.

(b) If a

n

D 0 the a

nC.kC2/m

D 0 for all m  0, from (A).

7.2.40. k D 2 and p.r/ D 1; (A)

m1

Y

j D0

p.4j /

4j C 3

D

1

Q

m1

j D0

.4j C 3/

; (B)

m1

Y

j D0

p.4j C 1/

.4j C 5/

D

1

Q

m1

j D0

4j C 5

.

Substituting (A) and (B) into the result of Exercise t.2.38(c) yields

y D a

0

1

X

mD0

.1/

m

x

4m

4

m

mŠ

Q

m1

j D0

.4j C 3/

C a

1

X

mD0

.1/

m

x

4mC1

4

m

mŠ

Q

m1

j D0

.4j C 5/

.

7.2.42. k D 6 and p.r/ D r.r 1/16r C72 D .r  9/.r 8/; (A)

m1

Y

j D0

p.8j /

8j C 7

D

m1

Y

j D0

8.j  1/.8j  9/

8j C 7

;

(B)

m1

Y

j D0

p.8j C 1/

.8j C 9/

D

m1

Y

j D0

8.j  1/.8j  7/

8j C 9

;

Substituting (A) and (B) in to the result of Exercise 7.2.38(c) yields

y D a

0



1 

9

7

x

8



C a

1



x 

7

9

x

9



.

7.2.44. k D 4 and p.r/ D r C 6; (A)

m1

Y

j D0

p.6j /

6j C 5

D

m1

Y

j D0

6.j C 1/

6j C 5

D

6

m

mŠ

Q

m1

j D0

.6j C 5/

;

(B)

m1

Y

j D0

p.6j C 1/

.6j C 7/

D 1;

Substituting (A) and (B) in to the result of Exercise 7.2.38(c) yields

y D a

0

1

X

mD0

.1/

m

x

6m

Q

m1

j D0

.6j C 5/

C a

1

X

mD0

.1/

m

x

6mC1

6

m

mŠ

.

7.3 SERIES SOLUTIONS NEAR AN ORDINARY POINT II

7.3.2. I f y D

1

X

nD0

a

n

x

n

, then .1 C x C 2x

2

/y

00

C .2 C 8x/y

0

C 4y D

1

X

nD2

n.n  1/a

n

x

n2

C

1

X

nD2

n.n 

1/a

n

x

n1

C 2

1

X

nD2

n.n  1/a

n

x

n

C 2

1

X

nD1

na

n

x

n1

C 8

1

X

nD1

na

n

x

n

C 4

1

X

nD0

a

n

x

n

D

1

X

nD0

.n C 2/.n C

1/.a

nC2

C a

nC1

C 2a

n

/x

n

D 0 if a

nC2

D a

nC1

 2a

n

, a

n

 0. Star ting with a

0

D 1 and a

1

D 2

yields y D 1 C 2x  4x

3

C 4x

4

C 4x

5

 12x

6

C 4x

7

C .

7.3.4. If y D

1

X

nD0

a

n

x

n

, then .1 Cx C3x

2

/y

00

C.2 C15x/y

0

C12y D

1

X

nD2

n.n 1/a

n

x

n2

C

1

X

nD2

n.n 

1/a

n

x

n1

C 3

1

X

nD2

n.n  1/a

n

x

n

C 2

1

X

nD1

na

n

x

n1

C 15

1

X

nD1

na

n

x

n

C 12

1

X

nD0

a

n

x

n

D

1

X

nD0

Œ.n C 2/.n C

1/a

nC2

C.n C1/.n C2/a

nC1

C3.n C2/

2

a

n

x

n

D 0 if a

nC2

D a

nC1



3.n C 2/

n C 1

a

n

, a

n

 0. Starting

with a

0

D 0 and a

1

D 1 yields y D x  x

2



7

2

x

3

C

15

2

x

4

C

45

8

x

5



261

8

x

6

C

207

16

x

7

C .

Section 7.3

Series So lutions Near an Ordinary Poin t II

97

7.3.6. If y D

1

X

nD0

a

n

x

n

, then .3 C 3x C x

2

/y

00

C .6 C 4x/y

0

C 2y D 3

1

X

nD2

n.n  1/a

n

x

n2

C

3

1

X

nD2

n.n  1/a

n

x

n1

C

1

X

nD2

n.n  1/a

n

x

n

C 6

1

X

nD1

na

n

x

n1

C 4

1

X

nD1

na

n

x

n

C 2

1

X

nD0

a

n

x

n

D

1

X

nD0

.n C

2/.n C 1/Œ3a

nC2

C 3a

nC1

C a

n

x

n

D 0 if a

nC2

D a

nC1

 a

n

=3, a

n

 0. Starting with a

0

D 7 and

a

1

D 3 yields y D 7 C 3x 

16

3

x

2

C

13

3

x

3



23

9

x

4

C

10

9

x

5



7

27

x

6



1

9

x

7

C .

7.3.8. The equation is equivalent to .1 C t C 2t

2

/y

00

C .2 C 6t/y

0

C 2y D 0 with t D x  1. If

y D

1

X

nD0

a

n

t

n

, then .1 Ct C2t

2

/y

00

C.2 C6t/y

0

C2y D

1

X

nD2

n.n 1/a

n

t

n2

C

1

X

nD2

n.n 1/a

n

t

n1

C

2

1

X

nD2

n.n  1/a

n

t

n

C 2

1

X

nD1

na

n

t

n1

C 6

1

X

nD1

na

n

t

n

C 2

1

X

nD0

a

n

t

n

D

1

X

nD0

.n C 1/Œ.n C 2/a

nC2

C .n C

2/a

nC1

C2.nC1/a

n

t

n

D 0 if a

nC2

D a

nC1



2.n C 1/

n C 2

a

n

, a

n

 0. Starting with a

0

D 1 and a

1

D 1

yields y D 1  .x  1/ C

4

3

.x  1/

3



4

3

.x  1/

4



4

5

.x  1/

5

C

136

45

.x  1/

6



104

63

.x  1/

7

C .

7.3.10. The equation is equivalent to .1 C t C t

2

/y

00

C .3 C 4t/y

0

C 2y D 0 with t D x  1. I f

y D

1

X

nD0

a

n

t

n

, then .1 Ct C t

2

/y

00

C.3 C4t/y

0

C 2y D

1

X

nD2

n.n  1/a

n

t

n2

C

1

X

nD2

n.n 1/a

n

t

n1

C

1

X

nD2

n.n1/a

n

t

n

C3

1

X

nD1

na

n

t

n1

C4

1

X

nD1

na

n

t

n

C2

1

X

nD0

a

n

t

n

D

1

X

nD0

.nC1/Œ.nC2/a

nC2

C.nC3/a

nC1

C

.n C 2/a

n

t

n

D 0 if a

nC2

D 

n C 3

n C 2

a

nC1

 a

n

, a

n

 0. Starting with a

0

D 2 and a

1

D 1 yields y D

2  .x 1/ 

1

2

.x  1/

2

C

5

3

.x  1/

3



19

12

.x  1/

4

C

7

30

.x  1/

5

C

59

45

.x  1/

6



1091

630

.x  1/

7

C 

7.3.12. The equation is equivalent to .1 C 2t C t

2

/y

00

C .1 C 7t/y

0

C 8y D 0 wi th t D x  1. If y D

1

X

nD0

a

n

t

n

, then .1C2t Ct

2

/y

00

C.1C7t/y

0

C8y D

1

X

nD2

n.n1/a

n

t

n2

C2

1

X

nD2

n.n1/a

n

t

n1

C

1

X

nD2

n.n

1/a

n

t

n

C

1

X

nD1

na

n

t

n1

C7

1

X

nD1

na

n

t

n

C8

1

X

nD0

a

n

t

n

D

1

X

nD0

Œ.nC2/.n C1/a

nC2

C.nC1/.2n C1/a

nC1

C

.nC2/.nC 4/a

n

t

n

D 0 if a

nC2

D 

2n C 1

n C 2

a

nC1



n C 4

n C 1

a

n

, a

n

 0. Starting wi th a

0

D 1 and a

1

D 2

yields y D 1  2.x  1/  3.x  1/

2

C 8.x  1/

3

 4.x  1/

4



42

5

.x  1/

5

C19.x  1/

6



604

35

.x  1/

7

C 

7.3.16. If y D

1

X

nD0

a

n

x

n

, then .1x/y

00

.2x/y

0

Cy D

1

X

nD2

n.n1/a

n

x

n2



1

X

nD2

n.n1/a

n

x

n1



2

1

X

nD1

na

n

x

n1

C

1

X

nD1

na

n

x

n

C

1

X

nD0

a

n

x

n

D

1

X

nD0

Œ.nC2/.nC1/a

nC2

.nC2/.nC1/a

nC1

C.nC1/a

n

x

n

D

0 if a

nC2

D a

nC1



a

n

n C 2

,a

n

 0.

98 Chapter 7

Series Solutions of Linear Second Order Equations

7.3.18. If y D

1

X

nD0

a

n

x

n

, then .1 C x

2

/y

00

C y

0

C 2y D

1

X

nD2

n.n  1/a

n

x

n2

C

1

X

nD2

n.n  1/a

n

x

n

C

1

X

nD1

na

n

x

n1

C 2

1

X

nD0

a

n

x

n

D

1

X

nD0

Œ.n C 2/.n C 1/a

nC2

C .n C 1/a

nC1

C .n

2

 n C 2/a

n

x

n

D 0 if

a

nC2

D 

1

n C 2

a

nC1



n

2

 n C2

.n C 2/.n C 1/

a

n

.

7.3.20. The equation is equivalent to .3 C 2t/y

00

C .1 C 2t/y

0

 .1  2t/y D 0 wit h t D x  1. If

y D

1

X

nD0

a

n

t

n

, then .3 C 2t/y

00

C .1 C 2t/y

0

 .1  2t /y D 3

1

X

nD2

n.n  1/a

n

t

n2

C 2

1

X

nD2

n.n 

1/a

n

t

n1

C

1

X

nD1

na

n

t

n1

C 2

1

X

nD1

na

n

t

n



1

X

nD0

a

n

t

n

C 2

1

X

nD0

a

n

t

nC1

D .6a

2

C a

1

 a

0

/ C

1

X

nD1

Œ3.n C

2/.n C 1/a

nC2

C .n C 1/.2n C 1/a

nC1

C .2n  1/a

n

C 2a

n1

t

n

D 0 if a

2

D 

a

1

 a

0

6

and a

nC2

D



2n C 1

3.n C 2/

a

nC1



2n  1

3.n C 2/.n C 1/

a

n



2

3.n C 2/.n C 1/

a

n1

, n  1. Starting with a

0

D 1 and

a

1

D 2 yields y D 1 2.x  1/ C

1

2

.x  1/

2



1

6

.x  1/

3

C

5

36

.x  1/

4



73

1080

.x  1/

5

C .

7.3.22. The equation is equivalent to .1Ct/y

00

C.22t/y

0

C.3Ct/y D 0 wit h t D xC3. If y D

1

X

nD0

a

n

t

n

,

then .1 Ct/y

00

C.2 2t/y

0

C.3 Ct /y D

1

X

nD2

n.n 1/a

n

t

n2

C

1

X

nD2

n.n 1/a

n

t

n1

C2

1

X

nD1

na

n

t

n1



2

1

X

nD1

na

n

t

n

C3

1

X

nD0

a

n

t

n

C

1

X

nD0

a

n

t

nC1

D .2a

2

C2a

1

C3a

0

/ C

1

X

nD1

Œ.n C2/.nC1/a

nC2

C.n C2/.n C

1/a

nC1

 .2n  3/a

n

C a

n1

t

n

D 0 if a

2

D 

2a

1

C 3a

0

2

and a

nC2

D a

nC1

C

.2n  3/a

n

 a

n1

.n C 2/.n C 1/

,

n  1. Starting with a

0

D 2 and a

1

D 2 yields

y D 2  2.x C3/  .x C 3/

2

C .x C 3/

3



11

12

.x C 3/

4

C

67

60

.x C 3/

5

C .

7.3.24. The equation is equivalent to .1C2t/y

00

C3y

0

C.1t/y D 0 with t D xC1. If y D

1

X

nD0

a

n

t

n

, then

.1C2t/y

00

C3y

0

C.1t/y D

1

X

nD2

n.n1/a

n

t

n2

C2

1

X

nD2

n.n1/a

n

t

n1

C3

1

X

nD1

na

n

t

n1

C

1

X

nD0

a

n

t

n



1

X

nD0

a

n

t

nC1

D .2a

2

C3a

1

Ca

0

/ C

1

X

nD1

Œ.n C2/.nC1/a

nC2

C.2n C3/.n C1/a

nC1

Ca

n

a

n1

t

n

D 0

if a

2

D 

3a

1

C a

0

2

and a

nC2

D 

2n C 3

n C 2

a

nC1



a

n

 a

n1

.n C 2/.n C 1/

, n  1. Starting with a

0

D 2 and

a

1

D 3 yields y D 2 3.x C 1/ C

7

2

.x C 1/

2

 5.x C 1/

3

C

197

24

.x C 1/

4



287

20

.x C 1/

5

C .

7.3.26. The equation is equivalent to .6  2t/y

00

C .3 C t /y D 0 with t D x  2. If y D

1

X

nD0

a

n

t

n

, then

Section 7.3

Series So lutions Near an Ordinary Poin t II

99

.6  2t/y

00

C .3 C t/y D 6

1

X

nD2

n.n  1/a

n

t

n2

 2

1

X

nD2

n.n  1/a

n

t

n1

C 3

1

X

nD0

a

n

t

n

C

1

X

nD0

a

n

t

nC1

D

.12a

2

C 3a

0

/ C

1

X

nD1

Œ6.n C 2/.n C 1/a

nC2

 2.n C 1/na

nC1

C 3a

n

C a

n1

t

n

D 0 if a

2

D 

a

0

4

and a

nC2

D

n

3.n C 2/

a

nC1



3a

n

C a

n1

6.n C 2/.n C 1/

, n  1. Starting with a

0

D 2 and a

1

D 4 yields

y D 2  4.x  2/ 

1

2

.x  2/

2

C

2

9

.x  2/

3

C

49

432

.x  2/

4

C

23

1080

.x  2/

5

C .

7.3.28. The equation is equivalent to .2 C4t/y

00

.1 2t/y D 0 with t D x C4. If y D

1

X

nD0

a

n

t

n

, then

.2 C4t/y

00

 .1 2t/y D 2

1

X

nD2

n.n 1/a

n

t

n2

C4

1

X

nD2

n.n 1/a

n

t

n1



1

X

nD0

a

n

t

n

C2

1

X

nD0

a

n

t

nC1

D

.4a

2

 a

0

/ C

1

X

nD1

Œ2.n C 2/.n C 1/a

nC2

C 4.n C 1/na

nC1

 a

n

C 2a

n1

t

n

D 0 if a

2

D

a

0

4

and

a

nC2

D 

2n

n C 2

a

nC1

C

a

n

 2a

n1

2.n C 2/.n C 1/

, n  1. Starting with a

0

D 1 and a

1

D 2 yield s y D

1 C 2.x C 1/ 

1

4

.x C 1/

2

C

1

2

.x C 1/

3



65

96

.x C 1/

4

C

67

80

.x C 1/

5

C.

N=5; b=zeros(N,1); b( 1)=-1;b(2)=2; b(3)=b(1)/4; for n=1:N-2 b(n+3)=-2*n*b(n+2) /(n+2)+(b(n+1)-

2*b(n))/(2*(n+2) *(n+1)); end

7.3.29. Let Ly D .1 C ˛x C ˇx

2

/y

00

C . C ıx/y

0

C y. If y D

1

X

nD0

a

n

x

n

, t hen Ly D

1

X

nD2

n.n 

1/a

n

x

n2

C˛

1

X

nD2

n.n1/a

n

x

n1

Cˇ

1

X

nD2

n.n1/a

n

x

n

C

1

X

nD1

na

n

x

n1

Cı

1

X

nD1

na

n

x

n

C

1

X

nD0

a

n

x

n

D

1

X

nD0

.n C 2/.n C 1/a

nC2

x

n

C ˛

1

X

nD0

.n C 1/na

nC1

x

n

C ˇ

1

X

nD0

n.n  1/a

n

x

n

C 

1

X

nD0

.n C 1/a

nC1

x

n

C

ı

1

X

nD0

na

n

x

n

C 

1

X

nD0

a

n

x

n

D

1

X

nD0

b

n

x

n

, where b

n

D .n C 1/.n C 2/a

nC2

C .n C 1/.˛n C /a

nC1

C

Œˇn.n  1/ C ın C a

n

, which implies the conclusion.

7.3.30. (a) Let  D 2˛, ı D 4ˇ, and  D 2ˇ in Exercise 7.3.29 t o obtain (B).

(b) If a

n

D c

1

r

n

1

C c

2

r

n

2

, then a

nC2

C ˛a

nC1

C ˇa

n

D c

1

r

n

1

.r

2

1

C ˛r C ˇ/ C c

2

r

n

2

.r

2

C ˛r

2

C

ˇ/ D c

1

r

n

1

P

0

.r

1

/ C c

2

r

n

2

P

0

.r

2

/ D 0, so fa

n

g satisﬁes (B). Since 1=r

1

and 1=r

2

are t he zeros of P

0

,

Theorem 7.2.1 implies that

P

1

nD0

.c

1

r

n

1

C c

2

r

n

2

/x

n

is a solution of (A) on .; /.

(c) If jxj < , then jr

1

xj <  and jr

2

xj < 1, so

1

X

nD0

r

n

i

x

n

D

1

1  r

i

x

D y

i

, i D 1; 2. Therefore, (b)

implies that fy

1

; y

2

g is a fundamental set of solutions of (A ) on .; /.

(d) (A) can writ ten as P

0

y

00

C 2P

0

y

0

C P

00

0

y D .P

0

y/

00

D 0. Therefore,P

0

y D a C bx where a and

b are arbitrary constants, and a par tial fraction expansion shows that the general solution of (A) on any

inter val not containing 1=r

1

or 1=r

2

is y D

a C bx

P

0

.x/

D

c

1

1  r

1

x

C

c

2

1  r

2

x

D c

1

y

1

Cc

2

y

2

.

(e) If a

n

D c

1

r

n

1

Cc

2

r

n

2

, then a

nC2

C˛a

nC1

Cˇa

n

D c

1

r

n

1

.r

2

1

C˛r Cˇ/ Cc

2

r

n

1

Œ.n C2/r

2

1

C˛.n C

1/r

2

C ˇn/ D .c

1

C nc

2

/r

n

1

P

0

.r

1

/ C c

2

r

n

1

P

0

.r

1

/ D 0, so fa

n

g satisﬁes (B). Since 1=r

1

is the only zero

100 Chapter 7

Series Solutions of Linear Second Order Equations

of P

0

, Theorem 7.2.1 implies that

P

1

nD0

.c

1

C c

2

n/r

n

1

/x

n

is a solution of (A) on .; /.

(f) If jxj < , th en jr

1

xj < , so

1

X

nD0

r

n

1

x

n

D

1

1  r

1

x

D y

1

. D ifferentiating this and multiplying

the result by x shows that

1

X

nD0

nr

n

1

x

n

D

r

1

x

.1  r

1

x/

2

D r

1

y

2

. Therefore, (e) implies that fy

1

; y

2

g is a

fundamental set of solutions of (A) on .; /.

(g) The argument is the same as in (c), but now the partial fracti on expansion can be written as y D

a C bx

P

0

.x/

D

c

1

1  r

1

x

C

c

2

x

.1  r

2

x/

2

D c

1

y

1

C c

2

y

2

.

7.3.32. If y D

1

X

nD0

a

n

x

n

, then y

00

C 2xy

0

C .3 C 2x

2

/y D

1

X

nD2

n.n  1/a

n

x

n2

C 2

1

X

nD1

na

n

x

n

C

3

1

X

nD0

a

n

x

n

C2

1

X

nD0

a

n

x

nC2

D .2a

2

C3a

0

/ C.6a

3

C5a

1

/x C

1

X

nD2

Œ.n C2/.n C1/a

nC2

C.2n C3/a

n

C

2a

n2

x

n

D 0 if a

2

D 3a

0

=2, a

3

D 5a

1

=6, and a

nC2

D 

.2n C 3/a

n

C 2a

n2

.n C 2/.n C1/

, n  2. Starting

with a

0

D 1 and a

1

D 2 yields y D 1  2x 

3

2

x

2

C

5

3

x

3

C

17

24

x

4



11

20

x

5

C .

7.3.34. If y D

1

X

nD0

a

n

x

n

, then y

00

C5xy

0

.3x

2

/y D

1

X

nD2

n.n1/a

n

x

n2

C5

1

X

nD1

na

n

x

n

3

1

X

nD0

a

n

x

n

C

1

X

nD0

a

n

x

nC2

D .2a

2

 3a

0

/ C .6a

3

C 2a

1

/x C

1

X

nD2

Œ.n C 2/.n C 1/a

nC2

C .5n  3/a

n

C a

n2

x

n

D 0

if a

2

D 3a

0

=2, a

3

D a

1

=3, and a

nC2

D 

.5n  3/a

n

C a

n2

.n C 2/.n C 1/

, n  2. St arting with a

0

D 6 and

a

1

D 2 yields y D 6 2x C 9x

2

C

2

3

x

3



23

4

x

4



3

10

x

5

C .

7.3.36. If y D

1

X

nD0

a

n

x

n

, then y

00

 3xy

0

C .2 C 4x

2

/y D

1

X

nD2

n.n  1/a

n

x

n2

 3

1

X

nD1

na

n

x

n

C

2

1

X

nD0

a

n

x

n

C4

1

X

nD0

a

n

x

nC2

D .2a

2

C2a

0

/ C .6a

3

 a

1

/x C

1

X

nD2

Œ.n C 2/.n C 1/a

nC2

 .3n  2/a

n

C

4a

n2

x

n

D 0 if a

2

D a

0

, a

3

D a

1

=6, and a

nC2

D

.3n  2/a

n

 4a

n2

.n C 2/.n C 1/

, n  2. Starting with a

0

D 3

and a

1

D 6 yields y D 3 C 6x  3x

2

C x

3

 2x

4



17

20

x

5

C .

7.3.38. If y D

1

X

nD0

a

n

x

n

, t hen 3y

00

C 2xy

0

C .4  x

2

/y D 3

1

X

nD2

n.n  1/a

n

x

n2

C 2

1

X

nD1

na

n

x

n

C

4

1

X

nD0

a

n

x

n



1

X

nD0

a

n

x

nC2

D .6a

2

C4a

0

/ C.18a

3

C6a

1

/x C

1

X

nD2

Œ3.n C2/.n C1/a

nC2

C.2n C4/a

n



a

n2

x

n

D 0 if a

2

D 2a

0

=3, a

3

D a

1

=3, and a

nC2

D 

.2n C 4/a

n

 a

n2

3.n C 2/.n C 1/

, n  2. Starting with

a

0

D 2 and a

1

D 3 yields y D 2 C 3x C

4

3

x

2

 x

3



19

54

x

4

C

13

60

x

5

C .

Section 7.3

Series Solutions Near an Ordinary Point II

101

7.3.40. If y D

1

X

nD0

a

n

x

n

, then .1 C x/y

00

C x

2

y

0

C .1 C 2x/y D

1

X

nD2

n.n  1/a

n

x

n2

C

1

X

nD2

n.n 

1/a

n

x

n1

C

1

X

nD1

na

n

x

nC1

C

1

X

nD0

a

n

x

n

C2

1

X

nD0

a

n

x

nC1

D .2a

2

Ca

0

/ C

1

X

nD1

Œ.n C2/.nC1/a

nC2

C.n C

1/na

nC1

Ca

n

C.nC1/a

n1

x

n

D 0 if a

2

D a

0

=2 and a

nC2

D 

.n C 1/na

nC1

C a

n

C .n C 1/a

n1

.n C 2/.n C1/

,

n  1. Starting with a

0

D 2 and a

1

D 3 yields y D 2 C 3x C x

2



1

6

x

3



3

4

x

4

C

31

120

x

5

C .

7.3.42. If y D

1

X

nD0

a

n

x

n

, then .1Cx

2

/y

00

C.2Cx

2

/y

0

Cxy D

1

X

nD2

n.n1/a

n

x

n2

C

1

X

nD2

n.n1/a

n

x

n

C

2

1

X

nD1

na

n

x

n1

C

1

X

nD1

na

n

x

nC1

C

1

X

nD1

a

n

x

nC1

D .2a

2

C2a

1

/C

1

X

nD1

Œ.nC2/.nC1/a

nC2

C2.nC1/a

nC1

C

n.n1/a

n

Cna

n1

x

n

D 0 if a

2

D a

1

and a

nC2

D 

Œ2.n C 1/a

nC1

C n.n  1/a

n

Cna

n1



.n C 2/.n C1/

, n  1.

Starti ng with a

0

D 3 and a

1

D 5 yields y D 3 C 5x  5x

2

C

23

6

x

3



23

12

x

4

C

11

30

x

5

C .

7.3.44. The equation is equivalent to y

00

C.1 C3t

2

/y

0

C.1 C2t/y D 0 with t D x 2. If y D

1

X

nD0

a

n

t

n

,

then y

00

C.1C3t

2

/y

0

C.1C2t/y D

1

X

nD2

n.n1/a

n

t

n2

C

1

X

nD1

na

n

t

n1

C3

1

X

nD1

na

n

t

nC1

C

1

X

nD0

a

n

t

n

C

2

1

X

nD0

a

n

t

nC1

D .2a

2

Ca

1

Ca

0

/ C

1

X

nD1

Œ.n C2/.nC1/a

nC2

C.n C1/a

nC1

Ca

n

C.3n 1/a

n1

t

n

D 0

if a

2

D .a

1

Ca

0

/=2 and a

nC2

D 

Œ.n C 1/a

nC1

C a

n

C .3n  1/a

n1



.n C 2/.n C 1/

, n  1. Starting with a

0

D 2

and a

1

D 3 yields

y D 2  3.x C 2/ C

1

2

.x C 2/

2



1

3

.x C 2/

3

C

31

24

.x C 2/

4



53

120

.x C 2/

5

C .

7.3.46. The equation is equivalent to .1t

2

/y

00

.78tCt

2

/y

0

Cty D 0 with t D xC2. I f y D

1

X

nD0

a

n

t

n

,

then .1  t

2

/y

00

 .7  8t C t

2

/y

0

C ty D

1

X

nD2

n.n  1/a

n

t

n2



1

X

nD2

n.n  1/a

n

t

n

 7

1

X

nD1

na

n

t

n1

C

8

1

X

nD1

na

n

t

n



1

X

nD1

na

n

t

nC1

C

1

X

nD0

a

n

t

nC1

D .2a

2

7a

1

/C

1

X

nD1

Œ.nC2/.nC1/a

nC2

7.nC1/a

nC1

n.n

9/a

n

 .n  2/a

n1

t

n

D 0 if a

2

D 7a

1

=2 and a

nC2

D

Œ7.n C 1/a

nC1

Cn.n  9/a

n

C .n  2/a

n1



.n C 2/.n C 1/

,

n  1. Starting with a

0

D 2 and a

1

D 1 yields

y D 2  .x C 2/ 

7

2

.x C 2/

2



43

6

.x C 2/

3



203

24

.x C 2/

4



167

30

.x C 2/

5

C .

7.3.48. The equation is equivalent to .1 C3t C2t

2

/y

00

.3 Ct t

2

/y

0

.3 Ct/y D 0 with t D x 1. If

y D

1

X

nD0

a

n

t

n

, then .1 C3t C2t

2

/y

00

.3 Ct t

2

/y

0

.3 Ct/y D

1

X

nD2

n.n 1/a

n

t

n2

C3

1

X

nD2

n.n 

102 Chapter 7

Series Solutions of Linear Second Order Equations

1/a

n

t

n1

C2

1

X

nD2

n.n1/a

n

t

n

3

1

X

nD1

na

n

t

n1



1

X

nD1

na

n

t

n

C

1

X

nD1

na

n

t

nC1

3

1

X

nD0

a

n

t

n



1

X

nD0

a

n

t

nC1

D

.2a

2

3a

1

3a

0

/C

1

X

nD1

Œ.nC2/.nC1/a

nC2

C3.n

2

1/a

nC1

C.2n

2

3n3/.nC1/a

n

C.n2/a

n1

t

n

D 0

if a

2

D 3.a

1

C a

0

/=2 and a

nC2

D 

Œ3.n

2

 1/a

nC1

C .2n

2

 3n  3/.n C 1/a

n

C .n  2/a

n1



.n C 2/.n C 1/

, n 

1. Starting with a

0

D 1 and a

1

D 0 yields y D 1 C

3

2

.x  1/

2

C

1

6

.x  1/

3



1

8

.x  1/

5

C .

7.4 REGULAR SINGULAR POI N TS; EULER EQUATIONS

7.4.2. p.r/ D r .r  1/  7r C 7 D .r  7/.r  1/; y D c

1

x C c

2

x

7

.

7.4.4. p.r/ D r .r  1/ C 5r C 4 D .r C 2/

2

;y D x

2

.c

1

C c

2

ln x/

7.4.6. p.r/ D r .r  1/  3r C 13 D .r  2/

2

C 9; y D x

2

Œc

1

cos.3 ln x/ C c

2

sin.3 l n x/.

7.4.8. p.r/ D 12r.r  1/  5r C 6 D .3r  2/.4r  3/; y D c

1

x

2=3

Cc

2

x

3=4

.

7.4.10. p.r/ D 3r.r  1/  r C 1 D .r  1/.3r  1/; y D c

1

x C c

2

x

1=3

.

7.4.12. p.r/ D r.r  1/ C 3r C 5 D .r C 1/

2

C 4; y D

1

x

Œc

1

cos.2 ln x/ C c

2

sin.2 l n x

7.4.14. p.r/ D r.r  1/  r C 10 D .r  1/

2

C 9; y D x Œc

1

cos.3 ln x/ C c

2

sin.3 ln x/.

7.4.16. p.r/ D 2r.r  1/ C 3r  1 D .r C 1/.2r  1/; y D

c

1

x

C c

2

x

1=2

.

7.4.18. p.r/ D 2r.r 1/C10r C9 D 2.r C2/

2

C1; y D

1

x

2



c

1

cos



1

p

2

ln x



C c

2

sin



1

p

2

ln x



.

7.4.20. If p.r/ D ar .r  1/ C br C c D a.r  r

1

/

2

, then (A) p.r

1

/ D p

0

.r

1

/ D 0. If y D ux

r

1

, then

y

0

D u

0

x

r

1

C r

1

ux

r

1

1

and y

00

D u

00

x

r

1

C 2r

1

u

0

x

r

1

1

1

C r

1

.r

1

 1/x

r

1

2

1

, so

ax

2

y

00

C bxy

0

C cy D ax

r

1

C2

u

00

C .2ar

1

C b/x

r

1

C1

u

0

C .ar

1

.r

1

 1/ C br

1

C c/ x

r

1

u

D ax

r

1

C2

u

00

C p

0

.r

1

/x

r

1

C1

1

u

0

Cp.r/x

r

1

u D ax

r

1

C2

u

00

;

from (A). Therefore,u

00

D 0, so u D c

1

C c

2

x and y D x

r

1

.c

1

C c

2

x/.

7.4.22. (a) If t D x  1 and Y.t/ D y.t C 1/ D y.x/, then .1  x

2

/y

00

 2xy

0

C ˛.˛ C 1/y D

t.2 C t/

d

2

Y

dt

2

 2.1 C t /

d Y

dt

C ˛.˛ C 1/Y D 0, so y satisﬁes Legendre’s equation if and only if Y

satisﬁes (A) t.2Ct/

d

2

Y

dt

2

C2.1Ct/

d Y

dt

˛.˛ C1/Y D 0. Since (A) can be rewritten as t

2

.2Ct/

d

2

Y

dt

2

C

2t.1 C t/

d Y

dt

 ˛.˛ C 1/tY D 0, (A) has a regular singular point at t D 0

0

.

(b) If t D x C1 and Y.t/ D y.t 1/ D y.x/, then .1 x

2

/y

00

2xy

0

C˛.˛ C1/y D t.2 t/

d

2

Y

dt

2

C

2.1 t/

d Y

dt

C˛.˛ C1/Y , so y satisﬁes Legendre’s equation if and only if Y satisﬁes (B) t.2t/

d

2

Y

dt

2

C

Section 7.5

The Method of Frobeni us I

103

2.1 t/

d Y

dt

C˛.˛ C1/Y , Since (B) can be rewritten as (B) t

2

.2t /

d

2

Y

dt

2

C2t.1 t/

d Y

dt

C˛.˛ C1/tY ,

(B) has a regular singular point at t D 0

0

.

7.5 The Method of Frobenius I

7.5.2. p

0

.r/ D r.3r  1/; p

1

.r/ D 2.r C 1/; p

2

.r/ D 4.r C 2/.

a

1

.r/ D 

2

3r C 2

; a

n

.r/ D 

2a

n1

.r/  4a

n2

.r/

3n C 3r  1

, n  1.

r

1

D 1=3; a

1

.1=3/ D 2=3; a

n

.1=3/ D 

2a

n1

.1=3/  4a

n2

.1=3/

3n

, n 1;

y

1

D x

1=3



1 

2

3

x C

8

9

x

2



40

81

x

3

C 



.

r

2

D 0; a

1

.0/ D 1; a

n

.0/ D 

2a

n1

.0/  4a

n2

.0/

3n  1

, n  1;

y

2

D 1  x C

6

5

x

2



4

5

x

3

C .

7.5.4. p

0

.r/ D .r C 1/.4r  1/; p

1

.r/ D 2.r C 2/; p

2

.r/ D 4r C 7.

a

1

.r/ D 

2

4r C 3

; a

n

.r/ D 

2

4n C 4r  1

a

n1

.r/ 

1

n C r C 1

a

n2

.r/, n  1.

r

1

D 1=4; a

1

.1=4/ D 1=2; a

n

.1=4/ D 

1

2n

a

n1

.1=4/ 

4

4n C 5

a

n2

.1=4/, n 1;

y

1

D x

1=4



1 

1

2

x 

19

104

x

2

C

1571

10608

x

3

C 



.

r

2

D 1; a

1

.1/ D 2; a

n

.1/ D 

2

4n  5

a

n1

.1/ 

1

n

a

n2

.1/, n  1;

y

2

D x

1



1 C 2x 

11

6

x

2



1

7

x

3

C 



.

7.5.6. p

0

.r/ D r.5r  1/; p

1

.r/ D .r C 1/

2

; p

2

.r/ D 2.r C 2/.5r C 9/.

a

1

.r/ D 

r C 1

5r C 4

; a

n

.r/ D 

n C r

5n C 5r  1

a

n1

.r/  2a

n2

.r/, n  1.

r

1

D 1=5; a

1

.1=5/ D 6=25; a

n

.1=5/ D 

5n C 1

25n

a

n1

.1=5/  2a

n2

.1=5/, n 1;

y

1

D x

1=5



1 

6

25

x 

1217

625

x

2

C

41972

46875

x

3

C 



.

r

2

D 0; a

1

.0/ D 1=4; a

n

.0/ D 

n

5n  1

a

n1

.0/  2a

n2

.0/, n  1;

y

2

D x 

1

4

x

2



35

18

x

3

C

11

12

x

4

C .

7.5.8. p

0

.r/ D .3r  1/.6r C 1/; p

1

.r/ D .3r C2/.6r C 1/; p

2

.r/ D 3r C 5.

a

1

.r/ D 

6r C 1

6r C 7

; a

n

.r/ D 

6n C 6r  5

6n C 6r C 1

a

n1

.r/ 

1

6n C 6r C 1

a

n2

.r/, n  1.

r

1

D 1=3; a

1

.1=3/ D 1=3; a

n

.1=3/ D 

2n  1

2n C 1

a

n1

.1=3/ 

1

6n C 3

a

n2

.1=3/, n 1;

y

1

D x

1=3



1 

1

3

x C

2

15

x

2



5

63

x

3

C 



.

r

2

D 1=6; a

1

.1=6/ D 0; a

n

.1=6/ D 

n  1

n

a

n1

.1=6/ 

1

6n

a

n2

.1=6/, n  1;

y

2

D x

1=6



1 

1

12

x

2

C

1

18

x

3

C 



.

104 Chapter 7

Series Solutions of Linear Second Order Equations

7.5.10. p

0

.r/ D .2r C1/.5r  1/; p

1

.r/ D .2r  1/.5r C 4/; p

2

.r/ D 2.2r C 5/.5r  1/.

a

1

.r/ D 

2r  1

2r C 3

; a

n

.r/ D 

2n C 2r  3

2n C 2r C 1

a

n1

.r/ 

10n C 10r  22

5n C 5r  1

a

n2

.r/, n  1.

r

1

D 1=5; a

1

.1=5/ D 3=17; a

n

.1=5/ D 

10n  13

10n C 7

a

n1

.1=5/ 

2n  4

n

a

n2

.1=5/, n 1;

y

1

D x

1=5



1 C

3

17

x 

7

153

x

2



547

5661

x

3

C 



.

r

2

D 1=2; a

1

.1=2/ D 1; a

n

.1=2/ D 

n  2

n

a

n1

.1=2/ 

20n  54

10n 7

a

n2

.1=2/, n  1;

y

2

D x

1=2



1 C x C

14

13

x

2



556

897

x

3

C 



.

7.5.14. p

0

.r/ D .r C 1/.2r  1/; p

1

.r/ D 2r C 1; a

n

.r/ D 

1

n C r C 1

a

n1

.r/.

r

1

D 1=2; a

n

.1=2/ D 

2

2n C 3

a

n1

.1=2/; y

1

D x

1=2

1

X

nD0

.2/

n

Q

n

j D1

.2j C 3/

x

n

.

r

2

D 1; a

n

.1/ D 

1

n

a

n1

.1/; y

2

D x

1

1

X

nD0

.1/

n

nŠ

x

n

.

7.5.16. p

0

.r/ D .r C 2/.2r  1/; p

1

.r/ D r C 3; a

n

.r/ D 

1

2n C 2r  1

a

n1

.r/.

r

1

D 1=2; a

n

.1=2/ D 

1

2n

a

n1

.1=2/; y

1

D x

1=2

1

X

nD0

.1/

n

2

n

nŠ

x

n

.

r

2

D 2; a

n

.2/ D 

1

2n  5

a

n1

.2/; y

2

D

1

x

2

1

X

nD0

.1/

n

Q

n

j D1

.2j  5/

x

n

.

7.5.18. p

0

.r/ D .r 1/.2r  1/; p

1

.r/ D 2; a

n

.r/ D

2

.n C r  1/.2n C 2r  1/

a

n1

.r/.

r

1

D 1; a

n

.1/ D

2

n.2n C 1

/a

n1

.1/; y

1

D x

1

X

nD0

2

n

nŠ

Q

n

j D1

.2j C 1/

x

n

.

r

2

D 1=2; a

n

.1=2/ D

2

n.2n  1

/a

n1

.1=2/; y

2

D x

1=2

1

X

nD0

2

n

nŠ

Q

n

j D1

.2j  1/

x

n

.

7.5.20. p

0

.r/ D .r 1/.3r C 1/; p

1

.r/ D r  3; a

n

.r/ D 

n C r  4

.n C r  1/.3n C 3r C 1/

a

n1

.r/.

r

1

D; a

n

.1/ D 

n  3

n.3n C 4/

a

n1

.1/; y

1

D x



1 C

2

7

x C

1

70

x

2



.

r

2

D 1=3; a

n

.1=3/ D 

3n  13

3n.3n  4/

a

n1

.1=3/; y

2

D x

1=3

1

X

nD0

.1/

n

3

n

nŠ

0

@

n

Y

j D1

3j  13

3j  4

1

A

x

n

.

7.5.22. p

0

.r/ D .r 1/.4r  1/; p

1

.r/ D r.r C 2/; a

n

.r/ D 

n C r C 1

4n C 4r  1

a

n1

.r/.

r

1

D 1; a

n

.1/ D 

n C 2

4n C 3

a

n1

.1/; y

1

D x

1

X

nD0

.1/

n

.n C 2/Š

2

Q

n

j D1

.4j C 3/

x

n

.

r

2

D 1=4; a

n

.1=4/ D 

4n C 5

16n

a

n1

.1=4/; y

2

D x

1=4

1

X

nD0

.1/

n

16

n

nŠ

n

Y

j D1

.4j C 5/x

n

Section 7.5

The Method of Frobeni us I

105

7.5.24. p

0

.r/ D .r C 1/.3r  1/; p

1

.r/ D 2.r C 2/.2r C 3/; a

n

.r/ D 2

2n C2r C 1

3n C3r  1

a

n1

.r/.

r

1

D 1=3; a

n

.1=3/ D 2

6n C 5

9n

a

n1

.1=3/; y

1

D x

1=3

1

X

nD0

.1/

n

nŠ



2

9



n

0

@

n

Y

j D1

.6j C 5/

1

A

x

n

;

r

2

D 1; a

n

.1/ D 2

2n  1

3n  4

a

n1

.1/; y

2

D x

1

1

X

nD0

.1/

n

2

n

0

@

n

Y

j D1

2j  1

3j  4

1

A

x

n

7.5.28. p

0

.r/ D .2r 1/.4r  1/; p

1

.r/ D .r C 1/

2

; a

n

.r/ D 

.n C r /

2

.2n C 2r  1/.4n C 4r  1/

a

n1

.r/.

r

1

D 1=2; a

n

.1=2/ D 

4n

2

C 4n C 1

8n.4n C 1/

a

n1

.1=2/; y

1

D x

1=2



1 

9

40

x C

5

128

x

2



245

39936

x

3

C 



.

r

2

D 1=4; a

n

.1=4/ D 

16n

2

C 8n C 1

32n.4n  1/

a

n1

.1=4/; y

2

D x

1=4



1 

25

96

x C

675

14336

x

2



38025

5046272

x

3

C 



.

7.5.30. p

0

.r/ D .2r 1/.2r C 1/; p

1

.r/ D .2r C 1/.3r C 1/; a

n

.r/ D 

.3n C 3r  2/

.2n C 2r C 1/

a

n

.r/.

r

1

D 1=2; a

n

.1=2/ D 

6n  1

4.n C 1/

a

n1

.1=2/; y

1

D x

1=2



1 

5

8

x C

55

96

x

2



935

1536

x

3

C 



.

r

2

D 1=2; a

n

.1=2/ D 

6n  7

4n

a

n1

.1=2/; y

2

D x

1=2



1 C

1

4

x 

5

32

x

2



55

384

x

3

C 



.

7.5.32. p

0

.r/ D .2r C1/.3r C1/; p

1

.r/ D .r C1/.r C2/; a

n

.r/ D

.n C r /.n C r C 1/

.2n C 2r C 1/.3n C 3r C 1/

a

n

.r/.

r

1

D 1=3; a

n

.1=3/ D 

.3n  1/.3n C 2/

9n.6n C 1/

a

n1

.1=3/; y

1

D x

1=3



1 

10

63

x C

200

7371

x

2



17600

3781323

x

3

C 



.

r

2

D 1=2; a

n

.1=2/ D 

.2n 1/.2n C 1/

4n.6n  1/

a

n1

.1=2/; y

2

D x

1=2



1 

3

20

x C

9

352

x

2



105

23936

x

3

C 



.

7.5.34. p

0

.r/ D .2r 1/.4r  1/; p

2

.r/ D .2r C 3/.4r C3/; a

2m

.r/ D

8m C4r  5

8m C4r  1

a

2m2

.r/.

r

1

D 1=2; a

2m

.1=2/ D

8m  3

8m C 1

a

2m2

.1=2/; y

1

D x

1=2

1

X

mD0

0

@

m

Y

j D1

8j  3

8j C 1

1

A

x

2m

.

r

2

D 1=4; a

2m

.1=4/ D

2m  1

2m

a

2m2

.1=4/; y

2

D x

1=4

1

X

mD0

1

2

m

mŠ

0

@

m

Y

j D1

.2j  1/

1

A

x

2m

7.5.36. p

0

.r/ D r.3r  1/; p

2

.r/ D .r  4/.r C 2/; a

2m

.r/ D 

2m C r  6

6m C 3r  1

a

2m2

.r/.

r

1

D 1=3; a

2m

.1=3/ D 

6m  17

18m

a

2m2

.1=3/; y

1

D x

1=3

1

X

mD0

.1/

m

18

m

mŠ

0

@

m

Y

j D1

.6j  17/

1

A

x

2m

.

r

2

D 0; a

2m

.0/ D 

2m  6

6m  1

a

2m2

.0/; y

2

D 1 C

4

5

x

2

C

8

55

x

4

7.5.38. p

0

.r/ D .2r 1/.3r  1/; p

2

.r/ D .r C 1/.3r C 5/; a

2m

.r/ D

2m C r  1

4m C 2r  1

a

2m2

.r/.

106 Chapter 7

Series Solutions of Linear Second Order Equations

r

1

D 1=2; a

2m

.1=2/ D

4m  1

8m

a

2m2

.1=2/; y

1

D x

1=2

1

X

mD0

1

8

m

mŠ

0

@

m

Y

j D1

.4j  1/

1

A

x

2m

.

r

2

D 1=3; a

2m

.1=3/ D

6m  2

12m  1

a

2m2

.1=3/; y

2

D x

1=3

1

X

mD0

2

m

0

@

m

Y

j D1

3j  1

12j  1

1

A

x

2m

.

7.5.40. p

0

.r/ D .2r 1/.2r C 1/; p

1

.r/ D .r C1/.2r C3/; a

2m

.r/ D 

2m C r  1

4m C2r C 1

a

2m2

.r/.

r

1

D 1=2; a

2m

.1=2/ D 

4m  1

4.2m C 1/

a

2m2

.1=2/; y

1

D x

1=2

1

X

mD0

.1/

m

4

m

0

@

m

Y

j D1

4j  1

2j C 1

1

A

x

2m

.

r

2

D 1=2; a

2m

.1=2/ D 

4m  3

8m

a

2m2

.1=2/; y

2

D x

1=2

1

X

mD0

.1/

m

8

m

mŠ

0

@

m

Y

j D1

.4j  3/

1

A

x

2m

7.5.42. p

0

.r/ D .r C 1/.3r  1/; p

1

.r/ D .r  1/.3r C 5/; a

2m

.r/ D 

2m C r  3

2m C r C 1

a

2m2

.r/.

r

1

D 1=3; a

2m

.1=3/ D 

3m  4

3m C 2

a

2m2

.1=3/; y

1

D x

1=3

1

X

mD0

.1/

m

0

@

m

Y

j D1

3j  4

3j C 2

1

A

x

2m

.

r

2

D 1; a

2m

.1/ D 

m  2

m

a

2m2

.1/; y

2

D x

1

.1 C x

2

/

7.5.44. p

0

.r/ D .r C 1/.2r  1/; p

1

.r/ D r

2

; a

2m

.r/ D 

.2m C r  2/

2

.2m C r C 1/.4m C 2r  1/

a

2m2

.r/.

r

1

D 1=2; a

2m

.1=2/ D 

.4m 3/

2

8m.4m C 3/

a

2m2

.1=2/; y

1

D x

1=2

1

X

mD0

.1/

m

8

m

mŠ

0

@

m

Y

j D1

.4j  3/

2

4j C 3

1

A

x

2m

.

r

2

D 1; a

2m

.1/ D 

.2m 3/

2

2m.4m  3/

a

2m2

.1/; y

2

D x

1

1

X

mD0

.1/

m

2

m

mŠ

0

@

m

Y

j D1

.2j  3/

2

4j  3

1

A

x

2m

.

7.5.46. p

0

.r/ D .3r  1/.3r C 1/; p

1

.r/ D 3r C 5; a

2m

.r/ D 

1

6m C 3r C 1

a

2m2

.r/.

r

1

D 1=3; a

2m

.1=3/ D 

1

2.3m C 1/

a

2m2

.1=3/; y

1

D x

1=3

1

X

mD0

.1/

m

2

m

Q

m

j D1

.3j C 1/

x

2m

.

r

2

D 1=3; a

2m

.1=3/ D 

1

6m

a

2m2

.1=3/; y

2

D x

1=3

1

X

mD0

.1/

m

6

m

mŠ

x

2m

7.5.48. p

0

.r/ D 2.r C1/.4r  1/; p

2

.r/ D .r C3/

2

; a

2m

.r/ D 

2m C r C 1

2.8m C 4r  1/

a

2m2

.r/.

r

1

D 1=4; a

2m

.1=4/ D 

8m C 5

64m

a

2m2

.1=4/; y

1

D x

1=4



1 

13

64

x

2

C

273

8192

x

4



2639

524288

x

6

C 



.

r

2

D 1; a

2m

.1/ D 

m

8m  5

a

2m2

.1/; y

2

D x

1



1 

1

3

x

2

C

2

33

x

4



2

209

x

6

C 



.

7.5.50. p

0

.r/ D .2r 1/.2r C 1/; p

2

.r/ D .2r C 5/

2

; a

2m

.r/ D 

4m C 2r C 1

4m C2r  1

a

2m2

.r/.

Section 7.5

The Method of Frobeni us I

107

r

1

D 1=2; a

2m

.1=2/ D 

2m C 1

2m

a

2m2

.1=2/; y

1

D x

1=2



1 

3

2

x

2

C

15

8

x

4



35

16

x

6

C 



.

r

2

D 1=2; a

2m

.1=2/ D 

2m

2m  1

a

2m2

.1=2/; y

2

D x

1=2



1  2x

2

C

8

3

x

4



16

5

x

6

C 



.

7.5.52. (a) Multiplying (A) c

1

y

1

Cc

2

y

2

 0 by x

r

2

yields c

1

x

r

1

r

2

P

1

nD0

a

n

x

n

Cc

2

P

1

nD0

b

n

x

n

D 0,

0 < x < . Letting x ! 0C shows that c

2

D 0, since b

0

D 1. Now (A) reduces to c

1

y

1

 0, so c

1

D 0.

Therefore,y

1

and y

2

are linearly independent on .0; /.

(b) Since y

1

D

P

1

nD0

a

n

.r

1

/x

n

and y

2

D

P

1

nD0

a

n

.r

2

/x

n

are linearly independent solutions of

Ly D 0 .0; /, fy

1

; y

2

g is a fundamental set of solutions of Ly D 0 on .0; /, by Theorem 5.1.6.

7.5.54. (a) If x > 0, then jxj

r

x

n

D x

nCr

, so the assertions are obvious. If x < 0, then jxj

r

D .x/

r

, so

d

dx

jxj

r

D r.x/

r1

D

r.x/

r

x

D

rjxj

r

x

. Therefore,(A)

d

dx

.jxj

r

x

n

/ D

rjxj

r

x

n

C jxj

r

.nx

n1

/ D

.n C r/jxj

r

x

n1

and

d

2

dx

2

.jxj

r

x

n

/ D .n C r/

d

dx

.jxj

r

x

n1

/ D .n C r /.n C r  1/jxj

r

x

n2

, from (A)

with n replaced by n  1.

7.5.56. (a) Here p

1

 0, so Eqn. (7.5.12) reduces to a

0

.r/ D 1, a

1

.r/ D 0, a

n

.r/ D 

p

2

.n C r  2/

p

0

.n C r /

a

n2

.r/,

r  0, which implies that a

2mC1

.r/ D 0 for m D 1; 2; 3; : : : . Therefore,Eqn. (7.5.12) actually reduces

to a

0

.r/ D 1, a

2m

.r/ D 

p

2

.2m C r  2/

p

0

.2m C r/

, which ho lds because of condition (A).

(b) Similar to the proof of Exercise 7.5.55(a).

(c) p

0

.2m C r

1

/ D 2m˛

0

.2m C r

1

 r

2

/, which is nonzero if m > 0, since r

1

 r

2

 0. Therefore,

the assumptions of Theorem 7.5.2 hold with r D r

1

, and Ly

1

D p

0

.r

1

/x

r

1

D 0. If r

1

 r

2

is no t an

even integer, then p

0

.2m C r

2

/ D 2m˛

0

.2m  r

1

C r

2

/ ¤ 0, m D 1; 2; . Hence, the assumptions

of Theorem 7.5.2 hold with r D r

2

and Ly

2

D p

0

.r

2

/x

r

2

D 0. From Exercise 7.5.52, fy

1

; y

2

g is a

fundamental set of solutions.

(d) Similar to the proof of Exercise 7.5.55(c).

7.5.58. (a) From Exercise 7.5.57, b

n

D 0 for n  1.

7.5.60. (a) .˛

0

C˛

1

xC˛

2

x

2

/

1

X

nD0

a

n

x

n

D ˛

0

a

0

C.˛

0

a

1

C˛

1

a

0

/xC

1

X

nD2

.˛

0

a

n

C˛

1

a

n1

C˛

2

a

n2

/x

n

D

1, so

1

X

nD0

a

n

x

n

D

˛

0

a

0

˛

0

C ˛

1

x C ˛

2

x

2

.

(b) If

p

1

.r  1/

p

0

.r/

D

˛

1

˛

0

and

p

2

.r  2/

p

0

.r/

D

˛

2

˛

0

, then Eqn. (7.5.12) is equivalent to a

0

.r/ D 1, ˛

0

a

1

.r/C

˛

1

a

0

.r/ D 0, ˛

0

a

n

.r/ C ˛

1

a

n1

.r/ C ˛

2

a

n2

.r/ D 0, n  2. Therefore,Theorem 7.5.2 implies the

conclusion.

7.5.62. p

0

.r/ D .2r  1/.3r  1/; p

1

.r/ D 0; p

2

.r/ D 2.2r C 3/.3r C 5/;

p

1

.r  1/

p

0

.r/

D 0 D

˛

1

˛

0

;

p

2

.r  2/

p

0

.r/

D 2 D

˛

2

˛

0

; y

1

D

x

1=3

1 C 2x

2

; y

2

D

x

1=2

1 C 2x

2

.

7.5.64. p

0

.r/ D 5.3r  1/.3r C 1/; p

1

.r/ D .3r C 2/.3r C 4/; p

2

.r/ D 0;

p

1

.r  1/

p

0

.r/

D

1

5

D

˛

1

˛

0

;

p

2

.r  2/

p

0

.r/

D 0 D

˛

2

˛

0

; y

1

D

x

1=3

5 C x

; y

2

D

x

1=3

5 C x

.

108 Chapter 7

Series Solutions of Linear Second Order Equations

7.5.66. p

0

.r/ D .2r 3/.2r 1/; p

1

.r/ D 3.2r 1/.2r C1/; p

2

.r/ D .2r C1/.2r C3/;

p

1

.r  1/

p

0

.r/

D

3 D

˛

1

˛

0

;

p

2

.r  2/

p

0

.r/

D 1 D

˛

2

˛

0

; y

1

D

x

1=2

1 C 3x C x

2

; y

2

D

x

3=2

1 C 3x C x

2

.

7.5.68. p

0

.r/ D 3.r 1/.4r 1/; p

1

.r/ D 2r.4r C3/; p

2

.r/ D .r C1/.4r C7/;

p

1

.r  1/

p

0

.r/

D

2

3

D

˛

1

˛

0

;

p

2

.r  2/

p

0

.r/

D

1

3

D

˛

2

˛

0

; y

1

D

x

3 C 2x C x

2

; y

2

D

x

1=4

3 C 2x C x

2

.

7.6 THE METHOD OF FROBENIUS II

7.6.2. p

0

.r/ D .r C 1/

2

; p

1

.r/ D .r C 2/.r C 3/; p

2

.r/ D .r C 3/.2r  1/;

a

1

.r/ D 

r C 3

r C 2

; a

n

.r/ D 

n C r C 2

n C r C 1

a

n1

.r/ 

2n C2r  5

n C r C 1

a

n2

.r/, n  2.

a

0

1

.r/ D

1

.r C 2/

2

; a

0

n

.r/ D 

n C r C 2

n C r C 1

a

0

n1

.r/ 

2n C2r  5

n C r C 1

a

0

n2

.r/ C

1

.n C r C 1/

2

a

n1

.r/ 

7

.n C r C 1/

2

a

n2

.r/, n  2.

r

1

D 1; a

1

.1/ D 2; a

n

.1/ D 

n C 1

n

a

n1

.1/ 

2n  7

n

a

n2

.1/, n  2;

y

1

D x

1



1  2x C

9

2

x

2



20

3

x

3

C 



;

a

0

1

.1/ D 1; a

0

n

.1/ D 

n C 1

n

a

n1

.1/ 

2n  7

n

a

n2

.1/ C

1

n

2

a

n1

.1/ 

7

n

2

a

n2

.1/, n  2;

y

2

D y

1

ln x C 1 

15

4

x C

133

18

x

2

C .

7.6.4. p

0

.r/ D .2r  1/

2

; p

1

.r/ D .2r C 1/.2r C 3/; p

2

.r/ D .2r C 1/.2r C 3/;

a

1

.r/ D 

2r C 3

2r C 1

; a

n

.r/ D 

.2n C 2r C 1/a

n1

.r/  .2n C 2r  3/a

n2

.r/

2n C2r  1

, n  2.

a

0

1

.r/ D

4

.2r C 1/

2

; a

0

n

.r/ D 

.2n C 2r C1/a

0

n1

.r/  .2n C 2r  3/a

0

n2

.r/

2n C 2r  1

C

4.a

n1

.r/  a

n2

.r//

.2n C 2r  1/

2

;

n  2.

r

1

D 1=2; a

1

.1=2/ D 2; a

n

.1=2/ D 

.n C 1/a

n1

.1=2/ C .n  1/a

n2

.1=2/

n

; n  2;

y

1

D x

1=2



1  2x C

5

2

x

2

 2x

3

C 



;

a

0

1

.1=2/ D 1; a

0

n

.1=2/ D 

.n C 1/a

0

n1

.1=2/ C .n  1/a

0

n2

.1=2/

n

C

a

n1

.1=2/  a

n2

.1=2/

n

2

, n 

2;

y

2

D y

1

ln x C x

3=2



1 

9

4

x C

17

6

x

2

C 



.

7.6.6. p

0

.r/ D .3r C 1/

2

; p

1

.r/ D 3.3r C 4/; p

2

.r/ D 2.3r C 7/;

a

1

.r/ D 

3

3r C 4

; a

n

.r/ D

3a

n1

.r/ C 2a

n2

.r/

3n C 3r C 1

; n  2;

a

0

1

.r/ D

9

.3r C 4/

2

; a

0

n

.r/ D

3a

0

n1

.r/ C 2a

0

n2

.r/

3n C 3r C 1

C

9a

n1

.r/  6a

n2

.r/

.3n C 3r C 1/

2

; n  2.

r

1

D 1=3; a

1

.1=3/ D 1; a

n

.1=3/ D

3a

n1

.1=3/ C 2a

n2

.1=3/

3n

, n  2;

y

1

D x

1=3



1  x C

5

6

x

2



1

2

x

3

C 



;

Section 7.6

The Method of Frobeni us II

109

a

0

1

.1=3/ D 1; a

0

n

.1=3/ D

3a

0

n1

.r/ C 2a

0

n2

.r/

3n

C

3a

n1

.r/  2a

n2

.r/

3n

2

; n  2;

y

2

D y

1

ln x C x

2=3



1 

11

12

x C

25

36

x

2

C 



.

7.6.8. p

0

.r/ D .r C 2/

2

; p

1

.r/ D 2.r C3/

2

; p

2

.r/ D 3.r C 4/;

a

1

.r/ D 2; a

n

.r/ D 2a

n1

.r/ 

3a

n2

.r/

n C r C 2

; n  2;

a

0

1

.r/ D 0; a

0

n

.r/ D 2a

0

n1

.r/ 

3a

0

n2

.r/

n C r C 2

C

3a

n2

.r/

.n C r C 2/

2

, n  2.

r

1

D 2; a

1

.2/ D 2; a

n

.2/ D 2a

n1

.2/ 

3a

n2

.2/

n

, n  2;

y

1

D x

2



1  2x C

5

2

x

2

 3x

3

C 



;

a

0

1

.2/ D 0; a

0

n

.2/ D 2a

n1

.2/ 

3a

n2

.2/

n

C

3a

n2

.2/

n

2

; n  2;

y

2

D y

1

ln x C

3

4



13

6

x C .

7.6.10. p

0

.r/ D .4r C1/

2

; p

1

.r/ D 4r C 5; p

2

.r/ D 2.4r C 9/;

a

1

.r/ D 

1

4r C 5

; a

n

.r/ D 

a

n1

.r/ C 2a

n2

.r/

4n C 4r C 1

; n  2;

a

0

1

.r/ D

4

.4r C 5/

2

; a

0

n

.r/ D 

a

0

n1

.r/ C 2a

0

n2

.r/

4n C 4r C 1

C

4a

n1

.r/ C 8a

n2

.r/

.4n C 4r C 1/

2

; n  2.

r

1

D 1=4; a

1

.1=4/ D 1=4; a

n

.1=4/ D 

a

n1

.1=4/ C 2a

n2

.1=4/

4n

; n  2;

y

1

D x

1=4



1 

1

4

x 

7

32

x

2

C

23

384

x

3

C 



;

a

0

1

.1=4/ D 1=4; a

0

n

.1=4/ D 

a

0

n1

.1=4/ C 2a

0

n2

.1=4/

4n

C

a

n1

.1=4/ C 2a

n2

.1=4/

4n

2

; n 

2;

y

2

D y

1

ln x C x

3=4



1

4

C

5

64

x 

157

2304

x

2

C 



.

7.6.12. p

0

.r/ D .2r 1/

2

; p

1

.r/ D 4;

a

n

.r/ D 

4

.2n C 2r  1/

2

a

n1

.r/;

a

n

.r/ D

.4/

n

Q

n

j D1

.2j C 2r  1/

.

By logarithmic differentiation, a

0

n

.r/ D a

n

.r/

n

X

j D1

2

2j C 2r  1

;

r

1

D 1=2; a

n

.1=2/ D

.1/

n

.nŠ/

2

;

a

0

n

.1=2/ D a

n

.1=2/

0

@

2

n

X

j D1

1

j

1

A

;

y

1

D x

1=2

1

X

nD0

.1/

n

.nŠ/

2

x

n

;

110 Chapter 7

Series Solutions of Linear Second Order Equations

y

2

D y

1

ln x 2x

1=2

1

X

nD1

.1/

n

.nŠ/

2

0

@

n

X

j D1

1

j

1

A

x

n

;

7.6.14. p

0

.r/ D .r  2/

2

; p

1

.r/ D r

2

; a

n

.r/ D 

.n C r  1/

2

.n C r  2/

2

a

n1

.r/; a

n

.r/ D .1/

n

.n C r  1/

2

.r  1/

2

;

a

0

n

.r/ D .1/

nC1

2n.r C n  1/

.r  1/

3

; r

1

D 2; a

n

.2/ D .1/

n

.n C 1/

2

; a

0

n

.2/ D .1/

nC1

2n.n C 1/;

y

1

D x

2

1

X

nD0

.1/

n

.n C 1/

2

x

n

; y

2

D y

1

ln x 2x

2

1

X

nD1

.1/

n

n.n C 1/x

n

.

7.6.16. p

0

.r/ D .5r 1/

2

; p

1

.r/ D r C 1;

a

n

.r/ D 

.n C r /

.5n C 5r  1/

2

a

n1

.r/;

a

n

.r/ D .1/

n

Y

j D1

.j C r/

.5j C 5r  1/

2

;

By logarithmic differentiation,

a

0

n

.r/ D a

n

.r/

n

X

j D1

.5j C 5r C 1/

.j C r/.5j C 5r  1/

;

r

1

D 1=5; a

n

.1=5/ D .1/

n

Y

j D1

.5j C 1/

125

n

.nŠ/

2

;

a

0

n

.1=5/ D a

n

.1=5/

n

X

j D1

5j C 2

j.5j C 1/

;

y

1

D x

1=5

1

X

nD0

.1/

n

Q

n

j D1

.5j C 1/

125

n

.nŠ/

2

x

n

;

y

2

D y

1

ln x x

1=5

1

X

nD1

.1/

n

Q

n

j D1

.5j C 1/

125

n

.nŠ/

2

0

@

n

X

j D1

5j C 2

j.5j C 1/

1

A

x

n

.

7.6.18. p

0

.r/ D .3r  1/

2

; p

1

.r/ D .2r  1/

2

;

a

n

.r/ D 

.2n C 2r  3/

2

.3n C 3r  1/

2

a

n1

.r/;

a

n

.r/ D .1/

n

Y

j D1

.2j C 2r  3/

2

.3j C 3r  1/

2

;

By logarithmic differentiation,

a

0

n

.r/ D 14a

n

.r/

n

X

j D1

1

.2j C 2r  3/.3j C 3r  1/

;

r

1

D 1=3; a

n

.1=3/ D

.1/

n

Q

n

j D1

.6j  7/

2

81

n

.nŠ/

2

;

a

0

n

.1=3/ D 14a

n

.1=3/

n

X

j D1

1

j.6j  7/

/;

y

1

D x

1=3

1

X

nD0

.1/

n

Q

n

j D1

.6j  7/

2

81

n

.nŠ/

2

x

n

;

Section 7.6

The Method of Frobeni us II

111

y

2

D y

1

ln x C 14x

1=3

1

X

nD1

.1/

n

Q

n

j D1

.6j  7/

2

81

n

.nŠ/

2

0

@

n

X

j D1

1

j.6j  7/

/

1

A

x

n

.

7.6.20. p

0

.r/ D .r C 1/

2

; p

1

.r/ D 2.r C 2/.2r C 3/;

a

n

.r/ D

2.2n C 2r C 1/

n C r C 1

a

n1

.r/, n  1; a

n

.r/ D 2

n

Y

j D1

2j C 2r C 1

j C r C 1

;

By logarithmic differentiation,

a

0

n

.r/ D a

n

.r/

n

X

j D1

1

.j C r C 1/.2j C 2r C 1/

;

r

1

D 1; a

n

.1/ D

2

n

Q

n

j D1

.2j  1/

nŠ

;

a

0

n

.1/ D a

n

.1/

n

X

j D1

1

j.2j  1/

;

y

1

D

1

x

1

X

nD0

2

n

Q

n

j D1

.2j  1/

nŠ

x

n

;

y

2

D y

1

ln x C

1

x

1

X

nD1

2

n

Q

n

j D1

.2j  1/

nŠ

0

@

n

X

j D1

1

j.2j  1/

1

A

x

n

.

7.6.22. p

0

.r/ D 2.r  2/

2

; p

1

.r/ D .r 1/.2r C 1/;

a

n

.r/ D 

2n C 2r  1

2.n C r  2/

a

n1

.r/;

a

n

.r/ D

.1/

n

2

n

Y

j D1

2j C 2r 1

j C r  2

;

By logarithmic differentiation,

a

0

n

.r/ D 3a

n

.r/

n

X

j D1

1

.j C r  2/.2j C 2r  1/

;

r

1

D 2; a

n

.2/ D

.1/

n

Q

n

j D1

.2j C 3/

2

n

nŠ

;

a

0

n

.2/ D 3a

n

.2/

n

X

j D1

1

j.2j C 3/

;

y

1

D x

2

1

X

nD0

.1/

n

Q

n

j D1

.2j C 3/

2

n

nŠ

x

n

;

y

2

D y

1

ln x 3x

2

1

X

nD0

.1/

n

Q

n

j D1

.2j C 3/

2

n

nŠ

0

@

n

X

j D1

1

j.2j C 3/

1

A

x

n

.

7.6.24. p

0

.r/ D .r 3/

2

; p

1

.r/ D 2.r  1/.r C 2/;

a

n

.r/ D

2.n C r  2/.n C r C 1/

.n C r  3/

2

a

n1

.r/;

a

0

n

.r/ D

2.n C r  2/.n C r C 1/

.n C r  3/

2

a

0

n1

.r/ 

2.5n C 5r  7/

.n C r  3/

3

a

n1

.r/;

r

1

D 3; a

n

.3/ D

2.n C 1/.n C 4/

n

2

a

n1

.3/;

112 Chapter 7

Series Solutions of Linear Second Order Equations

y

1

D x

3

.1 C 20x C 180x

2

C 1120x

3

C ;

a

0

n

.3/ D

2.n C 1/.n C 4/

n

2

a

0

n1

.3/ 

2.5n C8/

n

3

a

n1

.3/;

y

2

D y

1

ln x x

4



26 C 324x C

6968

3

x

2

C 



7.6.26. p

0

.r/ D r

2

; p

1

.r/ D r

2

C r C 1;

a

n

.r/ D 

.n

2

C n.2r  1/ C r

2

 r C 1/

.n C r /

2

a

n1

.r/;

a

0

n

.r/ D 

.n

2

C n.2r  1/ C r

2

 r C 1/

.n C r /

2

a

0

n1

.r/ 

.n C r  2/

.n C r /

3

a

n1

.r/;

r

1

D 0; a

n

.0/ D 

.n

2

 n C 1/

n

2

a

n1

.0/;

y

1

D 1  x C

3

4

x

2



7

12

x

3

C ;

a

0

n

.0/ D 

.n

2

 n C 1/

n

2

a

0

n1

.0/ 

.n  2/

n

3

a

n1

.0/;

y

2

D y

1

ln x C x



1 

3

4

x C

5

9

x

2

C 



.

7.6.28. p

0

.r/ D .r 1/

2

; p

2

.r/ D r C 1;

a

2m

.r/ D 

1

2m C r  1

a

2m2

.r/, n  1; a

2m

.r/ D

.1/

m

Q

m

j D1

.2j C r 1/

;

By logarithmic differentiation,

a

0

2m

.r/ D a

2m

.r/

m

X

j D1

;

r

1

D 1; a

2m

.1/ D

.1/

m

2

m

mŠ

;

a

0

2m

.1/ D 

1

2

a

2m

.1/

m

X

j D1

1

j

;

y

1

D x

1

X

mD0

.1/

m

2

m

mŠ

x

2m

;

y

2

D y

1

ln x 

x

2

1

X

mD1

.1/

m

2

m

mŠ

0

@

m

X

j D1

1

j

1

A

x

2m

.

7.6.30. p

0

.r/ D .2r 1/

2

; p

2

.r/ D 2r C 3;

a

2m

.r/ D 

1

4m C 2r  1

a

2m2

.r/;

a

2m

.r/ D

.1/

m

Q

m

j D1

.4j C 2r  1/

;

By logarithmic differentiation,

a

0

2m

.r/ D 2a

2m

.r/

m

X

j D1

1

4j C 2r  1

;

r

1

D 1=2; a

2m

.1=2/ D

.1/

m

4

m

mŠ

;

Section 7.6

The Method of Frobeni us II

113

a

0

2m

.1=2/ D 

1

2

a

2m

.1=2/

m

X

j D1

1

j

;

y

1

D x

1=2

1

X

mD0

.1/

m

4

m

mŠ

x

2m

;

y

2

D y

1

ln x 

x

1=2

2

1

X

mD1

.1/

m

4

m

mŠ

0

@

m

X

j D1

1

j

1

A

x

2m

.

7.6.32. p

0

.r/ D .2r 1/

2

; p

2

.r/ D .r C 1/.2r C 3/; a

2m

.r/ D 

2m C r  1

4m C 2r  1

a

2m2

.r/;

a

2m

.r/ D .1/

m

Y

j D1

2j C r  1

4j C 2r  1

;

By logarithmic differentiation,

a

0

2m

.r/ D a

2m

.r/

m

X

j D1

1

.2j C r 1/.4j C 2r  1/

;

r

1

D 1=2; a

2m

.1=2/ D

.1/

m

Q

m

j D1

.4j  1/

8

m

mŠ

;

a

0

2m

.1=2/ D a

2m

.1=2/

m

X

j D1

1

2j.4j  1/

;

y

1

D x

1=2

1

X

mD0

.1/

m

Q

m

j D1

.4j  1/

8

m

mŠ

x

2m

;

y

2

D y

1

ln x C

x

1=2

2

1

X

mD1

.1/

m

Q

m

j D1

.4j  1/

8

m

mŠ

0

@

m

X

j D1

1

j.4j  1/

1

A

x

2m

.

7.6.34. p

0

.r/ D .4r C1/

2

; p

2

.r/ D .r  1/.4r C 9/;

a

2m

.r/ D 

2m C r  3

8m C 4r C 1

a

2m2

.r/;

a

2m

.r/ D .1/

m

Y

j D1

2j C r  3

8j C 4r C 1

;

By logarithmic differentiation,

a

0

2m

.r/ D a

2m

.r/

m

X

j D1

13

.2j C r 3/.8j C 4r C 1/

;

r

1

D 1=4; a

2m

.1=4/ D

.1/

m

Q

m

j D1

.8j  13/

.32/

m

mŠ

;

a

0

2m

.1=4/ D a

2m

.1=4/

m

X

j D1

13

2j.8j  13/

;

y

1

D x

1=4

1

X

mD0

.1/

m

Q

m

j D1

.8j  13/

.32/

m

mŠ

x

2m

;

y

2

D y

1

ln x C

13

2

x

1=4

1

X

mD1

.1/

m

Q

m

j D1

.8j  13/

.32/

m

mŠ

0

@

m

X

j D1

1

j.8j  13/

1

A

x

2m

.

7.6.36. p

0

.r/ D .2r 1/

2

; p

2

.r/ D 16r.r C 1/;

114 Chapter 7

Series Solutions of Linear Second Order Equations

a

2m

.r/ D 

16.2m C r  2/.2m C r  1/

.4m C 2r  1/

2

a

2m2

.r/;

a

2m

.r/ D .16/

m

Y

j D1

.2j C r  2/.2j C r  1/

.4j C 2r  1/

2

;

By logarithmic differentiation,

a

0

2m

.r/ D a

2m

.r/

m

X

j D1

8j C 4r 5

.2j C r 2/.2j C r  1/.4j C 2r  1/

;

r

1

D 1=2; a

2m

.1=2/ D

.1/

m

Q

m

j D1

.4j  3/.4j  1/

4

m

.mŠ/

2

;

a

0

2m

.1=2/ D a

2m

.1=2/

m

X

j D1

8j  3

j.4j  3/.4j  1/

;

y

1

D x

1=2

1

X

mD0

.1/

m

Q

m

j D1

.4j  3/.4j  1/

4

m

.mŠ/

2

x

2m

;

y

2

D y

1

ln x C x

1=2

1

X

mD1

.1/

m

Q

m

j D1

.4j  3/.4j  1/

4

m

.mŠ/

2

0

@

m

X

j D1

8j  3

j.4j  3/.4j  1/

1

A

x

2m

.

7.6.38. p

0

.r/ D .r C 1/

2

; p

2

.r/ D .r C 3/.2r  1/;

a

2m

.r/ D 

4m C 2r  5

2m C r C 1

a

2m2

.r/;

a

2m

.r/ D .1/

m

Y

j D1

4j C 2r  5

2j C r C 1

;

By logarithmic differentiation,

a

0

2m

.r/ D a

2m

.r/

m

X

j D1

7

.2j C r C 1/.4j C 2r  5/

;

r

1

D 1; a

2m

.1/ D

.1/

m

Q

m

j D1

.4j  7/

2

m

mŠ

;

a

0

2m

.1/ D a

2m

.1/

m

X

j D1

7

2j.4j  7/

;

y

1

D

1

x

1

X

mD0

.1/

m

Q

m

j D1

.4j  7/

2

m

mŠ

x

2m

;

y

2

D y

1

ln x C

7

2x

1

X

mD1

.1/

m

Q

m

j D1

.4j  7/

2

m

mŠ

0

@

m

X

j D1

1

j.4j  7/

1

A

x

2m

.

7.6.40. p

0

.r/ D .r 1/

2

; p

2

.r/ D r C 1;

a

2m

.r/ D 

1

2m C r  1

a

2m2

.r/;

a

0

2m

.r/ D 

1

2m C r  1

a

0

2m2

.r/ C

1

.2m C r  1/

2

a

2m2

.r/;

r

1

D 1; a

2m

.1/ D 

1

2m

a

2m2

.1/;

y

1

D x



1 

1

2

x

2

C

1

8

x

4



1

48

x

6

C 



;

Section 7.6

The Method of Frobeni us II

115

a

0

2m

.1/ D 

1

2m

a

0

2m2

.1/ C

1

4m

2

a

2m2

.1/, m  1;

y

2

D y

1

ln x C x

3



1

4



3

32

x

2

C

11

576

x

4

C 



.

7.6.42. p

0

.r/ D 2.r C3/

2

; p

2

.r/ D r

2

 2r C2;

a

2m

.r/ D 

4m

2

C 4m.r  3/ C r

2

 6r C 10

2.2m C r C 3/

2

a

2m2

.r/;

a

0

2m

.r/ D 

4m

2

C 4m.r  3/ C r

2

 6r C 10

2.2m C r C 3/

2

a

0

2m2

.r/ 

12m C6r  19

.2m C r C 3/

3

a

2m2

.r/;

r

1

D 3; a

2m

.3/ D 

4m

2

 24m C37

8m

2

a

2m2

.3/;

y

1

D x

3



1 

17

8

x

2

C

85

256

x

4



85

18432

x

6

C 



;

a

0

2m

.3/ D 

4m

2

 24m C 37

8m

2

a

0

2m2

.3/ C

37  12m

8m

3

a

2m2

.3/, m  1;

y

2

D y

1

ln x C x

1



25

8



471

512

x

2

C

1583

110592

x

4

C 



.

7.6.44. p

0

.r/ D .r C 1/

2

; p

1

.r/ D 2.2 r/.r C 1/; r

1

D 1.

a

n

.r/ D

2.n C r/.n C r  3/

.n C r C 1/

2

a

n1

.r/; a

n

.r/ D 2

n

Y

j D1

.j C r/.j C r  3/

.j C r C 1/

2

, n  0. Therefore,a

n

.1/ D

0 if n  1 and y

1

D 1=x. If n  4, then a

n

.r/ D .rC1/

2

b

n

.r/, where b

0

n

.1/ exists; therefore a

0

n

.1/ D

0 if n  4. For r D 1; 2; 3, a

n

.r/ D .r C 1/c

n

.r/, where c

1

.r/ D

2.r  2/

.r C 2/

2

, c

2

.r/ D

4.r  2/.r  1/

.r C 2/.r C 3/

2

,

c

3

.r/ D

8r.r  2/.r  1/

.r C 2/.r C 3/.r C 4/

2

. Hence, a

0

1

.1/ D c

1

.1/ D 6, a

0

2

.1/ D c

2

.1/ D 6, a

0

3

.1/ D

c

3

.1/ D 8=3, and y

2

D y

1

ln x  6 C 6x 

8

3

x

2

.

7.6.46. p

0

.r/ D .r C 1/

2

; p

1

.r/ D .r  1/.r C 2/; r

1

D 1.

a

n

.r/ D

n C r  2

n C r C 1

a

n1

.r/; a

n

.r/ D

m

Y

j D1

j C r  2

j C r C 1

, n  0. Therefore,a

1

.1/ D 2, a

2

.1/ D 1,

and a

n

.1/ D 0 if n  3, so y

1

D

.x  1/

2

x

.

a

1

.r/ D

r  1

r C 2

, a

0

1

.r/ D

3

.r C 2/

2

, a

0

1

.1/ D 3; a

2

.r/ D

r.r  1/

.r C 2/.r C 3/

, a

0

2

.r/ D

6.r

2

C 2r  1/

.r C 2/

2

.r C 3/

2

,

a

0

2

.1/ D 3; if n  3 a

n

.r/ D .r C 1/c

n

.r/ where c

n

.r/ D

r.r  1/

.n C r /.n C r  1/.n C r C 1/

, so

a

0

n

.1/ D c

n

.1/ D

2

n.n  2/.n  1/

and y

2

D y

1

ln x C 3  3x C 2

1

X

nD2

1

n.n

2

 1/

x

n

.

7.6.48. p

0

.r/ D .r 2/

2

; p

1

.r/ D .r  5/.r  1/; r

1

D 2.

a

n

.r/ D

n C r  6

n C r  2

a

n1

.r/;

a

n

.r/ D

m

Y

j D1

j C r  6

j C r  2

, n  0. Therefore,a

1

.2/ D 3, a

2

.2/ D 3, a

3

.2/ D 1, and a

n

.2/ D 0 if

n  4, so y

1

D x

2

.1  x/

3

.

116 Chapter 7

Series Solutions of Linear Second Order Equations

a

1

.r/ D

r  5

r  1

, a

0

1

.r/ D

4

.r  1/

2

, a

0

1

.2/ D 4;

a

2

.r/ D

.r  5/.r  4/

r.r  1/

, a

0

2

.r/ D

4.2r

2

 10r C 5/

r

2

.r  1/

2

, a

0

2

.2/ D 7;

a

3

.r/ D

.r  5/.r  4/.r  3/

r.r  1/.r C 1/

, a

0

3

.r/ D

12.r

4

 8r

3

C 16r

2

 5/

r

2

.r  1/

2

.r C 1/

2

, a

0

3

.2/ D 11=3; if n  4, then

a

n

.r/ D .r  2/c

n

.r/ where c

n

.r/ D

.r  5/.r  4/.r  3/

.n C r  5/.n C r  4/.n C r  3/.n C r  2/

, so a

0

n

.2/ D

c

n

.2/ D 

6

n.n  2/.n

2

 1/

and

y

2

D y

1

ln x C x

3

4  7x C

11

3

x

2

 6

1

X

nD3

1

n.n  2/.n

2

 1/

x

n

!

.

7.6.50. p

0

.r/ D .3r  1/

2

; p

2

.r/ D 7  3r ; r

1

D 1=3.

a

2m

.r/ D

6m C 3r  13

.6m C 3r  1/

2

a

2m2

.r/;

a

2m

.r/ D

m

Y

j D1

6j C 3r  13

.6j C 3r  1/

2

, m  0. Therefore,a

2

.1=3/ D 1=6 and a

2m

.1=3/ D 0 if m  2, so

y

1

D x

1=3



1 

1

6

x

2



.

a

2

.r/ D

3r  7

.3r C 5/

2

; a

0

2

.r/ D

3.19  3r /

.3r C 5/

3

; a

0

2

.1=3/ D 1=4. If m  2, then a

2m

.r/ D .r 1=3/c

2m

.r/

where c

2m

.r/ D

3.3r  7/

.6m C 3r  7/.6m C 3r  1/

Q

m

j D1

.6j C 3r  1/

, so a

0

2m

.1=3/ D c

2m

.1=3/ D



1

12

1

6

m1

.m  1/m mŠ

, and

y

2

D y

1

ln x C x

7=3

1

4



1

12

1

X

mD1

1

6

m

m.m C 1/.m C 1/Š

x

2m

!

.

7.6.52. p

0

.r/ D .2r C1/

2

; p

2

.r/ D 7  2r; r

1

D 1=2.

a

2m

.r/ D

4m C 2r  11

.4m C 2r C 1/

2

a

2m2

.r/;

a

2m

.r/ D

m

Y

j D1

4j C 2r  11

.4j C 2r C 1/

2

, m  0. Therefore,a

2

.1=2/ D 1=2, a

4

.1=2/ D 1=32, and

a

2m

.1=2/ D 0 if m  3, so y

1

D x

1=2



1 

1

2

x

2

C

1

32

x

4



.

a

2

.r/ D

2r  7

.2r C 5/

2

, a

0

2

.r/ D

2.19 2r /

.2r C 5/

3

, a

0

2

.1=2/ D 5=8,

a

4

.r/ D

.2r  7/.2r 3/

.2r C 5/

2

.2r C 9/

2

, a

0

4

.r/ D 

4.8r

3

 60r

2

 146r C 519/

.2r C 5/

3

.2r C 9/

3

, a

0

4

.1=2/ D 9=128; if

m  3, then a

2m

.r/ D .r C 1=2/c

2m

.r/ where

c

2m

.r/ D

2.2r  7/.2r  3/

.4m C 2r  7/.4m C 2r  3/.4m C 2r C 1/

Q

m

j D1

.4j C 2r C 1/

, so a

0

2m

.1=2/ D c

2m

.1=2/ D

1

4

m

.m  2/.m  1/m mŠ

, and

Section 7.6

The Method of Frobeni us II

117

y

2

D y

1

ln x C x

3=2

5

8



9

128

x

2

C

1

X

mD2

1

4

mC1

.m  1/m.m C 1/.m C 1/Š

x

2m

!

.

7.6.54. (a) If p

0

.r/ D ˛

0

.r  r

1

/

2

, then (A) a

n

.r/ D

.1/

n

˛

n

0

n

Y

j D1

p

1

.j C r  1/

.j C r  r

1

/

2

. Therefore, a

n

.r

1

/ D

.1/

n

˛

n

0

.nŠ/

2

n

Y

j D1

p

1

.j C r

1

 1/. Theorem 7.6.2 implies Ly

1

D 0.

(b) From (A), ln ja

n

.r/j D n ln j˛

0

j C

n

X

j D1

.ln jp

1

.j C r  1/j  2 ln jj C r  r

1

j/, so a

0

n

.r/ D

a

n

.r/

n

X

j D1



p

0

1

.j C r  1/

p

1

.j C r  1/



2

j C r  r

1



and a

0

n

.r

1

/ D a

n

.r

1

/

n

X

j D1



p

0

1

.j C r

1

 1/

p

1

.j C r

1

 1/



2

j



. Theo-

rem 7.6.2 implies that Ly

2

D 0.

(c) Since p

1

.r/ D 

1

, y

1

and y

2

reduce to the stated forms. If 

1

D 0, then y

1

D x

r

1

and y

2

D

x

r

1

ln x, wh ich are solutions of the Euler equation ˛

0

x

2

y

00

C ˇ

0

xy

0

C 

0

y.

7.6.54. (a) Ly

1

D p

0

.r

1

/x

r

1

D 0. Now use t he fact that p

0

.j C r

1

/ D ˛

0

j

2

, so

Q

n

j D1

p

0

.j C r

1

/ D

˛

n

0

.nŠ/

2

.

(b) From Theorem 7.6.2, y

2

D y

1

ln x C x

r

1

X

nD1

a

0

n

.r

1

/x

n

is a second solution of Ly D 0. Since

a

n

.r/ D

.1/

n

˛

n

0

n

Y

j D1

p

1

.j C r  1/

.j C r  r

1

/

2

, (A) ln ja

n

.r/j D n ln j˛

0

jC

n

X

j D1

ln jp

1

.j Cr 1/j2

n

X

j D1

ln jj C

r r

1

j, provided that p

1

.j Cr 1/ and j Cr r

1

are nonzero for all positive integers j . Differentiating (A)

and then setting r D r

1

yields

a

0

n

.r

1

/

a

n

.r

1

/

D

n

X

j D1

p

0

1

.j C r

1

 1/

p

2

.j C r

1

 1/

 2

n

X

j D1

1

j

, which impli es the conclusion.

(c) In this case p

1

.r/ D 

1

and p

0

1

.r/ D 0, so a

n

.r

1

/ D

.1/

n

.nŠ/

2





1

˛

0



n

and J

n

D 2

n

X

j D1

1

j

. If



1

D 0, then y

1

D x

r

1

and y

2

D x

r

1

ln x, wh ile the differential equation is an Euler equation with

indicial polynomial ˛

0

.r  r

2

1

/. See Theorem 7.4.3.

7.6.56. p

0

.r/ D r

2

; p

1

.r/ D 1; r

1

D 0. a

2m

.r/ D 

a

2m1

.r/

.2m C r/

2

, m  1; a

2m

.r/ D

.1/

m

Q

m

j D1

.2j C r/

2

,

m  0. Therefore,a

2m

.0/ D

.1/

m

4

m

.mŠ/

2

, so y

1

D

1

X

mD0

.1/

m

4

m

.mŠ/

2

x

2m

.

By logarithmic differentiation, a

0

2m

.r/ D 2a

2m

.r/

m

X

j D1

1

2m C r

, so a

0

2m

.0/ D a

2m

.0/

m

X

j D1

1

j

and

y

2

D y

1

ln x 

1

X

mD1

.1/

m

4

m

.mŠ/

2

0

@

m

X

j D1

1

j

1

A

x

2m

.

7.6.58. p

0

.r/ D .2r 1/

2

; p

1

.r/ D .2r C1/

2

; p

2

.r/ D 0;

p

1

.r  1/

p

0

.r/

D 1 D

˛

1

˛

0

;

p

2

.r  2/

p

0

.r/

D 0 D

˛

2

˛

0

;

y

1

D

x

1=2

1 C x

; y

2

D

x

1=2

ln x

1 C x

.

118 Chapter 7

Series Solutions of Linear Second Order Equations

7.6.60. p

0

.r/ D 2.r  1/

2

; p

1

.r/ D 0; p

2

.r/ D .r C 1/

2

;

p

1

.r  1/

p

0

.r/

D 0 D

˛

1

˛

0

;

p

2

.r  2/

p

0

.r/

D

1=2 D

˛

2

˛

0

; y

1

D

x

2  x

2

; y

2

D

x ln x

2  x

2

.

7.6.62. p

0

.r/ D 4.r  1/

2

; p

1

.r/ D 3r

2

; p

2

.r/ D 0;

p

1

.r  1/

p

0

.r/

D 3=4 D

˛

1

˛

0

;

p

2

.r  2/

p

0

.r/

D 0 D

˛

2

˛

0

;

y

1

D

x

4 C 3x

; y

2

D

x ln x

4 C 3x

.

7.6.64. p

0

.r/ D .r 1/

2

; p

1

.r/ D 2r

2

; p

2

.r/ D .r C1/

2

;

p

1

.r  1/

p

0

.r/

D 2 D

˛

1

˛

0

;

p

2

.r  2/

p

0

.r/

D 1 D

˛

2

˛

0

; y

1

D

x

.1  x/

2

; y

2

D

x ln x

.1  x/

2

.

7.6.66. See the proofs of Theorems 7.6.1 and 7.6.2.

7.7 THE METHOD OF FROBENIUS III

7.7.2. p

0

.r/ D r.r  1/; p

1

.r/ D 1; r

1

D 1; r

2

D 0; k D r

1

 r

2

D 1;

a

n

.r/ D 

1

.n C r /.n C r  1/

a

n1

.r/;

a

n

.r/ D

.1/

n

Q

n

j D1

.j C r/.j C r  1/

;

a

n

.1/ D

.1/

n

nŠ.n C 1/Š

;

y

1

D x

1

X

nD0

.1/

n

nŠ.n C 1/Š

x

n

;

´ D 1; C D p

1

.0/a

0

.0/ D 1.

By logarithmic differentiation,

a

0

n

.r/ D a

n

.r/

n

X

j D1

2n C 2r  1

.n C r /.n C r  1/

;

a

0

n

.1/ D a

n

.1/

n

X

j D1

2j C 1

j.j C 1/

;

y

2

D 1  y

1

ln x C x

1

X

nD1

.1/

n

nŠ.n C 1/Š

0

@

n

X

j D1

2j C 1

j.j C 1/

1

A

x

n

.

7.7.4. p

0

.r/ D r.r 1/; p

1

.r/ D r C1; r

1

D 1; r

2

D 0; k D r

1

r

2

D 1; a

n

.r/ D 

a

n1

.r/

n C r  1

; a

n

.r/ D

.1/

n

Q

n

j D1

.j C r  1/

; a

n

.1/ D

.1/

n

nŠ

; y

1

D x

1

X

nD0

.1/

n

nŠ

x

n

D xe

x

; ´ D 1; C D p

1

.0/a

0

.0/ D 1.

By logarithmic differentiati on, a

0

n

.r/ D a

n

.r/

n

X

j D1

1

j C r  1

; a

0

n

.1/ D a

n

.1/

n

X

j D1

1

j

; y

2

D 1  y

1

ln x C x

1

X

nD1

.1/

n

nŠ

0

@

n

X

j D1

1

j

1

A

7.7.6. p

0

.r/ D .r  1/.r C 2/; p

1

.r/ D r C 3; r

1

D 1; r

2

D 2; k D r

1

 r

2

D 3. a

n

.r/ D



1

n C r  1

a

n1

.r/; a

n

.r/ D

.1/

n

Q

n

j D1

.j C r  1/

; a

n

.1/ D

.1/

n

nŠ

; y

1

D x

1

X

nD0

.1/

n

nŠ

x

n

D xe

x

;

Section 7.7

The Method of Frobenius III

119

´ D x

2



1 C

1

2

x C

1

2

x

2



; C D 

p

1

.0/

3

a

2

.2/ D 1=2. By logarithmic differentiation, a

0

n

.r/ D

a

n

.r/

n

X

j D1

1

j C r  1

; a

0

n

.1/ D a

n

.1/

n

X

j D1

1

j

; y

2

D x

2



1 C

1

2

x C

1

2

x

2





1

2

0

@

y

1

ln x  x

1

X

nD1

.1/

n

nŠ

0

@

n

X

j D1

1

j

1

A

x

n

1

A

;

7.7.8. p

0

.r/ D .r C 2/.r C 7/; p

1

.r/ D 1; r

1

D 2; r

2

D 7; k D r

1

 r

2

D 5; a

n

.r/ D



a

n1

.r/

.n C r C 2/.n C r C 7/

; a

n

.r/ D

.1/

n

Q

n

j D1

.j C r C2/.j C r C 7/

; a

n

.2/ D 120

n

Y

j D1

.1/

n

nŠ.n C 5/Š

;

y

1

D

120

x

2

1

X

nD0

.1/

n

nŠ.n C 5/Š

x

n

;

´ D x

7



1 C

1

4

x C

1

24

x

2

C

1

144

x

3

C

1

576

x

4



; C D 

p

1

.3/

5

a

4

.7/ D 1=2880. By logarith-

mic differentiation, a

0

n

.r/ D a

n

.r/

n

X

j D1



2j C 2r C 9

.j C r C 2/.j C r C 7/

; a

0

n

.2/ D a

n

.2/

n

X

j D1

2j C 5

j.j C 5/

;

y

2

D x

7



1 C

1

4

x C

1

24

x

2

C

1

144

x

3

C

1

576

x

4





1

2880

0

@

y

1

ln x 

120

x

2

1

X

nD1

.1/

n

nŠ.n C 5/Š

0

@

n

X

j D1

2j C 5

j.j C 5/

1

A

x

n

1

A

.

7.7.10. p

0

.r/ D r.r  4/; p

1

.r/ D .r  6/.r  5/; r

1

D 4; r

2

D 0; k D r

1

 r

2

D 4; a

n

.r/ D



.n C r  7/.n Cr  6/

.n C r /.n C r  4/

a

n1

.r/; a

n

.r/ D .1/

n

Y

j D1

.j C r  7/.j C r  6/

.j C r/.j C r  4/

. Setting r D 4 yields

y

1

D x

4



1 

2

5

x



. ´ D 1C10xC50x

2

C200x

3

; C D 

p

1

.3/

4

a

3

.0/ D 300. a

1

.r/ D 

.r  6/.r  5/

.r  3/.r C 1/

;

a

0

1

.r/ D 

3.3r

2

 22r C 31/

.r  3/

2

.r C 1/

2

; a

0

1

.4/ D 27=25. a

2

.r/ D .r4/c

2

.r/, with c

2

.r/ D

.r  6/.r  5/

2

.r  3/.r  2/.r C 1/.r C 2/

,

so a

0

2

.4/ D c

2

.4/ D 1=30. If n  3, then a

n

.r/ D .r  4/

2

b

n

.r/ where b

0

n

.4/ exists, so a

0

n

.4/ D 0 and

y

2

D 1 C 10x C 50x

2

C 200x

3

 300



y

1

ln x C

27

25

x

5



1

30

x

6



.

7.7.12. p

0

.r/ D .r  2/.r C 2/; p

1

.r/ D 2r  1; r

1

D 2; r

2

D 2; k D r

1

 r

2

D 4; a

n

.r/ D

2j C 2r  1

.j C r  2/.j C r C 2/

a

n1

.r/; a

n

.r/ D

n

Y

j D1

2n C 2r  1

.n C r  2/.n C r C 2/

; a

n

.2/ D

1

nŠ



Q

n

j D1

2jC3

j C4



;

y

1

D x

2

1

X

nD0

1

nŠ

0

@

n

Y

j D1

2j C 3

j C 4

1

A

x

n

; ´ D x

2



1 C x C

1

4

x

2



1

12

x

3



; C D 

p

1

.1/

4

a

3

.2/ D 1=16.

By logarithmic differentiation,

a

0

n

.r/ D 2a

n

.r/

n

X

j D1

j

2

C j.2r  1/ C r

2

 r C 4

.j C r  2/.j C r C 2/.2j C 2r  1/

; a

0

n

.2/ D 2a

n

.2/

n

X

j D1

.j

2

C 3j C 6/

j.j C 4/.2j C 3/

;

y

2

D x

2



1 C x C

1

4

x

2



1

12

x

3





1

16

y

1

ln x C

x

2

8

1

X

nD1

1

nŠ

0

@

n

Y

j D1

2j C 3

j C 4

1

A

0

@

n

X

j D1

.j

2

C 3j C 6/

j.j C 4/.2j C 3/

1

A

x

n

.

7.7.14. p

0

.r/ D .r C 1/.r C 7/; p

1

.r/ D .r C 5/.2r C 1/; r

1

D 1; r

2

D 7; k D r

1



r

2

D 6; a

n

.r/ D 

.n C r C 4/.2n C 2r  1/

.n C r C 1/.n C r C 7/

a

n1

.r/; a

n

.r/ D .1/

n

Y

j D1

.j C r C 4/.2j C 2r  1/

.j C r C 1/.j C r C 7/

;

120 Chapter 7

Series Solutions of Linear Second Order Equations

a

n

.1/ D

.1/

n

nŠ

0

@

n

Y

j D1

.j C 3/.2j  3/

j C 6

1

A

; y

1

D

1

x

1

X

nD0

.1/

n

nŠ

0

@

n

Y

j D1

.j C 3/.2j  3/

j C 6

1

A

x

n

; ´ D x

7



1 C

26

5

x C

143

20

x

2



;

C D 

p

1

.2/

6

a

5

.7/ D 0; y

2

D x

7



1 C

26

5

x C

143

20

x

2



.

7.7.16. p

0

.r/ D .3r  10/.3r C 2/; p

1

.r/ D r .3r  4/; r

1

D 10=3; r

2

D 2=3; k D r

1

 r

2

D 4;

a

n

.r/ D 

.n C r  1/.3n C 3r  7/

.3n C 3r  10/.3n C 3r C 2/

a

n1

.r/; a

n

.r/ D .1/

n

Y

j D1

.j C r  1/.3j C 3r  7/

.3j C 3r  10/.3j C 3r C 2/

;

a

n

.10=3/ D

.1/

n

.n C 1/

9

n

0

@

n

Y

j D1

3j C 7

j C 4

1

A

; y

1

D x

10=3

1

X

nD0

.1/

n

.n C 1/

9

n

0

@

n

Y

j D1

3j C 7

j C 4

1

A

x

n

; ´ D

x

2=3



1 C

4

27

x 

1

243

x

2



; C D 

p

1

.7=3/

36

a

3

.2=3/ D 0; y

2

D x

2=3



1 C

4

27

x 

1

243

x

2



.

7.7.18. p

0

.r/ D .r  3/.r C 2/; p

1

.r/ D .r C 1/

2

; r

1

D 3; r

2

D 2; k D r

1

 r

2

D 5;

a

n

.r/ D 

.n C r /

2

.n C r  3/.n C r C 2/

a

n1

.r/; a

n

.r/ D .1/

n

Y

j D1

.j C r/

2

.j C r  3/.j C r C 2/

; a

n

.3/ D

.1/

n

nŠ



Q

n

j D1

.j C3/

2

j C5



; y

1

D x

3

1

X

nD0

.1/

n

nŠ

0

@

n

Y

j D1

.j C 3/

2

j C 5

1

A

x

n

; ´ D x

2



1 C

1

4

x



; C D 

p

1

.2/

5

a

4

.2/ D

0; y

2

D x

2



1 C

1

4

x



.

7.7.20. p

0

.r/ D .r  6/.r  1/; p

1

.r/ D .r  8/.r  4/; r

1

D 6; r

2

D 1; k D r

1

 r

2

D 5; a

n

.r/ D



.n C r  9/.n Cr  5/

.n C r  6/.n Cr  1/

a

n1

.r/; y

1

D x

6



1 C

2

3

x C

1

7

x

2



; ´ D x



1 C

21

4

x C

21

2

x

2

C

35

4

x

3



;

C D 

p

1

.5/

6

a

5

.1/ D 0; y

2

D x



1 C

21

4

x C

21

2

x

2

C

35

4

x

3



.

7.7.22. p

0

.r/ D r.r  10/; p

1

.r/ D 2.r  6/.r C 1/; r

1

D 10; r

2

D 0; k D r

1

 r

2

D 10; a

n

.r/ D



2.n C r  7/

n C r  10

a

n1

.r/; a

n

.r/ D .2/

n

.n C r  9/.n C r  8/.n C r  7/

.r  9/.r  8/.r  7/

; a

n

.10/ D

.1/

n

2

n

.n C 1/.n C 2/.n C 3/

6

;

y

1

D

x

10

6

1

X

nD0

.1/

n

2

n

.n C 1/.n C2/.n C 3/x

n

; ´ D



1 

4

3

x C

5

3

x

2



40

21

x

3

C

40

21

x

4



32

21

x

5

C

16

21

x

6



;

C D 

p

1

.9/

10

a

9

.0/ D 0; y

2

D



1 

4

3

x C

5

3

x

2



40

21

x

3

C

40

21

x

4



32

21

x

5

C

16

21

x

6



.

Note: in the solutions to Exercises 7.7.23–7.7.40, ´ D x

r

2

P

k1

mD0

a

2m

.r

2

/x

2m

.

7.7.24. p

0

.r/ D .r  6/.r  2/; p

2

.r/ D r; r

1

D 6; r

2

D 2; k D .r

1

 r

2

/=2 D 2; a

2m

.r/ D



a

2m2

.r/

2m C r  6

; a

2m

.r/ D

.1/

m

Q

m

j D1

.2j C r  6/

; a

2m

.6/ D

.1/

m

2

m

mŠ

; y

1

D x

6

1

X

mD0

.1/

m

2

m

mŠ

x

2m

D x

6

e

x

2

=2

;

´ D x

2



1 C

1

2

x

2



; C D 

p

2

.4/

4

a

2

.2/ D 1=2. B y logarithmic differentiation, a

0

2m

.r/ D a

2m

.r/

m

X

j D1

1

2j C r  6

;

a

0

2m

.6/ D a

2m

.6/

m

X

j D1

1

2j

; y

2

D x

2



1 C

1

2

x

2





1

2

y

1

ln x C

x

6

4

1

X

mD1

.1/

m

2

m

mŠ

0

@

m

X

j D1

1

j

1

A

x

2m

.

Section 7.7

The Method of Frobenius III

121

7.7.26. p

0

.r/ D .r  1/.r C 1/; p

2

.r/ D 2r C 10; r

1

D 1; r

2

D 1; k D .r

1

 r

2

/=2 D 1;

a

2m

.r/ D 

2.2m Cr C 3/

.2m C r  1/.2m Cr C 1/

a

2m2

.r/; a

2m

.r/ D .2/

m

Y

j D1

2j C r C 3

.2j C r 1/.2j C r C 1/

;

a

2m

.1/ D

.1/

m

.m C 2/

2 mŠ

; y

1

D

x

2

1

X

mD0

.1/

m

.m C 2/

mŠ

x

2m

; ´ D x

1

; C D 

p

2

.1/

2

a

0

.1/ D 4.

By logarithmic differentiation,

a

0

2m

.r/ D a

2m

.r/

m

X

j D1

.4j

2

C 4j.r C 3/ C r

2

C 6r C 1/

.2j C r 1/.2j C r C 1/.2j C r C 3/

;

a

0

2m

.1/ D a

2m

.1/

m

X

j D1

j

2

C 4j C 2

2j.j C 1/.j C 2/

;

y

2

D x

1

 4y

1

ln x C x

1

X

mD1

.1/

m

.m C 2/

mŠ

0

@

m

X

j D1

j

2

C 4j C 2

j.j C 1/.j C 2/

1

A

x

2m

.

7.7.28. p

0

.r/ D .2r C 1/.2r C 5/; p

2

.r/ D 2r C 3; r

1

D 1=2; r

2

D 5=2; k D .r

1

 r

2

/=2 D 1;

a

2m

.r/ D 

.4m C 2r  1/

.4m C 2r C 1/.4m C 2r C 5/

a

2m2

.r/; a

2m

.r/ D .1/

m

Y

j D1

.4j C 2r  1/

.4j C 2r C 1/.4j C 2r C5/

;

a

2m

.1=2/ D

.1/

m

Q

m

j D1

.2j  1/

8

m

mŠ.m C 1/Š

; y

1

D x

1=2

1

X

mD0

.1/

m

Q

m

j D1

.2j  1/

8

m

mŠ.m C 1/Š

x

2m

; ´ D x

5=2

; C D



p

2

.5=2/

8

a

0

.5=2/ D 1=4. By logarithmic differentiation,

a

0

2m

.r/ D 2a

2m

.r/

m

X

j D1

.16j

2

C 8j.2r  1/ C 4r

2

 4r 11/

.4j C 2r  1/.4j C 2r C 1/.4j C 2r C 5/

; a

0

2m

.1=2/ D a

2m

.1=2/

m

X

j D1

2j

2

 2j  1

2j.j C 1/.2j  1/

;

y

2

D x

5=2

C

1

4

y

1

ln x  x

1=2

1

X

mD1

.1/

m

Q

m

j D1

.2j  1/

8

mC1

mŠ.m C 1/Š

0

@

m

X

j D1

2j

2

 2j  1

j.j C 1/.2j  1/

1

A

x

2m

.

7.7.30. p

0

.r/ D .r 2/.r C2/; p

2

.r/ D 2.r C4/; r

1

D 2; r

2

D 2; k D .r

1

r

2

/=2 D 2; a

2m

.r/ D

2

2m C r  2

a

2m2

.r/; a

2m

.r/ D

2

m

Q

m

j D1

.2j C r 2/

; a

2m

.2/ D

1

mŠ

; y

1

D x

2

1

X

mD0

1

mŠ

x

2m

D x

2

e

x

2

;

´ D x

2

.1x

2

/; C D 

p

2

.0/

4

a

2

.2/ D 2. By logarithmic differentiatio n, a

0

2m

.r/ D a

2m

.r/

m

X

j D1

1

2j C r  2

;

a

0

2m

.2/ D a

2m

.2/

m

X

j D1

1

2j

; y

2

D x

2

.1  x

2

/  2y

1

ln x C x

2

1

X

mD1

1

mŠ

0

@

m

X

j D1

1

j

1

A

x

2m

.

7.7.32. p

0

.r/ D .3r  13/.3r  1/; p

2

.r/ D 2.5  3r/; r

1

D 13=3; r

2

D 1=3; k D .r

1

 r

2

/=2 D 2;

a

2m

.r/ D

2.6m C 3r  11/

.6m C 3r  13/.6m C 3r  1/

a

2m2

.r/; a

2m

.r/ D 2

m

Y

j D1

.6j C 3r  11/

.6j C 3r  13/.6j C 3r  1/

;

a

2m

.13=3/ D

Q

m

j D1

.3j C 1/

9

m

mŠ.m C 2/Š

; y

1

D 2x

13=3

1

X

mD0

Q

m

j D1

.3j C 1/

9

m

mŠ.m C 2/Š

x

2m

; ´ D x

1=3



1 C

2

9

x

2



; C D



p

2

.7=3/

36

a

2

.1=3/ D 2=81. By logarithmic d ifferentiation, a

0

2m

.r/ D 9a

2m

.r/

m

X

j D1

.12j

2

C 4j.3r  11/ C3r

2

 22r C 47/

.6j C 3r  13/.6j C 3r  11/.6j C 3r  1/

;

122 Chapter 7

Series Solutions of Linear Second Order Equations

a

0

2m

.13=3/ D a

2m

.13=3/

m

X

j D1

3j

2

C 2j C 2

2j.j C 2/.3j C 1/

;

y

2

D x

1=3



1 C

2

9

x

2



C

2

81

0

@

y

1

ln x x

13=3

1

X

mD0

Q

m

j D1

.3j C 1/

9

m

mŠ.m C 2/Š

0

@

m

X

j D1

3j

2

C 2j C 2

j.j C 2/.3j C 1/

1

A

x

2m

1

A

.

7.7.34. p

0

.r/ D .r  2/.r C 2/; p

2

.r/ D 3.r  4/; r

1

D 2; r

2

D 2; k D .r

1

 r

2

/=2 D 2;

a

2m

.r/ D

3.2m C r  6/

.2m C r  2/.2m C r C 2/

a

2m2

.r/; y

1

D x

2



1 

1

2

x

2



; ´ D x

2



1 C

9

2

x

2



; C D



p

2

.0/

4

a

2

.2/ D 27=2; a

2

.r/ D

3.r  4/

r.r C 4/

, a

0

2

.r/ D 

3.r

2

 8r  16/

r

2

.r C 4/

2

, a

0

2

.2/ D 7=12. If m  2,

then a

2m

.r/ D .r  2/c

2m

.r/ where c

2m

.r/ D

3

m

.r  4/

.2m C r  4/.2m C r  2/

Q

m

j D1

.2j C r C 2/

, so

a

0

2m

.2/ D c

2m

.2/ D 



3

2



m

m.m  1/.m C 2/Š

; y

2

D x

2



1 C

9

2

x

2





27

2

y

1

ln x C

7

12

x

4

 x

2

1

X

mD2



3

2



m

m.m  1/.m C 2/Š

x

2m

!

.

7.7.36. p

0

.r/ D .2r  5/.2r C 7/; p

2

.r/ D .2r  1/

2

; r

1

D 5=2; r

2

D 7=2; k D .r

1

 r

2

/=2 D 3;

a

2m

.r/ D 

4m C2r  5

4m C 2r C 7

a

2m2

.r/; a

2m

.r/ D

.2r  1/.2r C 3/.2r C 7/

.4m C 2r  1/.4m C2r C 3/.4m C 2r C 7/

; a

2m

.5=2/ D

.1/

m

.m C 1/.m C 2/.m C 3/

; y

1

D x

5=2

1

X

mD0

.1/

m

.m C 1/.m C2/.m C 3/

x

2m

; ´ D x

7=2

.1 C x

2

/

2

C D



p

2

.1=2/

24

a

4

.7=2/ D 0; y

2

D x

7=2

.1 C x

2

/

2

.

7.7.38. p

0

.r/ D .r  3/.r C 7/; p

2

.r/ D r .r C 1/; r

1

D 3; r

2

D 7; k D .r

1

 r

2

/=2 D 5; a

2m

.r/ D



.2m C r  2/.2m C r  1/

.2m C r  3/.2m C r C 7/

a

2m2

.r/; a

2m

.r/ D .1/

m

Y

j D1

.2j C r 2/.2j C r  1/

.2j C r  3/.2j C r C 7/

; a

2m

.3/ D

.1/

m

m C 1

2

m

0

@

m

Y

j D1

2j C 1

j C 5

1

A

; y

1

D x

3

1

X

mD0

.1/

m

m C 1

2

m

0

@

m

Y

j D1

2j C 1

j C 5

1

A

x

2m

; ´ D x

7



1 C

21

8

x

2

C

35

16

x

4

C

35

64

x

6



C D 

p

2

.1/

10

a

8

.7/ D 0; y

2

D x

7



1 C

21

8

x

2

C

35

16

x

4

C

35

64

x

6



.

7.7.40. p

0

.r/ D .2r  3/.2r C 5/; p

2

.r/ D .2r  1/.2r C 1/; r

1

D 3=2; r

2

D 5=2; k D

.r

1

 r

2

/=2 D 2; a

2m

.r/ D 

4m C 2r  5

4m C 2r C 5

a

2m2

.r/; a

2m

.r/ D .1/

m

Y

j D1

4j C 2r  5

4j C 2r C 5

; a

2m

.3=2/ D

.1/

m

Q

m

j D1

.2j  1/

2

m1

.m C 2/Š

; y

1

D x

3=2

1

X

mD0

.1/

m

Q

m

j D1

.2j  1/

2

m1

.m C 2/Š

x

2m

; ´ D x

5=2



1 C

3

2

x

2



C D 

p

2

.1=2/

16

a

2

.5=2/ D

0; y

2

D x

5=2



1 C

3

2

x

2



.

7.7.42. p

0

.r/ D r

2

 

2

; p

2

.r/ D 1; r

1

D ; r

2

D ; k D .r

1

 r

2

/=2 D ; a

2m

.r/ D



a

2m2

.r/

.2m C r C /.2m C r  /

; a

2m

.r/ D

.1/

m

Q

m

j D1

.2j Cr C /.2j C r  /

; a

2m

./ D

.1/

m

4

m

mŠ

Q

m

j D1

.j C /

;

a

2m

./ D

.1/

m

4

m

mŠ

Q

m

j D1

.j  /

, j D 0; : : : ;   1; y

1

D x



1

X

mD0

.1/

m

4

m

mŠ

Q

m

j D1

.j C /

x

2m

; ´ D

Section 7.7

The Method of Frobenius III

123

x



1

X

mD0

.1/

m

4

m

mŠ

Q

m

j D1

.j  /

x

2m

; C D 

p

2

.  2/

2

a

22

./ D 

a

22

./

2

D 

2

4



Š.  1/Š

. By

logarithmic differentiation, a

0

2m

.r/ D 2a

2m

.r/

m

X

j D1

2j C 

.2j C r C /.2j C r  /

; a

0

2m

./ D a

2m

./

m

X

j D1

2j C 

2j.j C /

;

y

2

D x



1

X

mD0

.1/

m

4

m

mŠ

Q

m

j D1

.j  /

x

2m



2

4



Š.  1/Š

0

@

y

1

ln x 

x



2

1

X

mD1

.1/

m

4

m

mŠ

Q

m

j D1

.j C /

0

@

m

X

j D1

2j C 

j.j C /

1

A

x

2m

1

A

.

7.7.44. Since a

n

.r

2

/ D 

p

1

.n C r

2

 1/

p

0

.n C r

2

/

a

n1

.r

2

/, 1  n  k1, a

k1

.r

2

/ D .1/

k1

Y

j D1

p

1

.r

2

C j  1/

p

0

.r

2

Cj /

.

But C D 

p

1

.r

1

 1/

k˛

0

a

k1

.r

2

/ D 

p

1

.r

2

C k  1/

k˛

0

a

k1

.r

2

/ D ./

k

Q

k

j D1

p

1

.r

2

C j  1/

k˛

0

Q

k1

j D1

p

0

.r

2

C j /

D 0 if

and only if

k

Y

j D1

p

1

.r

2

C j  1/ D 0.

7.7.46. Since p

1

.r/ D 

1

, a

n

.r/ D 



1

˛

0

.n C r  r

1

/.n C r  r

2

/

a

n1

.r/ and (A) a

n

.r/ D .1/

n





1

˛

0



n

1

Q

n

j D1

.j C r  r

1

/.j C

Therefore, a

n

.r

1

/ D

.1/

n

nŠ





1

˛

0



n

1

Q

n

j D1

.j C k/

for n  0 (so Ly

1

D 0) and a

n

.r

2

/ D

.1/

n

nŠ





1

˛

0



n

1

Q

n

j D1

.j  k/

for n D 0; : : : ; k  1. Ly

2

D 0 if y

2

D x

r

2

k1

X

nD0

a

n

.r

2

/x

n

C C

y

1

ln x C x

r

1

X

nD1

a

0

n

.r

1

/x

n

!

if C D





1

k˛

0

a

k1

.r

2

/ D 



1

k˛

0

.1/

k1

.k  1/Š





1

˛

0



k1

.1/

k1

.k  1/Š

D 

1

kŠ.k  1/Š





1

˛

0



k

. From (A), ln ja

n

.r/j D

n ln

ˇ



1

˛

0

ˇ



n

X

j D1

..ln jj C r  r

1

j C ln jj C r  r

2

j/, so a

0

n

.r/ D a

n

.r/

n

X

j D1



1

j C r  r

1

C

1

j C r  r

2



and a

0

n

.r

1

/ D a

n

.r

1

/

n

X

j D1

2j C k

j.j C k/

.

7.7.48. (a) Fr om Exer cise 7.6.66( a) of Section 7.6, L



@y

@r

.x; r/



D p

0

.r/x

r

Cx

r

p

0

.r/ ln x. Setting r D

r

1

yields L

y

1

ln x C x

r

1

X

nD1

a

0

n

.r

1

/

!

D p

0

.r

1

/x

r

1

. Since p

0

.r/ D ˛

0

.2r r

1

r

2

/, p

0

.r

1

/ D k˛

0

.

(b) From Exercise 7.5.57 of Sect ion 7.5, L

x

r

2

1

X

nD0

a

n

.r

2

/x

n

!

D x

r

2

1

X

nD0

b

n

x

n

, where b

0

D p

0

.r

2

/ D

0 and b

n

D

n

X

j D0

p

j

.n C r

2

 j /a

nj

.r

2

/ if n  1. From the deﬁni tion of fa

n

.r

2

/g, b

n

D 0 if n ¤ k,

while b

k

D

k

X

j D0

p

k

.k C r

2

 j /a

kj

.r

2

/ D

k

X

j D1

p

j

.r

1

 j /a

kj

.r

2

/.

(d) Let fQa

n

.r

2

/g be the coefﬁcients that would obtained if Qa

k

.r

2

/ D 0. Then a

n

.r

2

/ D Qa

n

.r

2

/ if n D

124 Chapter 7

Series Solutions of Linear Second Order Equations

0; : : : ; k 1, and (A) a

n

.r

2

/  Qa

n

.r

2

/ D 

1

p

0

.n C r

2

/

nk

X

j D0

p

j

.n Cr

2

j /.a

nj

.r

2

/  Qa

nj

r

2

/ if n > k.

Now let c

m

D a

kCm

.r

2

/  Qa

kCm

.r

2

/. Sett ing n D m Ck in (A) and recalling the k Cr

2

D r

1

yields (B)

c

m

D 

1

p

0

.m C r

1

/

m

X

j D0

p

j

.m Cr

1

 j /c

mj

. Since c

k

D a

k

.r

2

/, (B) implies that c

m

D a

k

.r

2

/a

m

.r

1

/

for all m  0, which implies the conclusion.

CHAPTER 8

Laplace Transforms

8.1 INTRODUCTION TO THE LAPLACE TRANSFORM

8.1.2. (a) cosh t sin t D

1

2



e

t

sin t C e

t

sin t



$

1

2



1

.s  1/

2

C 1

C

1

.s C 1/

2

C 1



D

s

2

C 2

Œ.s  1/

2

C 1Œ.s C 1/

2

C 1

.

(b) sin

2

t D

1  cos 2t

2

$

1

2



1

s



s

.s

2

C 4/



D

2

s.s

2

C 4/

.

(c) cos

2

2t D

1

2



1

s

C

s

2

C 16



D

s

2

C 8

s.s

2

C 16/

.

(d) cosh

2

t D

.e

t

C e

t

/

2

/

4

D

.e

2t

C 2 C e

2t

/

4

$

1

4



1

s  2

C

2

s

C

1

s C 2



D

s

2

 2

s.s

2

 4/

.

(e) t sinh 2t D

te

2t

 te

2t

2

$

1

2



1

.s  2/

2



1

.s C 2/

2



D

4s

.s

2

 4/

2

.

(f) sin t cos t D

sin 2t

2

$

1

s

2

C 4

.

(g) sin.t C =4/ D sin t cos.=4/ C cos t cos.=4/ $

1

p

2

s C 1

s

2

C 1

.

(h) cos 2t  cos 3t $

s

2

C 4



s

2

C 9

D

5s

.s

2

C 4/.s

2

C 9/

.

(i) sin 2t C cos 4t $

2

s

2

C4

C

s

2

C 16

D

s

3

C 2s

2

C 4s C 32

.s

2

C 4/.s

2

C 16/

.

8.1.6. I f F.s/ D

Z

1

0

e

st

f .t/ dt, then F

0

.s/ D

Z

1

0

.te

st

/f .t/ dt D 

Z

1

0

e

st

.tf .t// dt. Apply-

ing this argument repeatedly yields the assertion.

8.1.8. Let f .t/ D 1 and F .s/ D 1=s. From Exercise 8.1.6, t

n

$ .1/

n

F

.n/

.s/ D nŠ=s

nC1

.

8.1.10. If jf .t/j  Me

s

0

t

for t  t

0

, then jf .t/e

st

j  Me

.ss

0

/t

for t  t

0

. Let g.t/ D e

st

f .t/,

w.t/ D Me

.ss

0

/t

, and  D t

0

. Since

R

1

t

0

w.t/ dt converges if s > s

0

, F .s/ is deﬁned for s > s

0

.

8.1.12.

Z

T

0

e

st



Z

t

0

f ./ d 



dt D 

e

st

s

Z

t

0

f ./ d 

ˇ

T

0

C

1

s

Z

T

0

e

st

f .t/ dt D 

e

sT

s

Z

T

0

f ./ d C

1

s

Z

T

0

e

st

f .t/ dt. Since f is of ex ponential order s

0

, the second integral on the right converges to

125

126 Chapter 8

Laplace Transforms

1

s

L.f / as T ! 1 (Exercise 8.1.10). Now it sufﬁces to show that (A) lim

T !1

e

sT

Z

T

0

f ./ d  D 0

if s > s

0

. Supp ose t hat jf .t/j  Me

s

0

t

if t  t

0

and jf .t/j  K if 0  t  t

0

, and let T > t

0

. Then

ˇ

Z

T

0

f ./ d 

ˇ



ˇ

Z

t

0

f ./ d 

ˇ

C

ˇ

Z

T

t

0

f ./ d 

ˇ

< Kt

0

C M

Z

T

t

0

e

s

0



d  < Kt

0

C

Me

s

0

T

s

0

, which

proves (A).

8.1.14. (a) If T > 0, then

Z

T

0

e

st

f .t/ dt D

Z

T

0

e

.ss

0

/t

.e

s

0

t

f .t// dt. Use integration by parts with

u D e

.ss

0

/t

, dv D e

s

0

t

f .t/ dt, du D .s  s

0

/e

.ss

0

/t

, and v D g t obtain

Z

T

0

e

st

f .t/ dt D

e

.ss

0

/t

g.t/

ˇ

T

0

C .s  s

0

/

Z

T

0

e

.ss

0

/t

g.t/ dt. Since g.0/ D 0 this reduces to

Z

T

0

e

st

f .t/ dt D

e

.ss

0

/T

g.T / C .s  s

0

/

Z

T

0

e

.ss

0

/t

g.t/ dt. Since jg.t/j  M for all t  0, we can let t ! 1 to

conclude that

Z

1

0

e

st

f .t/ dt D .s  s

0

/

Z

1

0

e

.ss

0

/t

g.t/ dt if s > s

0

.

(b) If F .s

0

/ exists, then g.t/ is bounded on Œ0; 1/. N ow apply ( a).

(c) Since f .t/ D

1

2

d

dt

sin.e

t

2

/,

ˇ

Z

t

0

f ./ d 

ˇ

D

jsin.e

t

2

/  sin.1/j

2

 1 for all t  0. Now apply (a)

with s

0

D 0.

8.1.16. (a) .˛/ D

Z

1

0

x

˛1

e

x

dx D

x

˛

e

x

˛

ˇ

1

0

C

1

˛

Z

1

0

x

˛

e

x

dx D

.˛ C 1/

˛

.

(b) Use indu ction. .1/ D

Z

1

0

e

x

dx D 1. If (A) .n C1/ D nŠ, then .n C2/ D .n C1/.n C1/

(from (a)) D .n C 1/nŠ (from (A)) D .n C 1/Š.

(c) .˛ C1/ D

Z

1

0

x

˛

e

x

dt. Let x D st. Then .˛ C1/ D

Z

1

0

.st/

˛

e

st

s dt, so

Z

1

0

e

st

t

˛

dt D

.˛ C 1/

˛

.

8.1.18. (a)

Z

2

0

e

st

f .t/ dt D

Z

1

0

e

st

t dtC

Z

2

1

e

st

.2t/ dt D



1

s

2



e

s

.s C 1/

s

2



C



e

s

.s  1/

s

2

C

e

2s

s

2



D



2e

s

s

2

C

e

2s

s

2

C

1

s

2

D

.1  e

s

/

2

s

2

. Therefore,F .s/ D

.1  e

s

/

2

s

2

.1  e

2s

/

D

1  e

s

s

2

.1 C e

s

/

D

1

s

2

tanh

s

2

.

(b)

Z

1

0

e

st

f .t/ dt D

Z

1=2

0

e

st

dt 

Z

1

1=2

e

st

dt D

1

s



e

s=2

s

C

e

s

s



e

s=2

s

D 

2e

s=2

s

C

e

s

s

C

1

s

D

.1  e

s=2

/

2

s

. Therefore,F .s/ D

.1  e

s=2

/

2

s.1  e

s

/

D

1  e

s=2

s.1 C e

s=2

/

D

1

s

tanh

s

4

.

(c)

Z



0

e

st

f .t/ dt D

Z



0

e

st

sin t dt D

1 C e

s

.s

2

C 1/

. Therefore,F.s/ D

1 C e

s

.s

2

C 1/.1  e

s

/

1

s

2

C 1

coth

s

2

.

(d)

Z

2

0

e

st

f .t/ dt D

Z



0

e

st

sin t dt D

1 C e

s

.s

2

C 1/

. Therefore,F .s/ D

1 C e

s

.s

2

C 1/1 C e

2s

D

1

.s

2

C 1/.1  e

s

/

.

Section 8.2

The Inverse Laplace Transform

127

8.2 THE INVERSE LAPLACE TRANSFORM

8.2.2. (a)

2s C 3

.s  7/

4

D

2.s  7/ C 17

.s  7/

4

D

2

.s  7/

3

C

17

.s  7/

4

D

2Š

.s  7/

3

C

17

6

3Š

.s  7/

4

$ e

7t



t

2

C

17

6

t

3



.

(b)

s

2

 1

.s  2/

6

D

Œ.s  2/ C 2

2

 1

.s  2/

6

D

.s  2/

2

C 4.s  2/ C 3

.s  2/

6

D

1

.s  2/

4

C

4

.s  2/

5

C

3

.s  2/

6

D

1

6

3Š

.s  2/

4

C

1

6

4Š

.s  2/

5

C

1

40

5Š

.s  2/

6

$



1

6

t

3

C

1

6

t

4

C

1

40

t

5



e

2t

.

(c)

s C 5

s

2

C 6s C 18

D

.s C 3/

2

C 9

C

2

3

.s C3/

2

C 9

$ e

3t



cos 3t C

2

3

sin 3t



.

(d)

2s C 1

s

2

C9

D 2

s

2

C 9

C

1

3

s

2

C 9

$ 2 cos 3t C

1

3

sin 3t.

(e)

s

2

C 2s C 1

D

.s C 1/  1

.s C 1/

2

D

1

s C 1



1

.s C1/

2

$ .1  t/e

t

.

(f)

s C 1

s

2

 9

D

s

2

 9

C

1

3

s

2

 9

$ cosh 3t C

1

3

sinh 3t.

(g) Expand t he numerator in powers of s C 1: s

3

C 2s

2

 s  3 D Œ.s C 1/  1

3

C 2Œ.s C 1/  1

2



Œ.s C1/1 3 D .s C1/

3

.s C1/

2

2.s C1/1; t herefore

s

3

C 2s

2

 s  3

.s C 1/

4

D

1

s C 1



1

.s C 1/

2



2

.s C 1/

3



1

6

.s C 1/

4

$



1  t  t

2



1

6

t

3



e

t

.

(h)

2s C 3

.s  1/

2

C 4

D 2

.s  1/

2

C 4

C

5

2

.s  1/

2

C 4

$ e

t



2 cos 2t C

5

2

sin 2t



.

(i)

1

s



s

2

C1

$ 1  cos t.

(j)

3s C 4

s

2

 1

D

3s

s

2

 1

C

4

s

2

 1

$ 3 cosh t C 4 sinh t. Alternatively,

3s C 4

s

2

 1

D

3s C 4

.s  1/.s C 1/

D

1

2



7

s  1



1

s C 1



$

7e

t

 e

t

2

.

(k)

3

s  1

C

4s C 1

s

2

C 9

D 3

1

s  1

C4

s

2

C 9

C

1

3

s

2

C9

$ 3e

t

C 4 cos 3t C

1

3

sin 3t.

(l)

3

.s C 2/

2



2s C 6

s

2

C 4

D 3

1

.s C 2/

2

 2

s

2

C4

 3

2

s

2

C 4

$ 3te

2t

 2 cos 2t  3 sin 2t.

8.2.4. ( a)

2 C 3s

.s

2

C 1/.s C 2/.s C 1/

D

A

s C 2

C

B

s C1

C

C s C D

s

2

C 1

;

where

A.s

2

C 1/.s C 1/ C B.s

2

C 1/.s C 2/ C .C s C D/.s C 2/.s C 1/ D 2 C 3s:

5A D 4 .set s D 2/I

2B D 1 .set s D 1/I

A C 2B C 2D D 2 .set s D 0/I

A C B C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D

4

5

, B D 

1

2

, C D 

3

10

, D D

11

10

. Therefore,

2 C 3s

.s

2

C 1/.s C 2/.s C 1/

D

4

5

1

s C 2



1

2

1

s C 1



1

10

3s  11

s

2

C 1

$

4

5

e

2t



1

2

e

t



3

10

cos t C

11

10

sin t:

128 Chapter 8

Laplace Transforms

(b)

3s

2

C 2s C 1

.s

2

C 1/.s

2

C 2s C 2/

D

As CB

s

2

C 1

C

C.s C 1/ C D

.s C 1/

2

C 1

;

where

.As CB/..s C 1/

2

C 1/ C.C.s C 1/ C D/.s

2

C 1/ D 3s

2

C 2s C 1:

2B C C C D D 1 .set s D 0/I

A C B C 2D D 2 .set s D 1/I

2B C C C D D 1 .set s D 0/I

A C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 6=5, B D 2=5, C D 6=5, D D 7=5. Therefore,

3s

2

C2s C 1

.s

2

C 1/.s

2

C 2s C 2/

D

1

5



6s C 2

s

2

C 1



6.s C 1/  7

.s C 1/

2

C 1



$

6

5

cos t C

2

5

sin t 

6

5

e

t

cos t C

7

5

e

t

sin t:

(c) s

2

C 2s C 5 D .s C 1/

2

C 4;

3s C 2

.s  2/..s C 1/

2

C 4/

D

A

s  2

C

B.s C 1/ C C

.s C 1/

2

C 4

;

where

A



.s C 1/

2

/ C 4



C .B.s C 1/ C C / .s  2/ D 3s C 2:

13A D 8 .set s D 2/I

4A  3C D 1 .set s D 1/I

A CB D 0 .equate coefﬁcients of s

2

/:

Solving this system yields A D

8

13

, B D 

8

13

, C D

15

13

. Therefore,

3s C 2

.s  2/..s C 1/

2

C 4/

D

1

13



8

s  2



8.s  1/  15

.s C 1/

2

C 4



$

8

13

e

2t



8

13

e

t

cos 2t C

15

26

e

t

sin 2t:

(d)

3s

2

C 2s C 1

.s  1/

2

.s C2/.s C 3/

D

A

s  1

C

B

.s  1/

2

C

s C 2

C

D

s C 3

;

where

.A.s  1/ C B/.s C 2/.s C 3/ C .C.s C 3/ C D.s C 2//.s  1/

2

D 3s

2

C 2s C 1:

12B D 6 .set s D 1/I

9C D 9 .set s D 2/I

16D D 22 .set s D 3/I

A C C C D D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 3=8, B D 1=2, C D 1, D D 11=8. Therefore,

3s

2

C2s C 1

.s  1/

2

.s C 2/.s C 3/

D

3

8

1

s  1

C

1

2

1

.s  1/

2

C

1

s C 2



11

8

1

s C3

$

3

8

e

t

C

1

2

te

t

C e

2t



11

8

e

3t

:

Section 8.2

The Inverse Laplace Transform

129

(e)

2s

2

C s C 3

.s  1/

2

.s C 2/

2

D

A

s  1

C

B

.s  1/

2

C

s C 2

C

D

.s C 2/

2

;

where

.A.s  1/ C B/.s C 2/

2

C .C.s C 2/ C D/.s  1/

2

D 2s

2

C s C 3:

9B D 6 .set s D 1/I

9D D 9 .set s D 2/I

4A C 4B C 2C C D D 3 .set s D 0/I

A C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1=9, B D 2=3, C D 1=9, D D 1. Therefore,

2s

2

C s C 3

.s  1/

2

.s C 2/

2

D

1

9

1

s  1

C

2

3

1

.s  1/

2



1

9

1

s C 2

C

1

.s C 2/

2

$

1

9

e

t

C

2

3

te

t



1

9

e

2t

C te

2t

:

(f)

3s C 2

.s

2

C 1/.s  1/

2

D

A

s  1

C

B

.s  1/

2

C

C s C D

s

2

C 1

;

where

A.s  1/.s

2

C 1/ CB.s

2

C 1/ C .C s C D/.s  1/

2

D 3s C 2: .A/

Setting s D 1 yields 2B D 5, so B D

5

2

. Substi tuting this into (A) shows t hat

A.s  1/.s

2

C 1/ C .C s C D/.s  1/

2

D 3s C 2 

5

2

.s

2

C 1/

D 

5s

2

 6s C 1

2

D 

.s  1/.5s  1/

2

:

Therefore,

A.s

2

C 1/ C .C s C D/.s  1/ D

1  5s

2

:

2A D 2 .set s D 1/I

A  D D 1=2 .set s D 0/I

A C C D 0 .equate coefﬁcients of s

2

/:

Solving this system yields A D 1, C D 1, D D 

3

2

. Therefore,

3s C 2

.s

2

C 1/.s  1/

2

D 

1

s  1

C

5

2

1

.s  1/

2

C

s  3=2

s

2

C 1

$ e

t

C

5

2

te

t

C cos t 

3

2

sin t:

8.2.6. ( a)

17s  15

.s

2

 2s C 5/.s

2

C 2s C 10/

D

A.s  1/ C B

.s  1/

2

C 4

C

C.s C 1/ C D

.s C 1/

2

C 9

where

.A.s  1/ C B/..s C 1/

2

C 9/ C .C.s C 1/ C D/..s  1/

2

C 4/ D 17s  15:

130 Chapter 8

Laplace Transforms

13B C 8C C 4D D 2 .set s D 1/I

18A C 9B C 8D D 32 .set s D 1/I

10A C 10B C 5C C 5D D 15 .set s D 0/I

A C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1, B D 2, C D 1, D D 4. Therefore,

17s  15

.s

2

 2s C 5/.s

2

C 2s C 10/

D

.s  1/ C 2

.s  1/

2

C 4



.s C 1/ C 4

.s C 1/

2

C 9

$ e

t

.cos 2t C sin 2t/  e

t



cos 3t C

4

3

sin 3t



:

(b)

8s C 56

.s

2

 6s C 13/.s

2

C 2s C 5/

D

A.s  3/ C B

.s  3/

2

C 4

C

C.s C 1/ C D

.s C 1/

2

C 4

where

.A.s  3/ C B/..s C 1/

2

C 4/ C .C.s C1/ C D/..s  3/

2

C 4/ D 8s C 56:

20B C 16C C 4D D 80 .set s D 3/I

16A C 4B C 20D D 48 .set s D 1/I

15A C 5B C 13C C 13D D 56 .set s D 0/I

A C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1, B D 3, C D 1, D D 1. Therefore,

8s C 56

.s

2

 6s C 13/.s

2

C 2s C 5/

D

.s  3/ C 3

.s  3/

2

C 4

C

.s C 1/ C 1

.s C 1/

2

C4

$ e

3t



cos 2t C

3

2

sin 2t



C e

t



cos 2t C

1

2

sin 2t



:

(c)

s C9

.s

2

C 4s C 5/.s

2

 4s C 13/

D

A.s C 2/ C B

.s C2/

2

C 1

C

C.s  2/ C D

.s  2/

2

C 9

where

.A.s C 2/ C B/..s  2/

2

C 9/ C .C.s  2/ C D/..s C 2/

2

C 1/ D s C 9:

25B  4C C D D 7 .set s D 2/I

36A C 9B C 17D D 11 .set s D 2/I

26A C 13B  10C C 5D D 9 .set s D 0/I

A C C D 0 .equate coefﬁcient s of s

3

/:

Solving this system yields A D 1=8, B D 1=4, C D 1=8, D D 1=4. Therefore,

s C 9

.s

2

C4s C 5/.s

2

 4s C 13/

D D



1

8

.s C 2/ C 2

.s C 2/

2

C 1



.s  2/  2

.s  2/

2

C 3



$ e

2t



1

8

cos t C

1

4

sin t



 e

2t



1

8

cos 3t 

1

12

sin 3t



:

(d)

3s  2

.s

2

 4s C 5/.s

2

 6s C 13/

D

A.s  2/ C B

.s  2/

2

C 1

C

C.s  3/ C D

.s  3/

2

C 4

where

.A.s  2/ C B/..s  3/

2

C 4/ C .C.s  3/ C D/..s  2/

2

C 1/ D 3s 2:

Section 8.2

The Inverse Laplace Transform

131

5B  C C D D 4 .set s D 2/I

4A C4B C 2D D 7 .set s D 3/I

26A C 13B  15C C 5D D 2 .set s D 0/I

A C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1, B D 1=2, C D 1, D D 1=2. Therefore,

3s  2

.s

2

 4s C 5/.s

2

 6s C 13/

D D

1

2



2.s  2/ C 1

.s  2/

2

C1



2.s  3/  1

.s  3/

2

C 4



$ e

2t



cos t C

1

2

sin t



 e

3t



cos 2t 

1

4

sin 2t



:

(e)

3s  1

.s

2

 2s C2/.s

2

C 2s C 5/

D

A.s  1/ C B

.s  1/

2

C 1

C

C.s C 1/ C D

.s C 1/

2

C 4

where

.A.s  1/ C B/..s C 1/

2

C 4/ C.C.s C 1/ C D/..s  1/

2

C 1/ D 3s  1:

8B C 2C C D D 2 .set s D 1/I

8A C 4B C 5D D 4 .set s D 1/I

5A C 5B C 2C C 2D D 1 .set s D 0/I

A C 5B C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1=5, B D 2=5, C D 1=5, D D 4=5. Therefore,

3s  1

.s

2

 2s C 2/.s

2

C 2s C 5/

D

1

5



.s  1/ C 2

.s  1/

2

C 1



.s C 1/ C 4

.s C 1/

2

C 4



:

$ e

t



1

5

cos t C

2

5

sin t



 e

t



1

5

cos 2t C

2

5

sin 2t



:

(f)

20s C 40

.4s

2

 4s C 5/.4s

2

C 4s C 5/

D Œ

A.s  1=2/ C B

.s  1=2/

2

C 1

C

C.s C 1=2/ C D

.s C 1=2/

2

C 1

where

.A.s  1=2/ C B/..s C 1=2/

2

C 1/ C .C.s C 1=2/ C D/..s  1=2/

2

C 1/ D

5s C 10

4

:

2B C C C D D 25=8 .set s D 1=2/I

A C B C 2D D 15=8 .set s D 1=2/I

5A C 10B C 5C C 10D D 20 .set s D 0/I

A CC D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1, B D 9=8, C D 1, D D 1=8. Therefore,

20s C 40

.4s

2

 4s C 5/.4s

2

C 4s C 5/

D

1

8



8.s  1=2/ C9

.s  1=2/

2

C 1

C

8.s C 1=2/

.s C 1=2/

2

C 1



$ e

t=2



cos t C

9

8

sin t



Ce

t=2



cos t 

1

8

sin t



:

8.2.8. ( a)

2s C 1

.s

2

C 1/.s  1/.s  3/

D

A

s  1

C

B

s  3

C

C s C D

s

2

C1

132 Chapter 8

Laplace Transforms

where

.A.s  3/ C B.s  1//.s

2

C 1/ C .C s C D/.s  1/.s  3/ D 2s C1:

4A D 3 .set s D 1/I

20B D 7 .set s D 3/I

3A  B C 3D D 1 .set s D 0/I

A CB C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 3=4, B D 7=20, C D 2=5, D D 3=10. Therefore,

2s C 1

.s

2

C 1/.s 1/.s  3/

D 

3

4

1

s  1

C

7

20

1

s  3

C

2

5

s

2

C 1



3

10

1

s

2

C 1

$ 

3

4

e

t

C

7

20

e

3t

C

2

5

cos t 

3

10

sin t:

(b)

s C 2

.s

2

C 2s C 2/.s

2

 1/

D

A

s  1

C

B

s C 1

C

C.s C 1/ CD

.s C 1/

2

C 1

where

.A.s C 1/ C B.s  1//..s C 1/

2

C 1/ C .C.s C 1/ C D/.s

2

 1/ D s C 2:

10A D 3 .set s D 1/I

2B D 1 .set s D 1/I

2A  2B  C  D D 2 .set s D 0/I

A C B C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 3=10, B D 1=2, C D 1=5, D D 3=5. Therefore,

s C 2

.s

2

C 2s C 2/.s

2

 1/

D

3

10

1

s  1



1

2

1

s C 1

C

1

5

s C 1

.s C 1/

2

C 1



3

5

1

.s C 1/

2

C 1

$

3

10

e

t



1

2

e

t

C

1

5

e

t

cos te

t

sin t:

(c)

2s  1

.s

2

 2s C 2/.s C 1/.s  2/

D

A

s  2

C

B

s C 1

C

C.s  1/ C D

.s  1/

2

C 1

where

.A.s C 1/ CB.s  2//..s  1/

2

C 1/ C .C.s  1/ CD/.s  2/.s C 1/ D 2s  1:

6A D 3 .set s D 2/I

15B D 3 .set s D 1/I

2A  4B C 2C  2D D 1 .set s D 0/I

A C B C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1=2, B D 1=5, C D 7=10, D D 1=10. Therefore,

2s  1

.s

2

 2s C 2/.s C 1/.s  2/

D D

1

2

1

s  2

C

1

5

1

s C 1



7

10

s  1

.s  1/

2

C 1



1

10

1

.s  1/

2

C 1

$

1

2

e

2t

C

1

5

e

t



7

10

e

t

cos t 

1

10

e

t

sin t:

(d)

s  6

.s

2

 1/.s

2

C 4/

D

A

s  1

C

B

s C 1

C

C s C D

s

2

C 4

Section 8.2

The Inverse Laplace Transform

133

where

.A.s C 1/ C B.s  1//.s

2

C 4/ C .C s C D/.s

2

 1/ D s  6:

10A D 5 .set s D 1/I

10B D 7 .set s D 1/I

4A  4B  D D 6 .set s D 0/I

A C B C C D 0 .equate coefﬁcient s of s

3

/:

Solving this system yields A D 1=2, B D 7=10, C D 1=5, D D 6=5. Therefore,

s  6

.s

2

 1/.s

2

C 4/

D D 

1

2

1

s  1

C

7

10

1

s C 1



1

5

s

2

C 4

C

3

5

C

1

s

2

C 4

$ 

1

2

e

t

C

7

10

e

t



1

5

cos 2t C

3

5

sin 2t:

(e)

2s  3

s.s  2/.s

2

 2s C 5/

D

A

s

C

B

s  2

C

C.s  1/ C D

.s  1/

2

C 4

where

.A.s  2/ C Bs/..s  1/

2

C 4/ C .C.s  1/ CD/s.s  2/ D 2s  3:

10A D 3 .set s D 0/I

10B D 1 .set s D 2/I

4A C 4B  D D 1 .set s D 1/I

A CB C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 3=10, B D 1=10, C D 2=5, D D 1=5. Therefore,

2s  3

s.s 2/.s

2

 2s C 5/

D D

3

10s

C

1

10

1

s  2



2

5

s  1

.s  1/

2

C 4

C

1

5

1

.s  1/

2

C 4

$

3

10

C

1

10

e

2t



2

5

e

t

cos 2t C

1

10

e

t

sin 2t:

(f)

5s  15

.s

2

 4s C 13/.s  2/.s  1/

D

A

s  1

C

B

s  2

C

C.s  2/ C D

.s  2/

2

C 9

where

.A.s  2/ C B.s  1//..s  2/

2

C 9/ C .C.s  2/ C D/.s  1/.s  2/ D 5s  15:

10A D 10 .set s D 1/I

9B D 5 .set s D 2/I

26A  13B  4C C 2D D 15 .set s D 0/I

A C B C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1, B D 5=9, C D 4=9, D D 1. Therefore,

5s  15

.s

2

 4s C 13/.s  2/.s 1/

D D

1

s  1



5

9

1

s  2



4

9

s  2

.s  2/

2

C 9

C

1

.s  2/

2

C 9

$ e

t



5

9

e

2t



4

9

e

2t

cos 3t C

1

3

e

2t

sin 3t:

134 Chapter 8

Laplace Transforms

8.2.10. (a) Let i D 1. (The proo f for i D 2; : : : ; n) is simi lar. Multiplying th e given equati on throu gh by

s  s

1

yields

P.s/

.s  s

2

/ .s  s

n

/

D A

1

C .s  s

1

/



A

2

s  s

2

C C

A

n

s  s

n



;

and setting s D s

1

yields A

1

D

P.s

1

/

.s

1

 s

2

/ .s

2

 s

n

/

.

(b) From calculus we know that F has a partial fractio n expansion of the form

P.s/

.s  s

1

/Q

1

.s/

D

A

s  s

1

C G.s/ where G is continuous at s

1

. Mul tiplying through by s  s

1

shows that

P.s/

Q

1

.s/

D A C

.s  s

1

/G.s/. Now set s D s

1

to obtain A D

P.s

1

/

Q.s

1

/

.

(c) The result in (b) is generalization of the result in (a), since it shows that if s

1

is a simple zero of the

denominator of the rational functio n, then Heaviside’s method can be used to determine the coefﬁcient of

1=.s s

1

/ in the partial fraction expansion even if some of the other zeros of the denominator are repeated

or complex.

8.3 SOLUTION OF INIT IAL VALUE PROBLEMS

8.3.2.

.s

2

 s  6/Y.s/ D

2

s

Cs  1 D

2 C s.s  1/

s

:

Since .s

2

 s  6/ D .s  3/.s C 2/,

Y.s/ D

2 C s.s  1/

s.s 3/.s C 2/

D 

1

3s

C

8

15

1

s  3

C

4

5

1

s C 2

and y D 

1

3

C

8

15

e

3t

C

4

5

e

2t

.

8.3.4.

.s

2

 4/Y.s/ D

2

s  3

C .1 C s/ D

2 C .s  1/.s  3/

s  3

:

Since s

2

 4 D .s  2/.s C 2/,

Y.s/ D

2 C .s  1/.s  3/

.s  2/.s C 2/.s  3/

D 

1

4

1

s  2

C

17

20

1

s C 2

C

2

5

1

s  3

and y D 

1

4

e

2t

C

17

20

e

2t

C

2

5

e

3t

.

8.3.6.

.s

2

C 3s C 2/Y.s/ D

6

s  1

C .1 C s/ C 3 D

6 C .s  1/.s C 2/

s  1

:

Since s

2

C 3s C 2 D .s C 2/.s C 1/,

Y.s/ D

6 C .s  1/.s C 2/

.s  1/.s C 2/.s C 1/

D

1

s  1

C

2

s C 2



2

s C 1

and y D e

t

C2e

2t

 2e

t

.

Section 8.3

Solution of Initial Value Problems

135

8.3.8.

.s

2

 3s C 2/Y.s/ D

2

s  3

C .1 C s/  3 D

2 C .s  3/.s  4/

s  3

:

Since s

2

 3s C 2 D .s  1/.s  2/,

Y.s/ D

2 C .s  3/.s  4/

.s  1/.s  2/.s  3/

D

4

s  1



4

s  2

C

1

s  3

and y D 4e

t

 4e

2t

C e

3t

.

8.3.10.

.s

2

 3s C 2/Y.s/ D

1

s  3

C .4  s/ C 3 D

1  .s  3/.s C 1/

s  3

:

Since s

2

 3s C 2 D .s  1/.s  2/,

Y.s/ D

1  .s  3/.s C1/

.s  1/.s  2/.s  3/

D

5

2

1

s  1



4

s  2

C

1

2

1

s  3

and y D

5

2

e

t

 4e

2t

C

1

2

e

3t

.

8.3.12.

.s

2

C s  2/Y.s/ D 

4

s

C .3 C 2s/ C 2 D

4 C s.5 C 2s/

s

:

Since .s

2

C s  2/ D .s C 2/.s  1/,

Y.s/ D

4 C s.5 C 2s/

s.s C2/.s  1/

D

2

s



1

s C 2

C

1

s  1

;

and y D 2 e

2t

C e

t

.

8.3.14.

.s

2

 s  6/Y.s/ D

2

s

Cs  1 D

2 C s.s  1/

s

:

Since s

2

 s  6 D .s  3/.s C 2/,

Y.s/ D

2 C s.s  1/

s.s 3/.s C 2/

D 

1

3s

C

8

15

1

s  3

C

4

5

1

s C 2

and y D 

1

3

C

8

15

e

3t

C

4

5

e

2t

.

8.3.16.

.s

2

 1/Y.s/ D

1

s

C s D

1 C s

2

s

:

Since s

2

 1 D .s  1/.s C 1/,

Y.s/ D

1 C s

2

s.s 1/.s C 1/

D 

1

s

C

1

s  1

C

1

s C 1

and y D 1 C e

t

Ce

t

.

136 Chapter 8

Laplace Transforms

8.3.18.

.s

2

C s/Y.s/ D

2

s  3

C .4  s/  1 D

2  .s  3/

2

s  3

:

Since s

2

C s D s.s C 1/,

Y.s/ D

2  .s 3/

2

s.s C 1/.s  3/

D

7

3s



7

2

1

s C 1

C

1

6

1

s  3

and y D

7

3



7

2

e

t

C

1

6

e

3t

.

8.3.20.

.s

2

C 1/Y.s/ D

1

s

2

C 2; so Y .s/ D

1

.s

2

C 1/s

2

C

2

s

2

C 1

:

Substituting x D s

2

into

1

.x C 1/x

D

1

x C 1



1

x

yields

1

.s

2

C 1/s

2

D

1

s

2



1

s

2

C 1

;

so Y .s/ D

1

s

2

C

1

s

2

C 1

and y D t C sin t.

8.3.22.

.s

2

C 5s C 6/Y.s/ D

2

s C 1

C .3 C s/ C 5 D

2 C .s C 1/.s C 8/

s C 1

:

Since s

2

C 5s C 6 D .s C 2/.s C 3/,

Y.s/ D

2 C .s C 1/.s C 8/

.s C 1/.s C 2/.s C 3/

D

1

s C 1

C

4

s C 2



4

s C 3

and y D e

t

C 4e

2t

 4e

3t

.

8.3.24.

.s

2

 2s  3/Y.s/ D

10s

s

2

C 1

C .7 C 2s/  4 D

10s

s

2

C 1

C.2s C 3/:

Since s

2

 2s  3 D .s  3/.s C 1/,

Y.s/ D

10s

.s  3/.s C 1/.s

2

C 1/

C

2s C 3

.s  3/.s C 1/

: .A/

2s C 3

.s  3/.s C 1/

D

9

4

1

s  3



1

4

1

s C 1

$

9

4

e

3t



1

4

e

t

: .B/

10s

.s  3/.s C 1/.s

2

C 1/

D

A

s  3

C

B

s C 1

C

C s C D

s

2

C 1

where

.A.s C 1/ C B.s  3//.s

2

C 1/ C .C s C D/.s  3/.s C 1/ D 10s:

40A D 30 .set s D 3/I

8B D 10 .set s D 1/I

A  3B  3D D 0 .set s D 0/I

A C B CC D 0 .equate coefﬁcient s of s

3

/:

Section 8.3

Solution of Initial Value Problems

137

Solving this system yields A D 3=4, B D 5=4, C D 2, D D 1. Therefore,

10s

.s  3/.s C 1/.s

2

C1/

D

3

4

1

s  3

C

5

4

1

s C 1



2s C1

s

2

C 1

$

3

4

e

3t

C

5

4

e

t

 2 cos t  sin t:

From this, (A), and (B), y D sin t  2 cos t C 3e

3t

C e

t

.

8.3.26.

.s

2

C 4/Y.s/ D

16

s

2

C 4

C

9s

s

2

C 1

C s; so

Y.s/ D

16

.s

2

C4/

2

C

9s

.s

2

C 4/.s

2

C 1/

C

s

2

C 4

:

From the table of Laplace transforms,

t cos 2t $

s

2

 4

.s

2

C 4/

2

D

s

2

C 4

.s

2

C 4/

2



8

.s

2

C 4/

2

D

1

s

2

C 4



8

.s

2

C 4/

2

:

Therefore,

8

.s

2

C 4/

2

D

1

s

2

C 4

 L.t cos 2t/; so

16

.s

2

C 4/

2

$ sin 2t  2t cos 2t: .A/

Substituting x D s

2

into

9

.x C 4/.x C 1/

D

3

x C 1



3

x C 4

and multiplying by s yields

9s

.s

2

C 4/.s

2

C 1/

D

3s

s

2

C 1



3s

s

2

C 4

$ 3 cos t  3 cos 2t: .B/

Finally,

s

2

C 4

$ cos 2t: .C/

Adding (A), (B ), and (C) yields y D .2t C 2/ cos 2t C sin 2t C 3 cos t.

28.

.s

2

C 2s C 2/Y.s/ D

2

s

2

C.7 C 2s/ C 4:

Since .s

2

C 2s C 2/ D .s C 1/

2

C 1,

Y.s/ D

2

s

2

..s C 1/

2

C 1/

C

2s  3

.s C 1/

2

C 1

: .A/

2s  3

.s C 1/

2

C 1

D

2.s C 1/  5

.s C 1/

2

C 1

$ e

t

.2 cos t  5 sin t/: .B/

2

s

2

..s C 1/

2

C 1/

D

A

s

C

B

s

2

C

C.s C 1/ C D

.s C 1/

2

C 1

;

138 Chapter 8

Laplace Transforms

where .As C B/



.s C 1/

2

C 1



C s

2

.C.s C 1/ C D/ D 2.

2B D 2 .set s D 0/I

A C B C D D 2 .set s D 1/I

A C C D 0 .equate coefﬁcients of s

3

/I

2A C B C C C D D 0 .equate coefﬁcients of s

2

/:

Solving this system yields A D 1, B D 1, C D 1, D D 0. Therefore,

2

s

2

..s C 1/

2

C 1/

D 

1

s

C

1

s

2

C

.s C 1/

.s C1/

2

C 1

$ 1 C t C e

t

cos t:

From this, (A), and (B), y D 1 C t C e

t

.cos t  5 sin t/.

8.3.30. .s

2

C 4s C 5/Y.s/ D

.s C 1/ C 3

.s C 1/

2

C 1

C 4. Since .s

2

C 4s C 5/ D .s C 2/

2

C 1,

Y.s/ D

s C 4

..s C 1/

2

C1/..s C 2/

2

C 1/

C

4

.s C2/

2

C 1

: .A/

4

.s C 2/

2

C 1

$ 4e

2t

sin t: .B/

s C 4

..s C 1/

2

C 1/..s C 2/

2

C 1/

D

A.s C 1/ C B

.s C 1/

2

C 1

C

C.s C 2/ C D

.s C 2/

2

C 1

;

where .A.s C 1/ C B/



.s C 2/

2

C 1



C .C.s C 2/ C D/



.s C 1/

2

C 1



D 4 C s.

5A C 5B C 4C C 2D D 4 .set s D 0/I

2B C C C D D 3 .set s D 1/I

A C B C 2D D 2 .set s D 2/I

A C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1, B D 1, C D 1, D D 0. Therefore,

s C4

..s C 1/

2

C 1/..s C 2/

2

C 1/

D

.s C1/ C 1

.s C 1/

2

C 1

C

s C2

.s C 2/

2

C1

; $ e

t

.cos t C sin t/ C e

2t

cos t:

From this, (A), and (B), y D e

t

.cos t C sin t/ C e

2t

.cos t C 4 sin t/.

8.3.32.

.2s

2

 3s  2/Y.s/ D

4

s  1

C 2.2 C s/  3 D

4 C .2s  7/.s  1/

s  1

Since 2s

2

 3s  2 D .s  2/.2s C 1/,

Y.s/ D

4 C .2s  7/.s  1/

2.s  2/.s  1/.s C 1=2/

D

1

5

1

s  2



4

3

1

s  1

C

32

15

1

s C 1=2

and y D

1

5

e

2t



4

3

e

t

C

32

15

e

t=2

.

8.3.34.

.2s

2

C 2s C 1/Y.s/ D

2

s

2

C 2.1 C s/ C 2 D

2

s

2

C 2s:

Section 8.3

Solution of Initial Value Problems

139

Since 2s

2

C 2s C 1 D 2..s C 1=2/

2

C 1=4/,

Y.s/ D

1

s

2

..s C 1=2/

2

C 1=4/

C

s

..s C 1=2/

2

C1=4/

: .A/

s

..s C 1=2/

2

C 1=4/

$ e

t=2

.cos.t=2/  sin.t=2//: .B/

1

s

2

..s C 1=2/

2

C 1=4/

D

A

s

C

B

s

2

C

C.s C 1=2/ CD

..s C 1=2/

2

C 1=4/

where

.As C B/..s C 1=2/

2

C 1=4/ C .C.s C 1=2/ CD/s

2

D 1:

B D 2 .set s D 0/I

A C 2B C 2D D 8 .set s D 1=2/I

5A C10B C 2C C 2D D 8 .set s D 1=2/I

A C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 4, B D 2, C D 4, D D 0. Therefore,

1

s

2

..s C 1=2/

2

C 1=4/

D 

4

s

C

2

s

2

C

4.s C 1=2/

.s C 1=2/

2

C 1=4

$ 4 C 2t C 4e

t=2

cos.t=2/:

This, (A), and (B) imply that y D e

t=2

.5 cos.t=2/  sin.t=2// C 2t  4.

8.3.36.

.4s

2

C 4s C 1/Y.s/ D

3 C s

s

2

C 1

C 4.1 C 2s/ C 8 D

3 C s

s

2

C1

C 4.1 C 2s/ C 8s C 4:

Since 4s

2

C 4s C 1 D 4.s C 1=2/

2

,

Y.s/ D

3 C s

4.s C 1=2/

2

.s

2

C 1/

C

2

s C 1=2

: .A/

3 C s

4.s C 1=2/

2

.s

2

C 1/

D

A

s C 1=2

C

B

.s C1=2/

2

C

C s C D

s

2

C 1

where

.A.s C 1=2/ C B/.s

2

C 1/ C .C s C D/.s C 1=2/

2

D

3 C s

4

:

10B D 5 .set s D 1=2/I

2A C 4B C D D 3 .set s D 0/I

12A C 8B C 9C C 9D D 4 .set s D 1/I

A C C D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 3=5, B D 1=2, C D 3=5, D D 1=5. Therefore,

3 C s

4.s C 1=2/

2

.s

2

C 1/

D

3

5

1

s C 1=2

C

1

2

1

.s C 1=2/

2



1

5

3s C 1

s

2

C 1

:

$

3

5

e

t=2

C

1

2

te

t=2



1

5

.3 cos t C sin t/:

140 Chapter 8

Laplace Transforms

Since

2

s C 1=2

$ 2e

t=2

, this and (A) imply that y D

e

t=2

10

.5t C 26/ 

1

5

.3 cos t C sin t/.

8.3.38. Transformin g the initial value problem

ay

00

C by

0

C cy D 0; y.0/ D 1; y

0

.0/ D 0

yields .as

2

Cbs Cc/Y.s/ D as Cb, so Y.s/ D

as C b

as

2

C bs C c

. Therefore, y

1

D L

1



as C b

as

2

C bs C c



satisﬁes the initial conditions y

1

.0/ D 1, y

0

1

.0/ D 0.

Transforming the initial value problem

ay

00

C by

0

C cy D 0; y.0/ D 0; y

0

.0/ D 1

yields .as

2

C bs C c/Y.s/ D a, so Y.s/ D

a

as

2

C bs C c

. Therefore, y

2

D L

1



a

as

2

C bs C c



satisﬁes the initial conditions y

1

.0/ D 0, y

0

1

.0/ D 1.

8.4 THE UNIT STEP FUNCTION

8.4.2.

L.f / D

Z

1

0

e

st

f .t/ dt D

Z

1

0

e

st

t dt C

Z

1

e

st

dt: .A/

To relate the ﬁrst term to a Laplace transform we add and su btract

R

1

e

st

t dt in (A) to obtain

L.f / D

Z

1

0

e

st

t dt C

Z

1

e

st

.1  t/ dt D L.t/ 

Z

1

e

st

.t  1/ dt: .B/

Letting t D x C 1 in the last integral yields

Z

1

e

st

.t  1/ dt D 

Z

1

0

e

s.xC1/

x dx D e

s

L.t/:

This and (B) imply that L.f / D .1  e

s

/L.t / D

1  e

s

s

2

.

Alternatively, f .t/ D t  u.t  1/.t  1/ $ .1  e

s

/L.t/ D

1  e

s

s

2

.

8.4.4.

L.f / D

Z

1

0

e

st

f .t/ dt D

Z

1

0

e

st

dt C

Z

1

e

st

.t C 2/ dt: .A/

To relate the ﬁrst term to a Laplace transform we add and su btract

R

1

e

st

dt i n (A) to obtain

L.f / D

Z

1

0

e

st

dt C

Z

1

e

st

.t C 1/ dt D L.t/ C

Z

1

e

st

.t C 1/ dt: .B/

Letting t D x C 1 in the last integral yields

Z

1

e

st

.t C 1/ dt D

Z

1

0

e

s.xC1/

.x C2/ dx D e

s

L.t C 2/:

This and (B) imply that L.f / D L.1/ Ce

s

L.t C 2/ D

1

s

C e

s



1

s

2

C

2

s



.

Section 8.4

The Unit Step Function

141

Alternatively,

f .t/ D 1 Cu.t  1/.t C 1/ $ L.1/ C e

s

L.t C 2/ D

1

s

C e

s



1

s

2

C

2

s



.

8.4.6.

L.f / D

Z

1

0

e

st

f .t/ dt D

Z

1

0

e

st

t

2

D L.t

2

/ 

Z

1

t

2

dt: .A/

Letting t D x C 1 in the last integral yields

Z

1

e

st

t

2

dt D

Z

1

0

e

s.xC1/

.t

2

C 2t C 1/ dx D e

s

L.t

2

C 2t C 1/:

This and (A) imply that

L.f / D L.t

2

/ C e

s

L.t

2

C 2t C 1/ D

2

s

3

 e

s



2

s

3

C

2

s

2

C

1

s



:

Alternatively,

f .t/ D t

2

.1  u.t  1// $ L.t

2

/ C e

s

L.t

2

C 2t C 1/ D

2

s

3

 e

s



2

s

3

C

2

s

2

C

1

s



8.4.8. f .t/ D t

2

C 2 C u.t  1/.t  t

2

 2/. Since t

2

C 2 $

2

s

3

C

2

s

and

L



u.t  1/.t  t

2

 2/



D e

s

L



.t C 1/  .t C 1/

2

 2



D e

s

L.t

2

C t C 2/ D e

s



2

s

3

C

1

s

2

C

2

s



;

it follows that F .s/ D

2

s

3

C

2

s

 e

s



2

s

3

C

1

s

2

C

2

s



.

8.4.10. f .t/ D e

t

C u.t  1/.e

2t

 e

t

/ $ L.e

t

/ C e

s

L.e

2.t C1/

/  e

s

L.e

t1

/ D L.e

t

/ C

e

.sC2/

L.e

2t

/  e

.sC1/

L.e

t

/ D

1  e

.sC1/

s C 1

C

e

.sC2/

s C 2

.

8.4.12. f .t/ D Œu.t  1/  u.t 2/ t $ e

s

L.t C1/  e

2s

L.t C 2/

D e

s



1

s

2

C

1

s



 e

2s



1

s

2

C

2

s



.

8.4.14.

f .t/ D t  2u.t  1/.t  1/ C u.t  2/.t C 4/ $

1

s

2

 2e

s

L.t/ C e

2s

L.t C 6/

D

1

s

2



2e

s

s

2

C e

2s



1

s

2

C

6

s



:

8.4.16. f .t/ D 2  2u.t  1/t C u.t  3/.5t  2/ $ L.2/  2e

s

L.t C 1/ C e

3s

L.5t C 13/ D

2

s

 e

s



2

s

2

C

2

s



C e

3s



5

s

2

C

13

s



.

142 Chapter 8

Laplace Transforms

8.4.18. f .t/ D .t C 1/

2

C u.t  1/



.t C 2/

2

 .t C 1/

2



D t

2

C 2t C 1 C u.t  1/.2t C 3/ $

L.t

2

C2t C 1/ C e

s

L.2t C 5/ D

2

s

3

C

2

s

2

C

1

s

C e

s



2

s

2

C

5

s



.

8.4.20.

1

s.s C 1/

D

1

s



1

s C 1

$ 1e

t

) e

s

1

s.s C 1/

$ u.t1/



1  e

.t1/



D

(

0; 0  t < 1;

1  e

.t1/

; t  1:

8.4.22.

3

s



1

s

2

$ 3  t ) e

s



3

s



1

s

2



$ u.t  1/ .3  .t  1// D u.t  1/.4  t/I

1

s

C

1

s

2

$ 1 C t ) e

3s



1

s

C

1

s

2



$ u.t  3/ .1 C .t  3// D u.t  3/.t  2/I

therefore

h.t/ D 2 C t C u.t  1/.4  t/ C u.t  3/.t  2/ D

8

ˆ

<

ˆ

:

2 C t; 0  t < 1;

6; 1  t < 3;

t C 4; t  3:

8.4.24.

1  2s

s

2

C 4s C 5

D

5  2.s C 2/

.s C 2/

2

C 1

$ e

2t

.5 sin t 2 cos t/I

therefore,

h.t/ D u.t   /e

2.t /

.5 sin.t  /  2 cos.t  //

D u.t   /e

2.t /

.2 cos t  5 sin t/

D

(

0; 0  t < ;

e

2.t /

.2 cos t  5 sin t/; t  :

:

8.4.26. Denote F.s/ D

3.s  3/

.s C 1/.s  2/



s C1

.s  1/.s  2/

. Since

3.s  3/

.s C 1/.s  2/

D

4

s C 1



1

s  2

and

s C 1

.s  1/.s  2/

D

3

s  2



2

s  1

, F.s/ D

4

s C 1



4

s  2

C

2

s  1

$ 4e

t

4e

2t

C2e

t

. Therefore,e

2s

F .s/ $

u.t  2/



4e

.t2/

 4e

2.t 2/

C 2e

.t2/



D

(

0; 0  t < 2;

4e

.t2/

 4e

2.t 2/

C 2e

.t2/

; t  2:

8.4.28.

3

s



1

s

3

$ 3 

t

2

) e

2s



3

s



1

s

3



$ u.t  2/



3 

.t  2/

2



D u.t  2/





t

2

C 2t C 1



I

1

s

2

$ t )

e

4s

s

2

$ u.t  4/.t  4/I

Section 8.5

Constant Coeefﬁcient Equations with Piecewise Continuous Forcing Functions

143

therefore

h.t/ D 1  t

2

C u.t  2/





t

2

C 2t C 1



C u.t  4/.t  4/

D

8

ˆ

<

ˆ

:

1  t

2

; 0  t < 2



3t

2

C 2t C 2; 2  t < 4;



3t

2

C3t  2; t  4:

8.4.30. Let T be an arbitrary p ositive number. Since lim

m!1

t

m

D 1, only ﬁnitely many members of

ft

m

g are in Œ0; T . Since f

m

is continuous on Œt

m

; 1/ for each m, f is piecewise continuous on Œ0; T .

If t

M

 t < t

M C1

, then u.t  t

m

/ D 1 if m  M , while u.t  t

m

/ D 0 if m > M . Therefore,

f .t/ D f

0

.t/ C

M

X

mD1

.f

m

.t/  f

m1

.t// D f

M

.t/

8.4.32. Since

1

X

mD0

e

Km

converges if  > 0,

1

X

mD0

e

t

m

converges if  > 0, by the comparison test.

Therefore,(C) of Exercise 8.3.31 holds if s > s

0

C if  is any p ositive number. This implies th at it holds

if s > s

0

.

8.4.34. Let t

m

D m and f

m

.t/ D .1/

m

, m D 0; 1; 2; : : : . Then f

m

.t/  f

m1

.t/ D .1/

m

2, so

f .t/ D 1 C 2

1

X

mD1

.1/

m

u.t  m/ and F.s/ D

1

s

1 C 2

1

X

mD1

.1/

m

e

ms

!

Substituting x D e

s

in the

identity

1

X

mD1

.1/

m

x

m

D 

x

1 C x

(jxj < 1) yields F.s/ D

1

s



1 

2e

s

1 C e

s



D

1

s

1  e

s

1 C e

s

.

8.4.36. Let t

m

D m and f

m

.t/ D .1/

m

m, m D 0; 1; 2; : : : . Then f

m

.t/  f

m1

.t/ D .1/

m

.2m  1/,

so f .t/ D

1

X

mD1

.1/

m

.2m  1/u.t  m/and F .s/ D

1

s

1

X

mD1

.1/

m

.2m  1/e

ms

. Substituting x D e

s

in the identities

1

X

mD1

.1/

m

x

m

D 

x

1 C x

and

1

X

mD1

.1/

m

mx

m

D 

x

.1 C x/

2

(jxj < 1) yields F .s/ D

1

s



e

s

1 Ce

s



2e

s

.1 C e

s

/

2



D

1

s

.1  e

s

/

.1 C e

s

/

2

.

8.5 CONSTANT COEEFFICIENT EQUATIONS WITH PIECE WISE CONTINUOUS FORCING

FUNCTIONS

8.5.2. y

00

C y D 3 C u.t  4/.2t  8/; y.0/ D 1; y

0

.0/ D 0. Since

L .u.t 4/.2t  8// D e

4s

L .2.t C 4/  8/ D e

4s

L.2t/ D

2e

4s

s

2

;

.s

2

C 1/Y.s/ D

3

s

C

2e

4s

s

2

C s:

144 Chapter 8

Laplace Transforms

Y.s/ D

3

s.s

2

C 1/

C

2e

4s

s

2

.s

2

C 1/

C

s

2

C 1

D 3



1

s



s

2

C 1



C 2e

4s



1

s

2



1

s

2

C 1



C

s

2

C 1

D

3

s



2s

s

2

C 1

C 2e

4s



1

s

2



1

s

2

C 1



:

Since

1

s

2



1

s

2

C 1

$ t  sin t ) e

4s



1

s

2



1

s

2

C 1



$ u.t  4/ .t  4  sin.t  4// ;

y D 3  2 cos t C 2u.t  4/ .t  4  sin.t  4//.

8.5.4. y

00

 y D e

2t

C u.t  2/.1  e

2t

/; y.0/ D 3; y

0

.0/ D 1. Since

L.u.t  2/.1  e

2t

// D e

2s

L.1  e

2.t C2/

/ D e

2s



1

s



e

4

s  2



;

.s

2

 1/Y.s/ D

1

s  2

C e

2s



1

s



e

4

s  2



C .1 C 3s/:

Therefore,

Y.s/ D

1

.s  1/.s C 1/.s 2/

C

3s  1

.s  1/.s C 1/

Ce

2s



1

s.s 1/.s C 1/



e

4

.s  1/.s C 1/.s  2/



:

1

.s  1/.s C 1/.s  2/

D 

1

2

1

s  1

C

1

6

1

s C 1

C

1

3

1

s  2

$ 

1

2

e

t

C

1

6

e

t

C

1

3

e

2t

I

e

2s

e

4

.s  1/.s C 1/.s  2/

$ u.t  2/





1

2

e

tC2

C

1

6

e

.t6/

C

1

3

e

2t



I

1

s.s  1/.s C 1/

D 

1

s

C

1

2

1

s  1

C

1

2

1

s C 1

$ 1 C

1

2

e

t

C

1

2

e

t

I

e

2s

s.s  1/.s C 1/

$ u.t  2/



1 C

1

2

e

t2

C

1

2

e

.t2/



I

3s  1

.s  1/.s C 1/

D

1

s  1

C

2

s C 1

$ e

t

C 2e

t

:

Therefore,

y D

1

2

e

t

C

13

6

e

t

C

1

3

e

2t

C u.t  2/



1 C

1

2

e

t2

C

1

2

e

.t2/

C

1

2

e

tC2



1

6

e

.t6/



1

3

e

2t



:

8.5.6. Note that jsin tj D sin t if 0  t <  , while jsin tj D sin t if   t < 2 . Rewrite the initial

value prob lem as

y

00

C 4y D sin t  2u.t  / sin t C u.t  2/ sin t; y.0/ D 3; y

0

.0/ D 1:

Section 8.5

Constant Coeefﬁcient Equations with Piecewise Continuous Forcing Functions

145

Since

L .u.t  / sin t/ D e

s

L.sin.t C // D e

s

L.sin t/

and

L .u.t 2/ sin t/ D e

2s

L.sin.t C 2// D e

2s

L.sin t/;

.s

2

C 4/Y.s/ D

1 C 2e

s

C e

2s

.s

2

C 1/

C 1  3s; so Y .s/ D

1 C 2e

s

C e

2s

.s

2

C 1/.s

2

C 4/

C

1  3s

s

2

C 4

:

1

.s

2

C 1/.s

2

C 4/

D



1

s

2

C 1



1

s

2

C 4



$

1

3

sin t 

1

6

sin 2tI

therefore

e

s

.s

2

C 1/.s

2

C 4/

$ u.t   /



1

3

sin.t  / 

1

6

sin 2.t   /



D u.t  /



1

3

sin t C

1

6

sin 2t



and

e

2s

.s

2

C 1/.s

2

C 4/

$ u.t  2/



1

3

sin.t  2/ 

1

6

sin 2.t  2/



D u.t  2 /



1

3

sin t 

1

6

sin 2t



I

therefore

y D

1

3

sin 2t 3 cos 2t C

1

3

sin t  2u.t   /



1

3

sin t C

1

6

sin 2t



C u.t  2/



1

3

sin t 

1

6

sin 2t



:

8.5.8. y

00

C 9y D cos t C u.t  3=2/.sin t  cos t/; y.0/ D 0; y

0

.0/ D 0. Si nce

L .u.t 3=2/.sin t  cos t// D e

3s=2

L .sin.t C 3=2/  cos.t C 3=2//

e

3s=2

L.cos t C sin t/;

.s

2

C9/Y .s/ D

1

s

2

C 1

e

3s=2

s C1

s

2

C 1

; so Y.s/ D

1

.s

2

C 1/.s

2

C 9/

e

3s=2

s C 1

.s

2

C 1/.s

2

C 9/

:

1

.s

2

C 1/.s

2

C 9/

D

1

8



1

s

2

C 1



1

s

2

C 9



$

1

8



sin t 

1

3

sin 3t



and

s

.s

2

C 1/.s

2

C 9/

D

1

8



s

2

C 1



s

2

C 9



$

1

8

.cos t  cos 3t/ :

s C 1

.s

2

C 1/.s

2

C 9/

D

s C 1

.s

2

C 1/.s

2

C 9/

D

s C 1

8



s C 1

s

2

C 1



s C 1

s

2

C 9



$

1

8



cos t C sin t  cos 3t 

1

3

sin 3t



; so

146 Chapter 8

Laplace Transforms

e

3s=2

s C 1

.s

2

C 1/.s

2

C9/

$

u.t  3=2/

8

.cos.t  3=2/ C sin.t  3=2/

cos 3.t  3=2/ 

1

3

sin 3.t  =2/



D

u.t  3=2/

8



sin t  cos t C sin 3t 

1

3

cos 3t



:

Therefore, y D

1

8

.cos t  cos 3t/ 

1

8

u.t  3=2/



sin t  cos t C sin 3t 

1

3

cos 3t



.

8.5.10. y

00

Cy D t  2u.t   /t; y.0/ D 0; y

0

.0/ D 0. Si nce

L .u.t  /t/ D e

s

L .t C / D e

s



1

s

2

C



s



;

.s

2

C 1/Y.s/ D

1

s

2

 2e

s



1

s

2

C



s



I

Y.s/ D

1

s

2

.s

2

C 1/

 2e

s



1

s

2

.s

2

C 1/

C



s.s

2

C 1/



D



1

s

2



1

s

2

C 1



 2e

s



1

s

2



1

s

2

C 1



 2e

s



1

s



s

2

C 1



:

Since

1

s

2



1

s

2

C 1

$ t  si n t ) e

s



1

s

2



1

s

2

C1



$ u.t   / .t    sin.t  // D u.t  /.t   C sin t /

and

1

s



s

2

C 1

$ 1  cos t ) e

s



1

s



s

2

C 1



$ u.t   / .1  cos.t  // D u.t   /.1 C cos t/;

y D t  sin t  2u.t   /.t C sin t C  cos t/.

8.5.12. y

00

Cy D t  3u.t  2/t; y.0/ D 1; y

0

.0/ D 2I

L.u.t  2/t/ D e

2s

L.t C 2/ D e

2s



1

s

2

C

2

s



I

.s

2

C 1/Y.s/ D

1  3e

2s

s

2



6e

2s

s

C 2 C sI

Y.s/ D

1  3e

2s

s

2

.s

2

C 1/



6e

2s

s.s

2

C1/

C

2 C s

s

2

C 1

I

1

s

2

.s

2

C1/

D

1

s

2



1

s

2

C1

$ t  sin tI

e

2s

s

2

.s

2

C 1/

$ u.t  2 /..t  2  sin.t  2 // D u.t  2/.t  2  sin t/I

Section 8.5

Constant Coeefﬁcient Equations with Piecewise Continuous Forcing Functions

147

1

s.s

2

C 1/

D

1

s



s

2

C 1

$ 1  cos tI

e

2s

s.s

2

C 1/

$ u.t  2/.1  cos.t  2// D u.t  2/.1 cos t/I

2 C s

s

2

C 1

$ 2 sin t C cos tI

y D t C sin t C cos t  u.t  2/.3t  3 sin t  6 cos t/.

8.5.14. y

00

 4y

0

C 3y D 1 C 2u.t  1/; y.0/ D 0; y

0

.0/ D 0;

.s

2

 4s C 3/Y.s/ D

1 C 2e

s

s

; Y.s/ D

1 C 2e

s

s.s  1/.s  3/

;

1

s.s 1/.s  3/

D

1

3s

C

1

6

1

s  3



1

2

1

s  1

$

1

3

C

1

6

e

3t



1

2

e

t

;

e

s

s.s 1/.s  3/

$ u.t  1/



1

3

C

1

6

e

3.t1/



1

2

e

t1



;

y D 

1

3



1

6

e

3t

C

1

2

e

t

C u.t  1/



2

3

C

1

3

e

3.t1/

 e

t1



.

8.5.16. y

00

C2y

0

C y D 4e

t

 4u.t  1/e

t

; y.0/ D 0; y

0

.0/ D 0. Since

L



4u.t  1/e

t



D e

s

L



4e

.tC1/



D

4e

sC1

s  1

;

.s

2

C 2s C 1/Y.s/ D

4

s  1



4e

sC1

s  1

; so

Y.s/ D

4

.s  1/.s C 1/

2



4e

sC1

.s  1/.s C 1/

2

:

1

.s  1/.s C 1/

2

D

A

s  1

C

B

s C 1

C

.s C1/

2

;

where

A.s C 1/

2

C B.s  1/.s C 1/ C C.s  1/ D 4:

A D 1 .set s D 1/I

C D 2 .set s D 1/I

A C B D 0 .equate coefﬁcients of s

2

/:

Solving this system yields A D 1, B D 1, C D 2. Therefore,

1

.s  1/.s C 1/

2

D

1

s  1



1

s C 1



2

.s C 1/

2

and

y D e

t

 e

t

 2te

t

 eu.t  1/



e

t1

 e

.t1/

 2.t  1/e

.t1/



D e

t

 e

t

 2te

t

 u.t  1/



e

t

 e

.t2/

 2.t  1/e

.t2/



:

8.5.18. y

00

 4y

0

C 4y D e

2t

 2u.t  2/e

2t

; y.0/ D 0; y

0

.0/ D 1. Since

L



u.t  2/e

2t



D e

2s

L



e

2t C4



D

e

2sC4

s  2

;

148 Chapter 8

Laplace Transforms

.s

2

 4s C 4/Y.s/ D

1

s  2



2e

2sC4

s  2

 1; so

Y.s/ D

1

.s  2/

3



2e

2sC4

.s  2/

3



1

.s  2/

2

:

1

.s  2/

3

$

t

2

e

2t

2

)

e

2sC4

.s  2/

3

$

e

4

2

u.t  2/e

2.t 2/

.t  2/

2

D u.t  2/

.t  2/

2

e

2t

2

I

therefore y D

t

2

e

2t

2

 te

2t

 u.t  2/.t  2/

2

e

2t

.

8.5.20. y

00

C2y

0

C 2y D 1 C u.t  2 /.t  1/  u.t  3 /.t C 1/; y.0/ D 2; y

0

.0/ D 1;

L.u.t  2/.t  1// D e

2s

L..t C 2  1// D e

2s



1

s

2

C

2  1

s



I

L.u.t  3/.t C 1// D e

3s

L..t C 3 C 1// D e

3s



1

s

2

C

3 C 1

s



I

.s

2

C 2s C 2/Y.s/ D

1

s

C e

2s



1

s

2

C

2  1

s



 e

3s



1

s

2

C

3 C 1

s



C .1 C 2s/ C 4:

Let G.s/ D

1

s.s

2

C 2s C 2/

, H.s/ D

1

s.s

2

C 2s C 2/

; then

Y.s/ D Y

1

.s/ C e

2s

Y

2

.s/  e

3s

Y

3

.s/; (A)

where

Y

1

.s/ D G.s/ C

2s C 3

s

2

C 2s C 2

; (B)

Y

2

.s/ D H.s/ C .2  1/G.s/; (C)

Y

3

.s/ D H.s/ C .3 C 1/G.s/: (D)

Let y

i

.t/ D L

1

.Y

i

.s//, .i D 1; 2; 3/. From (A),

y.t/ D y

1

.t/ C u.t  2/y

2

.t  2 /  u.t  3/y

3

.t  3/: (E)

Find L

1

.G.s//:

G.s/ D

A

s

C

B.s C 1/ CC

.s C 1/

2

C 1

where A..s C 1/

2

C 1/ C .B.s C 1/ C C /s D 1. Setting s D 0 yields A D 1=2; setting s D 1 yields

A  C D 1, so C D 1=2; since A C B D 0 (coefﬁcient of x

2

), B D 1=2. Therefore,

G.s/ D

1

2



1

s



.s C 1/ C 1

.s C 1/

2

C 1/



$

1

2



1

2

e

t

.cos t Csin t/: (F)

Find L

1

.H.s//:

H.s/ D

A

s

C

B

s C 2

C

C.s C 1/ C D

.s C 1/

2

C 1

Section 8.5

Constant Coeefﬁcient Equations with Piecewise Continuous Forcing Functions

149

where .As C B/..s C 1/

2

C 1/ C .C.s C 1/ C D/s

2

D 1.

2B D 1 .set s D 0/I

A C B C D D 1 .set s D 1/I

5A C 5B C 2C C D D 1 .set s D 1/I

A C B D 0 D 0 .equate coefﬁcients of s

3

/:

Solving this system yields A D 1=2, B D 1=2, C D 1=2, D D 0; therefore

H.s/ D 

1

2



1

s



1

s

2



s C 1

.s C 1/

2

C 1/



$ 

1

2

.1  t  e

t

cos t/: (G)

Since

2s C 3

s

2

C 2s C 2

D

2.s C 1/ C 1

.s C 1/

2

C 1

$ e

t

.2 cos t C sin t/;

(B) and (F)) imply that

y

1

.t/ D

1

2

e

t

.3 cos t C sin t/ C

1

2

: (H)

From (C), (F)), and (G),

y

2

.t/ D   1 C

t

2

C .  1/e

t

cos t 

2  1

2

e

t

sin t;

so

y

2

.t  2/ D 



e

.t2/



.  1/ cos t C

2  1

2

sin t



C 1 

t

2



: (I)

From (D), (F)), and (G),

y

3

.t/ D

1

2



e

t

.3 cos t C .3 C 1/ sin t C t C 3 /



;

so

y

3

.t  3/ D

1

2



e

.t3/

.3 cos t C .3 C 1/ sin t C t/



: (J)

Now (E), (20), (I), and (J)

y D

1

2

e

t

.3 cos t C sin t/ C

1

2

imply that

u.t  2 /



e

.t2/



.  1/ cos t C

2  1

2

sin t



C 1 

t

2





1

2

u.t  3 /



e

.t3/

.3 cos t C .3 C 1/ sin t/ C t



.

8.5.22. (a) f .t/ D

1

X

nD0

u.t  n /; F .s/ D

1

s

1

X

nD0

e

ns

; Y.s/ D

1

s.s

2

C 1/

1

X

nD0

e

ns

;

1

s.s

2

C 1/

D

1

s



s

2

C 1

$ 1  cos t;

e

ns

s.s

2

C 1/

$ u.t  n/.1  cos.t  n// D u.t  n/.1  .1/

n

cos t/;

y.t/ D

1

X

nD0

u.t n /.1 .1/

n

cos t/. If m  t < .mC1/, y.t/ D

m

X

nD0

.1.1/

n

cos t/. Therefore,

y.t/ D

(

2m C 1  cos t; 2m  t < .2m C1/ .m D 0; 1; : : : /

2m; .2m  1/  t < 2m .m D 1; 2; : : : /

.

150 Chapter 8

Laplace Transforms

(b) f .t/ D

1

X

nD0

u.t  2n/t ; F .s/ D

1

X

nD0

e

2ns

L.t C 2n s/ D

1

X

nD0

e

2ns



1

s

2

C

2n

s



; Y.s/ D

1

X

nD0

e

2ns

Y

n

.s/, where Y

n

.s/ D

1

s

2

.s

2

C 1/

C

2n

s.s

2

C 1/

D

1

s

2



1

s

2

C 1

C

2n

s



2n

s

2

C 1

$ y

n

.t/ D

t sin t C2n 2n cos t. Since cos.t 2n/ D cos t and sin.t 2n/ D sin t, e

2ns

Y

n

.s/ $ u.t 

2n/y

n

.t/ D u.t 2n/.t sin t 2n cos t/; theref ore y.t/ D

1

X

nD0

u.t 2n /.t sin t 2n cos t/.

If 2m  t < 2.m C 1/ , then

y.t/ D

m

X

nD0

.t  sin t  2n cos t/ D .m C 1/.t  sin t  m cos t/:

(c) f .t/ D 1C2

1

X

nD1

.1/

n

u.tn/; F .s/ D

1

s

1 C 2

1

X

nD1

.1/

n

e

ns

!

; Y.s/ D

1

s.s

2

C1/

1 C 2

1

X

nD1

.1/

n

e

ns

!

;

1

s.s

2

C 1/

D

1

s



s

2

C1

$ 1  cos t;

e

ns

s.s

2

C 1/

$ u.t  n/.1  cos.t  n // D u.t  n/.1 

.1/

n

cos t/; y.t/ D 1  cos t C 2

1

X

nD1

.1/

n

u.t  n/.1  .1/

n

cos t/. If m  t < .m C 1/,

y.t/ D 1  cos t C 2

m

X

nD1

.1/

n

.1  .1/

n

cos t/ D .1/

m

 .2m C 1/ cos t:

(d) f .t/ D

1

X

nD0

u.t  n/; F .s/ D

1

s

1

X

nD0

e

ns

; Y .s/ D

1

s.s

2

 1/

1

X

nD0

e

ns

;

1

s.s

2

 1/

D

1

2

1

s  1

C

1

2

1

s C 1



1

s

$

1

2

.e

t

Ce

t

2/;

e

ns

s.s

2

 1/

$

u.t  n/

2



e

t

C e

t

 2



; y.t/ D

1

2

1

X

nD0

u.tn/



e

tn

C e

.tn/

 2



.

If m  t < .m C1/,

y.t/ D

1

2

m

X

nD0



e

tn

C e

.tn/

 2



D

1

2

.e

tm

C e

t

/

m

X

nD0

e

n

 m  1

D

1  e

mC1

2.1  e/

.e

tm

C e

t

/  m  1:

(e) f .t/ D .sin tC2 cos t/

1

X

nD0

u.t2n/; F.s/ D

1 C 2s

s

2

C 1

1

X

nD0

e

2ns

; Y.s/ D

1 C 2s

.s

2

C 1/.s

2

C 2s C 2/

1

X

nD0

e

2ns

;

1 C 2s

.s

2

C 1/.s

2

C 2s C 2/

D

As C B

s

2

C 1

C

C.s C 1/ C D

.s C 1/

2

C 1

where

.As C B/..s C 1/

2

C 1/ C .C.s C 1/ C D/.s

2

C 1/ D 1 C 2s:

2B C C C D D 1 .set s D 0/I

A C B C 2D D 1 .set s D 1/I

5A C 5B C 4C C 2D D 3 .set s D 1/I

A C C D 0 .equate coefﬁcients of s

3

/:

Section 8.5

Constant Coeefﬁcient Equations with Piecewise Continuous Forcing Functions

151

Solving this system yields A D 0, B D 1, C D 0, D D 1. Therefore,

1 C2s

.s

2

C 1/.s

2

C 2s C 2/

D

1

s

2

C 1



1

.s C 1/

2

C 1

$



1  e

t



sin t:

Since sin.t  2n / D sin t,

e

2ns

1 C 2s

.s

2

C 1/.s

2

C 2s C 2/

$ u.t  2n/



1  e

.t2n/



sin t;

so

y.t/ D sin t

1

X

nD0

u.t  2n /



1  e

.t2n/



:

If 2m  t < 2.m C 1/ ,

y.t/ D sin t

m

X

nD0



1  e

.t2n/



D

m C 1 

1  e

2.mC1/

1  e

2

!

e

t

!

sin t:

(f) f .t/ D

1

X

nD0

u.t  n/; F .s/ D

1

s

1

X

nD0

e

ns

; Y.s/ D

1

s.s  1/.s  2/

;

1

s.s 1/.s  2/

D

1

2s



1

s  1

C

1

2

1

s  2

$

1

2



1  2e

t

C e

2t



I

e

ns

s.s 1/.s  2/

$

1

2

u.t  n/



1  2e

tn

C e

2.t n/



I

y.t/ D

1

2

1

X

nD0

u.t  n/



1  2e

tn

C e

2.t n/



:

If m  t < m C 1,

y.t/ D

m

X

nD0



1  2e

tn

C e

2.t n/



D

m C 1

2

 e

tm

m

X

nD0

e

n

C

1

2

e

2.t m/

m

X

nD0

e

2n

D

m C 1

2

 e

tm

1  e

mC1

1  e

C

1

2

e

2.t m/

1  e

2mC2

1  e

2

:

8.5.24. (a) The assumptions imply that y

00

.t/ D

f .t/  by

0

.t/  cy.t/

a

on .˛; t

0

/ and .t

0

; ˇ/, y

00

.t

0

C/ D

f .t

0

C/  by

0

.t

0

/  cy.t

0

/

a

, and y

00

.t

0

/ D

f .t

0

/  by

0

.t

0

/  cy.t

0

/

a

. This implies the conclusion.

(b) Since y

00

has a junp d iscontinouit y at t

0

, appl ying Exercise 8.4.23(c) to y

0

shows that y

0

is not

differentiable at t

0

. Therefore,y cannot satisfy (A) on .˛; ˇ/ if f has a jump discontinuity at some t

0

in

.˛; ˇ/.

8.5.26. If 0  t < t

0

, then y.t/ D ´

0

.t/. Therefore, y.0/ D ´

0

.0/ D k

0

and y

0

.0/ D ´

0

.0/ D k

1

, and

ay

00

C by

0

C cy D a´

00

0

Cb´

0

C c´

0

D f

0

.t/ D f .t/; 0 < t < t

0

:

152 Chapter 8

Laplace Transforms

Now suppo se that 1  m  n. For convenience, deﬁne t

nC1

D 1. If t

m

 t < t

mC1

, then

y.t/ D

P

m

kD0

´

m

.t/, so

ay

00

C by C cy D

m

X

kD0

.a´

00

k

Cb´

0

k

C c´

k

/ D f

0

C

m

X

kD1

.f

k

 f

k1

/ D f

m

D f; t

m

< t < t

mC1

:

Thus, y satisﬁes ay

00

C by

0

C cy D f on any open interval that does not contain any of the points t

1

,

t

2

,. . . , t

n

.

Since ´.t

m

/ D ´

0

.t

m

/ for m D 1; 2; : : : , y and y

0

are cont inuous on Œ0; 1/. Since y

00

.t/ D .by

0

.t/C

cy.t //=a if t ¤ t

m

(m D 1; 2; : : : ), y

00

has l imits from th e left at t

1

; : : : ; t

n

.

8.6 CONVOLUTION

8.6.2. ( a) sin at $

a

s

2

C a

2

and cos bt $

s

2

C b

2

, so H.s/ D

as

.s

2

C a

2

/.s

2

C b

2

/

.

(b) e

t

$

1

s  1

and sin at $

a

s

2

C a

2

, so H.s/ D

a

.s  1/.s

2

C a

2

/

.

(c) sinh at $

a

s

2

 a

2

and cosh at $

1

s

2

 a

2

, so H.s/ D

as

.s

2

 a

2

/

2

.

(d) t sin !t $

2!s

.s

2

C !

2

/

2

and t cos !t $

s

2

 !

2

.s

2

C !

2

/

2

, so H.s/ D

2!s.s

2

 !

2

/

.s

2

C !

2

/

4

.

(e) e

t

Z

t

0

sin ! cos !.t  / d  D

Z

t

0

.e



sin !/



e

.t/

cos !.t  /



d ; e

t

sin !t $

!

.s  1/

2

C !

2

and e

t

cos !t $

s  1

.s  1/

2

C !

2

, so H.s/ D

.s  1/!

..s  1/

2

C !

2

/

2

.

(f) e

t

Z

t

0



2

.t   /e



d  D

Z

t

0



2

e

2

.t   /e

.t/

d ; t

2

e

2t

$

2

.s  2/

3

and te

t

$

1

.s  1/

2

, so

H.s/ D

2

.s  2/

3

.s  1/

2

.

(g) e

t

Z

t

0

e



 cos !.t  / d  D

Z

t

0

e

2

e

.t/

cos !.t/ d ; te

2t

$

1

.s C 2/

2

and e

t

cos !t $

s C 1

.s C 1/

2

C !

2

, so H.s/ D

s C 1

.s C 2/

2

Œ.s C 1/

2

C !

2



.

(h) e

t

Z

t

0

e

2

sinh.t  / d  D

Z

t

0

e

3



e

.t/

sinh.t  /



d ; e

3t

$

1

s  3

and e

t

sinh t $

1

.s  1/

2

 1

,

so H.s/ D

1

.s  3/ ..s  1/

2

 1/

.

(i) t e

2t

$

1

.s  2/

2

and sin 2t $

2

s

2

C 4

, so H.s/ D

2

.s  2/

2

.s

2

C 4/

.

(j) t

3

$

6

s

4

and e

t

$

1

s  1

, so H.s/ D

6

s

4

.s  1/

.

(k) t

6

$

6Š

s

7

and e

t

sin 3t $

3

.s C 1/

2

C 9

, so H.s/ D

3  6Š

s

7

Œ.s C 1/

2

C 9

.

(l) t

2

$

2

s

3

and t

3

$

6

s

4

, so H.s/ D

12

s

7

.

(m) t

7

$

7Š

s

8

and e

t

sin 2t $

2

.s C1/

2

C 4

, so H.s/ D

2  7Š

s

8

Œ.s C 1/

2

C 4

.

(n) t

4

$

24

s

5

and sin 2t $

2

s

2

C 4

, so H.s/ D

48

s

5

.s

2

C 4/

.

Section 8.6

Convolution

153

8.6.4. ( a) Y.s/ D

1

s

2



Y.s/

s

2

; Y.s/



1 C

1

s

2



D

1

s

2

; Y.s/

s

2

C 1

s

2

D

1

s

2

; Y.s/ D

1

s

2

C 1

, so y D sin t.

(b) Y.s/ D

1

s

2

C 1



2sY.s/

s

2

C 1

; Y.s/



1 C

2s

s

2

C 1



D

1

s

2

C 1

; Y.s/

.s C 1/

2

s

2

C 1

D

1

s

2

C 1

; Y.s/ D

1

.s C 1/

2

, so y D te

t

.

(c) Y.s/ D

1

s

C

2sY.s/

s

2

C 1

; Y .s/



1 

2s

s

2

C 1



D

1

s

; Y.s/

.s  1/

2

s

2

C 1

D

1

s

; Y .s/ D

.s

2

C1/

s.s 1/

2

D

A

s

C

B

s

2

C

.s  1/

2

, where A.s 1/

2

CBs.s 1/ CC s D s

2

C1. Setting s D 0 and s D 1 shows that A D 1

and C D 2; equating coefﬁcients of s

2

yields A C B D 1, so B D 0. Therefore, Y.s/ D

1

s

C

1

.s  1/

2

,

so y D 1 C 2te

t

.

(d) Y.s/ D

1

s

2

C

Y.s/

s C 1

; Y.s/



1 

1

s C1



D

1

s

2

; Y.s/



s

s C 1



D

1

s

2

; Y.s/ D

s C 1

s

3

D

1

s

2

C

1

s

3

,

so y D t C

t

2

.

(e) sY.s/  4 D

1

s

2

C

sY.s/

s

2

C 1

; Y.s/



s 

s

2

C 1



D 4 C

1

s

2

; Y.s/

s

3

s

2

C 1

D

4s

2

C 1

s

2

; Y.s/ D

.4s

2

C 1/.s

2

C 1/

s

5

D

4s

4

C 5s

2

C 1

s

5

D

4

s

C

5

s

3

C

1

s

5

, so y D 4 C

5

2

t

2

C

1

24

t

4

.

(f) Y.s/ D

s  1

s

2

C 1

C

Y.s/

s

2

C 1

; Y .s/



1 

1

s

2

C 1



D

s  1

s

2

C 1

; Y .s/

s

2

s

2

C 1

D

s  1

s

2

C 1

; Y .s/ D

s  1

s

2

D

1

s



1

s

2

, so y D 1  t.

8.6.6. Substi tuting x D t  yields

Z

t

0

f .t /g./ d  D 

Z

0

t

f .x/g.t x/.dx/ D

Z

t

0

f .x/g.t 

x/ dx D

Z

t

0

f ./g.t  / d .

8.6.8. p.s/Y.s/ D F .s/ C a.k

1

C k

0

s/ C bk

0

, so (A) Y .s/ D

F .s/

p.s/

C

k

0

.as C b/ Ck

1

a

p.s/

. Since

p.s/ D a.s  r

1

/.s  r

2

/ and therefore b D a.r

1

C r

2

/, (A) can be rewritten as

Y.s/ D

F .s/

a.s  r

1

/.s  r

2

/

C

k

0

.s  r

1

 r

2

/

.s  r

1

/.s  r

2

/

C

k

1

.s  r

1

/.s  r

2

/

:

1

.s  r

1

/.s  r

2

/

D

1

r

2

 r

1



1

s  r

2



1

s  r

1



$

e

r

2

t

 e

r

1

t

r

2

 r

1

;

so the convolution theorem implies that

F .s/

a.s  r

1

/.s  r

2

/

$

1

a

Z

t

0

e

r

2



 e

r

1



r

2

 r

1

f .t  / d :

s  r

1

 r

2

.s  r

1

/.s  r

2

/

D

r

2

r

2

 r

1

s  r

1



r

1

r

2

 r

1

s  r

2

$

r

2

e

r

1

t

 r

1

e

r

2

t

r

2

 r

1

:

Therefore,

y.t/ D k

0

r

2

e

r

1

t

 r

1

e

r

2

t

r

2

 r

1

C k

1

e

r

2

t

 e

r

1

t

r

2

 r

1

C

1

a

Z

t

0

e

r

2



 e

r

1



r

2

 r

1

f .t  / d :

154 Chapter 8

Laplace Transforms

8.6.10. p.s/Y.s/ D F .s/ C a.k

1

C k

0

s/ C bk

0

, so (A) Y .s/ D

F .s/

p.s/

C

k

0

.as C b/ C k

1

a

p.s/

. Since

p.s/ D a.s  /

2

C !

2

and therefore b D 2a, (A) can be rew ritten as

Y.s/ D

F .s/

aŒ.s  /

2

C !

2

 C

k

0

.s  2/

.s  /

2

C !

2

C

k

1

.s  /

2

C !

2

:

1

.s  /

2

C !

2

$

1

!

e

t

sin !t, so the convolution theorem impl ies that

F .s/

aŒ.s  /

2

C !

2



$

1

a!

Z

t

0

e

t

f .t  / sin ! d :

s  2

.s  /

2

C !

2

D

.s  /  

.s  /

2

C !

2

$ e

t



cos !t 



!

sin !t



:

Therefore,

y.t/ D e

t



k

0



cos !t 



!

sin !t



C

k

1

!

sin !t



C

1

a!

Z

t

0

e

t

f .t  / sin ! d :

8.6.12. (a)

ay

00

C by

0

C cy D f

0

.t/ Cu.t  t

1

/.f

1

.t/  f

0

.t//; y.0/ D 0; y

0

.0/ D 0I

p.s/Y.s/ D F

0

.s/ C L.u.t  t

1

/.f

1

.t/  f

0

.t/// D F

0

.s/ C e

st

1

L.g/I

Y.s/ D

F

0

.s/ C e

st

1

G.s/

p.s/

: .B/

(b) Since F

0

.s/ $ f

0

.t/, G.s/ $ g.t/, and

1

p.s/

$ w.t/, the convolution theorem implies that

F

0

.s/

p.s/

$

Z

t

0

w.t  /f

0

./ d  and

G.s/

p.s/

$

Z

t

0

w.t  /g./ d :

Now Theorem 8.4.2 implies that

e

st

1

G.s/

p.s/

$ u.t  t

1

/

Z

t

0

w.t  t

1

 /g./ d , and (B) implies that

y.t/ D

Z

t

0

w.t  /f

0

./ d  C u.t  t

1

/

Z

tt

1

0

w.t  t

1

 /g./ d :

(c) Let ´

0

.t/ D

R

t

0

w.t  /f

0

./ d  and ´

1

.t/ D

R

t

0

w.t  /g./ d . Then y.t/ D ´

0

.t/ C u.t 

t

1

/´

1

.t  t

1

/. Using Leibniz’s rule as in the solution of Exercise 8.6.11(b) shows that

´

0

.t/ D

Z

t

0

w

0

.t   /f

0

./ d ; ´

0

1

.t/ D

Z

t

0

w

0

.t   /g./ d ; t > 0;

´

00

0

.t/ D

f

0

.t/

a

C

Z

t

0

w

00

.t  /f

0

./ d ; ´

00

1

.t/ D

g.t/

a

C

Z

t

0

w

00

.t   /g./ d ; t > 0;

if t > 0, and that

a´

00

0

C b´

0

C c´

0

D f

0

.t/ and a´

00

1

C b´

0

1

C c´

1

D f

1

.t C t

1

/  f

0

.t C t

1

/; t > 0:

Section 8.7

Constant Coefﬁcient Equations with Impulses

155

This implies the stated conclusion for y

0

and y

00

on .0; t/ and .t; 1/, and that ay

00

C by

0

C cy D f .t/

on these intervals.

(d) Since the functions ´

0

.t/ and h.t/ D u.t t

1

/´

1

.t t

1

/ are both continuous on Œ0; 1/ and h.t/ D 0

if 0  t  t

1

, y is contin uous on Œ0; 1/. From (c), y

0

is continuous on Œ0; t

1

/ and .t

1

; 1/, so we need

only show that y

0

is continuous at t

1

. For th is it sufﬁces to show that h

0

.t

1

/ D 0. Since h.t

1

/ D 0 if

t  t

1

, (B) lim

t!t

1



h.t/  h.t

1

/

t  t

1

D 0. If t > t

1

, then h.t/ D

Z

tt

1

0

w.t  t

1

/g./ d . Since h.t

1

/ D 0,

ˇ

h.t/  h.t

1

/

t  t

1

ˇ



Z

tt

1

0

jw.t  t

1

 /g./jd: .B/

Since g is continuous from the right at 0, we can choose constants T > 0 and M > 0 so that jg./j < M

if 0    T . Then (B) implies that

ˇ

h.t/  h.t

1

/

t  t

1

ˇ

 M

Z

tt

1

0

jw.t  t

1

 /jd ; t

1

< t < t

1

C T: .C/

Now suppose  > 0. Since w.0/ D 0, we can choose T

1

such that 0 < T

1

< T and jw.x/j < =M if

0  x < T

1

. If t

1

< t < t

1

C T

1

and 0    t  t

1

, then 0  t  t

1

  < T

1

, so (C) impli es that

ˇ

h.t/  h.t

1

/

t  t

1

ˇ

< ; t

1

< t < t

1

C T:

Therefore, li m

t!t

1

C

h.t/  h.t

1

/

t  t

1

D 0. This and (B) imply that h

0

.t

1

/ D 0.

8.7 CONSTANT COEFFICIENT EQUATIONS WITH IMPULSES

8.7.2. .s

2

Cs 2/

O

Y .s/ D 

10

s C 1

C.9 C7s/ C7;

O

Y .s/ D

10 C .s C 1/.7s  2/

.s  1/.s C 2/.s C 1/

D

2

s C 2

C

5

s C 1

;

Oy D 2e

2t

C 5e

t

;

1

p.s/

D

1

.s C 2/.s  1/

D

1

3



1

s  1



1

s C 2



; w D L

1



1

p.s/



D

e

t

 e

2t

3

;

y D 2e

2t

C 5e

t

C

5

3

u.t  1/



e

.t1/

 e

2.t 1/



.

8.7.4. .s

2

C 1/

O

Y .s/ D

3

s

2

C9

 1 C s;

O

Y .s/ D

3

.s

2

C 1/.s

2

C 9/

C

s  1

s

2

C 1

D

3

8



1

s

2

C 1



1

s

2

C9



C

s  1

s

2

C 1

D

1

8



8s  5

s

2

C 1



3

s

2

C 9



;

Oy D

1

8

.8 cos t 5 sin t sin 3t/;

1

p.s/

D

1

s

2

C 1

; w D L

1



1

p.s/



D sin t; y D

1

8

.8 cos t 5 sin t 

sin 3t/  2u.t  =2/ cos t.

8.7.6. .s

2

1/

O

Y .s/ D

8

s

C1  s;

O

Y .s/ D

8 C s.1  s/

s.s 1/.s C 1/

D

4

s  1

C

3

s C 1



8

s

; Oy D 4e

t

C3e

t

8;

1

p.s/

D

1

.s  1/.s C 1/

D

1

2

1

s  1



1

s C 1

; w D L

1



1

p.s/



D

e

t

C e

t

2

D sinh t; y D 4e

t

C

3e

t

 8 C 2u.t  2/ sinh.t  2/;

8.7.8. .s

2

C4/

O

Y .s/ D

8

s  2

C8s; (A)

O

Y .s/ D

8

.s  2/.s

2

C 4/

C

8s

s

2

C 4

;

8

.s  2/.s

2

C 4/

D

A

s  2

C

Bs C C

s

2

C 4

where A.s

2

C 4/ C .Bs C C /.s  2/ D 8. Setting s D 2 yields A D 1; setting s D 0

156 Chapter 8

Laplace Transforms

yields 4A  2C D 8, so C D 2; A C B D 0 (coefﬁcient of x

2

), so B D A D 1; therefore

8

.s  2/.s

2

C4/

D

1

s  2



s C 2

s

2

C 4

, so (A) impli es that Oy D e

2t

C7 cos 2t sin 2t;

1

p.s/

D

1

s

2

C 4

; w D

L

1



1

p.s/



D

1

2

sin 2t. Since sin.2t / D sin 2t, y D e

2t

C7 cos 2t sin 2t 

1

2

u.t =2/ sin 2t.

8.7.10. .s

2

C2s C1/

O

Y .s/ D

1

s  1

C.2s/2;

O

Y .s/ D

1  s.s  1/

.s  1/.s C 1/

2

D

A

s  1

C

B

s C 1

C

.s C 1/

2

where A.s C1/

2

C.B.s C1/CC /.s 1/ D 1 s.s 1/. Setting s D 1 yields A D 1=4; setting s D 1

yields C D 1=2; since A C B D 1 (coefﬁcient of s

2

), B D 1  A D 5=4. Therefore,

O

Y .s/ D

1

4

1

s  1



5

4

1

s C 1

C

1

2

1

.s C 1/

2

; Oy D

1

4

e

t

C

1

4

e

t

.2t 5/;

1

p.s/

D

1

.s C 1/

2

; w D L

1



1

p.s/



D te

t

;

y D

1

4

e

t

C

1

4

e

t

.2t  5/ C 2u.t  2/.t  2/e

.t2/

.

8.7.12. .s

2

C 2s C 2/

O

Y .s/ D .2  s/  2; Y.s/ D

.s C 1/ C 1

.s C 1/

2

C 1

; Oy D e

t

.sin t  cos t/;

1

p.s/

D

1

.s C 1/

2

C 1

; w D L

1



1

p.s/



D e

t

sin t. Since sin.t  / D sin t and si n.t  2 / D sin t,

y D e

t

.sin t  cos t/  e

.t/

u.t  / sin t  3u.t  2/e

.t2/

sin t.

8.7.14. .2s

2

3s2/

O

Y .s/ D

1

s

C2.2s/C3;

O

Y .s/ D

1 C s.7  2s/

2s.s C 1=2/.s  2/

D

7

10

1

s  2



6

5

1

s C 1=2



1

2s

;

Oy D

7

10

e

2t



6

5

e

t=2



1

2

;

1

p.s/

D

1

2.s C 1=2/.s  2/

D

1

5



1

s  2



1

s C 1=2



; w D L

1



1

p.s/



D

1

5

.e

2t

 e

t=2

/; y D

7

10

e

2t



6

5

e

t=2



1

2

C

1

5

u.t  2/



e

2.t 2/

 e

.t2/=2



;

8.7.16. .s

2

C 1/

O

Y .s/ D

s

2

C 4

 1;

O

Y .s/ D

s

.s

2

C 1/.s

2

C 4/



1

s

2

C 1

D

1

3



s

2

C1



s

2

C 4





1

s

2

C 1

; Oy D

1

3

.cos t  cos 2t  3 si n t/;

1

p.s/

D

1

s

2

C 1

; w D L

1



1

p.s/



D sin t. Since sin.t 

=2/ D cos t and sin .t   / D sin t,

y D

1

3

.cos t  cos 2t  3 sin t/  2u.t  =2/ cos t C 3u.t  / sin t:

8.7.18. .s

2

C 2s C 1/

O

Y .s/ D

1

s  1

 1; (A)

O

Y .s/ D

1

.s  1/.s C 1/

2



1

.s C 1/

2

;

1

.s  1/.s C 1/

2

D

A

s  1

C

B

s C 1

C

.s C 1/

2

where A.s C 1/

2

C .B.s C 1/ C C /.s  1/ D 1. Setting s D 1 yields A D 1=4; setting s D 1 yields

C D 1=2; since A C B D 0 ( coefﬁcient of s

2

), B D A D 1=4. Therefore,

1

.s  1/.s C 1/

2

D

1

4

1

s  1



1

4

1

s C 1



1

2

1

.s C 1/

2

:

This and (A) imply that

O

Y .s/ D

1

4

1

s  1



1

4

1

s C 1



3

2

1

.s C 1/

2

I

Section 8.7

Constant Coefﬁcient Equations with Impulses

157

Oy D

1

4



e

t

 e

t

.1 C 6t/



;

1

p.s/

D

1

.s C 1/

2

; w D L

1



1

p.s/



D te

t

;

y D

1

4



e

t

 e

t

.1 C 6t/



 u.t  1/.t  1/e

.t1/

C 2u.t  2/.t  2/e

.t2/

.

8.7.20. y

00

C4y D 1 2u.t =2/ Cı.t / 3ı.t 3=2/; y.0/ D 1; y

0

.0/ D 1. .s

2

C4/

O

Y .s/ D

1  2e

s=2

s

C s  1;

O

Y .s/ D

1  2e

s=2

s.s

2

C4/

C

s  1

s

2

C 4

. Sin ce

1

s.s

2

C 4/

D

1

4



1

s



s

2

C 4



,

O

Y .s/ D

1

4s

C

3

4

s

2

C 4



1

s

2

C 4

2e

s=2



1

s



s

2

C 4



. Oy D

3

4

cos 2t 

1

2

sin 2t C

1

4

C

1

4

u.t=2/.1Ccos 2t/.

w D L

1



1

p.s/



D

1

2

sin 2t. Since sin 2.t  / D sin 2t and sin 2.t  3=2/ D sin 2t,

y D

3

4

cos 2t 

1

2

sin 2t C

1

4

C

1

4

u.t  =2/.1 C cos 2t/ C

1

2

u.t   / sin 2t C

3

2

u.t 3=2/ sin 2t.

8.7.26. w.t/ D e

t

sin t; f

h

.t/ D

u.t  t

0

/  u.t  t

0

 h/

h

; .s

2

C2s C2/Y

h

.s/ D

1

h

e

st

0

 e

s.t

0

Ch/

s

;

Y

h

.s/ D

1

h

e

st

0

 e

s.t

0

Ch/

s.s

2

C 2s C 2/

;

1

s.s

2

C 2s C 2/

D 

.s C 1/ C 1

2 ..s C 1/

2

C 1/

C

1

2s

$

1

2



1  e

t

.cos t C sin t/



;

y

h

.t/ D

8

ˆ

<

ˆ

:

0; 0  t < t

0

;

1

2h

h

1  e

.tt

0

/

.cos.t  t

0

/ C sin.t  t

0

//

i

; t

0

 t < t

0

C h;

e

.tt

0

/

2h

h

e

h

.cos.t  t

0

 h/ C sin.t  t

0

 h//  cos.t  t

0

/  sin.t  t

0

/

i

; t  t

0

C h:

8.7.28. w.t/ D e

t

e

2t

; f

h

.t/ D

u.t  t

0

/  u.t  t

0

 h/

h

; .s

2

C3sC2/Y

h

.s/ D

1

h

e

st

0

 e

s.t

0

Ch/

s

;

Y

h

.s/ D

1

h

e

st

0

 e

s.t

0

Ch/

s.s C 1/.s C 2/

;

1

s.s C 1/.s C 2/

D

1

2.s C 2/



1

s C 1

C

1

2s

$

e

2t

2

 e

t

C

1

2

D

.e

t

 1/

2

;

y

h

.t/ D

8

ˆ

<

ˆ

:

0; 0  t < t

0

;

.e

.tt

0

/

 1/

2

2h

; t

0

 t < t

0

C h;

.e

.tt

0

/

 1/

2

 .e

.tt

0

h/

 1/

2

2h

; t  t

0

C h:

8.7.30. (a) .s

2

 1/

O

Y .s/ D 1, so Oy D w D L

1



1

s

2

 1



D

1

2



e

t

 e

t



; y D Oy C

1

X

kD0

u.t 

k/w.t  k/ D

1

2

1

X

kD0

u.t  k/



e

tk

 e

tk



. If m  t < m C 1, then y D

1

2

m

X

kD0



e

tk

 e

tk



D

1

2

.e

tm

 e

t

/

m

X

kD0

e

k

e

mC1

 1

2.e  1/

.e

tm

 e

t

/.

(b) .s

2

C 1/

O

Y .s/ D 1, so Oy D w D L

1



1

s

2

C 1



D sin t; y D Oy C

1

X

kD0

u.t  2k/w.t  2k/ D

158 Chapter 8

Laplace Transforms

sin t

1

X

kD0

u.t  2k/. If 2m  t < 2.m C1/, then y D .m C1/ sin t.

(c) .s

2

 3s C 2/

O

Y .s/ D 1, so Oy D w D L

1



1

.s  1/.s  2/



D .e

2t

 e

t

/; y D Oy C

1

X

kD0

u.t 

k/w.t  k/ D

1

X

kD0

u.t  k/



e

2.t k/

 e

tk



. If m  t < m C 1, then y D

m

X

kD0



e

2.t k/

 e

tk



D

e

2.t m/

m

X

kD0

e

2k

 e

tm

m

X

kD0

e

k

D e

2.t m/

e

2mC2

 1

e

2

 1

 e

.tm/

e

mC1

 1

e 1

.

(d) w D L

1



1

s

2

C 1



D sin t; y D

1

X

kD1

u.t  k/w.t  k / D sin t

1

X

kD1

.1/

k

u.t  k/, so

y D

(

0; 2m  t < .2m C 1/;

sin t; .2m C 1/  t < .2m C 2/;

.m D 0; 1; : : : /.

CHAPTER 9

Linear Higher Order Equations

9.1 INTRODUCTION TO LINEAR HIGHER ORDE R EQUATIONS

9.1.2. From Example 9.1.1, y D c

1

x

2

Cc

2

x

3

C

c

3

x

y

0

D 2c

1

xC3c

2

x

2



c

3

x

2

, and y

00

D 2c

1

C6c

2

xC

2c

3

x

3

,

where

c

1

 c

2

 c

3

D 4

2c

1

C 3c

2

 c

3

D 14

2c

1

 6c

2

 2c

3

D 20;

so c

1

D 2, c

2

D 3, c

3

D 1, and y D 2x

2

 3x

3

C

1

x

.

9.1.4. The general solu tion of y

.n/

D 0 can be written as y.x/ D

n1

X

mD0

c

m

.x  x

0

/

m

. Since y

.j /

.x/ D

n1

X

mDj

m.m1/ .m j C1/c

m

.xx

0

/

mj

, y

.j /

.x

0

/ D j Šc

j

. Therefore, y

i

D

.x  x

0

/

i1

.i  1/Š

; 1  i  n.

9.1.6. We omi t the veriﬁcation that the given functions are solutions of the given equations.

(a) The equati on is normal on .1; 1/. W.x/ D

ˇ

e

x

e

x

xe

x

e

x

e

x

e

x

.1  x/

e

x

e

x

e

x

.x  2/

ˇ

; W .0/ D

ˇ

1 1 0

1 1 1

1 1 2

ˇ

D

4. Apply Theorem 9.1.4.

(b) The equation is normal on .1; 1/.

W.x/ D

ˇ

e

x

e

x

cos 2x e

x

sin 2x

e

x

e

x

.cos 2x  2 sin 2x/ e

x

.2 cos 2x C sin 2x/

e

x

e

x

.3 cos 2x C 4 sin 2x/ e

x

.4 cos 2x  3 sin 2x/

ˇ

;

W.0/ D

ˇ

1 1 0

1 1 2

1 3 4

ˇ

8. Apply Theorem 9.1.4.

(c) The equation is normal on .1; 0/ and .0; 1/.

W.x/ D

ˇ

e

x

e

x

x

e

x

e

x

1

e

x

e

x

0

ˇ

D 2x. Apply Theorem 9.1.4.

(d) The equation is normal on .1; 0/ and .0; 1/.

W.x/ D

ˇ

e

x

=x e

x

=x 1

e

x

.1=x 1=x

2

/ e

x

.x C 1/=x

2

0

e

x

.1=x 2=x

2

C 2=x

3

/ e

x

.x

2

C 2x C 2/=x

3

0

ˇ

D 2=x

2

. Apply Theorem 9.1.4.

159

160 Chapter 9

Linear Higher Order Equations

(e) The equation is nor mal on .1; 1/. W .x/ D

ˇ

x x

2

e

x

1 2x e

x

0 2 e

x

ˇ

; W .0/ D

ˇ

0 0 1

1 0 1

0 2 1

ˇ

D 2; Apply

Theorem 9.1.4.

(f) The equation is normal on .1; 1=2/ and .1=2; 1/.

W.x/ D

ˇ

x e

x

e

x

e

2x

1 e

x

e

x

2e

2x

0 e

x

e

x

4e

.

2x/

0 e

x

e

x

8e

2x

ˇ

D e

2x

.12x 6/. Apply Theorem 9.1.4.

(g) The equation is normal on .1; 0/ and .0; 1/.

W.x/ D

ˇ

1 x

2

e

2x

e

2x

0 2x 2e

2x

2e

2x

0 2 4e

2x

4e

2x

0 0 8e

2x

8e

2x

ˇ

D 128x. Apply Theorem 9.1.4.

9.1.8. From Abel’s formula, (A) W .x/ D W.=2/ exp





Z

x

=4

tan t dt



;

Z

x

=4

tan t dt D ln cos t

ˇ

x

=4

D

ln.

p

2 cos x/; t herefore (A) i mplies that W.x/ D

p

2K cos x.

9.1.10. (a) W .x/ D

ˇ

1 e

x

e

x

0 e

x

e

x

0 e

x

e

x

ˇ

D .e

x

/.e

x

/

ˇ

1 1 1

0 1 1

0 1 1

ˇ

D 2.

(b) W .x/ D

ˇ

e

x

e

x

sin x e

x

cos x

e

x

e

x

.cos x C si n x/ e

x

.cos x  sin x/

e

x

2e

x

cos x 2e

x

sin x

ˇ

D

D e

3x

ˇ

1 sin x cos x

1 cos x C sin x cos x  sin x

1 2 co s x 2 sin x

ˇ

D e

3x

ˇ

1 sin x cos x

0 cos x sin x

1 2 cos x  sin x 2 sin x  cos x

ˇ

D e

3x

ˇ

1 sin x cos x

0 cos x sin x

0 sin x cos x

ˇ

D e

3x

(c) W.x/ D

ˇ

2 x C 1 x

2

C 2

0 1 2x

0 0 2

ˇ

D 4.

(d) W.x/ D

ˇ

x x ln jxj 1=x

1 ln jxj C 1 1=x

2

0 1=x 2=x

3

ˇ

D

ˇ

1 ln jxj 1=x

2

1 ln jxj C 1 1=x

2

0 1 2=x

2

ˇ

D

1

x

2

ˇ

1 ln jxj 1

1 ln jxj C1 1

0 1 2

ˇ

D

1

x

2

ˇ

1 ln jxj 1

0 1 2

0 1 2

ˇ

D

1

x

2

ˇ

1 ln jxj 1

0 1 2

0 0 4

ˇ

D 4=x

2

:

Section 9.1

Intr oduction to Linear Hi gher Order Equations

161

(e) W.x/ D

2

6

4

1 x x

2

=2 x

3

=3  x

n

=nŠ

0 1 x x

2

=2  x

n1

=.n  1/Š

0 0 1 x  x

n2

=.n  2/Š

0 0 0 1  x

n3

=.n  3/Š

:

0 0 0 0  1

3

7

5

D 1.

(f) W .x/ D

ˇ

e

x

e

x

x

e

x

e

x

1

e

x

e

x

0

ˇ

D

ˇ

1 1 x

1 1 1

1 1 0

ˇ

D

ˇ

1 1 x

0 2 1  x

0 0 x

ˇ

D 2x.

(g) W .x/ D

ˇ

e

x

=x e

x

=x 1

e

x

=x  e

x

=x

2

e

x

=x  e

x

=x

2

0

e

x

=x  2e

x

=x

2

C 2e

x

=x

3

e

x

=x C 2e

x

=x

2

C 2e

x

=x

3

0

ˇ

D

ˇ

1=x 1=x 1

1=x  1=x

2

1=x  1=x

2

0

1=x  2=x

2

C 2=x

3

1=x C 2=x

2

C 2=x

3

0

ˇ

D

ˇ

1=x  1=x

2

1=x  1=x

2

1=x  2=x

2

C 2=x

3

1=x C 2=x

2

C 2=x

3

ˇ

D

ˇ

1=x  1=x

2

2=x

1=x  2=x

2

C 2=x

3

4=x

2

ˇ

D 2=x

2

:

(h) W.x/ D

ˇ

x x

2

e

x

1 2x e

x

0 2 e

x

ˇ

D e

x

ˇ

x x

2

1

1 2x 1

0 2 1

ˇ

D e

x



x



2x 1

2 1







x

2

1

2 1



D e

x

.x

2

 2x C 2/.

(i) W .x/ D

ˇ

x x

3

1=x 1=x

2

1 3x

2

1=x

2

2=x

3

0 6x 2=x

3

6=x

4

0 6 6=x

4

24=x

5

ˇ

D

ˇ

0 2x

3

2=x 3=x

2

1 3x

2

1=x

2

2=x

3

0 6x 2=x

3

6=x

4

0 6 6=x

4

24=x

5

ˇ

D 

ˇ

2x

3

2=x 3=x

2

6x 2=x

3

6=x

4

6 6=x

4

24=x

5

ˇ

D x

4

ˇ

2 2=x

4

3=x

5

6 2=x

4

6=x

5

6 6=x

4

24=x

5

ˇ

D x

4

ˇ

2 2=x

4

3=x

5

0 8=x

4

15=x

5

0 0 15=x

5

ˇ

D 240=x

5

:

162 Chapter 9

Linear Higher Order Equations

(j) W.x/ D

ˇ

e

x

e

x

x e

2x

e

x

e

x

1 2e

2x

e

x

e

x

0 4e

2x

e

x

e

x

0 8e

2x

ˇ

D e

2x

ˇ

1 1 x 1

1 1 1 2

1 1 0 4

1 1 0 8

ˇ

D e

2x

ˇ

1  x 1 C x 0 1  2x

1 1 1 2

1 1 0 4

1 1 0 8

ˇ

D e

2x

ˇ

1  x 1 C x 1  2x

1 1 4

1 1 8

ˇ

D e

2x

ˇ

2 1 C x 1  2x

2 1 4

0 1 8

ˇ

D e

2x

ˇ

2 1 C x 1  2x

0 x 3 C 2x

0 1 8

ˇ

D 6e

2x

.2x  1/:

(k) W .x/ D

ˇ

e

2x

e

2x

1 x

2

2e

2x

2e

2x

0 2x

4e

2x

4e

2x

0 2

8e

2x

8e

2x

0 0

ˇ

D

ˇ

1 1 1 x

2

2 2 0 2x

4 4 0 2

8 8 0 0

ˇ

D

ˇ

2 2 2x

4 4 2

8 8 0

ˇ

D

ˇ

0 2 2x

8 4 2

0 8 0

ˇ

D 128x:

9.1.12. Let y be an arbitrary solution of Ly D 0 on .a; b/. Since f´

1

; : : : ; ´

n

g is a fundamental set of

solutions of Ly D 0 on .a; b/, t here are constants c

1

, c

2

,. . . , c

n

such that y D

n

X

iD1

c

i

y

i

. Therefore,

y D

n

X

iD1

c

i

n

X

j D1

a

ij

y

j

D

n

X

j D1

C

j

y

j

, with C

j

D

n

X

iD1

a

ij

c

i

. H ence fy

1

; : : : ; y

n

g is a fu ndamental set of

solutions of Ly D 0 on .a; b/.

9.1.14. Let y be a given sol ution of Ly D 0 and ´ D

n

X

j D1

y

.j 1/

.x

0

/y

j

Then ´

.r/

.x

0

/ D y

.r/

.x

0

/,

r D 0; : : : ; n  1. Since the solution of every initial value problem is unique (Theorem 9.1.1), ´ D y.

9.1.16. If fy

1

; y

2

; : : : ; y

n

g is linearly dependent on .a; b/ there are constants c

1

; : : : ; c

n

, not all zeros,

such that c

1

y

1

C c

2

y

2

C  C c

n

y

n

. Let k be the smallest integer such that c

k

¤ 0. If k D 1, then

y

1

D

1

c

1

.c

2

y

2

CCc

n

y

n

/; if 1 < k < n, then y

k

D 0y

1

CC0y

k1

C

1

c

k

.c

kC1

y

kC1

CCc

n

y

n

/;

if k D n, then y

n

D 0, so y

n

D 0  y

1

C 0  y

2

C C 0  y

n

.

9.1.18. Since F D

P

˙f

1i

1

f

2i

2

; : : : ; f

ni

n

,

F

0

D

X

˙f

0

1i

1

f

2i

2

; : : : ; f

ni

n

C

X

˙f

1i

1

f

0

2i

2

; : : : ; f

ni

n

C C

X

˙f

1i

1

f

2i

2

; : : : ; f

0

ni

n

D F

1

C F

2

C C F

n

:

Section 9.1

Intr oduction to Linear Hi gher Order Equations

163

9.1.20. Since y

.n/

j

D 

n

X

kD1

.P

k

=P

0

/y

.nk/

j

, Exercise 9.1.19 implies that

W

0

D 

ˇ

y

1

y

2

 y

n

y

0

1

y

0

2

 y

0

n

:

y

.n2/

1

y

.n2/

2

 y

.n2/

n

P

n

kD1

.P

k

=P

0

/y

.nk/

1

P

n

kD1

.P

k

=P

0

/y

.nk/

2



P

n

kD1

.P

k

=P

0

/y

.nk/

n

ˇ

;

so Exercise 9.1.17 implies that

W

0

D 

n

X

kD1

P

k

P

0

ˇ

y

1

y

2

 y

n

y

0

1

y

0

2

 y

0

n

:

y

.n2/

1

y

.n2/

2

 y

.n2/

n

y

.nk/

1

y

.nk/

2

 y

.nk/

n

ˇ

:

However, the determinants on the right each have two i dentical rows if k D 2; : : : ; n. Therefore,W

0

D



P

1

W

P

0

. Separating variables yields

W

0

W

D 

P

1

P

0

; hence ln

W.x/

W.x

0

/

D 

Z

x

0

P

1

.t/

P

0

.t/

dt, wh ich implies

Abel’s formula.

9.1.22. See the proof of Theorem 5.3.3.

9.1.24. (a)

P

0

.x/ D 

ˇ

x x

2

 1 x

2

C 1

1 2x 2x

0 2 2

ˇ

D 

ˇ

x x

2

 1 x

2

C1

1 0 0

0 2 2

ˇ

D

ˇ

x

2

 1 x

2

C 1

2 2

ˇ

D 4I

P

1

.x/ D

ˇ

x x

2

 1 x

2

C 1

1 2x 2x

0 0 0

ˇ

D 0; P

2

.x/ D 

ˇ

x x

2

 1 x

2

C 1

0 2 2

0 0 0

ˇ

D 0; P

3

.x/ D

ˇ

1 2x 2x

0 2 2

0 0 0

ˇ

D

0. Therefore, 4y

000

D 0, which is equivalent to y

000

D 0.

(b)

P

0

D 

ˇ

e

x

e

x

x

e

x

e

x

1

e

x

e

x

0

ˇ

D 

ˇ

1 1 x

1 1 1

1 1 0

ˇ

D 

ˇ

0 0 x

0 2 1

1 1 0

ˇ

D 2xI

P

1

D

ˇ

e

x

e

x

x

e

x

e

x

1

e

x

e

x

0

ˇ

D

ˇ

1 1 x

1 1 1

1 1 0

ˇ

D

ˇ

0 2 x

0 0 1

1 1 0

ˇ

D 2I

P

2

D 

ˇ

e

x

e

x

x

e

x

e

x

0

e

x

e

x

0

ˇ

D 

ˇ

1 1 x

1 1 0

1 1 0

ˇ

D 

ˇ

0 0 x

1 1 0

0 2 0

ˇ

D 2xI

164 Chapter 9

Linear Higher Order Equations

P

3

D

ˇ

e

x

e

x

1

e

x

e

x

0

e

x

e

x

0

ˇ

D

ˇ

1 1 1

1 1 0

1 1 0

ˇ

D

ˇ

0 0 1

1 2 0

1 1 0

ˇ

D 2:

Therefore, 2xy

000

C 2y

00

C 2xy

0

 2y D 0, which is equivalent to xy

000

 y

00

 xy

0

C y D 0.

(c)

P

0

.x/ D 

ˇ

e

x

xe

x

1

e

x

e

x

.1  x/ 0

e

x

e

x

.x  2/ 0

ˇ

D 

ˇ

1 x 1

1 1  x 0

1 x  2 0

ˇ

D 

ˇ

1 1  x

1 x  2

ˇ

D 3  2xI

P

1

.x/ D

ˇ

e

x

xe

x

1

e

x

e

x

.1  x/ 0

e

x

e

x

.3  x/ 0

ˇ

D

ˇ

1 x 1

1 1  x 0

1 3  x 0

ˇ

D

ˇ

1 1  x

1 3  x

ˇ

D 2I

P

2

.x/ D 

ˇ

e

x

xe

x

1

e

x

e

x

.x  2/ 0

e

x

e

x

.3  x/ 0

ˇ

D 

ˇ

1 x 1

1 x  2 0

1 3  x 0

ˇ

D 

ˇ

1 x  2

1 3  x

ˇ

D 2x  5I

P

3

.x/ D

ˇ

e

x

e

x

.1  x/ 0

e

x

e

x

.x  2/ 0

e

x

e

x

.3  x/ 0

ˇ

D 0:

Therefore, .3  2x/y

000

C 2y

00

C .2x  5/y

0

D 0.

(d)

P

0

.x/ D 

ˇ

x x

2

e

x

1 2x e

x

0 2 e

x

ˇ

D e

x

ˇ

x x

2

1

1 2x 1

0 2 1

ˇ

D e

x

ˇ

x x

2

 2 0

1 2x  2 0

0 2 1

ˇ

D e

x

ˇ

x x

2

 2

1 2x  2

ˇ

D e

x

.x

2

 2x C 2/I

P

1

.x/ D

ˇ

x x

2

e

x

1 2x e

x

0 0 e

x

ˇ

D e

x

ˇ

x x

2

1 2x

ˇ

D x

2

e

x

I

P

2

.x/ D 

ˇ

x x

2

e

x

0 2 e

x

0 0 e

x

ˇ

D e

x

ˇ

x x

2

0 2

ˇ

D 2xe

x

I

P

3

.x/ D

ˇ

1 2x e

x

0 2 e

x

0 0 e

x

ˇ

D e

x

ˇ

1 2x

0 2

ˇ

D 2e

x

:

Therefore, e

x

.x

2

 2x C 2/y

000

C x

2

e

x

y

00

 2xe

x

y

0

C 2e

x

y D 0; which is equivalent to .x

2

 2x C

2/y

000

 x

2

y

00

C 2xy

0

 2y D 0.

(e)

P

0

.x/ D 

ˇ

x x

2

1=x

1 2x 1=x

2

0 2 2=x

3

ˇ

D x

ˇ

1 x 1=x

2

1 2x 1=x

2

0 2 2=x

3

ˇ

D x

ˇ

1 x 1=x

2

0 x 2=x

2

0 2 2=x

3

ˇ

D x

ˇ

x 2=x

2

2 2=x

3

ˇ

D 

6

x

I

Section 9.1

Intr oduction to Linear Hi gher Order Equations

165

P

1

.x/ D

ˇ

x x

2

1=x

1 2x 1=x

2

0 0 6=x

4

ˇ

D 

6

x

4

ˇ

x x

2

1 2x

ˇ

D 

6

x

2

I

P

2

.x/ D 

ˇ

x x

2

1=x

0 2 2=x

3

0 0 6=x

4

ˇ

D

6

x

4

ˇ

x x

2

0 2

ˇ

D

12

x

3

I

P

3

.x/ D

ˇ

1 2x 1=x

2

0 2 2=x

3

0 0 6=x

4

ˇ

D 

6

x

4

ˇ

1 2x

0 2

ˇ

D 

12

x

4

:

Therefore, 

6

x

y

000



6

x

2

y

00

C

12

x

3

y

0



12

x

4

y D 0, which is equivalent to x

3

y

000

Cx

2

y

00

2xy

0

C2y D 0.

(f)

P

0

.x/ D 

ˇ

x C 1 e

x

e

3x

1 e

x

3e

3x

0 e

x

9e

3x

ˇ

D e

4x

ˇ

x C 1 1 1

1 1 3

0 1 9

ˇ

D e

4x

ˇ

x C 1 0 8

1 0 6

0 1 9

ˇ

D e

4x

ˇ

x C 1 8

1 6

ˇ

D 2e

4x

.1  3x/I

P

1

.x/ D

ˇ

x C 1 e

x

e

3x

1 e

x

3e

3x

0 e

x

27e

3x

ˇ

D e

4x

ˇ

x C1 1 1

1 1 3

0 1 27

ˇ

D e

4x

ˇ

x C 1 0 26

1 0 24

0 1 27

ˇ

D e

4x

ˇ

x C 1 26

1 24

ˇ

D 2e

4x

.12x 1/I

P

2

.x/ D 

ˇ

x C 1 e

x

e

3x

0 e

x

9e

3x

0 e

x

27e

3x

ˇ

D e

4x

ˇ

x C 1 1 1

0 1 9

0 1 27

ˇ

D e

4x

ˇ

x C 1 1 1

0 1 9

0 0 18

ˇ

D 18e

4x

.x C 1/I

P

3

.x/ D

ˇ

1 e

x

3e

3x

0 e

x

9e

3x

0 e

x

27e

3x

ˇ

D e

4x

ˇ

1 1 3

0 1 9

0 1 27

ˇ

D e

4x

ˇ

1 1 3

0 1 9

0 0 18

ˇ

D 18e

4x

:

Therefore,

2e

4x

.1  3x/y

000

C 2e

4x

.12x 1/y

00

 18e

4x

.x C 1/y

0

C 18e

4x

y D 0;

which is equivalent to

.3x  1/y

000

 .12x  1/y

00

C 9.x C 1/y

0

 9y D 0:

166 Chapter 9

Linear Higher Order Equations

(g)

P

0

.x/ D

ˇ

x x

3

1=x 1=x

2

1 3x

2

1=x

2

2=x

3

0 6x 2=x

3

6=x

4

0 6 6=x

4

24=x

5

ˇ

D x

ˇ

1 x

2

1=x

2

1=x

3

1 3x

2

1=x

2

2=x

3

0 6x 2=x

3

6=x

4

0 6 6=x

4

24=x

5

ˇ

D x

ˇ

1 x

2

1=x

2

1=x

3

0 2x

2

2=x

2

3=x

3

0 6x 2=x

3

6=x

4

0 6 6=x

4

24=x

5

ˇ

D x

ˇ

2x

2

2=x

2

3=x

3

6x 2=x

3

6=x

4

6 6=x

4

24=x

5

ˇ

D x

2

ˇ

2x 2=x

3

3=x

4

6x 2=x

3

6=x

4

6 6=x

4

24=x

5

ˇ

D x

2

ˇ

2x 2=x

3

3=x

4

0 8=x

3

15=x

4

0 0 15=x

5

ˇ

D 

240

x

5

P

1

.x/ D 

ˇ

x x

3

1=x 1=x

2

1 3x

2

1=x

2

2=x

3

0 6x 2=x

3

6=x

4

0 0 24=x

5

120=x

6

ˇ

D x

ˇ

1 x

2

1=x

2

1=x

3

1 3x

2

1=x

2

2=x

3

0 6x 2=x

3

6=x

4

0 0 24=x

5

120=x

6

ˇ

D x

ˇ

1 x

2

1=x

2

1=x

3

0 2x

2

2=x

2

3=x

3

0 6x 2=x

3

6=x

4

0 0 24=x

5

120=x

6

ˇ

D x

2

ˇ

2x 2=x

3

3=x

4

6x 2=x

3

6=x

4

0 24=x

5

120=x

6

ˇ

D x

2

ˇ

2x 2=x

3

3=x

4

0 8=x

3

15=x

4

0 24=x

5

120=x

6

ˇ

D 2x

3

ˇ

8=x

3

15=x

4

24=x

5

120=x

6

ˇ

D 

1200

x

6

I

P

2

.x/ D

ˇ

x x

3

1=x 1=x

2

1 3x

2

1=x

2

2=x

3

0 6 6=x

4

24=x

5

0 0 24=x

5

120=x

6

ˇ

D x

ˇ

1 x

2

1=x

2

1=x

3

1 3x

2

1=x

2

2=x

3

0 6 6=x

4

24=x

5

0 0 24=x

5

120=x

6

ˇ

D x

ˇ

1 x

2

1=x

2

1=x

3

0 2x

2

2=x

2

3=x

3

0 6 6=x

4

24=x

5

0 0 24=x

5

120=x

6

ˇ

D x

3

ˇ

2 2=x

4

3=x

5

6 6=x

4

24=x

5

0 24=x

5

120=x

6

ˇ

D x

3

ˇ

2 2=x

4

3=x

5

0 0 15=x

5

0 24=x

5

120=x

6

ˇ

D 2x

3

ˇ

0 15=x

5

24=x

5

120=x

6

ˇ

D

720

x

7

I

P

3

.x/ D 

ˇ

x x

3

1=x 1=x

2

0 6x 2=x

3

6=x

4

0 6 6=x

4

24=x

5

0 0 24=x

5

120=x

6

ˇ

D x

2

ˇ

6 2=x

4

6=x

5

6 6=x

4

24=x

5

0 24=x

5

120=x

6

ˇ

D x

2

ˇ

6 2=x

4

6=x

5

0 8=x

4

30=x

5

0 24=x

5

120=x

6

ˇ

D 6x

2

ˇ

8=x

4

30=x

5

24=x

5

120=x

6

ˇ

D

1440

x

6

I

Section 9.1

Intr oduction to Linear Hi gher Order Equations

167

P

4

.x/ D

ˇ

1 3x

2

1=x

2

2=x

3

0 6x 2=x

3

6=x

4

0 6 6=x

4

24=x

5

0 0 24=x

5

120=x

6

ˇ

D x

ˇ

6 2=x

4

6=x

5

6 6=x

4

24=x

5

0 0 24=x

5

120=x

6

ˇ

D x

ˇ

6 2=x

4

6=x

5

0 8=x

4

30=x

5

0 0 24=x

5

120=x

6

ˇ

D 6x

ˇ

8=x

4

30=x

5

24=x

5

120=x

6

ˇ

D 

1440

x

9

:

Therefore,



240

x

5

y

.4/



1200

x

6

y

000

C

720

x

7

y

00

C

1440

x

8

y

0



1440

x

9

y D 0;

which is equivalent to x

4

y

.4/

C 5x

3

y

000

 3x

2

y

00

 6xy

0

C 6y D 0.

(h)

P

0

.x/ D

ˇ

x x ln jxj 1=x x

2

1 ln jxjC 1 1=x

2

2x

0 1=x 2=x

3

2

0 1=x

2

6=x

4

0

ˇ

D x

ˇ

1 ln jxj 1=x

2

x

1 ln jxj C 1 1=x

2

2x

0 1=x 2=x

3

2

0 1=x

2

6=x

4

0

ˇ

D x

ˇ

1 ln jxj 1=x

2

x

0 1 2=x

2

x

0 1=x 2=x

3

2

0 1=x

2

6=x

4

0

ˇ

D x

ˇ

1 2=x

2

x

1=x 2=x

3

2

1=x

2

6=x

4

0

ˇ

D x

ˇ

1 2=x

2

x

1=x 2=x

3

2

1=x

2

6=x

4

0

ˇ

D x

ˇ

1 2=x

2

x

0 4=x

3

1

0 8=x

4

1=x

ˇ

D x

ˇ

4=x

3

1

8=x

4

1=x

ˇ

D

12

x

3

I

P

1

.x/ D 

ˇ

x x ln jxj 1=x x

2

1 ln jxj C 1 1=x

2

2x

0 1=x 2=x

3

2

0 2=x

3

24=x

5

0

ˇ

D x

ˇ

1 ln jxj 1=x

2

x

1 ln jxj C 1 1=x

2

2x

0 1=x 2=x

3

2

0 2=x

3

24=x

5

0

ˇ

D x

ˇ

1 ln jxj 1=x

2

x

0 1 2=x

2

x

0 1=x 2=x

3

2

0 2=x

3

24=x

5

0

ˇ

D x

ˇ

1 2=x

2

x

1=x 2=x

3

2

2=x

3

24=x

5

0

ˇ

D x

ˇ

1 2=x

2

x

0 4=x

3

1

0 28=x

5

2=x

2

ˇ

D x

ˇ

4=x

3

1

28=x

5

2=x

2

ˇ

D

36

x

4

I

168 Chapter 9

Linear Higher Order Equations

P

2

.x/ D

ˇ

x x ln jxj 1=x x

2

1 ln jxj C 1 1=x

2

2x

0 1=x

2

6=x

4

0

0 2=x

3

24=x

5

0

ˇ

D x

ˇ

1 ln jxj 1=x

2

x

1 ln jxj C 1 1=x

2

2x

0 1=x

2

6=x

4

0

0 2=x

3

24=x

5

0

ˇ

D x

ˇ

1 ln jxj 1=x

2

x

0 1 2=x

2

x

0 1=x

2

6=x

4

0

0 2=x

3

24=x

5

0

ˇ

D x

ˇ

1 2=x

2

x

1=x

2

6=x

4

0

2=x

3

24=x

5

0

ˇ

D x

ˇ

1 2=x

2

x

0 8=x

4

1=x

0 28=x

5

2=x

2

ˇ

D x

ˇ

8=x

4

1=x

28=x

5

2=x

2

ˇ

D 

12

x

5

I

P

3

.x/ D 

ˇ

x x ln jxj 1=x x

2

0 1=x 2=x

3

2

0 1=x

2

6=x

4

0

0 2=x

3

24=x

5

0

ˇ

D x

ˇ

1=x 2=x

3

2

1=x

2

6=x

4

0

2=x

3

24=x

5

0

ˇ

D x

ˇ

1=x 2=x

3

2

0 4=x

4

2=x

0 20=x

5

4=x

2

ˇ

D 

ˇ

4=x

4

2=x

20=x

5

4=x

2

ˇ

D

24

x

6

I

P

4

.x/ D

ˇ

1 ln jxj C 1 1=x

2

2x

0 1=x 2=x

3

2

0 1=x

2

6=x

4

0

0 2=x

3

24=x

5

0

ˇ

D

ˇ

1=x 2=x

3

2

1=x

2

6=x

4

0

2=x

3

24=x

5

0

ˇ

D 2

ˇ

1=x

2

6=x

4

2=x

3

24=x

5

ˇ

D 

24

x

7

:

Therefore,

12

x

3

y

.4/

C

36

x

4

y

000



12

x

5

y

00

C

24

x

6

y

0



24

x

7

y D 0;

which is equivalent to x

4

y

.4/

C 3x

2

y

000

 x

2

y

00

C2xy

0

 2y D 0.

(i)

P

0

.x/ D

ˇ

e

x

e

x

x e

2x

e

x

e

x

1 2e

2x

e

x

e

x

0 4e

2x

e

x

e

x

0 8e

2x

ˇ

D e

2x

ˇ

1 1 x 1

1 1 1 2

1 1 0 4

1 1 0 8

ˇ

D e

2x

ˇ

2 1 x 1

0 1 1 2

2 1 0 4

0 1 0 8

ˇ

D e

2x

ˇ

2 1 x 1

0 1 1 2

0 0 x 3

0 1 0 8

ˇ

D 2e

2x

ˇ

1 1 2

0 x 3

1 0 8

ˇ

D 2e

2x

ˇ

1 1 2

0 x 3

0 1 6

ˇ

D 2e

2x

ˇ

x 3

1 6

ˇ

D 6e

2x

.2x  1/I

Section 9.1

Intr oduction to Linear Hi gher Order Equations

169

P

1

.x/ D 

ˇ

e

x

e

x

x e

2x

e

x

e

x

1 2e

2x

e

x

e

x

0 4e

2x

e

x

e

x

0 16e

2x

ˇ

D e

2x

ˇ

1 1 x 1

1 1 1 2

1 1 0 4

1 1 0 16

ˇ

D e

2x

ˇ

0 1 x 1

2 1 1 2

0 1 0 4

0 1 0 16

ˇ

D 2e

2x

ˇ

1 x 1

1 0 4

1 0 16

ˇ

D 2e

2x

ˇ

1 x 1

0 x 3

0 x 15

ˇ

D 2e

2x

ˇ

x 3

x 15

ˇ

D 24xe

2x

I

P

2

.x/ D

ˇ

e

x

e

x

x e

2x

e

x

e

x

1 2e

2x

e

x

e

x

0 8e

2x

e

x

e

x

0 16e

2x

ˇ

D e

2x

ˇ

1 1 x 1

1 1 1 2

1 1 0 8

1 1 0 16

ˇ

D e

2x

ˇ

0 1 x 1

2 1 1 2

2 1 0 8

0 1 0 16

ˇ

D e

2x

ˇ

0 1 x 1

2 1 1 2

0 0 1 6

0 1 0 16

ˇ

D 2e

2x

ˇ

1 x 1

0 1 6

1 0 16

ˇ

D 2e

2x

ˇ

1 x 1

0 1 6

0 x 15

ˇ

D 2e

2x

ˇ

1 6

x 15

ˇ

D 6e

2x

.5  2x/I

P

3

.x/ D 

ˇ

e

x

e

x

x e

2x

e

x

e

x

0 4e

2x

e

x

e

x

0 8e

2x

e

x

e

x

0 16e

2x

ˇ

D e

2x

ˇ

1 1 x 1

1 1 0 4

1 1 0 8

1 1 0 16

ˇ

D e

2x

ˇ

0 1 x 1

0 1 0 4

2 1 0 8

0 1 0 16

ˇ

D 2e

2x

ˇ

1 x 1

0 x 3

0 x 15

ˇ

D 2e

2x

ˇ

x 3

x 15

ˇ

D 24xe

2x

I

P

4

.x/ D

ˇ

e

x

e

x

1 2e

2x

e

x

e

x

0 4e

2x

e

x

e

x

0 8e

2x

e

x

e

x

0 16e

2x

ˇ

D e

2x

ˇ

1 1 1 2

1 1 0 4

1 1 0 8

1 1 0 16

ˇ

D e

2x

ˇ

0 1 1 2

2 1 0 4

0 1 0 8

2 1 0 16

ˇ

D e

2x

ˇ

0 1 1 2

2 1 0 4

0 1 0 8

0 0 0 12

ˇ

D 2e

2x

ˇ

1 1 2

1 0 8

0 0 12

ˇ

D 2e

2x

ˇ

1 1 2

0 1 6

0 0 12

ˇ

D 24e

2x

:

Therefore,

6e

2x

.2x  1/y

.4/

 24xe

2x

y

000

C 6e

2x

.5  2x/y

00

C 24xe

2x

y

0

 24e

2x

y D 0;

170 Chapter 9

Linear Higher Order Equations

which is equivalent to .2x  1/y

.4/

 4xy

000

C.5  2x/y

00

C 4xy

0

 4y D 0.

9.1.24. (j)

P

0

.x/ D

ˇ

e

2x

e

2x

1 x

2

2e

2x

2e

2x

0 2x

4e

2x

4e

2x

0 2

8e

2x

8e

2x

0 0

ˇ

D

ˇ

1 1 1 x

2

2 2 0 2x

4 4 0 2

8 8 0 0

ˇ

D

ˇ

2 2 2x

4 4 2

8 8 0

ˇ

D

ˇ

2 2 2x

0 8 2  4x

0 0 8x

ˇ

D 128x

P

1

.x/ D 

ˇ

e

2x

e

2x

1 x

2

2e

2x

2e

2x

0 2x

4e

2x

4e

2x

0 2

16e

2x

16e

2x

0 0

ˇ

D 

ˇ

1 1 1 x

2

2 2 0 2x

4 4 0 2

16 16 0 0

ˇ

D 

ˇ

2 2 2x

4 4 2

16 16 0

ˇ

D 

ˇ

2 2 2x

0 8 2  4x

0 0 8

ˇ

D 128I

P

2

.x/ D

ˇ

e

2x

e

2x

1 x

2

2e

2x

2e

2x

0 2x

8e

2x

8e

2x

0 0

16e

2x

16e

2x

0 0

ˇ

D

ˇ

1 1 1 x

2

2 2 0 2x

8 8 0 0

16 16 0 0

ˇ

D

ˇ

2 2 2x

8 8 0

16 16 0

ˇ

D 2x

ˇ

8 8

16 16

ˇ

D 512xI

P

3

.x/ D 

ˇ

e

2x

e

2x

1 x

2

4e

2x

4e

2x

0 2

8e

2x

8e

2x

0 0

16e

2x

16e

2x

0 0

ˇ

D 

ˇ

1 1 1 x

2

4 4 0 2

8 8 0 0

16 16 0 0

ˇ

D 

ˇ

4 4 2

8 8 0

16 16 0

ˇ

D 2

ˇ

8 8

16 16

ˇ

D 512I

P

4

.x/ D

ˇ

2e

2x

2e

2x

0 2x

4e

2x

4e

2x

0 2

8e

2x

8e

2x

0 0

16e

2x

16e

2x

0 0

ˇ

D 0:

Therefore, 128xy

.4/

C128y

000

C512xy

00

512y D 0, which is equivalent to xy

.4/

y

000

4xy

00

C4y

0

D 0.

9.2 HIGHER ORDER CONSTANT COEFFICIENT HOMOGENEOUS EQUATIONS

9.2.2. p.r/ D r

4

C 8r

2

 9 D .r  1/.r C 1/.r

2

C 9/; y D c

1

e

x

Cc

2

e

x

C c

3

cos 3x C c

4

sin 3x.

9.2.4. p.r/ D 2r

3

C 3r

2

 2r  3 D .r  1/.r C 1/.2r C 3/; y D c

1

e

x

C c

2

e

x

C c

3

e

3x=2

.

Section 9.2

Higher Order Constant Coefﬁcient Ho mogeneous Equations

171

9.2.6. p.r/ D 4r

3

 8r

2

C 5r  1 D .r  1/.2r  1/

2

; y D c

1

e

x

C e

x=2

.c

2

C c

3

x/.

9.2.8. p.r/ D r

4

C r

2

D r

2

.r

2

C 1/; y D c

1

C c

2

x C c

3

cos x C c

4

sin x.

9.2.10. p.r/ D r

4

C 12r

2

C 36 D .r

2

C 6/

2

; y D .c

1

C c

2

x/ cos

p

6x C .c

3

C c

4

x/ sin

p

6x.

9.2.12. p.r/ D 6r

4

C 5r

3

C 7r

2

C 5r C 1 D .2r C 1/.3r C 1/.r

2

C 1/; y D c

1

e

x=2

C c

2

e

x=3

C

c

3

cos x C c

4

sin x.

9.2.14. p.r/ D r

4

4r

3

C7r

2

6r C2 D .r 1/

2

.r

2

2r C2/; y D e

x

.c

1

Cc

2

x Cc

3

cos x Cc

4

sin x/.

9.2.16. p.r/ D r

3

C 3r

2

 r  3 D .r  1/.r C 1/.r C 3/;

y D c

1

e

x

C c

2

e

x

C c

3

e

3x

y

0

D c

1

e

x

 c

2

e

x

 3c

3

e

3x

y

00

D c

1

e

x

C c

2

e

x

C 9c

3

e

3x

I

c

1

C c

2

C c

3

D 0

c

1

 c

2

 3c

3

D 14

c

1

C c

2

C9c

3

D 40

I

c

1

D 2, c

2

D 3, c

3

D 5; y D 2e

x

C3e

x

 5e

3x

.

9.2.18. p.r/ D r

3

 2r  4 D .r  2/.r

2

C 2r C 2/;

y D e

x

.c

1

cos x C c

2

sin x/ C c

3

e

2x

y

0

D e

x

..c

1

 c

2

/ cos x C .c

1

C c

2

/ sin x/ C 2c

3

e

2x

y

00

D e

x

.2c

1

sin x  2c

2

cos x/ C 4c

3

e

2x

I

c

1

C c

3

D 6

c

1

C c

2

C 2c

3

D 3

2c

2

C 4c

3

D 22

I

c

1

D 2, c

2

D 3, c

3

D 4; y D 2e

x

cos x  3e

x

sin x C 4e

2x

.

9.2.20. p.r/ D r

3

 6r

2

C 12r  8 D .r  2/

3

;

y D e

2x

.c

1

C c

2

x C c

3

x

2

/

y

0

D e

2x

.2c

1

C c

2

C .2c

2

C 2c

3

/x C2c

3

x

2

/

y

00

D 2e

2x

.2c

1

C 2c

2

C c

3

C 2.c

2

C 2c

3

/x C 2c

3

x

2

/

I

c

1

D 1

2c

1

C c

2

D 1

4c

1

C 4c

2

C 2c

3

D 4

c

1

D 1, c

2

D 3, c

3

D 2; y D e

2x

.1  3x C 2x

2

/.

9.2.22. p.r/ D 8r

3

 4r

2

 2r C 1 D .2r C 1/.2r  1/

2

;

y D e

x=2

.c

1

C c

2

x/ C c

3

e

x=2

y

0

D

1

2

e

x=2

.c

1

C 2c

2

C c

2

x/ 

1

2

c

3

e

x=2

y

00

D

1

4

e

x=2

.c

1

C 4c

2

C c

2

x/ C

1

4

c

3

e

x=2

I

c

1

C c

3

D 4

1

2

c

1

C c

2



1

2

c

3

D 3

1

4

c

1

C c

2

C

1

4

c

3

D 1

I

c

1

D 1, c

2

D 2, c

3

D 3; y D e

x=2

.1  2x/ C 3e

x=2

.

9.2.24. p.r/ D r

4

 6r

3

C 7r

2

C 6r  8 D .r  1/.r  2/.r  4/.r C 1/;

y D c

1

e

x

C c

2

e

2x

C c

3

e

4x

C c

4

e

x

y

0

D c

1

e

x

C 2c

2

e

2x

C 4c

3

e

4x

 c

4

e

x

y

00

D c

1

e

x

C 4c

2

e

2x

C 16c

3

e

4x

C c

4

e

x

y

000

D c

1

e

x

C 8c

2

e

2x

C 64c

3

e

4x

 c

4

e

x

I

c

1

C c

2

C c

3

C c

4

D 2

c

1

C 2c

2

C4c

3

 c

4

D 8

c

1

C 4c

2

C 16c

3

C c

4

D 14

c

1

C 8c

2

C 64c

3

 c

4

D 62

I

c

1

D 4, c

2

D 1, c

3

D 1, c

4

D 2; y D 4e

x

C e

2x

 e

4x

C 2e

x

.

172 Chapter 9

Linear Higher Order Equations

9.2.26. p.r/ D r

4

C 2r

3

 2r

2

 8r 8 D .r  2/.r C 2/.r

2

C 2r C2/;

y D c

1

e

2x

C c

2

e

2x

C e

x

.c

3

cos x C c

4

sin x/

y

0

D 2c

1

e

2x

 2c

2

e

2x

 e

x

..c

3

 c

4

/ cos x C .c

3

C c

4

/ sin x/

y

00

D 4c

1

e

2x

C 4c

2

e

2x

C e

x

.2c

3

sin x  2c

4

cos x/

y

000

D 8c

1

e

2x

 8c

2

e

2x

C e

x

..2c

3

C 2c

4

/ cos x C 2.c

4

 c

3

/ sin x/

I

c

1

C c

2

C c

3

D 5

2c

1

 2c

2

 c

3

C c

4

D 2

4c

1

C 4c

2

 2c

4

D 6

8c

1

 8c

2

C 2c

3

C 2c

4

D 8

I

c

1

D 1, c

2

D 1, c

3

D 3, c

4

D 1; y D e

2x

C e

2x

C e

x

.3 cos x C sin x/.

9.2.28. (a ) W .x/ D

ˇ

e

x

xe

x

e

2x

e

x

e

x

.x C 1/ 2e

2x

e

x

e

x

.x C 2/ 4e

2x

ˇ

I W .0/ D

ˇ

1 0 1

1 1 2

1 2 4

ˇ

D

ˇ

1 0 0

1 1 1

1 2 3

ˇ

D

ˇ

1 1

2 3

ˇ

D

1:

(b) W .x/ D

ˇ

cos 2x si n 2x e

3x

2 sin 2x 2 cos 2x 3e

3x

4 cos 2x 4 sin 2x 9e

3x

ˇ

IW .0/ D

ˇ

1 0 1

0 2 3

4 0 9

ˇ

D

ˇ

1 0 0

0 2 3

4 0 13

ˇ

D

ˇ

2 3

0 13

ˇ

D

26:

(c) W.x/ D

ˇ

e

x

cos x e

x

sin x e

x

e

x

.cos x C si n x/ e

x

.cos x  sin x/ e

x

2e

x

sin x 2e

x

cos x e

x

ˇ

IW.0/ D

ˇ

1 0 1

1 1 1

0 2 1

ˇ

D

ˇ

1 0 1

0 1 2

0 2 1

ˇ

D

ˇ

1 2

2 1

ˇ

D 5:

(d) W.x/ D

ˇ

1 x x

2

e

x

0 1 2x e

x

0 0 2 e

x

0 0 0 e

x

ˇ

I W .0/ D

ˇ

1 0 0 1

0 1 0 1

0 0 2 1

0 0 0 1

ˇ

D 1:

(e) W.x/ D

ˇ

e

x

e

x

cos x sin x

e

x

e

x

sin x cos x

e

x

e

x

cos x si n x

e

x

e

x

sin x cos x

ˇ

I

W.0/ D

ˇ

1 1 1 0

1 1 0 1

1 1 1 0

1 1 0 1

ˇ

D

ˇ

1 1 1 0

1 1 0 1

1 1 1 0

0 0 0 2

ˇ

D 2

ˇ

1 1 1

1 1 0

1 1 1

ˇ

D 2

ˇ

1 1 1

1 1 0

0 0 2

ˇ

D 4

ˇ

1 1

1 1

ˇ

D 8:

(f) W .x/ D

ˇ

cos x sin x e

x

cos x e

x

sin x

sin x cos x e

x

.cos x  sin x/ e

x

.cos x C si n x/

cos x si n x 2e

x

sin x 2e

x

cos x

sin x cos x e

x

.2 cos x C 2 sin x/ e

x

.2 cos x  2 sin x/

ˇ

I

Section 9.2

Higher Order Constant Coefﬁcient Ho mogeneous Equations

173

W.0/ D

ˇ

1 0 1 0

0 1 1 1

1 0 0 2

0 1 2 2

ˇ

D

ˇ

1 0 1 0

0 1 1 1

0 0 1 2

0 1 2 2

ˇ

D

ˇ

1 1 1

0 1 2

1 2 2

ˇ

D

ˇ

1 1 1

0 1 2

0 1 3

ˇ

D

ˇ

1 1 1

0 1 2

0 0 5

ˇ

D 5:

9.2.40. (a ) Si nce y D Q

1

.D/P

1

.D/y C Q

2

.D/P

2

.D/y and P

1

.D/y D P

2

.D/y D 0, i t follows that

y D 0.

(b) Suppose that (A) a

1

u

1

CCa

r

u

r

Cb

1

v

1

CCb

s

v

s

D 0, wher e a

1

; : : : ; a

r

and b

1

; : : : ; b

s

are

constants. Denote u D a

1

u

1

C C a

r

u

r

and v D b

1

v

1

C C b

s

v

s

. Then (B) P

1

.D/u D 0 and (C)

P

2

.D/v D 0. Since uCv D 0, P

2

.D/.uCv/ D 0. Therefore,0 D P

2

.D/.uCv/ D P

2

.D/uCP

2

.D/v.

Now (C) implies that P

2

.D/u D 0. This, (B), and (a) imply that u D a

1

u

1

C  C a

r

u

r

D 0, so

a

1

D  D a

r

D 0, since u

1

; : : : ; u

r

are linearly independent. Now (A) reduces to b

1

v

1

CCb

s

v

s

D 0,

so b

1

D c  D b

s

D 0, since v

1

; : : : ; v

s

are linearly independent. Therefore,u

1

; : : : ; u

r

; v

1

; : : : ; v

r

are

linearly independent.

(c) It sufﬁces to show that fy

1

; y

2

; : : : ; y

n

gis linearly independent. Suppose that c

1

y

1

CCc

n

y

n

D 0.

We may assume that y

1

; : : : ; y

r

are linearly independent solutions of p

1

.D/y D 0 and y

rC1

; : : : ; y

n

are

solutions of P

2

.D/ D p

2

.D/ p

k

.D/y D 0. Since p

1

.r/ and P

2

.r/ have no common factors, (b)

implies that (A) c

1

y

1

C  C c

r

y

r

D 0 and (B) c

rC1

y

rC1

C  C c

n

y

n

D 0. Now (A) implies that

c

1

D  D c

r

D 0, since y

1

; : : : ; y

r

are linearly independent. If k D 2, then y

rC1

; : : : ; y

n

are linearly

independent, so c

rC1

D  D c

n

D 0, and the proof is complete. If k > 2 repeat this argument, starting

from (B), with p

1

replaced by p

2

, and P

2

replaced by P

3

D p

3

p

n

.

9.2.42. (a)

.cos A C i sin A/.cos B C i sin B/ D .cos A cos B  sin A sin B/

C.cos A sin B C sin A cos B/

D cos.A C B/ C i sin.A CB/:

(b) Obvious for n D 0. If n D 1 write

1

cos  C i sin 

D

1

cos  C i sin 

cos   i sin 

D

cos   i sin 

cos

2

 C sin

2



D cos  i sin  D cos./ C i sin./:

(d) If n is a negative integer, then (B) .cos  C i sin  /

n

D

1

.cos  C i sin /

jnj

. From th e hint, (C)

1

.cos  C i sin /

jnj

D .cos   i sin /

jnj

D .cos./ C i sin.//

jnj

. Replacing  by  and n by

jnj in (A) shows that (D) .cos. / C i sin.//

jnj

D cos.jnj/ C i sin.jnj/. Since jnj D n, (E)

cos.jnj/ C i sin.jnj/ D cos n C i sin n. Now (B), (C), (D), and (E) imply (A).

(e) From (A), ´

n

k

D cos 2k C i sin 2k D 1 and 

n

k

D cos.2k C 1/ C i sin.2k C 1/ D cos.2k C

1/ D cos  D 1.

(f) From (e), 

1=n

´

0

; : : : ; 

1=n

´

n1

are all zeros of ´

n

. Si nce they are distinct numbers, ´

n

 has

the stated factoriztion.

174 Chapter 9

Linear Higher Order Equations

From (e), 

1=n



0

; : : : ; 

1=n



n1

are all zeros of ´

n

C . Since they are distinct numbers, ´

n

C  has

the stated factoriztion.

9.2.43. (a) p.r/ D r

3

 1 D .r  ´

0

/.r  ´

1

/.r  ´

2

/ where ´

k

D cos

2k

3

C i sin

2k

3

, k D 0; 1; 2.

Hence, ´

0

D 1, ´

1

D 

1

2

Ci

p

3

2

, and ´

2

D 

1

2

i

p

3

2

. Therefore, p.r/ D .r 1/



r C

1

2



2

C

3

4

!

,

so

(

e

x

; e

x=2

cos

p

3

2

x

!

; e

x=2

sin

p

3

2

x

!)

is a fundamental set of solutions.

(b) p.r/ D r

3

C1 D .r

0

/.r

1

/.r

2

/ where 

k

D cos

.2k C 1/

3

Ci sin

.2k C 1/

3

, k D 0; 1; 2.

Hence, 

0

D

1

2

C i

p

3

2

, 

1

D 1 

2

D

1

2

 i

p

3

2

. Therefore, p.r/ D .r C 1/



r 

1

2



2

C

3

4

!

, so

(

e

x

; e

x=2

cos

p

3

2

x

!

; e

x=2

sin

p

3

2

x

!)

is a fundamental set of solutions.

(c) p.r/ D r

4

C64 D .r 2

p

2

0

/.r 2

p

2

1

/.r 2

p

2

2

/.r 2

p

2

3

/, where 

k

D cos

.2k C 1/

4

C

i sin

.2k C 1/

4

, k D 0; 1; 2; 3. Therefore, 

0

D

1 Ci

p

2

, 

1

D

1 C i

p

2

, 

2

D

1  i

p

2

, and 

3

D

1  i

p

2

,

so p.r/ D ..r  2/

2

C 4/..r C 2/

2

C 4/ and fe

2x

cos 2x; e

2x

sin 2x; e

2x

cos 2x; e

2x

sin 2xg is a

fundamental set of solutions.

(d) p.r/ D r

6

1 D .r ´

0

/.r ´

1

/.r ´

2

/.r ´

3

/.r ´

4

/.r ´

5

/ where ´

k

D cos

2k

6

Ci sin

2k

6

,

k D 0; 1; 2; 3; 4; 5. Therefore, ´

0

D 1, ´

1

D

1

2

C i

p

3

2

, ´

2

D 

1

2

C i

p

3

2

, ´

3

D 1, ´

4

D 

1

2

 i

p

3

2

,

and ´

5

D

1

2

 i

p

3

2

, so p.r/ D .r  1/.r C 1/



r 

1

2



2

C

3

4

!



r C

1

2



2

C

3

4

!

and

(

e

x

; e

x

; e

x=2

cos

p

3

2

x

!

; e

x=2

sin

p

3

2

x

!

; e

x=2

cos

p

3

2

x

!

; e

x=2

sin

p

3

2

x

!)

is a funda-

mental set of solutions.

(e) p.r/ D r

6

C 64 D .r  2

0

/.r  2

1

/.r  2

2

/.r  2

3

/.r  2

4

/.r  2

5

/ where 

k

D

cos

.2k C 1/

6

Ci sin

.2k C 1/

6

, k D 0; 1; 2; 3; 4; 5. Therefore, 

0

D

p

3

2

C

i

2

, 

1

D i, 

2

D 

p

3

2

C

i

2

,



3

D 

p

3

2



i

2

, 

4

D i, and 

5

D

p

3

2



i

2

, so p.r/ D .r

2

C4/..r 

p

3/

2

C1/..r C

p

3/

2

C1/ and

fcos 2x; sin 2x; e



p

3x

cos x; e



p

3x

sin x; e

p

3x

cos x; e

p

3x

sin xg is a fundamental set of solutions.

(f) p.r/ D .r 1/

6

1 D .r 1´

0

/.r1´

1

/.r1´

2

/.r1´

3

/.r1´

4

/.r1´

5

/ wh ere ´

k

D

cos

2k

6

C i sin

2k

6

, k D 0; 1; 2; 3; 4; 5. Therefore, ´

0

D 1, ´

1

D

1

2

C i

p

3

2

, ´

2

D 

1

2

C i

p

3

2

, ´

3

D

1, ´

4

D 

1

2

 i

p

3

2

, and ´

5

D

1

2

 i

p

3

2

, so p.r/ D r .r  2/



r 

3

2



2

C

3

4

!



r 

1

2



2

C

3

4

!

and

(

1; e

2x

; e

3x=2

cos

p

3

2

x

!

; e

3x=2

sin

p

3

2

x

!

; e

x=2

cos

p

3

2

x

!

; e

x=2

sin

p

3

2

x

!)

is a funda-

mental set of solutions.

(g) p.r/ D r

5

C r

4

C r

3

C r

2

C r C 1 D

r

6

 1

r  1

. Therefore, from the solution of (d) p.r/ D

Section 9.3

Undetermined Coefﬁcients for Higher Order Equations

175

.r C 1/



r 

1

2



2

C

3

4

!



r C

1

2



2

C

3

4

!

and

(

e

x

; e

x=2

cos

p

3

2

x

!

; e

x=2

sin

p

3

2

x

!

; e

x=2

cos

p

3

2

x

!

; e

x=2

sin

p

3

2

x

!)

is a fundamen-

tal set of solutions.

9.3 UNDETERMINED COEFFICIENTS FOR HIGHER ORDER EQUATIONS

9.3.2. If y D u

3x

, then y

000

 2y

00

 5y

0

C 6y D e

3x

Œ.u

000

 11u

00

C 34u

0

 24u/  2.u

00

 6u

0

C

9u/  5.u

0

 3u/ C 6u D e

3x

.u

000

 11u

00

C 34u

0

 24u/. Let u

p

D A C Bx C Cx

2

, where

.24A C 34B  22C / C .24B C 68C /x  24Cx

2

D 32  23x C 6x

2

. Then C D 1=4, B D 1=4,

A D 3=4 and y

p

D 

e

3x

4

.3  x C x

2

/.

9.3.4. I f y D ue

2x

, then y

000

C 3y

00

 y

0

3y D e

2x

Œ.u

000

6u

00

C12u

0

 8u/ C3.u

00

 4u

0

C4u/ 

.u

0

 2u/  3u D e

2x

.u

000

 3u

00

 u

0

C 3u/. Let u

p

D A C Bx C Cx

2

, where .3A  B  6C / C

.3B  2C /x C 3Cx

2

D 2  17x C 3x

2

. Then C D 1, B D 5, A D 1, and y

p

D e

2x

.1  5x C x

2

/.

9.3.6. If y D ue

x

, then y

000

Cy

00

2y D e

x

Œ.u

000

C3u

00

C3u

0

Cu/C.u

00

C2u

0

Cu/2u D e

x

.u

000

C4u

00

C

5u

0

/. Let u

p

D x.ACBx CCx

2

/, where .5AC8B C6C /C.10B C24C /xC15Cx

2

D 14C34xC15x

2

.

Then C D 1, B D 1, A D 0, and y

p

D x

2

e

x

.1 C x/.

9.3.8. If y D ue

x

, then y

000

y

00

y

0

Cy D e

x

Œ.u

000

C3u

00

C3u

0

Cu/.u

00

C2u

0

Cu/.u

0

Cu/Cu D

e

x

.u

000

C 2u

00

/. Let u

p

D x

2

.A C Bx/ where .4A C 6B/ C 12Bx D 7 C 6x. Then B D 1=2, A D 1,

and y

p

D

x

2

e

x

2

.2 C x/.

9.3.10. If y D ue

3x

, then y

000

5y

00

C3y

0

C9y D e

3x

Œ.u

000

C9u

00

C27u

0

C27u/5.u

00

C6u

0

C9u/C3.u

0

C

3u/C9u D e

3x

.u

000

C4u

00

/. Let u

p

D x

2

.ACBxCCx

2

/, where .8AC6B/C.24B C24C /xC 48Cx

2

D

22  48x

2

. Then C D 1, B D 1, A D 2, and y

p

D x

2

e

3x

.2 C x  x

2

/.

9.3.12. If y D ue

x=2

, then 8y

000

12y

00

C6y

0

y D e

x=2

Œ8.u

000

C3u

00

=2 C3u

0

=4 Cu=8/ 12.u

00

Cu

0

C

u=4/ C 6.u

0

Cu=2/ u D 8e

x=2

u

000

, so u

000

D

1 C 4x

8

. Integrating three times and taking the constants

of in tegration to be zero yields u

p

D

x

3

48

.1 C x/. Therefore, y

p

D

x

3

e

x=2

48

.1 C x/.

9.3.14. If y D ue

2x

, then y

.4/

C3y

000

Cy

00

3y

0

2y D e

2x

Œ.u

.4/

C8u

000

C24u

00

C32u

0

C16u/C3.u

000

C

6u

00

C12u

0

C8u/C.u

00

C4u

0

C4u/ 3.u

0

C2u/ 2u D e

2x

.u

.4/

C11u

000

C43u

00

C69u

0

C36u/. Let

u

p

D A CBx where .36A C69B/ C36Bx D 33 36x. Then B D 1, A D 1, and y

p

D e

2x

.1 x/.

9.3.16. If y D ue

x

, then 4y

.4/

 11y

00

 9y

0

 2y D e

x

Œ4.u

.4/

C 4u

000

C 6u

00

C 4u

0

C u/  11.u

00

C

2u

0

C u/  9.u

0

C u/  2u D e

x

.4u

.4/

C 16u

000

C 13u

00

 15u

0

 18u/. Let u

p

D A C Bx where

.18A C 15B/  18Bx D 1 C 6x. Then B D 1=3, A D 1=3, and y

p

D

e

x

3

.1  x/.

9.3.18. If y D ue

x

, then y

.4/

4y

000

C6y

00

4y

0

C2y D e

x

Œ.u

.4/

C4u

000

C6u

00

C4u

0

Cu/4.u

000

C3u

00

C

3u

0

Cu/ C6.u

00

C2u

0

Cu/ 4.u

0

Cu/ C2u D e

x

.u

.4/

Cu/. Let u

p

D A CBx CCx

2

CDx

3

CEx

4

where .A C 24E/ C Bx C Cx

2

C Dx

3

C Ex

4

D 24 C x C x

4

. Then E D 1 D D 0, C D 0 B D 1,

A D 0, and y

p

D xe

x

.1 C x

3

/.

9.3.20. If y D ue

2x

, then y

.4/

C y

000

 2y

00

 6y

0

 4y D e

2x

Œ.u

.4/

C 8u

000

C 24u

00

C 32u

0

C 16u/ C

.u

000

C6u

00

C12u

0

C8u/2.u

00

C4u

0

C4u/ 6.u

0

C2u/ 4u D e

2x

.u

.4/

C9u

000

C28u

00

C30u

0

/. Let

176 Chapter 9

Linear Higher Order Equations

u

p

D x.ACBx CCx

2

/ where .30AC56B C54C /C.60B C168C/x C90Cx

2

D .4C28x C15x

2

/.

Then C D 1=6, B D 0, A D 1=6, and y

p

D

xe

2x

6

.1  x

2

/.

9.3.22. If y D ue

x

, then y

.4/

5y

00

C4y D e

x

Œ.u

.4/

C4u

000

C6u

00

C4u

0

Cu/5.u

00

C2u

0

Cu/C4u D

e

x

.u

.4/

C 4u

000

C u

00

 6u

0

/. Let u

p

D x.A C Bx C Cx

2

/ w here .6A C 2B C 24C / C .12B C

6C /x  18Cx

2

D 3 C x  3x

2

, so C D 1=6, B D 0, A D 1=6. Then y

p

D

xe

x

6

.1 C x

2

/.

9.3.24. If y D ue

2x

, then y

.4/

 3y

000

C 4y

0

D e

2x

Œ.u

.4/

C 8u

000

C 24u

00

C 32u

0

C 16u/  3.u

000

C

6u

00

C 12u

0

C 8u/ C 4.u

0

C 2u/ D e

2x

.u

.4/

C 5u

000

C 6u

00

/. Let u

p

D x

2

.A C Bx C Cx

2

/ w here

.12A C 30B C 24C / C .36B C 120C /x C 72Cx

3

D 15 C 26x C 12x

2

. Then C D 1=6, B D 1=6,

A D 1=2, and y

p

D

x

2

e

2x

6

.3 C x C x

2

/.

9.3.26. If y D ue

x

, then 2y

.4/

 5y

000

C3y

00

Cy

0

 y D e

x

Œ2.u

.4/

C4u

000

C6u

00

C4u

0

Cu/ 5.u

000

C

3u

00

C3u

0

Cu/ C3.u

00

C2u

0

Cu/ C.u

0

Cu/ u D e

x

.2u

.4/

C3u

000

/. Let u

p

D x

3

.A CBx/, where

.18A C 48B/ C 72Bx D 11 C 12x. Then B D 1=6, A D 1=6, and y

p

D

x

3

e

x

6

.1 C x/.

9.3.28. If y D ue

2x

, then y

.4/

 7y

000

C 18y

00

 20y

0

C 8y D e

2x

Œ.u

.4/

C 8u

000

C 24u

00

C 32u

0

C

16u/  7.u

000

C 6u

00

C 12u

0

C 8u/ C 18.u

00

C 4u

0

C 4u/  20.u

0

C 2u/ C 8u D e

2x

.u

.4/

C u

000

/. Let

u

p

D x

3

.A C Bx C Cx

2

/ where .6A C 24B/ C .24B C 120C /x C 60Cx

2

D 3  8x  5x

2

. Then so

C D 1=12 B D 1=12, A D 1=6, and y

p

D

x

3

e

2x

12

.2 C x  x

2

/.

9.3.30. If y D ue

x

, then y

000

Cy

00

4y

0

4y D e

x

Œ.u

000

3u

00

C3u

0

u/ C.u

00

2u

0

Cu/ 4.u

0



u/  4u D e

x

.u

000

 2u

00

 3u

0

/. Let u

p

D .A

0

C A

1

x/ cos 2x C .B

0

C B

1

x/ sin 2x, where

8A

1

 14B

1

D 22

14A

1

C 8B

1

D 6

8A

0

 14B

0

 15A

1

 8B

1

D 1

14A

0

C8B

0

C 8A

1

 15B

1

D 1:

Then A

1

D 1, B

1

D 1, A

0

D 1, B

0

D 1, and y

p

D e

x

Œ.1  x/ cos 2x C .1 C x/ sin 2x.

9.3.32. If y D ue

x

, then y

000

2y

00

Cy

0

2y D e

x

Œ.u

000

C3u

00

C3u

0

Cu/2.u

00

C2u

0

Cu/C.u

0

Cu/2u D

e

x

.u

000

C u

00

 2u/. Let u

p

D .A

0

C A

1

x C A

2

x

2

/ cos 2x C .B

0

C B

1

x CB

2

x

2

/ sin 2x where

6A

2

 8B

2

D 4

8A

2

 6B

2

D 3

6A

1

 8B

1

 24A

2

C 8B

2

D 5

8A

1

 6B

1

 8A

2

 24B

2

D 5

6A

0

 8B

0

 12A

1

C 4B

1

C 2A

2

C 12B

2

D 9

8A

0

 6B

0

 4A

1

 12B

1

 12A

2

C 2B

2

D 6:

Then A

2

D 0, B

2

D 1=2; A

1

D 1=2, B

1

D 1=2; A

0

D 1=1, B

0

D 1=2; and y

p

D

e

x

2

Œ.1 Cx/ cos 2x C

.1  x C x

2

/ sin 2x.

9.3.34. If y D ue

x

, then y

000

 y

00

C 2y D e

x

Œ.u

000

C 3u

00

C 3u

0

C u/  .u

00

C 2u

0

C u/ C 2u D

e

x

.u

000

C 2u

00

C u

0

C 2u/. Since cos x and sin x satisfy u

000

C 2u

00

C u

0

C 2u D 0, let u

p

D xŒ.A

0

C

Section 9.3

Undetermined Coefﬁcients for Higher Order Equations

177

A

1

x/ cos x C .B

0

C B

1

x/ sin x where

4A

1

C 8B

1

D 4

8A

1

 4B

1

D 12

2A

0

C 4B

0

C 4A

1

C 6B

1

D 20

4A

0

 2B

0

 6A

1

C 4B

1

D 12:

Then A

1

D 1, B

1

D 1; A

0

D 1, B

0

D 3; and y

p

D xe

x

Œ.1 C x/ cos x C .3 C x/ sin x.

9.3.36. If y D ue

3x

, then D e

3x

Œ.u

000

C 9u

00

C 27u

0

C 27u/  6.u

00

C 6u

0

C 9u/ C 18.u

0

C 3u/ D

e

3x

.u

000

C 3u

00

C 9u

0

C 27u/. Since cos 3x and sin 3x satisfy u

000

C 3u

00

C 9u

0

C 27u D 0, let u

p

D

xŒ.A

0

C A

1

x/ cos 3x C .B

0

C B

1

x/ sin 3x where

36A

1

C 36B

1

D 3

36A

1

 36B

1

D 3

18A

0

C 18B

0

C 6A

1

C 18B

1

D 2

18A

0

 18B

0

 18A

1

C 6B

1

D 3:

Then A

1

D 1=12, B

1

D 0; A

0

D, B

0

D 1=12; and y

p

D 

xe

3x

12

.x cos 3x C sin 3x/.

9.3.38. If y D ue

x

, then y

.4/

 3y

000

C 2y

00

C 2y

0

 4y D e

x

Œ.u

.4/

C 4u

000

C 6u

00

C 4u

0

C u/ 

3.u

000

C 3u

00

C 3u

0

C u/ C 2.u

00

C 2u

0

C u/ C 4.u

0

C u/ C u D e

x

.u

.4/

C u

000

 u

00

C u

0

 2u/. Let

u

p

D A cos 2x C B sin 2x where 18A  6B D 2 and 6A C 18B D 1. Then A D 1=12, B D 1=12,

and y

p

D

e

x

12

.cos 2x  sin 2x/.

9.3.40. If y D ue

x

, then y

.4/

C 6y

000

C 13y

00

C 12y

0

C 4y D e

x

Œ.u

.4/

 4u

000

C 6u

00

 4u

0

C

u/ C 6.u

000

 3u

00

C 3u

0

 u/ C 13.u

00

 2u

0

C u/ C 12u

0

 u/ C 4u D e

x

.u

.4/

C 2u

000

C u

00

/. Let

u

p

D .A

0

C A

1

x/ cos x C .B

0

C B

1

x/ sin x where

2B

1

D 1

2A

1

D 1

2B

0

 6A

1

 2B

1

D 4

2A

0

C 2A

1

 6B

1

D 5:

Then A

1

D 1=2, B

1

D 1=2, A

0

D 1=2, B

0

D 1, and y

p

D 

e

x

2

Œ.1 C x/ cos x C .2  x/ sin x.

9.3.42. If y D ue

x

, then y

.4/

5y

000

C13y

00

19y

0

C10y D e

x

Œ.u

.4/

C4u

000

C6u

00

C4u

0

Cu/5.u

000

C

3u

00

C3u

0

Cu/ C13.u

00

C2u

0

Cu/  19.u

0

Cu/ C10u D e

x

.u

.4/

 u

000

C4u

00

 4u

0

/. Since cos 2x

and sin 2x satisfy u

.4/

 u

000

C 4u

00

 4u

0

D 0, let u

p

D x.A cos 2x C B sin 2x/ where 8A  16B D 1

and 16A C 8B D 1. Then A D 3=40, B

0

D 1=40, and y

p

D

xe

x

40

.3 cos 2x  sin 2x/.

9.3.44. If y D ue

x

, then y

.4/

5y

000

C13y

00

19y

0

C10y D e

x

Œ.u

.4/

C4u

000

C6u

00

C4u

0

Cu/5.u

000

C

3u

00

C3u

0

Cu/ C13.u

00

C2u

0

Cu/  19.u

0

Cu/ C10u D e

x

.u

.4/

 u

000

C4u

00

 4u

0

/. Since cos 2x

and sin 2x satisfy u

.4/

 u

000

C 4u

00

 4u

0

D 0, l et u

p

D xŒ.A

0

C A

1

x/ cos 2x C .B

0

C B

1

x/ sin 2x/

where

16A

1

 32B

1

D 8

32A

1

C 16B

1

D 4

8A

0

 16B

0

 40A

1

 12B

1

D 7

16A

0

C8B

0

C 12A

1

 40B

1

D 8:

178 Chapter 9

Linear Higher Order Equations

Then A

1

D 0, B

1

D 1=4; A

0

D 0, B

0

D 1=4, and y

p

D 

xe

x

4

.1 C x/ sin 2x.

9.3.46. If y D ue

2x

, then y

.4/

8y

000

C32y

00

64y

0

C64y C4y D e

2x

Œ.u

.4/

C8u

000

C24u

00

C32u

0

C

16u/8.u

000

C6u

00

C12u

0

C8u/C32.u

00

C4u

0

C4u/64.u

0

C2u/C64u D e

2x

.u

.4/

C8u

00

C16u/. Since

cos 2x, sin 2x, x cos 2x, and x sin 2x satisfy u

.4/

C 8u

00

C 16u D 0, let u

p

D x

2

.A cos 2x C B sin 2x/

where 32A D 1 and 32B D 1. Then A D 1=32, B D 1=32, and y

p

D 

x

2

e

2x

32

.cos 2x  sin 2x/.

9.3.48. Find par ticular solutions of (a) y

000

4y

00

C5y

0

 2y D 4e

x

, (b) y

000

4y

00

C5y

0

 2y D e

2x

,

and (c) y

000

 4y

00

C 5y

0

 2y D 2 cos x C 4 sin x.

(a) I f y D ue

x

, then y

000

4y

00

C5y

0

2y D e

x

Œ.u

000

C3u

00

C3u

0

Cu/4.u

00

C2u

0

Cu/C5.u

0

Cu/2u D

e

x

.u

000

 u

00

/. Let u

1p

D Ax

2

where 2A D 4. Then A D 2, and y

1p

D 2x

2

e

x

.

(b) If y D ue

2x

, then y

000

 4y

00

C 5y

0

 2y D e

2x

Œ.u

000

C 6u

00

C 12u

0

C8u/  4.u

00

C 4u

0

C 4u/ C

5.u

0

C 2u/ 2u D e

2x

.u

000

C 2u

00

C u

0

/. Let u

2p

D x. Then y

2p

D xe

2x

.

(c) If y

3p

D A cos xCB sin x, then y

000

3p

4y

00

3p

C5y

0

3p

2y

3p

D .2AC4B/ cos xC.4AC2B/ sin x D

2 cos x C 4 sin x if A D 1 and B D 0, so y

3p

D cos x.

From the principle of superposition, y

p

D 2x

2

e

x

C xe

2x

 cos x.

9.3.50. Find particul ar solutions of (a) y

000

y

0

D 2.1 Cx/, (b) y

000

y

0

D 4e

x

, (c) y

000

y

0

D 6e

x

,

and (d) y

000

 y

0

D 96e

3x

(a) Let y

1p

D x.A CBx/. Then y

000

1p

y

0

1p

D A2Bx D 2.1Cx/ if A D 2 and B D 1; therefore

y

1p

D 2x C 2x

2

.

(b) If y D ue

x

, then y

000

 y

0

D e

x

Œ.u

000

C 3u

00

C 3u

0

C u/  .u

0

C u/ D e

x

.u

000

C 3u

00

C 2u

0

/. Let

u

2p

D 4x. Then y

2p

D 4xe

x

.

(c) If y D ue

x

, then y

000

y

0

D e

x

Œ.u

000

3u

00

C3u

0

u/ .u

0

u/ D e

x

.u

000

3u

00

C2u

0

/. Let

u

2p

D 3x. Then y

2p

D 6xe

x

.

(d) Since e

3x

does not satisfy the complementary equation, let y

4p

D Ae

3x

. Then y

000

4p

 y

0

4p

D

24Ae

3x

. Let A D 4; th en y

4p

D 4e

4x

.

From the principle of superposition, y

p

D 2x C x

2

C 2xe

x

 3xe

x

C 4e

3x

9.3.52. Find particular solutions of (a) y

000

C 3y

00

C 3y

0

C y D 12e

x

and (b) y

000

C 3y

00

C 3y

0

C y D

9 cos 2x  13 sin 2x.

(a) If y D ue

2x

, then y

000

C 3y

00

C 3y

0

C y D e

2x

Œ.u

000

 3u

00

C 3u

0

 u/ C 3.u

00

 2u

0

C u/ C

3.u

0

 u/ C u D e

x

u

000

. Let u

000

1p

D 12. Integrating three times and taking t he con stants of integration

to be zero yields u

1p

D 2x

3

. Therefore,y

1p

D 2x

3

.

(b) Let y

2p

D A cos 2x C B sin 2x where 11A  2B D 9 and 2A  11B D 13. Then A D 1,

B D 1, and y

2p

D cos 2x C sin 2x.

From the principle of superposition, y

p

D 2x

3

e

2x

 cos 2x Csin 2x.

9.3.54. Find par ticular solutions of (a) y

.4/

 5y

00

C4y D 12e

x

, (b) y

.4/

 5y

00

C4y D 6e

x

, and (c)

y

.4/

 5y

00

C 4y D 10 cos x.

(a) If y D ue

x

, then y

.4/

5y

00

C4y D e

x

Œ.u

.4/

C4u

000

C6u

00

C4u

0

Cu/ 5.u

00

C2u

0

Cu/ C4u D

e

x

.u

.4/

C 4u

000

C u

00

 6u

0

/. Let u

1p

D 2x. Then y

1p

D 2xe

x

.

(b) If y D ue

x

, then y

.4/

5y

00

C4y D e

x

Œ.u

.4/

4u

000

C6u

00

4u

0

Cu/5.u

00

2u

0

Cu/C4u D

e

x

.u

.4/

 4u

000

Cu

00

C 6u

0

/. Let u

2p

D x. Then y

2p

D xe

x

.

(c) Let y

3p

D A cos xCB sin x where 10A D 10 and 10B D 0. Then A D 1, B D 0, and y

3p

D cos x.

From the principle of superposition, y

p

D 2xe

x

C xe

x

C cos x.

9.3.56. Find particul ar solutions of (a) y

.4/

C2y

000

3y

00

4y

0

C4y D 2e

x

.1 Cx/ and (b) y

.4/

C2y

000



3y

00

 4y

0

C 4y D e

2x

.

Section 9.3

Undetermined Coefﬁcients for Higher Order Equations

179

(a) If y D ue

x

, then y

.4/

C 2y

000

 3y

00

 4y

0

C 4y D e

x

Œ.u

.4/

C 4u

000

C 6u

00

C 4u

0

C u/ C 2.u

000

C

3u

00

C3u

0

Cu/ 3.u

00

C2u

0

Cu/ 4.u

0

Cu/ C4u D e

x

.u

.4/

C6u

000

C9u

00

/. Let u

1p

D x

2

.A CBx/

where .18A C 36B/ C 54Bx D 2 C 2x. Then B D 1=27, A D 1=27, and y

1p

D

x

2

27

.1 C x/e

x

.

(b) If y D ue

2x

, then y

.4/

C 2y

000

 3y

00

4y

0

C4y D e

2x

Œ.u

.4/

 8u

000

C24u

00

32u

0

C16u/ C

2.u

000

 6u

00

C 12u

0

 8u/  3.u

00

 4u

0

C 4u/  4.u

0

 2u/ C 4u D e

2x

.u

.4/

 6u

000

C 9u

00

/. Let

u

2p

D Ax

2

where 18A D 1. Then A D 1=18 and y

p

D

x

2

18

e

2x

.

From the principle of superposition, y

p

D

x

2

54

Œ.2 C 2x/e

x

C 3e

2x

.

9.3.58. Find part icular sol utions of (a) y

.4/

C 5y

000

C 9y

00

C 7y

0

C 2y D e

x

.30 C 24x/ and (b)

y

.4/

C 5y

000

C 9y

00

C 7y

0

C 2y D e

2x

.

(a) If y D ue

x

, then y

.4/

C5y

000

C9y

00

C7y

0

C2y D e

x

Œ.u

.4/

4u

000

C6u

00

4u

0

Cu/ C5.u

000



3u

00

C3u

0

u/ C9.u

00

2u

0

Cu/ C7.u

0

u/ C2u D e

x

.u

.4/

Cu

000

/. Let u

1p

D x

3

.A CBx/ where

.6A C 24B/ C 24Bx D 30 C 24x. The B D 1, A D 1, and y

1p

D x

3

.1 C x/e

x

.

(b) If y D ue

2x

, then y

.4/

C5y

000

C9y

00

C7y

0

C2y D e

2x

Œ.u

.4/

 8u

000

C24u

00

32u

0

C16u/ C

5.u

000

6u

00

C12u

0

8u/ C9.u

00

4u

0

C4u/ C7.u

0

2u/ C2u D e

2x

.u

.4/

3u

000

C3u

00

u

0

/. Let

u

2p

D x. Then y

2p

D xe

2x

.

From the principle of superposition, y

p

D x

3

.1 C x/e

x

C xe

2x

.

9.3.60. If y D ue

2x

, then y

000

y

00

y

0

Cy D e

2x

Œ.u

000

C6u

00

C12u

0

C8u/.u

00

C4u

0

C4u/.u

0

C2u/C

u D e

2x

.u

000

C5u

00

C7u

0

C3u/. Let u

p

D A CBx, where .3A C7B/ C3x D 10 C 3x. Then B D 1,

A D 1 and y

p

D e

2x

.1 C x/. Since p.r/ D .r C 1/.r  1/

2

, y D e

2x

.1 C x/ C c

1

e

x

C e

x

.c

2

C c

3

x/

9.3.62. If y D ue

2x

, then y

000

6y

00

C11y

0

6y D e

2x

Œ.u

000

C6u

00

C12u

0

C8u/6.u

00

C4u

0

C4u/C 11.u

0

C

2u/6u D e

2x

.u

000

u

0

/. Let u

p

D x.ACBx CCx

2

/ where .AC6C/2Bx 3Cx

2

D 54x 3x

2

.

Then C D 1, B D 2, A D 1, and y

p

D xe

2x

.1 C x/

2

. Since p.r/ D .r  1/.r  2/.r  3/,

y D xe

2x

.1 C x/

2

Cc

1

e

x

C c

2

e

2x

C c

3

e

3x

.

9.3.64. If y D ue

x

, t hen y

000

 3y

00

C 3y

0

 y D e

x

Œ.u

000

C 3u

00

C 3u

0

C u/  3.u

00

C 2u

0

C u/ C

3.u

0

Cu/ u D e

x

u

000

. Let u

000

D 1 Cx. Integrating three times and taking the constants of integration

to be zero yields u D

x

3

24

.4 C x/. Therefore, y

p

D

x

3

e

x

24

.4 C x/. Since p.r/ D .r  1/

3

, y D

x

3

e

x

24

.4 C x/ C e

x

.c

1

C c

2

x C c

3

x

2

/.

9.3.66. If y D ue

2x

, then y

000

C2y

00

y

0

2y D e

2x

Œ.u

000

6u

00

C12u

0

8u/ C2.u

00

4u

0

C4u/ 

.u

0

 2u/  2u D e

2x

.u

000

 4u

00

C 3u

0

/. Let u

p

D .A

0

C A

1

x/ cos x C .B

0

C B

1

x/ sin x where

4A

1

C 2B

1

D 2

2A

1

C 4B

1

D 9

4A

0

C 2B

0

 8B

1

D 23

2A

0

C 4B

0

C8A

1

D 8:

Then A

1

D 1=2, B

1

D 2; A

0

D 1, B

0

D 3=2, and y

p

D e

2x





1 C

x

2



cos x C



3

2

 2x



sin x



.

Since p.r/ D .r  1/.r C 1/.r C2/, y D e

2x





1 C

x

2



cos x C



3

2

 2x



sin x



Cc

1

e

x

Cc

2

e

x

C

c

3

e

2x

.

180 Chapter 9

Linear Higher Order Equations

9.3.68. If y D ue

x

, then y

.4/

4y

000

C14y

00

20y

0

C25y D e

x

Œ.u

.4/

C4u

000

C6u

00

C4u

0

Cu/4.u

000

C

3u

00

C3u

0

Cu/ C14.u

00

C2u

0

Cu/ 20.u

0

Cu/ C25u D e

x

.u

.4/

C8u

00

C16u/. Since cos 2x, sin 2x,

x cos 2x, and x sin 2x satisfy u

.4/

C8u

00

C16u D 0, let u

p

D x

2

Œ.A

0

CA

1

x/ cos 2xC.B

0

CB

1

x/ sin 2x

where

96A

1

D 6

96B

1

D 0

32A

0

C 48B

1

D 2

48A

1

 32B

0

D 3:

Then A

1

D 1=16, B

1

D 0; A

0

D 1=16, B

0

D 0, and y

Œ

D 

x

2

e

x

16

.1 C x/ cos 2x. Since p.r/ D

Œ.r  1/

2

C 1

2

, y D 

x

2

e

x

16

.1 C x/ cos 2x C e

x

Œ.c

1

C c

2

x/ cos 2x C .c

3

Cc

4

x/ sin 2x.

9.3.70. If y D ue

x

, then y

000

 y

00

 y

0

C y D e

x

Œ.u

000

 3u

00

C 3u

0

 u/  .u

00

 2u

0

C u/  .u

0



u/ C u D e

x

.u

000

 4u

00

C 4u

0

/. Let u

p

D x.A C Bx/, where .4A  8B/ C 8Bx D 4 C 8x.

Then B D 1, A D 1, and y

p

D x.1 C x/e

x

. Since p.r/ D .r C 1/.r  1/

2

the general solution is

y D x.1 C x/e

x

C c

1

e

x

C c

2

e

x

C c

3

xe

x

. Therefore,

2

4

y

0

y

00

3

5

D

2

4

x.1 C x/e

x

e

x

.x

2

 x 1/

e

x

.x

2

 3x/

3

5

C

2

4

e

x

e

x

xe

x

e

x

e

x

e

x

.x C 1/

e

x

e

x

e

x

.x C 2/

3

5

2

4

c

1

c

2

c

3

5

:

Setting x D 0 and imposing the initial conditions yields

2

4

2

0

3

5

D

2

4

0

1

0

3

5

C

2

4

1 1 0

1 1 1

1 1 2

3

5

2

4

c

1

c

2

c

3

5

;

so c

1

D 1, c

2

D 1, c

3

D 1, and y D e

x

.1 C x C x

2

/ C .1  x/e

x

.

9.3.72. If y D ue

x

, t hen y

000

 2y

00

 5y

0

C 6y D e

x

Œ.u

.4/

 4u

000

C 6u

00

 4u

0

C u/ C 2.u

000



3u

00

C3u

0

u/ C 2.u

00

2u

0

Cu/ C2.u

0

u/ Cu D e

x

.u

.4/

2u

000

C2u

00

/. Let u

p

D x

2

.A C Bx/,

where .4A  12B/ C 12Bx D 20  12x. Then B D 1, A D 2, and y

p

D x

2

.2  x/e

x

. Since

p.r/ D .r C1/

2

.r

2

C1/, t he general solution is y D x

2

.2x/e

x

Ce

x

.c

1

Cc

2

x/Cc

3

cos x Cc

4

sin x.

Therefore,

2

6

4

y

0

y

00

y

000

3

7

5

D

2

6

4

x

2

.2  x/e

x

x.x

2

 5x C 4/e

x

.x

3

 8x

2

C 14x  4/e

x

.x

3

 11x

2

C 30x  18/e

x

3

7

5

C

2

6

4

e

x

xe

x

cos x sin x

e

x

.1  x/e

x

sin x cos x

e

x

.x  2/e

x

cos x sin x

e

x

.3  x/e

x

sin x cos x

3

7

5

2

6

4

c

1

c

2

c

3

c

4

3

7

5

Setting x D 0 and imposing the initial conditions yields

2

6

4

3

4

7

22

3

7

5

D

2

6

4

0

4

18

3

7

5

C

2

6

4

1 0 1 0

1 1 0 1

1 2 1 0

1 3 0 1

3

7

5

2

6

4

c

1

c

2

c

3

c

4

3

7

5

;

so c

1

D 2, c

2

D 1, c

3

D 1, c

4

D 1, and y D .2  x/.x

2

C 1/e

x

C cos x  si n x.

9.3.74. If y D ue

x

, then y

.4/

3y

000

C5y

00

2y

0

D e

x

Œ.u

.4/

C4u

000

C6u

00

C4u

0

Cu/ 3.u

000

C3u

00

C

3u

0

C u/ C 4.u

00

C 2u

0

C u/  2.u

0

C u/ D e

x

.u

.4/

C u

000

C u

00

C u

0

/. Since cos x and sin x satisfy

Section 9.4

Variation of Parameters for Higher Order Equations

181

u

.4/

C u

000

C u

00

C u

0

D 0, let u

p

D x.A cos x C B sin x/ where 2A  2B D 2 and 2A  2B D 2.

Then A D 1, B D 0, and y

p

D e

x

cos x. Since p.r/ D r.r  1/Œ.r  1/

2

C 1 the general solution is

y D e

x

cos x C c

1

C e

x

.c

2

C c

3

cos x C c

4

sin x/. Therefore,

2

6

4

y

0

y

00

y

000

3

7

5

D

2

6

4

xe

x

cos x

e

x

..x C 1/ cos x  x sin x/

e

x

.2 cos x  2.x C 1/ sin x/

e

x

.2x cos x C 2.x C 3/ sin x/

3

7

5

C

2

6

4

1 e

x

e

x

cos x e

x

sin x

0 e

x

e

x

.cos x  sin x/ e

x

.cos x Csin x/

0 e

x

2e

x

sin x 2e

x

cos x

0 e

x

e

x

.2 cos x C 2 sin x/ e

x

.2 cos x  2 sin x/

3

7

5

2

6

4

c

1

c

2

c

3

c

4

3

7

5

Setting x D 0 and imposing the initial conditions yields

2

6

4

2

0

1

5

3

7

5

D

2

6

4

0

1

2

0

3

7

5

C

2

6

4

1 1 1 0

0 1 1 1

0 1 0 2

0 1 2 2

3

7

5

2

6

4

c

1

c

2

c

3

c

4

3

7

5

;

so c

1

D 2, c

2

D 1, c

3

D 1, c

4

D 1, and 2 C e

x

Œ.1 C x/ cos x  sin x  1.

9.4 VARIATION OF PARAMETERS FOR HIGHER ORDER EQUATIONS

9.4.2. W D

ˇ

e

x

2

xe

x

2

x

2

e

x

2

2xe

x

2

e

x

2

.1  2x

2

/ 2xe

x

2

.1  x

2

/

e

x

2

.4x

2

 2/ 2xe

x

2

.2x

2

 3/ 2e

x

2

.2x

4

 5x

2

C 1/

ˇ

D 2e

3x

2

;

W

1

D

ˇ

xe

x

2

x

2

e

x

2

e

x

2

.1  2x

2

/ 2xe

x

2

.1  x

2

/

ˇ

D x

2

e

2x

2

; W

2

D

ˇ

e

x

2

x

2

e

x

2

2xe

x

2

2xe

x

2

.1  x

2

/

ˇ

D

2xe

2x

2

; W

3

D

ˇ

e

x

2

xe

x

2

2xe

x

2

e

x

2

.1  2x

2

/

ˇ

D e

2x

2

; u

0

1

D

F W

1

P

0

W

D

1

2

x

5=2

; u

0

2

D 

F W

2

P

0

W

D

x

3=2

; u

0

3

D

F W

2

P

0

W

D

p

x=2; u

1

D x

7=2

=7; u

2

D 

2

5

x

5=2

; u

3

D x

3=2

=3; y

p

D u

1

y

1

Cu

2

y

2

Cu

3

y

3

D

8

105

e

x

2

x

7=2

.

9.4.4. W D

ˇ

1

e

x

e

x

x

0

e

x

.x  1/

x

2



e

x

.x C 1/

x

2

0

e

x

.x

2

 2x C 2/

x

3

e

x

.x

2

C 2x C 2/

x

3

ˇ

D 2=x

2

; W

1

D

ˇ

e

x

e

x

x

e

x

.x  1/

x

2



e

x

.x C 1/

x

2

ˇ

D



2

x

2

; W

2

D

ˇ

1

e

x

x

0 

e

x

.x C 1/

x

2

ˇ

D 

e

x

.x C 1/

x

2

; W

3

D

ˇ

1

e

x

0

e

x

.x  1/

x

2

ˇ

D

e

x

.x  1/

x

2

; u

0

1

D

F W

1

P

0

W

D 2; u

0

2

D 

F W

2

P

0

W

D e

x

.x C 1/; u

0

3

D

F W

2

P

0

W

D e

x

.x  1/; u

1

D 2x; u

2

D e

x

.x C 2/;

u

3

D e

x

.x  2/; y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D 2.x

2

C 2/=x.

9.4.6. W D

ˇ

e

x

e

x

1

x

e

x

e

x

1=x

2

e

x

e

x

2

x

3

ˇ

D

2.x

2

 2/

x

3

; W

1

D

ˇ

e

x

1

x

e

x



1

x

2

ˇ

D

e

x

.x  1/

x

2

; W

2

D

182 Chapter 9

Linear Higher Order Equations

ˇ

e

x

1

x

e

x



1

x

2

ˇ

D 

e

x

.x C 1/

x

2

; W

3

D

ˇ

e

x

e

x

e

x

e

x

ˇ

D 2; u

0

1

D

F W

1

P

0

W

D e

x

.x  1/; u

0

2

D



F W

2

P

0

W

D e

x

.x C 1/; u

0

3

D

F W

2

P

0

W

D 2x

2

; y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D 2

x

2

3

.

9.4.8. W D

ˇ

p

x

1

p

x

2

1

2

p

x



1

2x

3=2

2x



1

4x

3=2

3

4x

5=2

2

ˇ

D 

15

4x

; W

1

D

ˇ

1

p

x

2



1

2x

3=2

2x

ˇ

D

5

p

x

2

; W

2

D

ˇ

p

x x

2

1

2

p

x

2x

ˇ

D

3x

3=2

2

; W

3

D

ˇ

p

x

1

p

x

1

2

p

x



1

2x

3=2

ˇ

D 

1

x

; u

0

1

D

F W

1

P

0

W

D 5

p

x; u

0

2

D 

F W

2

P

0

W

D 3x

3=2

; u

0

3

D

F W

2

P

0

W

D

2

x

; u

1

D 

10

3

x

3=2

; u

2

D

6

5

x

5=2

; u

3

D 2 ln jxj; y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D 2x

2

ln jxj 

32

15

x

2

. Since 

32

15

x

2

satisﬁes the complementary equation we take y

p

D ln jxj.

9.4.10. W D

ˇ

x 1=x

e

x

1 

1

x

2

e

x

.x  1/

x

2

0

2

x

3

e

x

.x

2

 2x C 2/

x

3

ˇ

D

2e

x

.1  x/

x

3

; W

1

D

ˇ

1

x

e

x



1

x

2

e

x

.x  1/

x

2

ˇ

D

e

x

2

;

W

2

D

ˇ

x

e

x

1

e

x

.x  1/

x

2

ˇ

D

e

x

.x  2/

x

; W

3

D

ˇ

x

1

x

1 

1

x

2

ˇ

D 

2

x

; u

0

1

D

F W

1

P

0

W

D 1; u

0

2

D 

F W

2

P

0

W

D

x.2  x/; u

0

3

D

F W

2

P

0

W

D 2xe

x

; u

1

D x; u

2

D

x

2

.3  x/

3

; u

3

D 2e

x

.x C 1/; y

p

D u

1

y

1

C

u

2

y

2

C u

3

y

3

D

2x

3

C3x

2

C 6x C 6

3x

. Since x C

2

x

satisﬁes the complementary equation we take

y

p

D

2x

2

C 6

3

.

9.4.12. W D

ˇ

x e

x

e

x

1 e

x

e

x

0 e

x

e

x

ˇ

D 2x; W

1

D

ˇ

e

x

e

x

e

x

e

x

ˇ

D 2; W

2

D

ˇ

x e

x

1 e

x

ˇ

D e

x

.x C

1/; W

3

D

ˇ

x e

x

1 e

x

ˇ

D e

x

.x  1/; u

0

1

D

F W

1

P

0

W

D 1; u

0

2

D 

F W

2

P

0

W

D e

x

.x C 1/=2; u

0

3

D

F W

2

P

0

W

D

e

x

.x1/=2; u

1

D x; u

2

D e

x

.xC2/=2; u

3

D e

x

.x2/=2; y

p

D u

1

y

1

Cu

2

y

2

Cu

3

y

3

D x

2

2.

Section 9.4

Variation of Parameters for Higher Order Equations

183

9.4.14. W D

ˇ

p

x 1=

p

x x

3=2

1

x

3=2

1

2

p

x



1

2x

3=2

3

p

x

2



3

2x

5=2



1

4x

3=2

3

4x

5=2

3

4

p

x

15

4x

7=2

3

8x

5=2



15

8x

7=2



3

8x

3=2



105

8x

9=2

ˇ

D

12

x

6

; W

1

D

ˇ

1

p

x

3=2

1

x

3=2



1

2x

3=2

3

p

x

2



3

2x

5=2

3

4x

5=2

3

4

p

x

15

4x

7=2

ˇ

D

6

x

7=2

; W

2

D

ˇ

p

x x

3=2

1

x

3=2

1

2

p

x

3

p

x

2



3

2x

5=2



1

4x

3=2

3

4

p

x

15

4x

7=2

ˇ

D

6

x

5=2

; W

3

D

ˇ

p

x

1

p

x

1

x

3=2

1

2

p

x



1

2x

3=2



3

2x

5=2



1

4x

3=2

3

4x

5=2

15

4x

7=2

ˇ

D



2

x

9=2

; W

4

D

ˇ

p

x

1

p

x

3=2

1

2

p

x



1

2x

3=2

3

p

x

2



1

4x

3=2

3

4x

5=2

3

4

p

x

ˇ

D 

2

x

3=2

; u

0

1

D 

F W

1

P

0

W

D 3x; u

0

2

D

F W

2

P

0

W

D

3x

2

; u

0

3

D 

F W

2

P

0

W

D 1; u

0

4

D

F W

4

P

0

W

D x

3

; u

1

D 

3x

2

; u

2

D x

3

; u

3

D x; u

4

D 

x

4

;

y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D

x

5=2

4

.

9.4.16. W D

ˇ

x x

2

x

3

x

4

1 2x 3x

2

4x

3

0 2 6x 12x

2

0 0 6 24x

ˇ

D 12x

4

; W

1

D

ˇ

x

2

x

3

x

4

2x 3x

2

4x

3

2 6x 12x

2

ˇ

D 2x

6

; W

2

D

ˇ

x x

3

x

4

1 3x

2

4x

3

0 6x 12x

2

ˇ

D

6x

5

; W

3

D

ˇ

x x

2

x

4

1 2x 4x

3

0 2 12x

2

ˇ

D 6x

4

; W

4

D

ˇ

x x

2

x

3

1 2x 3x

2

0 2 6x

ˇ

D 2x

3

; u

0

1

D 

F W

1

P

0

W

D 

x

2

6

;

u

0

2

D

F W

2

P

0

W

D

x

2

; u

0

3

D 

F W

2

P

0

W

D 

1

2

; u

0

4

D

F W

4

P

0

W

D

1

6x

; u

1

D 

x

3

18

; u

2

D

x

2

4

; u

3

D 

x

2

;

u

4

D

ln jxj

6

; y

p

D u

1

y

1

Cu

2

y

2

Cu

3

y

3

D

x

4

ln jxj

6



11x

4

36

. Since 

11x

4

36

satisﬁes the complementary

equation we take y

p

D

x

4

ln jxj

6

.

9.4.18. W D

ˇ

x x

2

1=x 1=x

2

1 2x 1=x

2

2=x

3

0 2 2=x

3

6=x

4

0 0 6=x

4

24=x

5

ˇ

D 72=x

6

; W

1

D

ˇ

x

2

1=x 1=x

2

2x 1=x

2

2=x

3

2 2=x

3

6=x

4

ˇ

D 12=x

4

;

W

2

D

ˇ

x 1=x 1=x

2

1 1=x

2

2=x

3

0 2=x

3

6=x

4

ˇ

D 6=x

5

; W

3

D

ˇ

x x

2

1=x

2

1 2x 2=x

3

0 2 6=x

4

ˇ

D 12=x

2

; W

4

D

ˇ

x x

2

1=x

1 2x 1=x

2

0 2 2=x

3

ˇ

D

6=x; u

0

1

D 

F W

1

P

0

W

D 2; u

0

2

D

F W

2

P

0

W

D 1=x; u

0

3

D 

F W

2

P

0

W

D 2x

2

; u

0

4

D

F W

4

P

0

W

D x

3

; u

1

D 2x;

u

2

D ln jxj; u

3

D 2x

3

=3; u

4

D x

4

=4; y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D x

2

ln jxj  19x

2

=12. Since

19x

2

=12 satisﬁes the complementary equation we take y

p

D x

2

ln jxj.

184 Chapter 9

Linear Higher Order Equations

9.4.20. W D

ˇ

e

x

e

2x

e

x

=x

e

2x

x

e

x

2e

2x

e

x

.x  1/

x

2

e

2x

.2x  1/

x

2

e

x

4e

2x

e

x

.x

2

 2x C 2/

x

3

2e

2x

.2x

2

 2x C 1/

x

3

e

x

8e

2x

e

x

.x

3

 3x

2

C 6x  6/

x

4

2e

2x

.4x

3

 6x

2

C 6x  3/

x

4

ˇ

D 

e

6x

x

4

;

W

1

D

ˇ

e

2x

e

x

e

2x

x

2e

2x

e

x

.x  1/

x

2

e

2x

.2x  1/

x

2

4e

2x

e

x

.x

2

 2x C 2/

x

3

2e

2x

.2x

2

 2x C 1/

x

3

ˇ

D

e

5x

x

3

;

W

2

D

ˇ

e

x

e

x

e

2x

x

e

x

e

x

.x  1/

x

2

e

2x

.2x  1/

x

2

e

x

e

x

.x

2

 2x C2/

x

3

2e

2x

.2x

2

 2x C 1/

x

3

ˇ

D 

e

4x

x

3

;

W

3

D

ˇ

e

x

e

2x

e

2x

x

e

x

2e

2x

e

2x

.2x  1/

x

2

e

x

4e

2x

2e

2x

.2x

2

 2x C 1/

x

3

ˇ

D

e

5x

.2  x/

x

3

;

W

4

D

ˇ

e

x

e

2x

e

x

e

x

2e

2x

e

x

.x  1/

x

2

e

x

4e

2x

e

x

.x

2

 2x C 2/

x

3

ˇ

D

e

4x

.x C 2/

x

3

;

u

0

1

D 

F W

1

P

0

W

D 3; u

0

2

D

F W

2

P

0

W

D 3e

x

; u

0

3

D 

F W

2

P

0

W

D 3.2  x/; u

0

4

D

F W

4

P

0

W

D 3e

x

.x C 2/;

u

1

D 3x; u

2

D 3e

x

; u

3

D 3x.4  x/=2; u

4

D 3e

x

.x C 3/; y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D

3e

x

.x

2

C 4x C 6/

2x

. Since

3e

x

.2x C 3/

x

is a solution of the complementary equation we t ake y

p

D

3xe

x

2

.

9.4.22. W D

ˇ

x x

3

x ln x

1 3x

2

1 C ln x

0 6x 1=x

ˇ

D 4x

2

; W

1

D

ˇ

x

3

x ln x

3x

2

1 C ln x

ˇ

D x

3

 2x

3

ln x; W

2

D

ˇ

x x ln x

1 1 C ln x

ˇ

D x; W

3

D

ˇ

x x

3

1 3x

2

ˇ

D 2x

3

; u

0

1

D

F W

1

P

0

W

D 2 ln x=x 

1

x

; u

0

2

D 

F W

2

P

0

W

D

1

x

3

;

u

0

3

D

F W

2

P

0

W

D 

2

x

; u

1

D .ln x/

2

 ln x; u

2

D 

1

2x

2

; u

3

D 2 ln x; y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D

x.ln x/

2

x ln x 

x

2

. Since x ln x 

x

2

satisﬁes the complementary equation we take y

p

D x.ln x/

2

Section 9.4

Variation of Parameters for Higher Order Equations

185

The general solution is y D x.ln x/

2

C c

1

x Cc

2

x

3

C c

3

x ln x, so

2

4

y

0

y

00

3

5

D

2

6

4

x.ln x/

2

.ln x/

2

 2 ln x



2 ln x

x



2

x

3

7

5

C

2

6

4

x x

3

x ln x

1 3x

2

1 Cln x

0 6x

1

x

3

7

5

2

4

c

1

c

2

c

3

5

Setting x D 1 and imposing the initial conditions yields

2

4

2

3

5

D

2

4

0

2

3

5

C

2

4

1 1 0

1 3 1

0 6 1

3

5

2

4

c

1

c

2

c

3

5

:

Solving this system yields c

1

D 3, c

2

D 1, c

3

D 2. Therefore,y D x.ln x/

2

C 3x C x

3

 2x ln x.

9.4.24. W D

ˇ

e

x

e

2x

xe

x

e

x

2e

2x

e

x

.1  x/

e

x

4e

2x

e

x

.x  2/

ˇ

D e

2x

.6x  5/; W

1

D

ˇ

e

2x

xe

x

2e

2x

e

x

.1  x/

ˇ

D e

x

.1  3x/;

W

2

D

ˇ

e

x

xe

x

e

x

e

x

.1  x/

ˇ

D 1  2x; W

3

D

ˇ

e

x

e

2x

e

x

2e

2x

ˇ

D e

3x

; u

0

1

D

F W

1

P

0

W

D 1  3x; u

0

2

D



F W

2

P

0

W

D e

x

.2x  1/; u

0

3

D

F W

2

P

0

W

D e

2x

; u

1

D

x.2  3x/

2

; u

2

D e

x

.2x C 1/; u

3

D

e

2x

2

;

y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D e

x

.3x

2

C x C 2/=2. Since 

e

x

2

is a solution of the complementary

equation we take y

p

D 

e

x

.3x C 1/x

2

.

The general solution is y D 

e

x

.3x C 1/x

2

C c

1

e

x

C c

2

e

2x

C c

3

xe

x

, so

2

4

y

0

y

00

3

5

D

2

6

4



e

x

.3x C 1/x

2



e

x

.3x

2

C7x C 1/

2



e

x

.3x

2

C 13x C 8/

2

3

7

5

C

ˇ

e

x

e

2x

xe

x

e

x

2e

2x

e

x

.1  x/

e

x

4e

2x

e

x

.x  2/

ˇ

2

4

c

1

c

2

c

3

5

:

Setting x D 0 and imposing the initial conditions yields

2

4

4



3

2

19

3

5

D

2

4

0



1

2

4

3

5

C

2

4

1 1 0

1 2 1

1 4 2

3

5

2

4

c

1

c

2

c

3

5

:

Solving this system yields c

1

D 3, c

2

D 1, c

3

D 4. Therefore, y D 

e

x

.3x C 1/x

2

 3e

x

 e

2x

C

4xe

x

.

9.4.26. W D

ˇ

x x

2

e

x

1 2x e

x

0 2 e

x

ˇ

D e

x

.x

2

2xC2/; W

1

D

ˇ

x

2

e

x

2x e

x

ˇ

D e

x

.x

2

2x/; W

2

D

ˇ

x e

x

1 e

x

ˇ

D

e

x

.x  1/; W

3

D

ˇ

x x

2

1 2x

ˇ

D x

2

; u

0

1

D

F W

1

P

0

W

D x.x  2/; u

0

2

D 

F W

2

P

0

W

D 1  x; u

0

3

D

F W

2

P

0

W

D

x

2

e

x

; y

p

D u

1

y

1

Cu

2

y

2

Cu

3

y

3

D 

x

4

C 6x

2

C 12x C 12

6

. Since 

6x

2

C 12x

6

is a solution of the

complementary equations we take y

p

D 

x

4

C 12

6

.

186 Chapter 9

Linear Higher Order Equations

The general solution is y D 

x

4

C 12

6

C c

1

x C c

2

x

2

C c

3

e

x

, so

2

4

y

0

y

00

3

5

D 

2

4

.x

4

C 12/=6

2x

3

=3

2x

2

3

5

C

ˇ

x x

2

e

x

1 2x e

x

0 2 e

x

ˇ

2

4

c

1

c

2

c

3

5

:

Setting x D 0 and imposing the initial conditions yields

2

4

0

5

0

3

5

D 

2

4

2

0

3

5

C

2

4

0 0 1

1 0 1

0 2 1

3

5

2

4

c

1

c

2

c

3

5

:

Solving this system yields c

1

D 3, c

2

D 1, c

3

D 2. Therefore, y D 

x

4

C 12

6

C3x  x

2

C 2e

x

.

9.4.28. W D

ˇ

x C 1 e

x

e

3x

1 e

x

3e

3x

0 e

x

9e

3x

ˇ

D 2e

4x

.3x1/; W

1

D

ˇ

e

x

e

3x

e

x

3e

3x

ˇ

D 2e

4x

; W

2

D

ˇ

x C 1 e

3x

1 3e

3x

ˇ

D

e

3x

.3x C 2/; W

3

D

ˇ

x C 1 e

x

1 e

x

ˇ

D xe

x

; u

0

1

D

F W

1

P

0

W

D 2e

x

; u

0

2

D 

F W

2

P

0

W

D 3x  2;

u

0

3

D

F W

2

P

0

W

D xe

2x

; u

1

D 2e

x

; u

2

D 

x.3x C 4/

2

; u

3

D 

e

2x

.2x C 1/

4

; y

p

D u

1

y

1

C

u

2

y

2

C u

3

y

3

D 

e

x

.6x

2

C 2x  7/

4

. Since

7e

x

4

is a solution of the complementary equation we take

y

p

D 

xe

x

.3x C 1/

2

The general solution is y D 

xe

x

.3x C 1/

2

C c

1

.x C 1/ C c

2

e

x

C c

3

e

2x

, so

2

4

y

0

y

00

3

5

D

2

4

xe

x

.3x C 1/=2

e

x

.3x

2

C 7x C 1/=2

e

x

.3x

2

C 13x C 8/=2

3

5

C

ˇ

x C 1 e

x

e

3x

1 e

x

3e

3x

0 e

x

9e

3x

ˇ

:

Setting x D 0 and imposing the initial conditions yields

2

4

3

4

5

4

1

4

3

5

D

2

4

0



1

2

4

3

5

C

2

4

1 1 1

1 1 3

0 1 9

3

5

2

4

c

1

c

2

c

3

5

:

Solving this system yields c

1

D

1

2

, c

2

D 

1

4

, c

3

D

1

2

. Therefore, y D 

xe

x

.3x C 1/

2

C

x C 1

2



e

x

4

C

e

2x

2

.

9.4.30. W D

ˇ

x x

2

1

x

x ln x

1 2x 

1

x

2

ln x C 1

0 2

2

x

3

1

x

0 0 

6

x

2



1

x

2

ˇ

D 

12

x

3

; W

1

D

ˇ

x

2

1

x

x ln x

2x 

1

x

2

ln x C 1

2

x

3

1

x

ˇ

D 6

ln x

x



3

x

;

Section 9.4

Variation of Parameters for Higher Order Equations

187

W

2

D

ˇ

x

1

x

x ln x

1 

1

x

2

ln x C 1

0

2

x

3

1

x

ˇ

D 

4

x

2

; W

3

D

ˇ

x x

2

x ln x

1 2x ln x C 1

0 2

1

x

ˇ

D x; W

4

D

ˇ

x x

2

1

x

1 2x 

1

x

2

0 2

2

x

3

ˇ

D

6

x

; u

0

1

D 

F W

1

P

0

W

D 9 ln x=2 

9

4

; u

0

2

D

F W

2

P

0

W

D

3

x

; u

0

3

D 

F W

2

P

0

W

D 

3x

2

4

; u

0

4

D

F W

4

P

0

W

D 

9

2

;

u

1

D

9x ln x

2



27x

4

; u

2

D 3 ln x; u

3

D 

x

3

4

; u

4

D 

9x

2

; y

p

D u

1

y

1

Cu

2

y

2

Cu

3

y

3

D 3x

2

ln x 7x

2

.

Since 7x

2

satisﬁes the complementary equation we take y

p

D 3x

2

ln x.

The general solution is y D 3x

2

ln x C c

1

x C c

2

x

2

C

c

3

x

C c

4

x ln x, so

2

6

4

y

0

y

00

y

000

3

7

5

D

2

6

4

3x

2

ln x

6x ln x C 3x

6 ln x C 9

6

x

3

7

5

C

ˇ

x x

2

1

x

x ln x

1 2x 

1

x

2

ln x C 1

0 2

2

x

3

1

x

0 0 

6

x

2



1

x

2

ˇ

2

6

4

c

1

c

2

c

3

c

4

3

7

5

:

Setting x D 1 and imposing the initial conditions yields

2

6

4

7

11

5

6

3

7

5

D

2

6

4

0

3

9

6

3

7

5

C

ˇ

1 1 1 0

1 2 1 1

0 2 2 1

0 0 6 1

ˇ

2

6

4

c

1

c

2

c

3

c

4

3

7

5

:

Solving this system yields c

1

D 0, c

2

D 7, c

3

D 0, c

4

D 0. Therefore, y D 3x

2

ln x  7x

2

.

9.4.32. W D

ˇ

x

p

x 1=x 1=

p

x

1 1=2

p

x 1=x

2

1=2x

3=2

0 1=4x

3=2

2=x

3

3=4x

5=2

0 3=8x

5=2

6=x

4

15=8x

7=2

ˇ

D 9=8x

6

; W

1

D

ˇ

p

x 1=x 1=

p

x

1=2

p

x 1=x

2

1=2x

3=2

1=4x

3=2

2=x

3

3=4x

5=2

ˇ

D

3=4x

4

; W

2

D

ˇ

x 1=x 1=

p

x

1 1=x

2

1=2x

3=2

0 2=x

3

3=4x

5=2

ˇ

D 3=2x

7=2

; W

3

D

ˇ

x

p

x 1=

p

x

1 1=2

p

x 1=2x

3=2

0 1=4x

3=2

3=4x

5=2

ˇ

D 3=4x

2

;

W

4

D

ˇ

x

p

x 1=x

1 1=2

p

x 1=x

2

0 1=4x

3=2

2=x

3

ˇ

D 3=2x

5=2

; u

0

1

D 

F W

1

P

0

W

D 1=x; u

0

2

D

F W

2

P

0

W

D 2=

p

x;

u

0

3

D 

F W

2

P

0

W

D x; u

0

4

D

F W

4

P

0

W

D 2

p

x; u

1

D ln x; u

2

D 4

p

x; u

3

D x

2

=2; u

4

D 4x

3=2

=3;

y

p

D u

1

y

1

C u

2

y

2

C u

3

y

3

D x ln x  19x=6. since 19x=6 satisﬁes t he complementary equation we

take y

p

D x ln x.

The general solution is y D x ln x C c

1

x C c

2

p

x C c

3

=x C c

4

=

p

x, so

2

6

4

y

0

y

00

y

000

3

7

5

D

2

6

4

x ln x

ln x C 1

1=x

1=x

2

3

7

5

C

ˇ

x

p

x 1=x 1=

p

x

1 1=2

p

x 1=x

2

1=2x

3=2

0 1=4x

3=2

2=x

3

3=4x

5=2

0 3=8x

5=2

6=x

4

15=8x

7=2

ˇ

2

6

4

c

1

c

2

c

3

c

4

3

7

5

:

188 Chapter 9

Linear Higher Order Equations

Setting x D 1 and imposing the initial conditions yields

2

6

4

2

0

4

37

4

3

7

5

D

2

6

4

0

1

1

3

7

5

C

ˇ

1 1 1 1

1 1=2 1 1=2

0 1=4 2 3=4

0 3=8 6 15=8

ˇ

2

6

4

c

1

c

2

c

3

c

4

3

7

5

:

Solving this system yields c

1

D 1, c

2

D 1, c

3

D 1, c

4

D 1. Therefore, y D x ln xCx 

p

x C

1

x

C

1

p

x

.

9.4.34. (a) Since u

0

j

D .1/

nj

F W

j

P

0

W

(1  j  n), the argument used in the derivation of the method of

variation o f parameters impl ies that y

p

is a solution of (A).

(b) Follows immediately from (a), since u

j

.x

0

/ D 0, j D 1; 2; : : : ; n.

(c) Expand the determinant in cofactors of its nth row.

(d) Just differentiate the determinan t n  1 times.

(e) If 0  j  n  2, then

@

j

G.x; t /

@x

j

ˇ

xDt

has tw o identical rows, and is therefore zero, while

@

n1

G.x; t /

@x

j

ˇ

xDt

D W.t/

(f) Since y

p

.x/ D

Z

x

0

G.x; t /F.t/ dt, y

0

p

.x/ D G.x; x/F .x/C

Z

x

0

@G.x; t/

@x

F .t/ dt. But G.x; x/ D

0 from (e), so y

0

p

.x/ D

Z

x

0

@G.x; t/

@x

F .t/ dt. Repeating this argument for j D 1; : : : ; n and invoking

(e) each time yield s the conclusion.

9.4.36.

ˇ

y

1

.t/ y

1

.t/ y

2

.t/

y

0

1

.t/ y

0

1

.t/ y

0

2

.t/

y

1

.x/ y

1

.x/ y

2

.x/

ˇ

D

ˇ

t t

2

1=t

1 2t 1=t

2

x x

2

1=x

ˇ

D x

ˇ

t

2

1=t

2t 1=t

2

ˇ

 x

2

ˇ

t 1=t

1 1=t

2

ˇ

C

1

x

ˇ

t t

2

1 2t

ˇ

D 3x C 2

x

2

t

C

t

2

x

D

.x  t/

2

.2x C t/

xt

:

Since P

0

.t/ D t

3

and W .t/ D

ˇ

t t

2

1=t

1 2t 1=t

2

x x

2

1=x

ˇ

D

6

t

, G.x; t/ D

.x  t/

2

.2x C t/

6xt

3

, so y

p

D

Z

x

0

.x  t/

2

.2x C t/

6xt

3

F .t/ dt .

9.4.38.

ˇ

y

1

.t/ y

1

.t/ y

2

.t/

y

0

1

.t/ y

0

1

.t/ y

0

2

.t/

y

1

.x/ y

1

.x/ y

2

.x/

ˇ

D

ˇ

t 1=t e

t

=t

1 1=t

2

e

t

.1=t  1=t

2

/

x 1=x e

x

=x

ˇ

D x

ˇ

1=t e

t

=t

1=t

2

e

t

.1=t  1=t

2

/

ˇ



1

x

ˇ

t e

t

=t

1 e

t

.1=t  1=t

2

/

ˇ

C

e

x

ˇ

t 1=t

1 1=t

2

ˇ

D

xe

t

2



e

t

.t  2/

xt



2e

x

xt

D

x

2

e

t

 e

t

t.t  2/  2te

x

xt

2

Section 9.4

Variation of Parameters for Higher Order Equations

189

Since P

0

.t/ D t.1  t/ and W.t/ D

ˇ

t 1=t e

t

=t

1 1=t

2

e

t

.1=t  1=t

2

/

0 2=t

3

e

t

.1=t  2=t

2

C 2=t

3

/

ˇ

D

2e

t

.1  t/

t

3

, G.x; t/ D

x

2

 t.t 2/  2te

.xt /

2x.t  1/

2

, so y

p

D

Z

x

0

x

2

 t.t 2/  2te

.xt /

2x.t  1/

2

F .t/ dt .

9.4.40.

ˇ

y

1

.t/ y

1

.t/ y

2

.t/ y

3

.t/

y

0

1

.t/ y

0

1

.t/ y

0

2

.t/ y

0

3

.t/

y

00

1

.t/ y

00

1

.t/ y

00

2

.t/ y

00

3

.t/

y

1

.x/ y

1

.x/ y

2

.x/ y

3

.x/

ˇ

D

ˇ

1 t t

2

1=t

0 1 2t 1=t

2

0 0 2 2=t

3

1 x x

2

1=x

ˇ

D 

ˇ

t t

2

1=t

1 2t 1=t

2

0 2 2=t

3

ˇ

C x

ˇ

1 t

2

1=t

0 2t 1=t

2

0 2 2=t

3

ˇ

x

2

ˇ

1 t 1=t

0 1 1=t

2

0 0 2=t

3

ˇ

C

1

x

ˇ

1 t t

2

0 1 2t

0 0 2

ˇ

D 

6

t

C

6x

t

2



2x

2

t

3

C

2

x

D

2.t  x/

3

xt

3

:

Since P

0

.t/ D t and W.t/ D

ˇ

1 t t

2

1=t

0 1 2t 1=t

2

0 0 2 2=t

3

0 0 0 6=t

4

ˇ

D 

12

t

4

, G.x; t/ D

.x  t/

3

6x

, so y

p

D

Z

x

0

.x  t/

3

6x

F .t/ dt.

9.4.42.

ˇ

y

1

.t/ y

1

.t/ y

2

.t/ y

3

.t/

y

0

1

.t/ y

0

1

.t/ y

0

2

.t/ y

0

3

.t/

y

00

1

.t/ y

00

1

.t/ y

00

2

.t/ y

00

3

.t/

y

1

.x/ y

1

.x/ y

2

.x/ y

3

.x/

ˇ

D

ˇ

1 t

2

e

2t

e

2t

0 2t 2e

2t

2e

2t

0 2 4e

2t

4e

2t

1 x

2

e

2x

e

2x

ˇ

D 

ˇ

t

2

e

2t

e

2t

2t 2e

2t

2e

2t

2 4e

2t

4e

2t

ˇ

C x

2

ˇ

1 e

2t

e

2t

0 2e

2t

2e

2t

0 4e

2t

4e

2t

ˇ

e

2x

ˇ

1 t

2

e

2t

0 2t 2e

2t

0 2 4e

2t

ˇ

C e

2x

ˇ

1 t

2

e

2t

0 2t 2e

2t

0 2 4e

2t

ˇ

D .16t

2

 8/ C 16x

2

 e

2.xt/ t

.8t C 4/ C e

2.xt/

.8t  4/:

Since P

0

.t/ D t and W .t/ D

ˇ

1 t

2

e

2t

e

2t

0 2t 2e

2t

2e

2t

0 2 4e

2t

4e

2t

0 0 8e

2t

8e

2t

ˇ

D 128t,

G.x; t / D

e

2.xt/

.1 C 2t/ C e

2.xt/

.1  2t/  4x

2

C 4t

2

 2

32t

2

, so

y

p

D

Z

x

0

e

2.xt/

.1 C 2t/ C e

2.xt/

.1  2t/  4x

2

C 4t

2

 2

32t

2

F .t/ dt.

CHAPTER 1 0

Linear Systems of D ifferential

Equations

10.1 INTRODUCTION TO SYST EMS OF DIFFERENTIAL EQUATIONS

10.1.2. Q

0

1

D .rate in/

1

 .rate out/

1

and Q

0

2

D .rate in/

2

 .rate out/

2

.

The volumes of the solutions in T

1

and T

2

are V

1

.t/ D 100 C 2t and V

2

.t/ D 100 C 3t, respectively.

T

1

receives salt from the external source at the rate of (2 lb/gal)  (6 gal/min) D 12 lb/min, and fr om

T

2

at the rate of (lb /gal in T

2

/  (1 gal/min) D

1

100 C 3t

Q

2

lb/min. Therefore, (A) (r ate in)

1

D 12 C

1

100 C 3t

Q

2

. Solution leaves T

1

at 5 gal/min, since 3 gal/min are dr ained and 2 gal/min are pumped to

T

2

; hence (B) .rate out/

1

D . lb/gal in T

1

/ (5 gal/min) D

1

100 C 2t

Q

1

5 D

5

100 C 2t

Q

1

. Now (A)

and (B) imply that (C) Q

0

1

D 12 

5

100 C 2t

Q

1

C

1

100 C 3t

Q

2

.

T

2

receives salt from the ex ternal source at the rate of (1 lb/gal)  (5 gal/min) D 5 lb/min, and from

T

1

at the rate of (lb/ gal in T

1

/  (2 gal/min) D

1

100 C 2t

Q

1

 2 D

1

50 C t

Q

1

lb/min. Therefore, (D)

(rate in)

2

D 5 C

1

50 C t

Q

1

. Solution leaves T

2

at 4 gal/min, since 3 gal/min are drained and 1 gal/mi n is

pumped to T

1

; hence (E) .rate out/

2

D . lb/gal in T

2

/(4 gal/ min) D

1

100 C 3t

Q

2

4 D

4

100 C 3t

Q

2

.

Now (D) and (E) imply that (F) Q

0

2

D 5 C

1

50 C t

Q

1



4

100 C 3t

Q

2

. Now (C) and (F) for m the desired

system.

10.1.4. mX

00

D ˛X

0

 mgR

2

X

kXk

3

; see Example 10.1.3.

10.1.8.

I

1i

D g

1

.t

i

; y

1i

; y

2i

/;

J

1i

D g

2

.t

i

; y

1i

; y

2i

/;

I

2i

D g

1

.t

i

C h; y

1i

C hI

1i

; y

2i

C hJ

1i

/ ;

J

2i

D g

2

.t

i

C h; y

1i

C hI

1i

; y

2i

C hJ

1i

/ ;

y

1;iC1

D y

1i

C

h

2

.I

1i

C I

2i

/;

y

2;i C1

D y

2i

C

h

2

.J

1i

C J

2i

/:

191

192 Chapter 10

Linear Systems of D ifferential Equations

10.2 LINEAR SYSTEMS OF DIFFEREN TIAL EQUATIONS

10.2.6. Let y

i

D y

.i1/

, i D 1; 2; : : : ; n; then y

0

i

D y

iC1

, i D 1; 2; : : :; n 1 and P

0

.t/y

0

n

CP

1

.t/y

n

C

 C P

n

.t/y

1

D F.t/, so

A D 

1

P

0

2

6

4

0 1 0  0

0 0 1  0

:

0 0 0  1

P

n

P

n1

P

n2

 P

1

3

7

5

and f D

1

P

0

2

6

4

0

:

0

F

3

7

5

:

If P

0

; P

1

; : : : ; P

n

and F are continuous and P

0

has no zer os on .a; b/, then P

1

=P

0

; : : : ; P

n

=P

0

and F=P

0

are contnuous on .a; b/.

10.2.7. (a) .c

1

P Cc

2

Q/

0

ij

D .c

1

p

ij

Cc

2

q

ij

/

0

D c

1

p

0

ij

Cc

2

q

0

ij

D .c

1

P

0

Cc

2

Q

0

/

ij

; hence .c

1

P Cc

2

Q/

0

D

c

1

P

0

C c

2

Q

0

.

(b) Let P be k  r and Q b e r  s; then PQ is k s and .PQ/

ij

D

r

X

łD1

p

ił

q

łj

. Therefore, .PQ/

0

ij

D

r

X

łD1

p

0

ił

q

łj

C

r

X

łD1

p

ił

q

0

łj

D .P

0

Q/

ij

C .PQ

0

/

ij

. Therefore, .PQ/

0

D P

0

Q C PQ

0

.

10.2.10. (a) From Exercise 10.2.7(b) with P D Q D X, .X

2

/

0

D .XX/

0

D X

0

X C XX

0

.

(b) By starting from Exercise 10.2.7(b) and using in duction it can be shown if P

1

; P

2

; : : : ; P

n

are

square matrices of the same order, then .P

1

P

2

P

n

/

0

D P

0

1

P

2

P

n

CP

1

P

0

2

P

n

CCP

1

P

2

P

0

n

.

Taking P

1

D P

2

D  D P

n

D X yields ( A ) .Y

n

/

0

D Y

0

Y

n1

C Y Y

0

Y

n2

C Y

2

Y

0

Y

n3

C  C

Y

n1

Y

0

D

n1

X

rD0

Y

r

Y

0

Y

nr1

.

(c) If Y is a scalar function, then (A) reduces to the familiar result .Y

n

/

0

D nY

n1

Y

0

.

10.2.12. From Exercise 10.2.6, the initial value problem (A) P

0

.x/y

.n/

CP

1

.x/y

.n1/

CCP

n

.x/y D

F .x/, y.x

0

/ D k

0

; y

0

.x

0

/ D k

1

; : : : ; y

.n1/

.x

0

/ D k

n1

is equivalent to the initial value problem (B)

y

0

D A.t/y C f.t/, with

A D 

1

P

0

2

6

4

0 1 0  0

0 0 1  0

:

0 0 0  1

P

n

P

n1

P

n2

 P

1

3

7

5

; f D

1

P

0

2

6

4

0

:

0

F

3

7

5

; and k D

2

6

4

k

0

k

1

:

k

n1

3

7

5

:

Since Theorem 10.2.1 implies that (B) has a unique solution on .a; b/, it f ollows that (A) does also.

10.3 BASIC THEORY OF HOMOGENEOUS LINEAR SYSTEM

10.3.2. (a) The system equivalent of (A) is (B) y

0

D 

1

P

0

.x/



0 1

P

2

.x/ P

1

.x/



y, where y D



y

0



.

Let y

1

D



y

1

y

0

1



and y

1

D



y

2

y

0

2



. Then t he Wronskian of fy

1

; y

2

g as deﬁned in this section is



y

1

y

2

y

0

1

y

0

2



D W .

Section 10.3

Basic Theory of Homogeneous Linear System

193

(b) The trace o f the matrix in (B) is P

1

.x/=P

0

.x/, so Eqn. 10.3.6 implies that W .x/ D W.x

0

/ exp





Z

x

0

P

1

.s/

P

0

.s/

ds



.

10.3.4. (a) See t he solution of Exercise 9.1.18.

(c)

ˇ

y

0

11

y

0

12

y

21

y

22

ˇ

D

ˇ

a

11

y

11

C a

12

y

21

a

11

y

12

C a

12

y

22

y

21

y

22

ˇ

D a

11

ˇ

y

11

y

12

y

21

y

22

ˇ

Ca

12

ˇ

y

21

y

22

y

21

y

22

ˇ

D

a

11

W C a

12

0 D a

11

W . Similarly,



y

11

y

12

y

0

21

y

0

22



D a

22

W .

10.3.6. (a) From t he equ ivalence of Theorem 10.3.3(b)and (e), Y.t

0

/ is invertible.

(b) From the equivalence of Theorem 10.3.3(a)and (b), the solution of the initial value problem is

y D Y.t/c, where c is a constant vector. To satisfy y.t

0

/ D k, we must have Y.t

0

/c D k, so c D Y

1

.t

0

/k

and y D Y

1

.t

0

/Y.t/k.

10.3.8. (b) y D



e

4t

e

4t



C c

2



2e

3t

5e

3t



where

c

1

 2c

2

D 10

c

1

C 5c

2

D 4

; so c

1

D 6, c

2

D 2, and

y D



6e

4t

C 4e

3t

6e

4t

 10e

3t



.

(c) Y .t/ D



e

4t

2e

3t

e

4t

5e

3t



; Y.0/ D



1 2

1 5



; Y

1

.0/ D

1

7



5 2

1 1



; y D Y .t/Y

1

.0/k D

1

7



5e

4t

C2e

3t

2e

4t

 2e

3t

5e

4t

 5e

3t

2e

4t

C5e

3t



k.

10.3.10. (b) y

1

D c

1



e

3t

e

3t



C c

2



e

t

e

t



, where

c

1

C c

2

D 2

c

1

 c

2

D 8

; so c

1

D 5, c

2

D 3, and

y D



5e

3t

 3e

t

5e

3t

C3e

t



.

(c) Y.t/ D



e

3t

e

t

3e

3t

e

t



; Y.0/ D



1 1

1 1



;

Y

1

.0/ D

1

2



1 1

1 1



; y D Y .t/Y

1

.0/k D

1

2



e

3t

C e

t

e

3t

 e

t

e

3t

 e

t

e

3t

Ce

t



k.

10.3.12. (b) y D c

1

2

4

e

2t

0

e

2t

3

5

Cc

2

4

e

2t

e

2t

0

3

5

Cc

3

2

4

e

4t

e

4t

e

4t

3

5

, where

c

1

 c

2

C c

3

D 0

c

2

C c

3

D 9

c

1

C c

3

D 12

; so

c

1

D 11, c

2

D 10, c

3

D 1, and y D

1

3

2

4

e

2t

C e

4t

10e

2t

C e

4t

11e

2t

C e

4t

3

5

.

(c) Y.t/ D

2

4

e

2t

e

2t

e

4t

0 e

2t

e

4t

e

2t

0 e

4t

3

5

; Y.0/ D

2

4

1 1 1

0 1 1

1 0 1

3

5

; Y

1

.0/ D

1

3

2

4

1 1 2

1 2 1

1 1 1

3

5

;

y D Y.t/Y

1

.0/k D

1

3

2

4

2e

2t

C e

4t

e

2t

C e

4t

e

2t

C e

4t

e

2t

Ce

4t

2e

2t

C e

4t

e

2t

C e

4t

e

2t

Ce

4t

e

2t

C e

4t

2e

2t

Ce

4t

3

5

k.

10.3.14. If Y and Z are both fund amental matrices for y

0

D A.t/y, then Z D C Y , where C is a constant

invertib le matrix. Therefore, ZY

1

D C and Y Z

1

D C

1

.

10.3.16. (a) The Wronskian of fy

1

; y

2

; : : : ; y

n

g equals one when t D t

0

. Apply Theorem 10.3.3.

(b) Let Y be the matrix with columns fy

1

; y

2

; : : : ; y

n

g. From (a), Y is a fundamental matrix for

y

0

D A.t/y on .a; b/. From Exercise 10.3.15(b), so is Z D Y C if C is any invertible constant matrix.

194 Chapter 10

Linear Systems of D ifferential Equations

10.3.18. (a) 

0

1

.t/ D Z

0

.t/Z.s/ D AZ.t/Z.s/ D A.t/ and 

1

.0/ D Z.s/, since Z.0/ D I . 

0

2

.t/ D

Z

0

.t Cs/ D AZ.t Cs/ D A

2

.t/ (since A is constant) and 

2

.0/ D Z.s/. Applying Theorem 10.2.1 t o

the columns of 

1

and 

2

shows that 

1

D 

2

.

(b) With s D t, (a ) implies th at Z.t /Z.t/ D Z.0/ D I ; therefore .Z.t//

1

D Z.t/.

(c) e

0A

D I is analogous to e

oa

D e

0

D 1 when a is a scalar, while e

.tCs/A

D e

tA

e

sA

is analagous

to e

.tCs/a

D e

ta

e

sa

when a is a scalar.

10.4 CONSTANT COEFFICIENT HOMOGENEOUS SYSTEMS I

10.4.2.

1

4

ˇ

5  4 3

3 5  4

ˇ

D . C1=2/. C2/. Eigenvectors associated with 

1

D 1=2 satisfy



3 3

4 4



x

1

x

2



D



0



, so x

1

D x

2

. Taking x

2

D 1 yields y

1

D



1



e

t=2

. Eigenvectors

associated with 

2

D 2 satisfy



3

4

3

4

1 1



x

1

x

2



D



0



, so x

1

D x

2

. Taking x

2

D 1 yields

y

2

D



1

1



e

2t

. Hence y D c

1



1



e

t=2

C c

2



1

1



e

2t

.

10.4.4.

ˇ

1   4

1 1  

ˇ

D .  1/. C 3/. Eigenvectors associated with 

1

D 3 satisfy



2 4

1 2



x

1

x

2



D



0



, so x

1

D 2x

2

. Taking x

2

D 1 yields y

1

D



2

1



e

3t

. Eigenvectors

associated with 

2

D 1 satisfy



2 4

1 2



x

1

x

2



D



0



, so x

1

D 2x

2

. Taking x

2

D 1 yields

y

2

D



2

1



e

t

. Hence y D c

1



2

1



e

3t

C c

2



2

1



e

t

.

10.4.6.

ˇ

4   3

2 1  

ˇ

D .2/.1/. Eigenvectors associated with 

1

D 2 satisfy



2 3



x

1

x

2



D



0



,

so x

1

D

3

2

x

2

. Taking x

2

D 2 yields y

1

D



3

2



e

2t

. Eigenvectors associated with 

2

D 1 sat-

isfy



3 3

2 2



x

1

x

2



D



0



, so x

1

D x

2

. Taking x

2

D 1 yields y

2

D



1



e

t

. Hence y D

c

1



3

2



e

2t

C c

2



1



e

t

.

10.4.8.

ˇ

1   1 2

1 2   3

4 1 1  

ˇ

D . C 3/. C 1/.  2/. The eigenvectors associated with

with 

1

D 3 satisfy the system with aug mented matrix

2

6

4

4 1 2

:

: 0

1 1 3

:

: 0

4 1 2

:

: 0

3

7

5

, which i s row

equivalent to

2

6

4

1 0 1

:

: 0

0 1 2

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D 2x

3

. Taking x

3

D 1 yields y

1

D

Section 10.4

Constant Coefﬁcient Homogeneous Systems I

195

2

4

1

2

1

3

5

e

3t

. The eigenvectors associated with with 

2

D 1 satisfy the system with augmented ma-

trix

2

6

4

2 1 2

:

: 0

1 1 3

:

: 0

4 1 0

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 4 0

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D 4x

3

. Taking x

3

D 1 yields y

2

D

2

4

1

4

1

3

5

e

t

. The eigenvectors associated w ith with



3

D 2 satisfy the system with augmented matri x

2

6

4

1 1 2

:

: 0

1 4 3

:

: 0

4 1 3

:

: 0

3

7

5

, which is row equivalent

to

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D x

3

. Taking x

3

D 1 yields y

3

D

2

4

1

1

3

5

e

2t

.

Hence y D c

1

2

4

1

2

1

3

5

e

3t

C c

2

4

1

4

1

3

5

e

t

C c

3

2

4

1

1

3

5

e

2t

.

10.4.10.

ˇ

3   5 8

1 1   2

1 1 1  

ˇ

D .  1/. C 2/.  2/. The eigenvectors associated with

with 

1

D 1 satisfy the system with augmented matrix

2

6

4

2 5 8

:

: 0

1 2 2

:

: 0

1 1 2

:

: 0

3

7

5

, which is row equiv-

alent to

2

6

4

1 0

2

3

:

: 0

0 1

4

3

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D 

2

3

x

3

and x

2

D 

4

3

x

3

. Taking x

3

D 3 yields y

1

D

2

4

2

4

3

5

e

t

. The eigenvectors associated with with 

2

D 2 satisfy the system with augmented ma-

trix

2

6

4

5 5 8

:

: 0

1 1 2

:

: 0

1 1 1

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 1 0

:

: 0

0 0 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

2

and x

3

D 0. Taking x

2

D 1 yields y

2

D

2

4

1

1

0

3

5

e

2t

. The ei genvectors associated with with

196 Chapter 10

Linear Systems of D ifferential Equations



3

D 2 satisfy the system with augmented matrix

2

6

4

1 5 8

:

: 0

1 3 2

:

: 0

1 1 3

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0

7

4

:

: 0

0 1

5

4

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D 

7

4

x

3

and x

2

D 

5

4

x

3

. Taking x

3

D 4 yields y

3

D

2

4

7

5

4

3

5

e

2t

.

Hence y D c

1

2

4

2

4

3

5

e

t

C c

2

4

1

1

0

3

5

e

2t

C c

3

2

4

7

5

4

3

5

e

2t

.

10.4.12.

ˇ

4   1 4

4 3   2

1 1 1  

ˇ

D .  3/. C 2/. C 1/. The eigenvectors associated with



1

D 3 satisfy the system with augmented matrix

2

6

4

1 1 4

:

: 0

4 6 2

:

: 0

1 1 4

:

: 0

3

7

5

, which is row equiva-

lent t o

2

6

4

1 0 11

:

: 0

0 1 7

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D 11x

3

and x

2

D 7x

3

. Taking x

3

D 1 yields y

1

D

2

4

11

7

1

3

5

e

3t

. The eigenvectors associated with 

2

D 2 satisfy the system with augmented matrix

2

6

4

6 1 4

:

: 0

4 1 2

:

: 0

1 1 1

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 2

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D

2x

3

. Taking x

3

D 1 yields y

2

D

2

4

1

2

1

3

5

e

2t

. The eigenvectors associated wi th 

3

D 1 satisfy the sys-

tem with augmented matrix

2

6

4

5 1 4

:

: 0

4 2 2

:

: 0

1 1 0

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

.

Hence x

1

D x

3

and x

2

D x

3

. Taking x

3

D 1 yields y

3

D

2

4

1

3

5

e

t

. Hence y D c

1

2

4

11

7

1

3

5

e

3t

C c

2

4

1

2

1

3

5

e

2t

C c

3

2

4

1

3

5

e

t

.

10.4.14.

ˇ

3   2 2

2 7   2

10 10 5  

ˇ

D . C 5/.  5/

2

. The eigenvectors associated with 

1

D

Section 10.4

Constant Coefﬁcient Homogeneous Systems I

197

5 satisfy the system with augmented matrix

2

6

4

8 2 2

:

: 0

2 12 2

:

: 0

10 10 0

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 

1

5

:

: 0

0 1 

1

5

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D

1

5

x

3

and x

2

D

1

5

x

3

. Taking x

3

D 5 yields y

1

D

2

4

1

5

3

5

e

5t

. The

eigenvectors associated with 

2

D 5 satisfy the system with augmented matrix

2

6

4

2 2 2

:

: 0

2 2 2

:

: 0

10 10 10

:

: 0

3

7

5

,

which is row equivalent to

2

6

4

1 1 1

:

: 0

0 0 0

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

2

 x

3

. Taking x

2

D 0 and x

3

D

1 yields y

2

D

2

4

1

0

1

3

5

e

5t

. Taking x

2

D 1 and x

3

D 0 yields y

3

D

2

4

1

0

3

5

e

5t

. Hence y D

c

1

2

4

1

5

3

5

e

5t

C c

2

4

1

0

1

3

5

e

5t

C c

3

2

4

1

0

3

5

e

5t

.

10.4.16.

ˇ

7   4

6 7  

ˇ

D .5/.C5/. Eigenvectors associated with 

1

D 5 satisfy



12 4

6 2



x

1

x

2



D



0



,

so x

1

D

x

2

3

. Taking x

2

D 3 yields y

1

D



1

3



e

5t

. Eigenvectors associated with 

2

D 5 satisfy



2 4

6 12



x

1

x

2



D



0



, so x

1

D 2x

2

. Taking x

2

D 1 yield s y

2

D



2

1



e

5t

. The general

solution is y D c

1



1

3



e

5t

C c

2



2

1



e

5t

. Now y.0/ D



2

4



) c

1



1

3



C c

2



2

1



D



2

4



,

so c

1

D 2 and c

2

D 2. Therefore, y D 



2

6



e

5t

C



4

2



e

5t

.

10.4.18.

ˇ

21   12

24 15  

ˇ

D .  9/. C 3/. Eigenvectors associated with 

1

D 9 satisfy



12 12

24 24



x

1

x

2



D



0



, so x

1

D x

2

. Taking x

2

D 1 yields y

1

D



1



e

9t

. Eigenvec-

tors associated with 

2

D 3



24 12



x

1

x

2



D



0



, so x

1

D

1

2

x

2

. Taking x

2

D 2 yields

y

2

D



1

2



e

3t

. The general solution is y D c

1



1



e

9t

C c

2



1

2



e

3t

. Now y.0/ D



5

3



)

c

1



1



C c

2



1

2



D



5

3



, so c

1

D 7 and c

2

D 2. Therefore, y D



7



e

9t





2

4



e

3t

.

198 Chapter 10

Linear Systems of D ifferential Equations

10.4.20.

ˇ

1

6

 

1

3

0

2

3



1

6

  0

0 0

1

2

 

ˇ

D . C 1=2/.  1=2/

2

. The eigenvectors associated with wi th



1

D 1=2 satisfy the system with augmented matrix

2

6

4

2

3

1

3

0

:

: 0

2

3

1

3

0

:

: 0

0 0 1

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1

2

0

:

: 0

0 0 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D 

x

2

and x

3

D 0. Taking x

2

D 2 yield s y

1

D

2

4

1

2

0

3

5

e

t=2

.

The eigenvectors associated wi th with 

2

D 

3

D 1=2 satisfy the system with augmented matrix

2

6

4



1

3

1

3

0

:

: 0

2

3



2

3

0

:

: 0

0 0 0

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 1 0

:

: 0

0 0 0

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

2

and

x

3

is arbitrary. Taking x

2

D 1 and x

3

D 0 yields y

2

D

2

4

1

0

3

5

e

t=2

. Taking x

2

D 0 and x

3

D 1 yields

y

3

D

2

4

0

1

3

5

e

t=2

. The general sol ution is y D c

1

2

4

1

2

0

3

5

e

t=2

C c

2

4

1

0

3

5

e

t=2

C c

3

2

4

0

1

3

5

e

t=2

.

Now y.0/ D

2

4

7

1

3

5

) c

1

2

4

1

2

0

3

5

C c

2

4

1

0

3

5

C c

3

2

4

0

1

3

5

e

t=2

D

2

4

7

1

3

5

, so c

1

D 1, c

2

D 5, and

c

3

D 1. Hence y D

2

4

1

2

0

3

5

e

t=2

C

2

4

5

0

3

5

e

t=2

C

2

4

0

1

3

5

e

t=2

.

10.4.22.

ˇ

6   3 8

2 1   2

3 3 5  

ˇ

D .  1/. C 2/.  3/. The eigenvectors associated with



1

D 1 satisfy the system with augmented matrix

2

6

4

5 3 8

:

: 0

2 0 2

:

: 0

3 3 6

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. H ence x

1

D x

3

and x

2

D x

3

. Taking x

3

D yields y

1

D

2

4

1

1

1

3

5

e

t

. The

eigenvectors associated with 

2

D 2 satisfy the system with augmented matrix

2

6

4

8 3 8

:

: 0

2 3 2

:

: 0

3 3 3

:

: 0

3

7

5

,

Section 10.4

Constant Coefﬁcient Homogeneous Systems I

199

which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 0

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D 0. Taking x

3

D 1 yields

y

2

D

2

4

1

0

1

3

5

e

2t

. The eigenvectors associated with 

3

D 3 satisfy the system with augmented matrix

2

6

4

3 3 8

:

: 0

2 2 2

:

: 0

3 3 8

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 1 0

:

: 0

0 0 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

2

and x

3

D

0. Taking x

2

D 1 yields y

3

D

2

4

1

0

3

5

e

3t

. The general solution is y D c

1

2

4

1

1

1

3

5

e

t

C c

2

4

1

0

1

3

5

e

2t

C

c

3

2

4

1

0

3

5

e

3t

. Now y.0/ D

2

4

0

1

3

5

) c

1

2

4

1

1

1

3

5

C c

2

4

1

0

1

3

5

C c

3

2

4

1

0

3

5

D

2

4

0

1

3

5

, so c

1

D 2,

c

2

D 3, and c

3

D 1. Therefore, y D

2

4

2

2

2

3

5

e

t



2

4

3

0

3

5

e

2t

C

2

4

1

0

3

5

e

3t

.

10.4.24.

ˇ

3   0 1

11 2  7

1 0 3  

ˇ

D .  2/. C 2/.  4/. The eigenvectors associated with

with 

1

D 2 satisfy the system with augmented matrix

2

6

4

1 0 1

:

: 0

11 4 7

:

: 0

1 0 1

:

: 0

3

7

5

, which is row equiv-

alent to

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D x

3

. Takin g x

3

D 1 yields y

1

D

2

4

1

1

3

5

e

2t

. The eigenvectors associated with w ith 

2

D 2 satisfy the system with augmented ma-

trix

2

6

4

5 0 1

:

: 0

11 0 7

:

: 0

1 0 5

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 0

:

: 0

0 0 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

D 0

and x

2

is arbitrary. Taking x

3

D 1 yield s y

2

D

2

4

0

1

0

3

5

e

2t

. The eigenvectors associated with with

200 Chapter 10

Linear Systems of D ifferential Equations



3

D 4 satisfy the system with augmented matri x

2

6

4

1 0 1

:

: 0

11 6 7

:

: 0

1 0 1

:

: 0

3

7

5

, which is row equivalent

to

2

6

4

1 0 1

:

: 0

0 1 3

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D 3x

3

. Taking x

3

D 1 yield s y

3

D

2

4

1

3

1

3

5

e

4t

.

The general solu tion is y D c

1

2

4

1

1

3

5

e

2t

C c

2

4

0

1

0

3

5

e

2t

C c

3

2

4

1

3

1

3

5

e

4t

. Now y.0/ D

2

4

2

7

6

3

5

)

c

1

2

4

1

1

3

5

C c

2

4

0

1

0

3

5

C c

3

2

4

1

3

1

3

5

D

2

4

2

7

6

3

5

, so c

1

D 2, c

2

D 3, and c

3

D 4. Hence y D

2

4

2

2

3

5

e

2t



2

4

0

3

0

3

5

e

2t

C

2

4

12

4

3

5

e

4t

10.4.26.

ˇ

3   1 0

4 2   0

4 4 2  

ˇ

D .C1/.2/

2

. The eigenvectors associated with 

1

D 1 sat-

isfy the system with augmented matrix

2

6

4

4 1 0

:

: 0

4 1 0

:

: 0

4 4 3

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 

1

4

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

Hence x

1

D x

2

=4 and x

2

D x

3

. Taking x

3

D 4 yields y

1

D

2

4

1

4

3

5

e

t

. The eigenvectors associated

with with 

2

D 

3

D 2 satisfy the system with augmented matri x

2

6

4

1 1 0

:

: 0

4 4 0

:

: 0

4 4 0

:

: 0

3

7

5

, which is row

equivalent to

2

6

4

1 1 0

:

: 0

0 0 0

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

2

and x

3

is arbitrary. Taking x

2

D 1 and x

3

D 0

yields y

2

D

2

4

1

0

3

5

e

2t

. Taking x

2

D 0 and x

3

D 1 yields y

3

D

2

4

0

1

3

5

e

2t

. The general solution is

y D c

1

2

4

1

4

3

5

e

t

C c

2

4

1

0

3

5

e

2t

C c

3

2

4

0

1

3

5

e

2t

. Now y.0/ D

2

4

7

10

2

3

5

) c

1

2

4

1

4

3

5

C c

2

4

1

0

3

5

C

c

3

2

4

0

1

3

5

D

2

4

7

10

2

3

5

, so c

1

D 1, c

2

D 6, and c

3

D 2. Hence y D

2

4

1

4

3

5

e

t

C

2

4

6

2

3

5

e

2t

.

Section 10.5

Constant Coefﬁcient Homogeneous Systems II

201

10.4.28. ( a) If y.t

0

/ D 0, then y is the solution of the initial value p roblem y

0

D Ay; y.t

0

/ D 0 . Sin ce

y  0 is a solution of this problem, Theorem 10.2.1 implies the conclusion.

(b) It is given that y

0

1

.t/ D Ay

1

.t/ for all t. Replacing t by t  shows that y

0

1

.t / D Ay

1

.t / D

Ay

2

.t/ for all t. Since y

0

2

.t/ D y

0

1

.t   / by the chain r ule, this implies that y

0

2

.t/ D Ay

2

.t/ for all t .

(c) If z.t/ D y

1

.t /, then z.t

2

/ D y

1

.t

1

/ D y

2

.t

2

/; therefore z and y

2

are both so lutions of the initial

value prob lem y

0

D Ay; y.t

2

/ D k, where k D y

2

.t

2

/.

10.4.42. The characteristic polynomial of A is p./ D 

2

 .a C b/ C ab  ˛ˇ, so the eigenvalues of

A are 

1

D

a C b  

2

and 

1

D

a C b C 

2

, where  D

p

.a  b/

2

C 4˛ˇ; x

1

D



b  a C 

2ˇ



and

x

2

D



b  a  

2ˇ



are associated eigenvectors. Since  > jb  aj, if L

1

and L

2

are l ines t hrough

the origin parallel to x

1

and x

2

, then L

1

is in the ﬁrst and third quadrants and L

2

is in the second and

fourth quadrants. The slope of L

1

is  D

2ˇ

b  a C 

> 0. I f Q

0

D P

0

there are three possibilities:

(i) if ˛ˇ D ab, then 

1

D 0 and P .t/ D P

0

, Q.t/ D Q

0

for all t > 0; (ii) if ˛ˇ < ab, then



1

> 0 and li m

t!1

P.t/ D lim

t!1

Q.t/ D 1 (monotonically); (iii) if ˛ˇ > ab, then 

1

< 0 and

lim

t!1

P.t/ D lim

t!1

Q.t/ D 0 (monotonically). Now suppo se Q

0

¤ P

0

, so that the trajectory

cannot intersect L

1

, and assume for the moment that ( A) makes sense for all t > 0; that is, even if

one or the other of P and Q is negative. Since 

2

> 0 it follows that either lim

t!1

P.t/ D 1 or

lim

t!1

Q.t/ D 1 (or both), and the trajectory is asymptotically parallel to L

2

. Therefore,the trajectory

must cross in to the third quadrant (so P .T / D 0 and Q.T / > 0 for some ﬁni te T ) if Q

0

> P

0

, or into

the fourth quadrant (so Q.T / D 0 and P .T / > 0 for some ﬁn ite T ) if Q

0

< P

0

.

10.5 CONSTANT COEFFICIENT HOMOGENEOUS SYSTEMS II

10.5.2.

ˇ

 1

1 2  

ˇ

D .C1/

2

. Hence 

1

D 1. Eigenvectors satisfy



1 1



x

1

x

2



D



0



,

so x

1

D x

2

. Taking x

2

D 1 yields y

1

D



1



e

t

. For a second solution we need a vector u such that



1 1



u

1

u

2



D



1



. Let u

1

D 1 and u

2

D 0. Then y

2

D



1

0



e

t

C



1



te

t

. The general

solution is y D c

1



1



e

t

C c

2



1

0



e

t

C



1



te

t



.

10.5.4. y

0

D

ˇ

3   1

1 1  

ˇ

D .2/

2

. Hence 

1

D 2. Eigenvectors satisfy



1 1

1 1



x

1

x

2



D



0



,

so x

1

D x

2

. Taking x

2

D 1 yields y

1

D



1

1



e

2t

. For a secon d solution we need a vecto r u such th at



1 1

1 1



u

1

u

2



D



1

1



. Let u

1

D 1 and u

2

D 0. Then y

2

D



1

0



e

2t

C



1

1



te

2t

.

The general solution is y D c

1



1

1



e

2t

C c

2



1

0



e

2t

C



1

1



te

2t



.

10.5.6.

ˇ

10   9

4 2  

ˇ

D .C4/

2

. Hence 

1

D 4. Eigenvectors satisfy



6 9

4 6



x

1

x

2



D



0



,

so x

1

D

3

2

x

2

. Taking x

2

D 2 yields y

1

D



3

2



e

4t

. For a second solution we need a vector u such that



6 9

4 6



u

1

u

2



D



3

2



. Let u

1

D 

1

2

and u

2

D 0. Then y

2

D



1

0



e

4t

2

C



3

2



te

4t

. The

202 Chapter 10

Linear Systems of D ifferential Equations

general solution is y D c

1



3

2



e

4t

C c

2



1

0



e

4t

2

C



3

2



te

4t



.

10.5.8.

2

4

 2 1

4 6   1

0 4 2  

3

5

D .  4/

2

. Hence 

1

D 0 and 

2

D 

3

D 4. The eigenvectors

associated with 

1

D 0 satisfy the system with augmented matrix

2

6

4

0 2 1

:

: 0

4 6 1

:

: 0

0 4 2

:

: 0

3

7

5

, which is

row equivalent to

2

6

4

1 0

1

2

:

: 0

0 1

1

2

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D 

1

2

x

3

and x

2

D 

1

2

x

3

. Taking x

3

D 2 yields

y

1

D

2

4

1

2

3

5

. The eigenvectors associated with 

2

D 4 satisfy the system with augmented matrix

2

6

4

4 2 1

:

: 0

4 2 1

:

: 0

0 4 2

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 

1

2

:

: 0

0 1 

1

2

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D

1

2

x

3

and

x

2

D

1

2

x

3

. Taking x

3

D 2 yields y

2

D

2

4

1

2

3

5

e

4t

. For a third solution we need a vector u such

that

2

4

4 2 1

0 4 2

3

5

2

4

u

1

u

2

u

3

5

D

2

4

1

2

3

5

. The augmented matrix of this system is row equivalent to

2

6

4

1 0 

1

2

:

: 0

0 1 

1

2

:

1

2

0 0 0

:

: 0

3

7

5

. Let u

3

D 0, u

1

D 0, and u

2

D

1

2

. Then y

3

D

2

4

0

1

0

3

5

e

4t

2

C

2

4

1

2

3

5

te

4t

. The

general solution is

y D c

1

2

4

1

2

3

5

C c

2

4

1

2

3

5

e

4t

C c

3

0

@

2

4

0

1

0

3

5

e

4t

2

C

2

4

1

2

3

5

te

4t

1

A

:

10.5.10.

2

4

1   1 1

2  2

1 3 1  

3

5

D .  2/. C 2/

2

. Hence 

1

D 2 and 

2

D 

3

D 2. The

eigenvectors associated with 

1

D 2 satisfy the system with augmented matrix

2

6

4

3 1 1

:

: 0

2 2 2

:

: 0

1 3 3

:

: 0

3

7

5

,

Section 10.5

Constant Coefﬁcient Homogeneous Systems II

203

which is row equivalent to

2

6

4

1 0 0

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D 0 and x

2

D x

3

. Taking x

3

D 1 yields

y

1

D

2

4

0

1

3

5

e

2t

. The eigenvectors associated with 

2

D 2 satisfy the system with augmented ma-

trix

2

6

4

1 1 1

:

: 0

2 2 2

:

: 0

1 3 1

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 0

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and

x

2

D 0. Taking x

3

D 1 yields y

2

D

2

4

1

0

1

3

5

e

2t

. For a third solution we need a vector u such

that

2

4

1 1 1

2 2 2

1 3 1

3

5

2

4

u

1

u

2

u

3

5

D

2

4

1

0

1

3

5

. The augmented matrix of this system is row equivalent to

2

6

4

1 0 1

:

1

2

0 1 0

:

1

2

0 0 0

:

: 0

3

7

5

. Let u

3

D 0, u

1

D

1

2

, and u

2

D

1

2

. Then y

3

D

2

4

1

0

3

5

e

2t

2

C

2

4

1

0

1

3

5

te

2t

.

The general solution is

y D c

1

2

4

0

1

3

5

e

2t

C c

2

4

1

0

1

3

5

e

2t

Cc

3

0

@

2

4

1

0

3

5

e

2t

2

C

2

4

1

0

1

3

5

te

2t

1

A

:

10.5.12.

2

4

6   5 3

2 1   3

2 1 1  

3

5

D . C 2/.  4/

2

. Hence 

1

D 2 and 

2

D 

3

D 4. The

eigenvectors associated with 

1

D 2 satisfy the system with augmented matrix

2

6

4

8 5 3

:

: 0

2 1 3

:

: 0

2 1 3

:

: 0

3

7

5

,

which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D x

3

. Taking x

3

D 1

yields y

1

D

2

4

1

1

3

5

e

2t

. The eigenvectors associated with 

2

D 4 satisfy the system with augmented

matrix

2

6

4

2 5 3

:

: 0

2 5 3

:

: 0

2 1 3

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

204 Chapter 10

Linear Systems of D ifferential Equations

and x

2

D x

3

. Taking x

3

D 1 yields y

2

D

2

4

1

3

5

e

4t

. For a third solution we need a vector u such

that

2

4

2 5 3

2 1 3

3

5

2

4

u

1

u

2

u

3

5

D

2

4

1

3

5

. The augmented matrix of this system is row equivalent to

2

6

4

1 0 1

:

1

2

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Let u

3

D 0, u

1

D

1

2

, and u

2

D 0. Then y

3

D

2

4

1

0

3

5

e

4t

2

C

2

4

1

3

5

te

4t

. The

general solution is y D c

1

2

4

1

1

3

5

e

2t

C c

2

4

1

3

5

e

4t

C c

3

0

@

2

4

1

0

3

5

e

4t

2

C

2

4

1

3

5

te

4t

1

A

.

10.5.14.

ˇ

15   9

16 9 

ˇ

D .3/

2

. Hence 

1

D 3. Eigenvectors satisfy



12 9

16 12



x

1

x

2



D



0



,

so x

1

D

3

4

x

2

. Takin g x

2

D 4 yields y

1

D



3

4



e

3t

. For a second solution we need a vector u such

that



12 9

16 12



u

1

u

2



D



3

4



. Let u

1

D

1

4

and u

2

D 0. Then y

2

D



1

0



e

3t

4

C



3

4



te

3t

.

The general solution is y D c

1



3

4



e

3t

C c

2



1

0



e

3t

4

C



3

4



te

3t



. Now y.0/ D



5

8



)

c

1



3

4



C c

2



1

4

0



D



5

8



, so c

1

D 2 and c

2

D 4. Therefore, y D



5

8



e

3t





12

16



te

3t

.

10.5.16.

ˇ

7   24

6 17 

ˇ

D .5/

2

. Hence 

1

D 5. Eigenvectors satisfy



12 24

6 12



x

1

x

2



D



0



,

so x

1

D 2x

2

. Taking x

2

D 1 yiel ds y

1

D



2

1



e

5t

. For a second solution we need a vector u such

that



12 24

6 12



u

1

u

2



D



2

1



. Let u

1

D

1

6

and u

2

D 0. Then y

2

D



1

0



e

5t

6

C



2

1



te

5t

.

The general solution is y D c

1



2

1



e

5t

C c

2



1

0



e

5t

6

C



2

1



te

5t



. Now y.0/ D



3

1



)

c

1



2

1



C c

2



1

6

0



D



3

1



, so c

1

D 1 and c

2

D 6. Therefore, y D



3

1



e

5t





12

6



te

5t

.

10.5.18.

2

4

1   1 0

1 1   2

1 1 1  

3

5

D . 1/. C2/

2

. Hence 

1

D 1 and 

2

D 

3

D 2. The

eigenvectors associated with 

1

D 1 satisfy the system with augmented matrix

2

6

4

2 1 0

:

: 0

1 2 2

:

: 0

1 1 2

:

: 0

3

7

5

,

which is row equivalent to

2

6

4

1 0

2

3

:

: 0

0 1

4

3

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D 

2

3

x

3

and x

2

D 

4

3

x

3

. Taking

Section 10.5

Constant Coefﬁcient Homogeneous Systems II

205

x

3

D 3 yields The eigenvectors associated with 

2

D 2 satisfy t he system with augmented matrix

2

6

4

1 1 0

:

: 0

1 1 2

:

: 0

1 1 1

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 1 0

:

: 0

0 0 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

2

and

x

3

D 0. Taking x

2

D 1 yields y

2

D

2

4

1

1

0

3

5

e

2t

. For a third solution we need a vector u such

that

2

4

1 1 0

1 1 2

1 1 1

3

5

2

4

u

1

u

2

u

3

5

D

2

4

1

1

0

3

5

. The augmented matrix of this system is row equiva-

lent to

2

6

4

1 1 0

:

: 1

0 0 1

:

: 1

0 0 0

:

: 0

3

7

5

. Let u

2

D 0, u

1

D 1, and u

3

D 1. Then y

3

D

2

4

1

0

1

3

5

e

2t

C

2

4

1

1

0

3

5

te

2t

. The general solution is y D c

1

2

4

2

4

3

5

e

t

Cc

2

4

1

1

0

3

5

e

2t

Cc

3

0

@

2

4

1

0

1

3

5

e

2t

C

2

4

1

1

0

3

5

te

2t

1

A

.

Now y.0/ D

2

4

6

5

7

3

5

) c

1

2

4

2

4

3

5

C c

2

4

1

1

0

3

5

C c

3

2

4

1

0

1

3

5

D

2

4

6

5

7

3

5

, so c

1

D 2, c

2

D 3,

and c

3

D 1. Therefore, y D

2

4

8

6

3

5

e

t

C

2

4

2

3

1

3

5

e

2t

C

2

4

1

1

0

3

5

te

2t

.

10.5.20.

2

4

7   4 4

1 0   1

9 5 6  

3

5

D . C 3/.  1/

2

. Hence 

1

D 3 and 

2

D 

3

D 1. The

eigenvectors associated with 

1

D 3 satisfy the system with augmented matrix

2

6

4

4 4 4

:

: 0

1 3 1

:

: 0

9 5 9

:

: 0

3

7

5

,

which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 0

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and x

2

D 0. Taking x

3

D 1 yields

y

1

D

2

4

1

0

1

3

5

e

3t

. The eigenvectors associated with 

2

D 1 satisfy the system with augmented ma-

trix

2

6

4

8 4 4

:

: 0

1 1 1

:

: 0

9 5 5

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 0

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D 0

206 Chapter 10

Linear Systems of D ifferential Equations

and x

2

D x

3

. Taking x

3

D 1 yields y

2

D

2

4

0

1

3

5

e

t

. For a third solution we need a vector u such

that

2

4

8 4 4

1 1 1

9 5 5

3

5

2

4

u

1

u

2

u

3

5

D

2

4

0

1

3

5

. The augmented matrix of this system is row equivalent to

2

6

4

1 0 0

:

: 1

0 1 1

:

: 2

0 0 0

:

: 0

3

7

5

. Let u

3

D 0, u

1

D 1, and u

2

D 2. Then y

3

D

2

4

1

2

0

3

5

e

t

C

2

4

0

1

3

5

te

t

.

The general solution is y D c

1

2

4

1

0

1

3

5

e

3t

C c

2

4

0

1

3

5

e

t

C c

3

0

@

2

4

1

2

0

3

5

e

t

C

2

4

0

1

3

5

te

t

1

A

. Now

y.0/ D

2

4

6

9

1

3

5

) c

1

2

4

1

0

1

3

5

C c

2

4

0

1

3

5

C c

3

2

4

1

2

0

3

5

D

2

4

6

9

1

3

5

, so c

1

D 2, c

2

D 1, and

c

3

D 4. Therefore, y D 

2

4

2

0

2

3

5

e

3t

C

2

4

4

9

1

3

5

e

t



2

4

0

4

3

5

te

t

.

10.5.22.

2

4

4   8 4

3 1   3

1 1 9  

3

5

D . C 4/.  8/

2

. Hence 

1

D 4 and 

2

D 

3

D 8. The

eigenvectors associated with 

1

D 4 satisfy the system with augmented matrix

2

6

4

8 8 4

:

: 0

3 3 3

:

: 0

1 1 13

:

: 0

3

7

5

,

which is row equivalent to

2

6

4

1 1 0

:

: 0

0 0 1

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

2

and x

3

D 0. Taking x

2

D 1 yields

y

1

D

2

4

1

0

3

5

e

t

. The eigenvectors associated with 

2

D 8 satisfy the system with augmented matrix

2

6

4

4 8 4

:

: 0

3 9 3

:

: 0

1 1 1

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 0

:

: 0

0 0 0

:

: 0

3

7

5

. Hence x

1

D x

3

and

x

2

D 0. Taking x

3

D 1 yields y

2

D

2

4

1

0

1

3

5

e

8t

. For a third solution we need a vector u such that

2

4

4 8 4

3 9 3

1 1 1

3

5

2

4

u

1

u

2

u

3

5

D

2

4

1

0

1

3

5

. The augmented matrix o f this system is row equivalent to

Section 10.5

Constant Coefﬁcient Homogeneous Systems II

207

2

6

4

1 0 1

:

3

4

0 1 0

:

: 

1

4

0 0 0

:

: 0

3

7

5

. Let u

3

D 0, u

1

D

3

4

, and u

2

D 

1

4

. Then y

3

D

2

4

3

1

0

3

5

e

8t

4

C

2

4

1

0

1

3

5

te

8t

.

The general solution is c

1

2

4

1

0

3

5

e

t

Cc

2

4

1

0

1

3

5

e

8t

Cc

3

0

@

2

4

3

1

0

3

5

e

8t

4

C

2

4

1

0

1

3

5

te

8t

1

A

. Now y.0/ D

2

4

4

1

3

3

5

) c

1

2

4

1

0

3

5

C c

2

4

1

0

1

3

5

C c

3

2

4

3

4



1

4

0

3

5

D

2

4

4

1

3

3

5

, so c

1

D 1, c

2

D 3, and c

3

D 8.

Therefore, y D 

2

4

1

0

3

5

e

4t

C

2

4

3

2

3

3

5

e

8t

C

2

4

8

0

8

3

5

te

8t

.

10.5.24.

2

4

5   1 1

1 9   3

2 2 4  

3

5

D .  6/

3

. Hence 

1

D 6. The eigenvectors satisfy the system

with augmented matrix

2

6

4

1 1 1

:

: 0

1 3 3

:

: 0

2 2 2

:

: 0

3

7

5

, which is row equival ent to

2

6

4

1 0 0

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

.

Hence x

1

D 0 and x

2

D x

3

. Taking x

3

D 1 yields y

1

D

2

4

0

1

3

5

e

6t

. For a second solution we need a

vector u such t hat

2

4

1 1 1

1 3 3

2 2 2

3

5

2

4

u

1

u

2

u

3

5

D

2

4

0

1

3

5

. The augmented matrix of this system is row

equivalent to

2

6

4

1 0 0

:

: 

1

4

0 1 1

:

1

4

0 0 0

:

: 0

3

7

5

. Let u

3

D 0, u

1

D 

1

4

, and u

2

D

1

4

. Then y

2

D

2

4

1

1

0

3

5

e

6t

4

C

2

4

0

1

3

5

te

6t

. For a third solution we need a vector v such that

2

4

1 1 1

1 3 3

2 2 2

3

5

2

4

v

1

v

2

v

3

5

D

2

6

4



1

4

1

4

0

3

7

5

.

The augmented matrix o f this system is row equivalent to

2

6

4

1 0 0

:

1

8

0 1 1

:

1

8

0 0 0

:

: 0

3

7

5

. Let v

3

D 0, v

1

D

1

8

,

and v

2

D

1

8

. Then y

3

D

2

4

1

0

3

5

e

6t

8

C

2

4

1

1

0

3

5

te

6t

4

C

2

4

0

1

3

5

t

2

e

6t

2

. The general solution is y D

208 Chapter 10

Linear Systems of D ifferential Equations

c

1

2

4

0

1

3

5

e

6t

C c

2

0

@

2

4

1

1

0

3

5

e

6t

4

C

2

4

0

1

3

5

te

6t

1

A

Cc

3

0

@

2

4

1

0

3

5

e

6t

8

C

2

4

1

1

0

3

5

te

6t

4

C

2

4

0

1

3

5

t

2

e

6t

2

1

A

:

10.5.26.

2

4

6   4 4

2 1   1

2 3 1  

3

5

D .C2/

3

. Hence 

1

D 2. The eigenvectors satisfy the sys-

tem with augmented matrix

2

6

4

4 4 4

:

: 0

2 1 1

:

: 0

2 3 3

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 0

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

.

Hence x

1

D 0 and x

2

D x

3

. Taking x

3

D 1 yields y

1

D

2

4

0

1

1

3

5

e

2t

. For a second solution we need a

vector u such that

2

4

4 4 4

2 1 1

2 3 3

3

5

2

4

u

1

u

2

u

3

5

D

2

4

0

1

1

3

5

. The augmented matri x of this system is row

equivalent to

2

6

4

1 0 0

:

: 1

0 1 1

:

: 1

0 0 0

:

: 0

3

7

5

. Let u

3

D 0, u

1

D 1, and u

2

D 1. Then y

2

D

2

4

1

1

0

3

5

e

2t

C

2

4

0

1

1

3

5

te

2t

. For a third solution we need a vect or v such that

2

4

4 4 4

2 1 1

2 3 3

3

5

2

4

v

1

v

2

v

3

5

D

2

4

1

1

0

3

5

. The augmented matrix of this system is row equivalent to

2

6

4

1 0 0

:

3

4

0 1 1

:

: 

1

2

0 0 0

:

: 0

3

7

5

. Let v

3

D 0,

v

1

D

3

4

, and v

2

D 

1

2

. Then y

3

D

2

4

3

2

0

3

5

e

2t

4

C

2

4

1

1

0

3

5

te

2t

C

2

4

0

1

1

3

5

t

2

e

2t

2

. The general

solution is y D c

1

2

4

0

1

1

3

5

e

2t

C c

2

0

@

2

4

1

1

0

3

5

e

2t

C

2

4

0

1

1

3

5

te

2t

1

A

Cc

3

0

@

2

4

3

2

0

3

5

e

2t

4

C

2

4

1

1

0

3

5

te

2t

C

2

4

0

1

1

3

5

t

2

e

2t

2

1

A

10.5.28.

2

4

2   12 10

2 24  11

2 24 8  

3

5

D . C 6/

3

. Hence 

1

D 6. The eigenvectors satisfy the

Section 10.5

Constant Coefﬁcient Homogeneous Systems II

209

system with augmented matrix

2

6

4

4 12 10

:

: 0

2 18 11

:

: 0

2 24 14

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 

1

2

:

: 0

0 0 0

:

: 0

3

7

5

.

Hence x

1

D x

3

and x

2

D

x

3

2

. Taking x

3

D 2 yields y

1

D

2

4

2

1

2

3

5

e

6t

. For a second solu-

tion we need a vector u su ch that

2

4

4 12 10

2 18 11

2 24 14

3

5

2

4

u

1

u

2

u

3

5

D

2

4

2

1

2

3

5

. The augmented matrix

of this system is row equivalent t o

2

6

4

1 0 1

:

: 1

0 1 

1

2

:

: 

1

6

0 0 0

:

: 0

3

7

5

. Let u

3

D 0, u

1

D 1, and u

2

D



1

6

. Then y

2

D 

2

4

6

1

0

3

5

e

6t

6

C

2

4

2

1

2

3

5

te

6t

. For a third solution we need a vector v such that

2

4

4 12 10

2 18 11

2 24 14

3

5

2

4

v

1

v

2

v

3

5

D

2

4

1



1

6

0

3

5

. The augmented matrix of this system is row equivalent to

2

6

4

1 0 1

:

: 

1

3

0 1 

1

2

:

: 

1

36

0 0 0

:

: 0

3

7

5

. Let v

3

D 0, v

1

D 

1

3

, and v

2

D 

1

36

. Then y

3

D 

2

4

12

1

0

3

5

e

6t

36



2

4

6

1

0

3

5

te

6t

6

C

2

4

2

1

2

3

5

t

2

e

6t

2

. The general solution is y D c

1

2

4

2

1

2

3

5

e

6t

C c

2

0

@



2

4

6

1

0

3

5

e

6t

6

C

2

4

2

1

2

3

5

te

6t

1

A

Cc

3

0

@



2

4

12

1

0

3

5

e

6t

36



2

4

6

1

0

3

5

te

6t

6

C

2

4

2

1

2

3

5

t

2

e

6t

2

1

A

:

10.5.30.

2

4

4   0 1

1 3   1

1 0 2  

3

5

D .C3/

3

. Hence 

1

D 3. The eigenvectors satisfy the sys-

tem with augmented matrix

2

6

4

1 0 1

:

: 0

1 0 1

:

: 0

1 0 1

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 0 0

:

: 0

0 0 0

:

: 0

3

7

5

.

Hence x

1

D x

3

and x

2

is arbitrary. Taking x

2

D 0 and x

3

D 1 yields y

1

D

2

4

1

0

1

3

5

e

3t

. Taking x

2

D

1 and x

3

D 0 yields y

2

D

2

4

0

1

0

3

5

e

3t

. For a third solution we need constants ˛ and ˇ and a vector u such

210 Chapter 10

Linear Systems of D ifferential Equations

that

2

4

1 0 1

1 0 1

3

5

2

4

u

1

u

2

u

3

5

D ˛

2

4

1

0

1

3

5

C ˇ

2

4

0

1

0

3

5

. The augmented matrix of this system is row

equivalent to

2

6

4

1 0 1

:

: ˛

0 0 0

:

: ˛ C ˇ

0 0 0

:

: 0

3

7

5

; hence the system has a solution if ˛ D ˇ D 1, whi ch yi elds

the eigenvector x

3

D

2

4

1

1

3

5

. Taking u

1

D 1 and u

2

D u

3

D 0 yields the solution y

3

D

2

4

1

0

3

5

e

3t

C

2

4

1

1

3

5

te

3t

. The general solution is y D c

1

2

4

1

0

1

3

5

e

3t

Cc

2

4

0

1

0

3

5

e

3t

C c

3

0

@

2

4

1

0

3

5

e

3t

C

2

4

1

1

3

5

te

3t

1

A

10.5.32.

2

4

3   1 0

1 1   0

1 1 2  

3

5

D . C 2/

3

. Hence 

1

D 2. The eigenvectors satisfy the

system with augmented matrix

2

6

4

1 1 0

:

: 0

1 1 0

:

: 0

1 1 0

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 1 0

:

: 0

0 0 0

:

: 0

0 0 0

:

: 0

3

7

5

.

Hence x

1

D x

2

and x

3

is arbitrary. Taking x

2

D 1 and x

3

D 0 yields y

1

D

2

4

1

1

0

3

5

e

2t

. Taking x

2

D

0 and x

3

D 1 yields y

2

D

2

4

0

1

3

5

e

2t

. For a third solution we need constants ˛ and ˇ and a vector u such

that

2

4

1 1 0

1 1 0

1 1 0

3

5

2

4

u

1

u

2

u

3

5

D ˛

2

4

1

1

0

3

5

C ˇ

2

4

0

1

3

5

. The augmented matrix of this system is row

equivalent to

2

6

4

1 1 0

:

: ˛

0 0 0

:

: ˛ C ˇ

0 0 0

:

: 0

3

7

5

; hence the system has a solution if ˛ D ˇ D 1, whi ch yi elds

the eigenvector x

3

D

2

4

1

1

1

3

5

. Taking u

1

D 1 and u

2

D u

3

D 0 yields the solut ion y

3

D

2

4

1

0

3

5

e

2t

C

2

4

1

1

1

3

5

te

2t

. The general solution is y D c

1

2

4

1

1

0

3

5

e

2t

C c

2

4

0

1

3

5

e

2t

C c

3

0

@

2

4

1

0

3

5

e

2t

C

2

4

1

1

1

3

5

te

2t

1

A

.

10.5.34.

y

0

3

 Ay

3

D .

1

I  A/ve



1

t

C .

1

I  A/ute



1

t

C ue



1

t

C.

1

I  A/x

t

2

e



1

t

2

C xte



1

t

D ue



1

t

 xte



1

t

C ue



1

t

C 0 C xte



1

t

D 0:

Section 10.6

Constant Coefﬁcient Homogeneous Systems III

211

Now suppose that c

1

y

1

C c

2

y

2

C c

3

y

3

D 0. Then

c

1

x C c

2

.u C tx/ C c

3



v C t u C

t

2

x



D 0: .A/

Differentiatin g this twice yields c

3

x D 0, so c

3

D 0 si nce x ¤ 0. Therefore,(A) reduces to (B) c

1

x C

c

2

.u C tx/ D 0. Differentiating this yields c

2

x D 0, so c

2

D 0 since x ¤ 0. Therefore,(B) reduces to

c

3

x D 0, so c

1

D 0 since x ¤ 0. Therefore,y

1

, y

2

, and y

3

are linearly independendent.

10.6 CONSTANT COEFFICIENT HOMOGENEOUS SYSTEMS III

10.6.2.

ˇ

11   4

26 9 

ˇ

D . C 1/

2

C 4. The augmented matrix of .A  .1 C 2i/ I / x D 0

is

2

4

10  2i 4

:

: 0

26 10  2i

:

: 0

3

5

, which is row equivalent t o

2

4

1

5Ci

13

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

.5  i/x

2

=13. Taking x

2

D 13 yields the eigenvector x D



5  i

13



. Taking real and imaginary parts of

e

t

.cos 2t C i sin 2t//



5  i

13



yields

y D c

1

e

t



5 cos 2t C sin 2t

13 cos 2t



C c

2

e

t



5 sin 2t  cos 2t

13 si n 2t



:

10.6.4.

ˇ

5   6

3 1  

ˇ

D .  2/

2

C 9. H ence,  D 2 C 3i is an eigenvalue of A. The associated

eigenvectors satisfy .A  .2 C 3i / I / x D 0. The augmented matrix of this system is

2

4

3  3i 6

:

: 0

3 3  3i

:

: 0

3

5

,

which is row equivalent to

2

4

1 1  i

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D .1 C i /x

2

. Takin g x

2

D 1 yields

x

1

D 1 C i , so x D



1 C i

1



is an eigenvector. Taking real and imaginary parts of e

2t

.cos 3t C

i sin 3t/



1 C i

1



yields y D c

1

e

2t



cos 3t  si n 3t

cos 3t



C c

2

e

2t



sin 3t C cos 3t

sin 3t



.

10.6.6.

ˇ

3   3 1

1 5   3

3 7 3 

ˇ

D . C 1/



. C 2/

2

C 4



. The augmented matrix of .A C

I /x D 0 is

2

6

4

2 3 1

:

: 0

1 4 3

:

: 0

3 7 4

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D

x

2

D x

3

. Taking x

3

D 1 yields y

1

D

2

4

1

1

3

5

e

t

. The augmented matrix of .A  .2 C 2i /I / x D 0

212 Chapter 10

Linear Systems of D ifferential Equations

is

2

6

4

1  2i 3 1

:

: 0

1 3  2i 3

:

: 0

3 7 5  2i

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 

1Ci

2

:

: 0

0 1

1i

2

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D

.1 C i/

2

x

3

and x

2

D 

.1  i/

2

x

3

. Taking x

3

D 2 yields the eigenvector x

2

D

2

4

1 C i

1 C i

2

3

5

. The real

and imaginary parts of e

2t

.cos 2t C i sin 2t/

2

4

1 C i

1 C i

2

3

5

are y

2

D e

2t

2

4

cos 2t  sin 2t

cos 2t  sin 2t

2 cos 2t

3

5

and

y

3

D e

2t

2

4

sin 2t C cos 2t

sin 2t C cos 2t

2 sin 2t

3

5

. Therefore,

y D c

1

2

4

1

1

3

5

e

t

C c

2

e

2t

2

4

cos 2t  sin 2t

cos 2t  sin 2t

2 cos 2t

3

5

C c

3

e

2t

2

4

sin 2t C cos 2t

sin 2t C cos 2t

2 sin 2t

3

5

:

10.6.8.

ˇ

3   1 3

4 1   2

4 2 3  

ˇ

D .1/



. C 1/

2

C 4



. The augmented matrix of .AI /x D 0

is

2

6

4

4 1 3

:

: 0

4 2 2

:

: 0

4 2 2

:

: 0

3

7

5

, which is row equival ent to

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D x

2

D

x

3

. Taking x

3

D 1 yields y

1

D

2

4

1

1

3

5

e

t

. The augmented matri x of .A  .1 C 2i /I / x D 0 is

2

6

4

2  2i 1 3

:

: 0

4 2i 2

:

: 0

4 2 4  2i

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0

1i

2

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D



1  i

2

x

3

and x

2

D x

3

. Taking x

3

D 2 yields the eigenvector x

2

D

2

4

1 C i

2

3

5

. The real and

imaginary parts of e

t

.cos 2t C i sin 2t/

2

4

1 C i

2

3

5

are y

2

D e

t

2

4

sin 2t  cos 2t

2 cos 2t

3

5

and y

3

D

e

t

2

4

cos 2t  sin 2t

2 sin 2t

3

5

. Therefore,

y D c

1

2

4

1

1

3

5

e

t

C c

2

e

t

2

4

sin 2t  cos 2t

2 cos 2t

3

5

C c

3

e

t

2

4

cos 2t  sin 2t

2 sin 2t

3

5

:

Section 10.6

Constant Coefﬁcient Homogeneous Systems III

213

10.6.10.

1

3

ˇ

7  3 5

2 5  3

ˇ

D .  2/

2

C 1. The augmented matrix of .A .2 C i/I /x D 0 is

1

3

2

4

1  3i 5

:

: 0

2 1  3i

:

: 0

3

5

, which is row equivalent to

2

4

1 

1C3i

2

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

1 C 3i

2

x

2

. Taking x

2

D 2 yields the eigenvector x D



1 C 3i

2



. Taking real and imaginary parts of

e

2t

.cos t C i sin t/



1 C 3i

2



yields

y D c

1

e

2t



cos t  3 sin t

2 cos t



C c

2

e

2t



sin t C 3 cos t

2 sin t



:

10.6.12.

ˇ

34   52

20 30  

ˇ

D .  2/

2

C 16. The augmented matrix of .A  .2 C 4i / I / x D 0

is

2

4

32  4i 52

:

: 0

20 32  4i

:

: 0

3

5

, which is row equivalent to

2

4

1

8Ci

5

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D



.8 C i/

5

x

2

. Taking x

2

D 5 yields the eigenvector x D



8  i

5



. Taking real and imag inary parts of

e

2t

.cos 4tCi si n 4t/



8  i

5



yields y D c

1

e

2t



sin 4t  8 cos 4t

5 cos 4t



C c

2

e

2t



cos 4t  8 sin 4t

5 sin 4t



.

10.6.14.

ˇ

3   4 2

5 7   8

10 13 8  

ˇ

D . C 2/



.  2/

2

C 9



. The augmented matrix of .A C

2I /x D 0 is

2

6

4

5 4 2

:

: 0

5 9 8

:

: 0

10 13 6

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 2

:

: 0

0 1 2

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D

x

2

D 2x

3

. Taking x

3

D 1 yields y

1

D

2

4

2

1

3

5

e

2t

. The augmented matrix of .A  .2 C 3i/I / x D 0 is

2

6

4

1  3i 4 2

:

: 0

5 5  3i 8

:

: 0

10 13 10 3i

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1  i

:

: 0

0 1 i

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D

.1  i /x

3

and x

2

D ix

3

. Taking x

3

D 1 yields t he eigenvector x

2

D

2

4

1 Ci

i

1

3

5

. The real

and imaginary parts of e

2t

.cos 3t C i sin 3t/

2

4

1 C i

i

1

3

5

are y

2

D e

2t

2

4

cos 3t  sin 3t

sin 3t

cos 3t

3

5

and

214 Chapter 10

Linear Systems of D ifferential Equations

y

3

D c

3

e

2t

2

4

sin 3t C cos 3t

cos 3t

sin 3t

3

5

. Therefore,

y D c

1

2

4

2

1

3

5

e

2t

C c

2

e

2t

2

4

cos 3t  sin 3t

sin 3t

cos 3t

3

5

C c

3

e

2t

2

4

sin 3t C cos 3t

cos 3t

sin 3t

3

5

:

10.6.16.

ˇ

1   2 2

0 2   1

1 0 

ˇ

D .  2/



.  1/

2

C 1



. The augmented matrix of .A  I /x D 0

is

2

6

4

0 2 2

:

: 0

0 1 1

:

: 0

1 0 1

:

: 0

3

7

5

, which is row equivalent t o

2

6

4

1 0 1

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D x

2

D 1.

Taking x

3

D 1 yields y

1

D

2

4

1

3

5

e

t

. The augmented matrix of .A  .1 C i /I/ x D 0 is

2

6

4

i 2 2

:

: 0

0 1 i 1

:

: 0

1 0 1  i

:

: 0

3

7

5

,

which is row equivalent to

2

6

4

1 0 1  i

:

: 0

0 1 

1Ci

2

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D .1 C i/x

3

and x

2

D

.1 C i/

2

x

3

.

Taking x

3

D 2 yields the eigenvector x

2

D

2

4

2 C 2i

1 C i

2

3

5

. The real and imaginary parts of e

4t

.cos t C

i sin t/

2

4

2 C 2i

1 C i

2

3

5

are y

2

D e

t

2

4

2 cos t  2 sin t

cos t  sin t

2 cos t

3

5

and y

3

D c

3

e

t

2

4

2 sin t C 2 cos t

cos t C sin t

2 sin t

3

5

. Therefore,

y D c

1

2

4

1

3

5

e

t

C c

2

e

t

2

4

2 cos t  2 sin t

cos t  sin t

2 cos t

3

5

C c

3

e

t

2

4

2 sin t C 2 cos t

cos t C sin t

2 sin t

3

5

:

10.6.18.

ˇ

7   15

3 1  

ˇ

D .  4/

2

C 36. The augmented matrix of .A  .4 C 6i / I / x D 0

is

2

4

3  6i 15

:

: 0

3 3  6i

:

: 0

3

5

, which is row equivalent to

2

4

1 1 C2i

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

.1C2i /x

2

. Taking x

2

D 1 yields the eigenvector x D



1  2i

1



. Taking real and i maginary parts of

e

4t

.cos 6tCi sin 6t/



1  2i

1



yields y D c

1

e

4t



2 sin 6t  cos 6t

cos 6t



C c

2

e

4t



2 cos 6t  sin 6t

sin 6t



.

Now y.0/ D



5

1



)



1 2

1 0



c

1

c

2



D



5

1



, so c

1

D 1, c

2

D 3, and y D e

4t



5 cos 6t C 5 sin 6t

cos 6t  3 sin 6t



.

Section 10.6

Constant Coefﬁcient Homogeneous Systems III

215

10.6.20.

1

6

ˇ

4  6 2

5 2  6

ˇ

D



 

1

2



2

C

1

4

. The augmented matrix of



A 

1 C i

2

I



x D 0

is

1

6

2

4

1  3i 2

:

: 0

5 1  3i

:

: 0

3

5

, which i s row equivalent to

2

4

1 

1C3i

5

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

1 C 3i

5

x

2

. Taking x

2

D 5 yields the eigenvector x D



1 C 3i

5



. Taking real and imaginary parts of

e

t=2

.cos t=2Ci sin t=2/



1 C 3i

5



yields y D c

1

e

t=2



cos t=2  3 sin t=2

5 cos t=2



C c

2

e

t=2



sin t=2 C 3 cos t=2

5 sin t=2



.

Now y.0/ D



1

1



)



1 3

5 0



c

1

c

2



D



1

1



, so c

1

D 

1

5

, c

2

D

2

5

, and y D e

t=2



cos.t=2/ C sin.t=2/

cos.t=2/ C 2 sin.t=2/



.

10.6.22.

ˇ

4   4 0

8 10   20

2 3 2  

ˇ

D .  8/



.  2/

2

C 4



. The augmented matrix of .A 

8I /x D 0 is

2

6

4

0 4 0

:

: 0

8 6 20

:

: 0

2 3 6

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 2

:

: 0

0 1 2

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D

x

2

D 2x

3

. Taking x

3

D 2 yields y

1

D

2

4

2

1

3

5

e

8t

. The augmented matrix of .A  .2 C 2i/I / x D 0 is

2

6

4

2  2i 4 0

:

: 0

8 8  2i 20

:

: 0

2 3 4  2i

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 2 C 2i

:

: 0

0 1 2i

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D

.2  2i /x

3

and x

2

D 2ix

3

. Taking x

3

D 1 yield s the eigenvector x

2

D

2

4

2  2i

2i

1

3

5

. The real and

imaginary parts of e

2t

.cos 2t C i sin 2t/

2

4

2  2i

2i

1

3

5

are y

2

D e

2t

2

4

2 cos 2t C 2 sin 2t

2 sin 2t

2 cos 2t

3

5

and y

3

D

e

2t

2

4

2 sin 2t C 2 cos 2t

2 cos 2t

sin 2t

3

5

, so the general solution is y D c

1

2

4

2

1

3

5

e

8t

Cc

2

e

2t

2

4

2 cos 2t C 2 sin 2t

2 sin 2t

2 cos 2t

3

5

C

c

3

e

2t

2

4

2 sin 2t C 2 cos 2t

2 cos 2t

sin 2t

3

5

. Now y.0/ D

2

4

8

6

5

3

5

)

2

4

2 2 2

2 0 2

1 1 0

3

5

2

4

c

1

c

2

c

3

5

D

2

4

8

6

5

3

5

, so c

1

D 2,

c

2

D 3, c

3

D 1, and y D

2

4

2

3

5

e

8t

C e

2t

2

4

4 cos 2t C 8 sin 2t

6 sin 2t C 2 cos 2t

3 cos 2t C sin 2t

3

5

.

10.6.24.

ˇ

4   4 4

10 3   15

2 3 1  

ˇ

D .  8/.

2

C 16/. The augmented matrix of .A  8I /x D 0 is

216 Chapter 10

Linear Systems of D ifferential Equations

2

6

4

4 4 4

:

: 0

10 5 15

:

: 0

2 3 7

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 2

:

: 0

0 1 1

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D 2x

3

and x

2

D x

3

. Taking x

3

D 1 yield s y

1

D

2

4

2

1

1

3

5

e

8t

. The augmented matrix of .A  4iI / x D 0 is

2

6

4

4  4i 4 4

:

: 0

10 3  4i 15

:

: 0

2 3 1  4i

:

: 0

3

7

5

, which is row equivalent to

2

6

4

1 0 1 C i

:

: 0

0 1 1 C 2i

:

: 0

0 0 0

:

: 0

3

7

5

. Therefore,x

1

D

.1  i /x

3

and x

2

D .1  2i/x

3

. Taking x

3

D 1 yields the eigenvector x

2

D

2

4

1  i

1  2i

1

3

5

. The

real and imaginary parts of .cos 4t C i sin 4t/

2

4

1  i

1  2i

1

3

5

are y

2

D

2

4

cos 4t C sin 4t

cos 4t C 2 sin 4t

cos 4t

3

5

and y

3

D

2

4

sin 4t  cos 4t

sin 4t  2 cos 4t

sin 4t

3

5

, so the general solution is y D c

1

2

4

2

1

1

3

5

e

8t

C c

2

4

cos 4t C sin 4t

cos 4t C 2 sin 4t

cos 4t

3

5

C

c

3

2

4

sin 4t  cos 4t

sin 4t  2 cos 4t

sin 4t

3

5

. Now y.0/ D

2

4

16

14

6

3

5

)

2

4

2 1 1

1 1 2

1 1 0

3

5

2

4

c

1

c

2

c

3

5

D

2

4

16

14

6

3

5

, so c

1

D 3,

c

2

D 3, c

3

D 7, and y D

2

4

6

3

3

5

e

8t

C

2

4

10 cos 4t  4 sin 4t

17 cos 4t  sin 4t

3 cos 4t  7 sin 4t

3

5

.

10.6.28. (a) From the quadratic formul a the root s are

k

1

D

kuk

2

 kv

2

k C

p

.kuk

2

 kv

2

k/

2

C 4.u; v/

2

2.u; v/

k

2

D

kuk

2

 kv

2

k 

p

.kuk

2

 kv

2

k/

2

C 4.u; v/

2

2.u; v/

:

Clearly k

1

> 0 and k

2

< 0. Moreover,

k

1

k

2

D

.kuk

2

 kv

2

k/

2





.kuk

2

 kv

2

k/

2

C 4.u; v/

2



4.u; v/

2

D 1:

(b) Since k

2

D 1= k

1

,

u

.2/

1

D u  k

2

v D u C

1

k

1

v D

1

k

1

.v C k

1

u/ D

1

k

1

v

.1/

1

v

.2/

1

D v C k

2

u D v 

1

k

1

u D 

1

k

1

.u  k

1

v/ D 

1

k

1

u

.1/

1

:

Section 10.6

Constant Coefﬁcient Homogeneous Systems III

217

10.6.30.

ˇ

15   10

25 15  

ˇ

D 

2

C25. The augmented matrix of .A5iI /x D 0 is

2

4

15  5i 10

:

: 0

25 15  5i

:

: 0

3

5

,

which is row equivalent to

2

4

1

3Ci

5

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

.3  i/

5

x

2

. Taking x

2

D 5 yields the

eigenvector x D



3  i

5



, so u D



3

5



and v D



1

0



. The quad ratic equation is 3k

2

33kC3 D

0, with positive root k  :0902. Routine calculations yield U 



:5257

:8507



, V 



:8507

:5257



.

10.6.32.

ˇ

3   15

3 3  

ˇ

D 

2

C36. The augmented matrix of .A6iI /x D 0 is

2

4

3  6i 15

:

: 0

3 3  6i

:

: 0

3

5

,

which is row equ ivalent to

2

4

1 1  2i

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D .1  2i/x

2

. Taking x

2

D 1

yields the eigenvector x D



1 C 2i

1



, so u D



1

1



and v D



2

0



. The quadratic equation is

2k

2

C 2k C 2 D 0, with positive root k  1:6180. Routine calculatio ns yield U 



:9732

:2298



,

V 



:2298

:9732



.

10.6.34.

ˇ

5   12

6 7  

ˇ

D . C 1/

2

C 36. The augmented matrix of .A  .1 C 6i /I /x D 0

is

2

4

6  6i 12

:

: 0

6 6  6i

:

: 0

3

5

, which is row equivalent to

2

4

1 .1 C i/

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

.1 C i/x

2

. Taking x

2

D 1 yields the eigenvector x D



1 C i

1



, so u D



1



and v D



1

0



.

The quadratic equation is k

2

 k  1 D 0, with positive root k  1:6180. Routine calculatio ns yield

U 



:5257

:8507



, V 



:8507

:5257



.

10.6.36.

ˇ

4   9

5 2  

ˇ

D . C 1/

2

C 36. The augmented matrix of .A  .1 C 6i /I /x D 0

is

2

4

3  6i 9

:

: 0

5 3  6i

:

: 0

3

5

, which is row equivalent to

2

4

1 

36i

5

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

3  6i

5

x

2

. Taking x

2

D 5 yields the eigenvector x D



3  6i

5



, so u D



3

5



and v D



6

0



. The

quadratic equation is 18k

2

C 2k C 18 D 0, with positive root k  1:0571. Routine calculations yield

U 



:8817

:4719



, V 



:4719

:8817



.

10.6.38.

ˇ

1   5

20 1  

ˇ

D . C 1/

2

C 100. The augmented matrix of .A  .1 C 10i/I /x D 0

218 Chapter 10

Linear Systems of D ifferential Equations

is

2

4

10i 5

:

: 0

20 10i

:

: 0

3

5

, which is row equivalent to

2

4

1 

i

2

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

i

2

x

2

.

Taking x

2

D 2 yields th e eigenvector x D



i

2



, so u D



0

2



and v D



1

0



. Since .u; v/ D 0 we

just normalize u and v to obtain U D



0

1



, V D



1

0



.

10.6.40.

ˇ

7   6

12 5 

ˇ

D . C 1/

2

C 36. The augmented matrix of .A  .1 C 6i /I /x D 0

is

2

4

6  6i 6

:

: 0

12 6  6i

:

: 0

3

5

, which is row equivalent to

2

4

1 

1i

2

:

: 0

0 0

:

: 0

3

5

. Therefore,x

1

D

1  i

2

x

2

. Taking x

2

D 2 yields the eigenvector x D



1  i

2



, so u D



1

2



and v D



1

0



. The

quadratic equation is k

2

 4k C 1 D 0, with positive root k  :2361. Routine calculations yield

U 



:5257

:8507



, V 



:8507

:5257



.

10.7 VARIATION OF PARA METERS FOR NONHOMOGENEOUS LINEAR SYSTEMS

10.7.2. Y D



3e

t

e

2t

e

t

2e

2t



; u

0

D Y

1

f D

1

5



2e

t

e

t

e

2t

3e

2t



50e

37

10e

3t



D



20e

4t

 2e

2t

10e

5t

C 6e

t



;

u D



e

2t

 5e

4t

2e

5t

 6e

t



; y

p

D Y u D



13e

3t

C 3e

3t

e

3t

 11e

3t



.

10.7.4. Y D



e

2t

e

t

2e

2t

e

t



; u

0

D Y

1

f D



e

2t

e

2t

2e

t

e

t



2

2e

t



D



2e

2t

 2e

t

2e

2t

 4e

t



;

u D



2e

t

 e

2t

e

2t

 4e

t



; y

p

D Y u D



5  3e

t

5e

t

 6



.

10.7.6. Y D



sin t cos t

cos t sin t



; u

0

D Y

1

f D



sin t cos t

cos t sin t



1

t



D



t cos t C sin t

t sin t  cos t



;

u D



t sin t

t cos t



; y

p

D Y u D



t

0



.

10.7.8. Y D

2

4

e

3t

e

2t

e

t

e

3t

0 3e

t

e

3t

e

2t

7e

t

3

5

; u

0

D Y

1

f D

1

6

2

4

3e

3t

6e

3t

3e

3t

4e

2t

6e

2t

2e

2t

e

t

0 e

t

3

5

2

4

1

e

t

e

t

3

5

D

1

6

2

4

3e

3t

 9e

2t

8e

t

C 4e

2t

e

2t

 e

t

3

5

; u D

1

12

2

4

9e

2t

 2e

3t

16e

t

 4e

2t

e

2t

 2e

t

3

5

; y

p

D Y u D 

1

6

2

4

3e

t

C 4

6e

t

 4

10

3

5

.

10.7.10. Y D

2

4

e

t

e

t

te

t

e

t

e

t

3e

t

 te

t

e

t

e

t

te

t

3

5

; u

0

D Y

1

f D

1

18

2

4

9e

t

0 9e

t

3e

t

.3  2t/ 6te

t

9e

t

6e

t

6e

t

0

3

5

2

4

e

t

e

t

e

t

3

5

D

1

3

2

4

0

e

2t

.3  2t/

2e

2t

3

5

; u D

1

3

2

4

0

e

2t

.2  t/

e

2t

3

5

; y

p

D Y u D

1

3

2

4

2e

t

e

t

2e

t

3

5

.

Section 10.7

Variation of Parameters for Nonhomogeneous Linear Systems

219

10.7.12. u

0

D Y

1

f D

1

2t



e

t

e

t

e

t

e

t



t

2



D

1

2



e

t

.t C 1/

e

t

.1  t/



; u D

1

2



e

t

.t C 2/

e

t

.2  t/



;

y

p

D Y u D

t

2



e

t

e

t

e

t

e

t



e

t

.t C 2/

e

t

.2  t/



D 



t

2

2t



.

10.7.14. u

0

D Y

1

f D

1

3



2 e

t

e

t

2



e

2t

e

2t



D

1

3



2e

2t

 e

3t

2e

2t

 e

3t



; u D

1

9



3e

2t

Ce

3t

e

3t

 3e

2t



;

y

p

D Y u D

1

9



2 e

t

e

t

2



3e

2t

C e

3t

e

3t

 3e

2t



D

1

9



5e

2t

 e

3t

e

3t

 5e

2t



.

10.7.16. u

0

D Y

1

f D

1

t

2

 1



t e

t

e

t



t

2

 1

t

2

 1



D



t  e

t

t  e

t



; u D

1

2



2e

t

C t

2

t

2

 2e

t



;

y

p

D Y u D

1

2



t e

t

e

t



2e

t

Ct

2

t

2

 2e

t



D

1

2



te

t

.t C 2/ C t

3

 2

te

t

.t  2/ C t

3

C 2



.

10.7.18. u

0

D Y

1

f D

1

3

2

4

e

5t

e

4t

e

3t

2e

2t

e

t

1

e

2t

2e

t

1

3

5

2

4

e

t

0

3

5

D

1

3

2

4

e

4t

2e

t

e

t

3

5

; u D

1

12

2

4

e

4t

8e

t

4e

t

3

5

;

y

p

D Y u D

1

12

2

4

e

5t

e

2t

0

e

4t

0 e

t

e

3t

1 1

3

5

2

4

e

4t

8e

t

4e

t

3

5

D

1

4

2

4

3e

t

1

e

t

3

5

.

10.7.20. u

0

D Y

1

f D

1

2t

2

4

e

2t

te

t

te

t

C e

2t

1 te

t

te

t

 1

2 0 2

3

5

2

4

e

t

0

e

t

3

5

D

2

4

1

e

2t

0

3

5

; u D

1

4

2

4

2t

e

2t

0

3

5

;

y

p

D Y u D Y D

1

4t

2

4

e

t

e

t

t

e

t

e

t

e

t

e

t

e

t

0

3

5

2

4

2t

e

2t

0

3

5

D

e

t

4t

2

4

2t C 1

2t  1

2t C 1

3

5

.

10.7.22. (c) If y

p

D Y u, then y

0

p

D Y

0

u CY u

0

D AY u CY u

0

, so (E) y

0

p

D Ay

p

CY u

0

. However, from

the derivation of the method of variation of parameters in Section 9.4, Y u

0

D f as d eﬁned in the solution

of (a). This and (E) imply the conclusion.

(d) Since Y u

0

D f with f as deﬁned in the solution of (a), u

1

; u

2

; : : : ; u

n

satisfy the condi tions required

in the derivation of the method of variation of parameters in Section 9.4; hence, y

p

D c

1

y

1

C c

2

y

2

C

 C c

n

y

n

is a particular solution of ( A ).

CHAPTER 1 1

Boundary Value Problems and Fourier

Expansions

11.1 EI GEN VA LUE PROBLEMS FOR y

00

C y D 0

11.1.2. From Theorem 11.1.2 with L D , 

n

D n

2

, y

n

D sin nx, n D 1; 2; 3; : : :

11.1.4. From Theorem 11.1.4 with L D , 

n

D

.2n  1/

2

4

, y

n

D sin

.2n  1/x

2

, n D 1; 2; 3; : : : ;

11.1.6. From Theorem 11.1.6 with L D  , 

0

D 0, y

0

D 1, 

n

D n

2

, y

1n

D cos nx, y

2n

D sin nx,

n D 1; 2; 3; : : :

11.1.8. From Theorem 11.1.5 with L D 1, 

n

D

.2n  1/

2



2

4

, y

n

D cos

.2n  1/ x

2

, n D 1; 2; 3; : : :

11.1.10. From Theorem 11.1.6 with L D 1, 

0

D 0, y

0

D 1, 

n

D n

2



2

, y

1n

D cos nx, y

2n

D

sin n x, n D 1; 2; 3; : : :

11.1.12. From Theorem 11.1.6 with L D 2, 

0

D 0, y

0

D 1, 

n

D

n

2



2

4

, y

1n

D cos

nx

2

, y

2n

D

sin

nx

2

, n D 1; 2; 3; : : :

11.1.14. From Theorem 11.1.5 wit h L D 3, 

n

D

.2n  1/

2



2

36

, y

n

D cos

.2n  1/ x

6

, n D 1; 2; 3; : : :

11.1.16. From Theorem 11.1.3 wit h L D 5, 

n

D

n

2



2

25

, y

n

D cos

nx

5

, n D 1; 2; 3; : : :

11.1.18. From Theorem 11.1.1, any eig envalues of Problem 11.1.4 must be positive. If  > 0, then

every solution of y

00

C y D 0 is of the form y D c

1

cos

p

 x C c

2

sin

p

 x where c

1

and c

2

are

constants. Therefore, y

0

D

p

 .c

1

sin

p

 x C c

2

cos

p

 x/. Since y

0

.0/ D 0, c

2

D 0. Therefore,

y D c

1

cos

p

 x. Since y.L/ D 0, c

1

cos

p

 L D 0. To make c

1

cos

p

 L D 0 with c

1

¤ 0 we must

choose

p

 D

.2n  1/

2L

, where n is a positive integer. Therefore,

n

D

.2n  1/

2



2

4L

2

is an eigenvalue

and y

n

D cos

.2n  1/ x

2L

is an associated eigenfunct ion.

221

222 Chapter 11

Boun dary Value Problems and Fourier Expansions

11.1.20. If r is a positive integer, then

Z

L

L

cos

r x

L

dx D

L

r

sin

r x

L

ˇ

L

L

D 0, so y

0

D 1 is ort hogonal

to all the other eigenfunctions. If m and n are distinct positive integers, then

Z

L

0

cos

mx

L

cos

nx

L

dx D

1

2

Z

L

L

cos

mx

L

cos

nx

L

dx D 0, from Example 11.1.4.

11.1.22. Let m and n be distinct positive integers. From th e identity cos A cos B D

1

2

Œcos.A  B/ C

cos.A C B/ with A D .2m  1/x=2L and B D .2n  1/x=2L,

Z

L

0

cos

.2m  1/ x

2L

cos

.2n  1/ x

2L

dx D

1

2

Z

L

0



cos

.m  n/x

L

C cos

.m C n  1/x

L



dx D 0:

11.1.24. If y D c

1

C c

2

x, then y

0

.0/ D 0 implies that c

2

D 0, so y D c

1

. Now

Z

L

0

y.x/ dx D

c

1

Z

L

0

dx D c

1

L D 0 only if c

1

D 0. Therefore,zero is not an eigenvalue.

If y D c

1

cosh kx C c

2

sinh kx, then y

0

.0/ D 0 implies that c

2

D 0, so y D c

1

cosh kx. Now

Z

L

0

y.x/ dx D c

1

Z

L

0

cosh kx dx D c

1

sinh kL

k

D 0 with k > 0 only if c

1

D 0. Therefore, there are no

negative ei genvalues.

If y D c

1

cos kx C c

2

sin kx, then y

0

.0/ D 0 implies that c

2

D 0, so y D c

1

cos kx. Now

Z

L

0

y.x/ dx D c

1

Z

L

0

cos kx dx D c

2

sin kL

k

D 0 if k D

n

L

, where n is a positive integer. Therefore,



n

D

n

2



2

L

2

and y

n

D cos

nx

L

, n D 1; 2; 3; : : : .

11.1.26. If y D c

1

C c

2

.x  L/, then y

0

.L/ D 0 implies that c

2

D 0, so y D c

1

. Now

Z

L

0

y.x/ dx D

c

1

Z

L

0

dx D c

1

L D 0 only if c

1

D 0. Therefore,zero is not an eigenvalue.

If y D c

1

cosh k.x L/Cc

2

sinh k.x L/, then y

0

.L/ D 0 i mplies that c

2

D 0, so y D c

1

cosh k.x 

L/. Now

Z

L

0

y.x/ dx D c

1

Z

L

0

cosh k.x  L/ dx D c

1

sinh kL

k

D 0 with k > 0 only if c

1

D 0.

Therefore,there are no negative eigenvalues.

If y D c

1

cos k.x L/Cc

2

sin k.x L/, then y

0

.L/ D 0 i mplies that c

2

D 0, so y D c

1

cos k.x L/.

Now

Z

L

0

y.x/ dx D c

1

Z

L

0

cos k.x  L/ dx D c

2

sin kL

k

D 0 if k D

n

L

, where n i s a positive integer.

Therefore, 

n

D

n

2



2

L

2

and y

n

D cos

n.x  L/

L

, or, equivalently, y

n

D cos

nx

L

, n D 1; 2; 3; : : : .

Section 11.2

Fourier Expansions I

223

11.2 FOURIER EXPANSIONS I

11.2.2.

a

0

D

1

2

Z

1

1

.2  x/ dx D

Z

1

0

2 dx D 2I

a

n

D

Z

1

1

.2  x/ cos nx dx D 4

Z

1

0

cos nx dx D

4

n

sin nx

ˇ

1

0

D 0I

b

n

D

Z

1

1

.2  x/ sin nx dx D 2

Z

1

0

x sin nx dx

D

2

n

"

x cos nx

ˇ

1

0



Z

1

0

cos n x dx

#

D

2

n

"

cos n 

1

n

sin nx

ˇ

1

0

#

D .1/

n

2

n

I

F .x/ D 2 C

2



1

X

nD1

.1/

n

sin n x. From Theorem 11.2.4,

F .x/ D

8

<

:

2; x D 1;

2  x; 1 < x < 1;

2; x D 1:

11.2.4. Since f is even, b

n

D 0 for n  1; a

0

D

Z

1

0

.1  3x

2

/ dx D .x  x

3

/

ˇ

1

0

D 0; if n  1, then

a

n

D 2

Z

1

0

.1  3x

2

/ cos nx dx D

2

n

"

.1  3x

2

/ sin nx

ˇ

1

0

C 6

Z

1

0

x sin nx dx

#

D 

12

n

2



2

"

x cos nx

ˇ

1

0



Z

1

0

cos n x dx

#

D 

12

n

2



2

"

cos n 

1

n

sin nx

ˇ

1

0

#

D .1/

nC1

12

n

2



2

I

F .x/ D 

12



2

1

X

nD1

.1/

n

cos nx

n

2

. From Theorem 11.2.4, F .x/ D 1  3x

2

, 1  x  1.

11.2.6. Since f is odd, a

n

D 0 if n  0;

b

1

D

2



Z



0

x cos x sin x dx D

1



Z



0

x sin 2x dx

D 

1

2



x cos 2x

ˇ



0



Z



0

cos 2x dx



D 

1

2



 

sin 2x

2

ˇ



0



D 

1

2

:

224 Chapter 11

Boun dary Value Problems and Fourier Expansions

if n  2, then

b

n

D

2



Z



0

x cos x sin nx dx D

1



Z



0

xŒsin.n C 1/x C sin.n  1/x dx

D 

1





x



cos.n C 1/x

n C 1

C

cos.n  1/x

n  1



ˇ



0



Z



0



cos.n C 1/x

n C 1

C

cos.n  1/x

n  1



dx



D .1/

n



1

n C 1

C

1

n  1



C

1





sin.n C 1/x

.n C 1/

2

C

sin.n  1/x

.n  1/

2



ˇ



0

D .1/

n

2n

n

2

 1

I

F .x/ D 

1

2

sin x C 2

1

X

nD2

.1/

n

2

 1

sin nx. Fr om Theorem 11.2.4, F .x/ D x cos x,   x   .

11.2.8. Since f is even, b

n

D 0 if n  1; a

0

D

1



Z



0

x sin x dx D 

1





x cos x

ˇ



0



Z



0

cos x dx



D

1C

sin x



ˇ



0

D 1; a

1

D

2



Z



0

x sin x cos x dx D

1



Z



0

x sin 2x dx D 

1

2



x cos 2x

ˇ



0



Z



0

cos 2x dx



D



1

2

C

sin 2x

4

ˇ



0

D 

1

2

; if n  2, then

a

n

D

2



Z



0

x sin x cos nx dx D

1



Z



0

xŒsin.n C 1/x  sin.n  1/x dx

D

1





x



cos.n  1/x

n  1



cos.n C 1/x

n C 1



ˇ



0



Z



0



cos.n  1/x

n  1



cos.n C 1/x

n C 1



dx



D .1/

nC1



1

n  1



1

n C 1





1





sin.n  1/x

.n  1/

2



sin.n C 1/x

.n C 1/

2



ˇ



0

D .1/

nC1

2

n

2

 1

I

F .x/ D 1 

1

2

cos x  2

1

X

nD2

.1/

n

2

 1

cos nx. From Theorem 11.2.4, F .x/ D x sin x,   x   .

11.2.10. Since f is even, b

n

D 0 if n  0; a

0

D

Z

1=2

0

cos x dx D

sin x



ˇ

1=2

0

D

1



; a

1

D

2

Z

1=2

0

cos

2

x dx D

Z

1=2

0

.1  cos 2x/ dx D

1

2



sin 2x

2

ˇ

1=2

0

D

1

2

; if n  2, then

a

n

D 2

Z

1=2

0

cos  x cos nx dx D

Z

1=2

0

Œcos.n C 1/x C cos.n  1/x dx

D

1





sin.n C 1/x

n C 1

C

sin.n  1/x

n  1



ˇ

1=2

0

D

1





1

n C 1



1

n  1



cos

n

2

D 

2

.n

2

 1/

cos

n

2

D

8

<

:

.1/

mC1

2

.4m

2

 1/

if n D 2m;

0 if n D 2m C 1I

F .x/ D

1



C

1

2

cos x 

2



1

X

nD1

.1/

n

4n

2

 1

cos 2nx. From Theorem 11.2.4, F .x/ D f .x/, 1  x  1.

Section 11.2

Fourier Expansions I

225

11.2.12. Since f is odd, a

n

D 0 if n  0; b

1

D 2

Z

1=2

0

sin

2

2x dx D

Z

1=2

0

.1  cos 4x/ dx D

1

2



sin 4x

4

ˇ

1=2

0

D

1

2

; if n  2, then

b

n

D 2

Z

1=2

0

sin x sin n x dx D

Z

1=2

0

Œcos.n  1/x  cos.n C 1/x dx

D

1





sin.n  1/x

n  1



sin.n C 1/x

n C 1



ˇ

1=2

0

D 

2n

.n

2

 1/

cos

n

2

D

(

.1/

mC1

4m

2

 1

if n D 2m;

0 if n D 2m C 1I

F .x/ D

1

2

sin x 

4



1

X

nD1

.1/

n

4n

2

 1

sin 2nx. From Theorem 11.2.4,

F .x/ D

8

ˆ

<

ˆ

:

0; 1  x <

1

2

;



1

2

; x D 

1

2

;

sin x; 

1

2

< x <

1

2

;

1

2

; x D

1

2

;

0;

1

2

< x  1:

11.2.14. Since f is even, b

n

D 0 if n  1;

a

0

D

Z

1=2

0

x sin x dx D 

1



"

x cos x

ˇ

1=2

0



Z

1=2

0

cos x dx

#

D

sin x



2

ˇ

1=2

0

D

1



2

I

a

1

D 2

Z

1=2

0

x sin x cos x dx D

Z

1=2

0

x sin 2x dx

D 

1

2

"

x cos 2 x

ˇ

1=2

0



Z

1=2

0

cos 2x dx

#

D

1

4

C

sin 2x

4

2

ˇ

1=2

0

D

1

4

I

if n  2, then

a

n

D 2

Z

1=2

0

x sin x cos nx dx D

Z

1=2

0

xŒsin.n C 1/x  sin.n  1/x dx

D

1



"

x



cos.n  1/x

n  1



cos.n C 1/x

n C 1



ˇ

1=2

0



Z

1=2

0



cos.n  1/x

n  1



cos.n C1/x

n C 1



dx

#

D

1

2



cos.n  1/=2

n  1



cos.n C 1/=2

n C 1





1



2



sin.n  1/=2

.n  1/

2



sin.n C 1/=2

.n C 1/

2



D

1



n

2

 1

sin

n

2

C

2



2

n

2

C 1

.n

2

 1/

2

cos

n

2

D

8

ˆ

<

ˆ

:

.1/

m

2



2

4m

2

C 1

.4m

2

 1/

2

if n D 2m;

.1/

m

1

4

2m C 1

m.m C 1/

if n D 2m C 1I

226 Chapter 11

Boun dary Value Problems and Fourier Expansions

F .x/ D

1



2

C

1

4

cos  xC

2



2

1

X

nD1

.1/

n

4n

2

C 1

.4n

2

 1/

2

cos 2nxC

1

4

1

X

nD1

.1/

n

2n C 1

n.n C 1/

cos.2nC1/x:

From Theorem 11.2.4,

F .x/ D

8

ˆ

<

ˆ

:

0; 1  x <

1

2

;

1

4

; x D 

1

2

;

x sin x; 

1

2

< x <

1

2

;

1

4

; x D

1

2

;

0;

1

2

< x  1:

11.2.16. Note that

Z

0

1

x

2

g.x/ dx D

Z

1

0

x

2

g.x/ dx; therefore, a

0

D

1

2



Z

0

1

x

2

dx C

Z

1

0

.1  x

2

/ dx



D

1

2

Z

1

0

dx D

1

2

, and if n  1, then

a

n

D

Z

0

1

x

2

cos nx dx C

Z

1

0

.1  x

2

/ cos nx dx D

Z

1

0

cos nx dx D

sin nx

n

ˇ

1

0

D 0

and

b

n

D

Z

0

1

x

2

sin nx dx C

Z

1

0

.1  x

2

/ sin nx dx D

Z

1

0

.1  2x

2

/ sin nx dx

D 

1

n

"

.1  2x

2

/ cos nx

ˇ

1

0

C4

Z

1

0

x cos nx dx

#

D

1 C cos n

n



4

n

2



2

"

x sin nx

ˇ

1

0



Z

1

0

sin nx dx

#

D

1 C cos n

n



4 cos nx

n

3



3

ˇ

1

0

D

1 C cos n

n

C

4.1  cos n/

n

3



3

D

8

ˆ

<

ˆ

:

1

m

if n D 2m;

8

.2m C 1/

3



3

if n D 2m C 1I

F .x/ D

1

2

C

1



1

X

nD1

1

n

sin 2nx C

8



3

1

X

nD0

1

.2n C 1/

3

sin.2n C 1/x:

From Theorem 11.2.4,

F .x/ D

8

ˆ

<

ˆ

:

1

2

; x D 1;

x

2

; 1 < x < 0;

1

2

; x D 0;

1  x

2

; 0 < x < 1;

1

2

; x D 1:

Section 11.2

Fourier Expansions I

227

11.2.18. a

0

D

1

6



Z

2

3

2 dx C

Z

2

2

3 dx C

Z

3

2

1 dx



D

5

2

. If n  1, then

a

n

D

1

3

Z

3

3

f .x/ cos

nx

3

dx

D

1

3



Z

2

3

2 cos

nx

3

dx C

Z

2

2

3 cos

nx

3

dx C

Z

3

2

cos

nx

3

dx



D

3

n

sin

2n

3

;

b

n

D

1

3



Z

2

3

2 sin

nx

3

dx C

Z

2

2

3 sin

nx

3

dx C

Z

3

2

sin

nx

3

dx



D

1

n



cos n  cos

2n

3



I

F .x/ D

5

2

C

3



1

X

nD1

1

n

sin

2n

3

cos

nx

3

C

1



1

X

nD1

1

n



cos n  cos

2n

3



sin

nx

3

:

11.2.20. (a) a

0

D

1

2

Z





e

x

dx D

e

x

2

ˇ





D

sinh 



. If n  1 then (A) a

n

D

1



Z





e

x

cos nx dx and

(B) b

n

D

1



Z





e

x

sin nx dx. Integrating (B) by parts yields

b

n

D

1





e

x

sin nx

ˇ





 n

Z





e

x

cos nx dx



D na

n

: .C/

Integrating (A) by parts yields

a

n

D

1





e

x

cos nx

ˇ





C n

Z





e

x

sin nx dx



D .1/

n

2 sin h 



C nb

n

D .1/

n

2 sin h 



 n

2

a

n

;

from (C). Therefore, a

n

D

2 sin h 



.1/

n

2

C 1

. Now (C) implies that b

n

D

2 sin h 



.1/

nC1

n

2

C 1

. Therefore,

F .x/ D

sinh 



1 C 2

1

X

nD1

.1/

n

2

C 1

cos nx  2

1

X

nD1

.1/

n

2

C 1

sin nx

!

:

(b) From Theorem 11.2.4, F ./ D cosh  , so

sinh 



1 C 2

1

X

nD1

1

n

2

C 1

!

D cosh  , which implies

the stated result.

11.2.24. Since f is even, b

n

D 0, n  1, a

0

D

1



Z



0

cos kx dx D

sin kx

k

ˇ



0

D

sin k

k

; if n  1 then

a

n

D

2



Z



0

cos kx cos nx dx D

1



Z



0

Œcos.n  k/x C cos.n C k/x dx

D

1





sin.n  k/x

n  k

C

sin.n C k/x

n C k



ˇ



0

D

cos n sin kx





1

n C k



1

n  k



D .1/

nC1

2k sin k

.n

2

 k

2

/

I

F .x/ D

sin k



"

1

k

 2k

1

X

nD1

.1/

n

2

 k

2

cos nx

#

.

228 Chapter 11

Boun dary Value Problems and Fourier Expansions

11.2.26. Since f is continuous on ŒL; L and f .L/ D f .L/, Theorem 11.2.4 implies that

f .x/ D a

0

C

1

X

nD1



a

n

cos

nx

L

C b

n

sin

nx

L



; L  x  L;

if a

0

D

1

2L

Z

L

L

f .x/ dx, and, for n  1,

a

n

D

1

L

Z

L

L

f .x/ cos

nx

L

dx D

1

n

"

f .x/ sin

nx

L

ˇ

L

L



Z

L

L

f

0

.x/ sin

nx

L

dx

#

D

L

n

2



2

"

f

0

.x/ cos

nx

L

ˇ

L

L



Z

L

L

f

00

.x/ cos

nx

L

dx

#

D 

L

n

2



2

Z

L

L

f

00

.x/ cos

nx

L

dx

(since f

0

.L/ D f

0

.L/), and

b

n

D

1

L

Z

L

L

f .x/ sin

nx

L

dx D 

1

n

"

f .x/ cos

nx

L

ˇ

L

L



Z

L

L

f

0

.x/ cos

nx

L

dx

#

D

1

n

Z

L

L

f

0

.x/ cos

nx

L

dx ( since f .L/ D f .L/)

D

L

n

2



2

"

f

0

.x/ sin

nx

L

ˇ

L

L



Z

L

L

f

00

.x/ sin

nx

L

dx

#

D 

L

n

2



2

Z

L

L

f

00

.x/ sin

nx

L

dx:

If f

000

is integrable on ŒL; L, then

a

n

D 

L

n

2



2

Z

L

L

f

00

.x/ cos

nx

L

dx D 

L

2

n

3



3

"

f

000

.x/ sin

nx

L

ˇ

L

L



Z

L

L

f

000

.x/ sin

nx

L

dx

#

D

L

2

n

3



3

Z

L

L

f

000

.x/ sin

nx

L

dx:

11.2.28. The Fourier series is a

0

C

1

X

nD1



a

n

cos

nx

L

C b

n

sin

nx

L



where

a

0

D

1

2L

Z

L

L

f .x/ dx D

1

2L

"

Z

0

L

f .x/ dx C

Z

L

0

f .x/ dx

#

: .A/

Since

Z

0

L

f .x/ dx D 

Z

0

L

f .x C L/ dx D 

Z

L

0

f .x/ dx, (A) implies that a

0

D 0. If n  1, then

a

n

D

1

L

Z

L

L

f .x/ cos

nx

L

dx D

1

L

"

Z

0

L

f .x/ cos

nx

L

dx C

Z

L

0

f .x/ cos

nx

L

dx

#

: .B/

Since

Z

0

L

f .x/ cos

nx

L

dx D 

Z

0

L

f .x C L/ cos

nx

L

dx D 

Z

L

0

f .x/ cos

n.x C L/

L

dx

D .1/

nC1

Z

L

0

f .x/ cos

nx

L

dx;

Section 11.3

Fourier Expansions II

229

(B) implies that a

2n1

D A

n

and a

2n

D 0, n  1. A similar argument showsthat b

2n1

D B

n

and

b

2n

D 0, n  1.

11.2.30.(b) Let 

0

D 1 and 

2m

D cos

mx

L

, 

2m1

D sin

mx

L

, m  1. Then c

0

D a

0

and c

2m

D a

m

,

c

2m1

D b

m

, m  1. Since

Z

L

L



2

0

.x/ dx D 2L an d

Z

L

L



2

2m1

.x/ dx D

1

2

Z

L

L



1  cos

2mx

L



dx D

L,

Z

L

L



2

2m

.x/ dx D

1

2

Z

L

L



1 C cos

2mx

L



dx D L, m  1, Exercise 12.2.29(d) implies the conclu-

sion.

11.3 FOURIER EXPANSIONS II

11.3.2. a

0

D

Z

1

0

.1  x/ dx D 

.1  x/

2

ˇ

1

0

D

1

2

; if n  1,

a

n

D 2

Z

1

0

.1  x/ cos nx dx D

2

n

"

.1  x/ sin nx

ˇ

1

0

C

Z

1

0

sin nx dx

#

D 

2

n

2



2

cos nx

ˇ

1

0

D

2

n

2



2

Œ1  .1/

n

 D

8

<

:

4

.2m  1/

2



2

if n D 2m  1;

0 if n D 2mI

C.x/ D

1

2

C

4



2

1

X

nD1

1

.2n 1/

2

cos.2n  1/x:

11.3.4. a

0

D

1



Z



0

sin kx dx D 

cos kx

k

ˇ



0

D

1  cos k

k

; if n  1, then

a

n

D

2



Z



0

sin kx cos nx dx D

1



Z



0

Œsin.n C k/x  sin.n  k/x dx

D

1





cos.n  k/x

n  k



cos.n C k/x

n C k



ˇ



0

D

1





cos.n  k/  1

n  k



cos.n Ck/  1

n C k



D 

2kŒ1  .1/

n

cos k 

.n

2

 k

2

/

I

C.x/ D

1  cos k

k



2k



1

X

nD1

Œ1  .1/

n

cos k

n

2

 k

2

cos nx:

11.3.6. a

0

D

1

L

Z

L

0

.x

2

 L

2

/ dx D

1

L



x

3

 L

2

x



ˇ

L

0

D 

2L

2

3

; if n  1,

a

n

D

2

L

Z

L

0

.x

2

 L

2

/ cos

nx

L

dx D

2

n

"

.x

2

 L

2

/ sin

nx

L

ˇ

L

0

 2

Z

L

0

x sin

nx

L

dx

#

D

4L

n

2



2

"

x cos

nx

L

ˇ

L

0



Z

L

0

cos

nx

L

dx

#

D .1/

n

4L

2

n

2



2



4L

2

n

3



3

sin

nx

L

ˇ

L

0

D .1/

n

4L

2

n

2



2

I

C.x/ D 

2L

2

3

C

4L

2



2

1

X

nD1

.1/

n

2

cos

nx

L

:

230 Chapter 11

Boun dary Value Problems and Fourier Expansions

11.3.8. a

0

D

Z



0

e

x

dx D e

x

ˇ



0

D

e



 1



; if n  1, then

a

n

D

2



Z



0

e

x

cos nx dx D

2





e

x

cos nx

ˇ



0

 n

Z



0

e

x

sin nx dx



D

2





.1/

n

e



 1  ne

x

sin nx

ˇ



0

 n

2

Z



0

e

x

cos nx dx



D

2



Œ.1/

n

e



 1  n

2

a

n

I

.1 C n

2

/a

n

D

2



Œ.1/

n

e



 1; a

n

D

2

.n

2

C 1/

Œ.1/

n

e



 1;

C.x/ D

e



 1



C

2



1

X

nD1

Œ.1/

n

e



 1

.n

2

C 1/

cos nx:

11.3.10. a

0

D

1

L

Z

L

0

.x

2

 2Lx/ dx D

1

L



x

3

 Lx

2



ˇ

L

0

D 

2L

2

3

; if n  1,

a

n

D

2

L

Z

L

0

.x

2

 2Lx/ cos

nx

L

dx D

2

n

"

.x

2

 2Lx/ sin

nx

L

ˇ

L

0

 2

Z

L

0

.x  L/ sin

nx

L

dx

#

D

4L

n

2



2

"

.x  L/ cos

nx

L

ˇ

L

0



Z

L

0

cos

nx

L

dx

#

D

4L

2

n

2



2



4L

3

n

3



3

sin

nx

L

ˇ

L

0

D

4L

2

n

2



2

I

C.x/ D 

2L

2

3

C

4L

2



2

1

X

nD1

1

n

2

cos

nx

L

:

11.3.12. b

n

D 2

Z

1

0

.1  x/ sin nx dx D 

2

n

"

.1  x/ cos n x

ˇ

1

0

C

Z

1

0

cos nx dx

#

D

2

n

C

2

n

2



2

sin nx

ˇ

1

0

D

2

n

; S.x/ D

2



1

X

nD1

1

n

sin nx.

11.3.14. b

n

D

2

L

Z

L=2

0

sin

nx

L

dx D 

2

n

cos

nx

L

ˇ

L=2

0

D

2

n

h

1  cos

n

2

i

;

S.x/ D

2



1

X

nD1

1

n

h

1  cos

n

2

i

sin

nx

L

:

11.3.16.

b

1

D

2



Z



0

x sin

2

x dx D

1



Z



0

x.1  cos 2x/ dx D

x

2

2

ˇ



0



1



Z



0

x cos 2x dx

D



2



1

2



x sin 2x

ˇ



0



Z



0

cos 2x dx



D



2

C

sin 2x

4

ˇ



0

D



2

I

Section 11.3

Fourier Expansions II

231

if n  2, then

b

n

D

2



Z



0

x sin x sin nx dx D

1



Z



0

xŒcos.n  1/x  cos.n C 1/x dx

D

1





x



sin.n  1/x

n  1



sin.n C 1/x

n C 1



ˇ



0



Z



0



sin.n  1/x

n  1



sin.n C 1/x

n C 1



dx



D

1





cos.n  1/x

.n  1/

2



cos.n C 1/x

.n C 1/

2



ˇ



0

D

1





1

.n  1/

2



1

.n C 1/

2





.1/

nC1

 1



D

4n

.n

2

 1/

2





.1/

nC1

 1



D

8

<

:

0 if n D 2m  1;



16m

.4m

2

 1/

if n D 2mI

S.x/ D



2

sin x 

16



1

X

nD1

n

.4n

2

 1/

2

sin 2nx:

11.3.18. c

n

D

2

L

Z

L

0

cos

.2n 1/x

2L

dx D

4

.2n  1/

sin

.2n 1/x

2L

ˇ

L

0

D .1/

nC1

4

.2n  1/

;

C

M

.x/ D 

4



1

X

nD1

.1/

n

2n  1

cos

.2n 1/x

2L

:

11.3.20.

d

n

D 2

Z

1

0

x cos

.2n  1/ x

2

dx

D

4

.2n 1/

"

x sin

.2n 1/x

2

ˇ

1

0



Z

1

0

sin

.2n  1/ x

2

dx

#

D

4

.2n 1/

"

.1/

nC1

C

2

.2n  1/

cos

.2n 1/x

2

ˇ

1

0

#

D 

4

.2n  1/



.1/

n

C

2

.2n  1/



I

C

M

.x/ D 

4



1

X

nD1



.1/

n

C

2

.2n  1/



cos

.2n  1/ x

2

:

11.3.22.

c

n

D

2



Z



0

cos x cos

.2n  1/x

2

dx D

1



Z



0



cos.2n C 1/x

2

C

cos.2n  3/x

2



dx

D

2





sin.2n C 1/x=2

2n C 1

C

sin.2n  3/x=2

2n  3



ˇ



0

D .1/

n

2





1

2n C 1

C

1

2n  3



D .1/

n

4.2n 1/

.2n 3/.2n C 1/

I

232 Chapter 11

Boun dary Value Problems and Fourier Expansions

C

M

.x/ D

4



1

X

nD1

.1/

n

2n  1

.2n  3/.2n C1/

cos

.2n  1/x

2

:

11.3.24.

c

n

D

2

L

Z

L

0

.Lx  x

2

/ cos

.2n  1/ x

2L

dx

D

4

.2n  1/

"

.Lx  x

2

/ sin

.2n 1/x

2L

ˇ

L

0



Z

L

0

.L  2x/ sin

.2n  1/ x

2L

dx

#

D

8L

.2n  1/

2



2

"

.L  2x/ cos

.2n 1/x

2L

ˇ

L

0

C 2

Z

L

0

cos

.2n  1/ x

2L

dx

#

D 

8L

2

.2n  1/

2



2

C

32L

2

.2n 1/

3



3

sin

.2n  1/ x

2L

ˇ

L

0

D

32L

2

.2n  1/

3



3

sin

.2n 1/x

2

D 

8L

2

.2n  1/

2



2

C .1/

n1

32L

2

.2n  1/

3



3

I

C

M

.x/ D 

8L

2



2

1

X

nD1

1

.2n 1/

2



1 C

4.1/

n

.2n  1/



cos

.2n 1/x

2L

:

11.3.26.

d

n

D

2

L

Z

L

0

x

2

sin

.2n 1/x

2L

dx

D 

4

.2n  1/

"

x

2

cos

.2n  1/ x

2L

ˇ

L

0

 2

Z

L

0

x cos

.2n 1/x

2L

dx

#

D

16L

.2n  1/

2



2

"

x sin

.2n  1/ x

2L

ˇ

L

0



Z

L

0

sin

.2n 1/x

2L

dx

#

D .1/

nC1

16L

2

.2n 1/

2



2

C

32L

2

.2n  1/

3



3

cos

.2n 1/x

2L

ˇ

L

0

D .1/

nC1

16L

2

.2n 1/

2



2



32L

2

.2n 1/

3



3

I

S

M

.x/ D 

16L

2



2

1

X

nD1

1

.2n 1/

2



.1/

n

C

2

.2n 1/



sin

.2n 1/x

2L

:

11.3.28.

d

n

D

2



Z



0

cos x sin

.2n 1/x

2

dx D

1



Z



0



sin.2n C 1/x

2

C

sin.2n  3/x

2



dx

D 

2





cos.2n C1/x=2

2n  1

C

cos.2n  3/x=2

2n  3



ˇ



0

D

2





1

2n C1

C

1

2n  3



D

4.2n 1/

.2n 3/.2n C 1/

I

Section 11.3

Fourier Expansions II

233

S

M

.x/ D

4



1

X

nD1

2n  1

.2n  3/.2n C1/

sin

.2n  1/x

2

:

11.3.30.

d

n

D

2

L

Z

L

0

.Lx  x

2

/ sin

.2n  1/ x

2L

dx

D 

4

.2n  1/

"

.Lx  x

2

/ cos

.2n  1/ x

2L

ˇ

L

0



Z

L

0

.L  2x/ cos

.2n 1/x

2L

dx

#

D

8L

.2n  1/

2



2

"

.L  2x/ sin

.2n  1/ x

2L

ˇ

L

0

C 2

Z

L

0

sin

.2n  1/ x

2L

dx

#

D .1/

n

8L

2

.2n  1/

2



2



32L

2

.2n  1/

3



3

cos

.2n 1/x

2L

ˇ

L

0

D .1/

n

8L

2

.2n  1/

2



2

C

32L

2

.2n 1/

3



3

I

S

M

.x/ D

8L

2



2

1

X

nD1

1

.2n  1/

2



.1/

n

C

4

.2n  1/



sin

.2n  1/ x

2L

:

11.3.32. a

0

D

1

L

Z

L

0

.3x

4

 4Lx

3

/ dx D

1

L



3x

5

 Lx

4



ˇ

L

0

D 

2L

4

5

. Since f

0

.0/ D f

0

.L/ D 0

and f

000

.x/ D 24.3x  L/,

a

n

D

48L

2

n

3



3

Z

L

0

.3x  L/ sin

nx

L

dx D 

48L

3

n

4



4

"

.3x  L/ cos

nx

L

ˇ

L

0

 3

Z

L

0

cos

nx

L

dx

#

D 

48L

3

n

4



4

Œ.1/

n

2L C L C

144L

4

n

5



5

sin

nx

L

ˇ

L

0

D 

48L

4

n

4



4

Œ1 C .1/

n

2 ; n  1I

C.x/ D 

2L

4

5



48L

4



4

1

X

nD1

1 C .1/

n

2

n

4

cos

nx

L

:

11.3.34. a

0

D

1

L

Z

L

0

.x

4

 2Lx

3

C L

2

x

2

/ dx D

1

L



x

5



Lx

4

2

C

L

2

x

3



ˇ

L

0

D

L

4

30

. Since f

0

.0/ D

f

0

.L/ D 0 and f

000

.x/ D 12.2x L/,

a

n

D

24L

2

n

3



3

Z

L

0

.2x  L/ sin

nx

L

dx D 

24L

3

n

4



4

"

.2x  L/ cos

nx

L

ˇ

L

0

 2

Z

L

0

cos

nx

L

dx

#

D 

24L

3

n

4



4

Œ.1/

n

L C L C

48L

4

n

5



5

sin

nx

L

ˇ

L

0

D 

24L

4

n

4



4

Œ1 C .1/

n



D

8

<

:

0 if n D 2m  1;



3L

4

m

4



4

if n D 2m;

n  1:

234 Chapter 11

Boun dary Value Problems and Fourier Expansions

C.x/ D

L

4

30



3L

4



4

1

X

nD1

1

n

4

cos

2nx

L

:

11.3.36. Since f .0/ D f .L/ D 0 and f

00

.x/ D 2,

b

n

D

4L

n

2



2

Z

L

0

sin

nx

L

dx D 

4L

2

n

3



3

cos

nx

L

ˇ

L

0

D 

4L

2

n

3



2

.cos n  1/

D

8

<

:

8L

2

.2m 1/

3



3

; if n D 2m  1;

0; if n D 2mI

S.x/ D

8L

2



3

1

X

nD1

1

.2n  1/

3

sin

.2n 1/x

L

:

11.3.38. Since f .0/ D f .L/ D 0 and f

00

.x/ D 6x,

b

n

D

12L

n

2



2

Z

L

0

x sin

nx

L

dx D 

12L

2

n

3



3

"

x cos

nx

L

ˇ

L

0



Z

L

0

cos

nx

L

dx

#

D .1/

nC1

12L

3

n

3



3

I

S.x/ D 

12L

3



3

1

X

nD1

.1/

n

3

sin

nx

L

:

11.3.40. Since f .0/ D f .L/ D f

00

.0/ D f

00

.L/ D 0 and f

.4/

D 360x,

b

n

D

720L

3

n

4



4

Z

L

0

x sin

nx

L

dx D 

720L

4

n

5



5

"

x cos

nx

L

ˇ

L

0



Z

L

0

cos

nx

L

dx

#

D .1/

nC1

720L

5

n

5



5

C

720L

5

n

6



6

sin

nx

L

ˇ

L

0

D .1/

nC1

720L

5

n

5



5

I

S.x/ D 

720L

5



5

1

X

nD1

.1/

n

5

sin

nx

L

:

11.3.42. (a) Since f is continuous on Œ0; L and f .L/ D 0, Theorem 11.3.3 implies that

f .x/ D

1

X

nD1

c

n

cos

.2n 1/x

2L

, L  x  L, with

c

n

D

2

L

Z

L

0

f .x/ cos

.2n  1/ x

2L

dx

D

4

.2n  1/

"

f .x/ sin

.2n 1/x

2L

ˇ

L

0



Z

L

0

f

0

.x/ sin

.2n 1/x

2L

dx

#

D 

4

.2n  1/

Z

L

0

f

0

.x/ sin

.2n 1/x

2L

dx (since f .L/ D 0)

D

8L

2

.2n  1/

2



2

"

f

0

.x/ cos

.2n  1/ x

2L

ˇ

L

0



Z

L

0

f

00

.x/ cos

.2n  1/ x

2L

dx

#

D 

8L

.2n  1/

2



2

Z

L

0

f

00

.x/ cos

.2n  1/ x

2L

dx ( since f

0

.0/ D 0):

Section 11.3

Fourier Expansions II

235

(b) Continuing the integration by parts yields

c

n

D 

16L

2

.2n  1/

3



3

"

f

00

.x/ sin

.2n  1/ x

2L

ˇ

L

0



Z

L

0

f

000

.x/ sin

.2n  1/ x

2L

dx

#

D

16L

2

.2n  1/

3



3

Z

L

0

f

000

.x/ sin

.2n  1/ x

2L

dx:

11.3.44. Since f

0

.0/ D f .L/ D 0 and f

00

.x/ D 2,

c

n

D

16L

.2n 1/

2



2

Z

L

0

cos

.2n  1/ x

2L

dx

D

32L

2

.2n 1/

3



3

sin

.2n  1/ x

2L

ˇ

L

0

D .1/

nC1

32L

2

.2n  1/

3



3

I

C

M

.x/ D 

32L

2



3

1

X

nD1

.1/

n

.2n 1/

3

cos

.2n 1/x

2L

:

11.3.46. Since f

0

.0/ D f .L/ D 0 and f

00

.x/ D 6.2x C L/,

c

n

D 

48L

.2n 1/

2



2

Z

L

0

.2x C L/ cos

.2n 1/x

2L

dx

D 

96L

2

.2n 1/

3



3

"

.2x C L/ sin

.2n 1/x

2L

ˇ

L

0

 2

Z

L

0

sin

.2n  1/ x

2L

#

dx

D 

96L

2

.2n 1/

3



3

"

.1/

nC1

3L 

4L

.2n 1/

cos

.2n  1/ x

2L

ˇ

L

0

#

D

96L

3

.2n 1/

3



3



.1/

n

3 C

4

.2n 1/



I

C

M

.x/ D

96L

3



3

1

X

nD1

1

.2n 1/

3



.1/

n

3 C

4

.2n  1/



cos

.2n  1/ x

2L

:

11.3.48. Since f

0

.0/ D f .L/ D f

00

.L/ D 0 and f

000

.x/ D 12.2x  L/,

c

n

D

192L

2

.2n  1/

3



3

Z

L

0

.2x  L/ sin

.2n  1/ x

2L

dx

D 

384L

3

.2n  1/

4



4

"

.2x  L/ cos

.2n  1/ x

2L

ˇ

L

0

 2

Z

L

0

cos

.2n  1/ x

2L

#

dx

D 

384L

3

.2n  1/

4



4

"

L 

4L

.2n 1/

sin

.2n  1/ x

2L

ˇ

L

0

#

D 

384L

4

.2n  1/

4



4



1 C

.1/

n

4

.2n 1/



I

C

M

.x/ D 

384L

4



4

1

X

nD1

1

.2n  1/

4



1 C

.1/

n

4

.2n 1/



cos

.2n 1/x

2L

:

236 Chapter 11

Boun dary Value Problems and Fourier Expansions

11.3.50. (a) Since f is continuous on Œ0; L and f .0/ D 0, Theorem 11.3.4 implies that

f .x/ D

1

X

nD1

d

n

sin

.2n  1/ x

2L

, L  x  L, with

d

n

D

2

L

Z

L

0

f .x/ sin

.2n 1/x

2L

dx

D 

4

.2n  1/

"

f .x/ cos

.2n 1/x

2L

ˇ

L

0



Z

L

0

f

0

.x/ cos

.2n  1/ x

2L

dx

#

D

4

.2n  1/

Z

L

0

f

0

.x/ cos

.2n  1/ x

2L

dx ( since f .0/ D 0)

D

8L

.2n  1/

2



2

"

f

0

.x/ sin

.2n  1/ x

2L

ˇ

L

0



Z

L

0

f

00

.x/ sin

.2n  1/ x

2L

dx

#

D 

8L

.2n  1/

2



2

Z

L

0

f

00

.x/ sin

.2n  1/ x

2L

dx since f

0

.L/ D 0:

(b) Continuing the integration by parts yields

d

n

D

16L

2

.2n 1/

3



3

"

f

00

.x/ cos

.2n  1/ x

2L

ˇ

L

0



Z

L

0

f

000

.x/ cos

.2n  1/ x

2L

dx

#

D 

16L

2

.2n 1/

3



3

Z

L

0

f

000

.x/ cos

.2n  1/ x

2L

dx:

11.3.52. Since f .0/ D f

0

.L/ D 0, and f

00

.x/ D 6.L  2x/

d

n

D 

48L

.2n  1/

2



2

Z

L

0

.L  2x/ sin

.2n  1/ x

2L

dx

D

96L

2

.2n  1/

3



3

"

.L  2x/ cos

.2n  1/ x

2L

ˇ

L

0

C 2

Z

L

0

cos

.2n  1/ x

2L

dx

#

D

96L

2

.2n  1/

3



3

"

L C

4L

.2n  1/

sin

.2n 1/x

2L

ˇ

L

0

#

D 

96L

3

.2n  1/

3



3



1 C .1/

n

4

.2n  1/



I

S

M

.x/ D 

96L

3



3

1

X

nD1

1

.2n  1/

3



1 C .1/

n

4

.2n  1/



sin

.2n  1/ x

2L

:

11.3.54. Since f .0/ D f

0

.L/ D f

00

.0/ D 0 and f

000

.x/ D 6,

d

n

D 

96L

2

.2n 1/

3



3

Z

L

0

cos

.2n 1/x

2L

dx

D 

192L

3

.2n 1/

4



4

sin

.2n  1/ x

2L

ˇ

L

0

D .1/

n

192L

3

.2n  1/

4



4

I

Section 11.3

Fourier Expansions II

237

S

M

.x/ D

192L

3



4

1

X

nD1

.1/

n

.2n 1/

4

sin

.2n 1/x

2L

:

11.3.56. Since f .0/ D f

0

.L/ D f

00

.0/ D 0 and f

000

.x/ D 12.2x  L/,

d

n

D 

192L

2

.2n  1/

3



3

Z

L

0

.2x  L/ cos

.2n  1/ x

2L

dx

D 

384L

3

.2n  1/

4



4

"

.2x  L/ sin

.2n 1/x

2L

ˇ

L

0

 2

Z

L

0

sin

.2n 1/x

2L

dx

#

D 

384L

3

.2n  1/

4



4

"

.1/

nC1

L C

4L

.2n  1/

cos

.2n  1/ x

2L

ˇ

L

0

#

D 

384L

3

.2n  1/

4



4



.1/

nC1

L 

4L

.2n  1/



D

384L

4

.2n  1/

4



4



.1/

n

C

4

.2n  1/



I

S

M

.x/ D

384L

4



4

1

X

nD1

1

.2n  1/

4



.1/

n

C

4

.2n  1/



sin

.2n  1/ x

2L

:

11.3.58. The Fourier sine series of f

4

on Œ0; 2L is

1

X

nD1

B

n

sin

nx

2L

, where

B

n

D

1

L

Z

2L

0

f

4

.x/ sin

nx

2L

dx D

1

L

"

Z

L

0

f .x/ sin

nx

2L

dx C

Z

2L

L

f .2L  x/ sin

nx

2L

dx

#

:

Replacing x by 2L  x y ields

Z

2L

L

f .2L  x/ sin

nx

2L

dx D

Z

L

0

f .x/ sin

n.2L  x/

2L

dx. Since

sin

n.2L  x/

2L

D .1/

nC1

sin

nx

2L

,

Z

2L

L

f .2L  x/ sin

nx

2L

dx D .1/

nC1

Z

L

0

f .x/ sin

nx

2L

dx;

so

B

n

D

1 C .1/

nC1

L

Z

L

0

f .x/ sin

nx

2L

dx D

8

<

:

2

L

Z

L

0

f .x/ sin

.2m  1/ x

2L

dx if n D 2m  1;

0 if n D 2m:

Therefore,the Fourier sine series of f

4

on Œ0; 2L is

1

X

nD1

d

n

sin

.2n 1/x

2L

with

d

n

D

2

L

Z

L

0

f .x/ sin

.2n  1/ x

2L

dx:

238 Chapter 11

Boun dary Value Problems and Fourier Expansions

11.3.60. The Fourier cosine series of f

4

on Œ0; 2L is A

0

C

1

X

nD1

A

n

cos

nx

2L

, where

A

0

D

1

2L

Z

2L

0

f

4

.x/ dx D

1

2L

"

Z

L

0

f .x/ dx C

Z

2L

L

f .2L  x/ dx

#

D

1

L

Z

L

0

f .x/ dx

and

A

n

D

1

L

Z

2L

0

f

4

.x/ cos

nx

2L

dx D

1

L

"

Z

L

0

f .x/ cos

nx

2L

dx C

Z

2L

L

f .2L  x/ cos

nx

2L

dx

#

:

Replacing x by 2L  x yields

Z

2L

L

f .2L  x/ cos

nx

2L

dx D 

Z

0

L

f .x/ cos

n.2L  x/

2L

dx D

Z

L

0

f .x/ cos

n.2L  x/

2L

dx:

Since cos

n.2L  x/

2L

D cos n cos

nx

2L

D .1/

n

cos

nx

2L

,

A

n

D

1 C.1/

n

L

Z

L

0

f .x/ cos

nx

2L

dx D

8

<

:

0 if n D 2m  1

2

L

Z

L

0

f .x/ cos

mx

L

dx if n D 2m:

Therefore,the Fourier cosine series of f

4

on Œ0; 2L is A

0

C

1

X

nD0

A

2n

cos

nx

L

= a

0

C

1

X

nD0

a

n

cos

nx

L

.

CHAPTER 1 2

Fo urier Solutions of Partial Differential

12.1 THE HEAT EQUATION

12.1.2. X.x/T .t/ satisﬁes u

t

D a

2

u

xx

if X

00

C X D 0 and ( A) T

0

D a

2

T for the same value

of . The p roduct also satisﬁes the boundary conditions u.0; t/ D u

x

.L; t / D 0; t > 0, if and only

if X.0/ D X

0

.L/ D 0. Since we are interested in nontrivial solutions, X must be a non trivial solution

of (B) X

00

C X D 0; X.0/ D 0; X

0

.L/ D 0. From Theorem 11.1.4, 

n

D .2n  1/

2



2

=4L

2

is an

eigenvalue of (B) with associated eig enfunction X

n

D sin

.2n  1/ x

2L

, n D 1; 2; 3; : : : . Substituting

 D .2n  1/

2



2

=4L

2

into (A) yields T

0

D ..2n  1/

2



2

a

2

=4L

2

/T , wh ich has the solution T

n

D

e

.2n1/

2



2

a

2

t=4L

2

.

We have now shown that the functions u

n

.x; t/ D e

.2n1/

2



2

a

2

t=4L

2

sin

.2n 1/x

2L

, n D 1; 2; 3; : : :

satisfy u

t

D a

2

u

xx

and the boundary conditions u.0; t/ D u

x

.L; t / D 0; t > 0. Any ﬁnite sum

m

X

nD1

d

n

e

.2n1/

2



2

a

2

t=4L

2

sin

.2n  1/ x

2L

also has these properties. Therefore,it is plausible to expect

that that this is also true of the inﬁnite series (C) u.x; t/ D

1

X

nD1

d

n

e

.2n1/

2



2

a

2

t=4L

2

sin

.2n 1/x

2L

under su itable conditions on the coefﬁcients fd

n

g. Since u.x; 0/ D

1

X

nD1

d

n

sin

.2n  1/ x

2L

, if fd

n

g are

the mixed Fourier sine coefﬁcients of f on Œ0; L, then u.x; 0/ D f .x/ at all points x in Œ0; L where the

mixed Fo urier sine series converges to f .x/. In this case (C) is a formal solution of the initial-boundary

value prob lem of Deﬁnition 12.1.3.

12.1.8. Since f .0/ D f .1/ D 0 and f

00

.x/ D 2, Theorem 11.3.5(b) implies that

˛

n

D

4

n

2



2

Z

1

0

sin nx dx D 

4

n

3



3

cos nx

ˇ

1

0

D 

4

n

3



2

.cos n  1/

D

8

<

:

8

.2m  1/

3



3

; if n D 2m  1;

0; if n D 2mI

S.x/ D

8



3

1

X

nD1

1

.2n  1/

3

sin

.2n  1/ x

L

. From Deﬁnition 12.1.1,

u.x; t/ D

8



3

1

X

nD1

1

.2n  1/

3

e

.2n1/

2



2

t

sin.2n  1/x:

239

240 Chapter 12

Fourier Solut ions of Partial Di fferential

12.1.10.

˛

1

D

2



Z



0

x sin

2

x dx D

1



Z



0

x.1  cos 2x/ dx D

x

2

2

ˇ



0



1



Z



0

x cos 2x dx

D



2



1

2



x sin 2x

ˇ



0



Z



0

cos 2x dx



D



2

C

sin 2x

4

ˇ



0

D



2

I

if n  2, then

˛

n

D

2



Z



0

x sin x sin nx dx D

1



Z



0

xŒcos.n  1/x  cos.n C 1/x dx

D

1





x



sin.n  1/x

n  1



sin.n C 1/x

n C 1



ˇ



0



Z



0



sin.n  1/x

n  1



sin.n C 1/x

n C 1



dx



D

1





cos.n  1/x

.n  1/

2



cos.n C 1/x

.n C 1/

2



ˇ



0

D

1





1

.n  1/

2



1

.n C 1/

2





.1/

nC1

 1



D

4n

.n

2

 1/

2





.1/

nC1

 1



D

8

<

:

0 i f n D 2m  1;



16m

.4m

2

 1/

if n D 2mI

S.x/ D



2

sin x 

16



1

X

nD1

n

.4n

2

 1/

2

sin 2nx. From Deﬁniti on 12.1.1,

u.x; t/ D



2

e

3t

sin x 

16



1

X

nD1

n

.4n

2

 1/

2

e

12n

2

t

sin 2nx:

12.1.12. Since f .0/ D f .L/ D 0 and f

00

.x/ D 6x, Theorem 11.3.5(b) implies that

˛

n

D

36

n

2



2

Z

3

0

x sin

nx

3

dx D 

108

n

3



3

"

x cos

nx

3

ˇ

3

0



Z

3

0

cos

nx

3

dx

#

D .1/

nC1

108

n

3



3

C

108

n

4



4

sin

nx

3

ˇ

3

0

D .1/

nC1

324

n

3



3

I

S.x/ D 

324



3

1

X

nD1

.1/

n

3

sin

nx

3

. From Deﬁnition 1 2.1.1, u.x; t/ D 

324



3

1

X

nD1

.1/

n

3

e

4n

2



2

t=9

sin

nx

3

.

12.1.14. Since f .0/ D f .1/ D f

00

.0/ D f

00

.L/ D 0 and f

.4/

D 360x, Theorem 11.3.5(b) and

Exercise 35(b) of Section 11.3 imply that

˛

n

D

720

n

4



4

Z

1

0

x sin nx dx D 

720

n

5



5

"

x cos nx

ˇ

1

0



Z

1

0

cos n x dx

#

D .1/

nC1

720

n

5



5

C

720

n

6



6

sin

nx

L

ˇ

1

0

D .1/

nC1

720

n

5



5

I

S.x/ D 

720



5

1

X

nD1

.1/

n

5

sin n x. From Deﬁnition 12.1.1, u.x; t/ D 

720



5

1

X

nD1

.1/

n

5

e

7n

2



2

t

sin nx.

Section 12.1

The Heat Equation

241

12.1.16. Since f .0/ D f .1/ D f

00

.0/ D f

00

.L/ D 0 and f

.4/

D 120.3x  1/, Theorem 11.3.5(b) and

Exercise 35(b) of Section 11.3 imply that

˛

n

D

240

n

4



4

Z

1

0

.3x  1/ sin nx dx D 

240

n

5



5

"

.3x  1/ cos nx

ˇ

1

0

 3

Z

1

0

cos nx dx

#

D 

240

n

5



5

Œ.1/

n

2 C 1 C

720

n

6



6

sin nx

ˇ

1

0

D 

240

n

5



5

Œ1 C .1/

n

2 I

S.x/ D 

240



5

1

X

nD1

1 C .1/

n

2

n

5

sin nx. From Deﬁnition 12.1.1,

u.x; t/ D 

240



5

1

X

nD1

1 C .1/

n

2

n

5

e

2n

2



2

t

sin n x:

12.1.18. ˛

0

D

1

2

Z

2

0

.x

2

 4x/ dx D

1

L



x

3

 2x

2



ˇ

2

0

D 

8

3

; if n  1,

˛

n

D

Z

2

0

.x

2

 4x/ cos

nx

2

dx D

2

n

"

.x

2

 4x/ sin

nx

2

ˇ

2

0

 2

Z

2

0

.x  2/ sin

nx

2

dx

#

D

8

n

2



2

"

.x  2/ cos

nx

2

ˇ

2

0



Z

2

0

cos

nx

2

dx

#

D

16

n

2



2



32

n

3



3

sin

nx

2

ˇ

2

0

D

16

n

2



2

I

C.x/ D 

8

3

C

16



2

1

X

nD1

1

n

2

cos

nx

2

. From Deﬁnition 12.1.3, u.x; t/ D 

8

3

C

16



2

1

X

nD1

1

n

2

e

n

2



2

t

cos

nx

2

.

12.1.20. From Example 11.3.5, C.x/ D 4

384



4

1

X

nD1

1

.2n  1/

4

cos

.2n  1/ x

2

. From Deﬁnition 12.1.3,

u.x; t/ D 4 

384



4

1

X

nD1

1

.2n  1/

4

e

3.2n1/

2



2

t=4

cos

.2n 1/x

2

.

12.1.22. ˛

0

D

1

L

Z

1

0

.3x

4

 4Lx

3

/ dx D

1

L



3x

5

 x

4



ˇ

1

0

D 

2

5

. Since f

0

.0/ D f

0

.1/ D 0 and

f

000

.x/ D 24.3x  1/, Theorem 11.3.5(a) implies that

˛

n

D

48

n

3



3

Z

1

0

.3x  1/ sin nx dx D 

48

n

4



4

"

.3x  1/ cos nx

ˇ

1

0

 3

Z

1

0

cos nx dx

#

D 

48

n

4



4

Œ.1/

n

2 C 1 C

144

n

5



5

sin nx

ˇ

1

0

D 

48

n

4



4

Œ1 C .1/

n

2 ; n  1I

C.x/ D 

2

5



48



4

1

X

nD1

1 C.1/

n

2

n

4

cos n x. From Deﬁnition 12.1.3,

u.x; t/ D 

2

5



48



4

1

X

nD1

1 C .1/

n

2

n

4

e

3n

2



2

t

cos nx:

242 Chapter 12

Fourier Solut ions of Partial Di fferential

12.1.24. ˛

0

D

1



Z



0

.x

4

 2x

3

C 

2

x

2

/ dx D

1





x

5



x

4

2

C



2

x

3



ˇ



0

D



4

30

. Since f

0

.0/ D

f

0

./ D 0 and f

000

.x/ D 12.2x  /, Theorem 11.3.5(a) implies that

˛

n

D

24

n

3



Z



0

.2x  / sin nx dx D 

24

n

4





.2x  / cos nx

ˇ



0

 2

Z



0

cos nx dx



D 

24

n

4



Œ.1/

n

 C   C

48

n

5



sin nx

ˇ



0

D 

24

n

4

Œ1 C .1/

n



D

(

0 if n D 2m  1;



3

m

4

if n D 2m;

n  1I

C.x/ D



4

30

 3

1

X

nD1

1

n

4

cos 2nx. From Deﬁnition 12.1.3, u.x; t/ D



4

30

 3

1

X

nD1

1

n

4

e

4n

2

t

cos 2nx.

12.1.26.

˛

n

D

2



Z



0

.x  x

2

/ sin

.2n  1/x

2

dx

D 

4

.2n  1/



.x  x

2

/ cos

.2n  1/x

2

ˇ



0



Z



0

.  2x/ cos

.2n  1/x

2

dx



D

8

.2n 1/

2





.  2x/ sin

.2n  1/x

2

ˇ



0

C 2

Z



0

sin

.2n  1/x

2

dx



D .1/

n

8

.2n  1/

2



32

.2n 1/

3



cos

.2n  1/x

2

ˇ



0

D .1/

n

8

.2n  1/

2

C

32

.2n  1/

3



I

S

M

.x/ D 8

1

X

nD1

1

.2n  1/

2



.1/

n

C

4

.2n  1/



sin

.2n  1/x

2

. From Deﬁnition 12.1.4,

u.x; t/ D 8

1

X

nD1

1

.2n  1/

2



.1/

n

C

4

.2n  1/



e

3.2n1/

2

t=4

sin

.2n  1/x

2

:

12.1.28. Since f .0/ D f

0

.1/ D 0, and f

00

.x/ D 6.1  2x/, Theorem 11.3.5(d) implies that

˛

n

D 

48

.2n 1/

2



2

Z

1

0

.1  2x/ sin

.2n  1/ x

2

dx

D

96

.2n 1/

3



3

"

.1  2x/ cos

.2n 1/x

2

ˇ

1

0

C 2

Z

1

0

cos

.2n  1/ x

2

dx

#

D

96

.2n 1/

3



3

"

1 C

4

.2n 1/

sin

.2n  1/ x

2

ˇ

1

0

#

D 

96

.2n 1/

3



3



1 C.1/

n

4

.2n 1/



I

Section 12.1

The Heat Equation

243

S

M

.x/ D 

96



3

1

X

nD1

1

.2n 1/

3



1 C .1/

n

4

.2n  1/



sin

.2n  1/ x

2

. From Deﬁnition 12.1.4,

u.x; t/ D 

96



3

1

X

nD1

1

.2n 1/

3



1 C .1/

n

4

.2n  1/



e

.2n1/

2



2

t

sin

.2n 1/x

2

:

12.1.30. Since f .0/ D f

0

.L/ D f

00

.0/ D 0 and f

000

.x/ D 6, Theorem 11.3.5(d) and Exercise 11.3.50(b)

imply that

˛

n

D 

96

.2n  1/

3



3

Z

1

0

cos

.2n  1/ x

2

dx

D 

192

.2n  1/

4



4

sin

.2n  1/ x

2

ˇ

1

0

D .1/

n

192

.2n  1/

4



4

I

S

M

.x/ D

192



4

1

X

nD1

.1/

n

.2n 1/

4

sin

.2n  1/ x

2

. From Deﬁnition 12.1.4,

u.x; t/ D

192



4

1

X

nD1

.1/

n

.2n 1/

4

e

.2n1/

2



2

t

sin

.2n 1/x

2

:

12.1.32. Since f .0/ D f

0

.1/ D f

00

.0/ D 0 and f

000

.x/ D 12.2x  1/, Theorem 11.3.5(d) and Exer-

cise 11.3.50(b) imply that

˛

n

D 

192

.2n  1/

3



3

Z

1

0

.2x  1/ cos

.2n 1/x

2

dx

D 

384

.2n  1/

4



4

"

.2x  1/ sin

.2n 1/x

2

ˇ

1

0

 2

Z

1

0

sin

.2n  1/ x

2

dx

#

D 

384

.2n  1/

4



4

"

.1/

nC1

1 C

4

.2n  1/

cos

.2n  1/ x

2

ˇ

1

0

#

D 

384

.2n  1/

4



4



.1/

nC1

1 

4

.2n  1/



D

384

.2n 1/

4



4



.1/

n

C

4

.2n  1/



I

S

M

.x/ D

384



4

1

X

nD1

1

.2n 1/

4



.1/

n

C

4

.2n 1/



sin

.2n 1/x

2

. From Deﬁnition 12.1.4,

u.x; t/ D

384



4

1

X

nD1

1

.2n 1/

4



.1/

n

C

4

.2n 1/



e

.2n1/

2



2

t

sin

.2n  1/ x

2

:

12.1.36. From Example 11.3.3, C

M

.x/ D

8



2

1

X

nD1

1

.2n  1/

2

cos

.2n  1/ x

2

. From Deﬁnition 12.1.5,

u.x; t/ D

8



2

1

X

nD1

1

.2n 1/

2

e

3.2n1/

2



2

t=4

cos

.2n  1/ x

2

:

244 Chapter 12

Fourier Solut ions of Partial Di fferential

12.1.38. Since f

0

.0/ D f ./ D 0 and f

00

.x/ D 2, Theorem 11.3.5(c) implies that

˛

n

D

16

.2n  1/

2



Z



0

cos

.2n  1/x

2

dx D

32

.2n  1/

3



sin

.2n 1/x

2

ˇ



0

D .1/

nC1

32

.2n 1/

3



I

C

M

.x/ D 

32



1

X

nD1

.1/

n

.2n  1/

3

cos

.2n 1/x

2

. From Deﬁni tion 12.1.5,

u.x; t/ D 

32



1

X

nD1

.1/

n

.2n 1/

3

e

7.2n1/

2

t=4

cos

.2n  1/x

2

:

12.1.40. Since f

0

.0/ D f .1/ D 0 and f

00

.x/ D 6.2x C1/, Theorem 11.3.5(c) implies that

˛

n

D 

48L

.2n  1/

2



2

Z

1

0

.2x C 1/ cos

.2n  1/ x

2

dx

D 

96

.2n  1/

3



3

"

.2x C 1/ sin

.2n  1/ x

2

ˇ

1

0

 2

Z

1

0

sin

.2n  1/ x

2

#

dx

D 

96

.2n  1/

3



3

"

.1/

nC1

3 

4

.2n  1/

cos

.2n 1/x

2

ˇ

1

0

#

D

96

.2n  1/

3



3



.1/

n

3 C

4

.2n  1/



I

C

M

.x/ D

96



3

1

X

nD1

1

.2n  1/

3



.1/

n

3 C

4

.2n  1/



cos

.2n  1/ x

2

. From Deﬁnition 12.1.5,

u.x; t/ D

96



3

1

X

nD1

1

.2n  1/

3



.1/

n

3 C

4

.2n 1/



e

.2n1/

2



2

t=4

cos

.2n  1/ x

2

:

12.1.42. Theorem 11.3.5(c) and Exercise 11.3.42(b) imply t hat Since f

0

.0/ D f .1/ D f

00

.1/ D 0 and

f

000

.x/ D 12.2x  1/,

˛

n

D

192

.2n  1/

3



3

Z

1

0

.2x  1/ si n

.2n  1/ x

2

dx

D 

384

.2n  1/

4



4

"

.2x  1/ cos

.2n  1/ x

2

ˇ

1

0

 2

Z

1

0

cos

.2n 1/x

2

#

dx

D 

384

.2n  1/

4



4

"

1 

4

.2n  1/

sin

.2n 1/x

2

ˇ

1

0

#

D 

384

.2n 1/

4



4



1 C

.1/

n

4

.2n 1/



I

C

M

.x/ D 

384



4

1

X

nD1

1

.2n  1/

4



1 C

.1/

n

4

.2n 1/



cos

.2n 1/x

2

. From Deﬁnition 12.1.5,

u.x; t/ D 

384



4

1

X

nD1

1

.2n  1/

4



1 C

.1/

n

4

.2n 1/



e

.2n1/

2



2

t=4

cos

.2n  1/ x

2

:

Section 12.1

The Heat Equation

245

12.1.44. ˛

n

D

2

L

Z

L=2

0

sin

nx

L

dx D 

2

n

cos

nx

L

ˇ

L=2

0

D

2

n

h

1  cos

n

2

i

;

S.x/ D

2



1

X

nD1

1

n

h

1  cos

n

2

i

sin

nx

L

. From Deﬁnition 12.1.1,

u.x; t/ D

2



1

X

nD1

1

n

h

1  cos

n

2

i

e

n

2



2

t

2

=L

2

sin

nx

L

:

12.1.46.

˛

n

D

2

L

Z

L=2

0

sin

.2n  1/ x

2L

dx D 

4

.2n  1/

cos

.2n 1/x

2L

ˇ

L=2

0

D

4

.2n 1/



1  cos

.2n 1//

4



I

S

M

.x/ D

4



1

X

nD1

1

2n  1



1  cos

.2n 1//

4



sin

.2n  1/ x

2L

. From Deﬁni tion 12.1.4,

u.x; t/ D

4



1

X

nD1

1

2n  1



1  cos

.2n 1//

4



e

.2n1/

2



2

a

2

t=4L

2

sin

.2n 1/x

2L

:

12.1.48. Let u.x; t/ D v.x; t/ C q.x/; t hen u

t

D v

t

and u

xx

D v

xx

C q

00

, so

v

t

D 9v

xx

C 9q

00

 54x; 0 < x < 4; t > 0;

v.0; t/ D 1 q.0/; v.4; t/ D 61  q.4/; t > 0;

v.x; 0/ D 2  x C x

3

 q.x/; 0  x  4:

.A/

We want q

00

.x/ D 6x; q.0/ D 1; q.4/ D 61; q.x/ D x

3

C a

1

C a

2

x; q.0/ D 1 ) a

1

D 1;

q.x/ D x

3

C 1 C a

2

x; q.4/ D 61 ) a

2

D 1; q.x/ D x

3

C 1  x. Now (A) redu ces to

v

t

D 9v

xx

; 0 < x < 4; t > 0;

v.0; t/ D 0; v.4; t/ D 0; t > 0;

v.x; 0/ D 1; 0  x  4;

which we so lve by separation of variables.

˛

n

D

1

2

Z

L

0

sin

nx

4

dx D 

2

n

cos

nx

4

ˇ

4

0

D

2

n

Œ1  .1/

n

 D

8

<

:

4

.2m 1/

if n D 2m  1;

0 if n D 2mI

S.x/ D

4



1

X

nD1

1

.2n  1/

sin

.2n  1/ x

4

. From Deﬁni tion 12.1.1,

v.x; t/ D

4



1

X

nD1

1

.2n  1/

e

9

2

n

2

t=16

sin

.2n 1/x

4

:

246 Chapter 12

Fourier Solut ions of Partial Di fferential

Therefore,

u.x; t/ D 1  x C x

3

C

4



1

X

nD1

e

9

2

n

2

t=16

.2n 1/

sin

.2n 1/x

4

:

12.1.50. Let u.x; t/ D v.x; t/ C q.x/; t hen u

t

D v

t

and u

xx

D v

xx

C q

00

, so

v

t

D 3u

xx

C3q

00

 18x; 0 < x < 1; t > 0;

v

x

.0; t/ D 1  q

0

.0/; v.1; t/ D 1  q.1/; t > 0;

v.x; 0/ D x

3

 2x  q.x/; 0  x  1:

.A/

We want q

00

.x/ D 6x; q

0

.0/ D 1; q.1/ D 1; q

0

.x/ D 3x

2

C a

2

; q

0

.0/ D 1 ) a

2

D 1;

q

0

.x/ D 3x

2

1; q.x/ D x

3

x Ca

1

x; q.1/ D 1 ) a

1

D 1; q.x/ D x

3

x 1. Now (A) reduces

to

v

t

D 3u

xx

; 0 < x < 1; t > 0;

v

x

.0; t/ D 0; v.1; t/ D 0; t > 0;

v.x; 0/ D 1  x; 0  x  1:

From Example 11.3.3, C

M

.x/ D

8



2

1

X

nD1

1

.2n  1/

2

cos

.2n  1/ x

2

. From Deﬁni tion 12.1.5, v.x; t/ D

8



2

1

X

nD1

1

.2n  1/

2

e

3.2n1/

2



2

t=4

cos

.2n  1/ x

2

. Therefore,

u.x; t/ D 1  x C x

3

C

8



2

1

X

nD1

1

.2n  1/

2

e

3.2n1/

2



2

t=4

cos

.2n 1/x

2

:

12.1.52. Let u.x; t/ D v.x; t/ C q.x/; t hen u

t

D v

t

and u

xx

D v

xx

C q

00

, so

v

t

D v

xx

C q

00

C 

2

sin x; 0 < x < 1; t > 0;

v.0; t/ D q.0/; v

x

.1; t/ D   q

0

.1/; t > 0;

v.x; 0/ D 2 sin x q.x/; 0  x  1:

.A/

We want q

00

.x/ D 

2

sin x; q.0/ D 0; q

0

.1/ D  ; q

0

.x/ D  cos  xCa

2

; q

0

.1/ D  ) a

2

D 0;

q

0

.x/ D  cos  x; q.x/ D sin  x C a

1

; q.0/ D 0 ) a

1

D 0; q.x/ D sin x. N ow (A) reduces to

v

t

D v

xx

; 0 < x < 1; t > 0;

v.0; t/ D 0; v

x

.1; t/ D 0; t > 0;

v.x; 0/ D sin x; 0  x  1:

˛

n

D 2

Z

1

0

sin x sin

.2n 1/x

2

dx D

Z

1

0



cos.2n  3/x

2



cos.2n C 1/ x

2



dx

D

2





sin.2n  3/x=2

.2n 3/



sin.2n C 1/x=2

.2n C 1/



ˇ

1

0

D .1/

n

2





1

2n  3



1

2n C 1



D .1/

n

8



1

.2n C 1/.2n 3/

I

S

M

.x/ D

8



1

X

nD1

.1/

n

.2n C 1/.2n  3/

sin

.2n  1/ x

2

. From Deﬁni tion 12.1.4,

v.x; t/ D

8



1

X

nD1

.1/

n

.2n C 1/.2n  3/

e

.2n1/

2



2

t=4

sin

.2n  1/ x

2

:

Section 12.2

The Wave Equation

247

Therefore, u.x; t/ D si n x C

8



1

X

nD1

.1/

n

.2n C 1/.2n  3/

e

.2n1/

2



2

t=4

sin

.2n  1/ x

2

.

12.1.54. (a) Since f is piecewise smooth of Œ0; L, there is a con stant K such that jf .x/j  K, 0  x 

L. Therefore, j˛

n

j D

2

L

ˇ

Z

L

0

f .x/ sin

nx

L

dx

ˇ



2

L

Z

L

0

jf .x/jdx D 2K. Hence, j˛

n

e

n

2



2

a

2

t=L

j 

2Ke

n

2



2

a

2

t=L

, so u.x; t/ converges for all x if t > 0, by the comparison test.

(b) Let t b e a ﬁxed positive number. Apply Theorem 12.1.2 with ´ D x and w

n

.x/ D ˛

n

e

n

2



2

t=L

2

sin

nx

L

.

Then w

0

n

.x/ D



L

n˛

n

e

n

2



2

t=L

2

cos

nx

L

, so jw

0

n

.x/j 

2K

L

ne

n

2



2

t=L

2

, 1 < x < 1. Since

1

X

nD1

ne

n

2



2

a

2

t=L

2

converges if t > 0, Theorem 12 .1.1 (with ´

1

D x

1

and ´

2

D x

2

arbitrary) implies

the concclusion.

(c) Since

1

X

nD1

n

2

e

n

2



2

a

2

t=L

2

also converges if t > 0, an argument like that in (b) w ith w

n

.x/ D

n˛

n

e

n

2



2

t=L

2

cos

nx

L

yields the conclusion.

(d) Let x be arbitrar y, but ﬁxed. Apply Theorem 12.1.2 with ´ D t and

w

n

.t/ D ˛

n

e

n

2



2

a

2

t=L

2

sin

nx

L

. Then w

0

n

.t/ D 



2

a

2

L

2

n

2

˛

n

e

n

2



2

a

2

t=L

2

sin

nx

L

, so jw

0

n

.t/j 

2K

2

a

2

L

n

2

e

n

2



2

a

2

t

0

=L

2

if t > t

0

. Since

1

X

nD1

n

2

e

n

2



2

a

2

t

0

=L

2

converges, Theorem 12.1.1 (with ´

1

D

t

0

> 0 and ´

2

D t

1

arbitrary impli es th e conclusion for t  t

0

. However, since t

0

is an arbitrary positive

number, this holds for t > 0.

12.2 THE WAVE EQUATION

12.2.1. ˇ

n

D 2

h

R

1=2

0

x sin nx C

R

1

1=2

.1  x/ sin n x dx

i

;

Z

1=2

0

x sin nx dx D 

1

n

"

x cos nx

ˇ

1=2

0



Z

1=2

0

cos nx dx

#

D 

1

2n

cos

n

2

C

1

n

2



2

sin nx

ˇ

1=2

0

D 

1

2n

cos

n

2

C

1

n

2



2

sin

n

2

I

Z

1=2

0

.1  x/ sin nx dx D 

1

n

"

.1  x/ cos n x

ˇ

1

1=2

C

Z

1=2

0

cos nx dx

#

D

1

2n

cos

n

2



1

n

2



2

sin nx

ˇ

1

1=2

D

1

2n

cos

n

2

C

1

n

2



2

sin

n

2

I

b

n

D

4

n

2



2

sin

n

2

D

8

<

:

.1/

mC1

4

.2m 1/

2



2

if n D 2m  1

0 if n D 2mI

248 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

S

g

.x/ D

4



2

1

X

nD1

.1/

nC1

.2n  1/

2

sin.2n  1/x. Fr om Deﬁnition 12.1.1,

u.x; t/ D

4

3

3

1

X

nD1

.1/

nC1

.2n 1/

3

sin 3.2n 1/t sin.2n  1/x:

12.2.2. Since f .0/ D f .1/ D 0 and f

00

.x/ D 2, Theorem 11.3.5(b) implies that

˛

n

D

4

n

2



2

Z

1

0

sin nx dx D 

4

n

3



3

cos nx

ˇ

1

0

D 

4

n

3



2

.cos n  1/

D

8

<

:

8

.2m  1/

3



3

; if n D 2m  1;

0; if n D 2mI

S

f

.x/ D

8



3

1

X

nD1

1

.2n  1/

3

sin.2n  1/x. Fr om Deﬁnition 12.1.1,

u.x; t/ D

8



3

1

X

nD1

1

.2n  1/

3

cos 3.2n  1/t sin.2n  1/x:

12.2.4. Since g.0/ D g.1/ D 0 and g

00

.x/ D 2, Theorem 11.3.5(b) implies that

ˇ

n

D

4

n

2



2

Z

1

0

sin nx dx D 

4

n

3



3

cos n x

ˇ

1

0

D 

4

n

3



2

.cos n  1/

D

8

<

:

8

.2m  1/

3



3

; if n D 2m  1;

0; if n D 2mI

S

g

.x/ D

8



3

1

X

nD1

1

.2n  1/

3

sin.2n  1/x. Fr om Deﬁnition 12.1.1,

u.x; t/ D

8

3

4

1

X

nD1

1

.2n 1/

4

sin 3.2n 1/t sin.2n  1/x:

12.2.6. From Example 11.2.6, S

f

.x/ D

324



3

1

X

nD1

.1/

n

3

sin

nx

3

. From Deﬁnition 12.1.1,

u.x; t/ D

324



3

1

X

nD1

.1/

n

3

cos

8 nt

3

sin

nx

3

:

12.2.8. From Example 11.2.6 S

g

.x/ D

324



3

1

X

nD1

.1/

n

3

sin

nx

3

. From Deﬁnition 12.1.1,

u.x; t/ D

81

2

4

1

X

nD1

.1/

n

4

sin

8 nt

3

sin

nx

3

:

Section 12.2

The Wave Equation

249

12.2.10.

˛

1

D

2



Z



0

x sin

2

x dx D

1



Z



0

x.1  cos 2x/ dx D

x

2

2

ˇ



0



1



Z



0

x cos 2x dx

D



2



1

2



x sin 2x

ˇ



0



Z



0

cos 2x dx



D



2

C

sin 2x

4

ˇ



0

D



2

I

if n  2, then

˛

n

D

2



Z



0

x sin x sin nx dx D

1



Z



0

xŒcos.n  1/x  cos.n C 1/x dx

D

1





x



sin.n  1/x

n  1



sin.n C 1/x

n C 1



ˇ



0



Z



0



sin.n  1/x

n  1



sin.n C 1/x

n C 1



dx



D

1





cos.n  1/x

.n  1/

2



cos.n C 1/x

.n C 1/

2



ˇ



0

D

1





1

.n  1/

2



1

.n C 1/

2





.1/

nC1

 1



D

4n

.n

2

 1/

2





.1/

nC1

 1



D

8

<

:

0 i f n D 2m  1;



16m

.4m

2

 1/

if n D 2mI

S

f

.x/ D



2

sin x 

16



1

X

nD1

n

.4n

2

 1/

2

sin 2nx. From Deﬁnition 12.1.1,

u.x; t/ D



2

cos

p

5 t sin x 

16



1

X

nD1

n

.4n

2

 1/

2

cos 2n

p

5 t sin 2nx:

12.2.12.

ˇ

1

D

2



Z



0

x sin

2

x dx D

1



Z



0

x.1  cos 2x/ dx D

x

2

2

ˇ



0



1



Z



0

x cos 2x dx

D



2



1

2



x sin 2x

ˇ



0



Z



0

cos 2x dx



D



2

C

sin 2x

4

ˇ



0

D



2

I

if n  2 then

ˇ

n

D

2



Z



0

x sin x sin nx dx D

1



Z



0

xŒcos.n  1/x  cos.n C 1/x dx

D

1





x



sin.n  1/x

n  1



sin.n C 1/x

n C 1



ˇ



0



Z



0



sin.n  1/x

n  1



sin.n C 1/x

n C 1



dx



D

1





cos.n  1/x

.n  1/

2



cos.n C 1/x

.n C 1/

2



ˇ



0

D

1





1

.n  1/

2



1

.n C 1/

2





.1/

nC1

 1



D

4n

.n

2

 1/

2





.1/

nC1

 1



D

8

<

:

0 if n D 2m  1;



16m

.4m

2

 1/

if n D 2mI

S

g

.x/ D



2

sin x 

16



1

X

nD1

n

.4n

2

 1/

2

sin 2nx. From Deﬁnition 12 .1.1,

u.x; t/ D



2

p

5

sin

p

5 t sin x 

8



p

5

1

X

nD1

1

.4n

2

 1/

2

sin 2n

p

5 t sin 2nx:

250 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

12.2.14. Since f .0/ D f .1/ D f

00

.0/ D f

00

.L/ D 0 and f

.4/

D 360x, Theorem 11.3.5(b) and

Exercise 35(b) of Section 11.3 imply that

˛

n

D

720

n

4



4

Z

1

0

x sin nx dx D 

720

n

5



5

"

x cos nx

ˇ

1

0



Z

1

0

cos n x dx

#

D .1/

nC1

720

n

5



5

C

720

n

6



6

sin

nx

L

ˇ

1

0

D .1/

nC1

720

n

5



5

I

S

f

.x/ D 

720



5

1

X

nD1

.1/

n

5

sin n x. From Deﬁnition 12.1.1, u.x; t/ D 

720



5

1

X

nD1

.1/

n

5

cos 3nt sin n x.

12.2.16. ( a) t must be in some interval of the form ŒmL=a; .m C 1/L=a. If

mL

a

 t 



m C

1

2



L

a

,

then (i) holds with 0    L=2a. If



m C

1

2



L

a

 t 

.m C 1/L

a

, then (ii) holds with 0    L=2a.

(b) Suppose that (i) holds. Since

cos

.2n  1/ a

L



 C

mL

a



D cos

.2n  1/ a

L

cos.2n  1/m D .1/

m

cos

.2n  1/ a

L

;

(A) implies that u.x; t/ D .1/

m

u.x; /.

Suppose that ( ii) holds. Since

cos

.2n  1/ a

L



 C

.m C 1/L

a



D cos

.2n  1/ a

L

cos.2n  1/.m C 1/

D .1/

mC1

cos

.2n  1/ a

L

;

(B) i mplies that that u.x; t/ D .1/

mC1

u.x; /.

12.2.18. Since f

0

.0/ D f .2/ D 0 and f

00

.x/ D 2, Theorem 11.3.5(c) implies that

˛

n

D

32

.2n 1/

2



2

Z

2

0

cos

.2n  1/ x

4

dx

D

128

.2n 1/

3



3

sin

.2n  1/ x

4

ˇ

4

0

D .1/

nC1

128

.2n  1/

3



3

I

C

Mf

.x/ D 

128



3

1

X

nD1

.1/

n

.2n  1/

3

cos

.2n  1/ x

4

. From Exercise 12.2.17,

u.x; t/ D 

128



3

1

X

nD1

.1/

n

.2n 1/

3

cos

3.2n  1/t

4

cos

.2n 1/x

4

:

12.2.20. Since g

0

.0/ D g.2/ D 0 and g

00

.x/ D 2, Theorem 11.3.5(c) implies that

ˇ

n

D

32

.2n  1/

2



2

Z

2

0

cos

.2n 1/x

4

dx

D

128

.2n  1/

3



3

sin

.2n  1/ x

4

ˇ

4

0

D .1/

nC1

128

.2n 1/

3



3

I

Section 12.2

The Wave Equation

251

C

Mf

.x/ D 

128



3

1

X

nD1

.1/

n

.2n  1/

3

cos

.2n  1/ x

4

. From Exercise 12.2.17,

u.x; t/ D 

512

3

4

1

X

nD1

.1/

n

.2n  1/

4

sin

3.2n  1/t

4

cos

.2n 1/x

4

:

12.2.22. Since f

0

.0/ D f .1/ D 0 and f

00

.x/ D 6.2x C1/, Theorem 11.3.5(c) implies that

˛

n

D 

48L

.2n  1/

2



2

Z

1

0

.2x C 1/ cos

.2n  1/ x

2

dx

D 

96

.2n  1/

3



3

"

.2x C 1/ sin

.2n  1/ x

2

ˇ

1

0

 2

Z

1

0

sin

.2n  1/ x

2

#

dx

D 

96

.2n  1/

3



3

"

.1/

nC1

3 

4

.2n  1/

cos

.2n 1/x

2

ˇ

1

0

#

D

96

.2n  1/

3



3



.1/

n

3 C

4

.2n  1/



I

C

Mf

.x/ D

96



3

1

X

nD1

1

.2n  1/

3



.1/

n

3 C

4

.2n 1/



cos

.2n 1/x

2

:

From Exercise 12.2.17,

u.x; t/ D

96



3

1

X

nD1

1

.2n  1/

3



.1/

n

3 C

4

.2n  1/



cos

.2n  1/

p

5 t

2

cos

.2n  1/ x

2

:

12.2.24. Since g

0

.0/ D g.1/ D 0 and g

00

.x/ D 6.2x C 1/, Theorem 11.3.5(c) implies that

ˇ

n

D 

48L

.2n  1/

2



2

Z

1

0

.2x C 1/ cos

.2n  1/ x

2

dx

D 

96

.2n  1/

3



3

"

.2x C 1/ sin

.2n  1/ x

2

ˇ

1

0

 2

Z

1

0

sin

.2n 1/x

2

#

dx

D 

96

.2n  1/

3



3

"

.1/

nC1

3 

4

.2n  1/

cos

.2n  1/ x

2

ˇ

1

0

#

D

96

.2n  1/

3



3



.1/

n

3 C

4

.2n  1/



I

C

Mg

.x/ D

96



3

1

X

nD1

1

.2n  1/

3



.1/

n

3 C

4

.2n  1/



cos

.2n 1/x

2

. From Exercise 12.2.17,

u.x; t/ D

192



4

p

5

1

X

nD1

1

.2n 1/

4



.1/

n

3 C

4

.2n  1/



sin

.2n  1/

p

5 t

2

cos

.2n  1/ x

2

:

252 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

12.2.26. Since f

0

.0/ D f .1/ D f

00

.1/ D 0 and f

000

.x/ D 24.x  1/, Theorem 11.3.5(c) and Exer-

cise 42(b) of Section 11.3 i mply that

˛

n

D

384

.2n  1/

3



3

Z

1

0

.x  1/ sin

.2n 1/x

2

dx

D 

768

.2n  1/

4



4

"

.x  1/ cos

.2n  1/ x

2

ˇ

1

0



Z

1

0

cos

.2n  1/ x

2

#

dx

D 

768

.2n  1/

4



4

"

1 

2

.2n  1/

sin

.2n 1/x

2

ˇ

1

0

#

D 

768

.2n  1/

4



4



1 C

.1/

n

2

.2n  1/



I

C

Mf

.x/ D 

384



4

1

X

nD1

1

.2n  1/

4



1 C

.1/

n

4

.2n  1/



cos

.2n  1/ x

2

. From Exercise 12.2.17,

u.x; t/ D 

384



4

1

X

nD1

1

.2n  1/

4



1 C

.1/

n

4

.2n 1/



cos

3.2n  1/t

2

cos

.2n 1/x

2

:

12.2.28. Since g

0

.0/ D g.1/ D g

00

.1/ D 0 and g

000

.x/ D 24.x  1/, Theorem 11.3.5(c) and Exer-

cise 11.2.42(b) imply that

ˇ

n

D

384

.2n 1/

3



3

Z

1

0

.x  1/ sin

.2n  1/ x

2

dx

D 

768

.2n 1/

4



4

"

.x  1/ cos

.2n  1/ x

2

ˇ

1

0



Z

1

0

cos

.2n  1/ x

2

#

dx

D 

768

.2n 1/

4



4

"

1 

2

.2n  1/

sin

.2n  1/ x

2

ˇ

1

0

#

D 

768

.2n 1/

4



4



1 C

.1/

n

2

.2n 1/



I

C

Mg

.x/ D 

384



4

1

X

nD1

1

.2n 1/

4



1 C

.1/

n

4

.2n  1/



cos

.2n  1/ x

2

:

From Exercise 12.2.17,

u.x; t/ D 

768

3

5

1

X

nD1

1

.2n  1/

5



1 C

.1/

n

4

.2n 1/



sin

3.2n  1/t

2

cos

.2n 1/x

2

:

12.2.30. Since f

0

.0/ D f .1/ D f

00

.1/ D 0 and f

000

.x/ D 24.x  1/, Theorem 11.3.5(c) and Exer-

Section 12.2

The Wave Equation

253

cise 42(b) of Section 11.3 i mply that

˛

n

D

384

.2n  1/

3



3

Z

1

0

.x  1/ sin

.2n 1/x

2

dx

D 

768

.2n  1/

4



4

"

.x  1/ cos

.2n  1/ x

2

ˇ

1

0



Z

1

0

cos

.2n  1/ x

2

#

dx

D 

768

.2n  1/

4



4

"

1 

2

.2n  1/

sin

.2n 1/x

2

ˇ

1

0

#

D 

768

.2n  1/

4



4



1 C

.1/

n

2

.2n  1/



I

C

Mf

.x/ D 

768



4

1

X

nD1

1

.2n  1/

4



1 C

.1/

n

2

.2n  1/



cos

.2n  1/ x

2

. From Exercise 12.2.17,

u.x; t/ D 

768



4

1

X

nD1

1

.2n 1/

4



1 C

.1/

n

2

.2n  1/



cos

.2n  1/ t

2

cos

.2n  1/ x

2

:

12.2.32. Setting A D .2n  1/x=2L and B D .2n  1/at=2L in the identities

cos A cos B D

1

2

Œcos.A C B/ C cos.A  B/ and cos A sin B D

1

2

Œsin.A C B/  sin.A  B/ yields

cos

.2n  1/ at

2L

cos

.2n 1/x

2L

D

1

2



cos

.2n 1/.x C at/

2L

C cos

.2n  1/.x  at/

2L



.A/

and

sin

.2n  1/ at

2L

cos

.2n  1/ x

2L

D

1

2



sin

.2n 1/.x C at/

2L

 sin

.2n 1/.x  at/

2L



D

.2n  1/

4L

Z

xCat

xat

cos

.2n 1/

2L

d :

.B/

Since C

Mf

.x/ D

1

X

nD1

˛

n

cos

.2n 1/x

2L

, (A) impli es th at

1

X

nD1

˛

n

cos

.2n  1/ at

2L

cos

.2n 1/x

2L

D

1

2

ŒC

Mf

.x C at/ C C

Mf

.x  at/: .C/

Since it can be shown th at a mixed Fourier cosine series can be integrated term by term between any two

limits, (B) implies that

1

X

nD1

2Lˇ

n

.2n  1/ a

sin

.2n 1/at

2L

cos

.2n  1/ x

2L

D

1

2a

1

X

nD1

ˇ

n

Z

xCat

xat

cos

.2n 1/

2L

d 

D

1

2a

Z

xCat

xat

1

X

nD1

ˇ

n

cos

.2n 1/

2L

!

d 

D

1

2a

Z

xCat

xat

C

Mg

./ d :

254 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

This and (C) imply that

u.x; t/ D

1

2

ŒC

Mf

.x C at/ C C

Mf

.x  at/ C

1

2a

Z

xCat

xat

C

Mg

./ d :

12.2.34. We begin by looking fo r functions of the form v.x; t/ D X.x/T .t/ that are no t identically zero

and satisfy v

tt

D a

2

v

xx

, v.0; t/ D 0, v

x

.L; t / D 0 for all .x; t/. As shown in the text, X and T must

satisfy X

00

C X D 0 and (B) T

00

C a

2

T D 0 for the same value of . Since v.0; t/ D X.0/T .t/

and v

x

.L; t / D X

0

.L/T .t/ and we don ’t want T to be identically zero, X.0/ D 0 and X

0

.L/ D 0.

Therefore, must be an eigenvalue of (C) X

00

C X D 0, X.0/ D 0, X

0

.L/ D 0, and X must be

a -eigenfunct ion. From Theorem 11.1.4, the eigenvalues of (C) are 

n

D

.2n 1/

2



2

=4L

2

, i nteger), with

associated eigenfunctions X

n

D sin

.2n 1/x

2L

, n D 1, 2, 3,. . . . Substituting  D

.2n  1/

2



2

4L

2

into

(B) yields T

00

C ..2n  1/

2



2

a

2

=4L

2

/T D 0, which has the general solution

T

n

D ˛

n

cos

.2n  1/ at

2L

C

2ˇ

n

L

.2n 1/a

sin

.2n  1/ at

2L

;

where ˛

n

and ˇ

n

are constants. Now let

v

n

.x; t/ D X

n

.x/T

n

.t/ D



˛

n

cos

.2n 1/at

2L

C

2ˇ

n

L

.2n  1/ a

sin

.2n 1/at

2L



sin

.2n  1/ x

2L

:

Then

@v

n

@t

.x; t/ D





.2n  1/ a

2L

˛

n

sin

.2n  1/ at

2L

C ˇ

n

cos

.2n  1/ at

2L



sin

.2n 1/x

2L

;

so

v

n

.x; 0/ D ˛

n

sin

.2n  1/ x

2L

and

@v

n

@t

.x; 0/ D ˇ

n

sin

.2n  1/ x

2L

:

Therefore,v

n

satisﬁes (A) with f .x/ D ˛

n

sin

.2n  1/ x

2L

and g.x/ D ˇ

n

sin

.2n  1/ x

2L

. More gen-

erally, if ˛

1

; ˛

2

; : : : ; ˛

m

and ˇ

1

; ˇ

2

; : : : ; ˇ

m

are constants and

u

m

.x; t/ D

m

X

nD1



˛

n

cos

.2n  1/ at

2L

C

2ˇ

n

L

.2n  1/ a

sin

.2n 1/at

2L



sin

.2n  1/ x

2L

;

then u

m

satisﬁes (A) with

f .x/ D

m

X

nD1

˛

n

sin

.2n  1/ x

2L

and g.x/ D

m

X

nD1

ˇ

n

sin

.2n  1/ x

2L

:

This motivates the deﬁnition.

Section 12.2

The Wave Equation

255

12.2.36. Since f .0/ D f

0

.1/ D 0, and f

00

.x/ D 6.1  2x/, Theorem 11.3.5(d) implies that

˛

n

D 

48

.2n 1/

2



2

Z

1

0

.1  2x/ sin

.2n  1/ x

2

dx

D

96

.2n 1/

3



3

"

.1  2x/ cos

.2n 1/x

2

ˇ

1

0

C 2

Z

1

0

cos

.2n  1/ x

2

dx

#

D

96

.2n 1/

3



3

"

1 C

4

.2n 1/

sin

.2n  1/ x

2

ˇ

1

0

#

D 

96

.2n 1/

3



3



1 C.1/

n

4

.2n 1/



I

S

Mf

.x/ D 

96



3

1

X

nD1

1

.2n 1/

3



1 C .1/

n

4

.2n  1/



sin

.2n  1/ x

2

. From Exercise 12.2.34,

u.x; t/ D 

96



3

1

X

nD1

1

.2n 1/

3



1 C .1/

n

4

.2n  1/



cos

3.2n  1/t

2

sin

.2n 1/x

2

:

12.2.38. Since g.0/ D g

0

.1/ D 0, and g

00

.x/ D 6.1  2x/, Theorem 11.3.5(d) implies that

ˇ

n

D 

48

.2n  1/

2



2

Z

1

0

.1  2x/ sin

.2n 1/x

2

dx

D

96

.2n  1/

3



3

"

.1  2x/ cos

.2n  1/ x

2

ˇ

1

0

C 2

Z

1

0

cos

.2n 1/x

2

dx

#

D

96

.2n  1/

3



3

"

1 C

4

.2n  1/

sin

.2n 1/x

2

ˇ

1

0

#

D 

96

.2n  1/

3



3



1 C .1/

n

4

.2n  1/



I

S

Mg

.x/ D 

96



3

1

X

nD1

1

.2n 1/

3



1 C .1/

n

4

.2n  1/



sin

.2n  1/ x

2

. From Exercise 12.2.34,

u.x; t/ D 

64



4

1

X

nD1

1

.2n  1/

4



1 C .1/

n

4

.2n  1/



sin

3.2n  1/t

2

sin

.2n  1/ x

2

:

12.2.40. Since f .0/ D f

0

./ D f

00

.0/ D 0 and f

000

.x/ D 6, Theorem 11.3.5(d) and Exercise 11.3.50(b)

imply that

˛

n

D 

96

.2n  1/

3



Z



0

cos

.2n 1/x

2

dx D 

192

.2n  1/

4



sin

.2n  1/x

2

ˇ



0

D .1/

n

192

.2n  1/

4



I

S

Mf

.x/ D

192



1

X

nD1

.1/

n

.2n  1/

4

sin

.2n 1/x

2

. From Exercise 12.2.34,

u.x; t/ D

192



1

X

nD1

.1/

n

.2n  1/

4

cos

.2n  1/

p

3 t

2

sin

.2n  1/x

2

:

256 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

12.2.42. Since g.0/ D g

0

./ D g

00

.0/ D 0 and g

000

.x/ D 6, Theorem 11.3.5(d) and Exercise 5 0(b) imply

that

ˇ

n

D 

96

.2n 1/

3



Z



0

cos

.2n  1/x

2

dx D 

192

.2n 1/

4



sin

.2n  1/x

2

ˇ



0

D .1/

n

192

.2n 1/

4



I

S

Mg

.x/ D

192



1

X

nD1

.1/

n

.2n 1/

4

sin

.2n 1/x

2

. From Exercise 12.2.34,

u.x; t/ D

384

p

3 

1

X

nD1

.1/

n

.2n  1/

5

sin

.2n 1/

p

3 t

2

sin

.2n 1/x

2

:

12.2.44. Since f .0/ D f

0

.1/ D f

00

.0/ D 0 and f

000

.x/ D 12.2x  1/, Theorem 11.3.5(d) and Exer-

cise 11.3.50(b) imply that

˛

n

D 

192

.2n  1/

3



3

Z

1

0

.2x  1/ cos

.2n  1/ x

2

dx

D 

384

.2n  1/

4



4

"

.2x  1/ sin

.2n  1/ x

2

ˇ

1

0

 2

Z

1

0

sin

.2n 1/x

2

dx

#

D 

384

.2n  1/

4



4

"

.1/

nC1

C

4

.2n 1/

cos

.2n  1/ x

2

ˇ

1

0

#

D 

384

.2n  1/

4



4



.1/

nC1



4

.2n  1/



D

384

.2n  1/

4



4



.1/

n

C

4

.2n 1/



I

S

Mf

.x/ D

384



4

1

X

nD1

1

.2n  1/

4



.1/

n

C

4

.2n  1/



sin

.2n  1/ x

2

. From Exercise 12.2.34,

u.x; t/ D

384



4

1

X

nD1

1

.2n  1/

4



.1/

n

C

4

.2n 1/



cos.2n  1/t sin

.2n  1/ x

2

:

12.2.46. Since g.0/ D g

0

.1/ D g

00

.0/ D 0 and g

000

.x/ D 12.2x  1/, Theorem 11.3.5(d) and Exer-

cise 11.3.50(b) imply that

ˇ

n

D 

192

.2n 1/

3



3

Z

1

0

.2x  1/ cos

.2n 1/x

2

dx

D 

384

.2n 1/

4



4

"

.2x  1/ sin

.2n 1/x

2

ˇ

1

0

 2

Z

1

0

sin

.2n 1/x

2

dx

#

D 

384

.2n 1/

4



4

"

.1/

nC1

C

4

.2n  1/

cos

.2n 1/x

2

ˇ

1

0

#

D 

384

.2n 1/

4



4



.1/

nC1



4

.2n 1/



D

384

.2n  1/

4



4



.1/

n

C

4

.2n  1/



I

S

Mg

.x/ D

384



4

1

X

nD1

1

.2n 1/

4



.1/

n

C

4

.2n  1/



sin

.2n 1/x

2

. From Exercise 12.2.34,

u.x; t/ D

384



5

1

X

nD1

1

.2n  1/

5



.1/

n

C

4

.2n  1/



sin.2n  1/t sin

.2n 1/x

2

:

Section 12.2

The Wave Equation

257

12.2.48. Since f is continuous on Œ0; L and f

0

.L/ D 0, Theorem 11.3.4 implies that S

Mf

.x/ D f .x/,

0  x  L. From Exercise 11.3.58, S

Mf

is the odd periodic extension (with period 2L) of the function

r.x/ D



f .x/; 0  x  L;

f .2L  x/; L < x  2L;

which is continuous on Œ0; 2L. Since r.0/ D r.2L/ D f .0/ D

0, S

Mf

is continuous on .1; 1/. Mo reover, r

0

.x/ D



f

0

.x/; 0 < x < L;

f

0

.2L x/; L < x < 2L;

r

0

C

.0/ D

f

0

C

.0/, r

0



.2L/ D f

0

C

.0/, and, sin ce f

0



.L/ D 0, r

0

.L/ D 0. Hence, r is differentiable on Œ0; 2L.

Since r .0/ D r.2L/ D f .0/ D 0, Theorem 12.2.3(a) with h D r, p D S

Mf

, and L replaced by 2L

implies that S

Mf

is differentiable o n .1; 1/. Similarly, S

Mg

is differentiable o n .1; 1/.

Now we n ote that r

00

.x/ D



f

00

.x/; 0 < x < L;

f

00

.2L  x/; L < x < 2L;

r

00

.L/ D f

00



.L/, and r

00

C

.0/ D r

00



.2L/ D

f

00

C

.0/ D 0. Since S

0

Mf

is the even periodic extension of r

0

, Theorem 12.2.3(b) with h D r

0

, q D S

0

Mf

,

and L replaced by 2L implies that S

0

Mf

is differentiable o n .1; 1/. Now follow the argument u sed t o

complete the proof of Theorem 12.2.4.

12.2.50. From Example 11.3.5, C

f

.x/ D 4

768



4

1

X

nD1

1

.2n  1/

4

cos

.2n 1/x

2

. From Exercise 12.2.49,

u.x; t/ D 4 

768



4

1

X

nD1

1

.2n 1/

4

cos

p

5.2n  1/t

2

cos

.2n 1/x

2

:

12.2.52. ˛

0

D

Z



0

.3x

4

 4Lx

3

/ dx D



3x

5

 x

4



ˇ



0

D 

2

4

5

. Since f

0

.0/ D f

0

./ D 0 and

f

000

.x/ D 24.3x  /, Theorem 11.3.5(a) i mplies that

˛

n

D

48

n

3



Z



0

.3x  / sin nx dx D 

48

n

4





.3x  / cos nx

ˇ



0

 3

Z



0

cos nx dx



D 

48

n

4



Œ.1/

n

2 C  C

144

n

5



sin nx

ˇ



0

D 

48

n

4

Œ1 C .1/

n

2 ; n  1I

C

f

.x/ D 

2

4

5

 48

1

X

nD1

1 C .1/

n

2

n

4

cos nx. From Exercise 12 .2.49,

u.x; t/ D 

2

4

5

 48

1

X

nD1

1 C .1/

n

2

n

4

cos 2nt cos nx:

12.2.54. ˇ

0

D

Z



0

.3x

4

 4Lx

3

/ dx D

1





3x

5

 x

4



ˇ



0

D 

2

4

5

. Since g

0

.0/ D g

0

./ D 0 and

g

000

.x/ D 24.3x  /, Theorem 11.3.5(a) implies that

ˇ

n

D

48

n

3



Z



0

.3x   / sin nx dx D 

48

n

4





.3x   / cos nx

ˇ



0

 3

Z



0

cos nx dx



D 

48

n

4



Œ.1/

n

2 C  C

144

n

5



sin nx

ˇ



0

D 

48

n

4

Œ1 C .1/

n

2 ; n  1I

258 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

C

g

.x/ D 

2

4

5

 48

1

X

nD1

1 C .1/

n

2

n

4

cos nx. From Exercise 12.2.49,

u.x; t/ D 

2

4

t

5

 24

1

X

nD1

1 C .1/

n

2

n

5

sin 2nt cos nx:

12.2.56. ˛

0

D

1



Z



0

.x

4

 2x

3

C 

2

x

2

/ dx D

1





x

5



x

4

2

C



2

x

3



ˇ



0

D



4

30

. Since f

0

.0/ D

f

0

./ D 0 and f

000

.x/ D 12.2x  /, Theorem 11.3.5(a) implies that

˛

n

D

24

n

3



Z



0

.2x  / sin nx dx D 

24

n

4





.2x  / cos nx

ˇ



0

 2

Z



0

cos nx dx



D 

24

n

4



Œ.1/

n

 C   C

48

n

5



sin nx

ˇ



0

D 

24

n

4

Œ1 C .1/

n



D

(

0 if n D 2m  1;



3

m

4

if n D 2m;

n  1I

C

f

.x/ D



4

30

 3

1

X

nD1

1

n

4

cos 2nx. From Exercise 12.2.49, u.x; t/ D



4

30

 3

1

X

nD1

1

n

4

cos 8nt cos 2nx.

12.2.58. ˇ

0

D

1



Z



0

.x

4

 2x

3

C 

2

x

2

/ dx D

1





x

5



x

4

2

C



2

x

3



ˇ



0

D



4

30

. Since g

0

.0/ D

g

0

./ D 0 and g

000

.x/ D 12.2x  /, Theorem 11.3.5(a) implies that

ˇ

n

D

24

n

3



Z



0

.2x   / sin nx dx D 

24

n

4





.2x   / cos nx

ˇ



0

 2

Z



0

cos nx dx



D 

24

n

4



Œ.1/

n

 C  C

48

n

5



sin nx

ˇ



0

D 

24

n

4

Œ1 C .1/

n



D

(

0 if n D 2m  1;



3

m

4

if n D 2m;

 1I

C

g

.x/ D



4

30

 3

1

X

nD1

1

n

4

cos 2nx. From Exercise 12.2.49, u.x; t/ D



4

t

30



3

8

1

X

nD1

1

n

5

sin 8nt cos 2nx.

12.2.60. Setting A D nx=L and B D nat=L in the iden tities cos A cos B D

1

2

Œcos.ACB/Ccos.A

B/ and cos A sin B D

1

2

Œsin.A C B/  sin.A  B/ yields

cos

nat

L

cos

nx

L

D

1

2



cos

n.x C at/

L

C cos

n.x  at/

L



.A/

and

sin

nat

L

cos

nx

L

D

1

2



sin

n.x C at/

L

 sin

n.x  at/

L



D

n

2L

Z

xCat

xat

cos

n

L

d :

.B/

Section 12.2

The Wave Equation

259

Since C

f

.x/ D ˛

0

C

1

X

nD1

˛

n

sin

nx

L

, (A) implies that

˛

0

C

1

X

nD1

˛

n

cos

nat

L

cos

nx

L

D

1

2

ŒC

f

.x C at/ C C

f

.x  at/: .C/

Since it can be shown that a Fourier sine series can be integrated term by term between any two limits,

(B) i mplies that

ˇ

0

t C

1

X

nD1

ˇ

n

L

na

sin

nat

L

cos

nx

L

D ˇ

0

t C

1

2a

1

X

nD1

ˇ

n

Z

xCat

xat

cos

n

L

d 

D

1

2a

Z

xCat

xat

ˇ

0

C

1

X

nD1

ˇ

n

cos

n

L

!

d 

D

1

2a

Z

xCat

xat

C

g

./ d :

This and (C) imply that

u.x; t/ D

1

2

ŒC

f

.x C at/ CC

f

.x  at/ C

1

2a

Z

xCat

xat

C

g

./ d :

12.2.62.(a). Since jp

n

.x/j  1 and jq

n

.t/j  1 for all t, jk

n

p

n

.x/q

n

.t/j  jk

n

j for all .x; t/, and th e

comparison test implies the conclusion.

(b) If t is ﬁxed but arbitrary, then jk

n

p

0

n

.x/q

n

.t/j  jjnjk

n

j, so Theorem 12.1.2 with ´ D x and

w

n

.x/ D k

n

p

n

.x/q

n

.t/ justiﬁes term by term differentiation with respect to x on .1; 1/. If x is ﬁxed

but arbitrary, then jk

n

p

n

.x/q

0

n

.t/j  jjnjk

n

j, so Theorem 12.1.2 with ´ D t and w

n

.t/ D k

n

p

n

.x/q

n

.t/

justiﬁes term by term differentiation with respect to t on .1; 1/.

(c) The argument is similar to argument use in (b).

(d) Apply (b) and (c) to the series

1

X

nD1

˛

n

cos

nat

L

sin

nx

L

and

1

X

nD1

ˇ

n

L

na

sin

nat

L

sin

nx

L

, recall-

ing that the individual terms in the series satisfy u

tt

D a

2

u

xx

for all .x; t/.

(d) u.x; t/ D

f .x C ct/ C f .x  ct/

2

C

1

2a

Z

xCat

xat

g.u/ du.

12.2.64.

u.x; t/ D

.x C at/ C .x  at/

2

C

1

2a

Z

xCat

xat

4au du D x C 2

Z

xCat

xat

u du D x C u

2

ˇ

xCat

xat

D x C .x C at/

2

 .x  at/

2

D x.1 C 4at/:

12.2.66.

u.x; t/ D

sin.x C at/ C sin.x  at/

2

C

1

2a

Z

xCat

xat

a cos u du

D

sin.x C at/ C sin.x  at/

2

C

sin.x C at/  sin.x  at/

2

D sin.x C at/:

260 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

12.2.68.

u.x; t/ D

.x Cat/ sin.x C at/ C .x  at/ sin .x  at/

2

C

1

2a

Z

xCat

xat

sin u du

D

xŒsin.x C at/ C sin.x  at/

2

C

atŒsin.x C at/  sin.x  at/

2

C

cos.x  at/ cos.x C at/

2a

D x sin x cos at C at cos x sin at C

sin x sin at

a

:

12.3 LAPLACE’S EQUATION IN RECTANGULAR COORDINATES

12.3.2. Since f .0/ D f .1/ D 0 and f

00

.x/ D 2 6x, Theorem 11.3.5(b) implies that

˛

n

D 

4

n

2



2

Z

1

0

.4  6x/ sin

nx

2

dx D

8

n

3



3

"

.4  6x/ cos

nx

2

ˇ

2

0

C6

Z

2

0

cos

nx

2

dx

#

D 

32

n

3



3

.1 C .1/

n

2/ C

96

n

4



4

sin

nx

2

ˇ

2

0

D 

32

n

3



3

Œ1 C .1/

n

2 I

S.x/ D 

32



3

1

X

nD1

Œ1 C .1/

n

2

n

3

sin

nx

2

. From Example 12.3.1,

u.x; y/ D 

32



3

1

X

nD1

Œ1 C .1/

n

2 si nh n.3  y/=2

n

3

sinh 3n=2

sin

nx

2

:

12.3.4.

˛

1

D

2



Z



0

x sin

2

x dx D

1



Z



0

x.1  cos 2x/ dx D

x

2

2

ˇ



0



1



Z



0

x cos 2x dx

D



2



1

2



x sin 2x

ˇ



0



Z



0

cos 2x dx



D



2

C

sin 2x

4

ˇ



0

D



2

I

if n  2, then

˛

n

D

2



Z



0

x sin x sin nx dx D

1



Z



0

xŒcos.n  1/x  cos.n C 1/x dx

D

1





x



sin.n  1/x

n  1



sin.n C 1/x

n C 1



ˇ



0



Z



0



sin.n  1/x

n  1



sin.n C 1/x

n C 1



dx



D

1





cos.n  1/x

.n  1/

2



cos.n C 1/x

.n C 1/

2



ˇ



0

D

1





1

.n  1/

2



1

.n C 1/

2





.1/

nC1

 1



D

4n

.n

2

 1/

2





.1/

nC1

 1



D

8

<

:

0 i f n D 2m  1;



16m

.4m

2

 1/

if n D 2mI

S.x/ D



2

sin x 

16



1

X

nD1

n

.4n

2

 1/

2

sin 2nx. From Example 12.3.1,

u.x; y/ D



2

sinh.1  y/

sinh 1

sin x 

16



1

X

nD1

n sinh 2n.1  y/

.4n

2

 1/

2

sinh 2n

sin 2nx:

Section 12.3

Laplace’s Equation in Rectangular Coordinates

261

12.3.6. ˛

0

D

Z

1

0

.1  x/ dx D 

.1  x/

2

ˇ

1

0

D

1

2

; if n  1,

˛

n

D 2

Z

1

0

.1  x/ cos n x dx D

2

n

"

.1  x/ sin n x

ˇ

1

0

C

Z

1

0

sin nx dx

#

D 

2

n

2



2

cos n x

ˇ

1

0

D

2

n

2



2

Œ1  .1/

n

 D

8

<

:

4

.2m 1/

2



2

if n D 2m  1;

0 if n D 2mI

C.x/ D

1

2

C

4



2

1

X

nD1

1

.2n  1/

2

cos.2n  1/x. From Example 12.3.3,

u.x; y/ D

y

2

C

4



3

1

X

nD1

sinh.2n  1/y

.2n  1/

3

cosh 2.2n  1/

cos.2n  1/x:

12.3.8. ˛

0

D

Z

1

0

.x  1/

2

dx D

.x  1/

3

ˇ

1

0

D

1

3

; if n  1, then

˛

n

D 2

Z

1

0

.x  1/

2

cos nx dx D

2

n

"

.x  1/

2

sin nx

ˇ

1

0

 2

Z

1

0

.x  1/ sin nx dx

#

D

4

n

2



2

"

.x  1/ cos nx

ˇ

1

0



Z

1

0

cos nx dx

#

D

4

n

2



2



4

n

3



3

sin n x

ˇ

1

0

D

4

n

2



2

I

C.x/ D

1

3

C

4



2

1

X

nD1

1

n

2

cos n x. From Example 12.3.3, u.x; y/ D

y

3

C

4



3

1

X

nD1

sinh ny

n

3

cosh n

cos n x.

12.3.10. Since g.0/ D g

0

.1/ D 0, and g

00

.y/ D 6.1  2y/, Theorem 11.3.5(d) implies that

˛

n

D 

48

.2n  1/

2



2

Z

1

0

.1  2y/ sin

.2n  1/y

2

dy

D

96

.2n  1/

3



3

"

.1  2y/ cos

.2n 1/y

2

ˇ

1

0

C 2

Z

1

0

cos

.2n 1/y

2

dy

#

D

96

.2n  1/

3



3

"

1 C

4

.2n  1/

sin

.2n  1/y

2

ˇ

1

0

#

D 

96

.2n  1/

3



3



1 C .1/

n

4

.2n  1/



I

S

M

.y/ D 

96



3

1

X

nD1

1

.2n 1/

3



1 C .1/

n

4

.2n  1/



sin

.2n  1/y

2

. From Example 12.3.5,

u.x; y/ D 

96



3

1

X

nD1



1 C .1/

n

4

.2n 1/



cosh.2n 1/.x  2/=2

.2n  1/

3

cosh 2.2n  1/=2

sin

.2n  1/y

2

:

262 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

12.3.12. From Example 11.3.8.3,

S

M

.y/ D

96



3

1

X

nD1

1

.2n  1/

3



3 C .1/

n

4

.2n  1/



sin

.2n  1/y

2

:

From Example 12.3.5,

u.x; y/ D

96



3

1

X

nD1



3 C .1/

n

4

.2n  1/



cosh.2n 1/.x  3/=2

.2n 1/

3

cosh 3.2n  1/=2

sin

.2n  1/y

2

:

12.3.14.

c

n

D

2

3

Z

3

0

.3y  y

2

/ cos

.2n  1/y

6

dy

D

4

.2n  1/

"

.3y  y

2

/ sin

.2n  1/y

6

ˇ

3

0



Z

3

0

.3  2y/ sin

.2n  1/y

6

dy

#

D

24

.2n  1/

2



2

"

.3  2y/ cos

.2n  1/y

6

ˇ

3

0

C 2

Z

3

0

cos

.2n 1/y

6

dy

#

D 

72

.2n  1/

2



2

C

288

.2n 1/

3



3

sin

.2n  1/y

6

ˇ

3

0

D

288

.2n 1/

3



3

sin

.2n  1/y

2

D 

72

.2n  1/

2



2

C .1/

n1

288

.2n  1/

3



3

I

C

M

.y/ D 

72



2

1

X

nD1

1

.2n  1/

2



1 C

4.1/

n

.2n 1/



cos

.2n  1/y

6

. From Example 12.3.7,

u.x; y/ D 

432



3

1

X

nD1



1 C

4.1/

n

.2n  1/



cosh.2n  1/x=6

.2n 1/

3

sinh.2n  1/=3

cos

.2n 1/y

6

:

12.3.16. Since g

0

.0/ D g.1/ D 0 and g

00

.y/ D 6y, Theorem 11.3.5(c) implies that

˛

n

D

48

.2n 1/

2



2

Z

1

0

y cos

.2n 1/y

2

dy

D

96

.2n 1/

3



3

"

y sin

.2n 1/y

2

ˇ

1

0



Z

1

0

sin

.2n  1/y

2

dy

#

D

96

.2n 1/

3



3

"

.1/

nC1

C

2

.2n  1/

cos

.2n 1/y

2

ˇ

1

0

#

D 

96

.2n 1/

3



3



.1/

n

C

2

.2n  1/



dyI

C

M

.y/ D 

96



3

1

X

nD1

1

.2n  1/

3



.1/

n

C

2

.2n  1/



cos

.2n  1/y

2

. From Example 12.3.7,

u.x; y/ D 

192



4

1

X

nD1

cosh.2n 1/x=2

.2n  1/

4

sinh.2n  1/=2



.1/

n

C

2

.2n  1/



cos

.2n 1/y

2

:

Section 12.3

Laplace’s Equation in Rectangular Coordinates

263

12.3.18. The boundary conditions require products v.x; y/ D X.x/Y.y/ such that (A) X

00

C X D 0,

X

0

.0/ D 0, X

0

.a/ D 0, and ( B) Y

00

Y D 0, Y.0/ D 1, Y.b/ D 0. From Theorem 11.1.3, the eigenval-

ues of (A) are  D 0, with associated eigenfu nction X

0

D 1, and 

n

D

n

2



2

a

2

, with associated eigenfunc-

tions Y

n

D cos

nx

a

, n D 1, 2, 3,. . . . Substituting  D 0 into (B) yields Y

00

0

D 0, Y

0

.0/ D 1, Y

0

.b/ D 0,

so Y

0

.y/ D 1 

y

b

. Substi tuting  D

n

2



2

a

2

into (B) yields Y

00

n

.n

2



2

=a

2

/Y

n

D 0, Y

n

.0/ D 1, Y

n

.b/ D

0, so Y

n

D

sinh n.b  y/=a

sinh nb=a

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D

sinh n.b  y/=a

sinh n b=a

cos

nx

a

, so

v

n

.x; 0/ D cos

nx

a

. Therefore,v

n

is solution of the given problem with f .x/ D cos

nx

a

. More gener-

ally, if ˛

0

; : : : ; ˛

m

are arbitrary constants, then u

m

.x; y/ D ˛

0



1 

y

b



C

m

X

nD1

˛

n

sinh n.b  y/=a

sinh nb=a

cos

nx

a

is a solution of the given problem with f .x/ D ˛

0

C

m

X

nD1

˛

n

cos

nx

a

. Therefore, if f is an arbi-

trary piecewise smooth function on Œ0; a we d eﬁne the formal solution of the given problem to b e

u.x; y/ D ˛

0



1 

y

b



C

1

X

nD1

˛

n

sinh n.b  y/=a

sinh n b=a

cos

nx

a

, where C.x/ D ˛

0

C

1

X

nD1

˛

n

cos

nx

a

is

the Fourier cosi ne series of f on Œ0; a; t hat is, ˛

0

D

1

a

Z

a

0

f .x/ dx and ˛

n

D

2

a

Z

a

0

f .x/ cos

nx

a

dx,

n  1.

Now consider the special case. ˛

0

D

1

2

Z

2

0

.x

4

 4x

3

C 4x

2

/ dx D

1

2



x

5

 x

4

C

4x

3



ˇ

2

0

D

6

5

.

Since f

0

.0/ D f

0

.2/ D 0 and f

000

.x/ D 12.2x  2/, Theorem 11 .3.5(a) implies that

˛

n

D

96

n

3



3

Z

2

0

.2x  2/ sin

nx

2

dx D 

192

n

4



4

"

.2x  2/ cos

nx

2

ˇ

2

0

 2

Z

2

0

cos

nx

2

dx

#

D 

192

n

4



4

Œ.1/

n

2 C 2 C

768

n

5



5

sin

nx

2

ˇ

2

0

D 

384

n

4



4

Œ1 C .1/

n



D

(

0 if n D 2m  1;



48

m

4



4

if n D 2m;

n  1:

C.x/ D

8

15



48



4

1

X

nD1

1

n

4

cos n x; u.x; y/ D

8.1  y/

15



48



4

1

X

nD1

1

n

4

sinh n.1 y/

sinh n

cos n x.

12.3.20. The boundary conditions require products v.x; y/ D X.x/Y.y/ such that (A) X

00

C X D 0,

X.0/ D 0, X

0

.a/ D 0, and (B) Y

00

 Y D 0, Y .0/ D 1, Y .b/ D 0. From Theorem 11.1.4, the

eigenvalues of (A) are 

n

D

.2n 1/

2



2

4a

2

, with associated eigenfun ctions Y

n

D sin

.2n  1/ x

2a

,

n D 1, 2, 3,. . . . Substituting  D

.2n  1/

2



2

4a

2

into (B) yields Y

00

n

 ..2n  1/

2



2

=4a

2

/Y

n

D 0,

Y

n

.0/ D 1, Y

n

.b/ D 0, so Y

n

D

sinh.2n  1/.b  y/=2a

sinh.2n  1/b=2a

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D

sinh.2n  1/.b  y/=2a

sinh.2n  1/b=2a

sin

.2n 1/x

2a

, so v

n

.x; 0/ D sin

.2n  1/ x

2a

. Therefore,v

n

is solution of

264 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

the given problem with f .x/ D sin

.2n  1/ x

2a

. More generally, if ˛

1

; : : : ; ˛

m

are arbitrary constants,

then u

m

.x; y/ D

m

X

nD1

˛

n

sinh.2n  1/.b  y/=2a

sinh.2n  1/b=2a

cos

.2n  1/ x

2a

is a solution o f the given problem

with f .x/ D

m

X

nD1

˛

n

sin

.2n  1/ x

2a

. Therefore, if f is an arbitrary piecewise smooth function on Œ0; a

we deﬁne the formal solution of the given problem to be u.x; y/ D

1

X

nD1

˛

n

sinh.2n  1/.b  y/=2a

sinh.2n  1/b=2a

sin

.2n  1/ x

2a

,

where S

m

.x/ D

1

X

nD1

˛

n

sin

.2n  1/ x

2a

is the mixed Fourier sine series of f on Œ0; a; that is, ˛

n

D

2

a

Z

a

0

f .x/ sin

.2n  1/ x

2a

.

Now consider the special case. Since f .0/ D f

0

.L/ D 0 and f

00

.x/ D 2, Theorem 11.3.5(d) implies

that

˛

n

D

48

.2n 1/

2



2

Z

3

0

sin

.2n  1/ x

6

dx D 

288

.2n 1/

3



3

cos

.2n  1/ x

6

ˇ

3

0

D

288

.2n  1/

3



3

I

S

M

.x/ D

288



3

1

X

nD1

1

.2n 1/

3

sin

.2n  1/ x

6

I

u.x; y/ D

288



3

1

X

nD1

sinh.2n  1/.2  y/=6

.2n 1/

3

sinh.2n  1/=3

sin

.2n 1/x

6

:

12.3.22. The boundary conditions require products v.x; y/ D X.x/Y.y/ such that (A) X

00

C X D 0,

X

0

.0/ D 0, X

0

.a/ D 0, and (B) Y

00

 Y D 0, Y

0

.0/ D 0, Y.b/ D 1. From Theorem 1 1.1.3, the

eigenvalues of (A) are  D 0, with associated eigenfunction X

0

D 1, and 

n

D

n

2



2

a

2

, wit h associated

eigenfunctions Y

n

D cos

nx

a

, n D 1, 2, 3,. . . . Substituting  D 0 into (B) yields Y

00

0

D 0, Y

0

.0/ D 0,

Y

0

.b/ D 1, so Y

0

D 1. Substituti ng  D

n

2



2

a

2

into (B) y ields Y

00

n

 .n

2



2

=a

2

/Y

n

D 0, Y

0

n

.0/ D

0, Y

n

.b/ D 1, so Y

n

D

cosh ny=a

cosh nb=a

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D

sinh ny=a

cosh nb=a

cos

nx

a

, so

v

n

.x; b/ D cos

nx

a

. Therefore,v

n

is solu tion of the given problem with f .x/ D cos

nx

a

. More

generally, i f ˛

0

; : : : ; ˛

m

are arbitrary constants, then u

m

.x; y/ D ˛

0

C

m

X

nD1

˛

n

cosh ny=a

cosh nb=a

cos

nx

a

is

a sol ution of the given problem with f .x/ D ˛

0

C

m

X

nD1

˛

n

cos

nx

a

. Therefore, if f is an arbitrary

piecewise smooth funct ion on Œ0; a we deﬁne the formal solution of the given prob lem to be u.x; y/ D

˛

0

C

1

X

nD1

˛

n

cosh ny=a

cosh nb=a

cos

nx

a

, where C.x/ D ˛

0

C

1

X

nD1

˛

n

cos

nx

a

is the Fourier cosine series of

f on Œ0; a; that is, ˛

0

D

1

a

Z

a

0

f .x/ dx and ˛

n

D

2

a

Z

a

0

f .x/ cos

nx

a

dx, n  1.

Section 12.3

Laplace’s Equation in Rectangular Coordinates

265

Now consider the special case.

˛

0

D

1



Z



0

.x

4

 2x

3

C 

2

x

2

/ dx D

1





x

5



x

4

2

C



2

x

3



ˇ



0

D



4

30

:

Since f

0

.0/ D f

0

./ D 0 and f

000

.x/ D 12.2x  /, Theorem 11.3.5(a) implies that

˛

n

D

24

n

3



Z



0

.2x  / sin nx dx D 

24

n

4





.2x  / cos nx

ˇ



0

 2

Z



0

cos nx dx



D 

24

n

4



Œ.1/

n

 C   C

48

n

5



sin nx

ˇ



0

D 

24

n

4

Œ1 C .1/

n



D

(

0 if n D 2m  1;



3

m

4

if n D 2m;

n  1I

C.x/ D



4

30

 3

1

X

nD1

1

n

4

cos 2nx; u.x; y/ D



4

30

 3

1

X

nD1

1

n

4

cosh 2ny

cos 2n

cos 2nx

12.3.24. The boundary conditions require products v.x; y/ D X.x/Y .y/ such that (A) X

00

 X D

0, X

0

.0/ D 0, X.a/ D 1, and (B) Y

00

C Y D 0, Y.0/ D 0, Y .b/ D 0. From Theorem 11.1.2,

the eigenvalues of (B ) are 

n

D

n

2



2

b

2

, with associated eigenfunctions Y

n

D sin

ny

b

, n D 1, 2,

3,. . . . Substituting  D

n

2



2

b

2

into ( A ) yields X

00

n

 .n

2



2

=b

2

/X

n

D 0, X

0

n

.0/ D 0, X

n

.a/ D 1, so

X

n

D

cosh nx=b

cosh na=b

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D

cosh nx=b

cosh na=b

sin

ny

b

, so v

n

.a; y/ D sin

ny

b

.

Therefore,v

n

is solu tion of the given problem with g.y/ D sin

ny

b

. More generally, if ˛

1

; : : : ; ˛

m

are arbitrary constants, then u

m

.x; y/ D

m

X

nD1

˛

n

cosh nx=b

cosh na=b

sin

ny

b

is a solution of the given problem

with g.y/ D

m

X

nD1

˛

n

sin

ny

b

. Therefore, if g is an arbitrary piecewise smooth function on Œ0; b we

deﬁne the formal solution of the given problem to be u.x; y/ D

1

X

nD1

˛

n

cosh nx=b

cosh na=b

sin

ny

b

, where

S.y/ D

1

X

nD1

˛

n

sin

ny

b

is the Fourier sine series of g on Œ0; b; that is, ˛

n

D

2

b

Z

b

0

g.y/ sin

ny

b

dy.

Now consider t he special case. Since g.0/ D g.1/ D g

00

.0/ D g

00

.L/ D 0 and f

.4/

.y/ D 24,

Theorem 11.3.5(b) and Exercise 35(b) of Section 11.3 imply that

˛

n

D

48

n

4



4

Z

1

0

sin ny dy D 

48

n

5



5

cos ny

ˇ

1

0

D 

48

n

5



5

Œ.1/

n

 1 D

8

<

:

96

.2m  1/

5



5

if n D 2m  1

0 if n D 2mI

S.y/ D

96



5

1

X

nD1

1

.2n  1/

5

sin.2n 1/y; u.x; y/ D

96



5

1

X

nD1

cosh.2n  1/x

.2n 1/

5

cosh.2n 1/

sin.2n 1/y.

266 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

12.3.26. The boundary conditions require p roducts v.x; y/ D X.x/Y.y/ such th at (A) X

00

 X D 0,

X

0

.0/ D 0, X

0

.a/ D 1, and (B) Y

00

C Y D 0, Y .0/ D 0, Y.b/ D 0. From Theorem 11.1.2, the

eigenvalues of (B) are 

n

D

n

2



2

b

2

, wi th associated eigenfunctions Y

n

D sin

ny

b

, n D 1, 2, 3,. . . .

Substituting  D

n

2



2

b

2

into (A) yields X

00

n

 .n

2



2

=b

2

/X

n

D 0, X

0

n

.0/ D 0, X

0

n

.a/ D 1, so X

n

D

b

n

cosh nx=b

sinh na=b

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D

b

n

cosh nx=b

sinh na=b

sin

ny

b

, so

@v

n

@x

.a; y/ D sin

ny

b

.

Therefore,v

n

is solut ion of the given problem with g.y/ D sin

ny

b

. More generally, if ˛

1

; : : : ; ˛

m

are

arbitrary constants, then u

m

.x; y/ D

b



m

X

nD1

˛

n

cosh nx=b

n sinh n a=b

sin

ny

b

is a solution of the given problem

with g.y/ D

m

X

nD1

˛

n

sin

ny

b

. Therefore, if g is an arbitrary piecewise smooth function on Œ0; b we

deﬁne the formal solution of the given problem to be u.x; y/ D

b



1

X

nD1

˛

n

cosh nx=b

n sinh na=b

sin

ny

b

, where

S.y/ D

1

X

nD1

˛

n

sin

ny

b

is the Fourier sine series of g on Œ0; b; that is, ˛

n

D

2

b

Z

b

0

g.y/ sin

ny

b

dy.

Now consider the special case. ˛

n

D

1

2



Z

2

0

y sin

ny

4

C

Z

4

2

.4  y/ sin

ny

4

dy



;

Z

2

0

y sin

ny

4

dy D 

4

n

"

y cos

ny

4

ˇ

2

0



Z

2

0

cos

ny

4

dy

#

D 

2

n

cos

n

2

C

4

n

2



2

sin

ny

4

ˇ

2

0

D 

2

n

cos

n

2

C

4

n

2



2

sin

n

2

I

Z

2

0

.4  y/ sin

ny

4

dy D 

2

n

"

.4  y/ cos

ny

4

ˇ

4

2

C

Z

2

0

cos

ny

4

dy

#

D

2

n

cos

n

2



4

n

2



2

sin

ny

4

ˇ

4

2

D

2

n

cos

n

2

C

4

n

2



2

sin

n

2

I

˛

n

D

16

n

2



2

sin

n

2

D

8

<

:

.1/

mC1

16

.2m  1/

2



2

if n D 2m  1

0 if n D 2mI

S.y/ D

16



2

1

X

nD1

.1/

nC1

.2n 1/

2

sin

.2n  1/y

4

I

u.x; y/ D

64



3

1

X

nD1

.1/

nC1

cosh.2n  1/x=4

.2n  1/

3

sinh.2n  1/=4

sin

.2n  1/y

4

:

12.3.28. The boundary conditions require p roducts v.x; y/ D X.x/Y.y/ such th at (A) X

00

 X D 0,

X

0

.0/ D 1, X.a/ D 0, and (B) Y

00

C Y D 0, Y

0

.0/ D 0, Y

0

.b/ D 0. From Theorem 11.1.3, the

Section 12.3

Laplace’s Equation in Rectangular Coordinates

267

eigenvalues of (B) are 

0

D 0, with associated ei genfunction Y

0

D 1, and 

n

D

n

2



2

b

2

, with associ-

ated eigenfunctions Y

n

D cos

ny

b

, n D 1, 2, 3,. . . . Substituting 

0

D 0 into (A) yield s X

00

0

D 0,

X

0

.0/ D 1 X.a/ D 0, so X

0

D x  a. Substituting  D

n

2



2

b

2

into (A) yields X

00

n

 .n

2



2

=b

2

/X

n

D

0, X

0

n

.0/ D 1, X

n

.a/ D 0, so X

n

D

b

n

sinh n.x  a/=b

cosh na=b

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D

b

n

sinh n.x  a/=b

cosh na=b

cos

ny

b

, so

@v

n

@x

.0; y/ D cos

ny

b

. Therefore,v

n

is solution of the given prob-

lem with g.y/ D cos

ny

b

. More generally, if ˛

0

; : : : ; ˛

m

are arbitrary constants, th en u

m

.x; y/ D

˛

0

.x  a/ C

b



m

X

nD1

˛

n

sinh n.x  a/=b

n cosh na=b

cos

ny

b

is a solution of t he given problem with g.y/ D

m

X

nD1

˛

n

cos

ny

b

. Therefore, if g is an arbitrary piecewise smooth function on Œ0; b we deﬁne the formal

solution of the given problem to be u.x; y/ D ˛

0

.x  a/ C

b



1

X

nD1

˛

n

sinh n.x  a/=b

n cosh na=b

cos

ny

b

where

C.y/ D ˛

0

C

1

X

nD1

˛

n

cos

ny

b

is the Fourier co sine series of g on Œ0; b; that is, ˛

0

D

1

b

Z

b

0

g.y/ cos

ny

b

dy,

˛

n

D

2

b

Z

b

0

g.y/ cos

ny

b

dy, n  1.

Now consider the special case. From Example 11.3.1,

C.y/ D



2



4



1

X

nD1

1

.2n  1/

2

cos.2n  1/yI

u.x; y/ D

.x  2/

2



4



1

X

nD1

sinh.2n 1/.x  2/

.2n  1/

3

cosh 2.2n  1/

cos.2n  1/y:

12.3.30. The boundary conditions require products v.x; y/ D X.x/Y.y/ such that (A) X

00

C X D 0,

X

0

.0/ D 0, X.a/ D 0, and (B) Y

00

 Y D 0, Y.0/ D 1, and Y is bounded. From Theorem 1 1.1.5, the

eigenvalues of (A) are 

n

D

.2n 1/

2



2

4a

2

, with associated eigenfuncti ons Y

n

D cos

.2n  1/ x

2a

, n D 1,

2, 3,. . . . Substitut ing  D

.2n  1/

2



2

4a

2

into (B) yields Y

00

n

 ..2n  1/

2



2

=4a

2

/Y

n

D 0, Y

n

.0/ D 1, so

Y

n

D e

.2n1/y=2a

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D e

.2n1/y=2a

cos

.2n 1/x

2a

, so v

n

.x; 0/ D

cos

.2n 1/x

2a

. Therefore,v

n

is solution of the given problem with f .x/ D cos

.2n 1/x

2a

. More

generally, if ˛

1

; : : : ; ˛

m

are arbitrary constants, then u

m

.x; y/ D

m

X

nD1

˛

n

e

.2n1/y=2a

cos

.2n 1/x

2a

is a solution of the given problem with f .x/ D

m

X

nD1

˛

n

cos

.2n  1/ x

2a

. Therefore, i f f is an ar-

bitrary piecewise smooth fu nction on Œ0; a we deﬁne the formal solution o f the given prob lem to be

268 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

u.x; y/ D

1

X

nD1

˛

n

e

.2n1/y=2a

cos

.2n  1/ x

2a

, where C

m

.x/ D

1

X

nD1

˛

n

cos

.2n  1/ x

2a

is the mixed

Fourier cosine series of f on Œ0; a; that is, ˛

n

D

2

a

Z

a

0

f .x/ cos

.2n  1/ x

2a

.

Now consider the special case. Since f

0

.0/ D f .L/ D 0 and f

00

.x/ D 2, Theorem 11.3.5(d) implies

that

˛

n

D

16L

.2n 1/

2



2

Z

3

0

cos

.2n  1/ x

6

dx

D

288

.2n 1/

3



3

sin

.2n  1/ x

6

ˇ

3

0

D .1/

nC1

288

.2n  1/

3



3

I

C

M

.x/ D 

288



3

1

X

nD1

.1/

n

.2n  1/

3

cos

.2n  1/ x

6

I

u.x; y/ D 

288



3

1

X

nD1

.1/

n

.2n  1/

3

e

.2n1/y=6

cos

.2n  1/ x

6

:

12.3.32. The boundary conditions require pro ducts v.x; y/ D X.x/Y.y/ such th at (A) X

00

C X D

0, X.0/ D 0, X.a/ D 0, and (B) Y

00

 Y D 0, Y

0

.0/ D 1, and Y is boun ded. From Theo-

rem 11.1.2, the eigenvalues of (A) are 

n

D

n

2



2

a

2

, with associated eigenfunctions Y

n

D sin

nx

a

,

n D 1, 2, 3,. . . . Substituting  D

n

2



2

a

2

into (B) yields Y

00

n

 .n

2



2

=a

2

/Y

n

D 0, Y

0

n

.0/ D 1, so

Y

n

D 

a

n

e

ny=a

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D 

a

n

e

ny=a

sin

nx

a

, so

@v

n

@y

.x; 0/ D sin

nx

a

.

Therefore,v

n

is solution of the given problem with f .x/ D sin

nx

a

. Mor e generally, if ˛

1

; : : : ; ˛

m

are

arbitrary constants, then u

m

.x; y/ D 

a



m

X

nD1

˛

n

e

ny=a

sin

nx

a

is a solution of the given problem

with f .x/ D

m

X

nD1

˛

n

sin

nx

a

. Therefore, if f is an arbitrary piecewise smooth function on Œ0; a we

deﬁne the formal solution of the given problem to be u.x; y/ D 

a



1

X

nD1

˛

n

e

ny=a

sin

nx

a

, where

C.x/ D

1

X

nD1

˛

n

sin

nx

a

is the Fourier sine series of f on Œ0; a; that is, ˛

n

D

2

a

Z

a

0

f .x/ sin

nx

a

dx.

Now consider the special case. Since f .0/ D f ./ D 0 and f

00

.x/ D 2  6x, Theorem 11.3.5(b)

implies that

˛

n

D 

2

n

2



Z



0

.2  6x/ sin nx dx D

2

n

3





.2  6x/ cos nx

ˇ



0

C 6

Z



0

cos nx dx



D 

4

n

3

Œ1 C .1/

n

2 C

12

n

4



sin nx

ˇ



0

D 

4

n

3

Œ1 C .1/

n

2 I

S.x/ D 4

1

X

nD1

Œ1 C .1/

n

2

n

3

sin nx; u.x/ D 4

1

X

nD1

Œ1 C .1/

n

2

n

4

e

ny

sin nx;

Section 12.3

Laplace’s Equation in Rectangular Coordinates

269

12.3.34. The boundary conditions require products v.x; y/ D X.x/Y.y/ such that (A) X

00

C X D 0,

X.0/ D 0, X

0

.a/ D 0, and (B) Y

00

 Y D 0, Y

0

.0/ D 1, and Y is bounded. From Theorem 11.1.4, the

eigenvalues of (A) are 

n

D

.2n 1/

2



2

4a

2

, with associated eigenfunctions Y

n

D sin

.2n 1/x

2a

, n D 1,

2, 3,. . . . Substitut ing  D

.2n  1/

2



2

4a

2

into (B) yields Y

00

n

 ..2n  1/

2



2

=4a

2

/Y

n

D 0, Y

0

n

.0/ D 1, so

Y

n

D 

2a

.2n  1/

e

.2n1/y=2a

. Then v

n

.x; y/ D X

n

.x/Y

n

.y/ D 

2a

.2n 1/

e

.2n1/y=2a

sin

.2n  1/ x

2a

,

so

@v

n

@y

.x; 0/ D sin

.2n  1/ x

2a

. Therefore,v

n

is solution of the given problem with f .x/ D sin

.2n 1/x

2a

.

More generally, if ˛

1

; : : : ; ˛

m

are arbitrary constants, then u

m

.x; y/ D 

2a



m

X

nD1

˛

n

2n  1

e

.2n1/y=2a

sin

.2n  1/ x

2a

is a sol ution of the given p roblem with f .x/ D

m

X

nD1

˛

n

sin

.2n  1/ x

2a

. Therefore, if f is an ar-

bitrary piecewise smooth fu nction on Œ0; a we deﬁne the formal solution o f the given prob lem to be

u.x; y/ D 

2a



1

X

nD1

˛

n

2n  1

e

.2n1/y=2a

sin

.2n  1/ x

2a

,where S

m

.x/ D

1

X

nD1

˛

n

sin

.2n 1/x

2a

is

the mixed Fourier sine series of f on Œ0; a; that is, ˛

n

D

2

a

Z

a

0

f .x/ sin

.2n  1/ x

2a

.

Now consider the special case.

˛

n

D

2

5

Z

5

0

.5x  x

2

/ sin

.2n  1/ x

10

dx

D 

4

.2n  1/

"

.5x  x

2

/ cos

.2n  1/ x

10

ˇ

5

0



Z

5

0

.5  2x/ cos

.2n  1/ x

10

dx

#

D

40

.2n  1/

2



2

"

.5  2x/ sin

.2n  1/ x

10

ˇ

5

0

C 2

Z

5

0

sin

.2n  1/ x

10

dx

#

D .1/

n

200

.2n 1/

2



2



800

.2n  1/

3



3

cos

.2n  1/ x

10

ˇ

5

0

D .1/

n

200

.2n 1/

2



2

C

800

.2n  1/

3



3

I

S

M

.x/ D

200



2

1

X

nD1

1

.2n  1/

2



.1/

n

C

4

.2n  1/



sin

.2n  1/ x

10

I

u.x; y/ D 

2000



3

1

X

nD1

1

.2n 1/

3



.1/

n

C

4

.2n 1/



e

.2n1/y=10

sin

.2n 1/x

10

:

12.3.36. Solving BVP.1; 1; 1; 1/.f

0

; 0; 0; 0/ requires products X.x/Y.y/ such that

X

00

C X D 0; X

0

.0/ D 0; X

0

.a/ D 0I Y

00

 Y D 0; Y

0

.b/ D 0; Y

0

.0/ D 1:

Hence, X

n

D cos

nx

a

, Y

n

D 

a cosh n.y  b/=a

n sinh nb=a

, and c

1



a



1

X

nD1

A

n

cosh n.y  b/=a

n sinh nb=a

cos

nx

a

is

270 Chapter 12

Fourier Solut ions of Partial Di fferential Equation s

a formal solution of BVP.1; 1; 1; 1/.f

0

; 0; 0; 0/ if c

1

is any constant and

1

X

nD1

A

n

cos

nx

a

is the Fourier

cosine expansion of f

0

on Œ0; a, which is possible if and o nly if

Z

a

0

f

0

.x/ dx D 0.

Similarly, c

2

C

a



1

X

nD1

B

n

cosh ny=a

n sinh nb=a

cos

nx

a

is a formal solution of BVP.1; 1; 1; 1/.0; f

1

; 0; 0/ if

c

2

is any constant and

1

X

nD1

B

n

cos

nx

a

is the Fourier cosine exp ansion of f

1

on Œ0; a, w hich is possible

if and only if

Z

a

0

f

1

.x/ dx D 0.

Interchanging x and y and a and b shows that c

3



b



1

X

nD1

C

n

cosh n.x  a/=b

n sinh na=b

cos

ny

b

is a formal so-

lution of BVP.1; 1; 1; 1/.0; 0; g

0

; 0/ i f c

3

is any constant and

1

X

nD1

C

n

cos

ny

b

is the Fourier cosine expan-

sion of g

0

on Œ0; b, which is possible if an d only if

Z

b

0

g

0

.x/ dx D 0, and c

4

C

b



1

X

nD1

D

n

cosh nx=b

n sinh na=b

cos

ny

b

is a formal solu tion of BVP.1; 1; 1; 1/.0; 0; 0; g

1

/ if c

4

is any constant and

1

X

nD1

D

n

cos

ny

b

is the Fourier

cosine expansion of g

1

on Œ0; b, w hich is possible if and only if

Z

b

0

g

1

.x/ dx D 0.

Adding the four solutions yields

u.x; y/ D C C

a



1

X

nD1

B

n

cosh ny=a A

n

cosh n.y  b/=a

n sinh nb=a

cos

nx

a

C

b



1

X

nD1

D

n

cosh nx=b  C

n

cosh n.x  a/=b

n sinh n a=b

cos

ny

b

;

where C is an arbitr ary constant.

12.4 LAPLACE’S EQUATION IN POLAR COORDINATES

12.4.2. v.r; / D R.r/‚. / where (A) r

2

R

00

C rR

0

 R D 0 and ‚

00

C ‚ D 0, ‚.0/ D 0,

‚./ D 0. From Theorem 11.1.2, 

n

D

n

2



2



2

, ‚

n

D sin

n



, n D 1, 2, 3,. . . . Substituting  D

n

2



2



2

into (A) yields the Euler equation r

2

R

00

n

C rR

0

n



n

2



2



2

R

n

D 0 for R

n

. The indicial polynomial is



s 

n





s C

n





, so R

n

D c

1

r

n=

C c

2

r

n=

, by Theorem 7.4.3. We want R

n

./ D 1 and

R

n

.

0

/ D 0, so R

n

.r/ D



n=

0

r

n=

 

n=

0

r

n=



n=

0



n=

 

n=

0



n=

;

v

n

.r; / D



n=

0

r

n=

 

n=

0

r

n=



n=

0



n=

 

n=

0



n=

sin

n



I

Section 12.4

Laplace’s Equation in Polar Co ordinates

271

u.r; / D

1

X

nD1

˛

n



n=

0

r

n=

 

n=

0

r

n=



n=

0



n=

 

n=

0



n=

sin

n



, where S./ D

1

X

nD1



n

sin

n



is the Fourier

sine series if f on Œ0;  ; that is, ˛

n

D

1



Z



0

f ./ sin

n



d, n D 1, 2, 3,. . . .

12.4.4. v.r; / D R.r/‚./ where (A) r

2

R

00

CrR

0

R D 0 and ‚

00

C‚ D 0, ‚

0

.0/ D 0, ‚./ D 0.

From Theorem 11.1.5, 

n

D

.2n  1/

2



2

4

2

, ‚

n

D cos

.2n  1/ 

2

, n D 1, 2, 3,. . . . Substitut ing

 D

.2n  1/

2



2

4

2

into (A) yields the Euler equation r

2

R

00

n

C rR

0

n



.2n  1/

2



2

4

2

R

n

D 0 for R

n

. The

indicial polynomial is



s 

.2n  1/

2



s C

.2n 1/

2



, so R

n

D c

1

r

.2n1/=2

C c

2

r

.2n1/=2

,

by Theorem 7.4.3. We want R

n

to be bou nded as r ! 0C and R

n

./ D 1, so we take R

n

.r/ D

r

.2n1/=2



.2n1/=2

; v

n

.r; / D

r

.2n1/=2



.2n1/=2

cos

.2n  1/ 

2

; u.r; / D

1

X

nD1

˛

n

r

.2n1/=2



.2n1/=2

cos

.2n  1/ 

2

,

where C

M

./ D

1

X

nD1

˛

n

cos

.2n  1/ 

2

is the mixed Fourier cosine series of f on Œ0; ; that is, ˛

n

D

2



Z



0

f ./ cos

.2n  1/ 

2

d, n D 1, 2, 3,. . . .

12.4.6. v.r; / D R.r/‚./ where (A) r

2

R

00

CrR

0

R D 0 and ‚

00

C‚ D 0, ‚

0

.0/ D 0, ‚

0

./ D 0.

From Theorem 11.1.3, 

0

D 0, ‚

0

D 1; 

n

D

n

2



2



2

, ‚

n

D cos

n



, n D 1, 2, 3,. . . . Substituting

 D 0 into (A) yields the equation r

2

R

00

0

C rR

0

D 0 for R

0

; R

0

D c

1

C c

2

ln r . Since we want R

0

to be

bounded as r ! 0C and R

0

./ D 1, R

0

.r/ D 1; therefore v

0

.r; / D 1.

Substituting  D

n

2



2



2

into (A) yields the Euler equation r

2

R

00

n

C rR

0

n



n

2



2



2

R

n

D 0 for R

n

. The

indicial polynomial is



s 

n





s C

n





, so R

n

D c

1

r

n=

C c

2

r

n=

, by Theorem 7.4.3. Since

we want R

n

to be bounded as r ! 0C and R

n

./ D 1, R

n

.r/ D

r

n=



n=

; v

n

.r; / D

r

n=



n=

cos

n



,

n D 1, 2, 3,. . . ; u.r; / D ˛

0

C

1

X

nD1

˛

n

r

n=



n=

cos

n



, where F ./ D ˛

0

C

1

X

nD1

˛

n

cos

n



is the

Fourier cosine series of f on Œ0; ; that is, ˛

0

D

1



Z



0

f ./ d and ˛

n

D

2



Z



0

f ./ cos

n



d,

n D 1, 2, 3,. . . .

CHAPTER 1 3

Boundary Value Problems for Second

Order Ordinary Differential Equations

13.1 BOUNDARY VALUE PROBLEMS

13.1.2. By inspection, y

p

D x; y D x C c

1

e

x

C c

2

e

x

; y.0/ D 2 H) c

1

C c

2

D 2;

y.1/ D 1 H) 1 C c

1

e C c

2

=e D 1;



1 1

e 1=e



c

1

c

2



D



2

2



; c

1

D

2

e  1

; c

2

D

2e

1  e

;

y D x C

2



e

x

 e

.x1/



e 1

13.1.4. By i nspection, y

p

D x; y D x C c

1

e

x

C c

2

e

x

; y

0

D 1 C c

1

e

x

 c

2

e

x

; y.0/ C y

0

.0/ D

3 H) 1 C 2c

1

D 3; c

1

D 2; y.1/  y

0

.1/ D 2 H)

2c

2

e

D 2; c

2

D e; y D x C 2e

x

C e

.x1/

13.1.6. y

p

D Ax

2

e

x

; y

0

p

D A.x

2

C2xe

x

/; y

00

p

D A.x

2

e

x

C4xe

x

C2e

x

/; y

00

p

2y

0

p

Cy

p

D 2Ae

x

D e

x

if A D 1; y

p

D x

2

e

x

; y D .x

2

C c

1

C c

2

x/e

x

; y

0

D .x

2

C 2x C c

1

C c

2

C c

2

x/e

x

; B

1

.y/ D 3 and

B

2

.y/ D 6e H) c

1

 2c

2

D 3, 2c

1

C 3c

2

D 24; c

1

D 13; c

2

D 8; y D .x

2

 8x C 13/e

x

.

13.1.8. B

1

.y/ D y.0/; B

2

.y/ D y.1/  y

0

.1/. Let y

1

D x, y

2

D 1; B

1

.y

1

/ D B

2

.y

1

/ D 0. By

variation of parameters, if y

p

D u

1

x C u

2

where u

0

1

x C u

0

2

D 0 and u

0

1

D F , then y

00

p

D F .x/. Let

u

0

1

D F , u

0

2

D xF ; u

1

D 

Z

1

x

F .t/ dt, u

2

D 

Z

x

0

tF.t/ dt; y

p

D x

Z

1

x

F .t/ dt 

Z

x

0

tF.t/ dt;

y

0

p

D 

Z

1

x

F .t/ dt; y D y

p

C c

1

x C c

2

. Since B

1

.y

p

/ D 0, B

1

.x/ D 0 and B

1

.1/ D 1, B

1

.y/ D

0 H) c

2

D 0; hence, y D y

p

Cc

1

x. Since B

2

.y

p

/ D 

Z

1

0

tF.t/ dt and B

2

.x/ D 0, B

2

.y/ D 0 H)

Z

1

0

tF.t/ dt D 0: There is no solution if this conditions does not hold. If it does hold, then the solutions

are y D y

p

C c

1

x, with c

1

arbitrary.

13.1.10. (a) The condition is ba ¤ .kC1=2/ (k D integer). Let y

1

D sin.xa/ and y

2

D cos.xb/.

Then y

1

.a/ D y

0

2

.b/ D 0 and fy

1

; y

2

g is linearly independent if b  a ¤ .k C 1=2/ (k D integer),

since

ˇ

sin.x  a/ cos.x  b/

cos.x  a/ sin.x  b/

ˇ

D cos.b a/ ¤ 0:

273

274 Chapter 13

Boun dary Value Problems for Second Order Ordinary Differential Equati ons

Now Theorem 13.1.2 implies that (A) has a unique solution for any continuous F and constants k

1

and

k

2

. If y D u

1

sin.x  a/ C u

2

cos.x  b/ where

u

0

1

sin.x  a/ C u

0

2

cos.x  b/ D 0

u

0

1

cos.x  a/  u

0

2

sin.x  b/ D F;

then y

00

C y D F .

u

0

1

D F.x/

cos.x  b/

cos.b  a/

; u

0

2

D F .x/

sin.x  a/

cos.b  a/

;

u

1

D 

1

cos.b a/

Z

b

x

F .t/ cos.t  b/ dt; u

2

D 

1

cos.b a/

Z

x

a

F .t/ sin.t b/ dt I

y D 

sin.x  a/

cos.b  a/

Z

b

x

F .t/ cos.t  b/ dt 

cos.x  b/

cos.b a/

Z

x

a

F .t/ sin.t a/ dt:

(b) If b  a D .k C 1=2/ (k D integer), then y

1

D sin.x  a/ satisﬁes both boundary conditions

y.a/ D 0 and y

0

.b/ D 0. Let y

2

D cos.x  a/. If y

p

D u

1

sin.x  a/ C u

2

cos.x/ where

u

0

1

sin.x  a/ C u

0

2

cos.x  a/ D 0;

u

0

1

cos.x  a/  u

0

2

sin.x  a/ D F;

then y

00

p

C y

p

D F ; u

0

1

D F cos.x  a/; u

0

2

D F sin.x  a/;

u

1

D 

Z

b

x

F .t/ cos.t  a/ dt; u

2

D 

Z

x

a

F .t/ sin.t a/ dtI

y

p

D sin.x  a/

Z

b

x

F .t/ cos.t  a/ dt  cos.x  a/

Z

x

a

F .t/ sin.t a/ dtI

y

0

p

D cos.x  a/

Z

b

x

F .t/ cos.t  a/ dt C sin.x  a/

Z

x

a

F .t/ sin.t a/ dt:

The general solution of y

00

Cy D F is y D y

p

Cc

1

sin.xa/Cc

2

cos.xa/. Since b a D .kC1=2/,

y

0

.b/ D 0 H) y

0

p

.b/ D .1/

k

Z

b

a

F .t/ sin.t  a/ dt D 0; ther efore, F must satisfy

Z

b

a

F .t/ sin.t 

a/ dt D 0. In this case, the solutions of the boundary value problem ar e y D y

p

Cc

1

sin.x a/, with c

1

arbitrary.

13.1.12. Let y

1

D sinh.x  a/ and y

2

D sinh.x  b/. Then y

1

.a/ D 0, y

2

.b/ D 0, and

W.x/ D

ˇ

sinh.x  a/ sinh.x  b/

cosh.x  a/ cosh.x  b/

ˇ

D sinh.b a/ ¤ 0:

(Since W is constant (Theorem 5.1.4), evaluate it by setting x D b.) From Theorem 13.1.2, (A) has a

unique solution for any continuous F and constants k

1

and k

2

. If y D u

1

sinh.x  a/ C u

2

sinh.x  b/

where

u

0

1

sinh.x  a/ C u

0

2

sinh.x  b/ D 0

u

0

1

cosh.x  a/ C u

0

2

cosh.x  b/ D F;

then y

00

 y D F .

u

0

1

D F.x/

sinh.x  b/

sinh.b  a/

; u

0

2

D F .x/

sinh.x  a/

sinh.b  a/

;

Section 13.1

Boun dary Value Problems

275

u

1

D

1

sinh.b  a/

Z

b

x

F .t/ sinh.t  b/ dt; u

2

D

1

sinh.b  a/

Z

x

a

F .t/ sinh.t  a/ dtI

y D

sinh.x  a/

sinh.b  a/

Z

b

x

F .t/ sinh.t  b/ dt C

sinh.x  b/

sinh.b  a/

Z

x

a

F .t/ sinh.t  a/ dt:

13.1.14. Let y

1

D cosh.x  a/ and y

2

D cosh.x  b/. Then y

0

1

.a/ D y

0

2

.b/ D 0 and

W.x/ D

ˇ

cosh.x  a/ cosh.x  b/

sinh.x  a/ sinh.x  b/

ˇ

D sinh.b  a/ ¤ 0:

(Since W is constant (Theorem 5.1.40, evaluate it by setting x D b.) If

y D u

1

cosh.x  a/ C u

2

cosh.x  b/ where

u

0

1

cosh.x  a/ C u

0

2

cosh.x  b/ D 0

u

0

1

sinh.x  a/ C u

0

2

sinh.x  b/ D F;

then y

00

 y D F .

u

0

1

D F.x/

cosh.x  b/

sinh.b  a/

; u

0

2

D F .x/

cosh.x  a/

sinh.b  a/

;

u

1

D 

1

sinh.b  a/

Z

b

x

F .t/ cosh.t  b/ dt; u

2

D 

1

sinh.b  a/

Z

x

a

F .t/ cosh.t  a/ dtI

y D 

cosh.x  a/

sinh.b  a/

Z

b

x

F .t/ cosh.t  b/ dt 

cosh.x  b/

sinh.b  a/

Z

x

a

F .t/ cosh.t  a/ dt:

13.1.16. Let y

1

D sin !x, y

2

sin !.x  /; then y

1

.0/ D 0, y

2

./ D 0,

W.x/ D

ˇ

sin !x sin !.x   /

! cos !x ! cos !.x   /

ˇ

D ! sin ! ¤ 0

if and only if ! is not an integer. If this is so, then y D u

1

sin !x C u

2

sin !.x  / if

u

0

1

sin !x C u

0

2

sin !.x  / D 0

!.u

0

1

cos !x C u

0

2

cos !.x  // D F I

u

0

1

D F

sin !.x  /

! sin !

; u

0

2

D F

sin !x

! sin !

I

u

1

D

1

! sin !

Z



x

F .t/ sin !.t  / dtI u

2

D

1

! sin !

Z

x

0

F .t/ sin !t dtI

y D

1

! sin !



sin !x

Z



x

F .t/ sin !.t  / dt C sin !.x  /

Z



0

F .t/ sin !t dt



:

If ! D n (positive integer ), then y

1

D sin nx i s a nontrivial solution o f y

00

Cy D 0, y.0/ D 0, y./ D

0. Let y

2

D cos nx; then W.x/ D

ˇ

sin nx cos nx

n cos nx n sin nx

ˇ

D n, and y

p

D u

1

sin nx C u

2

cos nx

satisﬁes y

00

p

C n

2

y

p

D 0 if

u

0

1

sin nx C u

0

2

cos nx D 0

nu

0

1

cos nx  nu

0

2

sin nx D F I

276 Chapter 13

Boun dary Value Problems for Second Order Ordinary Differential Equati ons

u

0

1

D

1

n

F cos nx, u

0

2

D 

1

n

F sin nx; u

1

D 

1

n

Z



x

F .t/ cos nt dt ; u

2

D 

1

n

Z

x

0

F .t/ sin nt dt;

y

p

D 

1

n



sin nx

Z



x

F .t/ cos nt dt C cos nx

Z

x

0

F .t/ sin nt dt



I

y D y

p

C c

1

sin nx C c

2

cos nx. Since y

p

D 0, y.0/ D 0, so c

2

D 0; y D y

p

C c

1

sin nx. Since

y./ D 0,

Z



0

F .t/ sin nt dt D 0 is necessary for existence of a solution. I f this hold, then the solut ions

are y D y

p

C c

1

sin nx, with c

1

arbitrary.

13.1.18. Let y

1

D cos !x; y

2

D sin !.x /; t hen y

0

1

.0/ D y

2

./ D 0, and

W.x/ D

ˇ

cos !x sin !.x  /

! sin !x ! cos !.x  /

ˇ

D ! cos ! ¤ 0

if and only if ! ¤ n C 1=2 (n D integer). If this is so, then y D u

1

cos !x C u

2

sin !.x  / satisﬁes

y

00

C!

2

y D F .x/ if

u

0

1

cos !x C u

0

2

sin !.x  / D 0

!.u

0

1

sin !x Cu

0

2

cos !.x  //! D F I

then

u

0

1

D 

F sin !.x  /

! cos !

; u

0

2

D

F cos !x

! cos !

;

u

1

D

1

! cos !

Z



x

F .t/ sin !.t  /; dt; u

2

D

1

! cos !

Z

x

0

F .t/ cos !t dt;

y D

1

! cos !



sin !x

Z



x

F .t/ sin !.t  /; dt C sin !.x  /

Z

x

0

F .t/ cos !t dt



:

If ! D n C 1=2 (n D integer), then y

1

D cos.n C 1=2/x is a nontrivial solution y

00

C y D 0,

y

0

.0/ D y./ D 0. Let y

2

D sin.n C 1=2/x; then

W.x/ D

ˇ

cos.n C 1=2/x sin.n C1=2/x

.n C 1=2/ sin.n C 1=2/x .n C 1=2/ cos.n C 1=2/x

ˇ

D n C 1=2;

so y

p

D u

1

cos.n C 1=2/x C u

2

sin.n C 1=2/x satisﬁes y

00

p

C .n C 1=2/

2

y

p

D F if

u

0

1

cos.n C 1=2/x C u

0

2

sin.n C 1=2/x D 0

.n C 1=2/u

0

1

sin.n C 1=2/x C .n C 1=2/u

0

2

cos.n C 1=2/x D F:

u

0

1

D 

F sin.n C 1=2/x

n C 1=2

I u

0

2

D

F cos.n C 1=2/x

n C 1=2

I

u

1

D

Z



x

F .t/ sin.n C 1=2/t

n C 1=2

dtI u

2

D

Z

x

0

F .t/ cos.n C 1=2/t

n C 1=2

dtI

y

p

D

1

n C 1=2



cos.n C 1=2/x

Z



x

F .t/ sin.n C 1=2/t dt C sin .n C 1=2/x

Z

x

0

F .t/ cos.n C 1=2/t dt



I

y

0

p

D sin.n C 1=2/x

Z



x

F .t/ sin.n C 1=2/t dt C cos.n C 1=2/x

Z

x

0

F .t/ cos.n C 1=2/t dtI

Section 13.1

Boun dary Value Problems

277

y D y

p

C c

1

cos.n C 1=2/x C c

2

sin.n C 1=2/xI

y

0

D y

0

p

C .n C 1=2/.c

1

sin.n C 1=2/x C c

2

cos.n C 1=2//x:

Since y

0

p

.0/ D 0, y

0

.0/ D 0 H) c

2

D 0; y D y

p

C c

1

cos.n C 1=2/x;

y

0

D y

0

p

C.nC1=2/c

1

.nC1=2/x; y./ D 0 H) y

p

./ D 0. Hence,

Z



0

F .y/ cos.nC1=2/t dt D 0

is a necessary condition for existence of a solution. If th is holds, then the so lutions are y D y

p

C

c

1

cos.n C 1=2/x with c

1

arbitrary.

13.1.20. Suppose y D c

1

´

1

C c

2

´

2

is a nontrivial solution of the homogeneo us boundary value prob-

lem. Then B

1

.y/ D c

1

B

1

.´

1

/ C c

2

B

1

.´

2

/ D 0. From Theorem 13.1.1 we may assume without

loss of generality that B

1

.´

2

/ ¤ 0. Then c

2

D 

B

1

.´

1

/

B

1

.´

2

/

c

1

. Therefore, y is constant mul tiple of

y

0

D B

1

.´

2

/´

1

 B

1

.´

1

/´

2

¤ 0. To that check y satisﬁes the boun dary conditions, note that B

1

.y

0

/ D

B

1

.´

2

/B

1

.´

1

/B

1

.´

1

/B

1

.´

2

/ D 0 B

2

.y

0

/ D B

1

.´

2

/B

2

.´

1

/B

1

.´

1

/B

2

.´

2

/ D 0, by Theorem 13.1.2.

13.1.22. y

1

D a

1

Ca

2

x; y

1

.0/2y

0

1

.0/ D a

1

2a

2

D 0 if a

1

D 2, a

2

D 1; y

1

D 2Cx. y

2

D b

1

Cb

2

x;

y

2

.1/ D 2y

0

1

.1/ D b

1

C 3b

2

D 0 if b

1

D 3, b

2

D 1; y

2

D 3  x.

W.x/ D

ˇ

2 C x 3  x

1 1

ˇ

D 5I G.x; t / D

8

ˆ

<

ˆ

:



.2 C t/.3  x/

5

; 0  t  x;



.2 C x/.3  t/

5

; x  t  1:

y D 

1

5



.2 C x/

Z

1

x

.3  t/F .t/ dt C .3  x/

Z

x

0

.2 C t/F .t/ dt



: (B)

(a) With F.x/ D 1, (B) becomes

y D 

1

5



.2 C x/

Z

1

x

.3  t/ dt C .3  x/

Z

x

0

.2 C t/ dt



D 

1

5



.2 C x/



x

2

 6x C 5

2



C .3  x/



x

2

C 4x

2



D

x

2

 x  2

2

:

(b) With F .x/ D x, (B ) becomes

y D 

1

5



.2 C x/

Z

1

x

.3t  t

2

/ dt C .3  x/

Z

x

0

.2t C t

2

/ dt



D 

1

5



.2 C x/



2x

3

 9x

2

C 7

6



C .3  x/



x

3

C 3x

2

3



D

5x

3

 7x  14

30

:

(b) With F .x/ D x

2

, (B) becomes

y D 

1

5



.2 C x/

Z

1

x

.3t

2

 t

3

/ dt C .3  x/

Z

x

0

.2t

2

C t

3

/ dt



D 

1

5



.2 C x/



x

4

 4x

2

C 3

4



C .3  x/



3x

4

C 8x

3

12



D

5x

4

 9x  18

60

:

278 Chapter 13

Boun dary Value Problems for Second Order Ordinary Differential Equati ons

13.1.24. y

1

D x

2

x, y

2

D x

2

2x; th en y

1

.1/ D 0, y

2

.2/ D 0; W .x/ D

ˇ

x

2

 x x

2

 2x

2x  1 2x  2

ˇ

D x

2

.

Since P

0

.x/ D x

2

, G.x; t/ D

8

ˆ

<

ˆ

:

.t  1/x.x  2/

t

3

; 1  t  x;

x.x  1/.t  2/

t

3

; x  t  2:

:

y D x.x  1/

Z

2

x

t  2

t

3

F .t/ dt C x.x  2/

Z

x

1

F .t/ dt: (B)

(a) With F.x/ D 2x

3

, (B) becomes

y D 2x.x  1/

Z

2

x

.t  2/ dt C 2x.x  2/

Z

x

1

.t  1/ dt

D x.x  1/.x  2/

2

C x.x  2/.x  1/

2

D x.x  1/.x  2/:

(b) With F .x/ D 6x

4

, (B) becomes

y D 6x.x  1/

Z

2

x

.t  2/t dt C 6x.x  2/

Z

x

1

.t  1/t dt

D 2x.x  1/.x C 1/.x  2/

2

C x.x 2/.x  1/

2

.2x C 1/ D x.x  1/.x  2/.x C 3/:

13.1.26. y

1

D a

1

C a

2

x; y

0

1

D a

2

; B

1

.y

1

/ D ˛a

1

C ˇa

2

D 0 if a

1

D ˇ, a

2

D ˛; y

1

D ˇ  ˛x.

y

2

D b

1

C b

2

x; y

0

2

D b

2

; B

2

.y

2

/ D b

1

C . C ı/b

2

D 0 if b

1

D  C ı, b

2

D ; y

2

D  C ı  x;

W.x/ D



ˇ  ˛x  C ı  x

˛ 



D ˛. C ı/  ˇ. From Theorem 13.1.2, (A ) has a unique so lution

if and only if ˛. C ı/  ˇ ¤ 0. Then

G.x; t / D

8

ˆ

<

ˆ

:

.ˇ  ˛t/. Cı  x/

˛. C ı/  ˇ

; 0  t  x;

.ˇ  ˛x/. C ı  t/

˛. C ı/  ˇ

; x  t  1:

13.1.28. y

1

D a

1

cos x Ca

2

sin x; y

0

1

D a

1

sin x Ca

2

cos x; B

1

.y

1

/ D ˛a

1

Cˇa

2

D 0 if a

1

D ˇ, a

2

D

˛. y

1

D ˇ cos x ˛ sin x. y

2

D b

1

cos x Cb

2

sin x; y

0

2

D b

1

sin x Cb

2

cos x; B

2

.y

2

/ D b

2

ıb

1

D

0 if b

1

D , b

2

D ı; y

2

D  cos x Cı sin x; W.x/ D



ˇ cos x  ˛ sin x  cos x C ı sin x

ˇ sin x ˛ cos x  sin x C ı cos x



Since

W is constant, we can evaluate it with x D 0: W D



ˇ 

˛ ı



D ˛ Cˇı. From Theorem 13.1.2, (A)

has a unique solution if and only if ˛ C ˇı ¤ 0. Then

G.x; t / D

8

ˆ

<

ˆ

:

.ˇ cos t  ˛ sin t/. cos x C ı sin x/

˛ C ˇı

; 0  t  x;

.ˇ cos x  ˛ sin x/. cos t C ı sin t//

˛ C ˇı

; x  t  :

13.1.30. y

1

D e

x

.a

1

cos x C a

2

sin x/; y

0

1

D e

x

Œa

1

.cos x  sin x/ C a

2

.sin x C cos x/;

B

1

.y

1

/ D .˛ C ˇ/a

1

C ˇa

2

D 0 if a

1

D ˇ, a

2

D .˛ C ˇ/.

Section 13.2

Sturm-Liouville Problems

279

y

1

D e

x

.ˇ cos x  .˛ C ˇ/ sin x. y

2

D e

x

.b

1

cos x C b

2

sin x/;

y

0

2

D e

x

Œ.b

1

.cos x  sin x// C b

2

.sin x C cos x/;

B

2

.y

2

/ D e

=2

Œ. Cı/b

2

 ıb

1

 D 0 if b

1

D ı, b

2

D . C ı/;

y

2

D e

x

Œ. C ı/ cos x C ı sin x/;

To evaluate W.x/, we write y

1

D e

x

v

1

and y

2

D e

x

v

2

, where

v

1

D ˇ cos x .˛ C ˇ/ sin x and v

2

D . C ı/ cos x C ı sin x.

Then y

0

1

D y

1

C e

x

v

0

1

and y

2

D y

2

C e

x

y

0

2

,

W.x/ D

ˇ

y

1

y

2

y

1

C e

x

v

0

1

y

2

C e

x

v

0

2

ˇ

D

ˇ

y

1

y

2

e

x

v

0

1

xv

0

2

ˇ

D e

2x

ˇ

v

1

v

2

v

0

1

xv

0

2

ˇ

D

ˇ

.ˇ cos x  .˛ C ˇ/ sin x . C ı/ cos x C ı sin x

.ˇ sin x  .˛ C ˇ/ cos x .. C ı/ sin x C ı cos x

ˇ

:

Since v

00

i

C v

i

D 0, i D 1, 2, Theorem 5.1.4 implies that W .x/ D Ke

2x

, where is a constant that can be

determined by setting x D 0 in the determinant :

W.x/e

2x

ˇ

ˇ  C ı

˛ ˇ ı

ˇ

D Œˇı C .˛ C ˇ/. C ı/:

From Theorem 13.1.2, the bo undary value problem has a unique solution if and only if ˇı C.˛ Cˇ/. C

ı/ ¤ 0. In this case the Green’s function is

G.x; t / D

8

ˆ

<

ˆ

:

e

xt

Œˇ cos t  .˛ C ˇ/ sin tŒ C ı/ cos x C ı sin x

ˇı C .˛ C ˇ/. C ı/

; a  t  x

e

xt

Œˇ cos x  .˛ C ˇ/ sin xŒ C ı/ cos t C ı sin t

ˇı C .˛ C ˇ/. C ı/

; x  t  =2:

13.1.32. Let y

p

D

Z

b

a

G.x; t /F.t/ dt. From Theorem 13.1.3, Ly

p

D F , B

1

.y

p

/ D 0, and B

2

.y

p

/ D 0.

The so lution of Ly D F , B

1

.y/ D k

1

, and B

2

.y/ D k

2

is of the form y D y

p

C c

1

y

1

C c

2

y

2

. Since

B

1

.y

p

/ D 0 and B

1

.y

1

/ D 0, B

1

.y/ D k

1

H) k

1

D c

2

B

1

.y

2

/ H) c

2

D

k

1

B

1

.y

2

/

. Since

B

2

.y

p

/ D 0 and B

2

.y

2

/ D 0, B

2

.y/ D k

2

H) k

2

D c

1

B

2

.y

1

/ H) c

1

D

k

2

B

2

.y

1

/

.

13.2 STURM-LIOUVILLE PROBLEMS

13.2.2. y

00

C

1

x

y

0

C



1 



2

x

2



y D 0;

p

0

p

D

1

x

; ln jpj D ln jxj; p D x; xy

00

C y

0

D



x 



2

x



y D 0;

.xy

0

/

0

C



x 



2

x



y D 0.

13.2.4. y

00

C

b

x

y

0

C

c

x

2

y D 0;

p

0

p

D

b

x

; ln jpj D b ln jxj; p D x

b

;

x

b

y

00

C bx

b1

y

0

C cx

b2

y D 0; .x

b

y

0

/

0

C cx

b2

y D 0.

13.2.6. xy

00

C .1  x/y

0

C ˛y D 0; y

00

C



1

x

 1



y

0

C

˛

x

y D 0;

p

0

p

D

1

x

 1; ln jpj D l n jxj  x;

p D xe

x

; xe

x

y

00

C .1  x/y

0

C ˛e

x

y D 0; .xe

x

y

0

/

0

C ˛e

x

y D 0.

280 Chapter 13

Boun dary Value Problems for Second Order Ordinary Differential Equati ons

13.2.8. If  is an eigenvalues of (A) and y is a -eigenfunction, multiplying the differential equation in

(B) by y yields .xy

0

/y C



x

y

2

D 0;



Z

2

1

y

2

.x/

x

2

dx D 

Z

2

1

.xy

0

.x//

0

y.x/ dx D xy

0

.x/y.x/

ˇ

2

1

C

Z

2

1

x.y

0

.x//

2

dxI

y.1/ D y

.

2/ D 0 H) xy

0

.x/y.x/

ˇ

2

1

D 0I 

Z

2

1

y

2

.x/

x

dx D

Z

2

1

x.y

0

.x//

2

dx:

Therefore   0: We must still show that  D 0 is not an eigenvalue. To th is end , suppose th at .xy

0

/

0

D 0;

then xy

0

D c

1

; y

0

D

c

1

x

; y D c

1

ln jxj C c

2

; y.1/ D 0 H) c

2

D 0; y D c

1

ln jxj; y.2/ D 0 H)

c

1

D 0; y  0; therefore  D 0 is not an eigenvalue.

13.2.10. Characteristic equation: r

2

C 2r C 1 C  D 0; r D 1 ˙

p

.

 D 0: y D e

x

.c

1

C c

2

x/; y

0

D e

x

.c

1

 c

2

C c

2

x/; y

0

.0/ D 0 H) c

1

D c

2

; y

0

D c

2

xe

x

;

y

0

.1/ D 0 H) c

2

=e D 0 H) c

2

D 0;  D 0 is not an eigenvalue.

 D k

2

, k > 0: r D 1 ˙ k; y D e

x

.c

1

cosh kx C c

2

sinh kx/;

y

0

D c

1

e

x

.cosh kx C k sinh kx/ C c

2

e

x

.sinh kx C k cosh kx/.

The boundary conditions require th at

c

1

C c

2

k D 0 and .cosh k C k sinh k/c

1

C.sinh k C k cosh k/c

2

D 0.

This system has a nontrivial solution if and only if .1 k

2

/ sinh k D 0. Let k D 1 and c

1

D c

2

D 1; then

 D 1 is the only negative eigenvalue, with associated eigenfunction y D 1.

 D k

2

, k > 0: r D 1 ˙ ik; y D e

x

.c

1

cos kx C c

2

sin kx/;

y

0

D c

1

e

x

.cos kx  k sin kx/ Cc

2

e

x

.sin x C k cos kx/. The boundary condit ions require that

c

1

C c

2

k D 0 and .cos k  k sin k/c

1

C .sin k C k cos k/c

2

D 0.

This system has a nontrivial solution if and only if .1 C k

2

/ sin k D 0. Let k D n (k a p ositive

integer)and c

1

D n, c

2

D 1; then 

n

D n

2



2

is an eigenvalue, with associated eigenfunction y

n

D

e

x

.n cos nx C sin nx/.

13.2.12. Characteristic equation: r

2

C  D 0.

 D 0 W y D c

1

C c

2

x. y.0/ D 0 H) c

1

D 0, so y D c

2

x. Now y.1/  2y

0

.1/ D 0 H) c

2

D 0.

Therefore  D 0 is not an eigenvalue.

 D k

2

, k > 0: y D c

1

cosh kx Cc

2

sinh kx; y

0

D k.c

1

sinh kx Cc

2

cosh kx/. y

0

.0/ H) c

2

D 0,

so y D c

1

cosh kx. Now y.1/  2y

0

.1/ D 0 H) c

1

.cosh k  2k sinh k/ D 0, which is possible with

c

1

¤ 0 if and only i f tanh k D

1

2k

. Graphing both sides of this equation on the same axes show that it

has on e positive solution k

0

; y

0

D cosh k

0

x is a k

2

0

-eigefunction.

 D k

2

, k > 0: y D c

1

cos kx C c

2

sin kx; y

0

D k.c

1

sin kx C c

2

cos kx/. y

0

.0/ H) c

2

D 0, so

y D c

1

cos kx. Now y.1/  2y

0

.1/ D 0 H) c

1

.cos k C 2k sin k/ D 0, which is possib le with c

1

¤ 0

if and only if tan k D 

1

2k

. Graphing both sides of this equation on the same axes shows that it has a

solution k

n

in ..2n  1/=2; n/, n D 1, 2, 3, . . . ; y

n

D cos k

n

x is a k

2

n

-eigenfunction.

13.2.14. Characteristic equation: r

2

C  D 0.

 D 0 W y D c

1

C c

2

x. The boundary conditions require that c

1

C 2c

2

D 0 and c

1

C c

2

D 0, which

imply that c

1

D c

2

D 0, so  D 0 i s not an eigenvalue.

 D k

2

, k > 0: y D c

1

cosh kx C c

2

sinh kx; y

0

D k.c

1

sinh kx C c

2

cosh kx/. The boundary

conditions require that

c

1

C 2kc

2

D 0 and c

1

cosh k C c

2

sinh 2k D 0.

This system has a nontrivial solution if and only if tanh k D 2k. G raphing both sides o f this equation

Section 13.2

Sturm-Liouville Problems

281

on the same axes shows that it has a solution k

0

in .0; /; y

0

D 2k

0

cosh k

0

x  sin h k

0

x is a k

2

0

-

eigenfunction.

 D k

2

, k > 0: y D c

1

cos kx Cc

2

sin kx; y

0

D k.c

1

sin kx Cc

2

cos kx/. The boundary conditions

require th at

c

1

C 2kc

2

D 0 and c

1

cos k C c

2

sin k D 0.

This system has a nontrivial solution if and only if tan k D 2k. Graphing both sides of this equation on

the same axes shows that it has a solu tion k

n

in .n; n C1=2/, n D 1, 2,3, . . . ; y

n

D 2k

n

cos k

n

x sin k

n

x

is a k

2

n

-eigenfunction.

13.2.16. Characteristic equation: r

2

C  D 0.

 D 0 W y D c

1

C c

2

x. The bou ndary conditions r equire that c

1

C c

2

D 0 and c

1

C 4c

2

D 0, so

c

1

D c

2

D 0. Therefore  D 0 is not an eigenvalue.

 D k

2

, k > 0: y D c

1

cosh kx C c

2

sinh kx; y

0

D k.c

1

sinh kx C c

2

cosh kx/. The boundary

conditions require that

c

1

C kc

2

D 0 and .cosh 2k C 2k sinh 2k/c

1

C.sinh 2k C 2k cosh 2k/c

2

D 0.

This system has a nontrivial solution if and only if tanh 2k D 

k

1  2k

2

. Graphi ng both sides of this

equation on the same axes shows that it has a solution k

0

in .1=

p

2/; y

0

D k

0

cosh k

0

x  sinh k

0

x is a

k

2

0

- eigenfunction.

 D k

2

, k > 0: y D c

1

cos kx Cc

2

sin kx; y

0

D k.c

1

sin kx Cc

2

cos kx/. The boundary conditions

require th at

c

1

C kc

2

D 0 and .cos 2k  2k sin 2k/c

1

C .sin 2k C 2k cos 2k/c

2

D 0.

This system has a nontrivial solution if and only if tan 2k D 

k

1 C 2k

2

. Graphing b oth sides of this

equation on the same axes shows that it has a solution k

n

in ..2n  1/=4; n=2/, n D 1, 2,3, . . . ;

y

n

D k

n

cos k

n

x sin k

n

x is a k

2

n

-eigenfunction.

13.2.18. Characteristic equation: r

2

C  D 0.

 D 0 W y D c

1

C c

2

x. The boundary conditions require that 3c

1

C 2c

2

D 0 and 3c

1

C 4c

2

D 0, so

c

1

D c

2

D 0. Therefore  D 0 is not an eigenvalue.

 D k

2

, k > 0: y D c

1

cosh kx C c

2

sinh kx; y

0

D k.c

1

sinh kx C c

2

cosh kx/. The boundary

conditions require that

3c

1

C kc

2

D 0 and .3 cosh 2k  2k sinh 2k/c

1

C .3 sinh 3k  2k cosh 2k/c

2

D 0.

This system has a nontrivial solution if and only if tanh 2k D

9k

9 C 2k

2

. Graphing both si des of this equa-

tion on t he same axes shows t hat it has so lutions y

1

in .1; 2/ and y

2

in .5=2; 7=2/; y

n

D k

n

cosh k

n

x 

3 sin h k

n

x is a k

2

n

-eigenfunction, k D 1, 2.

 D k

2

, k > 0: y D c

1

cos kx Cc

2

sin kx; y

0

D k.c

1

sin kx Cc

2

cos kx/. The boundary conditions

require th at

3c

1

C kc

2

D 0 and .3 cos 2k C 2k sin 2k/c

1

C .3 sin 2k  2k cos 2k/c

2

D 0.

This system has a nontrivial solution if and only i f tan 2k D 

9k

9  2k

2

. Graphing both sides of this

equation on the same axes shows that it has solutions k

0

in .3=

p

2;  / and k

n

in ..2n C 3/=4; .n C

2/=3/, n D 1, 2,3, . . . ; y

n

D k

n

cos k

n

x 3 sin k

n

x is a k

2

n

-eigenfunction.

13.2.20. Characteristic equation: r

2

C  D 0.

 D 0 W y D c

1

C c

2

x. The bou ndary conditions require th at 5c

1

C 2c

2

D 0 and 5c

1

C 3c

2

, so

c

1

D c

2

D 0. Therefore  D 0 is not an eigenvalue.

 D k

2

, k > 0: y D c

1

cosh kx C c

2

sinh kx; y

0

D k.c

1

sinh kx C c

2

cosh kx/. The boundary

conditions require that

5c

1

C 2kc

2

D 0 and .5 cosh k  2k sin h k/c

1

C .5 sinh k  2k cosh k/c

2

D 0.

282 Chapter 13

Boun dary Value Problems for Second Order Ordinary Differential Equati ons

This system has a nontrivial solution if and only if tanh k D

20k

25 C 4k

2

. Graphing both sides of this equa-

tion on the same axes shows that it has solutions k

1

in .1; 2/ and k

2

in .5=2; 7=2/; y

n

D 2k

n

cosh k

n

x 

sinh k

n

x is k

n

-eigenfunction, n D 1, 2.

 D k

2

, k > 0: y D c

1

cos kx Cc

2

sin kx; y

0

D k.c

1

sin kx Cc

2

cos kx/. The boundary conditions

require th at

5c

1

C2kc

2

D 0 and .5 cos k C 2k sin k/c

1

C .5 sin k  2k cos k/c

2

D 0.

This system has a nontrivial solution if and only if tan k D 

20k

25  4k

2

. Graphing both sides of this

equation on the same axes shows that it has a solution k

n

in

..2n C 1/=2; .n C 1//, n D 1, 2,3, . . . ; y

n

D 2k

n

cos k

n

x 3 sin k

n

x is a k

2

n

-eigenfunction.

13.2.22.  D 0: x

2

y

00

 2xy

0

C 2y D 0 is an Euler equation with indicial equation r.r  1/ 2r C2 D

.r1/.r2/ D 0. y D x.c

1

Cc

2

x/; y.1/ D y.2/ D 0 H) c

1

Cc

2

D c

1

C2c

2

D 0 H) c

1

D c

2

D 0,

so  D 0 is not an eigenvalue.

 D k

2

; k > 0: y D x.c

1

cosh k.x  1/ C c

2

sinh k.x  1//; y.1/ D 0 H) c

1

D 0; y D

c

2

x sin h k.x  1/; y.2/ D 0 H) 2c

2

sinh k D 0 H) c

2

D 0;  is not an eigenvalue.

 D k

2

; k > 0: y D x.c

1

cos k.x1/Cc

2

sin k.x 1//; y.1/ D 0 H) c

1

D 0; y D c

2

x sin k.x1/;

y.2/ D 0 wi th c

2

¤ 0 if k D n (n a positive integer); 

n

D n

2



2

; y

n

D x sin n.x  1/ is a k

2

n

-

eigenfunction.

13.2.24.  D 0: x

2

y

00

 2xy

0

C 2y D 0 is an Euler equation with indicial equation r.r  1/ 2r C2 D

.r 1/.r 2/ D 0. y D x.c

1

Cc

2

x/; y

0

D c

1

C2c

2

x; y.1/ D y

0

.2/ D 0 H) c

1

Cc

2

D c

1

C4c

2

D

0 H) c

1

D c

2

D 0, so  D 0 i s not an eigenvalue.

 D k

2

; k > 0: y D x.c

1

cosh k.x  1/ C c

2

sinh k.x  1//; y.1/ D 0 H) c

1

D 0; y D

c

2

x sin h k.x 1/; y

0

D c

2

.sinh k.x1/Ckx cosh k.x 1//; y

0

.2/ D 0 H) c

2

.sinh k Ck cosh k/ H)

c

2

D 0;  is not an eigenvalue.

 D k

2

; k > 0: y D x.c

1

cos k.x1/Cc

2

sin k.x 1//; y.1/ D 0 H) c

1

D 0; y D c

2

x sin k.x1/;

y

0

D c

2

.sin k.x  1/ C kx cos k.x  1//; y

0

.2/ D 0 with c

2

¤ 0 if and only if sin k C 2k cos k D 0

or, equivalently, tan k D 2k. Graphing both sides of this equation on the same axes shows that it has a

solution k

n

in ..2n  1/=2; n/, n D 1, 2,3, . . . ; y

n

D x sin k

n

.x  1/ is a k

2

n

-eigenfunction.

13.2.26.  D 0: y D c

1

Cc

2

x. The bound ary conditions require that c

1

C˛c

2

D 0 and c

1

C. C˛/c

2

D

0, so c

1

D c

2

D 0. Therefore  D 0 is not an eigenvalue of (A).

 D k

2

, k > 0: y D c

1

cosh kx C c

2

sinh kx; y

0

D k.c

1

sinh kx C c

2

cosh kx/. The boundary

conditions require that

c

1

C˛kc

2

D 0

.cosh k C ˛k sinh k/c

1

C .sinh k C ˛k cosh k/c

2

D 0:

(D)

This system has a nontrivial solution if and only if .1k

2

˛

2

/ sinh k D 0, which holds with k > 0 if and

only if k

2

D ˙1=˛. Therefore  D 1=˛

2

is the only negative eig envalue. We can choose k D ˙1=˛.

Either way, the ﬁrst equation in (D) implies that e

x=˛

is an associated eigenfunction.

 D k

2

, k > 0: y D c

1

cos kx Cc

2

sin kx; y

0

D k.c

1

sin kx Cc

2

cos kx/. The boundary conditions

require th at

c

1

C˛kc

2

D 0

.cos k  ˛k sin k /c

1

C .sin k C ˛k cos k/c

2

D 0:

(E)

This system h as a nontrivial solution if and o nly if .1 C k

2

˛

2

/ sin k D 0. Choosing k D n produces

eigenvalues 

n

D n

2



2

. Setting k D n in the ﬁrst equation in (E) yields c

1

C ˛ nc

2

D 0, so y

n

D

n˛ cos nx  sin nx.

Section 13.2

Sturm-Liouville Problems

283

13.2.28. y D c

1

C c

2

x. The boundary conditions require that

˛c

1

C ˇc

2

D 0 and c

1

C .L C ı/c

2

D 0.

This system has a nontrivial solution if and only if ˛.L C ı/  ˇ D 0.

13.2.30. (a) y D c

1

cos kx C c

2

sin kx; y

0

D k.c

1

sin kx C c

2

cos kx/. The bou ndary cond itions

require th at

˛c

1

C ˇkc

2

D 0 and . cos kL  ık sin kL/c

1

C . sin kL C ık cos kL/c

2

D 0.

This system has a nontrivial solution if and only if its determinant is zero. This implies the conclusio n.

(b) If ˛ı  ˇ D 0, (A) reduces to

.˛ C k

2

ˇı/ sin kL D 0: (B)

From the solution of Exercise 13.2.29(b), ˛ C k

2

ˇı > 0 for all k > 0. Therefore the positive zeros o f

(B) are k

n

D n=L, n D 1, 2, 3, . . . , so the positive eigenvalues (SL) are 

n

D n

2



2

=L

2

, n D 1, 2, 3,

. . . .

13.2.32. Suppose  is an eigenvalue and y is an associated eigenfunction. From the solution of Exer-

cise 13.2.31,



Z

b

a

r.x/y

2

.x/ dx D p.a/y.a/y

0

.a/  p.b/y.b/y

0

.b/ C

Z

b

a

p.x/.y

0

.x//

2

dx: (A)

If ˛ˇ D 0 then either y.a/ D 0 or y

0

.a/ D 0, so y.a/y

0

.a/ D 0. If ˛ˇ < 0 then y.a/ D 

ˇ

˛

y

0

.a/, so

y.a/y

0

.a/ D 

ˇ

˛

.y

0

.a//

2

: (B)

Moreover, y

0

.a/ ¤ 0 because if y

0

.a/ D 0 then y.a/ D 0, from (B), and y  0, a contradiction. Si nce



ˇ

˛

> 0 if ˛ˇ < 0, we conclude that if ˛ˇ  0, then

p.a/y.a/y

0

.a/  0; (C)

with equality if and only if ı D 0. A similar arg ument shows that if ı  0, then

p.b/y.b/y

0

.b/  0; (D)

with equality if and only if ˛ˇ D 0. Since .˛ˇ/

2

C .ı/

2

> 0, the inequality must hold in at least one of

(C) and (D). Now (A) implies that  > 0.