Visual Chirality

Zhiqiu Lin

Jin Sun

1,2

Abe Davis

1,2

Noah Snavely

1,2

Cornell University

Cornell Tech

Abstract

How can we tell whether an image has been mirrored?

While we understand the geometry of mirror reﬂections very

well, less has been said about how it affects distributions of

imagery at scale, despite widespread use for data augmenta-

tion in computer vision. In this paper, we investigate how the

statistics of visual data are changed by reﬂection. We refer to

these changes as “visual chirality,” after the concept of geo-

metric chirality—the notion of objects that are distinct from

their mirror image. Our analysis of visual chirality reveals

surprising results, including low-level chiral signals pervad-

ing imagery stemming from image processing in cameras, to

the ability to discover visual chirality in images of people

and faces. Our work has implications for data augmentation,

self-supervised learning, and image forensics.

1. Introduction

“...there’s a room you can see through the glass—that’s just the

same as our drawing room, only the things go the other way.”

— Lewis Carroll,

“Alice’s Adventures in Wonderland & Through the Looking-Glass”

There is a rich history of lore involving reﬂections. From

the stories of Perseus and Narcissus in ancient Greek mythol-

ogy to the adventures of Lewis Carroll’s Alice and J.K. Rowl-

ing’s Harry Potter, ﬁction is full of mirrors that symbolize

windows into worlds similar to, yet somehow different from,

our own. This symbolism is rooted in mathematical fact:

what we see in reﬂections is consistent with a world that

differs in subtle but meaningful ways from the one around

us—right hands become left, text reads backward, and the

blades of a fan spin in the opposite direction. What we see

is, as Alice puts it, “just the same... only the things go the

other way”.

Geometrically, these differences can be attributed to

a world where distances from the reﬂecting surface are

negated, creating an orientation-reversing isometry with ob-

jects as we normally see them. While the properties of such

isometries are well-understood in principle, much less is

known about how they affect the statistics of visual data

at scale. In other words, while we understand a great deal

about how reﬂection changes image data, we know much

(a) (b) (c)

Figure 1.

Which images have been mirrored?

Our goal is to

understand how distributions of natural images differ from their

reﬂections. Each of the images here appears plausible, but some

subset have actually been ﬂipped horizontally. Figuring out which

can be a challenging task even for humans. Can you tell which are

ﬂipped? Answers are in Figure 2.

less about how it changes what we learn from that data—this,

despite widespread use of image reﬂection (e.g., mirror-ﬂips)

for data augmentation in computer vision.

This paper is guided by a very simple question: How do

the visual statistics of our world change when it is reﬂected?

One can understand some aspects of this question by con-

sidering the images in Figure 1. For individual objects, this

question is closely related to the concept of chirality [

An object is said to be chiral if it cannot be rotated and

translated into alignment with its own reﬂection, and achiral

otherwise.

Put differently, we can think of chiral objects

as being fundamentally changed by reﬂection—these are

the things that “go the other way” when viewed through a

mirror—and we can think of achiral objects as simply be-

ing moved by reﬂection. Chirality provides some insight

into our guiding question, but remains an important step re-

moved from telling us how reﬂections impact learning. For

this, we need a different measure of chirality—one we call

visual chirality—that describes the impact of reﬂection on

distributions of imagery.

In this paper, we deﬁne the notion of visual chirality,

and analyze visual chirality in real world imagery, both

through new theoretical tools, and through empirical analysis.

Our analysis has some unexpected conclusions, including 1)

deep neural networks are surprisingly good at determining

whether an image is mirrored, indicating a signiﬁcant degree

More generally, any ﬁgure is achiral if its symmetry group contains

any orientation-reversing isometries.

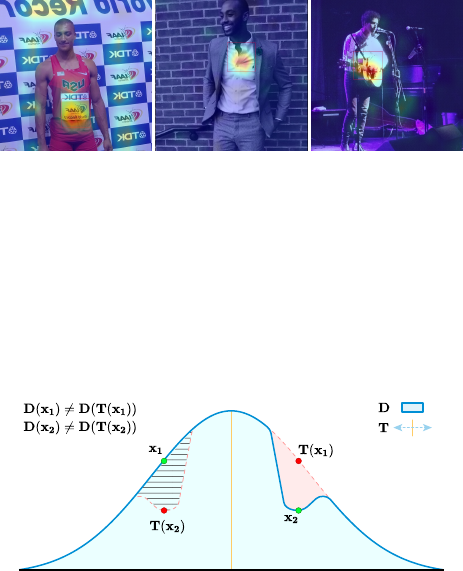
(a) (b) (c)

Figure 2. Images from Figure 1 with chirality-revealing regions

highlighted. These regions are automatically found by our approach

to chiral content discovery. (a,

ﬂipped

) Text chirality. Text (in any

language) is strongly chiral. (b,

not ﬂipped

) Object chirality. The

shirt collar, and in particular which side the buttons are on, exhibit

more subtle visual chirality. (c,

ﬂipped

) Object interaction chirality.

While guitars are often (nearly) symmetric, the way we hold them

is not (the left hand is usually on the fretboard).

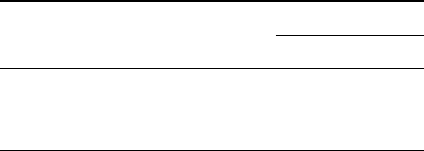
A Simple Example of Distribution Chirality

Figure 3. The curve above represents a distribution over images

(shown as a 1D distribution for simplicity). Using a transformation

to augment a sample-based approximation of the distribution

assumes symmetry with respect to

. We deﬁne visual chirality in

terms of approximation error induced by this assumed symmetry

when T is image reﬂection.

of visual chirality in real imagery, 2) we can automatically

discover high-level cues for visual chirality in imagery, in-

cluding text, watches, shirt collars, face attributes, etc, and

3) we theoretically and empirically demonstrate the exis-

tence of low-level chiral cues that are imprinted in images by

common image processing operations, including Bayer de-

mosaicing and JPEG compression. These conclusions have

implications in topics ranging from data augmentation to

self-supervised learning and image forensics. For instance,

our analysis suggests that low-level cues can reveal whether

an image has been ﬂipped, a common operation in image

manipulation.

1.1. Deﬁning visual chirality

To deﬁne visual chirality, we ﬁrst consider data augmen-

tation for learning in computer vision to build intuition. Ma-

chine learning algorithms are based on the idea that we can

approximate distributions by ﬁtting functions to samples

drawn from those distributions. Viewed in this light, data

augmentation can be seen as a way to improve sampling

efﬁciency for approximating a distribution

D(x)

(where

represents data from some domain, e.g., images) by assum-

ing that

is invariant to some transformation

. More

precisely, augmenting a training sample

with the function

T assumes symmetry of the form:

D(x) = D(T(x)) (1)

which allows us to double our effective sampling efﬁciency

for

at the cost of approximation error wherever the as-

sumed symmetry does not hold. This idea is illustrated in

Figure 3.

Recall that for achiral objects reﬂection is equivalent to

a change in viewpoint. Therefore, if we consider the case

where

is a uniform distribution over all possible views of

an object, and

is image reﬂection, then Equation 1 reduces

to the condition for achirality. We can then deﬁne visual

chirality by generalizing this condition to arbitrary visual

distributions. In other words, we deﬁne visual chirality as a

measure of the approximation error associated with assuming

visual distributions are symmetric under reﬂection. Deﬁning

visual chirality in this way highlights a close connection with

data augmentation. Throughout the paper we will also see

implications to a range of other topics in computer vision,

including self-supervised learning and image forensics.

Note that our deﬁnition of visual chirality can also be

generalized to include other transformations. In this paper

we focus on reﬂection, but note where parts of our analysis

could also apply more broadly.

Notes on visual chirality vs. geometric chirality.

Here we

make a few clarifying observations about visual chirality.

First, while geometric chirality is a binary property of ob-

jects, visual chirality can be described in terms of how much

Equation 1 is violated, letting us discuss it as a continuous

or relative property of visual distributions, their samples, or,

as we will see in Section 4, functions applied to visual dis-

tributions. Second, visual chirality and geometric chirality

need not imply one another. For example, human hands have

chiral geometry, but tend to be visually achiral because the

right and left form a reﬂective pair and each occurs with

similar frequency. Conversely, an achiral object with one

plane of symmetry will be visually chiral when it is only

viewed from one side of that plane. For the remainder of the

paper we will refer to geometric chirality as such to avoid

confusion.

2. Related work

Chirality has strong connections to symmetry, a long-

studied topic in computer vision. Closely related to our work

is recent work exploring the asymmetry of time (referred to

as “Time’s arrow”) in videos, by understanding what makes

videos look like they are being played forwards or back-

wards [

]—a sort of temporal chirality. We explore the

spatial version of this question, by seeking to understand

what makes images look normal or mirrored. This spatial

chirality is related to other orientation problems in graphics

in vision, such as detecting “which way is up” in an image

or 3D model that might be oriented incorrectly [

]. Com-

pared to upright orientation, chirality is potentially much

more subtle—many images may exhibit quite weak visual

chirality cues, including a couple of the images in Figure 1.

Upright orientation and other related tasks have also been

used as proxy tasks for unsupervised learning of feature

representations [

]. Such tasks include the arrow of time

task mentioned above [

], solving jigsaw puzzles [

], and

reasoning about relative positions of image patches [2].

Our problem represents an interesting variation on the

classic task of detecting symmetries in images [

]. As

such, our work is related to the detection and classiﬁcation

of asymmetric, chiral objects, as explored by Hel-Or et al.in

their work on “how to tell left from right” [

], e.g., how to

tell a left hand in an image from a right hand. However,

this prior work generally analyzed geometric chirality, as

opposed to the visual chirality we explore, as deﬁned above—

for instance, a right hand might be geometrically chiral but

not visually chiral, while a right hand holding a pencil might

visually chiral due to the prevalence of right-handed people.

Our work also relates to work on unsupervised discovery

from large image collections, including work on identifying

distinctive visual characteristics of cities or other image

collections [3, 18] or of yearbook photos over time [6].

Finally, a speciﬁc form of chirality (sometimes referred to

as cheirality) has been explored in geometric vision. Namely,

there is an asymmetry between 3D points in front of a camera

and points in back of a camera. This asymmetry can be

exploited in various geometric ﬁtting tasks [7].

3. Measuring visual chirality

In principle, one way to measure visual chirality would

be to densely sample a distribution and analyze symmetry

in the resulting approximation. However, this approach

is inefﬁcient and in most cases unnecessary; we need not

represent an entire distribution just to capture its asymmetry.

Instead, we measure visual chirality by training a network to

distinguish between images and their reﬂections. Intuitively,

success at this task should be bound by the visual chirality

of the distribution we are approximating.

Given a set of images sampled from a distribution, we

cast our investigation of visual chirality as a simple classi-

ﬁcation task. Let us denote a set of training images from

some distribution as

positive

= {I

, I

, · · · , I

}

(we as-

sume these images are photos of the real world and have not

been ﬂipped). We perform a horizontal ﬂip on each image

to produce its reﬂected version

. Let us denote the mirrored

set as

negative

= {I

, I

, · · · , I

}

. We then assign a binary

label y

to each image I

in C

positive

∪ C

negative



0 if I

∈ C

negative

, i.e., ﬂipped

1 if I

∈ C

positive

, i.e., non-ﬂipped

(2)

We train deep Convolutional Neural Nets (CNNs) with stan-

dard classiﬁcation losses for this problem, because they are

good at learning complex distribution of natural images [

Measuring a trained CNNs performance on a validation set

provides insight on the visual chirality of data distribution

we are investigating on.

Next we discuss details on training such a network and the

techniques we use to discover the sources of visual chriality

of the data distribution using a trained model as a proxy.

Network architecture.

We adopt a ResNet network [

], a

widely used deep architecture for image classiﬁcation tasks.

In particular, we use ResNet-50 and replace the last average

pooling layer of the network with a global average pooling

layer [16] in order to support variable input sizes.

Optimization.

We train the network in a mini-batch set-

ting using a binary cross-entropy loss. We optionally ap-

ply random cropping, and discuss the implications of such

data augmentation below. We normalize pixel values by

per-channel mean-subtraction and dividing by the standard

deviation. We use a stochastic gradient descent optimizer [

]

with momentum 0.9 and L

weight decay of 10

−5

Hyperparameter selection.

Finding a suitable learning rate

is important for this task. We perform a grid search in the log

domain and select the best learning rate for each experiment

by cross-validation.

Shared-batch training.

During training, we include both

and

(i.e., positive and negative chirality versions of the

same image) in the same mini-batch. We observe signiﬁcant

improvements in model performance using this approach, in

alignment with prior self-supervised learning methods [5].

Discovering sources of visual chirality.

If a trained model

is able to predict whether an image is ﬂipped or not with high

accuracy, it must be using a reliable set of visual features

from the input image for this task. We consider those cues

as the source of visual chrility in the data distribution.

We use Class Activation Maps (CAM) [

] as a pow-

erful tool to visualize those discriminative regions from a

trained model. Locations with higher activation values in

CAM make correspondingly larger contributions to predict-

ing ﬂipped images.

Throughout this paper, we visualize these activation maps

as heatmaps using the Jet color scheme (red=higher acti-

vations, blue=lower activations). We only compute CAM

heatmaps corresponding to an image’s correct label. Figure 2

shows examples of such class activation maps.

In the following sections, we analyze visual chirality discov-

ered in different settings using the tools described above.

(a) Resizing (b) Random Cropping

Figure 4.

Resizing vs. random cropping as dataset preprocess-

ing

. This ﬁgure shows CAM heatmaps for an image from models

trained with two preprocessing methods: (a) resizing and (b) ran-

dom cropping. We observe that the resizing scheme learns cues

in the edges or corners of images (note the focus on the lower left

corner of (a)), where JPEG encoding can be asymmetric. On the

other hand, the random cropping scheme captures the meaningful

high-level cue—the chiral shirt collar.

4. The chirality of image processing

When we ﬁrst attempted to train our model to distinguish

between images and their reﬂections, we quickly observed

that the network would ﬁnd ways to accomplish this task

using low-level cues that appeared only loosely correlated

with the image’s content. Furthermore, the strength of these

cues seemed to vary a great deal with changes in how data

was prepared. For example, Figure 4 shows two different

CAM heatmaps for the same sample image. The left is

derived from a network trained on resized data, and the right

is derived from a network trained on random crops of the

same data. Both maps identify a dark corner of the image as

being discriminative, as well as part of the shirt on one of

the the image’s human subjects. However, these networks

appear to disagree about the relative strength of the chiral

cues in these regions. This result illustrates how the way we

capture and process visual data—even down to the level of

Bayer mosaics in cameras or JPEG compression—can have

a signiﬁcant impact on its chirality. In this section and the

supplemental material we develop theoretical tools to help

reason about that impact, and use this theory to predict what

networks will learn in experiments.

4.1. Transformation commutativity

The key challenge of predicting how an imaging process

will affect chirality is ﬁnding a way to reason about its be-

havior under minimal assumptions about the distribution to

which it will be applied. For this, we consider what it means

for an arbitrary imaging transformation

to preserve the

symmetry of a distribution

(satisfying Equation 1) under

a transformation

. There are two ways we can deﬁne this.

The ﬁrst is simply to say that if some symmetry exists in the

distribution

then the same symmetry should exist in

the transformation of that distribution by

. The second is

to say that if elements

and

are related by

= Tx

then this relationship should be preserved by

, meaning

= TJx

. In our supplemental material we show that

both deﬁnitions hold when

commutes with

, and that the

second deﬁnition does not hold when

does not commute

with

. With these observations, commutativity becomes a

powerful tool for predicting how a given process

can affect

chirality.

4.2. Predicting chirality with commutativity

In our supplemental material we provide a detailed analy-

sis of the commutativity of Bayer demosaicing, JPEG com-

pression, demosaicing + JPEG compression, and all three of

these again combined with random cropping. We then show

that, in all six cases, our analysis of commutativity predicts

the performance of a network trained from scratch to dis-

tinguish between random noise images and their reﬂection.

These predictions also explain our observations in Figure

4. While the full details are presented in the supplemental

material, some key highlights include:

•

Demosaicing and JPEG compression are both individu-

ally chiral and chiral when combined.

•

When random cropping is added to demosaicing or

JPEG compression individually, they become achiral.

•

When demosaicing, JPEG compression, and random

cropping are all combined, the result is chiral.

This last conclusion is especially surprising—it implies that

common image processing operations inside our cameras

may leave a chiral imprint, i.e., that they imprint chiral cues

that are imperceptible to people, but potentially detectable

by neural networks, and that these features are robust to

random cropping. Thus, these conclusions have implications

on image forensics. For instance, our analysis gives us

new theoretical and practical tools for determining if image

content has been ﬂipped, a common operation in image

editing.

Finally, our analysis of how commutativity relates to

the preservation of symmetries makes only very general

assumptions about

, and

, making it applicable to

more arbitrary symmetries. For example, Doersch et al. [

]

found that when they used the relative position of different

regions in an image as a signal for self-supervised learning,

the networks would “cheat” by utilizing chromatic aberra-

tion for prediction. Identifying the relative position of image

patches requires asymmetry with respect to image transla-

tion. Applied to their case, our analysis is able to predict

that chromatic aberration, which does not commute with

translation, can provide this asymmetry.

5. High-level visual chirality

While analysis of chiralities that arise in image processing

have useful implications in forensics, we are also interested

in understanding what kinds of high-level visual content

(objects, object regions, etc.) reveals visual chirality, and

whether we can discover these cues automatically. As de-

scribed in Section 4, if we try to train a network from scratch,

it invariably starts to pick up on uninterpretable, low-level

image signals. Instead, we hypothesize that if we start with

a ResNet network that has been pre-trained on ImageNet ob-

ject classiﬁcation, then it will have a familiarity with objects

that will allow it to avoid picking up on low-level cues. Note,

that such ImageNet-trained networks should not have fea-

tures sensitive to speciﬁcally to chirality—indeed, as noted

above, many ImageNet classiﬁers are trained using random

horizontal ﬂips as a form of data augmentation.

Data.

What distribution of images do we use for training?

We could try to sample from the space of all natural images.

However, because we speculate that many chirality cues have

to do with people, and with manmade objects and scenes, we

start with images that feature people. In particular, we utilize

the StreetStyle dataset of Matzen et al. [

], which consists

of millions of images of people gathered from Instagram.

For our work, we select a random subset of 700K images

from StreetStyle, and refer to this as the Instagram dataset;

example images are shown in Figures 1 and 5. We randomly

sample 5K images as a test set

test

, and split the remaining

images into training and validation sets with a ratio of 9:1

(unless otherwise stated, we use this same train/val/test split

strategy for all experiments in this paper).

Training.

We trained the chirality classiﬁcation approach

described in Section 3 on Instagram, starting from an

ImageNet-pretrained model. As it turns out, the transfor-

mations applied to images before feeding them to a network

are crucial to consider. Initially, we downsampled all input

images bilinearly to a resolution of 512

512. A network so

trained achieves a

92%

accuracy on the Instagram test set,

a surprising result given that determining whether an image

has been ﬂipped can be difﬁcult even for humans.

As discussed above, it turns out that our networks were

still picking up on traces left by low-level processing, such

as boundary artifacts produced by JPEG encoding, as evi-

denced by CAM heatmaps that often ﬁred near the corners of

images. In addition to pre-training on ImageNet, we found

that networks can be made more resistant to the most obvi-

ous such artifacts by performing random cropping of input

images. In particular, we randomly crop a 512

512 window

from the input images during training and testing (rather than

simply resizing the images). A network trained in such a

way still achieves a test accuracy to 80%, still a surprisingly

high result.

Non-text cues.

Examining the most conﬁdent classiﬁca-

Training set Preprocessing Test Accuracy

Instagram F100M

Instagram Resizing 0.92 0.57

Instagram RandCrop 0.80 0.59

Instagram (no-text) RandCrop 0.74 0.55

Table 1.

Chirality classiﬁcation performance of models trained

on Instagram.

Hyper-parameters were selected by cross valida-

tion. The ﬁrst column indicates the training dataset, and the second

column the processing that takes place on input images. The last

columns report on a held-out test set, and on an unseen dataset

(Flickr100M, or F100M for short). Note that the same preprocess-

ing scheme (resize vs. random crop) is applied to both the training

and test sets, and the model trained on Instagram without text is

also tested on Instagram without text.

tions, we found that many involved text (e.g., on clothing or

in the background), and that CAM heatmaps often predomi-

nantly focused on text regions. Indeed, text is such a strong

signal for chirality that it seems to drown out other signals.

This yields a useful insight: we may be able to leverage

chirality to learn a text detector via self-supervision, for any

language (so long as the writing is chiral, which is true for

many if not all languages).

However, for the purpose of the current analysis, we wish

to discover non-text chiral cues as well. To make it easier

to identify such cues, we ran an automatic text detector [

]

on Instagram, split it into text and no-text subsets, and then

randomly sampled the no-text subset to form new training

and text set. On the no-text subset, chirality classiﬁcation

accuracy drops from 80% to 74%—lower, but still well

above chance.

Generalization.

Perhaps our classiﬁer learns features spe-

ciﬁc to Instagram images. To test this, Table 1 (last column)

shows the evaluation accuracy of all models (without ﬁne-

tuning) on another dataset of Internet photos, a randomly

selected subset of photos from Flickr100M [

]. Note that

there is a signiﬁcant domain gap between Instagram and

Flickr100M, in that images in our Instagram dataset all

contain people, whereas Flickr100M features more general

content (landscapes, macro shots, etc.) in addition al people.

While the performance on Flickr100M is naturally lower

than on Instagram, our Instagram-trained models still per-

form above chance rates, with an accuracy of 55% (or 59% if

text is considered), suggesting that our learned chiral features

can generalize to new distributions of photos.

5.1. Revealing object-level chiral features

Inspecting the CAM heatmaps derived from our non-text-

trained Instagram model reveals a network that focuses on

a coherent set of local regions, such as smart phones and

shirt pockets, across different photos. To further understand

SmartphonesGuitarsWatchesShirt collarsShirt pockets

Faces

Figure 5.

Chiral clusters discovered in the Instagram dataset.

Each row shows selected images from a single discovered cluster. Each

image is shown with its corresponding CAM heatmap superimposed, where red regions are highly correlated with its true chirality. We

discover a range of object-level chiral clusters, such as cellphones, watches, and shirts.

what the network has learned, we develop a way to group

the images, as well as their CAM heatmaps, to determine

which cues are most common and salient. Inspired by work

on mid-level discriminative patch mining [

], we

propose a method built upon CAM that we call chiral feature

clustering, which automatically groups images based on the

similarity of features extracted by the network, in regions

deemed salient by CAM.

Chiral feature clustering.

First, we extract the most dis-

criminative local chiral feature from each image to use as

input to our clustering stage. To do so, we consider the fea-

ture maps that are output from the last convolutional layer

of our network. As is typical of CNNs, these features are

maps with low spatial resolution, but with high channel di-

mensionality (e.g., 2048).

Given an input image, let us denote the output of this last

convolutional layer as

, which in our case is a feature map

of dimensions

16×16×2048

(

w×h×c

). Let

f (x, y)

denote

the 2048-D vector at location

(x, y)

. We apply CAM,

using the correct chirality label for the image, to obtain a

16 × 16

weight activation map

. Recall that the higher

the value of

A(x, y)

, the higher the contribution of the local

region corresponding to

(x, y)

to the prediction of the correct

chirality label.

We then locate the spatial maxima of

∗

, y

∗

) =

arg max

(x,y )

A(x, y)

in each image. These correspond to

points deemed maximally salient for the chirality task by

the network. We extract

f (x

∗

, y

∗

)

as a local feature vector

describing this maximally chiral region. Running this proce-

dure for each image yields a collection for feature vectors,

on which we run k-means clustering.

Results of chiral feature clustering.

We apply this clus-

tering procedure to our no-text Instagram test set, using

k = 500

clusters. We observe that this method is surpris-

ingly effective and identiﬁes a number of intriguing object-

level chiral cues in our datasets. We refer to these clusters

as chiral clusters. Examples of striking high-level chiral

clusters are shown in Figure 5, and include phones (e.g.,

held in a speciﬁc way to take photos in a mirror), watches

(typically worn on the left hand), shirt collars (shirts with

buttoned collared typically button on a consistent side), shirt

pockets, pants, and other objects.

Many of these discovered chiral clusters are highly inter-

pretable. However, some clusters are difﬁcult to understand.

For instance, in the face cluster shown in the last row of Fig-

ure 5, the authors could not ﬁnd obvious evidence of visual

chirality, leading us to suspect that there may be subtle chi-

rality cues in faces. We explore this possibility in Section 6.

We also observe that some clusters focus on sharp edges in

the image, leading us to suspect that some low-level image

processing cues are being learned in spite of the ImageNet

initialization and random cropping.

6. Visual chirality in faces

Inspired by our results on the Instagram dataset in Sec-

tion 5, we now analyze chirality in face images. To do so, we

use the FFHQ dataset [

] as the basis for learning. FFHQ is

a recent dataset of 70K high-quality faces introduced in the

context of training generative methods. We use 7% of the

images as a test set and the remaining images for training and

validation. We train various models on FFHQ, ﬁrst down-

sampling images to a resolution of 520

520, then randomly

cropping to 512

512. We train a standard model starting

from ImageNet pre-trained features. This model achieves

an accuracy of 81%, which is a promising indicator that our

network can indeed learn to predict the chirality of faces

with accuracy signiﬁcantly better than chance.

However, perhaps there is some bias in FFHQ that leads

to spurious chirality signals. For instance, since a face detec-

tor is used to create FFHQ, there is the possibility that the

detector is biased, e.g., for left-facing faces vs. right-facing

faces. To test this, we evaluate how well our FFHQ-trained

model generalizes to other independent datasets. In particu-

lar, we evaluate this model (without ﬁne-tuning) on another

dataset, LFW, a standard face dataset [

]. We upsample

the low-resolution images in LFW to 512

512 to match our

input resolution. This yields an accuracy of 60%—not as

high as FFHQ, perhaps due to different distributions of faces,

but still signiﬁcantly better than chance.

To qualitatively explore the chirality cues the model has

identiﬁed, we show a sample of chiral clusters derived from

the FFHQ test set in Figure 6. We can see that the CAM

heatmaps in each cluster focus on speciﬁc facial regions.

Based on these cluster, we have identiﬁed some intriguing

preliminary hypotheses about facial chirality:

Hair part

. The ﬁrst cluster in Figure 6 indicates a region

around the part of the hair on the left side of the forehead. We

conjecture that this could be due to bias in hair part direction.

We manually inspected a subset of the FFHQ test set, and

found that a majority of people pictured parted their hair

from left to right (the ratio is

∼

2:1 for photos with visible

hair part), indicating a bias for asymmetry in hair, possibly

due to people preferentially using their dominant right hand

to part their hair.

Predominant gaze direction

, aka ocular dominance

. The

second cluster cluster in Figure 6 highlights a region around

the corner of the right eye. We conjectured that this may

have to do with bias in gaze direction, possibly due to ocular

dominance. We use gaze detection software

to determine

and compare the locations of the pupil in the left and right

eyes. We found that indeed more than two thirds of people

in portrait photographs gaze more towards the left.

https://en.wikipedia.org/wiki/Ocular dominance

https://github.com/shaoanlu/GazeML-keras

Hair part

Eyes

Beard

Figure 6.

Chiral clusters found in FFHQ.

It shows 3 chiral clusters of FFHQ dataset. The leftmost image of each row is the average face +

CAM heatmap for all non-ﬂipped images inside the each cluster. We also show some random non-ﬂipped examples for each cluster.

Note that there are also other clusters left to be explained

(for example the “beard” cluster, which may perhaps be due

to males tending to use right hands to shave or groom their

beard). Exploring such cues would make for interesting

future work and perhaps reveal interesting asymmetries in

our world.

7. Conclusion

We propose to discover visual chirality in image distribu-

tions using a self-supervised learning approach by predicting

whether a photo is ﬂipped or not, and by analyzing proper-

ties of transformations that yield chirality. We report various

visual chirality cues identiﬁed using our tool on a variety of

datasets such as Instagram photos and FFHQ face images.

We also ﬁnd that low-level chiral cues are likely pervasive

in images, due to chiralities inherent in standard image pro-

cessing pipelines. Our analysis has implications in data

augmentation, self-supervised learning, and image forensics.

Our results implies that visual chirality indeed exists in many

vision datasets and such properties should be taken into ac-

count when developing real-world vision systems. However,

our work suggests that it can also be used as a signal that can

be leveraged in interesting new ways. For instance, since

text is highly chiral, our work points to interesting future

direction in utilizing chirality in a self-supervised way to

learn to detect text in images in the wild. We hope that our

work will also inspire further investigation into subtle biases

imprinted our visual world.

Acknowledgements.

This research was supported in part

by the generosity of Eric and Wendy Schmidt by recommen-

dation of the Schmidt Futures program.

References

[1]

L. Bottou. Stochastic gradient descent tricks. In Neural

networks: Tricks of the trade. Springer, page 421–436, 2012.

[2]

C. Doersch, A. Gupta, and A. A. Efros. Unsupervised visual

representation learning by context prediction. ICCV, 2015. 3,

[3]

C. Doersch, S. Singh, A. Gupta, J. Sivic, and A. A. Efros.

What makes Paris look like Paris? SIGGRAPH, 31(4), 2012.

3, 7

[4]

H. Fu, D. Cohen-Or, G. Dror, and A. Sheffer. Upright orien-

tation of man-made objects. In SIGGRAPH, 2008. 3

[5]

S. Gidaris, P. Singh, and N. Komodakis. Unsupervised rep-

resentation learning by predicting image rotations. In ICLR,

2018. 3

[6]

S. Ginosar, K. Rakelly, S. Sachs, B. Yin, and A. A. Efros. A

Century of Portraits: A visual historical record of american

high school yearbooks. In ICCV Workshops, December 2015.

[7]

R. Hartley. Cheirality invariants. In Proc. DARPA Image

Understanding Workshop, 1993. 3

[8] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning

for image recognition. In CVPR, pages 770–778, 2016. 3

[9]

Y. Hel-Or, S. Peleg, and H. Hel-Or. How to tell right from

left. In CVPR, 1988. 3

[10]

G. B. Huang, M. Ramesh, T. Berg, and E. Learned-Miller. La-

beled faces in the wild: A database for studying face recogni-

tion in unconstrained environments. Technical Report 07-49,

University of Massachusetts, Amherst, October 2007. 7

[11]

T. Karras, S. Laine, and T. Aila. A style-based genera-

tor architecture for generative adversarial networks. CoRR,

abs/1812.04948, 2018. 7

[12]

W. T. Kelvin. The molecular tactics of a crystal. J. Oxford

Univ. Jr. Sci. Club, 18:3–57, 1894. 1

[13]

A. Krizhevsky, I. Sutskever, and G. E. Hinton. ImageNet

classiﬁcation with deep convolutional neural networks. In

NeurIPS, 2012. 3

[14]

Y. Li, L. Liu, C. Shen, and A. van den Hengel. Mid-level

deep pattern mining. In CVPR, 2015. 7

[15]

Y. Liu, H. Hel-Or, C. S. Kaplan, and L. J. V. Gool. Computa-

tional symmetry in computer vision and computer graphics.

Foundations and Trends in Computer Graphics and Vision,

5(1-2):1–195, 2010. 3

[16]

Q. C. M. Lin and S. Yan. Network in network. In International

Conference on Learning Representations, pages 2921–2929,

2014. 3

[17]

K. Matzen, K. Bala, and N. Snavely. StreetStyle: Exploring

world-wide clothing styles from millions of photos. CoRR,

abs/1706.01869, 2017. 5

[18]

K. Matzen and N. Snavely. BubbLeNet: Foveated imaging

for visual discovery. In ICCV, 2015. 3, 7

[19]

M. Noroozi and P. Favaro. Unsupervised learning of visual

representations by solving jigsaw puzzles. In ECCV, 2016. 3

[20]

L. C. Pickup, Z. Pan, D. Wei, Y.-C. Shih, C. Zhang, A. Zisser-

man, B. Sch

olkopf, and W. T. Freeman. Seeing the arrow of

time. In CVPR, 2014. 2

[21]

S. Singh, A. Gupta, and A. A. Efros. Unsupervised discovery

of mid-level discriminative patches. In ECCV, 2012. 7

[22]

B. Thomee, D. A. Shamma, G. Friedland, B. Elizalde, K. Ni,

D. Poland, D. Borth, and L.-J. Li. Yfcc100m: The new data

in multimedia research. CACM, 59(2), Jan. 2016. 5

[23]

A. Vailaya, H. Zhang, C. Yang, F.-I. Liu, and A. K. Jain. Au-

tomatic image orientation detection. Trans. Image Processing,

11(7):746–55, 2002. 3

[24]

D. Wei, J. Y. S. Lim, A. Zisserman, and W. T. Freeman.

Learning and using the arrow of time. In CVPR, 2018. 2, 3

[25]

H. W. Y. W. S. Z. W. H. X. Zhou, C. Yao and J. Liang. East:

An efﬁcient and accurate scene text detector. In CVPR, 2017.

[26]

B. Zhou, A. Khosla, A. Lapedriza, A. Oliva, and A. Torralba.

Learning deep features for discriminative localization. In

Proceedings of the IEEE conference on computer vision and

pattern recognition, pages 2921–2929, 2016. 3