Contents
Preface 2
1 The Wave Function 3
2 Time-Independent Schrödinger Equation 14
3 Formalism 62
4 Quantum Mechanics in Three Dimensions 87
5 Identical Particles 132
6 Time-Independent Perturbation Theory 154
7 The Variational Principle 196
8 The WKB Approximation 219
9 Time-Dependent Perturbation Theory 236
10 The Adiabatic Approximation 254
11 Scattering 268
12 Afterword 282
Appendix Linear Algebra 283
2
nd
Edition – 1
st
Edition Problem Correlation Grid 299
2
Preface
These are my own solutions to the problems in Introduction to Quantum Mechanics, 2nd ed. I have made every
effort to insure that they are clear and correct, but errors are bound to occur, and for this I apologize in advance.
I would like to thank the many people who pointed out mistakes in the solution manual for the first edition,
and encourage anyone who finds defects in this one to alert me (griffi[email protected]). I’ll maintain a list of errata
on my web page (http://academic.reed.edu/physics/faculty/griffiths.html), and incorporate corrections in the
manual itself from time to time. I also thank my students at Reed and at Smith for many useful suggestions,
and above all Neelaksh Sadhoo, who did most of the typesetting.
At the end of the manual there is a grid that correlates the problem numbers in the second edition with
those in the first edition.
David Griffiths
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 1. THE WAVE FUNCTION 3
Chapter 1
The Wave Function
Problem 1.1
(a)
j
2
=21
2
= 441.
j
2
=
1
N
j
2
N(j)=
1
14
(14
2
) + (15
2
) + 3(16
2
) + 2(22
2
) + 2(24
2
) + 5(25
2
)
=
1
14
(196 + 225 + 768 + 968 + 1152 + 3125) =
6434
14
=
459.571.
(b)
j ∆j = j −j
14 14 − 21 = −7
15 15 − 21 = −6
16 16 − 21 = −5
22 22 − 21 = 1
24 24 − 21 = 3
25 25 − 21 = 4
σ
2
=
1
N
(∆j)
2
N(j)=
1
14
(−7)
2
+(−6)
2
+(−5)
2
· 3 + (1)
2
· 2 + (3)
2
· 2 + (4)
2
· 5
=
1
14
(49+36+75+2+18+80)=
260
14
=
18.571.
σ =
√
18.571 = 4.309.
(c)
j
2
−j
2
= 459.571 − 441=18.571. [Agrees with (b).]
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

4 CHAPTER 1. THE WAVE FUNCTION
Problem 1.2
(a)
x
2
=
h
0
x
2
1
2
√
hx
dx =
1
2
√
h
2
5
x
5/2
h
0
=
h
2
5
.
σ
2
= x
2
−x
2
=
h
2
5
−
h
3
2
=
4
45
h
2
⇒ σ =
2h
3
√
5
=0.2981h.
(b)
P =1−
x
+
x
−
1
2
√
hx
dx =1−
1
2
√
h
(2
√
x)
x
+
x
−
=1−
1
√
h
√
x
+
−
√
x
−
.
x
+
≡x + σ =0.3333h +0.2981h =0.6315h; x
−
≡x−σ =0.3333h − 0.2981h =0.0352h.
P =1−
√
0.6315 +
√
0.0352 = 0.393.
Problem 1.3
(a)
1=
∞
−∞
Ae
−λ(x−a)
2
dx. Let u ≡ x − a, du = dx, u : −∞ → ∞.
1=A
∞
−∞
e
−λu
2
du = A
π
λ
⇒
A =
λ
π
.
(b)
x = A
∞
−∞
xe
−λ(x−a)
2
dx = A
∞
−∞
(u + a)e
−λu
2
du
= A
∞
−∞
ue
−λu
2
du + a
∞
−∞
e
−λu
2
du
= A
0+a
π
λ
=
a.
x
2
= A
∞
−∞
x
2
e
−λ(x−a)
2
dx
= A
∞
−∞
u
2
e
−λu
2
du +2a
∞
−∞
ue
−λu
2
du + a
2
∞
−∞
e
−λu
2
du
= A
1
2λ
π
λ
+0+a
2
π
λ
=
a
2
+
1
2λ
.
σ
2
= x
2
−x
2
= a
2
+
1
2λ
− a
2
=
1
2λ
;
σ =
1
√
2λ
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 1. THE WAVE FUNCTION 5
(c)
A
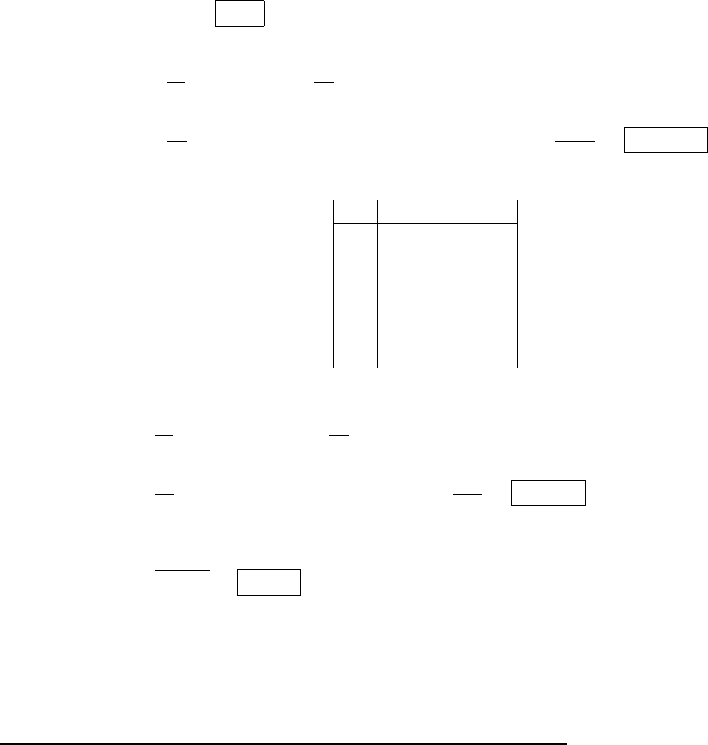
x
a
ρ(x)
Problem 1.4
(a)
1=
|A|
2
a
2
a
0
x
2
dx +
|A|
2
(b − a)
2
b
a
(b − x)
2
dx = |A|
2
1
a
2
x
3
3
a
0
+
1
(b − a)
2
−
(b − x)
3
3
b
a
= |A|
2
a
3
+
b − a
3
= |A|
2
b
3
⇒
A =
3
b
.
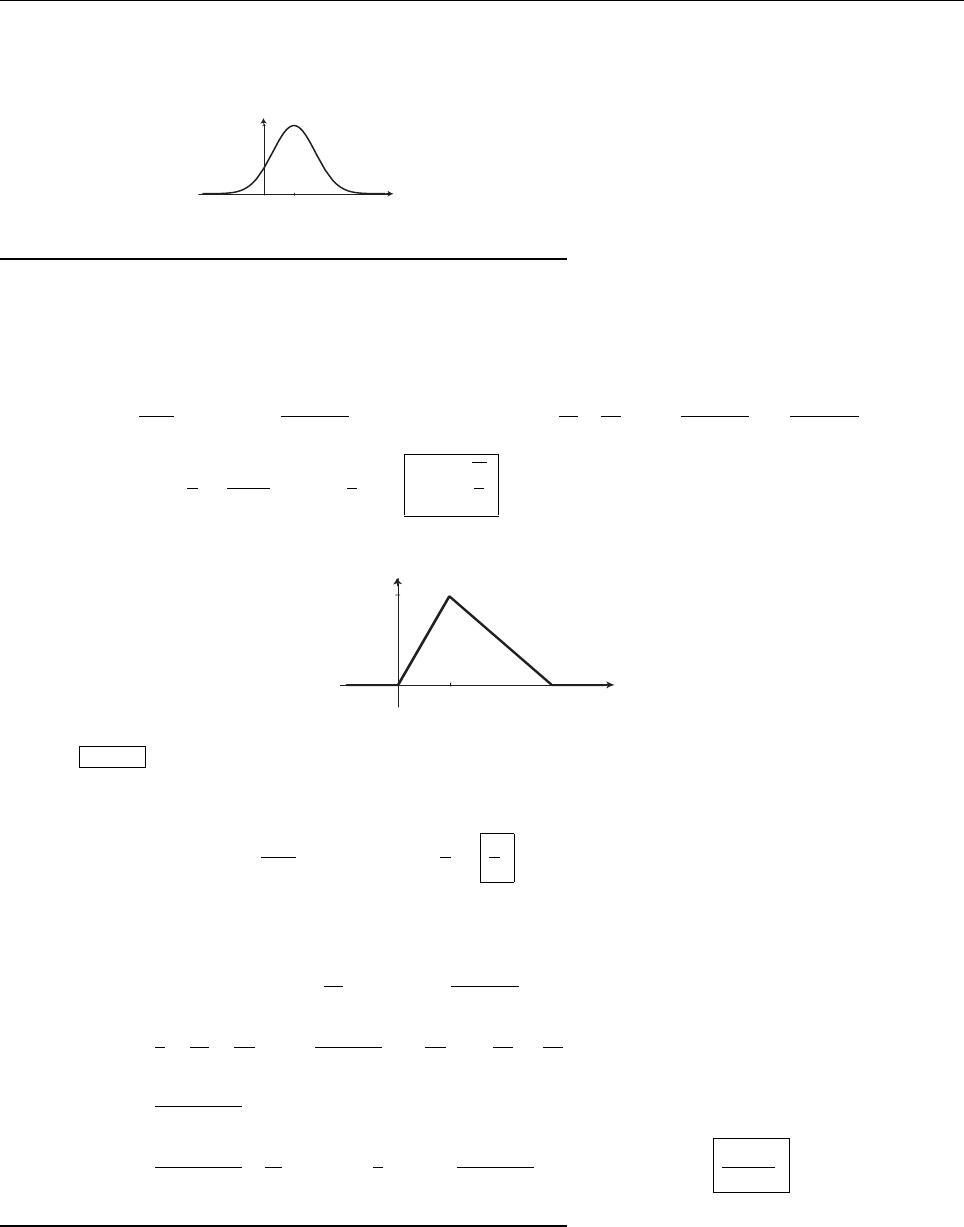
(b)
x
a
A
b
Ψ
(c) At x = a.
(d)
P =
a
0
|Ψ|
2
dx =
|A|
2
a
2
a
0
x
2
dx = |A|
2
a
3
=
a
b
.
P =1 if b = a,
P =1/2if b =2a.
(e)
x =
x|Ψ|
2
dx = |A|
2
1
a
2
a
0
x
3
dx +
1
(b − a)
2
b
a
x(b − x)
2
dx
=
3
b
1
a
2
x
4
4
a
0
+
1
(b − a)
2
b
2
x
2
2
− 2b
x
3
3
+
x
4
4
b
a
=
3
4b(b − a)
2
a
2
(b − a)
2
+2b
4
− 8b
4
/3+b
4
− 2a
2
b
2
+8a
3
b/3 − a
4
=
3
4b(b − a)
2
b
4
3
− a
2
b
2
+
2
3
a
3
b
=
1
4(b − a)
2
(b
3
− 3a
2
b +2a
3
)=
2a + b
4
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
6 CHAPTER 1. THE WAVE FUNCTION
Problem 1.5
(a)
1=
|Ψ|
2
dx =2|A|
2
∞
0
e
−2λx
dx =2|A|
2
e
−2λx
−2λ
∞
0
=
|A|
2
λ
;
A =
√
λ.
(b)
x =
x|Ψ|
2
dx = |A|
2
∞
−∞
xe
−2λ|x|
dx = 0. [Odd integrand.]
x
2
=2|A|
2
∞
0
x
2
e
−2λx
dx =2λ
2
(2λ)
3
=
1
2λ
2
.
(c)
σ
2
= x
2
−x
2
=
1
2λ
2
; σ =
1
√
2λ
.
|Ψ(±σ)|
2
= |A|
2
e
−2λσ
= λe
−2λ/
√
2λ
= λe
−
√
2
=0.2431λ.
|Ψ|
2
λ
σ−σ
+
x
.24λ
Probability outside:
2
∞
σ
|Ψ|
2
dx =2|A|
2
∞
σ
e
−2λx
dx =2λ
e
−2λx
−2λ
∞
σ
= e
−2λσ
= e
−
√
2
=0.2431.
Problem 1.6
For integration by parts, the differentiation has to be with respect to the integration variable – in this case the
differentiation is with respect to t, but the integration variable is x. It’s true that
∂
∂t
(x|Ψ|
2
)=
∂x
∂t
|Ψ|
2
+ x
∂
∂t
|Ψ|
2
= x
∂
∂t
|Ψ|
2
,
but this does not allow us to perform the integration:
b
a
x
∂
∂t
|Ψ|
2
dx =
b
a
∂
∂t
(x|Ψ|
2
)dx =(x|Ψ|
2
)
b
a
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 1. THE WAVE FUNCTION 7
Problem 1.7
From Eq. 1.33,
dp
dt
= −i
∂
∂t
Ψ
∗
∂Ψ
∂x
dx. But, noting that
∂
2
Ψ
∂x∂t
=
∂
2
Ψ
∂t∂x
and using Eqs. 1.23-1.24:
∂
∂t
Ψ
∗
∂Ψ
∂x
=
∂Ψ
∗
∂t
∂Ψ
∂x
+Ψ
∗
∂
∂x
∂Ψ
∂t
=
−
i
2m
∂
2
Ψ
∗
∂x
2
+
i
V Ψ
∗
∂Ψ
∂x
+Ψ
∗
∂
∂x
i
2m
∂
2
Ψ
∂x
2
−
i
V Ψ
=
i
2m
Ψ
∗
∂
3
Ψ
∂x
3
−
∂
2
Ψ
∗
∂x
2
∂Ψ
∂x
+
i
V Ψ
∗
∂Ψ
∂x
− Ψ
∗
∂
∂x
(V Ψ)
The first term integrates to zero, using integration by parts twice, and the second term can be simplified to
V Ψ
∗
∂Ψ
∂x
− Ψ
∗
V
∂Ψ
∂x
− Ψ
∗
∂V
∂x
Ψ=−|Ψ|
2
∂V
∂x
. So
dp
dt
= −i
i
−|Ψ|
2
∂V
∂x
dx = −
∂V
∂x
. QED
Problem 1.8
Suppose Ψ satisfies the Schr¨odinger equation without V
0
: i
∂Ψ
∂t
= −
2
2m
∂
2
Ψ
∂x
2
+ V Ψ. We want to find the solution
Ψ
0
with V
0
: i
∂Ψ
0
∂t
= −
2
2m
∂
2
Ψ
0
∂x
2
+(V + V
0
)Ψ
0
.
Claim:Ψ
0
=Ψe
−iV
0
t/
.
Proof: i
∂Ψ
0
∂t
= i
∂Ψ
∂t
e
−iV
0
t/
+ iΨ
−
iV
0
e
−iV
0
t/
=
−
2
2m
∂
2
Ψ
∂x
2
+ V Ψ
e
−iV
0
t/
+ V
0
Ψe
−iV
0
t/
= −
2
2m
∂
2
Ψ
0
∂x
2
+(V + V
0
)Ψ
0
. QED
This has no effect on the expectation value of a dynamical variable, since the extra phase factor, being inde-
pendent of x, cancels out in Eq. 1.36.
Problem 1.9
(a)
1=2|A|
2
∞
0
e
−2amx
2
/
dx =2|A|
2
1
2
π
(2am/)
= |A|
2
π
2am
;
A =
2am
π
1/4
.
(b)
∂Ψ
∂t
= −iaΨ;
∂Ψ
∂x
= −
2amx
Ψ;
∂
2
Ψ
∂x
2
= −
2am
Ψ+x
∂Ψ
∂x
= −
2am
1 −
2amx
2
Ψ.
Plug these into the Schr¨odinger equation, i
∂Ψ
∂t
= −
2
2m
∂
2
Ψ
∂x
2
+ V Ψ:
V Ψ=i(−ia)Ψ +
2
2m
−
2am
1 −
2amx
2
Ψ
=
a − a
1 −
2amx
2
Ψ=2a
2
mx
2
Ψ, so V (x)=2ma
2
x
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

8 CHAPTER 1. THE WAVE FUNCTION
(c)
x =
∞
−∞
x|Ψ|
2
dx = 0. [Odd integrand.]
x
2
=2|A|
2
∞
0
x
2
e
−2amx
2
/
dx =2|A|
2
1
2
2
(2am/)
π
2am
=
4am
.
p = m
dx
dt
=
0.
p
2
=
Ψ
∗
i
∂
∂x
2
Ψdx = −
2
Ψ
∗
∂
2
Ψ
∂x
2
dx
= −
2
Ψ
∗
−
2am
1 −
2amx
2
Ψ
dx =2am
|Ψ|
2
dx −
2am
x
2
|Ψ|
2
dx
=2am
1 −
2am
x
2
=2am
1 −
2am
4am
=2am
1
2
=
am.
(d)
σ
2
x
= x
2
−x
2
=
4am
=⇒
σ
x
=
4am
; σ
2
p
= p
2
−p
2
= am =⇒ σ
p
=
√
am.
σ
x
σ
p
=
4am
√
am =
2
. This is (just barely) consistent with the uncertainty principle.
Problem 1.10
From Math Tables: π =3.141592653589793238462643 ···
(a)
P (0) = 0 P (1) = 2/25 P (2) = 3/25 P (3) = 5/25 P (4) = 3/25
P (5) = 3/25 P (6) = 3/25 P (7) = 1/25 P (8) = 2/25 P (9) = 3/25
In general, P (j)=
N(j)
N
.
(b) Most probable:
3. Median: 13 are ≤ 4, 12 are ≥ 5, so median is 4.
Average: j =
1
25
[0 · 0+1· 2+2· 3+3· 5+4· 3+5· 3+6· 3+7· 1+8· 2+9· 3]
=
1
25
[0+2+6+15+12+15+18+7+16+27]=
118
25
= 4.72.
(c) j
2
=
1
25
[0+1
2
· 2+2
2
· 3+3
2
· 5+4
2
· 3+5
2
· 3+6
2
· 3+7
2
· 1+8
2
· 2+9
2
· 3]
=
1
25
[0+2+12+45+48+75+108+49+128+243] =
710
25
= 28.4.
σ
2
= j
2
−j
2
=28.4 − 4.72
2
=28.4 − 22.2784 = 6.1216; σ =
√
6.1216 = 2.474.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 1. THE WAVE FUNCTION 9
Problem 1.11
(a) Constant for 0 ≤ θ ≤ π, otherwise zero. In view of Eq. 1.16, the constant is 1/π.
ρ(θ)=
1/π, if 0 ≤ θ ≤ π,
0, otherwise.
1/π
−π/2
0
π
3π/2
ρ(θ)
θ
(b)
θ =
θρ(θ) dθ =
1
π
π
0
θdθ =
1
π
θ
2
2
π
0
=
π
2
[of course].
θ
2
=
1
π
π
0
θ
2
dθ =
1
π
θ
3
3
π
0
=
π
2
3
.
σ
2
= θ
2
−θ
2
=
π
2
3
−
π
2
4
=
π
2
12
;
σ =
π
2
√
3
.
(c)
sin θ =
1
π
π
0
sin θdθ=
1
π
(−cos θ)|
π
0
=
1
π
(1 − (−1)) =
2
π
.
cos θ =
1
π
π
0
cos θdθ=
1
π
(sin θ)|
π
0
= 0.
cos
2
θ =
1
π
π
0
cos
2
θdθ=
1
π
π
0
(1/2)dθ =
1
2
.
[Because sin
2
θ + cos
2
θ = 1, and the integrals of sin
2
and cos
2
are equal (over suitable intervals), one can
replace them by 1/2 in such cases.]
Problem 1.12
(a) x = r cos θ ⇒ dx = −r sin θdθ. The probability that the needle lies in range dθ is ρ(θ)dθ =
1
π
dθ, so the
probability that it’s in the range dx is
ρ(x)dx =
1
π
dx
r sin θ
=
1
π
dx
r
1 − (x/r)
2
=
dx
π
√
r
2
− x
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

10 CHAPTER 1. THE WAVE FUNCTION
ρ(x)
x
r
2r
-r
-2r
∴ ρ(x)=
1
π
√
r
2
−x
2
, if − r<x<r,
0, otherwise.
[Note: We want the magnitude of dx here.]
Total:
r
−r
1
π
√
r
2
−x
2
dx =
2
π
r
0
1
√
r
2
−x
2
dx =
2
π
sin
−1
x
r
r
0
=
2
π
sin
−1
(1) =
2
π
·
π
2
=1.
(b)
x =
1
π
r
−r
x
1
√
r
2
− x
2
dx = 0 [odd integrand, even interval].
x
2
=
2
π
r
0
x
2
√
r
2
− x
2
dx =
2
π
−
x
2
r
2
− x
2
+
r
2
2
sin
−1
x
r
r
0
=
2
π
r
2
2
sin
−1
(1) =
r
2
2
.
σ
2
= x
2
−x
2
= r
2
/2=⇒ σ = r/
√
2.
To get x and x
2
from Problem 1.11(c), use x = r cos θ,sox = rcos θ =0, x
2
= r
2
cos
2
θ = r
2
/2.
Problem 1.13
Suppose the eye end lands a distance y up from a line (0 ≤ y<l), and let x be the projection along that same
direction (−l ≤ x<l). The needle crosses the line above if y + x ≥ l (i.e. x ≥ l − y), and it crosses the line
below if y + x<0 (i.e. x<−y). So for a given value of y, the probability of crossing (using Problem 1.12) is
P (y)=
−y
−l
ρ(x)dx +
l
l−y
ρ(x)dx =
1
π
−y
−l
1
√
l
2
− x
2
dx +
l
l−y
1
√
l
2
− x
2
dx
=
1
π
sin
−1
x
l
−y
−l
+ sin
−1
x
l
l
l−y
=
1
π
−sin
−1
(y/l)+2sin
−1
(1) − sin
−1
(1 − y/l)
=1−
sin
−1
(y/l)
π
−
sin
−1
(1 − y/l)
π
.
Now, all values of y are equally likely, so ρ(y)=1/l, and hence the probability of crossing is
P =
1
πl
l
0
π − sin
−1
y
l
− sin
−1
l − y
l
dy =
1
πl
l
0
π − 2 sin
−1
(y/l)
dy
=
1
πl
πl −2
y sin
−1
(y/l)+l
1 − (y/l)
2
l
0
=1−
2
πl
[l sin
−1
(1) − l]=1−1+
2
π
=
2
π
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 1. THE WAVE FUNCTION 11
Problem 1.14
(a) P
ab
(t)=
b
a
|Ψ(x, t)
2
dx, so
dP
ab
dt
=
b
a
∂
∂t
|Ψ|
2
dx. But (Eq. 1.25):
∂|Ψ|
2
∂t
=
∂
∂x
i
2m
Ψ
∗
∂Ψ
∂x
−
∂Ψ
∗
∂x
Ψ
= −
∂
∂t
J(x, t).
∴
dP
ab
dt
= −
b
a
∂
∂x
J(x, t)dx = − [J(x, t)]|
b
a
= J(a, t) −J(b, t). QED
Probability is dimensionless, so J has the dimensions 1/time, and units
seconds
−1
.
(b) Here Ψ(x, t)=f(x)e
−iat
, where f (x) ≡ Ae
−amx
2
/
,soΨ
∂Ψ
∗
∂x
= fe
−iat
df
dx
e
iat
= f
df
dx
,
and Ψ
∗
∂Ψ
∂x
= f
df
dx
too, so J(x, t)=0.
Problem 1.15
(a) Eq. 1.24 now reads
∂Ψ
∗
∂t
= −
i
2m
∂
2
Ψ
∗
∂x
2
+
i
V
∗
Ψ
∗
, and Eq. 1.25 picks up an extra term:
∂
∂t
|Ψ|
2
= ···+
i
|Ψ|
2
(V
∗
− V )=···+
i
|Ψ|
2
(V
0
+ iΓ − V
0
+ iΓ) = ···−
2Γ
|Ψ|
2
,
and Eq. 1.27 becomes
dP
dt
= −
2Γ
∞
−∞
|Ψ|
2
dx = −
2Γ
P . QED
(b)
dP
P
= −
2Γ
dt =⇒ ln P = −
2Γ
t + constant =⇒
P (t)=P (0)e
−2Γt/
, so τ =
2Γ
.
Problem 1.16
Use Eqs. [1.23] and [1.24], and integration by parts:
d
dt
∞
−∞
Ψ
∗
1
Ψ
2
dx =
∞
−∞
∂
∂t
(Ψ
∗
1
Ψ
2
) dx =
∞
−∞
∂Ψ
∗
1
∂t
Ψ
2
+Ψ
∗
1
∂Ψ
2
∂t
dx
=
∞
−∞
−i
2m
∂
2
Ψ
∗
1
∂x
2
+
i
V Ψ
∗
1
Ψ
2
+Ψ
∗
1
i
2m
∂
2
Ψ
2
∂x
2
−
i
V Ψ
2
dx
= −
i
2m
∞
−∞
∂
2
Ψ
∗
1
∂x
2
Ψ
2
− Ψ
∗
1
∂
2
Ψ
2
∂x
2
dx
= −
i
2m
∂Ψ
∗
1
∂x
Ψ
2
∞
−∞
−
∞
−∞
∂Ψ
∗
1
∂x
∂Ψ
2
∂x
dx − Ψ
∗
1
∂Ψ
2
∂x
∞
−∞
+
∞
−∞
∂Ψ
∗
1
∂x
∂Ψ
2
∂x
dx
=0. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

12 CHAPTER 1. THE WAVE FUNCTION
Problem 1.17
(a)
1=|A|
2
a
−a
a
2
− x
2
2
dx =2|A|
2
a
0
a
4
− 2a
2
x
2
+ x
4
dx =2|A|
2
a
4
x − 2a
2
x
3
3
+
x
5
5
a
0
=2|A|
2
a
5
1 −
2
3
+
1
5
=
16
15
a
5
|A|
2
, so A =
15
16a
5
.
(b)
x =
a
−a
x|Ψ|
2
dx = 0. (Odd integrand.)
(c)
p =
i
A
2
a
−a
a
2
− x
2
d
dx
a
2
− x
2
−2x
dx = 0. (Odd integrand.)
Since we only know x at t = 0 we cannot calculate dx/dt directly.
(d)
x
2
= A
2
a
−a
x
2
a
2
− x
2
2
dx =2A
2
a
0
a
4
x
2
− 2a
2
x
4
+ x
6
dx
=2
15
16a
5
a
4
x
3
3
− 2a
2
x
5
5
+
x
7
7
a
0
=
15
8a
5
a
7
1
3
−
2
5
+
1
7
=
✚
✚
15a
2
8
35 − 42+15
✁
3 ·
✁
5 · 7
=
a
2
8
·
8
7
=
a
2
7
.
(e)
p
2
= −A
2
2
a
−a
a
2
− x
2
d
2
dx
2
a
2
− x
2
−2
dx =2A
2
2
2
a
0
a
2
− x
2
dx
=4·
15
16a
5
2
a
2
x −
x
3
3
a
0
=
15
2
4a
5
a
3
−
a
3
3
=
15
2
4a
2
·
2
3
=
5
2
2
a
2
.
(f)
σ
x
=
x
2
−x
2
=
1
7
a
2
=
a
√
7
.
(g)
σ
p
=
p
2
−p
2
=
5
2
2
a
2
=
5
2
a
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 1. THE WAVE FUNCTION 13
(h)
σ
x
σ
p
=
a
√
7
·
5
2
a
=
5
14
=
10
7
2
>
2
.
Problem 1.18
h
√
3mk
B
T
>d ⇒ T<
h
2
3mk
B
d
2
.
(a) Electrons (m =9.1 ×10
−31
kg):
T<
(6.6 × 10
−34
)
2
3(9.1 × 10
−31
)(1.4 × 10
−23
)(3 × 10
−10
)
2
= 1.3 × 10
5
K.
Sodium nuclei (m =23m
p
= 23(1.7 × 10
−27
)=3.9 × 10
−26
kg):
T<
(6.6 × 10
−34
)
2
3(3.9 × 10
−26
)(1.4 × 10
−23
)(3 × 10
−10
)
2
= 3.0K.
(b) PV = Nk
B
T ; volume occupied by one molecule (N =1,V= d
3
) ⇒ d =(k
B
T/P)
1/3
.
T<
h
2
2mk
B
P
k
B
T
2/3
⇒ T
5/3
<
h
2
3m
P
2/3
k
5/3
B
⇒ T<
1
k
B
h
2
3m
3/5
P
2/5
.
For helium (m =4m
p
=6.8 × 10
−27
kg) at 1 atm = 1.0 × 10
5
N/m
2
:
T<
1
(1.4 × 10
−23
)
(6.6 × 10
−34
)
2
3(6.8 × 10
−27
)
3/5
(1.0 × 10
5
)
2/5
= 2.8 K.
For hydrogen (m =2m
p
=3.4 × 10
−27
kg) with d =0.01 m:
T<
(6.6 × 10
−34
)
2
3(3.4 × 10
−27
)(1.4 × 10
−23
)(10
−2
)
2
= 3.1 × 10
−14
K.
At 3 K it is definitely in the classical regime.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

14 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Chapter 2
Time-IndependentSchr¨odinger
Equation
Problem 2.1
(a)
Ψ(x, t)=ψ(x)e
−i(E
0
+iΓ)t/
= ψ(x)e
Γt/
e
−iE
0
t/
=⇒|Ψ|
2
= |ψ|
2
e
2Γt/
.
∞
−∞
|Ψ(x, t)|
2
dx = e
2Γt/
∞
−∞
|ψ|
2
dx.
The second term is independent of t, so if the product is to be 1 for all time, the first term (e
2Γt/
) must
also be constant, and hence Γ = 0. QED
(b) If ψ satisfies Eq. 2.5, −
2
2m
∂
2
ψ
dx
2
+ Vψ = Eψ, then (taking the complex conjugate and noting that V and
E are real): −
2
2m
∂
2
ψ
∗
dx
2
+ Vψ
∗
= Eψ
∗
,soψ
∗
also satisfies Eq. 2.5. Now, if ψ
1
and ψ
2
satisfy Eq. 2.5, so
too does any linear combination of them (ψ
3
≡ c
1
ψ
1
+ c
2
ψ
2
):
−
2
2m
∂
2
ψ
3
dx
2
+ Vψ
3
= −
2
2m
c
1
∂
2
ψ
1
dx
2
+ c
2
∂
2
ψ
2
∂x
2
+ V (c
1
ψ
1
+ c
2
ψ
2
)
= c
1
−
2
2m
d
2
ψ
1
dx
2
+ Vψ
1
+ c
2
−
2
2m
d
2
ψ
2
dx
2
+ Vψ
2
= c
1
(Eψ
1
)+c
2
(Eψ
2
)=E(c
1
ψ
1
+ c
2
ψ
2
)=Eψ
3
.
Thus, (ψ + ψ
∗
) and i(ψ − ψ
∗
) – both of which are real – satisfy Eq. 2.5. Conclusion: From any complex
solution, we can always construct two real solutions (of course, if ψ is already real, the second one will be
zero). In particular, since ψ =
1
2
[(ψ + ψ
∗
) − i(i(ψ − ψ
∗
))],ψ can be expressed as a linear combination of
two real solutions. QED
(c) If ψ(x) satisfies Eq. 2.5, then, changing variables x →−x and noting that ∂
2
/∂(−x)
2
= ∂
2
/∂x
2
,
−
2
2m
∂
2
ψ(−x)
dx
2
+ V (−x)ψ(−x)=Eψ(−x);
so if V (−x)=V (x) then ψ(−x) also satisfies Eq. 2.5. It follows that ψ
+
(x) ≡ ψ(x)+ψ(−x) (which is
even: ψ
+
(−x)=ψ
+
(x)) and ψ
−
(x) ≡ ψ(x) − ψ(−x) (which is odd: ψ
−
(−x)=−ψ
−
(x)) both satisfy Eq.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 15
2.5. But ψ(x)=
1
2
(ψ
+
(x)+ψ
−
(x)), so any solution can be expressed as a linear combination of even and
odd solutions. QED
Problem 2.2
Given
d
2
ψ
dx
2
=
2m
2
[V (x) −E]ψ,ifE<V
min
, then ψ
and ψ always have the same sign: If ψ is positive(negative),
then ψ
is also positive(negative). This means that ψ always curves away from the axis (see Figure). However,
it has got to go to zero as x →−∞(else it would not be normalizable). At some point it’s got to depart from
zero (if it doesn’t, it’s going to be identically zero everywhere), in (say) the positive direction. At this point its
slope is positive, and increasing,soψ gets bigger and bigger as x increases. It can’t ever “turn over” and head
back toward the axis, because that would requuire a negative second derivative—it always has to bend away
from the axis. By the same token, if it starts out heading negative, it just runs more and more negative. In
neither case is there any way for it to come back to zero, as it must (at x →∞) in order to be normalizable.
QED
x
ψ
Problem 2.3
Equation 2.20 says
d
2
ψ
dx
2
= −
2mE
2
ψ; Eq. 2.23 says ψ(0) = ψ(a) = 0. If E =0,d
2
ψ/dx
2
=0,soψ(x)=A + Bx;
ψ(0) = A =0⇒ ψ = Bx; ψ(a)=Ba =0⇒ B =0,soψ =0. IfE<0, d
2
ψ/dx
2
= κ
2
ψ, with κ ≡
√
−2mE/
real, so ψ(x)=Ae
κx
+ Be
−κx
. This time ψ(0) = A + B =0⇒ B = −A,soψ = A(e
κx
− e
−κx
), while
ψ(a)=A
e
κa
− e
iκa
=0⇒ either A =0,soψ = 0, or else e
κa
= e
−κa
,soe
2κa
=1,so2κa = ln(1) = 0,
so κ = 0, and again ψ = 0. In all cases, then, the boundary conditions force ψ = 0, which is unacceptable
(non-normalizable).
Problem 2.4
x =
x|ψ|
2
dx =
2
a
a
0
x sin
2
nπ
a
x
dx. Let y ≡
nπ
a
x, so dx =
a
nπ
dy; y :0→ nπ.
=
2
a
a
nπ
2
nπ
0
y sin
2
ydy=
2a
n
2
π
2
y
2
4
−
y sin 2y
4
−
cos 2y
8
nπ
0
=
2a
n
2
π
2
n
2
π
2
4
−
cos 2nπ
8
+
1
8
=
a
2
.
(Independent of n.)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

16 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
x
2
=
2
a
a
0
x
2
sin
2
nπ
a
x
dx =
2
a
a
nπ
3
nπ
0
y
2
sin
2
ydy
=
2a
2
(nπ)
3
y
3
6
−
y
3
4
−
1
8
sin 2y −
y cos 2y
4
nπ
0
=
2a
2
(nπ)
3
(nπ)
3
6
−
nπ cos(2nπ)
4
=
a
2
1
3
−
1
2(nπ)
2
.
p = m
dx
dt
=
0. (Note :Eq. 1.33 is much faster than Eq. 1.35.)
p
2
=
ψ
∗
n
i
d
dx
2
ψ
n
dx = −
2
ψ
∗
n
d
2
ψ
n
dx
2
dx
=(−
2
)
−
2mE
n
2
ψ
∗
n
ψ
n
dx =2mE
n
=
nπ
a
2
.
σ
2
x
= x
2
−x
2
= a
2
1
3
−
1
2(nπ)
2
−
1
4
=
a
2
4
1
3
−
2
(nπ)
2
;
σ
x
=
a
2
1
3
−
2
(nπ)
2
.
σ
2
p
= p
2
−p
2
=
nπ
a
2
; σ
p
=
nπ
a
.
∴ σ
x
σ
p
=
2
(nπ)
2
3
− 2.
The product σ
x
σ
p
is smallest for n =1; in that case, σ
x
σ
p
=
2
π
2
3
− 2=(1.136)/2 > /2.
Problem 2.5
(a)
|Ψ|
2
=Ψ
2
Ψ=|A|
2
(ψ
∗
1
+ ψ
∗
2
)(ψ
1
+ ψ
2
)=|A|
2
[ψ
∗
1
ψ
1
+ ψ
∗
1
ψ
2
+ ψ
∗
2
ψ
1
+ ψ
∗
2
ψ
2
].
1=
|Ψ|
2
dx = |A|
2
[|ψ
1
|
2
+ ψ
∗
1
ψ
2
+ ψ
∗
2
ψ
1
+ |ψ
2
|
2
]dx =2|A|
2
⇒ A =1/
√
2.
(b)
Ψ(x, t)=
1
√
2
ψ
1
e
−iE
1
t/
+ ψ
2
e
−iE
2
t/
(but
E
n
= n
2
ω)
=
1
√
2
2
a
sin
π
a
x
e
−iωt
+ sin
2π
a
x
e
−i4ωt
=
1
√
a
e
−iωt
sin
π
a
x
+ sin
2π
a
x
e
−3iωt
.
|Ψ(x, t)|
2
=
1
a
sin
2
π
a
x
+ sin
π
a
x
sin
2π
a
x
e
−3iωt
+ e
3iωt
+ sin
2
2π
a
x
=
1
a
sin
2
π
a
x
+ sin
2
2π
a
x
+ 2 sin
π
a
x
sin
2π
a
x
cos(3ωt)
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 17
(c)
x =
x|Ψ(x, t)|
2
dx
=
1
a
a
0
x
sin
2
π
a
x
+ sin
2
2π
a
x
+ 2 sin
π
a
x
sin
2π
a
x
cos(3ωt)
dx
a
0
x sin
2
π
a
x
dx =
x
2
4
−
x sin
2π
a
x
4π/a
−
cos
2π
a
x
8(π/a)
2
a
0
=
a
2
4
=
a
0
x sin
2
2π
a
x
dx.
a
0
x sin
π
a
x
sin
2π
a
x
dx =
1
2
a
0
x
cos
π
a
x
− cos
3π
a
x
dx
=
1
2
a
2
π
2
cos
π
a
x
+
ax
π
sin
π
a
x
−
a
2
9π
2
cos
3π
a
x
−
ax
3π
sin
3π
a
x
a
0
=
1
2
a
2
π
2
cos(π) −cos(0)
−
a
2
9π
2
cos(3π) −cos(0)
= −
a
2
π
2
1 −
1
9
= −
8a
2
9π
2
.
∴ x =
1
a
a
2
4
+
a
2
4
−
16a
2
9π
2
cos(3ωt)
=
a
2
1 −
32
9π
2
cos(3ωt)
.
Amplitude:
32
9π
2
a
2
=0.3603(a/2);
angular frequency: 3ω =
3π
2
2ma
2
.
(d)
p = m
dx
dt
= m
a
2
−
32
9π
2
(−3ω) sin(3ωt)=
8
3a
sin(3ωt).
(e) You could get either E
1
= π
2
2
/2ma
2
or E
2
=2π
2
2
/ma
2
, with equal probability P
1
= P
2
=1/2.
So H =
1
2
(E
1
+ E
2
)=
5π
2
2
4ma
2
; it’s the average of E
1
and E
2
.
Problem 2.6
From Problem 2.5, we see that
Ψ(x, t)=
1
√
a
e
−iωt
sin
π
a
x
+ sin
2π
a
x
e
−3iωt
e
iφ
;
|Ψ(x, t)|
2
=
1
a
sin
2
π
a
x
+ sin
2
2π
a
x
+ 2 sin
π
a
x
sin
2π
a
x
cos(3ωt − φ)
;
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
18 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
and hence x =
a
2
1 −
32
9π
2
cos(3ωt − φ)
. This amounts physically to starting the clock at a different time
(i.e., shifting the t = 0 point).
If φ =
π
2
, so Ψ(x, 0) = A[ψ
1
(x)+iψ
2
(x)], then cos(3ωt −φ) = sin(3ωt); x starts at
a
2
.
If φ = π, so Ψ(x, 0) = A[ψ
1
(x) − ψ
2
(x)], then cos(3ωt −φ)=−cos(3ωt); x starts at
a
2
1+
32
9π
2
.
Problem 2.7
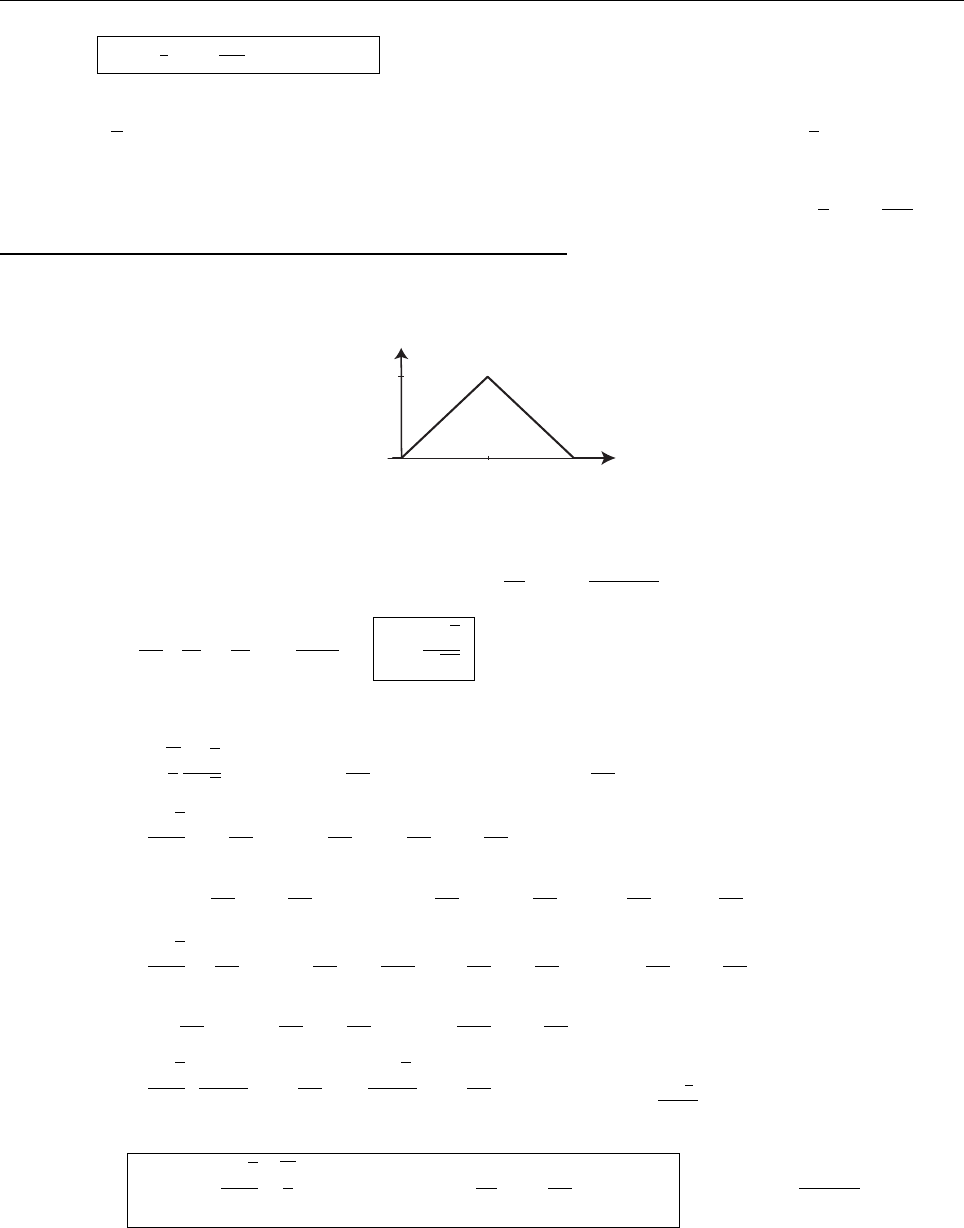
Ψ(x,0)
x
a
a
/2
Aa/2
(a)
1=A
2
a/2
0
x
2
dx + A
2
a
a/2
(a − x)
2
dx = A
2
x
3
3
a/2
0
−
(a − x)
3
3
a
a/2
=
A
2
3
a
3
8
+
a
3
8
=
A
2
a
3
12
⇒
A =
2
√
3
√
a
3
.
(b)
c
n
=
2
a
2
√
3
a
√
a
a/2
0
x sin
nπ
a
x
dx +
a
a/2
(a − x) sin
nπ
a
x
dx
=
2
√
6
a
2
a
nπ
2
sin
nπ
a
x
−
xa
nπ
cos
nπ
a
x
a/2
0
+ a
−
a
nπ
cos
nπ
a
x
a
a/2
−
a
nπ
2
sin
nπ
a
x
−
ax
nπ
cos
nπ
a
x
a
a/2
=
2
√
6
a
2
a
nπ
2
sin
nπ
2
−
✘
✘
✘
✘
✘
✘
✘
a
2
2nπ
cos
nπ
2
−
✟
✟
✟
✟
✟
a
2
nπ
cos nπ +
✟
✟
✟
✟
✟
✟
✟
a
2
nπ
cos
nπ
2
+
a
nπ
2
sin
nπ
2
+
✟
✟
✟
✟
✟
a
2
nπ
cos nπ −
✘
✘
✘
✘
✘
✘
✘
a
2
2nπ
cos
nπ
2
=
2
√
6
a
2
2
a
2
(nπ)
2
sin
nπ
2
=
4
√
6
(nπ)
2
sin
nπ
2
=
0,neven,
(−1)
(n−1)/2
4
√
6
(nπ)
2
,nodd.
So
Ψ(x, t)=
4
√
6
π
2
2
a
n=1,3,5,...
(−1)
(n−1)/2
1
n
2
sin
nπ
a
x
e
−E
n
t/
, where E
n
=
n
2
π
2
2
2ma
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 19
(c)
P
1
= |c
1
|
2
=
16 · 6
π
4
= 0.9855.
(d)
H =
|c
n
|
2
E
n
=
96
π
4
π
2
2
2ma
2
1
1
+
1
3
2
+
1
5
2
+
1
7
2
+ ···
π
2
/8
=
48
2
π
2
ma
2
π
2
8
=
6
2
ma
2
.
Problem 2.8
(a)
Ψ(x, 0) =
A, 0 <x<a/2;
0, otherwise.
1=A
2
a/2
0
dx = A
2
(a/2) ⇒ A =
2
a
.
(b) From Eq. 2.37,
c
1
= A
2
a
a/2
0
sin
π
a
x
dx =
2
a
−
a
π
cos
π
a
x
a/2
0
= −
2
π
cos
π
2
− cos 0
=
2
π
.
P
1
= |c
1
|
2
= (2/π)
2
=0.4053.
Problem 2.9
ˆ
HΨ(x, 0) = −
2
2m
∂
2
∂x
2
[Ax(a − x)] = −A
2
2m
∂
∂x
(a − 2x)=A
2
m
.
Ψ(x, 0)
∗
ˆ
HΨ(x, 0) dx = A
2
2
m
a
0
x(a − x) dx = A
2
2
m
a
x
2
2
−
x
3
3
a
0
= A
2
2
m
a
3
2
−
a
3
3
=
30
a
5
2
m
a
3
6
=
5
2
ma
2
(same as Example 2.3).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

20 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Problem 2.10
(a) Using Eqs. 2.47 and 2.59,
a
+
ψ
0
=
1
√
2mω
−
d
dx
+ mωx
mω
π
1/4
e
−
mω
2
x
2
=
1
√
2mω
mω
π
1/4
−
−
mω
2
2x + mωx
e
−
mω
2
x
2
=
1
√
2mω
mω
π
1/4
2mωxe
−
mω
2
x
2
.
(a
+
)
2
ψ
0
=
1
2mω
mω
π
1/4
2mω
−
d
dx
+ mωx
xe
−
mω
2
x
2
=
1
mω
π
1/4
−
1 − x
mω
2
2x
+ mωx
2
e
−
mω
2
x
2
=
mω
π
1/4
2mω
x
2
− 1
e
−
mω
2
x
2
.
Therefore, from Eq. 2.67,
ψ
2
=
1
√
2
(a
+
)
2
ψ
0
=
1
√
2
mω
π
1/4
2mω
x
2
− 1
e
−
mω
2
x
2
.
(b)
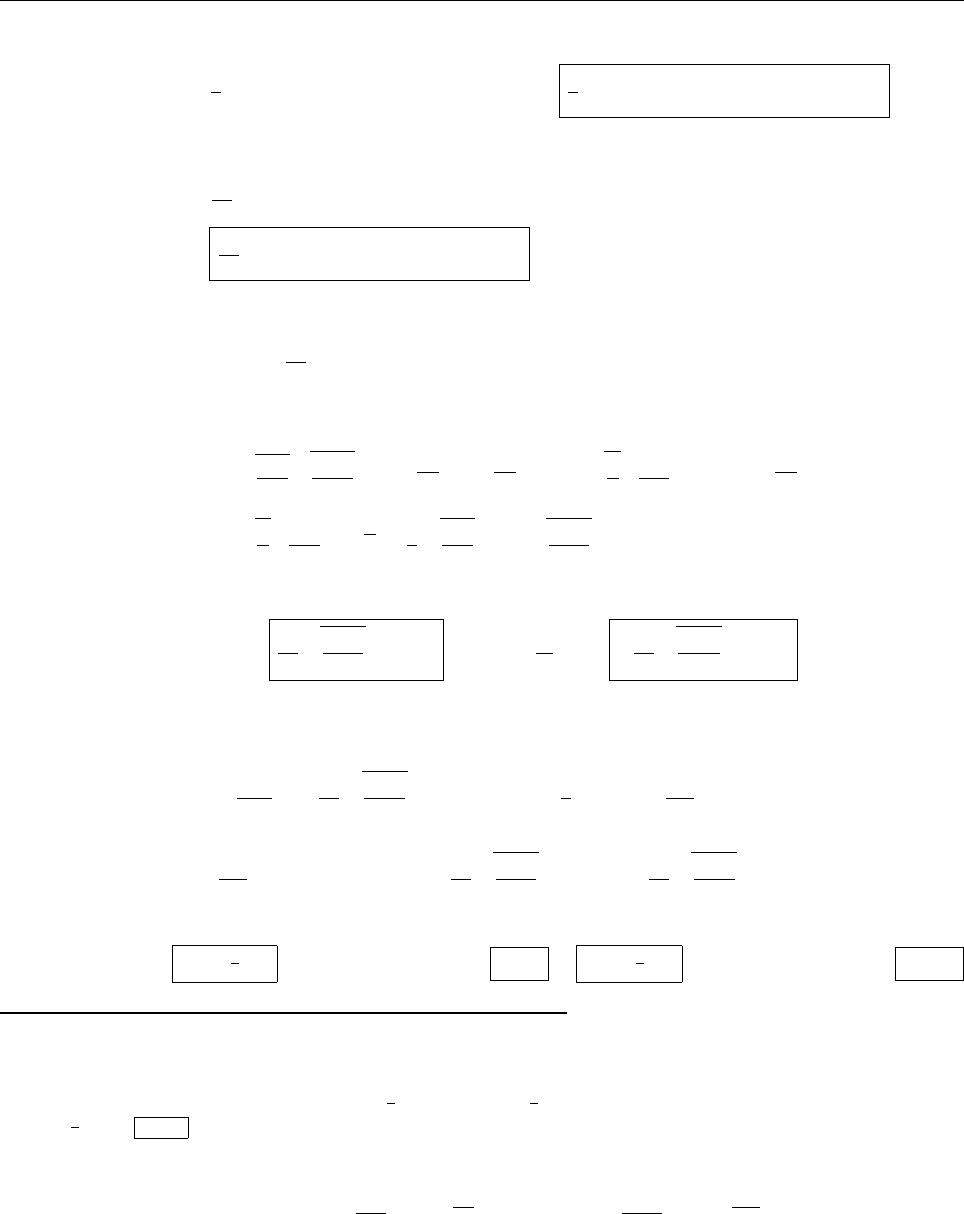
ψψ
ψ
1
2
0
(c) Since ψ
0
and ψ
2
are even, whereas ψ
1
is odd,
ψ
∗
0
ψ
1
dx and
ψ
∗
2
ψ
1
dx vanish automatically. The only one
we need to check is
ψ
∗
2
ψ
0
dx:
ψ
∗
2
ψ
0
dx =
1
√
2
mω
π
∞
−∞
2mω
x
2
− 1
e
−
mω
x
2
dx
= −
mω
2π
∞
−∞
e
−
mω
x
2
dx −
2mω
∞
−∞
x
2
e
−
mω
x
2
dx
= −
mω
2π
π
mω
−
2mω
2mω
π
mω
=0.
Problem 2.11
(a) Note that ψ
0
is even, and ψ
1
is odd. In either case |ψ|
2
is even, so x =
x|ψ|
2
dx = 0. Therefore
p = mdx/dt =
0. (These results hold for any stationary state of the harmonic oscillator.)
From Eqs. 2.59 and 2.62, ψ
0
= αe
−ξ
2
/2
,ψ
1
=
√
2αξe
−ξ
2
/2
.So
n =0
:
x
2
= α
2
∞
−∞
x
2
e
−ξ
2
/2
dx = α
2
mω
3/2
∞
−∞
ξ
2
e
−ξ
2
dξ =
1
√
π
mω
√
π
2
=
2mω
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 21
p
2
=
ψ
0
i
d
dx
2
ψ
0
dx = −
2
α
2
mω
∞
−∞
e
−ξ
2
/2
d
2
dξ
2
e
−ξ
2
/2
dξ
= −
mω
√
π
∞
−∞
ξ
2
− 1
e
−ξ
2
/2
dξ = −
mω
√
π
√
π
2
−
√
π
=
mω
2
.
n =1:
x
2
=2α
2
∞
−∞
x
2
ξ
2
e
−ξ
2
dx =2α
2
mω
3/2
∞
−∞
ξ
4
e
−ξ
2
dξ =
2
√
πmω
3
√
π
4
=
3
2mω
.
p
2
= −
2
2α
2
mω
∞
−∞
ξe
−ξ
2
/2
d
2
dξ
2
ξe
−ξ
2
/2
dξ
= −
2mω
√
π
∞
−∞
ξ
4
− 3ξ
2
e
−ξ
2
dξ = −
2mω
√
π
3
4
√
π − 3
√
π
2
=
3mω
2
.
(b) n =0:
σ
x
=
x
2
−x
2
=
2mω
; σ
p
=
p
2
−p
2
=
mω
2
;
σ
x
σ
p
=
2mω
mω
2
=
2
. (Right at the uncertainty limit.)
n =1
:
σ
x
=
3
2mω
; σ
p
=
3mω
2
; σ
x
σ
p
=3
2
>
2
.
(c)
T =
1
2m
p
2
=
1
4
ω (n =0)
3
4
ω (n =1)
;
V =
1
2
mω
2
x
2
=
1
4
ω (n =0)
3
4
ω (n =1)
.
T + V = H =
1
2
ω (n =0)=E
0
3
2
ω (n =1)=E
1
, as expected.
Problem 2.12
From Eq. 2.69,
x =
2mω
(a
+
+ a
−
),p= i
mω
2
(a
+
− a
−
),
so
x =
2mω
ψ
∗
n
(a
+
+ a
−
)ψ
n
dx.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

22 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
But (Eq. 2.66)
a
+
ψ
n
=
√
n +1ψ
n+1
,a
−
ψ
n
=
√
nψ
n−1
.
So
x =
2mω
√
n +1
ψ
∗
n
ψ
n+1
dx +
√
n
ψ
∗
n
ψ
n−1
dx
= 0 (by orthogonality).
p = m
dx
dt
=
0. x
2
=
2mω
(a
+
+ a
−
)
2
=
2mω
a
2
+
+ a
+
a
−
+ a
−
a
+
+ a
2
−
.
x
2
=
2mω
ψ
∗
n
a
2
+
+ a
+
a
−
+ a
−
a
+
+ a
2
−
ψ
n
. But
a
2
+
ψ
n
= a
+
√
n +1ψ
n+1
=
√
n +1
√
n +2ψ
n+2
=
(n + 1)(n +2)ψ
n+2
.
a
+
a
−
ψ
n
= a
+
√
nψ
n−1
=
√
n
√
nψ
n
= nψ
n
.
a
−
a
+
ψ
n
= a
−
√
n +1ψ
n+1
=
n +1)
√
n +1ψ
n
=(n +1)ψ
n
.
a
2
−
ψ
n
= a
−
√
nψ
n−1
=
√
n
√
n − 1ψ
n−2
=
(n − 1)nψ
n−2
.
So
x
2
=
2mω
0+n
|ψ
n
|
2
dx +(n +1)
|ψ
n
|
2
dx +0
=
2mω
(2n +1)=
n +
1
2
mω
.
p
2
= −
mω
2
(a
+
− a
−
)
2
= −
mω
2
a
2
+
− a
+
a
−
− a
−
a
+
+ a
2
−
⇒
p
2
= −
mω
2
[0 − n − (n +1)+0]=
mω
2
(2n +1)=
n +
1
2
mω.
T = p
2
/2m =
1
2
n +
1
2
ω
.
σ
x
=
x
2
−x
2
=
n +
1
2
mω
; σ
p
=
p
2
−p
2
=
n +
1
2
√
mω; σ
x
σ
p
=
n +
1
2
≥
2
.
Problem 2.13
(a)
1=
|Ψ(x, 0)|
2
dx = |A|
2
9|ψ
0
|
2
+12ψ
∗
0
ψ
1
+12ψ
∗
1
ψ
0
+16|ψ
1
|
2
dx
= |A|
2
(9+0+0+16)=25|A|
2
⇒ A =1/5.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 23
(b)
Ψ(x, t)=
1
5
3ψ
0
(x)e
−iE
0
t/
+4ψ
1
(x)e
−iE
1
t/
=
1
5
3ψ
0
(x)e
−iωt/2
+4ψ
1
(x)e
−3iωt/2
.
(Here ψ
0
and ψ
1
are given by Eqs. 2.59 and 2.62; E
1
and E
2
by Eq. 2.61.)
|Ψ(x, t)|
2
=
1
25
9ψ
2
0
+12ψ
0
ψ
1
e
iωt/2
e
−3iωt/2
+12ψ
0
ψ
1
e
−iωt/2
e
3iωt/2
+16ψ
2
1
=
1
25
9ψ
2
0
+16ψ
2
1
+24ψ
0
ψ
1
cos(ωt)
.
(c)
x =
1
25
9
xψ
2
0
dx +16
xψ
2
1
dx + 24 cos(ωt)
xψ
0
ψ
1
dx
.
But
xψ
2
0
dx =
xψ
2
1
dx = 0 (see Problem 2.11 or 2.12), while
xψ
0
ψ
1
dx =
mω
π
2mω
xe
−
mω
2
x
2
xe
−
mω
2
x
2
dx =
2
π
mω
∞
−∞
x
2
e
−
mω
x
2
dx
=
2
π
mω
2
√
π2
'
1
2
mω
(
3
=
2mω
.
So
x =
24
25
2mω
cos(ωt);
p = m
d
dt
x =
−
24
25
mω
2
sin(ωt).
(With ψ
2
in place of ψ
1
the frequency would be (E
2
− E
0
)/ = [(5/2)ω − (1/2)ω]/ =2ω.)
Ehrenfest’s theorem says dp/dt = −∂V/∂x. Here
dp
dt
= −
24
25
mω
2
ω cos(ωt),V=
1
2
mω
2
x
2
⇒
∂V
∂x
= mω
2
x,
so
−
)
∂V
∂x
*
= −mω
2
x = −mω
2
24
25
2mω
cos(ωt)=−
24
25
mω
2
ω cos(ωt),
so Ehrenfest’s theorem holds.
(d) You could get
E
0
=
1
2
ω, with probability |c
0
|
2
= 9/25, or E
1
=
3
2
ω, with probability |c
1
|
2
= 16/25.
Problem 2.14
The new allowed energies are E
n
=(n +
1
2
)ω
=2(n +
1
2
)ω = ω, 3ω, 5ω,.... So the probability of
getting
1
2
ω is zero. The probability of getting ω (the new ground state energy) is P
0
= |c
0
|
2
, where c
0
=
Ψ(x, 0)ψ
0
dx, with
Ψ(x, 0) = ψ
0
(x)=
mω
π
1/4
e
−
mω
2
x
2
,ψ
0
(x)
=
m2ω
π
1/4
e
−
m2ω
2
x
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

24 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
So
c
0
=2
1/4
mω
π
∞
−∞
e
−
3mω
2
x
2
dx =2
1/4
mω
π
2
√
π
'
1
2
2
3mω
(
=2
1/4
2
3
.
Therefore
P
0
=
2
3
√
2=0.9428.
Problem 2.15
ψ
0
=
mω
π
1/4
e
−ξ
2
/2
, so P =2
mω
π
∞
x
0
e
−ξ
2
dx =2
mω
π
mω
∞
ξ
0
e
−ξ
2
dξ.
Classically allowed region extends out to:
1
2
mω
2
x
2
0
= E
0
=
1
2
ω, or x
0
=
mω
, so ξ
0
=1.
P =
2
√
π
∞
1
e
−ξ
2
dξ = 2(1 − F (
√
2)) (in notation of CRC Table) = 0.157.
Problem 2.16
n =5:j =1⇒ a
3
=
−2(5−1)
(1+1)(1+2)
a
1
= −
4
3
a
1
; j =3⇒ a
5
=
−2(5−3)
(3+1)(3+2)
a
3
= −
1
5
a
3
=
4
15
a
1
; j =5⇒ a
7
=0. So
H
5
(ξ)=a
1
ξ −
4
3
a
1
ξ
3
+
4
15
a
1
ξ
5
=
a
1
15
(15ξ − 20ξ
3
+4ξ
5
). By convention the coefficient of ξ
5
is 2
5
,soa
1
=15· 8,
and
H
5
(ξ) = 120ξ − 160ξ
3
+32ξ
5
(which agrees with Table 2.1).
n =6:
j =0⇒ a
2
=
−2(6−0)
(0+1)(0+2)
a
0
= −6a
0
; j =2⇒ a
4
=
−2(6−2)
(2+1)(2+2)
a
2
= −
2
3
a
2
=4a
0
; j =4⇒ a
6
=
−2(6−4)
(4+1)(4+2)
a
4
= −
2
15
a
4
= −
8
15
a
0
; j =6⇒ a
8
=0. So H
6
(ξ)=a
0
−6a
0
ξ
2
+4a
0
ξ
4
−
8
15
ξ
6
a
0
. The coefficient of ξ
6
is 2
6
,so2
6
= −
8
15
a
0
⇒ a
0
= −15 · 8=−120. H
6
(ξ)=−120 + 720ξ
2
− 480ξ
4
+64ξ
6
.
Problem 2.17
(a)
d
dξ
(e
−ξ
2
)=−2ξe
−ξ
2
;
d
dξ
2
e
−ξ
2
=
d
dξ
(−2ξe
−ξ
2
)=(−2+4ξ
2
)e
−ξ
2
;
d
dξ
3
e
−ξ
2
=
d
dξ
(−2+4ξ
2
)e
−ξ
2
=
8ξ +(−2+4ξ
2
)(−2ξ)
e
−ξ
2
= (12ξ −8ξ
3
)e
−ξ
2
;
d
dξ
4
e
−ξ
2
=
d
dξ
(12ξ − 8ξ
3
)e
−ξ
2
=
12 − 24ξ
2
+ (12ξ − 8ξ
3
)(−2ξ)
e
−ξ
2
= (12 − 48ξ
2
+16ξ
4
)e
−ξ
2
.
H
3
(ξ)=−e
ξ
2
d
dξ
3
e
−ξ
2
= −12ξ +8ξ
3
; H
4
(ξ)=e
ξ
2
d
dξ
4
e
−ξ
2
= 12 − 48ξ
2
+16ξ
4
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 25
(b)
H
5
=2ξH
4
− 8H
3
=2ξ(12 − 48ξ
2
+16ξ
4
) − 8(−12ξ +8ξ
3
)= 120ξ − 160ξ
3
+32ξ
5
.
H
6
=2ξH
5
− 10H
4
=2ξ(120ξ − 160ξ
3
+32ξ
5
) − 10(12 − 48ξ
2
+16ξ
4
)= −120 + 720ξ
2
− 480ξ
4
+64ξ
6
.
(c)
dH
5
dξ
= 120 − 480ξ
2
+ 160ξ
4
= 10(12 − 48ξ
2
+16ξ
4
) = (2)(5)H
4
.
dH
6
dξ
= 1440ξ −1920ξ
3
+ 384ξ
5
= 12(120ξ −160ξ
3
+32ξ
5
) = (2)(6)H
5
.
(d)
d
dz
(e
−z
2
+2zξ
)=(−2z + ξ)e
−z
2
+2zξ
; setting z =0, H
0
(ξ)=2ξ.
d
dz
2
(e
−z
2
+2zξ
)=
d
dz
(−2z +2ξ)e
−z
2
+2zξ
=
− 2+(−2z +2ξ)
2
e
−z
2
+2zξ
; setting z =0, H
1
(ξ)=−2+4ξ
2
.
d
dz
3
(e
−z
2
+2zξ
)=
d
dz
− 2+(−2z +2ξ)
2
e
−z
2
+2zξ
=
2(−2z +2ξ)(−2) +
− 2+(−2z +2ξ)
2
(−2z +2ξ)
e
−z
2
+2zξ
;
setting z =0,H
2
(ξ)=−8ξ +(−2+4ξ
2
)(2ξ)= −12ξ +8ξ
3
.
Problem 2.18
Ae
ikx
+ Be
−ikx
= A(cos kx + i sin kx)+B(cos kx − i sin kx)=(A + B) cos kx + i(A − B) sin kx
= C cos kx + D sin kx, with
C = A + B; D = i(A − B).
C cos kx + D sin kx = C
e
ikx
+ e
−ikx
2
+ D
e
ikx
− e
−ikx
2i
=
1
2
(C − iD)e
ikx
+
1
2
(C + iD)e
−ikx
= Ae
ikx
+ Be
−ikx
, with A =
1
2
(C − iD); B =
1
2
(C + iD).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

26 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Problem 2.19
Equation 2.94 says Ψ = Ae
i(kx−
k
2
2m
t)
,so
J =
i
2m
Ψ
∂Ψ
∗
∂x
− Ψ
∗
∂Ψ
∂x
=
i
2m
|A|
2
e
i(kx−
k
2
2m
t)
(−ik)e
−i(kx−
k
2
2m
t)
− e
−i(kx−
k
2
2m
t)
(ik)e
i(kx−
k
2
2m
t)
=
i
2m
|A|
2
(−2ik)=
k
m
|A|
2
.
It flows in the positive (x) direction (as you would expect).
Problem 2.20
(a)
f(x)=b
0
+
∞
n=1
a
n
2i
e
inπx/a
− e
−inπx/a
+
∞
n=1
b
n
2
e
inπx/a
+ e
−inπx/a
= b
0
+
∞
n=1
a
n
2i
+
b
n
2
e
inπx/a
+
∞
n=1
−
a
n
2i
+
b
n
2
e
−inπx/a
.
Let
c
0
≡ b
0
; c
n
=
1
2
(−ia
n
+ b
n
) , for n =1, 2, 3,... ; c
n
≡
1
2
(ia
−n
+ b
−n
) , for n = −1, −2, −3,... .
Then f(x)=
∞
n=−∞
c
n
e
inπx/a
. QED
(b)
a
−a
f(x)e
−imπx/a
dx =
∞
n=−∞
c
n
a
−a
e
i(n−m)πx/a
dx. But for n = m,
a
−a
e
i(n−m)πx/a
dx =
e
i(n−m)πx/a
i(n − m)π/a
a
−a
=
e
i(n−m)π
− e
−i(n−m)π
i(n − m)π/a
=
(−1)
n−m
− (−1)
n−m
i(n − m)π/a
=0,
whereas for n = m,
a
−a
e
i(n−m)πx/a
dx =
a
−a
dx =2a.
So all terms except n = m are zero, and
a
−a
f(x)e
−imπx/a
=2ac
m
, so c
n
=
1
2a
a
−a
f(x)e
−inπx/a
dx. QED
(c)
f(x)=
∞
n=−∞
π
2
1
a
F (k)e
ikx
=
1
√
2π
F (k)e
ikx
∆k,
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 27
where ∆k ≡
π
a
is the increment in k from n to (n + 1).
F (k)=
2
π
a
1
2a
a
−a
f(x)e
−ikx
dx =
1
√
2π
a
−a
f(x)e
−ikx
dx.
(d) As a →∞, k becomes a continuous variable,
f(x)=
1
√
2π
∞
−∞
F (k)e
ikx
dk; F (k)=
1
√
2π
∞
−∞
f(x)e
ikx
dx.
Problem 2.21
(a)
1=
∞
−∞
|Ψ(x, 0)|
2
dx =2|A|
2
∞
0
e
−2ax
dx =2|A|
2
e
−2ax
−2a
∞
0
=
|A|
2
a
⇒ A =
√
a.
(b)
φ(k)=
A
√
2π
∞
−∞
e
−a|x|
e
−ikx
dx =
A
√
2π
∞
−∞
e
−a|x|
(cos kx − i sin kx)dx.
The cosine integrand is even, and the sine is odd, so the latter vanishes and
φ(k)=2
A
√
2π
∞
0
e
−ax
cos kx dx =
A
√
2π
∞
0
e
−ax
e
ikx
+ e
−ikx
dx
=
A
√
2π
∞
0
e
(ik−a)x
+ e
−(ik+a)x
dx =
A
√
2π
e
(ik−a)x
ik −a
+
e
−(ik+a)x
−(ik + a)
∞
0
=
A
√
2π
−1
ik −a
+
1
ik + a
=
A
√
2π
−ik −a + ik − a
−k
2
− a
2
=
a
2π
2a
k
2
+ a
2
.
(c)
Ψ(x, t)=
1
√
2π
2
a
3
2π
∞
−∞
1
k
2
+ a
2
e
i(kx−
k
2
2m
t)
dk =
a
3/2
π
∞
−∞
1
k
2
+ a
2
e
i(kx−
k
2
2m
t)
dk.
(d) For large a,Ψ(x, 0) is a sharp narrow spike whereas φ(k)
∼
=
2/πa is broad and flat; position is well-
defined but momentum is ill-defined. For small a,Ψ(x, 0) is a broad and flat whereas φ(k)
∼
=
(
2a
3
/π)/k
2
is a sharp narrow spike; position is ill-defined but momentum is well-defined.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

28 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Problem 2.22
(a)
1=|A|
2
∞
−∞
e
−2ax
2
dx = |A|
2
π
2a
;
A =
2a
π
1/4
.
(b)
∞
−∞
e
−(ax
2
+bx)
dx =
∞
−∞
e
−y
2
+(b
2
/4a)
1
√
a
dy =
1
√
a
e
b
2
/4a
∞
−∞
e
−y
2
dy =
π
a
e
b
2
/4a
.
φ(k)=
1
√
2π
A
∞
−∞
e
−ax
2
e
−ikx
dx =
1
√
2π
2a
π
1/4
π
a
e
−k
2
/4a
=
1
(2πa)
1/4
e
−k
2
/4a
.
Ψ(x, t)=
1
√
2π
1
(2πa)
1/4
∞
−∞
e
−k
2
/4a
e
i(kx−k
2
t/2m)
e
−[(
1
4a
+it/2m)k
2
−ixk]
dk
=
1
√
2π(2πa)
1/4
√
π
1
4a
+ it/2m
e
−x
2
/4(
1
4a
+it/2m)
=
2a
π
1/4
e
−ax
2
/(1+2iat/m)
1+2iat/m
.
(c)
Let θ ≡ 2at/m. Then |Ψ|
2
=
2a
π
e
−ax
2
/(1+iθ)
e
−ax
2
/(1−iθ)
(1 + iθ)(1 −iθ)
. The exponent is
−
ax
2
(1 + iθ)
−
ax
2
(1 − iθ)
= −ax
2
(1 − iθ +1+iθ)
(1 + iθ)(1 −iθ)
=
−2ax
2
1+θ
2
; |Ψ|
2
=
2a
π
e
−2ax
2
/(1+θ
2
)
√
1+θ
2
.
Or, with w ≡
a
1+θ
2
, |Ψ|
2
=
2
π
we
−2w
2
x
2
. As t increases, the graph of |Ψ|
2
flattens out and broadens.
|Ψ|
2
|Ψ|
2
xx
t = 0
t > 0
(d)
x =
∞
−∞
x|Ψ|
2
dx = 0 (odd integrand); p = m
dx
dt
=
0.
x
2
=
2
π
w
∞
−∞
x
2
e
−2w
2
x
2
dx =
2
π
w
1
4w
2
π
2w
2
=
1
4w
2
. p
2
= −
2
∞
−∞
Ψ
∗
d
2
Ψ
dx
2
dx.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 29
Write Ψ = Be
−bx
2
, where B ≡
2a
π
1/4
1
√
1+iθ
and b ≡
a
1+iθ
.
d
2
Ψ
dx
2
= B
d
dx
−2bxe
−bx
2
= −2bB(1 −2bx
2
)e
−bx
2
.
Ψ
∗
d
2
Ψ
dx
2
= −2b|B|
2
(1 − 2bx
2
)e
−(b+b
∗
)x
2
; b + b
∗
=
a
1+iθ
+
a
1 − iθ
=
2a
1+θ
2
=2w
2
.
|B|
2
=
2a
π
1
√
1+θ
2
=
2
π
w. So Ψ
∗
d
2
Ψ
dx
2
= −2b
2
π
w(1 −2bx
2
)e
−2w
2
x
2
.
p
2
=2b
2
2
π
w
∞
−∞
(1 − 2bx
2
)e
−2w
2
x
2
dx
=2b
2
2
π
w
π
2w
2
− 2b
1
4w
2
π
2w
2
=2b
2
1 −
b
2w
2
.
But 1 −
b
2w
2
=1−
a
1+iθ
1+θ
2
2a
=1−
(1 − iθ)
2
=
1+iθ
2
=
a
2b
, so
p
2
=2b
2
a
2b
=
2
a. σ
x
=
1
2w
;
σ
p
=
√
a.
(e)
σ
x
σ
p
=
1
2w
√
a =
2
1+θ
2
=
2
1+(2at/m)
2
≥
2
.
Closest at
t =0, at which time it is right at the uncertainty limit.
Problem 2.23
(a)
(−2)
3
− 3(−2)
2
+2(−2) − 1=−8 − 12 − 4 − 1= −25.
(b)
cos(3π)+2=−1+2=
1.
(c)
0 (x = 2 is outside the domain of integration).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

30 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Problem 2.24
(a) Let y ≡ cx, so dx =
1
c
dy.
If c>0,y: −∞→∞.
If c<0,y: ∞→−∞.
∞
−∞
f(x)δ(cx)dx =
1
c
∞
−∞
f(y/c)δ(y)dy =
1
c
f(0) (c>0); or
1
c
−∞
∞
f(y/c)δ(y)dy = −
1
c
∞
−∞
f(y/c)δ(y)dy = −
1
c
f(0) (c<0).
In either case,
∞
−∞
f(x)δ(cx)dx =
1
|c|
f(0) =
∞
−∞
f(x)
1
|c|
δ(x)dx. So δ(cx)=
1
|c|
δ(x).
(b)
∞
−∞
f(x)
dθ
dx
dx = fθ
∞
−∞
−
∞
−∞
df
dx
θdx (integration by parts)
= f(∞) −
∞
0
df
dx
dx = f(∞) − f(∞)+f (0) = f (0) =
∞
−∞
f(x)δ(x)dx.
So dθ/dx = δ(x). [Makes sense: The θ function is constant (so derivative is zero) except at x = 0, where
the derivative is infinite.]
Problem 2.25
ψ(x)=
√
mα
e
−mα|x|/
2
=
√
mα
e
−mαx/
2
, (x ≥ 0),
e
mαx/
2
, (x ≤ 0).
x = 0 (odd integrand).
x
2
=
∞
−∞
x
2
|ψ|
2
dx =2
mα
2
∞
0
x
2
e
−2mαx/
2
dx =
2mα
2
2
2
2mα
3
=
4
2m
2
α
2
; σ
x
=
2
√
2mα
.
dψ
dx
=
√
mα
−
mα
2
e
−mαx/
2
, (x ≥ 0)
mα
2
e
mαx/
2
, (x ≤ 0)
=
√
mα
3
−θ(x)e
−mαx/
2
+ θ(−x)e
mαx/
2
.
d
2
ψ
dx
2
=
√
mα
3
−δ(x)e
−mαx/
2
+
mα
2
θ(x)e
−mαx/
2
− δ(−x)e
mαx/
2
+
mα
2
θ(−x)e
mαx/
2
=
√
mα
3
−2δ(x)+
mα
2
e
−mα|x|/
2
.
In the last step I used the fact that δ(−x)=δ(x) (Eq. 2.142), f (x)δ(x)=f(0)δ(x) (Eq. 2.112), and θ(−x)+
θ(x) = 1 (Eq. 2.143). Since dψ/dx is an odd function, p =0.
p
2
= −
2
∞
−∞
ψ
d
2
ψ
dx
2
dx = −
2
√
mα
√
mα
3
∞
−∞
e
−mα|x|/
2
−2δ(x)+
mα
2
e
−mα|x|/
2
dx
=
mα
2
2 − 2
mα
2
∞
0
e
−2mαx/
2
dx
=2
mα
2
1 −
mα
2
2
2mα
=
mα
2
.
Evidently
σ
p
=
mα
, so σ
x
σ
p
=
2
√
2mα
mα
=
√
2
2
>
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 31
Problem 2.26
Put f(x)=δ(x) into Eq. 2.102: F (k)=
1
√
2π
∞
−∞
δ(x)e
−ikx
dx =
1
√
2π
.
∴ f(x)=δ(x)=
1
√
2π
∞
−∞
1
√
2π
e
ikx
dk =
1
2π
∞
−∞
e
ikx
dk. QED
Problem 2.27
(a)
V(x)
-a a
x
(b) From Problem 2.1(c) the solutions are even or odd. Look first for even solutions:
ψ(x)=
Ae
−κx
(x<a),
B(e
κx
+ e
−κx
)(−a<x<a),
Ae
κx
(x<−a).
Continuity at a : Ae
−κa
= B(e
κa
+ e
−κa
), or A = B(e
2κa
+1).
Discontinuous derivative at a, ∆
dψ
dx
= −
2mα
2
ψ(a):
−κAe
−κa
− B(κe
κa
− κe
−κa
)=−
2mα
2
Ae
−κa
⇒ A + B(e
2κa
− 1) =
2mα
2
κ
A;or
B(e
2κa
− 1) = A
2mα
2
κ
− 1
= B(e
2κa
+1)
2mα
2
κ
− 1
⇒ e
2κa
− 1=e
2κa
2mα
2
κ
− 1
+
2mα
2
κ
− 1.
1=
2mα
2
κ
− 1+
2mα
2
κ
e
−2κa
;
2
κ
mα
=1+e
−2κa
, or e
−2κa
=
2
κ
mα
− 1.
This is a transcendental equation for κ (and hence for E). I’ll solve it graphically: Let z ≡ 2κa, c ≡
2
2amα
,
so e
−z
= cz − 1. Plot both sides and look for intersections:
1
z
1/c
cz-1
e
-z
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

32 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
From the graph, noting that c and z are both positive, we see that there is one (and only one) solution
(for even ψ). If α =
2
2ma
,soc = 1, the calculator gives z =1.278, so κ
2
= −
2mE
2
=
z
2
(2a)
2
⇒ E =
−
(1.278)
2
8
2
ma
2
= −0.204
2
ma
2
.
Now look for odd solutions:
ψ(x)=
Ae
−κx
(x<a),
B(e
κx
− e
−κx
)(−a<x<a),
−Ae
κx
(x<−a).
Continuity at a : Ae
−κa
= B(e
κa
− e
−κa
), or A = B(e
2κa
− 1).
Discontinuity in ψ
: −κAe
−κa
− B(κe
κa
+ κe
−κa
)=−
2mα
2
Ae
−κa
⇒ B(e
2κa
+1)=A
2mα
2
κ
− 1
,
e
2κa
+1=(e
2κa
− 1)
2mα
2
κ
− 1
= e
2κa
2mα
2
κ
− 1
−
2mα
2
κ
+1,
1=
2mα
2
κ
− 1 −
2mα
2
κ
e
−2κa
;
2
κ
mα
=1− e
−2κa
, e
−2κa
=1−
2
κ
mα
,
or e
−z
=1− cz.
1/c
1/c
1
z
This time there may or may not be a solution. Both graphs have their y-intercepts at 1, but if c is too
large (α too small), there may be no intersection (solid line), whereas if c is smaller (dashed line) there
will be. (Note that z =0⇒ κ =0isnot a solution, since ψ is then non-normalizable.) The slope of e
−z
(at z =0)is−1; the slope of (1 − cz)is−c. So there is an odd solution ⇔ c<1, or α>
2
/2ma.
Conclusion:
One bound state if α ≤
2
/2ma; two if α>
2
/2ma.
ψ
ψ
x
x
a-a a
-a
Even Odd
α =
2
ma
⇒ c =
1
2
.
Even: e
−z
=
1
2
z − 1 ⇒ z =2.21772,
Odd: e
−z
=1−
1
2
z ⇒ z =1.59362.
E = −0.615(
2
/ma
2
); E = −0.317(
2
/ma
2
).
α =
2
4ma
⇒ c =2. Only even: e
−z
=2z − 1 ⇒ z =0.738835; E = −0.0682(
2
/ma
2
).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 33
Problem 2.28
ψ =
Ae
ikx
+ Be
−ikx
(x<−a)
Ce
ikx
+ De
−ikx
(−a<x<a)
Fe
ikx
(x>a)
. Impose boundary conditions:
(1) Continuity at −a : Ae
ika
+ Be
ika
= Ce
−ika
+ De
ika
⇒ βA + B = βC + D, where β ≡ e
−2ika
.
(2) Continuity at +a : Ce
ika
+ De
−ika
= Fe
ika
⇒ F = C + βD.
(3) Discontinuity in ψ
at −a : ik(Ce
−ika
− De
ika
) − ik(Ae
−ika
− Be
ika
)=−
2mα
2
(Ae
−ika
+ Be
ika
)
⇒ βC − D = β(γ +1)A + B(γ −1), where γ ≡ i2mα/
2
k.
(4) Discontinuity in ψ
at +a : ikF e
ika
− ik(Ce
ika
− De
−ika
)=−
2mα
2
(Fe
ika
)
⇒ C − βD =(1− γ)F.
To solve for C and D,
add (2) and (4) : 2C = F +(1− γ)F ⇒ 2C =(2− γ)F.
subtract (2) and (4) : 2βD = F − (1 − γ)F ⇒ 2D =(γ/β)F.
add (1) and (3) : 2βC = βA + B + β(γ +1)A + B(γ − 1) ⇒ 2C =(γ +2)A +(γ/β)B.
subtract (1) and (3) : 2D = βA + B −β(γ +1)A − B(γ −1) ⇒ 2D = −γβA +(2− γ)B.
Equate the two expressions for 2C :(2− γ)F =(γ +2)A +(γ/β)B.
Equate the two expressions for 2D :(γ/β)F = −γβA +(2− γ)B.
Solve these for F and B, in terms of A. Multiply the first by β(2 − γ), the second by γ, and subtract:
β(2 − γ)
2
F = β(4 − γ
2
)A + γ(2 − γ)B
;
(γ
2
/β)F = −βγ
2
A + γ(2 − γ)B
.
⇒
β(2 − γ)
2
− γ
2
/β
F = β
4 − γ
2
+ γ
A =4βA ⇒
F
A
=
4
(2 − γ)
2
− γ
2
/β
2
.
Let g ≡ i/γ =
2
k
2mα
; φ ≡ 4ka, so γ =
i
g
,β
2
= e
−iφ
. Then:
F
A
=
4g
2
(2g − i)
2
+ e
iφ
.
Denominator: 4g
2
− 4ig − 1 + cos φ + i sin φ =(4g
2
− 1 + cos φ)+i(sin φ − 4g).
|Denominator|
2
=(4g
2
− 1 + cos φ)
2
+ (sin φ −4g)
2
=16g
4
+1+cos
2
φ − 8g
2
− 2 cos φ +8g
2
cos φ + sin
2
φ − 8g sin φ +16g
2
=16g
4
+8g
2
+2+(8g
2
− 2) cos φ − 8g sin φ.
T =
F
A
2
=
8g
4
(8g
4
+4g
2
+1)+(4g
2
− 1) cos φ − 4g sin φ
, where g ≡
2
k
2mα
and φ ≡ 4ka.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
34 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Problem 2.29
In place of Eq. 2.151, we have: ψ(x)=
Fe
−κx
(x>a)
D sin(lx)(0<x<a)
−ψ(−x)(x<0)
.
Continuity of ψ : Fe
−κa
= D sin(la); continuity of ψ
: −Fκe
−κa
= Dl cos(la).
Divide: −κ = l cot(la), or − κa = la cot(la) ⇒
z
2
0
− z
2
= −z cot z, or −cot z =
(z
0
/z)
2
− 1.
Wide, deep well: Intersections are at π, 2π, 3π, etc. Same as Eq. 2.157, but now for n even. This fills in the
rest of the states for the infinite square well.
Shallow, narrow well: If z
0
<π/2, there is no odd bound state. The corresponding condition on V
0
is
V
0
<
π
2
2
8ma
2
⇒ no odd bound state.
π2π
z
z
0
Problem 2.30
1=2
∞
0
|ψ|
2
dx =2
|D|
2
a
0
cos
2
lx dx + |F |
2
∞
a
e
−2κx
dx
=2
|D|
2
x
2
+
1
4l
sin 2lx
a
0
+ |F |
2
−
1
2κ
e
−2κx
∞
a
=2
|D|
2
a
2
+
sin 2la
4l
+ |F |
2
e
−2κa
2κ
.
But F = De
κa
cos la (Eq. 2.152), so 1 = |D|
2
a +
sin(2la)
2l
+
cos
2
(la)
κ
.
Furthermore κ = l tan(la) (Eq. 2.154), so
1=|D|
2
a +
2 sin la cos la
2l
+
cos
3
la
l sin la
= |D|
2
a +
cos la
l sin la
(sin
2
la + cos
2
la)
= |D|
2
a +
1
l tan la
= |D|
2
a +
1
κ
.
D =
1
a +1/κ
,
F =
e
κa
cos la
a +1/κ
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 35
Problem 2.31
Equation 2.155 ⇒ z
0
=
a
√
2mV
0
. We want α = area of potential =2aV
0
held constant as a → 0. Therefore
V
0
=
α
2a
; z
0
=
a
2m
α
2a
=
1
√
mαa → 0. So z
0
is small, and the intersection in Fig. 2.18 occurs at very small
z. Solve Eq. 2.156 for very small z, by expanding tan z:
tan z
∼
=
z =
(z
0
/z)
2
− 1=(1/z)
z
2
0
− z
2
.
Now (from Eqs. 2.146, 2.148 and 2.155) z
2
0
−z
2
= κ
2
a
2
, so z
2
= κa. But z
2
0
−z
2
= z
4
1 ⇒ z
∼
=
z
0
, so κa
∼
=
z
2
0
.
But we found that z
0
∼
=
1
√
mαa here, so κa =
1
2
mαa,orκ =
mα
2
. (At this point the a’s have canceled, and
we can go to the limit a → 0.)
√
−2mE
=
mα
2
⇒−2mE =
m
2
α
2
2
. E = −
mα
2
2
2
(which agrees with Eq. 2.129).
In Eq. 2.169, V
0
E ⇒ T
−1
∼
=
1+
V
2
0
4EV
0
sin
2
2a
√
2mV
0
. But V
0
=
α
2a
, so the argument of the sine is small,
and we can replace sin 9 by 9: T
−1
∼
=
1+
V
0
4E
2a
2
2mV
0
=1+(2aV
0
)
2
m
2
2
E
. But 2aV
0
= α, so T
−1
=1+
mα
2
2
2
E
,
in agreement with Eq. 2.141.
Problem 2.32
Multiply Eq. 2.165 by sin la, Eq. 2.166 by
1
l
cos la, and add:
C sin
2
la + D sin la cos la = Fe
ika
sin la
C cos
2
la −D sin la cos la =
ik
l
Fe
ika
cos la
C = Fe
ika
sin la +
ik
l
cos la
.
Multiply Eq. 2.165 by cos la, Eq. 2.166 by
1
l
sin la, and subtract:
C sin la cos la + D cos
2
la = Fe
ika
cos la
C sin la cos la −D sin
2
la =
ik
l
Fe
ika
sin la
D = Fe
ika
cos la −
ik
l
sin la
.
Put these into Eq. 2.163:
(1) Ae
−ika
+ Be
ika
= −Fe
ika
sin la +
ik
l
cos la
sin la + Fe
ika
cos la −
ik
l
sin la
cos la
= Fe
ika
cos
2
la −
ik
l
sin la cos la − sin
2
la −
ik
l
sin la cos la
= Fe
ika
cos(2la) −
ik
l
sin(2la)
.
Likewise, from Eq. 2.164:
(2) Ae
−ika
− Be
ika
= −
il
k
Fe
ika
sin la +
ik
l
cos la
cos la +
cos la −
ik
l
sin la
sin la
= −
il
k
Fe
ika
sin la cos la +
ik
l
cos
2
la + sin la cos la −
ik
l
sin
2
la
= −
il
k
Fe
ika
sin(2la)+
ik
l
cos(2la)
= Fe
ika
cos(2la) −
il
k
sin(2la)
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

36 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Add (1) and (2):2Ae
−ika
= Fe
ika
2 cos(2la) − i
k
l
+
l
k
sin(2la)
, or:
F =
e
−2ika
A
cos(2la) −i
sin(2la)
2kl
(k
2
+ l
2
)
(confirming Eq. 2.168). Now subtract (2) from (1):
2Be
ika
= Fe
ika
i
l
k
−
k
l
sin(2la)
⇒ B = i
sin(2la)
2kl
(l
2
− k
2
)F (confirming Eq. 2.167).
T
−1
=
A
F
2
=
cos(2la) −i
sin(2la)
2kl
(k
2
+ l
2
)
2
= cos
2
(2la)+
sin
2
(2la)
(2lk)
2
(k
2
+ l
2
)
2
.
But cos
2
(2la)=1− sin
2
(2la), so
T
−1
= 1 + sin
2
(2la)
(k
2
+ l
2
)
2
(2lk)
2
− 1
1
(2kl)
2
[k
4
+2k
2
l
2
+l
4
−4k
2
l
2
]=
1
(2kl)
2
[k
4
−2k
2
l
2
+l
4
]=
(k
2
−l
2
)
2
(2kl)
2
.
=1+
(k
2
− l
2
)
2
(2kl)
2
sin
2
(2la).
But k =
√
2mE
,l=
2m(E + V
0
)
;so(2la)=
2a
2m(E + V
0
); k
2
− l
2
= −
2mV
0
2
, and
(k
2
− l
2
)
2
(2kl)
2
=
2m
2
2
V
2
0
4
2m
2
2
E(E + V
0
)
=
V
2
0
4E(E + V
0
)
.
∴ T
−1
=1+
V
2
0
4E(E + V
0
)
sin
2
2a
2m(E + V
0
)
, confirming Eq. 2.169.
Problem 2.33
E < V
0
.ψ=
Ae
ikx
+ Be
−ikx
(x<−a)
Ce
κx
+ De
−κx
(−a<x<a)
Fe
ikx
(x>a)
k =
√
2mE
; κ =
2m(V
0
− E)
.
(1) Continuity of ψ at −a: Ae
−ika
+ Be
ika
= Ce
−κa
+ De
κa
.
(2) Continuity of ψ
at −a: ik(Ae
−ika
− Be
ika
)=κ(Ce
−κa
− De
κa
).
⇒ 2Ae
−ika
=
1 − i
κ
k
Ce
−κa
+
1+i
κ
k
De
κa
.
(3) Continuity of ψ at +a: Ce
κa
+ De
−κa
= Fe
ika
.
(4) Continuity of ψ
at +a: κ(Ce
κa
− De
−κa
)=ikF e
ika
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 37
⇒ 2Ce
κa
=
1+
ik
κ
Fe
ika
;2De
−κa
=
1 −
ik
κ
Fe
ika
.
2Ae
−ika
=
1 −
iκ
k
1+
ik
κ
Fe
ika
e
−2κa
2
+
1+
iκ
k
1 −
ik
κ
Fe
ika
e
2κa
2
=
Fe
ika
2
1+i
k
κ
−
κ
k
+1
e
−2κa
+
1+i
κ
k
−
k
κ
+1
e
2κa
=
Fe
ika
2
2
e
−2κa
+ e
2κa
+ i
(κ
2
− k
2
)
kκ
e
2κa
− e
−2κa
.
But sinh x ≡
e
x
− e
−x
2
, cosh x ≡
e
x
+ e
−x
2
, so
=
Fe
ika
2
4 cosh(2κa)+i
(κ
2
− k
2
)
kκ
2 sinh(2κa)
=2Fe
ika
cosh(2κa)+i
(κ
2
− k
2
)
2kκ
sinh(2κa)
.
T
−1
=
A
F
2
= cosh
2
(2κa)+
(κ
2
− k
2
)
2
(2κk)
2
sinh
2
(2κa). But cosh
2
= 1 + sinh
2
, so
T
−1
=1+
1+
(κ
2
− k
2
)
2
(2κk)
2
sinh
2
(2κa)= 1+
V
2
0
4E(V
0
− E)
sinh
2
2a
2m(V
0
− E)
,
where =
4κ
2
k
2
+ k
4
+ κ
4
− 2κ
2
k
2
(2κk)
2
=
(κ
2
+ k
2
)
2
(2κk)
2
=
2mE
2
+
2m(V
0
−E)
2
2
4
2mE
2
2m(V
0
−E)
2
=
V
2
0
4E(V
0
− E)
.
(You can also get this from Eq. 2.169 by switching the sign of V
0
and using sin(iθ)=i sinh θ.)
E = V
0
.ψ=
Ae
ikx
+ Be
−ikx
(x<−a)
C + Dx (−a<x<a)
Fe
ikx
(x>a)
(In central region −
2
2m
d
2
ψ
dx
2
+ V
0
ψ = Eψ ⇒
d
2
ψ
dx
2
=0, so ψ = C + Dx.)
(1) Continuous ψ at −a : Ae
−ika
+ Be
ika
= C − Da.
(2) Continuous ψ at +a : Fe
ika
= C + Da.
⇒ (2.5)2Da = Fe
ika
− Ae
−ika
− Be
ika
.
(3) Continuous ψ
at −a : ik
Ae
−ika
− Be
ika
= D.
(4) Continuous ψ
at +a : ikF e
ika
= D.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

38 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
⇒ (4.5) Ae
−2ika
− B = F.
Use (4) to eliminate D in (2.5): Ae
−2ika
+ B = F −2aikF =(1− 2iak)F , and add to (4.5):
2Ae
−2ika
=2F (1 − ika), so T
−1
=
A
F
2
=1+(ka)
2
= 1+
2mE
2
a
2
.
(You can also get this from Eq. 2.169 by changing the sign of V
0
and taking the limit E → V
0
, using sin 9
∼
=
9.)
E > V
0
. This case is identical to the one in the book, only with V
0
→−V
0
.So
T
−1
=1+
V
2
0
4E(E − V
0
)
sin
2
2a
2m(E − V
0
)
.
Problem 2.34
(a)
ψ =
Ae
ikx
+ Be
−ikx
(x<0)
Fe
−κx
(x>0)
where k =
√
2mE
; κ =
2m(V
0
− E)
.
(1) Continuity of ψ : A + B = F.
(2) Continuity of ψ
: ik(A − B)=−κF.
⇒ A + B = −
ik
κ
(A − B) ⇒ A
1+
ik
κ
= −B
1 −
ik
κ
.
R =
B
A
2
=
|(1 + ik/κ)|
2
|(1 − ik/κ)|
2
=
1+(k/κ)
2
1+(k/κ)
2
= 1.
Although the wave function penetrates into the barrier, it is eventually all reflected.
(b)
ψ =
Ae
ikx
+ Be
−ikx
(x<0)
Fe
ilx
(x>0)
where k =
√
2mE
; l =
2m(E − V
0
)
.
(1) Continuity of ψ : A + B = F.
(2) Continuity of ψ
: ik(A − B)=ilF.
⇒ A + B =
k
l
(A − B); A
1 −
k
l
= −B
1+
k
l
.
R =
B
A
2
=
(1 − k/l)
2
(1 + k/l)
2
=
(k −l)
2
(k + l)
2
=
(k −l)
4
(k
2
− l
2
)
2
.
Now k
2
− l
2
=
2m
2
(E − E + V
0
)=
2m
2
V
0
; k − l =
√
2m
[
√
E −
E − V
0
], so
R =
(
√
E −
√
E − V
0
)
4
V
2
0
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 39
(c)
v
i
v
i
v
t
v
t
dt
dt
From the diagram, T = P
t
/P
i
= |F |
2
v
t
/|A|
2
v
i
, where P
i
is the probability of finding the incident particle
in the box corresponding to the time interval dt, and P
t
is the probability of finding the transmitted
particle in the associated box to the right of the barrier.
But
v
t
v
i
=
√
E − V
0
√
E
(from Eq. 2.98). So T =
E − V
0
E
F
A
2
. Alternatively, from Problem 2.19:
J
i
=
k
m
|A|
2
; J
t
=
l
m
|F |
2
; T =
J
t
J
i
=
F
A
2
l
k
=
F
A
2
E − V
0
E
.
For E<V
0
, of course, T =0.
(d)
For E>V
0
,F= A + B = A + A
k
l
− 1
k
l
+1
= A
2k/l
k
l
+1
=
2k
k + l
A.
T =
F
A
2
l
k
=
2k
k + l
2
l
k
=
4kl
(k + l)
2
=
4kl(k − l)
2
(k
2
− l
2
)
2
=
4
√
E
√
E − V
0
(
√
E −
√
E − V
0
)
2
V
2
0
.
T + R =
4kl
(k + l)
2
+
(k −l)
2
(k + l)
2
=
4kl + k
2
− 2kl + l
2
(k + l)
2
=
k
2
+2kl + l
2
(k + l)
2
=
(k + l)
2
(k + l)
2
=1.
Problem 2.35
(a)
ψ(x)=
Ae
ikx
+ Be
−ikx
(x<0)
Fe
ilx
(x>0)
where k ≡
√
2mE
,l≡
2m(E + V
0
)
.
Continuity of ψ ⇒ A + B = F
Continuity of ψ
⇒ ik(A − B)=ilF
=⇒
A + B =
k
l
(A − B); A
1 −
k
l
= −B
1+
k
l
;
B
A
= −
1 − k/l
1+k/l
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

40 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
R =
B
A
2
=
l − k
l + k
2
=
'
√
E + V
0
−
√
E
√
E + V
0
+
√
E
(
2
=
'
1+V
0
/E − 1
1+V
0
/E +1
(
2
=
√
1+3− 1
√
1+3+1
2
=
2 − 1
2+1
2
=
1
9
.
(b) The cliff is two-dimensional, and even if we pretend the car drops straight down, the potential as a function
of distance along the (crooked, but now one-dimensional) path is −mgx (with x the vertical coordinate),
as shown.
V(x)
x
-V
0
(c) Here V
0
/E =12/4 = 3, the same as in part (a), so R =1/9, and hence T = 8/9 = 0.8889.
Problem 2.36
Start with Eq. 2.22: ψ(x)=A sin kx + B cos kx. This time the boundary conditions are ψ(a)=ψ(−a)=0:
A sin ka + B cos ka =0; −A sin ka + B cos ka =0.
Subtract : A sin ka =0⇒ ka = jπ or A =0,
Add : B cos ka =0⇒ ka =(j −
1
2
)π or B =0,
(where j =1, 2, 3,...).
If B = 0 (so A = 0), k = jπ/a. In this case let n ≡ 2j (so n is an even integer); then k = nπ/2a,
ψ = A sin(nπx/2a). Normalizing: 1 = |A|
2
a
−a
sin
2
(nπx/2a) dx = |A|
2
/2 ⇒ A =
√
2.
If A = 0 (so B = 0), k =(j −
1
2
)π/a. In this case let n ≡ 2j − 1(n is an odd integer); again k = nπ/2a,
ψ = B cos(nπx/2a). Normalizing: 1 = |B|
2
a
−a
cos
2
(nπx/2a)dx = |a|
2
/2 ⇒ B =
√
2.
In either case Eq. 2.21 yields E =
2
k
2
2m
=
n
2
π
2
2
2m(2a)
2
(in agreement with Eq. 2.27 for a well of width 2a).
The substitution x → (x + a)/2 takes Eq. 2.28 to
2
a
sin
nπ
a
(x + a)
2
=
2
a
sin
nπx
2a
+
nπ
2
=
(−1)
n/2
2
a
sin
nπx
2a
(n even),
(−1)
(n−1)/2
2
a
cos
nπx
2a
(n odd).
So (apart from normalization) we recover the results above. The graphs are the same as Figure 2.2, except that
some are upside down (different normalization).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 41
cos(πx/2a)
sin(2πx/2a) cos(3πx/2a)
Problem 2.37
Use the trig identity sin 3θ = 3 sin θ −4 sin
3
θ to write
sin
3
πx
a
=
3
4
sin
πx
a
−
1
4
sin
3πx
a
. So (Eq. 2.28): Ψ(x, 0) = A
a
2
3
4
ψ
1
(x) −
1
4
ψ
3
(x)
.
Normalize using Eq. 2.38: |A|
2
a
2
9
16
+
1
16
=
5
16
a|A|
2
=1⇒ A =
4
√
5a
.
So Ψ(x, 0) =
1
√
10
[3ψ
1
(x) − ψ
3
(x)] , and hence (Eq. 2.17)
Ψ(x, t)=
1
√
10
3ψ
1
(x)e
−iE
1
t/
− ψ
3
(x)e
−iE
3
t/
.
|Ψ(x, t)|
2
=
1
10
9ψ
2
1
+ ψ
2
3
− 6ψ
1
ψ
3
cos
E
3
− E
1
t
;so
x =
a
0
x|Ψ(x, t)|
2
dx =
9
10
x
1
+
1
10
x
3
−
3
5
cos
E
3
− E
1
t
a
0
xψ
1
(x)ψ
3
(x)dx,
where x
n
= a/2 is the expectation value of x in the nth stationary state. The remaining integral is
2
a
a
0
x sin
πx
a
sin
3πx
a
dx =
1
a
a
0
x
cos
2πx
a
− cos
4πx
a
dx
=
1
a
a
2π
2
cos
2πx
a
+
xa
2π
sin
2πx
a
−
a
4π
2
cos
4πx
a
−
xa
4π
sin
4πx
a
a
0
=0.
Evidently then,
x =
9
10
a
2
+
1
10
a
2
=
a
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

42 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Problem 2.38
(a) New allowed energies: E
n
=
n
2
π
2
2
2m(2a)
2
;Ψ(x, 0) =
2
a
sin
π
a
x
,ψ
n
(x)=
2
2a
sin
nπ
2a
x
.
c
n
=
√
2
a
a
0
sin
π
a
x
sin
nπ
2a
x
dx =
√
2
2a
a
0
+
cos
n
2
− 1
πx
a
− cos
n
2
+1
πx
a
,
dx.
=
1
√
2a
sin
n
2
− 1
πx
a
n
2
− 1
π
a
−
sin
n
2
+1
πx
a
n
2
+1
π
a
a
0
(for n =2)
=
1
√
2π
sin
n
2
− 1
π
n
2
− 1
−
sin
n
2
+1
π
n
2
+1
=
sin
n
2
+1
π
√
2π
1
n
2
− 1
−
1
n
2
+1
=
4
√
2
π
sin
n
2
+1
π
(n
2
− 4)
=
0, if n is even
±
4
√
2
π(n
2
−4)
, if n is odd
.
c
2
=
√
2
a
a
0
sin
2
π
a
x
dx =
√
2
a
a
0
1
2
dx =
1
√
2
. So the probability of getting E
n
is
P
n
= |c
n
|
2
=
1
2
, if n =2
32
π
2
(n
2
−4)
2
, if n is odd
0, otherwise
.
Most probable
: E
2
=
π
2
2
2ma
2
(same as before). Probability: P
2
= 1/2.
(b) Next most probable: E
1
=
π
2
2
8ma
2
, with probability P
1
=
32
9π
2
=0.36025.
(c) H =
Ψ
∗
HΨ dx =
2
a
a
0
sin
π
a
x
−
2
2m
d
2
dx
2
sin
π
a
x
dx, but this is exactly the same as before the wall
moved – for which we know the answer:
π
2
2
2ma
2
.
Problem 2.39
(a) According to Eq. 2.36, the most general solution to the time-dependent Schr¨odinger equation for the
infinite square well is
Ψ(x, t)=
∞
n=1
c
n
ψ
n
(x)e
−i(n
2
π
2
/2ma
2
)t
.
Now
n
2
π
2
2ma
2
T =
n
2
π
2
2ma
2
4ma
2
π
=2πn
2
,soe
−i(n
2
π
2
/2ma
2
)(t+T )
= e
−i(n
2
π
2
/2ma
2
)t
e
−i2πn
2
, and since n
2
is
an integer, e
−i2πn
2
=1. Therefore Ψ(x, t + T )=Ψ(x, t). QED
(b) The classical revival time is the time it takes the particle to go down and back: T
c
=2a/v, with the
velocity given by
E =
1
2
mv
2
⇒ v =
2E
m
⇒
T
c
= a
2m
E
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 43
(c) The two revival times are equal if
4ma
2
π
= a
2m
E
, or
E =
π
2
2
8ma
2
=
E
1
4
.
Problem 2.40
(a) Let V
0
≡ 32
2
/ma
2
. This is just like the odd bound states for the finite square well, since they are the
ones that go to zero at the origin. Referring to the solution to Problem 2.29, the wave function is
ψ(x)=
D sin lx, l ≡
2m(E + V
0
)/ (0 <x<a),
Fe
−κx
,κ≡
√
−2mE/ (x>a),
and the boundary conditions at x = a yield
−cot z =
(z
0
/z)
2
− 1
with
z
0
=
√
2mV
0
a =
2m(32
2
/ma
2
)
a =8.
Referring to the figure (Problem 2.29), and noting that (5/2)π =7.85 <z
0
< 3π =9.42, we see that there
are
three bound states.
(b) Let
I
1
≡
a
0
|ψ|
2
dx = |D|
2
a
0
sin
2
lx dx = |D|
2
x
2
−
1
2l
sin lx cos lx
a
0
= |D|
2
a
2
−
1
2l
sin lz cos la
;
I
2
≡
∞
a
|ψ|
2
dx = |F |
2
∞
a
e
−2κx
dx = |F |
2
−
e
−2κx
2κ
∞
a
= |F |
2
e
−2κa
2κ
.
But continuity at x = a ⇒ Fe
−κa
= D sin la,soI
2
= |D|
2
sin
2
la
2κ
.
Normalizing:
1=I
1
+ I
2
= |D|
2
a
2
−
1
2l
sin la cos la +
sin
2
la
2κ
=
1
2κ
|D|
2
κa −
κ
l
sin la cos la + sin
2
la
But (referring again to Problem 2.29) κ/l = −cot la, so
=
1
2κ
|D|
2
κa + cot la sin la cos la + sin
2
la
= |D|
2
(1 + κa)
2κ
.
So |D|
2
=2κ/(1 + κa), and the probability of finding the particle outside the well is
P = I
2
=
2κ
1+κa
sin
2
la
2κ
=
sin
2
la
1+κa
.
We can express this interms of z ≡ la and z
0
: κa =
z
2
0
− z
2
(page 80),
sin
2
la = sin
2
z =
1
1 + cot
2
z
=
1
1+(z
0
/z)
2
− 1
=
z
z
0
2
⇒ P =
z
2
z
2
0
(1 +
z
2
0
− z
2
)
.
So far, this is correct for any bound state. In the present case z
0
= 8 and z is the third solution
to −cot z =
(8/z)
2
− 1, which occurs somewhere in the interval 7.85 <z<8. Mathematica gives
z =7.9573 and
P =0.54204.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

44 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Problem 2.41
(a) In the standard notation ξ ≡
mω/x, α ≡ (mω/π)
1/4
,
Ψ(x, 0) = A(1 − 2ξ)
2
e
−ξ
2
/2
= A(1 − 4ξ +4ξ
2
)e
−ξ
2
/2
.
It can be expressed as a linear combination of the first three stationary states (Eq. 2.59 and 2.62, and
Problem 2.10):
ψ
0
(x)=αe
−ξ
2
/2
,ψ
1
(x)=
√
2 αξe
−ξ
2
/2
,ψ
2
(x)=
α
√
2
(2ξ
2
− 1)e
−ξ
2
/2
.
So Ψ(x, 0) = c
0
ψ
0
+ c
1
ψ
1
+ c
2
ψ
2
= α(c
0
+
√
2ξc
1
+
√
2ξ
2
c
2
−
1
√
2
c
2
)e
−ξ
2
/2
with (equating like powers)
α
√
2c
2
=4A ⇒ c
2
=2
√
2A/α,
α
√
2c
1
= −4A ⇒ c
1
= −2
√
2A/α,
α(c
0
− c
2
/
√
2) = A ⇒ c
0
=(A/α)+c
2
/
√
2=(1+2)A/α =3A/α.
Normalizing: 1 = |c
0
|
2
+ |c
1
|
2
+ |c
2
|
2
=(8+8+9)(A/α)
2
= 25(A/α)
2
⇒ A = α/5.
c
0
=
3
5
,c
1
= −
2
√
2
5
,c
2
=
2
√
2
5
.
H =
|c
n
|
2
(n +
1
2
)ω =
9
25
1
2
ω
+
8
25
3
2
ω
+
8
25
5
2
ω
=
ω
50
(9+24+40)=
73
50
ω.
(b)
Ψ(x, t)=
3
5
ψ
0
e
−iωt/2
−
2
√
2
5
ψ
1
e
−3iωt/2
+
2
√
2
5
ψ
2
e
−5iωt/2
= e
−iωt/2
3
5
ψ
0
−
2
√
2
5
ψ
1
e
−iωt
+
2
√
2
5
ψ
2
e
−2iωt
.
To change the sign of the middle term we need e
−iωT
= −1 (then e
−2iωT
= 1); evidently ωT = π,or
T = π/ω.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 45
Problem 2.42
Everything in Section 2.3.2 still applies, except that there is an additional boundary condition: ψ(0) = 0. This
eliminates all the even solutions (n =0, 2, 4,...), leaving only the odd solutions. So
E
n
=
n +
1
2
ω, n =1, 3, 5,... .
Problem 2.43
(a) Normalization is the same as before: A =
2a
π
1/4
.
(b) Equation 2.103 says
φ(k)=
1
√
2π
2a
π
1/4
∞
−∞
e
−ax
2
e
ilx
e
−ikx
dx [same as before, only k → k − l]=
1
(2πa)
1/4
e
−(k−l)
2
/4a
.
Ψ(x, t)=
1
√
2π
1
(2πa)
1/4
∞
−∞
e
−(k−l)
2
/4a
e
i(kx−k
2
t/2m)
e
−l
2
/4a
e
−
[(
1
4a
+i
t
2m
)
k
2
−
(
ix+
l
2a
)
k
]
dk
=
1
√
2π
1
(2πa)
1/4
e
−l
2
/4a
π
1
4a
+ i
t
2m
e
(ix+l/2a)
2
/[4(1/4a+it/2m)]
=
2a
π
1/4
1
1+2iat/m
e
−l
2
/4a
e
a(ix+l/2a)
2
/(1+2iat/m)
.
(c) Let θ ≡ 2at/m, as before: |Ψ|
2
=
2a
π
1
√
1+θ
2
e
−l
2
/2a
e
a
(ix+l/2a)
2
(1+iθ)
+
(−ix+l/2a)
2
(1−iθ)
. Expand the term in
square brackets:
[]=
1
1+θ
2
(1 − iθ)
ix +
l
2a
2
+(1+iθ)
−ix +
l
2a
2
=
1
1+θ
2
−x
2
+
ixl
a
+
l
2
4a
2
+
−x
2
−
ixl
a
+
l
2
4a
2
+iθ
x
2
−
ixl
a
−
l
2
4a
2
+ iθ
−x
2
−
ixl
a
+
l
2
4a
2
=
1
1+θ
2
−2x
2
+
l
2
2a
2
+2θ
xl
a
=
1
1+θ
2
−2x
2
+2θ
xl
a
−
θ
2
l
2
2a
2
+
θ
2
l
2
2a
2
+
l
2
2a
2
=
−2
1+θ
2
x −
θl
2a
2
+
l
2
2a
2
.
|Ψ(x, t)|
2
=
2
π
a
1+θ
2
e
−l
2
/2a
e
−
2a
1+θ
2
(x−θl/2a)
2
e
l
2
/2a
=
2
π
we
−2w
2
(x−θl/2a)
2
,
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

46 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
where w ≡
a/(1 + θ
2
). The result is the same as before, except x →
x −
θl
2a
=
x −
l
m
t
,so|Ψ|
2
has
the same (flattening Gaussian) shape – only this time the center moves at constant speed v = l/m.
(d)
x =
∞
−∞
x|Ψ(x, t)|
2
dx. Let y ≡ x − θl/2a = x − vt, so x = y + vt.
=
∞
−∞
(y + vt)
2
π
we
−2w
2
y
2
dy = vt.
(The first integral is trivially zero; the second is 1 by normalization.)
=
l
m
t;
p = m
dx
dt
=
l.
x
2
=
∞
−∞
(y + vt)
2
2
π
we
−2w
2
y
2
dy =
1
4w
2
+0+(vt)
2
(the first integral is same as before).
x
2
=
1
4w
2
+
lt
m
2
. p
2
= −
2
∞
−∞
Ψ
∗
d
2
Ψ
dx
2
dx.
Ψ=
2a
π
1/4
1
√
1+iθ
e
−l
2
/4a
e
a(ix+l/2a)
2
/(1+iθ)
, so
dΨ
dx
=
2ia
ix +
l
2a
(1 + iθ)
Ψ;
d
2
Ψ
dx
2
=
2ia(ix + l/2a)
1+iθ
dΨ
dx
+
2i
2
a
1+iθ
Ψ=
−4a
2
(ix + l/2a)
2
(1 + iθ)
2
−
2a
1+iθ
Ψ.
p
2
=
4a
2
2
(1 + iθ)
2
∞
−∞
ix +
l
2a
2
+
(1 + iθ)
2a
|Ψ|
2
dx
=
4a
2
2
(1 + iθ)
2
∞
−∞
−
y + vt −
il
2a
2
+
(1 + iθ)
2a
|Ψ|
2
dy
=
4a
2
2
(1 + iθ)
2
−
∞
−∞
y
2
|Ψ|
2
dy − 2
vt −
il
2a
∞
−∞
y|Ψ|
2
dy
+
−
vt −
il
2a
2
+
(1 + iθ)
2a
∞
−∞
|Ψ|
2
dy
=
4a
2
2
(1 + iθ)
2
−
1
4w
2
+0−
vt −
il
2a
2
+
(1 + iθ)
2a
=
4a
2
2
(1 + iθ)
2
−
1+θ
2
4a
−
−il
2a
(1 + iθ)
2
+
(1 + iθ)
2a
=
a
1+iθ
−(1 − iθ)+
l
2
a
(1 + iθ)+2
=
a
2
1+iθ
(1 + iθ)
1+
l
2
a
=
2
(a + l
2
).
σ
2
x
= x
2
−x
2
=
1
4w
2
+
lt
m
2
−
lt
m
2
=
1
4w
2
⇒ σ
x
=
1
2w
;
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 47
σ
2
p
= p
2
−p
2
=
2
a +
2
l
2
−
2
l
2
=
2
a, so σ
p
=
√
a.
(e) σ
x
and σ
p
are same as before, so the uncertainty principle still holds.
Problem 2.44
Equation 2.22 ⇒ ψ(x)=A sin kx + B cos kx, 0 ≤ x ≤ a, with k =
√
2mE/
2
.
Even solutions: ψ(x)=ψ(−x)=A sin(−kx)+B cos(−kx)=−A sin kx + B cos kx (−a ≤ x ≤ 0).
Boundary
conditions
ψ continuous at 0 : B = B (no new condition).
ψ
discontinuous (Eq. 2.125 with sign of α switched): Ak + Ak =
2mα
2
B ⇒ B =
2
k
mα
A.
ψ → 0atx = a : A sin(ka)+
2
k
mα
A cos(ka)=0⇒ tan(ka)=−
2
k
mα
.
ψ(x)=A
sin kx +
2
k
mα
cos kx
(0 ≤ x ≤ a); ψ(−x)=ψ(x).
π2π
3π
tan(ka)
-h k
mα
2
ka
From the graph, the allowed energies are slightly above
ka =
nπ
2
(n =1, 3, 5,...)so
E
n
n
2
π
2
2
2m(2a)
2
(n =1, 3, 5,...).
These energies are somewhat higher than the corresponding energies for the infinite square well (Eq. 2.27, with
a → 2a). As α → 0, the straight line (−
2
k/mα) gets steeper and steeper, and the intersections get closer to
nπ/2; the energies then reduce to those of the ordinary infinite well. As α →∞, the straight line approaches
horizontal, and the intersections are at nπ (n =1, 2, 3,...), so E
n
→
n
2
π
2
2
2ma
2
– these are the allowed energies for
the infinite square well of width a. At this point the barrier is impenetrable, and we have two isolated infinite
square wells.
Odd solutions: ψ(x)=−ψ(−x)=−A sin(−kx) −B cos(−kx)=A sin(kx) − B cos(kx)(−a ≤ x ≤ 0).
Boundary conditions
ψ continuous at 0 : B = −B ⇒ B =0.
ψ
discontinuous: Ak −Ak =
2mα
2
(0) (no new condition).
ψ(a)=0⇒ A sin(ka)=0⇒ ka =
nπ
2
(n =2, 4, 6,...).
ψ(x)=A sin(kx), (−a<x<a); E
n
=
n
2
π
2
2
2m(2a)
2
(n =2, 4, 6,...).
These are the exact (even n) energies (and wave functions) for the infinite square well (of width 2a). The point
is that the odd solutions (even n) are zero at the origin, so they never “feel” the delta function at all.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

48 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Problem 2.45
−
2
2m
d
2
ψ
1
dx
2
+ Vψ
1
= Eψ
1
⇒−
2
2m
ψ
2
d
2
ψ
1
dx
2
+ Vψ
1
ψ
2
= Eψ
1
ψ
2
−
2
2m
d
2
ψ
2
dx
2
+ Vψ
2
= Eψ
2
⇒−
2
2m
ψ
1
d
2
ψ
2
dx
2
+ Vψ
1
ψ
2
= Eψ
1
ψ
2
⇒−
2
2m
ψ
2
d
2
ψ
1
dx
2
− ψ
1
d
2
ψ
2
dx
2
=0.
But
d
dx
ψ
2
dψ
1
dx
− ψ
1
dψ
2
dx
=
dψ
2
dx
dψ
1
dx
+ ψ
2
d
2
ψ
1
dx
2
−
dψ
1
dx
dψ
2
dx
− ψ
1
d
2
ψ
2
dx
2
= ψ
2
d
2
ψ
1
dx
2
− ψ
1
d
2
ψ
2
dx
2
. Since this is
zero, it follows that ψ
2
dψ
1
dx
− ψ
1
dψ
2
dx
= K (a constant). But ψ → 0at∞ so the constant must be zero. Thus
ψ
2
dψ
1
dx
= ψ
1
dψ
2
dx
, or
1
ψ
1
dψ
1
dx
=
1
ψ
2
dψ
2
dx
, so ln ψ
1
=lnψ
2
+ constant, or ψ
1
= (constant)ψ
2
. QED
Problem 2.46
−
2
2m
d
2
ψ
dx
2
= Eψ (where x is measured around the circumference), or
d
2
ψ
dx
2
= −k
2
ψ, with k ≡
√
2mE
,so
ψ(x)=Ae
ikx
+ Be
−ikx
.
But ψ(x + L)=ψ(x), since x + L is the same point as x,so
Ae
ikx
e
ikL
+ Be
−ikx
e
−ikL
= Ae
ikx
+ Be
−ikx
,
and this is true for all x. In particular, for x =0:
(1) Ae
ikL
+ Be
−ikL
= A + B. And for x =
π
2k
:
Ae
iπ/2
e
ikL
+ Be
−iπ/2
e
−ikL
= Ae
iπ/2
+ Be
−iπ/2
, or iAe
ikL
− iBe
−ikL
= iA − iB, so
(2) Ae
ikL
− Be
−ikL
= A − B. Add (1) and (2): 2Ae
ikL
=2A.
Either A = 0, or else e
ikL
= 1, in which case kL =2nπ (n =0, ±1, ±2,...). But if A = 0, then Be
−ikL
= B,
leading to the same conclusion. So for every positive n there are two solutions: ψ
+
n
(x)=Ae
i(2nπx/L)
and
ψ
−
n
(x)=Be
−i(2nπx/L)
(n = 0 is ok too, but in that case there is just one solution). Normalizing:
L
0
|ψ
±
|
2
dx =
1 ⇒ A = B =1/
√
L. Any other solution (with the same energy) is a linear combination of these.
ψ
±
n
(x)=
1
√
L
e
±i(2nπx/L)
; E
n
=
2n
2
π
2
2
mL
2
(n =0, 1, 2, 3,...).
The theorem fails because here ψ does not go to zero at ∞; x is restricted to a finite range, and we are unable
to determine the constant K (in Problem 2.45).
Problem 2.47
(a) (i) b =0⇒ ordinary finite square well. Exponential decay outside; sinusoidal inside (cos for ψ
1
, sin for
ψ
2
). No nodes for ψ
1
, one node for ψ
2
.
(ii) Ground state is even. Exponential decay outside, sinusoidal inside the wells, hyperbolic cosine in
barrier. First excited state is odd – hyperbolic sine in barrier. No nodes for ψ
1
, one node for ψ
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 49
x
x
ψ
ψ
1
2
-a
-a
aa
x
x
b/2
b/2
-b/2
b/2+a
-b/
2
-(b/2+a)
-(b/
2+a)
b/
2+a
ψ
1
2
ψ
(iii) For b a, same as (ii), but wave function very small in barrier region. Essentially two isolated finite
square wells; ψ
1
and ψ
2
are degenerate (in energy); they are even and odd linear combinations of the
ground states of the two separate wells.
ψ
ψ
1
2
x
x
-(b/
2+a)
-(b/
2+a)
-b/
2
-b/2
b/2
b/2
b/2+a
b/
2+a
(b) From Eq. 2.157 we know that for b = 0 the energies fall slightly below
E
1
+ V
0
≈
π
2
2
2m(2a)
2
=
h
4
E
2
+ V
0
≈
4π
2
2
2m(2a)
2
= h
where h ≡
π
2
2
2ma
2
.
For b a, the width of each (isolated) well is a,so
E
1
+ V
0
≈ E
2
+ V
0
≈
π
2
2
2ma
2
= h (again, slightly below this).
Hence the graph (next page). [Incidentally, within each well,
d
2
ψ
dx
2
= −
2m
2
(V
0
+ E)ψ, so the more curved
the wave function, the higher the energy. This is consistent with the graphs above.]
(c) In the (even) ground state the energy is lowest in configuration (i), with b → 0, so the electron tends to
draw the nuclei
together, promoting bonding of the atoms. In the (odd) first excited state, by contrast,
the electron drives the nuclei
apart.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
50 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
h
h/4
b
E+V
0
E +V
E +V
0
0
1
2
Problem 2.48
(a)
dΨ
dx
=
2
√
3
a
√
a
·
1, (0 <x<a/2)
−1, (a/2 <x<a)
=
2
√
3
a
√
a
1 − 2θ
x −
a
2
.
(b)
d
2
Ψ
dx
2
=
2
√
3
a
√
a
− 2δ
x −
a
2
=
−
4
√
3
a
√
a
δ
x −
a
2
.
(c)
H = −
2
2m
−
4
√
3
a
√
a
Ψ
∗
δ
x −
a
2
dx =
2
√
3
2
ma
√
a
Ψ
∗
a
2
√
3/a
=
2 · 3 ·
2
m · a · a
=
6
2
ma
2
.
Problem 2.49
(a)
∂Ψ
∂t
=
−
mω
2
a
2
2
−2iωe
−2iωt
+
i
m
− 2ax(−iω)e
−iωt
Ψ, so
i
∂Ψ
∂t
=
−
1
2
ma
2
ω
2
e
−2iωt
+
1
2
ω + maxω
2
e
−iωt
Ψ.
∂Ψ
∂x
=
−
mω
2
2x − 2ae
−iωt
Ψ=−
mω
x − ae
−iωt
Ψ;
∂
2
Ψ
∂x
2
= −
mω
Ψ −
mω
x − ae
−iωt
∂Ψ
∂x
=
−
mω
+
mω
2
x − ae
−iωt
2
Ψ.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 51
−
2
2m
∂
2
Ψ
∂x
2
+
1
2
mω
2
x
2
Ψ=−
2
2m
−
mω
+
mω
2
x − ae
−iωt
2
Ψ+
1
2
mω
2
x
2
Ψ
=
1
2
ω −
1
2
mω
2
x
2
− 2axe
−iωt
+ a
2
e
−2iωt
+
1
2
mω
2
x
2
Ψ
=
1
2
ω + maxω
2
e
−iωt
−
1
2
mω
2
a
2
e
−2iωt
Ψ
= i
∂Ψ
∂t
(comparing second line above).
(b)
|Ψ|
2
=
mω
π
e
−
mω
2
x
2
+
a
2
2
(
1+e
2iωt
)
−
it
m
−2axe
iωt
+
x
2
+
a
2
2
(
1+e
−2iωt
)
+
it
m
−2axe
−iωt
=
mω
π
e
−
mω
2
[
2x
2
+a
2
+a
2
cos(2ωt)−4ax cos(ωt)
]
. But a
2
[1 + cos(2ωt)] = 2a
2
cos
2
ωt, so
=
mω
π
e
−
mω
[
x
2
−2ax cos(ωt)+a
2
cos
2
(ωt)
]
=
mω
π
e
−
mω
(x−a cos ωt)
2
.
The wave packet is a Gaussian of fixed shape, whose center oscillates back and forth sinusoidally, with
amplitude a and angular frequency ω.
(c) Note that this wave function is correctly normalized (compare Eq. 2.59). Let y ≡ x − a cos ωt :
x =
x|Ψ|
2
dx =
(y + a cos ωt)|Ψ|
2
dy =0+a cos ωt
|Ψ|
2
dy = a cos ωt.
p = m
dx
dt
=
−maω sin ωt.
dp
dt
= −maω
2
cos ωt. V =
1
2
mω
2
x
2
=⇒
dV
dx
= mω
2
x.
−
dV
dx
= −mω
2
x = −mω
2
a cos ωt =
dp
dt
, so Ehrenfest’s theorem is satisfied.
Problem 2.50
(a)
∂Ψ
∂t
=
−
mα
2
∂
∂t
|x − vt|−i
(E +
1
2
mv
2
)
Ψ;
∂
∂t
|x − vt| =
−v, if x − vt > 0
v, if x − vt < 0
.
We can write this in terms of the θ-function (Eq. 2.143):
2θ(z) −1=
1, if z>0
−1, if z<0
, so
∂
∂t
|x − vt| = −v[2θ(x − vt) − 1].
i
∂Ψ
∂t
=
i
mαv
[2θ(x −vt) − 1] + E +
1
2
mv
2
Ψ. []
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
52 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
∂Ψ
∂x
=
−
mα
2
∂
∂x
|x − vt|+
imv
Ψ
∂
∂x
|x − vt| = {1, if x>vt; −1, if x<vt} =2θ(x − vt) −1.
=
−
mα
2
[2θ(x −vt) − 1] +
imv
Ψ.
∂
2
Ψ
∂x
2
=
−
mα
2
[2θ(x −vt) − 1] +
imv
2
Ψ −
2mα
2
∂
∂x
θ(x −vt)
Ψ.
But (from Problem 2.24(b))
∂
∂x
θ(x −vt)=δ(x − vt), so
−
2
2m
∂
2
Ψ
∂x
2
− αδ(x −vt)Ψ
=
'
−
2
2m
−
mα
2
[2θ(x −vt) − 1] +
imv
2
+ αδ(x −vt) −αδ(x − vt)
(
Ψ
= −
2
2m
m
2
α
2
4
[2θ(x −vt) − 1]
2
1
−
m
2
v
2
2
− 2i
mv
mα
2
[2θ(x −vt) − 1]
Ψ
=
−
mα
2
2
2
+
1
2
mv
2
+ i
mvα
[2θ(x −vt) − 1]
Ψ=i
∂Ψ
∂t
(compare []).
(b)
|Ψ|
2
=
mα
2
e
−2mα|y|/
2
(y ≡ x − vt).
Check normalization: 2
mα
2
∞
0
e
−2mαy/
2
dy =
2mα
2
2
2mα
=1.
H =
∞
−∞
Ψ
∗
HΨdx. But HΨ=i
∂Ψ
∂t
, which we calculated above [].
=
imαv
[2θ(y) − 1] + E +
1
2
mv
2
|Ψ|
2
dy = E +
1
2
mv
2
.
(Note that [2θ(y)−1] is an odd function of y.) Interpretation: The wave packet is dragged along (at speed
v) with the delta-function. The total energy is the energy it would have in a stationary delta-function
(E), plus kinetic energy due to the motion (
1
2
mv
2
).
Problem 2.51
(a) Figure at top of next page.
(b)
dψ
0
dx
= −Aa sech(ax) tanh(ax);
d
2
ψ
0
dx
2
= −Aa
2
−sech(ax) tanh
2
(ax) + sech(ax) sech
2
(ax)
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 53
V(x)
x
Hψ
0
= −
2
2m
d
2
ψ
0
dx
2
−
2
a
2
m
sech
2
(ax)ψ
0
=
2
2m
Aa
2
−sech(ax) tanh
2
(ax) + sech
3
(ax)
−
2
a
2
m
A sech
3
(ax)
=
2
a
2
A
2m
−sech(ax) tanh
2
(ax) + sech
3
(ax) − 2 sech
3
(ax)
= −
2
a
2
2m
A sech(ax)
tanh
2
(ax) + sech
2
(ax)
.
But (tanh
2
θ + sech
2
θ)=
sinh
2
θ
cosh
2
θ
+
1
cosh
2
θ
=
sinh
2
θ +1
cosh
2
θ
=1, so
= −
2
a
2
2m
ψ
0
. QED Evidently E = −
2
a
2
2m
.
1=|A|
2
∞
−∞
sech
2
(ax)dx = |A|
2
1
a
tanh(ax)
∞
−∞
=
2
a
|A|
2
=⇒ A =
a
2
.
x
ψ(x)
(c)
dψ
k
dx
=
A
ik + a
(ik −a tanh ax)ik − a
2
sech
2
ax
e
ikx
.
d
2
ψ
k
dx
2
=
A
ik + a
-
ik
(ik −a tanh ax)ik − a
2
sech
2
ax
− a
2
ik sech
2
ax +2a
3
sech
2
ax tanh ax
.
e
ikx
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
54 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
−
2
2m
d
2
ψ
k
dx
2
+ Vψ
k
=
A
ik + a
−
2
ik
2m
−k
2
− iak tanh ax − a
2
sech
2
ax
+
2
a
2
2m
ik sech
2
ax
−
2
a
3
m
sech
2
ax tanh ax −
2
a
2
m
sech
2
ax(ik −a tanh ax)
e
ikx
=
Ae
ikx
ik + a
2
2m
ik
3
− ak
2
tanh ax + ia
2
k sech
2
ax + ia
2
k sech
2
ax
−2a
3
sech
2
ax tanh ax − 2ia
2
k sech
2
ax +2a
3
sech
2
ax tanh ax
=
Ae
ikx
ik + a
2
2m
k
2
(ik −a tanh ax)=
2
k
2
2m
ψ
k
= Eψ
k
. QED
As x → +∞, tanh ax → +1, so
ψ
k
(x) → A
ik −a
ik + a
e
ikx
, which represents a transmitted wave.
R =0. T =
ik −a
ik + a
2
=
−ik −a
−ik + a
ik −a
ik + a
=
1.
Problem 2.52
(a) (1) From Eq. 2.133: F + G = A + B.
(2) From Eq. 2.135: F −G =(1+2iβ)A − (1 − 2iβ)B, where β = mα/
2
k.
Subtract: 2G = −2iβA + 2(1 − iβ)B ⇒ B =
1
1 − iβ
(iβA + G). Multiply (1) by (1 − 2iβ) and add:
2(1 − iβ)F − 2iβG =2A ⇒ F =
1
1 − iβ
(A + iβG).
S =
1
1 − iβ
iβ 1
1 iβ
.
(b) For an even potential, V (−x)=V (x), scattering from the right is the same as scattering from the left, with
x ↔−x, A ↔ G, B ↔ F (see Fig. 2.22): F = S
11
G + S
12
A, B = S
21
G + S
22
A. So S
11
= S
22
,S
21
= S
12
.
(Note that the delta-well S matrix in (a) has this property.) In the case of the finite square well, Eqs. 2.167
and 2.168 give
S
21
=
e
−2ika
cos 2la − i
(k
2
+l
2
)
2kl
sin 2la
; S
11
=
i
(l
2
−k
2
)
2kl
sin 2la e
−2ika
cos 2la − i
(k
2
+l
2
)
2kl
sin 2la
. So
S =
e
−2ika
cos 2la − i
(k
2
+l
2
)
2kl
sin 2la
'
i
(l
2
−k
2
)
2kl
sin 2la 1
1 i
(l
2
−k
2
)
2kl
sin 2la
(
.
Problem 2.53
(a)
B = S
11
A + S
12
G ⇒ G =
1
S
12
(B − S
11
A)=M
21
A + M
22
B ⇒ M
21
= −
S
11
S
12
,M
22
=
1
S
12
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION 55
F = S
21
A + S
22
B = S
21
A +
S
22
S
12
(B − S
11
A)=−
(S
11
S
22
− S
12
S
21
)
S
12
A +
S
22
S
12
B = M
11
A + M
12
B.
⇒ M
11
= −
det S
S
12
,M
12
=
S
22
S
12
. M =
1
S
12
−det(S) S
22
−S
11
1
.
Conversely:
G = M
21
A + M
22
B ⇒ B =
1
M
22
(G − M
21
A)=S
11
A + S
12
G ⇒ S
11
= −
M
21
M
22
; S
12
=
1
M
22
.
F = M
11
A + M
12
B = M
11
A +
M
12
M
22
(G − M
21
A)=
(M
11
M
22
− M
12
M
21
)
M
22
A +
M
12
M
22
G = S
21
A + S
22
G.
⇒ S
21
=
det M
M
22
; S
22
=
M
12
M
22
. S =
1
M
22
−M
21
1
det(M) M
12
.
[It happens that the time-reversal invariance of the Schr¨odinger equation, plus conservation of probability,
requires M
22
= M
∗
11
,M
21
= M
∗
12
, and det(M) = 1, but I won’t use this here. See Merzbacher’s Quantum
Mechanics. Similarly, for even potentials S
11
= S
22
,S
12
= S
21
(Problem 2.52).]
R
l
= |S
11
|
2
=
M
21
M
22
2
, T
l
= |S
21
|
2
=
det(M)
M
22
2
, R
r
= |S
22
|
2
=
M
12
M
22
2
, T
r
= |S
12
|
2
=
1
|M
22
|
2
.
(b)
A
B
C
D
F
G
x
M
M
1
2
F
G
= M
2
C
D
,
C
D
= M
1
A
B
, so
F
G
= M
2
M
1
A
B
= M
A
B
, with M = M
2
M
1
. QED
(c)
ψ(x)=
Ae
ikx
+ Be
−ikx
(x<a)
Fe
ikx
+ Ge
−ikx
(x>a)
.
Continuity of ψ : Ae
ika
+ Be
−ika
= Fe
ika
+ Ge
−ika
Discontinuity of ψ
: ik
Fe
ika
− Ge
−ika
− ik
Ae
ika
− Be
−ika
= −
2mα
2
ψ(a)=−
2mα
2
Ae
ika
+ Be
−ika
.
(1) Fe
2ika
+ G = Ae
2ika
+ B.
(2) Fe
2ika
− G = Ae
2ika
− B + i
2mα
2
k
Ae
2ika
+ B
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

56 CHAPTER 2. THE TIME-INDEPENDENT SCHR
¨
ODINGER EQUATION
Add (1) and (2):
2Fe
2ika
=2Ae
2ika
+ i
2mα
2
k
Ae
2ika
+ B
⇒ F =
1+i
mα
2
k
A + i
mα
2
k
e
−2ika
B = M
11
A + M
12
B.
So M
11
=(1+iβ); M
12
= iβe
−2ika
; β ≡
mα
2
k
.
Subtract (2) from (1):
2G =2B −2iβe
2ika
A − 2iβB ⇒ G =(1−iβ)B − iβe
2ika
A = M
21
A + M
22
B.
So M
21
= −iβe
2ika
; M
22
=(1− iβ). M =
(1 + iβ) iβe
−2ika
−iβe
2ika
(1 − iβ)
.
(d)
M
1
=
(1 + iβ) iβe
−2ika
−iβe
2ika
(1 − iβ)
; to get M
2
, just switch the sign of a: M
2
=
(1 + iβ) iβe
2ika
−iβe
−2ika
(1 − iβ)
.
M = M
2
M
1
=
[1+2iβ + β
2
(e
4ika
− 1)] 2iβ[cos 2ka + β sin 2ka]
−2iβ[cos 2ka + β sin 2ka][1− 2iβ + β
2
(e
−4ika
− 1)]
.
T = T
l
= T
r
=
1
|M
22
|
2
⇒
T
−1
=[1+2iβ + β
2
(e
4ika
− 1)][1 − 2iβ + β
2
(e
−4ika
− 1)]
=1− 2iβ + β
2
e
−4ika
− β
2
+2iβ +4β
2
+2iβ
3
e
−4ika
− 2iβ
3
+ β
2
e
4ika
− β
2
− 2iβ
3
e
4ika
+2iβ
3
+ β
4
(1 − e
4ika
− e
−4ika
+1)
=1+2β
2
+ β
2
(e
4ika
+ e
−4ika
) − 2iβ
3
(e
4ika
− e
−4ika
)+2β
4
− β
4
(e
4ika
+ e
−4ika
)
=1+2β
2
+2β
2
cos 4ka − 2iβ
3
2i sin 4ka +2β
4
− 2β
4
cos 4ka
=1+2β
2
(1 + cos 4ka)+4β
3
sin 4ka +2β
4
(1 − cos 4ka)
=1+4β
2
cos
2
2ka +8β
3
sin 2kacos 2ka +4β
4
sin
2
2ka
T =
1
1+4β
2
(cos 2ka + β sin 2ka)
2
Problem 2.54
I’ll just show the first two graphs, and the last two. Evidently K lies between 0.9999 and 1.0001.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
57
Problem 2.55
The correct values (in Eq. 2.72) are K =2n + 1 (corresponding to E
n
=(n +
1
2
)ω). I’ll start by “guessing”
2.9, 4.9, and 6.9, and tweaking the number until I’ve got 5 reliable significant digits. The results (see below)
are
3.0000, 5.0000, 7.0000. (The actual energies are these numbers multiplied by
1
2
ω.)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
58
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
59
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

60
Problem 2.56
The Schr¨odinger equation says −
2
2m
ψ
= Eψ, or, with the correct energies (Eq. 2.27) and a =1,ψ
+(nπ)
2
ψ =
0. I’ll start with a “guess” using 9 in place of π
2
(that is, I’ll use 9 for the ground state, 36 for the first excited
state, 81 for the next, and finally 144). Then I’ll tweak the parameter until the graph crosses the axis right
at x = 1. The results (see below) are, to five significant digits:
9.8696, 39.478, 88.826, 157.91. (The actual
energies are these numbers multiplied by
2
/2ma
2
.)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
61
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
62 CHAPTER 3. FORMALISM
Chapter 3
Formalism
Problem 3.1
(a) All conditions are trivial except Eq. A.1: we need to show that the sum of two square-integrable functions
is itself square-integrable. Let h(x)=f(x)+g(x), so that |h|
2
=(f + g)
∗
(f + g)=|f|
2
+ |g|
2
+ f
∗
g + g
∗
f
and hence
|h|
2
dx =
|f|
2
dx +
|g|
2
dx +
f
∗
gdx+
f
∗
gdx
∗
.
If f(x) and g(x) are square-integrable, then the first two terms are finite, and (by Eq. 3.7) so too are the
last two. So
|h|
2
dx is finite. QED
The set of all normalized functions is certainly not a vector space: it doesn’t include 0, and the sum of
two normalized functions is not (in general) normalized—in fact, if f(x) is normalized, then the square
integral of 2f(x)is4.
(b) Equation A.19 is trivial:
g|f =
b
a
g(x)
∗
f(x) dx =
'
b
a
f(x)
∗
g(x) dx
(
∗
= f|g
∗
.
Equation A.20 holds (see Eq. 3.9) subject to the understanding in footnote 6. As for Eq. A.21, this is
pretty obvious:
f|(b|g+ c|h)=
f(x)
∗
(bg(x)+ch(x)) dx = b
f
∗
gdx+ c
f
∗
hdx= bf |g + cf|h.
Problem 3.2
(a)
f|f =
1
0
x
2ν
dx =
1
2ν +1
x
2ν+1
1
0
=
1
2ν +1
1 − 0
2ν+1
.
Now 0
2ν+1
is finite (in fact, zero) provided (2ν +1)> 0, which is to say, ν>−
1
2
. If (2ν +1)< 0 the
integral definitely blows up. As for the critical case ν = −
1
2
, this must be handled separately:
f|f =
1
0
x
−1
dx =lnx
1
0
=ln1−ln 0 = 0 + ∞.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 63
So f(x) is in Hilbert space only for ν strictly greater than -1/2.
(b) For ν =1/2, we know from (a) that f(x) is in Hilbert space:
yes.
Since xf = x
3/2
, we know from (a) that it is in Hilbert space: yes.
For df/dx =
1
2
x
−1/2
, we know from (a) that it is not in Hilbert space: no.
[Moral: Simple operations, such as differenting (or multiplying by 1/x), can carry a function out of Hilbert
space.]
Problem 3.3
Suppose h|
ˆ
Qh =
ˆ
Qh|h for all functions h(x). Let h(x)=f(x)+cg(x) for some arbitrary constant c. Then
h|
ˆ
Qh = (f + cg)|
ˆ
Q(f + cg) = f|
ˆ
Qf + cf|
ˆ
Qg+ c
∗
g|
ˆ
Qf + |c|
2
g|
ˆ
Qg;
ˆ
Qh|h =
ˆ
Q(f + cg)|(f + cg) =
ˆ
Qf|f + c
ˆ
Qf|g+ c
∗
ˆ
Qg|f + |c|
2
ˆ
Qg|g.
Equating the two and noting that f |
ˆ
Qf =
ˆ
Qf|f and g|
ˆ
Qg =
ˆ
Qg|g leaves
cf|
ˆ
Qg+ c
∗
g|
ˆ
Qf = c
ˆ
Qf|g+ c
∗
ˆ
Qg|f.
In particlar, choosing c =1:
f|
ˆ
Qg+ g|
ˆ
Qf =
ˆ
Qf|g+
ˆ
Qg|f,
whereas if c = i:
f|
ˆ
Qg−g|
ˆ
Qf =
ˆ
Qf|g−
ˆ
Qg|f.
Adding the last two equations:
f|
ˆ
Qg =
ˆ
Qf|g. QED
Problem 3.4
(a) f|(
ˆ
H +
ˆ
K)g = f |
ˆ
Hg+ f|
ˆ
Kg =
ˆ
Hf|g +
ˆ
Kf|g = (
ˆ
H +
ˆ
K)f|g.
(b) f|α
ˆ
Qg = αf|
ˆ
Qg; α
ˆ
Qf|g = α
∗
ˆ
Qf|g. Hermitian ⇔ α is real.
(c) f|
ˆ
H
ˆ
Kg =
ˆ
Hf|
ˆ
Kg =
ˆ
K
ˆ
Hf|g,so
ˆ
H
ˆ
K is hermitian ⇔
ˆ
H
ˆ
K =
ˆ
K
ˆ
H,or [
ˆ
H,
ˆ
K]=0.
(d) f|ˆxg =
f
∗
(xg) dx =
(xf)
∗
gdx= ˆxf|g.
f|
ˆ
Hg =
f
∗
−
2
2m
d
2
dx
2
+ V
gdx= −
2
2m
f
∗
d
2
g
dx
2
dx +
f
∗
V g dx.
Integrating by parts (twice):
∞
−∞
f
∗
d
2
g
dx
2
dx = f
∗
dg
dx
∞
−∞
−
∞
−∞
df
∗
dx
dg
dx
dx = f
∗
dg
dx
∞
−∞
−
df
∗
dx
g
∞
−∞
+
∞
−∞
d
2
f
∗
dx
2
g dx.
But for functions f(x) and g(x) in Hilbert space the boundary terms vanish, so
∞
−∞
f
∗
d
2
g
dx
2
dx =
∞
−∞
d
2
f
∗
dx
2
gdx, and hence (assuming that V (x) is real):
f|
ˆ
Hg =
∞
−∞
−
2
2m
d
2
f
dx
2
+ Vf
∗
gdx=
ˆ
Hf|g.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
64 CHAPTER 3. FORMALISM
Problem 3.5
(a) f|xg =
f
∗
(xg) dx =
(xf)
∗
gdx= xf|g,so x
†
= x.
f|ig =
f
∗
(ig) dx =
(−if)
∗
gdx= −if|g,so i
†
= −i.
f|
dg
dx
=
∞
−∞
f
∗
dg
dx
dx = f
∗
g
∞
−∞
−
∞
−∞
df
dx
∗
gdx= −xf|g,so
d
dx
†
= −
d
dx
.
(b) a
+
=
1
√
2mω
(−ip + mωx). But p and x are hermitian, and i
†
= −i,so(a
+
)
†
=
1
√
2mω
(ip + mωx), or
(a
+
)
†
=(a
−
).
(c) f|(
ˆ
Q
ˆ
R)g =
ˆ
Q
†
f|
ˆ
Rg =
ˆ
R
†
ˆ
Q
†
f|g = (
ˆ
Q
ˆ
R)
†
f|g,so(
ˆ
Q
ˆ
R)
†
=
ˆ
R
†
ˆ
Q
†
.
Problem 3.6
f|
ˆ
Qg =
2π
0
f
∗
d
2
g
dφ
2
dφ = f
∗
dg
dφ
2π
0
−
2π
0
df
∗
dφ
dg
dφ
dφ = f
∗
dg
dφ
2π
0
−
df
∗
dφ
g
2π
0
+
2π
0
d
2
f
∗
dφ
2
g dφ.
As in Example 3.1, for periodic functions (Eq. 3.26) the boundary terms vanish, and we conclude that f |
ˆ
Qg =
ˆ
Qf|g,so
ˆ
Q is hermitian:
yes.
ˆ
Qf = qf ⇒
d
2
f
dφ
2
= qf ⇒ f
±
(φ)= Ae
±
√
qφ
.
The periodicity condition (Eq. 3.26) requires that
√
q(2π)=2nπi,or
√
q = in, so the eigenvalues are
q = −n
2
, (n =0, 1, 2,...). The spectrum is doubly degenerate; for a given n there are two eigenfunctions
(the plus sign or the minus sign, in the exponent), except for the special case n = 0, which is not degenerate.
Problem 3.7
(a) Suppose
ˆ
Qf = qf and
ˆ
Qg = qg. Let h(x)=af(x)+bg(x), for arbitrary constants a and b. Then
ˆ
Qh =
ˆ
Q(af + bg)=a(
ˆ
Qf)+b(
ˆ
Qg)=a(qf)+b(qg)=q(af + bg)=qh.
(b)
d
2
f
dx
2
=
d
2
dx
2
(e
x
)=
d
dx
(e
x
)=e
x
= f,
d
2
g
dx
2
=
d
2
dx
2
e
−x
=
d
dx
−e
−x
= e
−x
= g.
So both of them are eigenfunctions, with the same eigenvalue 1. The simplest orthogonal linear combina-
tions are
sinh x =
1
2
e
x
− e
−x
=
1
2
(f − g) and cosh x =
1
2
e
x
+ e
−x
=
1
2
(f + g).
(They are clearly orthogonal, since sinh x is odd while cosh x is even.)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 65
Problem 3.8
(a) The eigenvalues (Eq. 3.29) are 0, ±1, ±2,..., which are obviously real. For any two eigenfunctions,
f = A
q
e
−iqφ
and g = A
q
e
−iq
φ
(Eq. 3.28), we have
f|g = A
∗
q
A
q
2π
0
e
iqφ
e
−iq
φ
dφ = A
∗
q
A
q
e
i(q−q
)φ
i(q − q
)
2π
0
=
A
∗
q
A
q
i(q − q
)
e
i(q−q
)2π
− 1
.
But q and q
are integers,soe
i(q−q
)2π
= 1, and hence f|g = 0 (provided q = q
, so the denominator is
nonzero).
(b) In Problem 3.6 the eigenvalues are q = −n
2
, with n =0, 1, 2,..., which are obviously real. For any
two eigenfunctions, f = A
q
e
±inφ
and g = A
q
e
±in
φ
,wehave
f|g = A
∗
q
A
q
2π
0
e
∓inφ
e
±in
φ
dφ = A
∗
q
A
q
e
±i(n
−n)φ
±i(n
− n)
2π
0
=
A
∗
q
A
q
±i(n
− n)
e
±i(n
−n)2π
− 1
=0
(provided n = n
). But notice that for each eigenvalue (i.e. each value of n) there are two eigenfunctions
(one with the plus sign and one with the minus sign), and these are not orthogonal to one another.
Problem 3.9
(a) Infinite square well (Eq. 2.19).
(b)
Delta-function barrier (Fig. 2.16), or the finite rectangular barrier (Prob. 2.33).
(c)
Delta-function well (Eq. 2.114), or the finite square well (Eq. 2.145) or the sech
2
potential (Prob. 2.51).
Problem 3.10
From Eq. 2.28, with n =1:
ˆpψ
1
(x)=
i
d
dx
2
a
sin
π
a
x
=
i
2
a
π
a
cos
π
a
x
=
−i
π
a
cot
π
a
x
ψ
1
(x).
Since ˆpψ
1
is not a (constant) multiple of ψ
1
, ψ
1
is not an eigenfunction of ˆp: no. It’s true that the magnitude
of the momentum,
√
2mE
1
= π/a, is determinate, but the particle is just as likely to be found traveling to the
left (negative momentum) as to the right (positive momentum).
Problem 3.11
Ψ
0
(x, t)=
mω
π
1/4
e
−
mω
2
x
2
e
−iωt/2
;Φ(p, t)=
1
√
2π
mω
π
1/4
e
−iω/2
∞
−∞
e
−ipx/
e
−
mω
2
x
2
dx.
From Problem 2.22(b):
Φ(p, t)=
1
√
2π
mω
π
1/4
e
−iωt/2
2π
mω
e
−p
2
/2mω
=
1
(πmω)
1/4
e
−p
2
/2mω
e
−iωt/2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

66 CHAPTER 3. FORMALISM
|Φ(p, t)|
2
=
1
√
πmω
e
−p
2
/mω
. Maximum classical momentum:
p
2
2m
= E =
1
2
ω =⇒ p =
√
mω.
So the probability it’s outside classical range is:
P =
−
√
mω
−∞
|Φ|
2
dp +
∞
√
mω
|Φ|
2
dp =1−2
√
mω
0
|Φ|
2
dp. Now
√
mω
0
|Φ|
2
dp =
1
√
πmω
√
mω
0
e
−p
2
/mω
dp. Let z ≡
2
mω
p, so dp =
mω
2
dz.
=
1
√
2π
√
2
0
e
−z
2
/2
dz = F (
√
2) −
1
2
, in CRC Table notation.
P =1− 2
(F (
√
2) −
1
2
=1− 2F (
√
2) + 1 = 2
1 − F (
√
2)
=0.157.
To two digits:
0.16 (compare Prob. 2.15).
Problem 3.12
From Eq. 3.55: Ψ(x, t)=
1
√
2π
∞
−∞
e
ipx/
Φ(p, t)dp.
x =
Ψ
∗
xΨdx =
1
√
2π
e
−ip
x/
Φ
∗
(p
,t)dp
x
1
√
2π
e
+ipx/
Φ(p, t)dp
dx.
But xe
ipx/
= −i
d
dp
e
ipx/
, so (integrating by parts):
x
e
ipx/
Φ dp =
i
d
dp
e
ipx/
)Φ dp =
e
ipx/
−
i
∂
∂p
Φ(p, t)
dp.
So x =
1
2π
e
−ip
x/
Φ
∗
(p
,t)e
ipx/
−
i
∂
∂p
Φ(p, t)
dp
dp dx.
Do the x integral first, letting y ≡ x/:
1
2π
e
−ip
x/
e
ipx/
dx =
1
2π
e
i(p−p
)y
dy = δ(p −p
), (Eq. 2.144), so
x =
Φ
∗
(p
,t)δ(p − p
)
−
i
∂
∂p
Φ(p, t)
dp
dp =
Φ
∗
(p, t)
−
i
∂
∂p
Φ(p, t)
dp. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 67
Problem 3.13
(a) [AB, C]=ABC −CAB = ABC − ACB + ACB − CAB = A[B,C]+[A, C]B.
(b) Introducing a test function g(x), as in Eq. 2.50:
[x
n
,p]g = x
n
i
dg
dx
−
i
d
dx
(x
n
g)=x
n
i
dg
dx
−
i
nx
n−1
g + x
n
dg
dx
= inx
n−1
g.
So, dropping the test function, [x
n
,p]=inx
n−1
.
(c) [f,p]g = f
i
dg
dx
−
i
d
dx
(fg)=f
i
dg
dx
−
i
df
dx
g + f
dg
dx
= i
df
dx
g ⇒ [f,p]=i
df
dx
.
Problem 3.14
x,
p
2
2m
+ V
=
1
2m
x, p
2
+[x, V ];
x, p
2
= xp
2
− p
2
x = xp
2
− pxp + pxp − p
2
x =[x, p]p + p[x, p].
Using Eq. 2.51:
x, p
2
= ip + pi =2ip. And [x, V ]=0, so
x,
p
2
2m
+ V
=
1
2m
2ip =
ip
m
.
The generalized uncertainty principle (Eq. 3.62) says, in this case,
σ
2
x
σ
2
H
≥
1
2i
i
m
p
2
=
2m
p
2
⇒ σ
x
σ
H
≥
2m
|p|. QED
For stationary states σ
H
= 0 and p = 0, so it just says 0 ≥ 0.
Problem 3.15
Suppose
ˆ
Pf
n
= λ
n
f
n
and
ˆ
Qf
n
= µ
n
f
n
(that is: f
n
(x) is an eigenfunction both of
ˆ
P and of
ˆ
Q), and the set {f
n
}
is complete, so that any function f(x) (in Hilbert space) can be expressed as a linear combination: f =
/
c
n
f
n
.
Then
[
ˆ
P,
ˆ
Q]f =(
ˆ
P
ˆ
Q −
ˆ
Q
ˆ
P )
c
n
f
n
=
ˆ
P
c
n
µ
n
f
n
−
ˆ
Q
c
n
λ
n
f
n
=
c
n
µ
n
λ
n
f
n
−
c
n
λ
n
µ
n
f
n
=0.
Since this is true for any function f, it follows that [
ˆ
P,
ˆ
Q]=0.
Problem 3.16
dΨ
dx
=
i
(iax − iax + p)Ψ =
a
−x + x +
i
a
p
Ψ.
dΨ
Ψ
=
a
− x + x +
ip
a
dx ⇒ ln Ψ =
a
−
x
2
2
+ xx +
ip
a
x
+ constant.
Let constant = −
x
2
a
2
+ B (B a new constant). Then ln Ψ = −
a
2
(x −x)
2
+
ip
x + B.
Ψ=e
−
a
2
(x−x)
2
e
ipx/
e
B
= Ae
−a(x−x)
2
/2
e
ipx/
, where A ≡ e
B
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

68 CHAPTER 3. FORMALISM
Problem 3.17
(a) 1 commutes with everything, so
d
dt
Ψ|Ψ =0
(this is the conservation of normalization, which we origi-
nally proved in Eq. 1.27).
(b) Anything commutes with itself, so [H, H] = 0, and hence
d
dt
H =0
(assuming H has no explicit time
dependence); this is conservation of energy, in the sense of the comment following Eq. 2.40.
(c) [H, x]=−
ip
m
(see Problem 3.14). So
dx
dt
=
i
−
ip
m
=
p
m
(Eq. 1.33).
(d) [H, p]=
p
2
2m
+ V,p
=[V,p]=i
dV
dx
(Problem 3.13(c)). So
dp
dt
=
i
i
0
∂V
∂x
1
=
−
0
∂V
∂x
1
.
This is Ehrenfest’s theorem (Eq. 1.38).
Problem 3.18
Ψ(x, t)=
1
√
2
ψ
1
e
−iE
1
t/
+ ψ
2
e
−E
2
t/
.H
2
Ψ=
1
√
2
(H
2
ψ
1
)e
−E
1
t/
+(H
2
ψ
2
)e
−iE
n
t/
.
Hψ
1
= E
1
ψ
1
⇒ H
2
ψ
1
= E
1
Hψ
1
= E
2
1
ψ
1
, and H
2
ψ
2
= E
2
2
ψ
2
, so
H
2
=
1
2
ψ
1
e
−iE
1
t/
+ ψ
2
e
−iE
2
t/
|
E
2
1
ψ
1
e
−iE
1
t/
+ E
2
2
ψ
2
e
−iE
2
t/
=
1
2
ψ
1
|ψ
1
e
iE
1
t/
E
2
1
e
−iE
1
t/
+ ψ
1
|ψ
2
e
iE
1
t/
E
2
2
e
−iE
2
t/
+ ψ
2
|ψ
1
e
iE
2
t/
E
2
1
e
−iE
1
t/
+ ψ
2
|ψ
2
e
iE
2
t/
E
2
2
e
−iE
2
t/
=
1
2
E
2
1
+ E
2
2
.
Similarly, H =
1
2
(E
1
+ E
2
) (Problem 2.5(e)).
σ
2
H
= H
2
−H
2
=
1
2
E
2
1
+ E
2
2
−
1
4
(E
1
+ E
2
)
2
=
1
4
2E
2
1
+2E
2
2
− E
2
2
− E
2
1
− 2E
1
E
2
− E
2
2
=
1
4
E
2
1
− 2E
1
E
2
+ E
2
2
=
1
4
(E
2
− E
1
)
2
. σ
H
=
1
2
(E
2
− E
1
).
x
2
=
1
2
ψ
1
|x
2
|ψ
1
+ ψ
2
|x
2
|ψ
2
+ ψ
1
|x
2
|ψ
2
e
i(E
1
−E
2
)t/
+ ψ
2
|x
2
|ψ
1
e
i(E
2
−E
1
)t/
.
ψ
n
|x
2
|ψ
m
=
2
a
a
0
x
2
sin
nπ
a
x
sin
mπ
a
x
dx =
1
a
a
0
x
2
cos
n − m
a
πx
− cos
n + m
a
πx
dx.
Now
a
0
x
2
cos
k
a
πx
dx =
2a
2
x
k
2
π
2
cos
k
a
πx
+
a
kπ
3
kπx
a
2
− 2
sin
k
a
πx
a
0
=
2a
3
k
2
π
2
cos(kπ)=
2a
3
k
2
π
2
(−1)
k
(for k = nonzero integer).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 69
∴ ψ
n
|x
2
|ψ
m
=
2a
2
π
2
(−1)
n−m
(n − m)
2
−
(−1)
n+m
(n + m)
2
=
2a
2
π
2
(−1)
n+m
4nm
(n
2
− m
2
)
2
.
So ψ
1
|x
2
|ψ
2
= ψ
2
|x
2
|ψ
1
= −
16a
2
9π
2
. Meanwhile, from Problem 2.4, ψ
n
|x
2
|ψ
n
= a
2
1
3
−
1
2(nπ)
2
.
Thus x
2
=
1
2
a
2
1
3
−
1
2π
2
+ a
2
1
3
−
1
8π
2
−
16a
2
9π
2
e
i(E
2
−E
1
)t/
+ e
−i(E
2
−E
1
)t/
2cos
(
E
2
−E
1
t
)
.
E
2
− E
1
=
(4 − 1)π
2
2
2ma
2
=
3π
2
2ma
2
=3ω [in the notation of Problem 2.5(b)].
x
2
=
a
2
2
2
3
−
5
8π
2
−
32
9π
2
cos(3ωt)
. From Problem 2.5(c), x =
a
2
1 −
32
9π
2
cos(3ωt)
.
So σ
2
x
= x
2
−x
2
=
a
2
4
4
3
−
5
4π
2
−
64
9π
2
cos(3ωt) −1+
64
9π
2
cos(3ωt) −
32
9π
2
2
cos
2
(3ωt)
.
σ
2
x
=
a
2
4
1
3
−
5
4π
2
−
32
9π
2
2
cos
2
(3ωt)
. And, from Problem 2.5(d):
dx
dt
=
8
3ma
sin(3ωt).
Meanwhile, the energy-time uncertainty principle (Eq. 3.72) says σ
2
H
σ
2
x
≥
2
4
dx
dt
2
. Here
σ
2
H
σ
2
x
=
1
4
(3ω)
2
a
2
4
1
3
−
5
4π
2
−
32
9π
2
2
cos
2
(3ωt)
=(ωa)
2
3
4
2
1
3
−
5
4π
2
−
32
9π
2
2
cos
2
(3ωt)
.
2
4
dx
dt
2
=
2
8
3ma
2
2
sin
2
(3ωt)=
8
3π
2
2
(ωa)
2
sin
2
(3ωt), since
ma
=
2aω
π
.
So the uncertainty principle holds if
3
4
2
1
3
−
5
4π
2
−
32
9π
2
2
cos
2
(3ωt)
≥
8
3π
2
2
sin
2
(3ωt),
which is to say, if
1
3
−
5
4π
2
≥
32
9π
2
2
cos
2
(3ωt)+
4
3
8
3π
2
2
sin
2
(3ωt)=
32
9π
2
2
.
Evaluating both sides:
1
3
−
5
4π
2
=0.20668;
32
9π
2
2
=0.12978. So it holds. (Whew!)
Problem 3.19
From Problem 2.43, we have:
x =
l
m
t, so
dx
dt
=
l
m
,
σ
2
x
=
1
4w
2
=
1+θ
2
4a
,
where θ =
2at
m
; H =
1
2m
p
2
=
1
2m
2
(a + l
2
).
We need H
2
(to get σ
H
). Now, H =
p
2
2m
, so
H
2
=
1
4m
2
p
4
=
1
4m
2
∞
−∞
p
4
|Φ(p, t)|
2
dp, where (Eq. 3.54): Φ(p, t)=
1
√
2π
∞
−∞
e
−ipx/
Ψ(x, t) dx.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

70 CHAPTER 3. FORMALISM
From Problem 2.43: Ψ(x, t)=
2a
π
1/4
1
√
1+iθ
e
−
l
2
4a
e
a
(
ix+
l
2a
)
2
/(1+iθ)
.
So Φ(p, t)=
1
√
2π
2a
π
1/4
1
√
1+iθ
e
−l
2
/4a
∞
−∞
e
−ipx/
e
a
(
ix+
l
2a
)
2
/(1+iθ)
dx. Let y ≡ x −
il
2a
.
=
1
√
2π
2a
π
1/4
1
√
1+iθ
e
−l
2
/4a
e
pl/2a
∞
−∞
e
−ipy/
e
−ay
2
/(1+iθ)
dy.
[See Prob. 2.22(a) for the integral.]
=
1
√
2π
2a
π
1/4
1
√
1+iθ
e
−l
2
/4a
e
pl/2a
π(1 + iθ)
a
e
−
p
2
(1+iθ)
4a
2
=
1
√
1
2aπ
1/4
e
−
l
2
4a
e
pl
2a
e
−
p
2
(1+iθ)
4a
2
.
|Φ(p, t)|
2
=
1
√
2aπ
1
e
−l
2
/2a
e
pl/a
e
−p
2
/2a
2
=
1
√
2aπ
e
1
2a
l
2
−
2pl
+
p
2
2
=
1
√
2aπ
e
−(l−p/)
2
/2a
.
p
4
=
1
√
2aπ
∞
−∞
p
4
e
−(l−p/)
2
/2a
dp. Let
p
− l ≡ z, so p = (z + l).
=
1
√
2aπ
5
∞
−∞
(z + l)
4
e
−z
2
/2a
dz. Only even powers of z survive:
=
4
√
2aπ
∞
−∞
z
4
+6z
2
l
2
+ l
4
e
−z
2
/2a
dz =
4
√
2aπ
3(2a)
2
4
√
2aπ +6l
2
(2a)
2
√
2aπ + l
4
√
2aπ
=
4
3a
2
+6al
2
+ l
4
. ∴ H
2
=
4
4m
2
3a
2
+6al
2
+ l
4
.
σ
2
H
= H
2
−H
2
=
2
4m
2
3a
2
+6al
2
+ l
4
− a
2
− 2al
2
− l
4
=
4
4m
2
2a
2
+4al
2
=
4
a
2m
2
a +2l
2
.
σ
2
H
σ
2
x
=
4
a
2m
2
a +2l
2
1
4a
1+
2at
m
2
=
4
l
2
4m
2
1+
a
2l
2
1+
2at
m
2
≥
4
l
2
4m
2
=
2
4
l
m
2
=
2
4
dx
dt
2
, so it works.
Problem 3.20
For Q = x, Eq. 3.72 says σ
H
σ
x
≥
2
dx
dt
. But p = m
dx
dt
,soσ
x
σ
H
≥
2m
|p|, which is the Griffiths
uncertainty principle of Problem 3.14.
Problem 3.21
P
2
|β = P (P |β)=P (α|β|α)=α|β(P |α)=α|βα|α
1
|α = α|β|α = P |β.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 71
Since P
2
|β = P |β for any vector |β,P
2
= P . QED [Note: To say two operators are equal means that
they have the same effect on all vectors.]
If |γ is an eigenvector of
ˆ
P with eigenvalue λ, then
ˆ
P |γ = λ|γ, and it follows that
ˆ
P
2
|γ = λ
ˆ
P |γ = λ
2
|γ.
But
ˆ
P
2
=
ˆ
P , and |γ=0,soλ
2
= λ, and hence the eigenvalues of
ˆ
P are 0 and 1. Any (complex) multiple of
|α is an eigenvector of
ˆ
P , with eigenvalue 1; any vector orthogonal to |α is an eigenvector of
ˆ
P , with eigenvalue
0.
Problem 3.22
(a) α| = −i1|−22| + i3|; β| = −i1|+23|.
(b) α|β =(−i1|−22|+ i3|)(i|1 +2|3)=(−i)(i)1|1 +(i)(2)3|3 = 1+2i.
β|α =(−i1|+23|)(i|1−2|2−i|3)=(−i)(i)1|1 + (2)(−i)3|3 = 1 − 2i = α|β
∗
.
(c)
A
11
= 1|αβ|1 =(i)(−i)=1;A
12
= 1|αβ|2 =(i)(0) = 0; A
13
= 1|αβ|3 =(i)(2) = 2i;
A
21
= 2|αβ|1 =(−2)(−i)= 2i; A
22
= 2|αβ|2 =(−2)(0) = 0; A
23
= 2|αβ|3 =(−2)(2) = −4;
A
31
= 3|αβ|1 =(−i)(−i)=−1; A
32
= 3|αβ|2 =(−i)(0) = 0; A
33
= 3|αβ|3 =(−i)(2) = −2i.
A =
102i
2i 0 −4
−10−2i
.
No, it’s not hermitian.
Problem 3.23
Write the eigenvector as |ψ = c
1
|1 + c
2
|2, and call the eigenvalue E. The eigenvalue equation is
ˆ
H|ψ = 9 (|11|−|22| + |12| + |21|)(c
1
|1 + c
2
|2)=9 (c
1
|1 + c
1
|2−c
2
|2 + c
2
|1)
= 9 [(c
1
+ c
2
)|1 +(c
1
− c
2
)|2]=E|ψ = E(c
1
|1 + c
2
|2).
9(c
1
+ c
2
)=Ec
1
⇒ c
2
=
E
9
− 1
c
1
; 9(c
1
− c
2
)=Ec
2
⇒ c
1
=
E
9
+1
c
2
.
c
2
=
E
9
− 1
E
9
+1
c
2
⇒
E
9
2
− 1=1 ⇒ E = ±
√
2 9.
The eigenvectors are: c
2
=(±
√
2 − 1)c
1
⇒ |ψ
±
= c
1
|1 +(±
√
2 − 1)|2
.
The Hamiltonian matrix is H = 9
11
1 −1
.
Problem 3.24
|α =
n
c
n
|e
n
⇒
ˆ
Q|α =
n
c
n
ˆ
Q|e
n
=
n
e
n
|αq
n
|e
n
=
'
n
q
n
|e
n
e
n
|
(
|α⇒
ˆ
Q =
n
q
n
|e
n
e
n
|.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
72 CHAPTER 3. FORMALISM
Problem 3.25
|e
1
=1; e
1
|e
1
=
1
−1
1 dx =2. So |e
1
=
1
√
2
.
|e
2
= x; e
1
|e
2
=
1
√
2
1
−1
xdx=0; e
2
|e
2
=
1
−1
x
2
dx =
x
3
3
1
−1
=
2
3
. So
|e
2
=
3
2
x.
|e
3
= x
2
; e
1
|e
3
=
1
√
2
1
−1
x
2
dx =
1
√
2
2
3
; e
2
|e
3
=
2
3
1
−1
x
3
dx =0.
So (Problem A.4): |e
3
= |e
3
−
1
√
2
2
3
|e
1
= x
2
−
1
3
.
e
3
|e
3
=
1
−1
x
2
−
1
3
2
dx =
x
5
5
−
2
3
·
x
3
3
+
x
9
1
−1
=
2
5
−
4
9
+
2
9
=
8
45
. So
|e
3
=
45
8
x
2
−
1
3
=
5
2
3
2
x
2
−
1
2
.
|e
4
= x
3
. e
1
|e
4
=
1
√
2
1
−1
x
3
dx =0; e
2
|e
4
=
3
2
1
−1
x
4
dx =
3
2
·
2
5
;
e
3
|e
4
=
5
2
1
−1
3
2
x
5
−
1
2
x
3
dx =0. |e
4
= |e
4
−e
2
|e
4
|e
2
= x
3
−
3
2
2
5
3
2
x = x
3
−
3
5
x.
e
4
|e
4
=
1
−1
x
3
−
3
5
x
2
dx =
x
7
7
−
2 · 3
5
x
5
5
+
9
25
x
3
3
1
−1
=
2
7
−
12
25
+
18
75
=
8
7 · 25
.
|e
4
=
5
2
7
2
x
3
−
3
5
x
=
7
2
5
2
x
3
−
3
2
x
.
Problem 3.26
(a) Q = ψ|
ˆ
Qψ =
ˆ
Q
†
ψ|ψ = −
ˆ
Qψ|ψ = −(ψ|
ˆ
Qψ)
∗
= −Q
∗
, so Q is imaginary.
(b) From Problem 3.5(c) we know that (
ˆ
P
ˆ
Q)
†
=
ˆ
Q
†
ˆ
P
†
,soif
ˆ
P =
ˆ
P
†
and
ˆ
Q =
ˆ
Q
†
then
[
ˆ
P,
ˆ
Q]
†
=(
ˆ
P
ˆ
Q −
ˆ
Q
ˆ
P )
†
=
ˆ
Q
†
ˆ
P
†
−
ˆ
P
†
ˆ
Q
†
=
ˆ
Q
ˆ
P −
ˆ
P
ˆ
Q = −[
ˆ
P,
ˆ
Q].
If
ˆ
P = −
ˆ
P
†
and
ˆ
Q = −
ˆ
Q
†
, then [
ˆ
P,
ˆ
Q]
†
=
ˆ
Q
†
ˆ
P
†
−
ˆ
P
†
ˆ
Q
†
=(−
ˆ
Q)(−
ˆ
P ) − (−
ˆ
P )(−
ˆ
Q)=−[
ˆ
P,
ˆ
Q].
So in either case the commutator is antihermitian.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 73
Problem 3.27
(a) ψ
1
.
(b) b
1
(with probability 9/25) or b
2
(with probability 16/25).
(c) Right after the measurement of B:
• With probability 9/25 the particle is in state φ
1
=(3ψ
1
+4ψ
2
)/5; in that case the probability of
getting a
1
is 9/25.
• With probability 16/25 the particle is in state φ
2
=(4ψ
1
− 3ψ
2
)/5; in that case the probability of
getting a
1
is 16/25.
So the total probability of getting a
1
is
9
25
·
9
25
+
16
25
·
16
25
=
337
625
=0.5392.
[Note: The measurment of B (even if we don’t know the outcome of that measurement) collapses the wave
function, and thereby alters the probabilities for the second measurment of A. If the graduate student
inadvertantly neglected to measure B, the second measurement of A would be certain to reproduce the
result a
1
.]
Problem 3.28
Ψ
n
(x, t)=
2
a
sin
nπ
a
x
e
−iE
n
t/
, with E
n
=
n
2
π
2
2
2ma
2
.
Φ
n
(p, t)=
1
√
2π
∞
−∞
e
−ipx/
Ψ
n
(x, t) dx =
1
√
2π
2
a
e
−iE
n
t/
a
0
e
−ipx/
sin
nπ
a
x
dx
=
1
√
πa
e
−iE
n
t/
1
2i
a
0
e
i(nπ/a−p/)x
− e
i(−nπ/a−p/)x
dx
=
1
√
πa
e
−iE
n
t/
1
2i
e
i(nπ/a−p/)x
i(nπ/a −p/)
−
e
i(−nπ/a−p/)x
i(−nπ/a −p/)
a
0
=
−1
2
√
πa
e
−iE
n
t/
e
i(nπ−pa/)
− 1
(nπ/a −p/)
+
e
−i(nπ+pa/)
− 1
(nπ/a + p/)
=
−1
2
√
πa
e
−iE
n
t/
(−1)
n
e
−ipa/
− 1
(nπ − ap/)
a +
(−1)
n
e
−ipa/
− 1
(nπ + ap/)
a
= −
1
2
a
π
e
−iE
n
t/
2nπ
(nπ)
2
− (ap/)
2
(−1)
n
e
−ipa/
− 1
=
aπ
ne
−iE
n
t/
(nπ)
2
− (ap/)
2
1 − (−1)
n
e
−ipa/
.
Noting that
1 − (−1)
n
e
−ipa/
= e
−ipa/2
e
ipa/2
− (−1)
n
e
−ipa/2
=2e
−ipa/2
cos(pa/2)(n odd),
i sin(pa/2)(n even),
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

74 CHAPTER 3. FORMALISM
we have
|Φ
1
(p, t)|
2
=
4πa
cos
2
(pa/2)
[π
2
− (pa/)
2
]
2
, |Φ
2
(p, t)|
2
=
16πa
sin
2
(pa/2)
[(2π)
2
− (pa/)
2
]
2
.
Mathematica has no trouble with the points p = ±nπ/a, where the denominator vanishes. The reason is that
the numerator is also zero there, and the function as a whole is finite—in fact, the graphs show no interesting
behavior at these points.
pp
|Φ |
1
2
2
2
|Φ |
p
2
=
∞
−∞
p
2
|Φ
n
(p, t)|
2
dp =
4n
2
πa
∞
−∞
p
2
[(nπ)
2
− (ap/)
2
]
2
cos
2
(pa/2)
sin
2
(pa/2)
dp [let x ≡
ap
nπ
]
=
4n
2
a
2
∞
−∞
x
2
(1 − x
2
)
2
T
n
(x) dx =
4n
2
a
2
I
n
,
where
T
n
(x) ≡
cos
2
(nπx/2), if n is odd,
sin
2
(nπx/2), if n is even.
The integral can be evaluated by partial fractions:
x
2
(x
2
− 1)
2
=
1
4
1
(x − 1)
2
+
1
(x +1)
2
+
1
(x − 1)
−
1
(x +1)
⇒
I
n
=
1
4
∞
−∞
1
(x − 1)
2
T
n
(x) dx +
∞
−∞
1
(x +1)
2
T
n
(x) dx +
∞
−∞
1
(x − 1)
T
n
(x) dx −
∞
−∞
1
(x +1)
T
n
(x) dx
.
For odd n:
∞
−∞
1
(x ± 1)
k
cos
2
nπx
2
dx =
∞
−∞
1
y
k
cos
2
nπ
2
(y ∓ 1)
dy =
∞
−∞
1
y
k
sin
2
nπy
2
dy.
For even n:
∞
−∞
1
(x ± 1)
k
sin
2
nπx
2
dx =
∞
−∞
1
y
k
sin
2
nπ
2
(y ∓ 1)
dy =
∞
−∞
1
y
k
sin
2
nπy
2
dy.
In either case, then,
I
n
=
1
2
∞
−∞
1
y
2
sin
2
nπy
2
dy =
nπ
4
∞
−∞
sin
2
u
u
2
du =
nπ
2
4
.
Therefore
p
2
=
4n
2
a
2
I
n
=
4n
2
a
2
nπ
2
4
=
nπ
a
2
(same as Problem 2.4).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
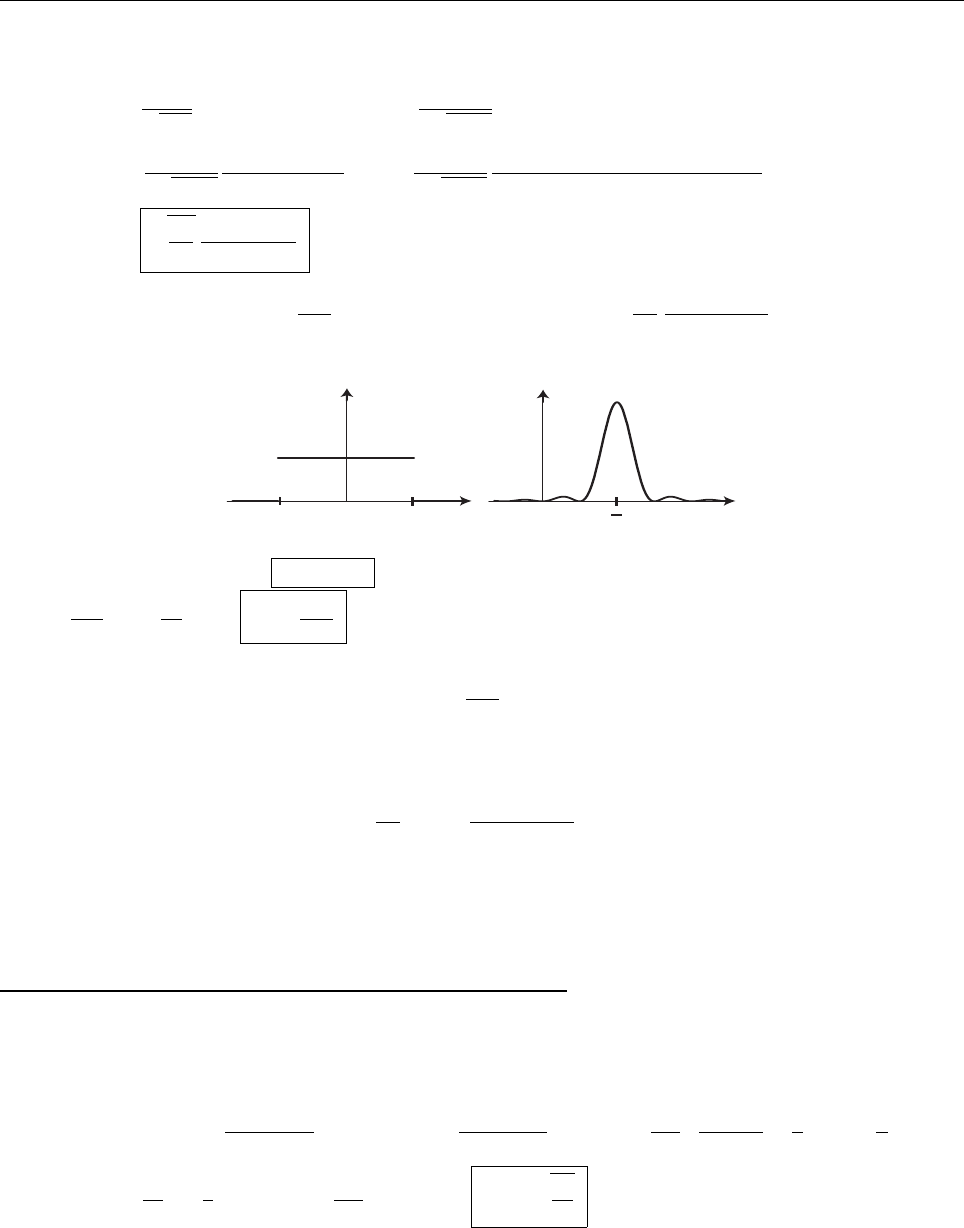
CHAPTER 3. FORMALISM 75
Problem 3.29
Φ(p, 0) =
1
√
2π
∞
−∞
e
−ipx/
Ψ(x, 0) dx =
1
2
√
nπλ
nλ
−nλ
e
i(2π/λ−p/)x
dx
=
1
2
√
nπλ
e
i(2π/λ−p/)x
i(2π/λ − p/)
nλ
−nλ
=
1
2
√
nπλ
e
i2πn
e
−ipnλ/)
− e
−i2πn
e
ipnλ/)
i(2π/λ − p/)
=
λ
nπ
sin(npλ/)
(pλ − 2π)
.
|Ψ(x, 0)|
2
=
1
2nλ
(−nλ < x < nλ); |Φ(p, 0)|
2
=
λ
nπ
sin
2
(npλ/)
(pλ − 2π)
2
.
|Ψ|
2
|Φ|
2
-nλ
nλ
p
x
2πh/λ
The width of the |Ψ|
2
graph is w
x
=2nλ. The |Φ|
2
graph is a maximum at 2π/λ, and goes to zero on either
side at
2π
λ
1 ±
1
2n
,so
w
p
=
2π
nλ
.
As n →∞,w
x
→∞and w
p
→ 0; in this limit the particle has a
well-defined momentum, but a completely indeterminate position. In general,
w
x
w
p
=(2nλ)
2π
nλ
=4π > /2,
so the uncertainty principle is satisfied (using the widths as a measure of uncertainty). If we try to check the
uncertainty principle more rigorously, using standard deviation as the measure, we get an uninformative result,
because
p
2
=
λ
nπ
∞
−∞
p
2
sin
2
(npλ/)
(pλ − 2π)
2
dp = ∞.
(At large |p| the integrand is approximately (1/λ
2
) sin
2
(npλ/), so the integral blows up.) Meanwhile p is
zero, so σ
p
= ∞, and the uncertainty principle tells us nothing. The source of the problem is the discontinuity
in Ψ at the end points; here ˆp Ψ=−i dΨ/dx picks up a delta function, and Ψ|ˆp
2
Ψ = ˆp Ψ|ˆp Ψ→∞because
the integral of the square of the delta function blows up. In general, if you want σ
p
to be finite, you cannot
allow discontinuities in Ψ.
Problem 3.30
(a)
1=|A|
2
∞
−∞
1
(x
2
+ a
2
)
2
dx =2|A|
2
∞
0
1
(x
2
+ a
2
)
2
dx =2|A|
2
1
2a
2
x
x
2
+ a
2
+
1
a
tan
−1
x
a
∞
0
=
1
a
2
|A|
2
1
a
tan
−1
(∞)=
π
2a
3
|A|
2
⇒ A = a
2a
π
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

76 CHAPTER 3. FORMALISM
(b)
x = A
2
∞
−∞
x
(a
2
+ x
2
)
2
dx = 0.
x
2
=2A
2
∞
0
x
2
(a
2
+ x
2
)
2
dx. [Let y ≡
x
2
a
2
,x= a
√
y, dx =
a
2
√
y
dy.]
=
2a
2
π
∞
0
y
1/2
(1 + y)
2
dy =
2a
2
π
Γ(3/2)Γ(1/2)
Γ(2)
=
2a
2
π
(
√
π/2)(
√
π)
1
=
a
2
.
σ
x
=
x
2
−x
2
= a.
(c)
Φ(p, 0) =
A
√
2π
∞
−∞
e
−ipx/
1
x
2
+ a
2
dx. [But e
−ipx/
= cos
px
− i sin
px
, and sine is odd.]
=
2A
√
2π
∞
0
cos(px/)
x
2
+ a
2
dx =
2A
√
2π
π
2a
e
−|p|a/
=
a
e
−|p|a/
.
∞
−∞
|Φ(p, 0)|
2
dp =
a
∞
−∞
e
−2|p|a/
dp =
2a
e
−2pa/
−2a/
∞
0
=1.
(d)
p =
a
∞
−∞
pe
−2|p|a/
dp = 0.
p
2
=2
a
∞
0
p
2
e
−2pa/
dp =
2a
2
2a
3
=
2
2a
2
. σ
p
=
p
2
−p
2
=
√
2 a
.
(e) σ
x
σ
p
= a
√
2 a
=
√
2
2
>
2
.
Problem 3.31
Equation 3.71 ⇒
d
dt
xp =
i
[H, xp]; Eq. 3.64 ⇒ [H, xp]=[H, x]p + x[H, p]; Problem 3.14 ⇒ [H, x]=
−
ip
m
; Problem 3.17(d) ⇒ [H, p]=i
dV
dx
. So
d
dt
xp =
i
−
i
m
p
2
+ ix
dV
dx
=2
p
2
2m
−x
dV
dx
=2T −x
dV
dx
. QED
In a stationary state all expectation values (at least, for operators that do not depend explicitly on t) are
time-independent (see item 1 on p. 26), so dxp/dt = 0, and we are left with Eq. 3.97.
For the harmonic oscillator:
V =
1
2
mω
2
x
2
⇒
dV
dx
= mω
2
x ⇒ x
dV
dx
= mω
2
x
2
=2V ⇒ 2T =2V ⇒T = V . QED
In Problem 2.11(c) we found that T = V =
1
4
ω (for n = 0); T = V =
3
4
ω (for n = 1).
In Problem 2.12 we found that T =
1
2
n+
1
2
ω, while x
2
=(n+
1
2
)/mω,soV =
1
2
mω
2
x
2
=
1
2
(n+
1
2
)ω,
and hence T = V for all stationary states.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 77
Problem 3.32
Ψ(x, t)=
1
√
2
ψ
1
e
−iE
1
t/
+ ψ
2
e
−iE
2
t/
; Ψ(x, t)|Ψ(x, 0) =0⇒
1
2
e
iE
1
t/
ψ
1
|ψ
1
+ e
iE
1
t/
ψ
1
|ψ
2
+ e
iE
2
t/
ψ
2
|ψ
1
+ e
iE
2
t/
ψ
2
|ψ
2
=
1
2
e
iE
1
t/
+ e
iE
2
t/
=0, or e
iE
2
t/
= −e
iE
1
t/
, so e
i(E
2
−E
1
)t/
= −1=e
iπ
.
Thus (E
2
− E
1
)t/ = π (orthogonality also at 3π, 5π, etc., but this is the first occurrence).
∴ ∆t ≡
t
π
=
E
2
− E
1
. But ∆E = σ
H
=
1
2
(E
2
− E
1
) (Problem 3.18). So ∆t ∆E =
2
.
Problem 3.33
Equation 2.69: x =
2mω
(a
+
+ a
−
),p= i
mω
2
(a
+
− a
−
); Eq. 2.66 :
a
+
|n =
√
n +1|n +1,
a
−
|n =
√
n |n −1.
n|x|n
=
2mω
n|(a
+
+ a
−
)|n
=
2mω
√
n
+1n|n
+1 +
√
n
n|n
− 1
=
2mω
√
n
+1δ
n,n
+1
+
√
n
δ
n,n
−1
=
2mω
√
nδ
n
,n−1
+
√
n
δ
n,n
−1
.
n|p|n
= i
mω
2
√
nδ
n
,n−1
−
√
n
δ
n,n
−1
.
Noting that n and n
run from zero to infinity, the matrices are:
X =
2mω
0
√
10000
√
10
√
20 0 0
0
√
20
√
30 0
.
:
00
√
30
√
40
000
√
40
√
5
···
; P = i
mω
2
0 −
√
10000
√
10−
√
2000
0
√
20−
√
30 0
.
:
00
√
30−
√
40
00 0
√
4 −
√
5
···
.
Squaring these matrices:
X
2
=
2mω
10
√
1 · 20 0 0
030
√
2 · 30 0
√
1 · 20 5 0
√
3 · 40
.
:
0
√
2 · 30 7 0
√
4 · 5
···
;
P
2
= −
mω
2
−10
√
1 · 20 0 0
0 −30
√
2 · 30 0
√
1 · 20 −50
√
3 · 40
.
:
0
√
2 · 30 −70
√
4 · 5
···
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

78 CHAPTER 3. FORMALISM
So the Hamiltonian, in matrix form, is
H =
1
2m
P
2
+
mω
2
2
X
2
= −
ω
4
−10
√
1 · 20 0 0
0 −30
√
2 · 30 0
√
1 · 20 −50
√
3 · 40
.
:
0
√
2 · 30 −70
√
4 · 5
···
+
ω
4
10
√
1 · 20 0 0
030
√
2 · 30 0
√
1 · 20 5 0
√
3 · 40
.
:
0
√
2 · 30 7 0
√
4 · 5
···
=
ω
2
1000
0300
0050
0007
.
.
.
.
It’s plainly diagonal, and the nonzero elements are H
nn
=
n +
1
2
ω, as they should be.
Problem 3.34
Evidently Ψ(x, t)=c
0
ψ
0
(x)e
−iE
0
t/
+ c
1
ψ
1
(x)e
−iE
1
t/
, with |c
0
|
2
= |c
1
|
2
=1/2, so c
0
= e
iθ
0
/
√
2,c
1
= e
iθ
1
/
√
2,
for some real θ
0
,θ
1
.
p = |c
0
|
2
ψ
0
|pψ
0
+ |c
1
|
2
ψ
1
|pψ
1
+ c
∗
0
c
1
e
i(E
0
−E
1
)t/
ψ
0
|pψ
1
+ c
∗
1
c
0
e
i(E
1
−E
0
)t/
ψ
1
|pψ
0
.
But E
1
− E
0
=(
3
2
ω) −(
1
2
ω)=ω, and (Problem 2.11) ψ
0
|pψ
0
= ψ
1
|pψ
1
= 0, while (Eqs. 2.69 and 2.66)
ψ
0
|pψ
1
= i
mω
2
ψ
0
|(a
+
− a
−
)ψ
1
= i
mω
2
ψ
0
|
√
2ψ
2
−ψ
0
|
√
1ψ
0
= −i
mω
2
; ψ
1
|pψ
0
= i
mω
2
.
p =
1
√
2
e
−iθ
0
1
√
2
e
iθ
1
e
−iωt
'
−i
mω
2
(
+
1
√
2
e
−iθ
1
1
√
2
e
iθ
0
e
iωt
'
i
mω
2
(
=
i
2
mω
2
−e
−i(ωt−θ
1
+θ
0
)
+ e
i(ωt−θ
1
+θ
0
)
= −
mω
2
sin(ωt + θ
0
− θ
1
).
The maximum is
mω/2; it occurs at t =0⇔ sin(θ
0
− θ
1
)=−1, or θ
1
= θ
0
+ π/2. We might as well pick
θ
0
=0,θ
1
= π/2; then
Ψ(x, t)=
1
√
2
ψ
0
e
−iωt/2
+ ψ
1
e
iπ/2
e
−3iωt/2
=
1
√
2
e
−iωt/2
ψ
0
+ iψ
1
e
−iωt
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 79
Problem 3.35
(a) x = α|xα =
2mω
α|(a
+
+ a
−
)α =
2mω
(a
−
α|α + α|a
−
α)=
2mω
(α + α
∗
).
x
2
=
2mω
a
2
+
+ a
+
a
−
+ a
−
a
+
+ a
2
−
. But a
−
a
+
=[a
−
,a
+
]+a
+
a
−
=1+a
+
a
−
(Eq. 2.55).
=
2mω
a
2
+
+2a
+
a
−
+1+a
2
−
.
x
2
=
2mω
α|
a
2
+
+2a
+
a
−
+1+a
2
−
α =
2mω
a
2
−
α|α +2a
−
α|a
−
α + α|α + α|a
2
−
α
=
2mω
(α
∗
)
2
+2(α
∗
)α +1+α
2
=
2mω
1+(α + α
∗
)
2
.
p = α|pα = i
mω
2
α|(a
+
− a
−
)α = i
mω
2
(a
−
α|α−α|a
−
α)= −i
mω
2
(α − α
∗
).
p
2
= −
mω
2
a
2
+
− a
+
a
−
− a
−
a
+
+ a
2
−
= −
mω
2
a
2
+
− 2a
+
a
−
− 1+a
2
−
.
p
2
= −
mω
2
α|
a
2
+
− 2a
+
a
−
− 1+a
2
−
α = −
mω
2
a
2
−
α|α−2a
−
α|a
−
α−α|α + α|a
2
−
α
= −
mω
2
(α
∗
)
2
− 2(α
∗
)α − 1+α
2
=
mω
2
1 − (α − α
∗
)
2
.
(b)
σ
2
x
= x
2
−x
2
=
2mω
1+(α + α
∗
)
2
− (α + α
∗
)
2
=
2mω
;
σ
2
p
= p
2
−p
2
=
mω
2
1 − (α − α
∗
)
2
+(α − α
∗
)
2
=
mω
2
.σ
x
σ
p
=
2mω
mω
2
=
2
. QED
(c) Using Eq. 2.67 for ψ
n
:
c
n
= ψ
n
|α =
1
√
n!
(a
+
)
n
ψ
0
|α =
1
√
n!
ψ
0
|(a
−
)
n
α =
1
√
n!
α
n
ψ
0
|α =
α
n
√
n!
c
0
.
(d) 1=
∞
n=0
|c
n
|
2
= |c
0
|
2
∞
n=0
|α|
2n
n!
= |c
0
|
2
e
|α|
2
⇒ c
0
= e
−|α|
2
/2
.
(e) |α(t) =
∞
n=0
c
n
e
−iE
n
t/
|n =
∞
n=0
α
n
√
n!
e
−|α|
2
/2
e
−i(n+
1
2
)ωt
|n = e
−iωt/2
∞
n=0
αe
−iωt
n
√
n!
e
−|α|
2
/2
|n.
Apart form the overall phase factor e
−iωt/2
(which doesn’t affect its status as an eigenfunction of a
−
,or
its eigenvalue), |α(t) is the same as |α, but with eigenvalue α(t)=e
−iωt
α.
(f) Equation 2.58 says a
−
|ψ
0
=0,so yes, it is a coherent state, with eigenvalue α =0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

80 CHAPTER 3. FORMALISM
Problem 3.36
(a) Equation 3.60 becomes |z|
2
= [Re(z)]
2
+ [Im(z)]
2
=
1
2
(z + z
∗
)
2
+
1
2i
(z − z
∗
)
2
; Eq. 3.61 generalizes to
σ
2
A
σ
2
B
≥
1
2
(f|g+ g|f)
2
+
1
2i
(f|g−g|f)
2
.
But f|g−g|f = [
ˆ
A,
ˆ
B] (p. 111), and, by the same argument,
f|g+ g|f =
ˆ
A
ˆ
B−AB+
ˆ
B
ˆ
A−AB =
ˆ
A
ˆ
B +
ˆ
B
ˆ
A − 2AB = D.
So σ
2
A
σ
2
B
≥
1
4
D
2
+ C
2
.
(b) If
ˆ
B =
ˆ
A, then
ˆ
C =0,
ˆ
D =2
ˆ
A
2
−A
2
; D =2
ˆ
A
2
−A
2
=2σ
2
A
. So Eq. 3.99 says
σ
2
A
σ
2
A
≥ (1/4)4σ
4
A
= σ
4
A
, which is true, but not very informative.
Problem 3.37
First find the eigenvalues and eigenvectors of the Hamiltonian. The characteristic equation says
(a − E)0 b
0(c − E)0
b 0(a − E)
=(a − E)(c − E)(a −E) − b
2
(c − E)=(c − E)
(a − E)
2
− b
2
=0,
Either E = c, or else (a − E)
2
= b
2
⇒ E = a ± b. So the eigenvalues are
E
1
= c, E
2
= a + b, E
3
= a − b.
To find the corresponding eigenvectors, write
a 0 b
0 c 0
b 0 a
α
β
γ
= E
n
α
β
γ
.
(1)
aα + bγ = cα ⇒ (a − c)α + bγ =0;
cβ = cβ (redundant) ;
bα + aγ = cγ ⇒ (a − c)γ + bα =0.
⇒
(a − c)
2
− b
2
α =0.
So (excluding the degenerate case a − c = ±b) α = 0, and hence also γ =0.
(2)
aα + bγ =(a + b)α ⇒ α − γ =0;
cβ =(a + b)β ⇒ β =0;
bα + aγ =(a + b)γ (redundant).
So α = γ and β =0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 3. FORMALISM 81
(3)
aα + bγ =(a − b)α ⇒ α + γ =0;
cβ =(a −b)β ⇒ β =0;
bα + aγ =(a − b)γ (redundant).
So α = −γ and β =0.
Conclusion: The (normalized) eigenvectors of H are
|s
1
=
0
1
0
, |s
2
=
1
√
2
1
0
1
, |s
3
=
1
√
2
1
0
−1
.
(a) Here |S(0) = |s
1
,so
|S(t) = e
−iE
1
t/
|s
1
= e
−ict/
0
1
0
.
(b)
|S(0) =
1
√
2
(|s
2
+ |s
3
) .
|S(t) =
1
√
2
e
−iE
2
t/
|s
2
+ e
−iE
3
t/
|s
3
=
1
√
2
e
−i(a+b)t/
1
√
2
1
0
1
+ e
−i(a−b)t/
1
√
2
1
0
−1
=
1
2
e
−iat/
e
−ibt/
+ e
ibt/
0
e
−ibt/
− e
ibt/
=
e
−iat/
cos(bt/)
0
−i sin(bt/)
.
Problem 3.38
(a) H:
E
1
= ω, E
2
= E
3
=2ω; |h
1
=
1
0
0
, |h
2
=
0
1
0
, |h
3
=
0
0
1
.
A:
−aλ 0
λ −a 0
00(2λ − a)
= a
2
(2λ − a) − (2λ − a)λ
2
=0⇒ a
1
=2λ, a
2
= λ, a
3
= −λ.
λ
010
100
002
α
β
γ
= a
α
β
γ
⇒
λβ = aα
λα = aβ
2λγ = aγ
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
82 CHAPTER 3. FORMALISM
(1)
λβ =2λα ⇒ β =2α,
λα =2λβ ⇒ α =2β,
2λγ =2λγ;
α = β =0;
|a
1
=
0
0
1
.
(2)
λβ = λα ⇒ β = α,
λα = λβ ⇒ α = β,
2λγ = λγ; ⇒ γ =0.
|a
2
=
1
√
2
1
1
0
.
(3)
λβ = −λα ⇒ β = −α,
λα = −λβ ⇒ α = −β,
2λγ = −λγ; ⇒ γ =0.
|a
3
=
1
√
2
1
−1
0
.
B:
(2µ − b)0 0
0 −bµ
0 µ −b
= b
2
(2µ − b) − (2µ − b)µ
2
=0⇒ b
1
=2µ, b
2
= µ, b
3
= −µ.
µ
200
001
010
α
β
γ
= b
α
β
γ
⇒
2µα = bα
µγ = bβ
µβ = bγ
(1)
2µα =2µα,
µγ =2µβ ⇒ γ =2β,
µβ =2µγ ⇒ β =2γ;
β = γ =0;
|b
1
=
1
0
0
.
(2)
2µα = µα ⇒ α =0,
µγ = µβ ⇒ γ = β,
µβ = µγ; ⇒ β = γ.
|b
2
=
1
√
2
0
1
1
.
(3)
2µα = −µα ⇒ α =0,
µγ = −µβ ⇒ γ = −β,
µβ = −µγ; ⇒ β = −γ.
|b
3
=
1
√
2
0
1
−1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 83
(b)
H = S(0)|H|S(0) = ω
c
∗
1
c
∗
2
c
∗
3
100
020
002
c
1
c
2
c
3
=
ω
|c
1
|
2
+2|c
2
|
2
+2|c
3
|
2
.
A = S(0)|A|S(0) = λ
c
∗
1
c
∗
2
c
∗
3
010
100
002
c
1
c
2
c
3
=
λ
c
∗
1
c
2
+ c
∗
2
c
1
+2|c
3
|
2
.
B = S(0)|B|S(0) = µ
c
∗
1
c
∗
2
c
∗
3
200
001
010
c
1
c
2
c
3
=
µ
2|c
1
|
2
+ c
∗
2
c
3
+ c
∗
3
c
2
.
(c)
|S(0) = c
1
|h
1
+ c
2
|h
2
+ c
3
|h
3
⇒
|S(t) = c
1
e
−iE
1
t/
|h
1
+ c
2
e
−iE
2
t/
|h
2
+ c
3
e
−iE
3
t/
|h
3
= c
1
e
−iωt
|h
1
+ c
2
e
−2iωt
|h
2
+ c
3
e
−2iωt
|h
3
= e
−2iωt
c
1
e
iωt
1
0
0
+ c
2
0
1
0
+ c
3
0
0
1
=
e
−2iωt
c
1
e
iωt
c
2
c
3
.
H: h
1
= ω, probability |c
1
|
2
; h
2
= h
3
=2ω, probability (|c
2
|
2
+ |c
3
|
2
).
A: a
1
=2λ, a
1
|S(t) = e
−2iωt
001
c
1
e
iωt
c
2
c
3
= e
−2iωt
c
3
⇒ probability |c
3
|
2
.
a
2
= λ, a
2
|S(t) = e
−2iωt
1
√
2
110
c
1
e
iωt
c
2
c
3
=
1
√
2
e
−2iωt
c
1
e
iωt
+ c
2
⇒
probability =
1
2
c
∗
1
e
−iωt
+ c
∗
2
c
1
e
iωt
+ c
2
=
1
2
|c
1
|
2
+ |c
2
|
2
+ c
∗
1
c
2
e
−iωt
+ c
∗
2
c
1
e
iωt
.
a
3
= −λ, a
3
|S(t) = e
−2iωt
1
√
2
1 −10
c
1
e
iωt
c
2
c
3
=
1
√
2
e
−2iωt
c
1
e
iωt
− c
2
⇒
probability =
1
2
c
∗
1
e
−iωt
− c
∗
2
c
1
e
iωt
− c
2
=
1
2
|c
1
|
2
+ |c
2
|
2
− c
∗
1
c
2
e
−iωt
− c
∗
2
c
1
e
iωt
.
Note that the sum of the probabilities is 1.
B:
b
1
=2µ, b
1
|S(t) = e
−2iωt
100
c
1
e
iωt
c
2
c
3
= e
−2iωt
c
1
⇒ probability |c
1
|
2
.
b
2
= µ, b
2
|S(t) = e
−2iωt
1
√
2
011
c
1
e
iωt
c
2
c
3
=
1
√
2
e
−2iωt
(c
2
+ c
3
) ⇒
probability =
1
2
(c
∗
1
+ c
∗
2
)(c
1
+ c
2
)=
1
2
|c
1
|
2
+ |c
2
|
2
+ c
∗
1
c
2
+ c
∗
2
c
1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

84 CHAPTER 3. FORMALISM
b
3
= −µ, b
3
|S(t) = e
−2iωt
1
√
2
01−1
c
1
e
iωt
c
2
c
3
=
1
√
2
e
−2iωt
(c
2
− c
3
) ⇒
probability =
1
2
(c
∗
2
− c
∗
3
)(c
2
− c
3
)=
1
2
|c
2
|
2
+ |c
3
|
2
− c
∗
2
c
3
− c
∗
3
c
2
.
Again, the sum of the probabilities is 1.
Problem 3.39
(a)
Expanding in a Taylor series: f (x + x
0
)=
∞
n=0
1
n!
x
n
0
d
dx
n
f(x).
But p =
i
d
dx
, so
d
dx
=
ip
. Therefore f(x + x
0
)=
∞
n=0
1
n!
x
n
0
ip
n
f(x)=e
ipx
0
/
f(x).
(b)
Ψ(x, t + t
0
)=
∞
n=0
1
n!
t
n
0
∂
∂t
n
Ψ(x, t); i
∂Ψ
∂t
= HΨ.
[Note: It is emphatically not the case that i
∂
∂t
= H. These two operators have the same effect only when
(as here) they are acting on solutions to the (time-dependent) Schr¨odinger equation.] Also,
i
∂
∂t
2
Ψ=i
∂
∂t
(HΨ) = H
i
∂Ψ
∂t
= H
2
Ψ,
provided H is not explicitly dependent on t. And so on. So
Ψ(x, t + t
0
)=
∞
n=0
1
n!
t
n
0
−
i
H
n
Ψ=e
−iHt
0
/
Ψ(x, t).
(c)
Q
t+t
0
= Ψ(x, t + t
0
)|Q(x, p, t + t
0
)|Ψ(x, t + t
0
).
But Ψ(x, t + t
0
)=e
−iHt
0
/
Ψ(x, t), so, using the hermiticity of H to write
e
−iHt
0
/
†
= e
iHt
0
/
:
Q
t+t
0
= Ψ(x, t)|e
iHt
0
/
Q(x, p, t + t
0
)e
−iHt
0
/
|Ψ(x, t).
If t
0
= dt is very small, expanding to first order, we have:
Q
t
+
dQ
dt
dt = Ψ(x, t)|
1+
iH
dt
Q(x, p, t)+
∂Q
∂t
dt
1 −
iH
dt
|Ψ(x, t)
= Q(x, p, t)+
iH
dt Q −Q
iH
dt
+
∂Q
∂t
dt = Q +
i
[H, Q]dt +
∂Q
∂t
dt
= Q
t
+
i
[H, Q]dt +
∂Q
∂t
dt.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 3. FORMALISM 85
∴
dQ
dt
=
i
[H, Q]+
∂Q
∂t
. QED
Problem 3.40
(a) For the free particle, V (x) = 0, so the time-dependent Schr¨odinger equation reads
i
∂Ψ
∂t
= −
2
2m
∂
2
Ψ
∂x
2
. Ψ(x, t)=
1
√
2π
∞
−∞
e
ipx/
Φ(p, t) dp ⇒
∂Ψ
∂t
=
1
√
2π
∞
−∞
e
ipx/
∂Φ
∂t
dp,
∂
2
Ψ
∂x
2
=
1
√
2π
∞
−∞
−
p
2
2
e
ipx/
Φ dp. So
1
√
2π
∞
−∞
e
ipx/
i
∂Φ
∂t
dp =
1
√
2π
∞
−∞
e
ipx/
p
2
2m
Φ
dp.
But two functions with the same Fourier transform are equal (as you can easily prove using Plancherel’s
theorem), so
i
∂Φ
∂t
=
p
2
2m
Φ.
1
Φ
dΦ=−
ip
2
2m
dt ⇒
Φ(p, t)=e
−ip
2
t/2m
Φ(p, 0).
(b)
Ψ(x, 0) = Ae
−ax
2
e
ilx
,A=
2a
π
1/4
(Problem2.43(a)).
Φ(p, 0) =
1
√
2π
2a
π
1/4
∞
−∞
e
−ipx/
e
−ax
2
e
ilx
dx =
1
(2πa
2
)
1/4
e
−(l−p/)
2
/4a
(Problem2.43(b)).
Φ(p, t)=
1
(2πa
2
)
1/4
e
−(l−p/)
2
/4a
e
−ip
2
t/2m
; |Φ(p, t)|
2
=
1
√
2πa
e
−(l−p/)
2
/2a
.
(c)
p =
∞
−∞
p|Φ(p, t)|
2
dp =
1
√
2πa
∞
−∞
pe
−(l−p/)
2
/2a
dp
[Let y ≡ (p/) − l, so p = (y + l) and dp = dy.]
=
√
2πa
∞
−∞
(y + l)e
−y
2
/2a
dy [but the first term is odd]
=
2l
√
2πa
∞
0
e
−y
2
/2a
dy =
2l
√
2πa
πa
2
=
l [as in Problem 2.43(d)].
p
2
=
∞
−∞
p
2
|Φ(p, t)|
2
dp =
1
√
2πa
∞
−∞
p
2
e
−(l−p/)
2
/2a
dp =
2
√
2πa
∞
−∞
(y
2
+2yl + l
2
)e
−y
2
/2a
dy
=
2
2
√
2πa
∞
0
y
2
e
−y
2
/2a
dy + l
2
∞
0
e
−y
2
/2a
dy
=
2
2
√
2πa
2
√
π
a
2
3
+ l
2
πa
2
=
(a + l
2
)
2
[as in Problem 2.43(d)].
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

86 CHAPTER 3. FORMALISM
(d) H =
p
2
2m
; H =
1
2m
p
2
=
2
2m
(l
2
+a)=
1
2m
p
2
+
2
a
2m
. But H
0
=
1
2m
p
2
0
=
2
a
2m
(Problem 2.22(d)).
So H =
1
2m
p
2
+ H
0
. QED Comment: The energy of the traveling gaussian is the energy of the
same gaussian at rest, plus the kinetic energy (p
2
/2m) associated with the motion of the wave packet
as a whole.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 87
Chapter 4
Quantum Mechanics in Three
Dimensions
Problem 4.1
(a)
[x, y]=xy − yx =0, etc., so
[r
i
,r
j
]=0.
[p
x
,p
y
]f =
i
∂
∂x
i
∂f
∂y
−
i
∂
∂y
i
∂f
∂x
= −
2
∂
2
f
∂x∂y
−
∂
2
f
∂y∂x
=0
(by the equality of cross-derivatives), so
[p
i
,p
j
]=0.
[x, p
x
]f =
i
x
∂f
∂x
−
∂
∂x
(xf)
=
i
x
∂f
∂x
− x
∂f
∂x
− f
= if,
so [x, p
x
]=i (likewise [y, p
y
]=i and [z, p
z
]=i).
[y, p
x
]f =
i
y
∂f
∂x
−
∂
∂x
(yf)
=
i
y
∂f
∂x
− y
∂f
∂y
= 0 (since
∂y
∂x
=0). So [y, p
x
]=0,
and same goes for the other “mixed” commutators. Thus
[r
i
,p
j
]=−[p
j
,r
i
]=iδ
ij
.
(b) The derivation of Eq. 3.71 (page 115) is identical in three dimensions, so
dx
dt
=
i
[H, x];
[H, x]=
p
2
2m
+ V,x
=
1
2m
[p
2
x
+ p
2
y
+ p
2
z
,x]=
1
2m
[p
2
x
,x]
=
1
2m
(p
x
[p
x
,x]+[p
x
,x]p
x
)=
1
2m
[(−i)p
x
+(−i)p
x
]=−i
m
p
x
.
∴
dx
dt
=
i
−i
m
p
x
=
1
m
p
x
. The same goes for y and z, so:
dr
dt
=
1
m
p.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

88 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
dp
x
dt
=
i
[H, p
x
];[H, p
x
]=
p
2
2m
+ V,p
x
=[V,p
x
]=i
∂V
∂x
(Eq. 3.65)
=
i
(i)
0
∂V
∂x
1
=
0
−
∂V
∂x
1
. Same for y and z, so:
dp
dt
= −∇V .
(c) From Eq. 3.62: σ
x
σ
p
x
≥
1
2i
[x, p
x
]
=
1
2i
i
=
2
. Generally,
σ
r
i
σ
p
j
≥
2
δ
ij
.
Problem 4.2
(a) Equation 4.8 ⇒−
2
2m
∂
2
ψ
∂x
2
+
∂
2
ψ
∂y
2
+
∂
2
ψ
∂z
2
= Eψ (inside the box). Separable solutions: ψ(x, y, z)=
X(x)Y (y)Z(z). Put this in, and divide by XY Z:
1
X
d
2
X
dx
2
+
1
Y
d
2
X
dy
2
+
1
Z
d
2
Z
dz
2
= −
2m
2
E.
The three terms on the left are functions of x, y, and z, respectively, so each must be a constant. Call the
separation constants k
2
x
, k
2
y
, and k
2
z
(as we’ll soon seen, they must be positive).
d
2
X
dx
2
= −k
2
x
X;
d
2
Y
dy
2
= −k
2
y
Y ;
d
2
Z
dz
2
= −k
2
z
Z, with E =
2
2m
(k
2
x
+ k
2
y
+ k
2
z
).
Solution:
X(x)=A
x
sin k
x
x + B
x
cos k
x
x; Y (y)=A
y
sin k
y
y + B
y
cos k
y
y; Z(z)=A
z
sin k
z
z + B
z
cos k
z
z.
But X(0) = 0, so B
x
=0;Y (0) = 0, so B
y
=0;Z(0) = 0, so B
z
= 0. And X(a)=0⇒ sin(k
x
a)=0⇒
k
x
= n
x
π/a (n
x
=1, 2, 3,...). [As before (page 31), n
x
= 0, and negative values are redundant.] Likewise
k
y
= n
y
π/a and k
z
= n
z
π/a.So
ψ(x, y, z)=A
x
A
y
A
z
sin
n
x
π
a
x
sin
n
y
π
a
y
sin
n
z
π
a
z
,E=
2
2m
π
2
a
2
(n
2
x
+ n
2
y
+ n
2
z
).
We might as well normalize X, Y, and Z separately: A
x
= A
y
= A
z
=
2/a. Conclusion:
ψ(x, y, z)=
2
a
3/2
sin
n
x
π
a
x
sin
n
y
π
a
y
sin
n
z
π
a
z
; E =
π
2
2
2ma
2
(n
2
x
+ n
2
y
+ n
2
z
); n
x
,n
y
,n
z
=1, 2, 3,...
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 89
(b)
n
x
n
y
n
z
(n
2
x
+ n
2
y
+ n
2
z
)
111 3
112 6
121 6
211 6
122 9
212 9
221 9
113 11
131 11
311 11
222 12
123 14
132 14
213 14
231 14
312 14
321 14
Energy Degeneracy
E
1
=3
π
2
2
2ma
2
; d =1
E
2
=6
π
2
2
2ma
2
; d =3.
E
3
=9
π
2
2
2ma
2
; d =3.
E
4
=11
π
2
2
2ma
2
; d =3.
E
5
=12
π
2
2
2ma
2
; d =1.
E
6
=14
π
2
2
2ma
2
; d =6.
(c) The next combinations are: E
7
(322),E
8
(411),E
9
(331),E
10
(421),E
11
(332),E
12
(422),E
13
(431), and
E
14
(333 and 511). The degeneracy of E
14
is 4. Simple combinatorics accounts for degeneracies of 1
(n
x
= n
y
= n
z
), 3 (two the same, one different), or 6 (all three different). But in the case of E
14
there is
a numerical “accident”: 3
2
+3
2
+3
2
= 27, but 5
2
+1
2
+1
2
is also 27, so the degeneracy is greater than
combinatorial reasoning alone would suggest.
Problem 4.3
Eq. 4.32 ⇒ Y
0
0
=
1
√
4π
P
0
0
(cos θ); Eq. 4.27 ⇒ P
0
0
(x)=P
0
(x); Eq. 4.28 ⇒ P
0
(x)=1. Y
0
0
=
1
√
4π
.
Y
1
2
= −
5
4π
1
3 · 2
e
iφ
P
1
2
(cos θ); P
1
2
(x)=
1 − x
2
d
dx
P
2
(x);
P
2
(x)=
1
4 · 2
d
dx
2
x
2
− 1
2
=
1
8
d
dx
2(x
2
− 1)2x
=
1
2
x
2
− 1+x(2x)
=
1
2
3x
2
− 1
;
P
1
2
(x)=
1 − x
2
d
dx
3
2
x
2
−
1
2
=
1 − x
2
3x; P
1
2
(cos θ) = 3 cos θ sin θ. Y
1
2
= −
15
8π
e
iφ
sin θ cos θ.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

90 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Normalization:
|Y
0
0
|
2
sin θdθdφ=
1
4π
π
0
sin θdθ
2π
0
dφ
=
1
4π
(2)(2π)=1.
|Y
1
2
|
2
sin θdθdφ=
15
8π
π
0
sin
2
θ cos
2
θ sin θdθ
2π
0
dφ =
15
4
π
0
cos
2
θ(1 −cos
2
θ) sin θdθ
=
15
4
−
cos
3
θ
3
+
cos
5
θ
5
π
0
=
15
4
2
3
−
2
5
=
5
2
−
3
2
=1
Orthogonality:
Y
0
0
∗
Y
1
2
sin θdθdφ= −
1
√
4π
15
8π
π
0
sin θ cos θ sin θdθ
(sin
3
θ)/3|
π
0
=0
2π
0
e
iφ
dφ
(e
iφ
)/i|
2π
0
=0
=0.
Problem 4.4
dΘ
dθ
=
A
tan(θ/2)
1
2
sec
2
(θ/2) =
A
2
1
sin(θ/2) cos(θ/2)
=
A
sin θ
. Therefore
d
dθ
sin θ
dΘ
dθ
=
d
dθ
(A)=0.
With l = m =0, Eq. 4.25 reads:
d
dθ
sin θ
dΘ
dθ
=0. So A ln[tan(θ/2)] does satisfy Eq. 4.25. However,
Θ(0) = A ln(0) = A(−∞); Θ(π)=A ln
tan
π
2
= A ln(∞)=A(∞).
Θ blows up at θ = 0 and at θ = π.
Problem 4.5
Y
l
l
=(−1)
l
(2l +1)
4π
1
(2l)!
e
ilφ
P
l
l
(cos θ).P
l
l
(x)=(1− x
2
)
l/2
d
dx
l
P
l
(x).
P
l
(x)=
1
2
l
l!
d
dx
l
(x
2
− 1)
l
, so P
l
l
(x)=
1
2
l
l!
(1 − x
2
)
l/2
d
dx
2l
(x
2
− 1)
l
.
Now (x
2
−1)
l
= x
2l
+ ···, where all the other terms involve powers of x less than 2l, and hence give zero when
differentiated 2l times. So
P
l
l
(x)=
1
2
l
l!
(1 − x
2
)
l/2
d
dx
2l
x
2l
. But
d
dx
n
x
n
= n!, so P
l
l
=
(2l)!
2
l
l!
(1 − x
2
)
l/2
.
∴ Y
l
l
=(−1)
l
(2l +1)
4π(2l)!
e
ilφ
(2l)!
2
l
l!
(sin θ)
l
=
1
l!
(2l + 1)!
4π
−
1
2
e
iφ
sin θ
l
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 91
Y
2
3
=
7
4π
·
1
5!
e
2iφ
P
2
3
(cos θ); P
2
3
(x)=(1− x
2
)
d
dx
2
P
3
(x); P
3
(x)=
1
8 · 3!
d
dx
3
(x
2
− 1)
3
.
P
3
=
1
8 · 3 · 2
d
dx
2
6x(x
2
− 1)
2
=
1
8
d
dx
(x
2
− 1)
2
+4x
2
(x
2
− 1)
=
1
8
4x(x
2
− 1)+8x(x
2
− 1)+4x
2
· 2x
=
1
2
x
3
− x +2x
3
− 2x +2x
3
=
1
2
5x
3
− 3x
.
P
2
3
(x)=
1
2
1 − x
2
d
dx
2
5x
3
− 3x
=
1
2
1 − x
2
d
dx
15x
2
− 3
=
1
2
(1 − x
2
)30x =15x(1 − x
2
).
Y
2
3
=
7
4π
1
5!
15e
2iφ
cos θ sin
2
θ =
1
4
105
2π
e
2iφ
sin
2
θ cos θ.
Check that Y
l
l
satisfies Eq. 4.18: Let
1
l!
(2l + 1)!
4π
−
1
2
l
≡ A,so Y
l
l
= A(e
iφ
sin θ)
l
.
∂Y
l
l
∂θ
= Ae
ilφ
l(sin θ)
l−1
cos θ; sin θ
∂Y
l
l
∂θ
= l cos θY
l
l
;
sin θ
∂
∂θ
sin θ
∂Y
l
l
∂θ
= l cos θ
sin θ
∂Y
l
l
∂θ
− l sin
2
θY
l
l
=
l
2
cos
2
θ −l sin
2
θ
Y
l
l
.
∂
2
Y
l
l
∂φ
2
= −l
2
Y
l
l
.
So the left side of Eq. 4.18 is
l
2
(1 − sin
2
θ) −l sin
2
θ −l
2
Y
l
l
= −l(l + 1) sin
2
θY
l
l
, which matches the right side.
Check that Y
2
3
satisfies Eq. 4.18: Let B ≡
1
4
105
2π
, so Y
2
3
= Be
2iφ
sin
2
θ cos θ.
∂Y
2
3
∂θ
= Be
2iφ
2 sin θ cos
2
θ −sin
3
θ
; sin θ
∂
∂θ
sin θ
∂Y
2
3
∂θ
= Be
2iφ
sin θ
∂
∂θ
2 sin
2
θ cos
2
θ −sin
4
θ
= Be
2iφ
sin θ
4 sin θ cos
3
θ −4 sin
3
θ cos θ − 4 sin
3
θ cos θ
=4Be
2iφ
sin
2
θ cos θ
cos
2
θ −2 sin
2
θ
= 4(cos
2
θ −2 sin
2
θ)Y
2
3
.
∂
2
Y
2
3
∂φ
2
= −4Y
2
3
. So the left side of Eq. 4.18 is
4(cos
2
θ −2 sin
2
θ −1)Y
2
3
=4(−3 sin
2
θ)Y
2
3
= −l(l + 1) sin
2
θY
2
3
,
where l = 3, so it fits the right side of Eq. 4.18.
Problem 4.6
1
−1
P
l
(x)P
l
(x)dx =
1
2
l
l!
1
2
l
l
!
1
−1
d
dx
l
(x
2
− 1)
l
d
dx
l
(x
2
− 1)
l
dx.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

92 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
If l = l
, we may as well let l be the larger of the two (l>l
). Integrate by parts, pulling successively each
derivative off the first term onto the second:
2
l
l!2
l
l
!
1
−1
P
l
(x)P
l
(x)dx =
d
dx
l−1
(x
2
− 1)
l
d
dx
l
(x
2
− 1)
l
1
−1
−
1
−1
d
dx
l−1
(x
2
− 1)
l
d
dx
l
+1
(x
2
− 1)
l
dx
= ...(boundary terms) ...+(−1)
l
1
−1
(x
2
− 1)
l
d
dx
l
+l
(x
2
− 1)
l
dx.
But (d/dx)
l
+l
(x
2
− 1)
l
= 0, because (x
2
− 1)
l
is a polynomial whose highest power is 2l
, so more than 2l
derivatives will kill it, and l
+ l>2l
. Now, the boundary terms are of the form:
d
dx
l−n
(x
2
− 1)
l
d
dx
l
+n−1
(x
2
− 1)
l
+1
−1
,n=1, 2, 3,... ,l.
Look at the first term: (x
2
− 1)
l
=(x
2
− 1)(x
2
− 1) ...(x
2
− 1); l factors. So 0, 1, 2,... ,l− 1 derivatives will
still leave at least one overall factor of (x
2
− 1). [Zero derivatives leaves l factors; one derivative leaves l − 1:
d/dx(x
2
−1)
l
=2lx(x
2
−1)
l−1
; two derivatives leaves l−2: d
2
/dx
2
(x
2
−1)
l
=2l(x
2
−1)
l−1
+2l(l−1)2x
2
(x
2
−1)
l−2
,
and so on.] So the boundary terms are all zero, and hence
1
−1
P
l
(x)P
l
(x)dx =0.
This leaves only the case l = l
. Again the boundary terms vanish, but this time the remaining integral does
not:
(2
l
l!)
2
1
−1
[P
l
(x)]
2
dx =(−1)
l
1
−1
(x
2
− 1)
l
d
dx
2l
(x
2
− 1)
l
(d/dx)
2l
(x
2l
)=(2l)!
dx
=(−1)
l
(2l)!
1
−1
(x
2
− 1)
l
dx = 2(2l)!
1
0
(1 − x
2
)
l
dx.
Let x ≡ cos θ,sodx = −sin θdθ, (1 − x
2
) = sin
2
θ, θ : π/2 → 0. Then
1
0
(1 − x
2
)
l
dx =
0
π/2
(sin θ)
2l
(−sin θ)dθ =
π/2
0
(sin θ)
2l+1
dθ
=
(2)(4) ···(2l)
(1)(3)(5) ···(2l +1)
=
(2
l
l!)
2
1 · 2 · 3 ····(2l +1)
=
(2
l
l!)
2
(2l + 1)!
.
∴
1
−1
[P
l
(x)]
2
dx =
1
(2
l
l!)
2
2(2l)!
(2
l
l!)
2
(2l + 1)!
=
2
2l +1
. So
1
−1
P
l
(x)P
l
(x)dx =
2
2l +1
δ
ll
. QED
Problem 4.7
(a)
n
1
(x)=−(−x)
1
x
d
dx
cos x
x
= −
cos x
x
2
−
sin x
x
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 93
n
2
(x)=−(−x)
2
1
x
d
dx
2
cos x
x
= −x
2
1
x
d
dx
1
x
d
dx
cos x
x
= −x
d
dx
1
x
·
−x sin x − cos x
x
2
= x
d
dx
sin x
x
2
+
cos x
x
3
= x
x
2
cos x −2x sin x
x
4
+
−x
3
sin x −3x
2
cos x
x
6
=
cos x
x
− 2
sin x
x
2
−
sin x
x
2
−
3 cos x
x
3
= −
3
x
3
−
1
x
cos x −
3
x
2
sin x.
(b) Letting sin x ≈ x and cos x ≈ 1, and keeping only the lowest power of x:
n
1
(x) ≈−
1
x
2
+
1
x
x ≈
−
1
x
2
. As x → 0, this blows up.
n
2
(x) ≈−
3
x
3
−
1
x
−
3
x
2
x ≈ −
3
x
3
, which again blows up at the origin.
Problem 4.8
(a)
u = Arj
1
(kr)=A
sin(kr)
k
2
r
−
cos(kr)
k
=
A
k
sin(kr)
(kr)
− cos(kr)
.
du
dr
=
A
k
k
2
r cos(kr) − k sin(kr)
(kr)
2
+ k sin(kr)
= A
cos(kr)
kr
−
sin(kr)
(kr)
2
+ sin(kr)
.
d
2
u
dr
2
= A
−k
2
r sin(kr) − k cos(kr)
(kr)
2
−
k
3
r
2
cos(kr) − 2k
2
r sin(kr)
(kr)
4
+ k cos(kr)
= Ak
−
sin(kr)
(kr)
−
cos(kr)
(kr)
2
−
cos(kr)
(kr)
2
+2
sin(kr)
(kr)
3
+ cos(kr)
= Ak
1 −
2
(kr)
2
cos(kr)+
2
(kr)
3
−
1
(kr)
sin(kr)
.
With V = 0 and l = 1, Eq. 4.37 reads:
d
2
u
dr
2
−
2
r
2
u = −
2mE
2
u = −k
2
u. In this case the left side is
Ak
1 −
2
(kr)
2
cos(kr)+
2
(kr)
3
−
1
(kr)
sin(kr) −
2
(kr)
2
sin(kr)
(kr)
− cos(kr)
= Ak
cos(kr) −
sin(kr)
kr
= −k
2
u. So this u does satisfy Eq. 4.37.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
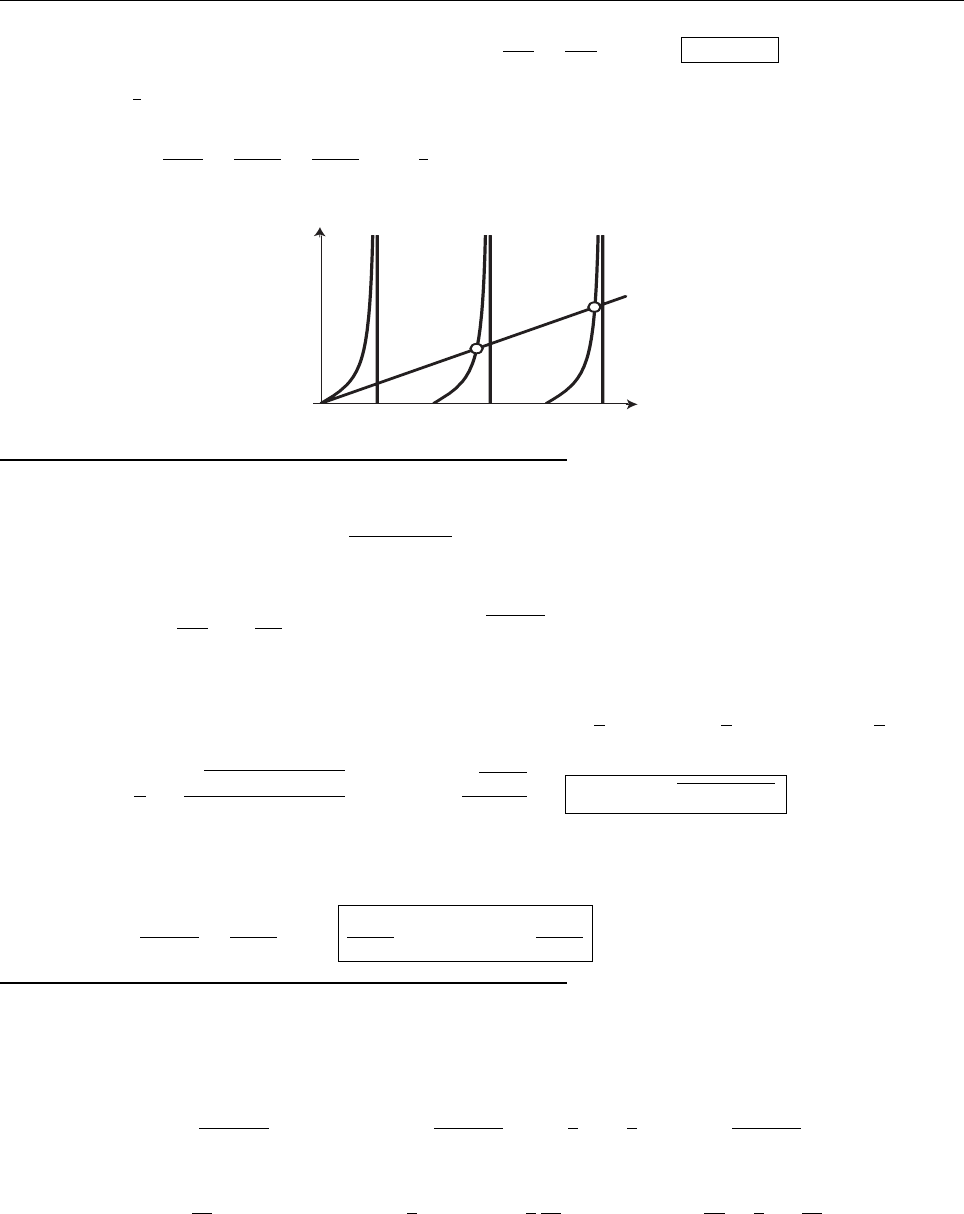
94 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
(b) Equation 4.48 ⇒ j
1
(z) = 0, where z = ka.Thus
sin z
z
2
−
cos z
z
=0,or tan z = z. For high z (large n,
if n =1, 2, 3,... counts the allowed energies in increasing order), the intersections occur slightly below
z =(n +
1
2
)π.
∴ E =
2
k
2
2m
=
2
z
2
2ma
2
=
2
π
2
2ma
2
n +
1
2
2
. QED
π/2 3π/2
z
5π/2
z
tan z
Problem 4.9
For r ≤ a, u(r)=A sin(kr), with k ≡
2m(E + V
0
)/.Forr ≥ a, Eq. 4.37 with l =0,V = 0, and (for a bound
state) E<0 ⇒:
d
2
u
dr
2
= −
2m
2
Eu = κ
2
u, with κ ≡
√
−2mE/ ⇒ u(r)=Ce
κr
+ De
−κr
.
But the Ce
κr
term blows up as r →∞,sou(r)=De
−κr
.
Continuity of u at r = a : A sin(ka)=De
−κa
Continuity of u
at r = a : Ak cos(ka)=−Dκe
−κa
divide:
1
k
tan(ka)=−
1
κ
, or −cot ka =
κ
k
.
Let ka ≡ z;
κ
k
=
2mV
0
a
2
/
2
− z
2
z
. Let z
0
≡
√
2mV
0
a.
−cot z =
(z
0
/z)
2
− 1. This is exactly the
same transcendental equation we encountered in Problem 2.29—see graph there. There is no solution if z
0
<π/2,
which is to say, if 2mV
0
a
2
/
2
<π
2
/4, or V
0
a
2
<π
2
2
/8m. Otherwise, the ground state energy occurs somewhere
between z = π/2 and z = π:
E + V
0
=
2
k
2
a
2
2ma
2
=
2
2ma
2
z
2
, so
2
π
2
8ma
2
< (E
0
+ V
0
) <
2
π
2
2ma
2
(precise value depends on V
0
).
Problem 4.10
R
30
(n =3,l = 0) : Eq. 4.62 ⇒ v(ρ)=
/
j=0
c
j
ρ
j
.
Eq. 4.76 ⇒ c
1
=
2(1 − 3)
(1)(2)
c
0
= −2c
0
; c
2
=
2(2 − 3)
(2)(3)
c
1
= −
1
3
c
1
=
2
3
c
0
; c
3
=
2(3 − 3)
(3)(4)
c
2
=0.
Eq. 4.73 ⇒ ρ =
r
3a
; Eq. 4.75 ⇒ R
30
=
1
r
ρe
−ρ
v(ρ)=
1
r
r
3a
e
−r/3a
c
0
− 2c
0
r
3a
+
2
3
c
0
r
3a
2
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 95
R
30
=
c
0
3a
1 −
2
3
r
a
+
2
27
r
a
2
e
−r/3a
.
R
31
(n =3,l =1): c
1
=
2(2 − 3)
(1)(4)
c
0
= −
1
2
c
0
; c
2
=
2(3 − 3)
(2)(5)
c
1
=0.
R
31
=
1
r
r
3a
2
e
−r/3a
c
0
−
1
2
c
0
r
3a
=
c
0
9a
2
r
1 −
1
6
r
a
e
−r/3a
.
R
32
(n =3,l =2): c
1
=
2(3 − 3)
(1)(6)
c
0
=0.R
32
=
1
r
r
3a
3
e
−r/3a
(c
0
)=
c
0
27a
3
r
2
e
−r/3a
.
Problem 4.11
(a)
Eq. 4.31 ⇒
∞
0
|R|
2
r
2
dr =1. Eq. 4.82 ⇒ R
20
=
c
0
2a
1 −
r
2a
e
−r/2a
. Let z ≡
r
a
.
1=
c
0
2a
2
a
3
∞
0
1 −
z
2
2
e
−z
z
2
dz =
c
2
0
a
4
∞
0
z
2
− z
3
+
1
4
z
4
e
−z
dz =
c
2
0
a
4
2 − 6+
24
4
=
a
2
c
2
0
.
∴
c
0
=
2
a
.
Eq. 4.15 ⇒ ψ
200
= R
20
Y
0
0
. Table 4.3 ⇒ Y
0
0
=
1
√
4π
.
∴ ψ
200
=
1
√
4π
2
a
1
2a
1 −
r
2a
e
−r/2a
⇒ ψ
200
=
1
√
2πa
1
2a
1 −
r
2a
e
−r/2a
.
(b)
R
21
=
c
0
4a
2
re
−r/2a
;1=
c
0
4a
2
2
a
5
∞
0
z
4
e
−z
dz =
c
2
0
a
16
24 =
3
2
ac
2
0
, so c
0
=
2
3a
.
R
21
=
1
√
6a
1
2a
2
re
−r/2a
; ψ
21±1
=
1
√
6a
1
2a
2
re
−r/2a
'
∓
3
8π
sin θe
±iφ
(
=
∓
1
√
πa
1
8a
2
re
−r/2a
sin θe
±iφ
;
ψ
210
=
1
√
6a
1
2a
2
re
−r/2a
'
3
4π
cos θ
(
=
1
√
2πa
1
4a
2
re
−r/2a
cos θ.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

96 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Problem 4.12
(a)
L
0
= e
x
e
−x
= 1. L
1
= e
x
d
dx
e
−x
x
= e
x
e
−x
− e
−x
x
= 1 − x.
L
2
= e
x
d
dx
2
e
−x
x
2
= e
x
d
dx
2xe
−x
− e
−x
x
2
= e
x
2e
−x
− 2xe
−x
+ e
−x
x
2
− 2xe
−x
= 2 − 4x + x
2
.
L
3
= e
x
d
dx
3
e
−x
x
3
= e
x
d
dx
2
−e
−x
x
3
+3x
2
e
−x
= e
x
d
dx
e
−x
x
3
− 3x
2
e
−x
− 3x
2
e
−x
+6xe
−x
= e
x
−e
−x
x
3
+3x
2
e
−x
+6x
2
e
−x
− 12xe
−x
− 6xe
−x
+6e
−x
=
6 − 18x +9x
2
− x
3
.
(b)
v(ρ)=L
5
2
(2ρ); L
5
2
(x)=L
5
7−5
(x)=(−1)
5
d
dx
5
L
7
(x).
L
7
(x)=e
x
d
dx
7
x
7
e
−x
= e
x
d
dx
6
7x
6
e
−x
− x
7
e
−x
= e
x
d
dx
5
42x
5
e
−x
− 7x
6
e
−x
− 7x
6
e
−x
+ x
7
e
−x
= e
x
d
dx
4
210x
4
e
−x
− 42x
5
e
−x
− 84x
5
e
−x
+14x
6
e
−x
+7x
6
e
−x
− x
7
e
−x
= e
x
d
dx
3
840x
3
e
−x
− (210 + 630)x
4
e
−x
+ (126 + 126)x
5
e
−x
− (21+7)x
6
e
−x
+ x
7
e
−x
= e
x
d
dx
2
2520x
2
e
−x
− (840 + 3360)x
3
e
−x
+(840 + 1260)x
4
e
−x
− (252 + 168)x
5
e
−x
+ (28 + 7)x
6
e
−x
− x
7
e
−x
= e
x
d
dx
5040xe
−x
− (2520 + 12600)x
2
e
−x
+ (4200 + 8400)x
3
e
−x
− (2100 + 2100)x
4
e
−x
+ (420 + 210)x
5
e
−x
− (35+7)x
6
e
−x
+ x
7
e
−x
= e
x
5040e
−x
− (5040 + 30240)xe
−x
+ (15120 + 37800)x
2
e
−x
− (12600 + 8400 + 8400)x
3
e
−x
+ (2100 + 2100 + 3150)x
4
e
−x
− (630 + 252)x
5
e
−x
+(42+7)x
6
e
−x
− x
7
e
−x
= 5040 − 35280x + 52920x
2
− 29400x
3
+ 7350x
4
− 882x
5
+49x
6
− x
7
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 97
L
5
2
= −
d
dx
5
−882x
5
+49x
6
− x
7
= −
−882(5 · 4 · 3 · 2) + 49(6 · 5 · 4 · 3 · 2)x − 7 · 6 · 5 ·4 ·3x
2
=60
(882 × 2) − (49 × 12)x +42x
2
= 2520(42 − 14x + x
2
).
v(ρ) = 2520(42 −28ρ +4ρ
2
)= 5040
21 − 14ρ +2ρ
2
.
(c)
Eq. 4.62 ⇒ v(ρ)=
∞
j=0
c
j
ρ
j
. Eq. 4.76 ⇒ c
1
=
2(3 − 5)
(1)(6)
c
0
= −
2
3
c
0
.
c
2
=
2(4 − 5)
(2)(7)
c
1
= −
1
7
c
1
=
2
21
c
0
; c
3
=
2(5 − 5)
(3)(8)
c
2
=0.
v(ρ)=c
0
−
2
3
c
0
ρ +
2
21
c
0
ρ
2
=
c
0
21
21 − 14ρ +2ρ
2
.
Problem 4.13
(a)
ψ =
1
√
πa
3
e
−r/a
, so r
n
=
1
πa
3
r
n
e
−2r/a
r
2
sin θdrdθdφ
=
4π
πa
3
∞
0
r
n+2
e
−2r/a
dr.
r =
4
a
3
∞
0
r
3
e
−2r/a
dr =
4
a
3
3!
a
2
4
=
3
2
a;
r
2
=
4
a
3
∞
0
r
4
e
−2r/a
dr =
4
a
3
4!
a
2
5
= 3a
2
.
(b)
x =0; x
2
=
1
3
r
2
= a
2
.
(c)
ψ
211
= R
21
Y
1
1
= −
1
√
πa
1
8a
2
re
−r/2a
sin θe
iφ
(Problem 4.11(b)).
x
2
=
1
πa
1
(8a
2
)
2
r
2
e
−r/a
sin
2
θ
r
2
sin
2
θ cos
2
φ
r
2
sin θdrdθdφ
=
1
64πa
5
∞
0
r
6
e
−r/a
dr
π
0
sin
5
θdθ
2π
0
cos
2
φdφ
=
1
64πa
5
6!a
7
2
2 · 4
1 · 3 · 5
1
2
· 2π
=
12a
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

98 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Problem 4.14
ψ =
1
√
πa
3
e
−r/a
; P = |ψ|
2
4πr
2
dr =
4
a
3
e
−2r/a
r
2
dr = p(r) dr; p(r)=
4
a
3
r
2
e
−2r/a
.
dp
dr
=
4
a
3
2re
−2r/a
+ r
2
−
2
a
e
−2r/a
=
8r
a
3
e
−2r/a
1 −
r
a
=0⇒
r = a.
Problem 4.15
(a) Ψ(r,t)=
1
√
2
ψ
211
e
−iE
2
t/
+ ψ
21−1
e
−iE
2
t/
=
1
√
2
(ψ
211
+ ψ
21−1
) e
−iE
2
t/
; E
2
=
E
1
4
= −
2
8ma
2
.
From Problem 4.11(b):
ψ
211
+ ψ
21−1
= −
1
√
πa
1
8a
2
re
−r/2a
sin θ
e
iφ
− e
−iφ
= −
i
√
πa 4a
2
re
−r/2a
sin θ sin φ.
Ψ(r,t)=−
i
√
2πa 4a
2
re
−r/2a
sin θ sin φe
−iE
2
t/
.
(b)
V =
|Ψ|
2
−
e
2
4π9
0
1
r
d
3
r =
1
(2πa)(16a
4
)
−
e
2
4π9
0
r
2
e
−r/a
sin
2
θ sin
2
φ
1
r
r
2
sin θdrdθdφ
=
1
32πa
5
−
2
ma
2
∞
0
r
3
e
−r/a
dr
π
0
sin
3
θdθ
2π
0
sin
2
φdφ= −
2
32πma
6
3!a
4
4
3
(π)
=
−
2
4ma
2
=
1
2
E
1
=
1
2
(−13.6eV) = −6.8eV
(independent of t).
Problem 4.16
E
n
(Z)=Z
2
E
n
; E
1
(Z)=Z
2
E
1
; a(Z)=a/Z; R(Z)=Z
2
R.
Lyman lines range from n
i
=2ton
i
= ∞ (with n
f
= 1); the wavelengths range from
1
λ
2
= R
1 −
1
4
=
3
4
R ⇒ λ
2
=
4
3R
down to
1
λ
1
= R
1 −
1
∞
= R ⇒ λ
1
=
1
R
.
For Z =2: λ
1
=
1
4R
=
1
4(1.097 × 10
7
)
=
2.28 × 10
−8
m to λ
2
=
1
3R
=
3.04 × 10
−8
m, ultraviolet.
For Z =3: λ
1
=
1
9R
=
1.01 × 10
−8
m to λ
2
=
4
27R
=
1.35 × 10
−8
m, also ultraviolet.
Problem 4.17
(a) V (r)=−G
Mm
r
.
So
e
2
4π9
0
→ GM m translates hydrogen results to the gravitational analogs.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 99
(b) Equation 4.72: a =
4π9
0
e
2
2
m
, so
a
g
=
2
GMm
2
=
(1.0546 × 10
−34
Js)
2
(6.6726 × 10
−11
m
3
/kg · s
2
)(1.9892 × 10
30
kg)(5.98 × 10
24
kg)
2
= 2.34 × 10
−138
m.
(c) Equation 4.70 ⇒ E
n
= −
m
2
2
(GMm)
2
1
n
2
.
E
c
=
1
2
mv
2
− G
Mm
r
o
. But G
Mm
r
2
o
=
mv
2
r
o
⇒
1
2
mv
2
=
GMm
2r
o
, so
E
c
= −
GMm
2r
o
= −
m
2
2
(GMm)
2
1
n
2
⇒ n
2
=
GMm
2
2
r
o
=
r
o
a
g
⇒ n =
r
o
a
g
.
r
o
= earth-sun distance = 1.496 ×10
11
m ⇒ n =
1.496 × 10
11
2.34 × 10
−138
= 2.53 × 10
74
.
(d)
∆E = −
G
2
M
2
m
3
2
2
1
(n +1)
2
−
1
n
2
.
1
(n +1)
2
=
1
n
2
(1 + 1/n)
2
≈
1
n
2
1 −
2
n
.
So
1
(n +1)
2
−
1
n
2
≈
1
n
2
1 −
2
n
− 1
= −
2
n
3
;∆E =
G
2
M
2
m
3
2
n
3
.
∆E =
(6.67 × 10
−11
)
2
(1.99 × 10
30
)
2
(5.98 × 10
24
)
3
(1.055 × 10
−34
)
2
(2.53×
74
)
3
= 2.09 × 10
−41
J. E
p
=∆E = hν =
hc
λ
.
λ =(3×10
8
)(6.63 × 10
−34
)/(2.09 × 10
−41
)= 9.52 × 10
15
m.
But 1 ly = 9.46 × 10
15
m. Is it a coincidence that λ ≈ 1 ly? No: From part (c), n
2
= GM m
2
r
o
/
2
,so
λ =
ch
∆E
= c2π
2
n
3
G
2
M
2
m
3
= c
2π
3
G
2
M
2
m
3
GMm
2
r
o
2
3/2
= c
'
2π
r
3
o
GM
(
.
But (from (c)) v =
GM/r
o
=2πr
o
/T , where T is the period of the orbit (in this case one year), so
T =2π
r
3
o
/GM, and hence λ = cT (one light year). [Incidentally, the same goes for hydrogen: The
wavelength of the photon emitted in a transition from a highly excited state to the next lower one is equal
to the distance light would travel in one orbital period.]
Problem 4.18
f|L
±
g = f|L
x
g±if|L
y
g = L
x
f|g±iL
y
f|g = (L
x
∓ iL
y
)f|g = L
∓
f|g, so (L
±
)
†
= L
∓
.
Now, using Eq. 4.112, in the form L
∓
L
±
= L
2
− L
2
z
∓ L
z
:
f
m
l
|L
∓
L
±
f
m
l
= f
m
l
|(L
2
− L
2
z
∓ L
z
)f
m
l
= f
m
l
|
2
l(l +1)−
2
m
2
∓
2
m
f
m
l
=
2
[l(l +1)− m(m ± 1)] f
m
l
|f
m
l
=
2
[l(l +1)− m(m ± 1)]
= L
±
f
m
l
|L
±
f
m
l
= A
m
l
f
m±1
l
|A
m
l
f
m±1
l
= |A
m
l
|
2
f
m±1
l
|f
m±1
l
= |A
m
l
|
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

100 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Conclusion: A
m
l
=
l(l +1)− m(m ± 1).
Problem 4.19
(a)
[L
z
,x]=[xp
y
− yp
x
,x]=[xp
y
,x] − [yp
x
,x]=0− y[p
x
,x]=iy.
[L
z
,y]=[xp
y
− yp
x
,y]=[xp
y
,y] − [yp
x
,y]=x[p
y
,y] − 0=−ix.
[L
z
,z]=[xp
y
− yp
x
,z]=[xp
y
,z] − [yp
x
,z]=0− 0=0.
[L
z
,p
x
]=[xp
y
− yp
x
,p
x
]=[xp
y
,p
x
] − [yp
x
,p
x
]=p
y
[x, p
x
] − 0=ip
y
.
[L
z
,p
y
]=[xp
y
− yp
x
,p
y
]=[xp
y
,p
y
] − [yp
x
,p
y
]=0− p
x
[y, p
y
]=−ip
x
.
[L
z
,p
z
]=[xp
y
− yp
x
,p
z
]=[xp
y
,p
z
] − [yp
x
,p
z
]=0− 0=0.
(b)
[L
z
,L
x
]=[L
z
,yp
z
− zp
y
]=[L
z
,yp
z
] − [L
z
,zp
y
]=[L
z
,y]p
z
− [L
z
,p
y
]z
= −ixp
z
+ ip
x
z = i(zp
x
− xp
z
)=iL
y
.
(So, by cyclic permutation of the indices, [L
x
,L
y
]=iL
z
.)
(c)
[L
z
,r
2
]=[L
z
,x
2
]+[L
z
,y
2
]+[L
z
,z
2
]=[L
z
,x]x + x[L
z
,x]+[L
z
,y]y + y[L
z
,y]+0
= iyx + xiy +(−ix)y + y(−ix)=
0.
[L
z
,p
2
]=[L
z
,p
2
x
]+[L
z
,p
2
y
]+[L
z
,p
2
z
]=[L
z
,p
x
]p
x
+ p
x
[L
z
,p
x
]+[L
z
,p
y
]p
y
+ p
y
[L
z
,p
y
]+0
= ip
y
p
x
+ p
x
ip
y
+(−ip
x
)p
y
+ p
y
(−ip
x
)= 0.
(d) It follows from (c) that all three components of L commute with r
2
and p
2
, and hence with the whole
Hamiltonian, since H = p
2
/2m + V (
√
r
2
). QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 101
Problem 4.20
(a)
Equation 3.71 ⇒
dL
x
dt
=
i
[H, L
x
]. [H, L
x
]=
1
2m
[p
2
,L
x
]+[V,L
x
].
The first term is zero (Problem 4.19(c)); the second would be too if V were a function only of r = |r|, but
in general
[H, L
x
]=[V,yp
z
− zp
y
]=y[V,p
z
] − z[V,p
y
]. Now (Problem 3.13(c)):
[V,p
z
]=i
∂V
∂z
and [V,p
y
]=i
∂V
∂y
. So [H, L
x
]=yi
∂V
∂z
− zi
∂V
∂y
= i[r × (∇V )]
x
.
Thus
dL
x
dt
= −[r × (∇V )]
x
, and the same goes for the other two components:
dL
dt
= [r × (−∇V )] = N. QED
(b)
If V (r)=V (r), then ∇V =
∂V
∂r
ˆr, and r × ˆr =0, so
dL
dt
=0. QED
Problem 4.21
(a)
L
+
L
−
f = −
2
e
iφ
∂
∂θ
+ i cot θ
∂
∂φ
e
−iφ
∂f
∂θ
− i cot θ
∂f
∂φ
= −
2
e
iφ
e
−iφ
∂
2
f
∂θ
2
− i
−csc
2
θ
∂f
∂φ
+ cot θ
∂
2
f
∂θ ∂φ
+i cot θ
−ie
−iφ
∂f
∂θ
− i cot θ
∂f
∂φ
+ e
−iφ
∂
2
f
∂φ∂θ
− i cot θ
∂
2
f
∂φ
2
= −
2
∂
2
f
∂θ
2
+ i csc
2
θ
∂f
∂φ
− i cot θ
∂
2
f
∂θ ∂φ
+ cot θ
∂f
∂θ
− i cot
2
θ
∂f
∂φ
+ i cot θ
∂
2
f
∂φ∂θ
+ cot
2
θ
∂
2
f
∂φ
2
= −
2
∂
2
∂θ
2
+ cot θ
∂
∂θ
+ cot
2
θ
∂
2
∂φ
2
+ i(csc
2
θ −cot
2
θ)
∂
∂φ
f, so
L
+
L
−
= −
2
∂
2
∂θ
2
+ cot θ
∂
∂θ
+ cot
2
θ
∂
2
∂φ
2
+ i
∂
∂φ
. QED
(b) Equation 4.129 ⇒ L
z
=
i
∂
∂φ
, Eq. 4.112 ⇒ L
2
= L
+
L
−
+ L
2
z
− L
z
, so, using (a):
L
2
= −
2
∂
2
∂θ
2
+ cot θ
∂
∂θ
+ cot
2
θ
∂
2
∂φ
2
+ i
∂
∂φ
−
2
∂
2
∂φ
2
−
i
∂
∂φ
= −
2
∂
2
∂θ
2
+ cot θ
∂
∂θ
+ (cot
2
θ +1)
∂
2
∂φ
2
+ i
∂
∂φ
− i
∂
∂φ
= −
2
∂
2
∂θ
2
+ cot θ
∂
∂θ
+
1
sin
2
θ
∂
2
∂φ
2
= −
2
1
sin θ
∂
∂θ
sin θ
∂
∂θ
+
1
sin
2
θ
∂
2
∂φ
2
. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

102 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Problem 4.22
(a) L
+
Y
l
l
=0 (top of the ladder).
(b)
L
z
Y
l
l
= lY
l
l
⇒
i
∂
∂φ
Y
l
l
= lY
l
l
, so
∂Y
l
l
∂φ
= ilY
l
l
, and hence Y
l
l
= f(θ)e
ilφ
.
[Note: f(θ) is the “constant” here—it’s constant with respect to φ... but still can depend on θ.]
L
+
Y
l
l
=0⇒ e
iφ
∂
∂θ
+ i cot θ
∂
∂φ
f(θ)e
ilφ
=0, or
df
dθ
e
ilφ
+ if cot θile
ilφ
=0, so
df
dθ
= l cot θf ⇒
df
f
= l cot θdθ ⇒
df
f
= l
cos θ
sin θ
dθ ⇒ ln f = l ln(sin θ)+constant.
ln f = ln(sin
l
θ)+K ⇒ ln
f
sin
l
θ
= K ⇒
f
sin
l
θ
= constant ⇒ f(θ)=A sin
l
θ.
Y
l
l
(θ, φ)=A(e
iφ
sin θ)
l
.
(c)
1=A
2
sin
2l
θ sin θdθdφ=2πA
2
π
0
sin
(2l+1)
θdθ=2πA
2
2
(2 · 4 · 6 ·····(2l))
1 · 3 · 5 ·····(2l +1)
=4πA
2
(2 · 4 · 6 ·····2l)
2
1 · 2 · 3 · 4 · 5 ·····(2l +1)
=4πA
2
(2
l
l!)
2
(2l + 1)!
, so
A =
1
2
l+1
l!
(2l + 1)!
π
,
the same as Problem 4.5, except for an overall factor of (−1)
l
, which is arbitrary anyway.
Problem 4.23
L
+
Y
1
2
= e
iφ
∂
∂θ
+ i cot θ
∂
∂θ
−
15
8π
sin θ cos θe
iφ
= −
15
8π
e
iφ
e
iφ
(cos
2
θ −sin
2
θ)+i
cos θ
sin θ
sin θ cos θie
iφ
= −
15
8π
e
2iφ
cos
2
θ −sin
2
θ −cos
2
θ
=
15
8π
e
iφ
sin θ
2
=
√
2 · 3 − 1 · 2 Y
2
2
=2Y
2
2
. ∴ Y
2
2
=
1
4
15
2π
e
iφ
sin θ
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 103
Problem 4.24
(a)
H =2
1
2
mv
2
= mv
2
; |L| =2
a
2
mv = amv, so L
2
= a
2
m
2
v
2
, and hence H =
L
2
ma
2
.
But we know the eigenvalues of L
2
:
2
l(l + 1); or, since we usually label energies with n:
E
n
=
2
n(n +1)
ma
2
(n =0, 1, 2,...).
(b) ψ
nm
(θ, φ)=Y
m
n
(θ, φ), the ordinary spherical harmonics. The degeneracy of the nth energy level is the
number of m-values for given n:
2n +1.
Problem 4.25
r
c
=
(1.6 × 10
−19
)
2
4π(8.85 ×10
−12
)(9.11 × 10
−31
)(3.0 × 10
8
)
2
=2.81 × 10
−15
m.
L =
1
2
= Iω =
2
5
mr
2
v
r
=
2
5
mrv so
v =
5
4mr
=
(5)(1.055 × 10
−34
)
(4)(9.11 × 10
−31
)(2.81 × 10
−15
)
=
5.15 × 10
10
m/s.
Since the speed of light is 3 × 10
8
m/s, a point on the equator would be going more than 100 times the speed
of light.
Nope : This doesn’t look like a very realistic model for spin.
Problem 4.26
(a)
[S
x
, S
y
]=S
x
S
y
− S
y
S
x
=
2
4
01
10
0 −i
i 0
−
0 −i
i 0
01
10
=
2
4
i 0
0 −i
−
−i 0
0 i
=
2
4
2i 0
0 −2i
= i
2
10
0 −1
= iS
z
.
(b)
σ
x
σ
x
=
10
01
=1=σ
y
σ
y
= σ
z
σ
z
, so σ
j
σ
j
= 1 for j = x, y, or z.
σ
x
σ
y
=
i 0
0 −i
= iσ
z
; σ
y
σ
z
=
0 i
i 0
= iσ
x
; σ
z
σ
x
=
01
−10
= iσ
y
;
σ
y
σ
x
=
−i 0
0 i
= −iσ
z
; σ
z
σ
y
=
0 −i
−i 0
= −iσ
x
; σ
x
σ
z
=
0 −1
10
= −iσ
y
.
Equation 4.153 packages all this in a single formula.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
104 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Problem 4.27
(a)
χ
†
χ = |A|
2
(9 + 16) = 25|A|
2
=1⇒ A =1/5.
(b)
S
x
= χ
†
S
x
χ =
1
25
2
−3i 4
01
10
3i
4
=
50
−3i 4
4
3i
=
50
(12i +12i)=
0.
S
y
= χ
†
S
y
χ =
1
25
2
−3i 4
0 −i
i 0
3i
4
=
50
−3i 4
−4i
−3
=
50
(−12 − 12) =
−
12
25
.
S
z
= χ
†
S
z
χ =
1
25
2
−3i 4
10
0 −1
3i
4
=
50
−3i 4
3i
−4
=
50
(9 − 16) =
−
7
50
.
(c)
S
2
x
= S
2
y
= S
2
z
=
2
4
(always, for spin 1/2), so σ
2
S
x
= S
2
x
−S
x
2
=
2
4
− 0,
σ
S
x
=
2
.
σ
2
S
y
= S
2
y
−S
y
2
=
4
−
12
25
2
2
=
2
2500
(625 − 576) =
49
2500
2
, σ
S
y
=
7
50
.
σ
2
S
z
= S
2
z
−S
z
2
=
2
4
−
7
50
2
2
=
2
2500
(625 − 49) =
576
2500
2
, σ
S
z
=
12
25
.
(d)
σ
S
x
σ
S
y
=
2
·
7
50
?
≥
2
|S
z
| =
2
·
7
50
(right at the uncertainty limit).
σ
S
y
σ
S
z
=
7
50
·
12
25
?
≥
2
|S
x
| = 0 (trivial).
σ
S
z
σ
S
x
=
12
25
·
2
?
≥
2
|S
y
| =
2
·
12
25
(right at the uncertainty limit).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 105
Problem 4.28
S
x
=
2
a
∗
b
∗
01
10
a
b
=
2
a
∗
b
∗
b
a
=
2
(a
∗
b + b
∗
a) = Re(ab
∗
).
S
y
=
2
a
∗
b
∗
0 −i
i 0
a
b
=
2
a
∗
b
∗
−ib
ia
=
2
(−ia
∗
b + iab
∗
)=
2
i(ab
∗
− a
∗
b) = − Im(ab
∗
).
S
z
=
2
a
∗
b
∗
10
0 −1
a
b
=
2
a
∗
b
∗
a
−b
=
2
(a
∗
a − b
∗
b)=
2
(|a|
2
−|b|
2
).
S
2
x
=
2
4
01
10
01
10
=
2
4
10
01
=
2
4
; S
2
y
=
2
4
0 −i
i 0
0 −i
i 0
=
2
4
;
S
2
z
=
2
4
10
0 −1
10
0 −1
=
2
4
;so
S
2
x
= S
2
y
= S
2
z
=
2
4
.
S
2
x
+ S
2
y
+ S
2
z
=
3
4
2
?
= s(s +1)
2
=
1
2
(
1
2
+1)
2
=
3
4
2
= S
2
.
Problem 4.29
(a)
S
y
=
2
0 −i
i 0
;
−λ −i/2
i/2 −λ
= λ
2
−
2
4
⇒
λ = ±
2
(of course).
2
0 −i
i 0
α
β
= ±
2
α
β
⇒−iβ = ±α; |α|
2
+ |β|
2
=1⇒|α|
2
+ |α|
2
=1⇒ α =
1
√
2
.
χ
(y)
+
=
1
√
2
1
i
; χ
(y)
−
=
1
√
2
1
−i
.
(b)
c
+
=
χ
(y)
+
†
χ =
1
√
2
1 −i
a
b
=
1
√
2
(a − ib);
+
2
, with probability
1
2
|a − ib|
2
.
c
−
=
χ
(y)
−
†
χ =
1
√
2
1 i
a
b
=
1
√
2
(a + ib);
−
2
, with probability
1
2
|a + ib|
2
.
P
+
+ P
−
=
1
2
[(a
∗
+ ib
∗
)(a − ib)+(a
∗
− ib
∗
)(a + ib)]
=
1
2
|a|
2
− ia
∗
b + iab
∗
+ |b|
2
+ |a|
2
+ ia
∗
b − iab
∗
+ |b|
2
= |a|
2
+ |b|
2
=1.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

106 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
(c)
2
4
, with probability 1.
Problem 4.30
S
r
= S · ˆr = S
x
sin θ cos φ + S
y
sin θ sin φ + S
z
cos θ
=
2
0 sin θ cos φ
sin θ cos φ 0
+
0 −i sin θ sin φ
i sin θ sin φ 0
+
cos θ 0
0 −cos θ
=
2
cos θ sin θ(cos φ −i sin φ)
sin θ(cos φ + i sin φ) −cos θ
=
2
cos θe
−iφ
sin θ
e
iφ
sin θ −cos θ
.
(
2
cos θ − λ)
2
e
−iφ
sin θ
2
e
iφ
sin θ (−
2
cos θ − λ)
= −
2
4
cos
2
θ + λ
2
−
2
4
sin
2
θ =0 ⇒
λ
2
=
2
4
(sin
2
θ + cos
2
θ)=
2
4
⇒
λ = ±
2
(of course).
2
cos θe
−iφ
sin θ
e
iφ
sin θ −cos θ
α
β
= ±
2
α
β
⇒ α cos θ + βe
−iφ
sin θ = ±α; β = e
iφ
(±1 − cos θ)
sin θ
α.
Upper sign: Use 1 − cos θ = 2 sin
2
θ
2
, sin θ = 2 sin
θ
2
cos
θ
2
. Then β = e
iφ
sin(θ/2)
cos(θ/2)
α. Normalizing:
1=|α|
2
+|β|
2
= |α
2
|+
sin
2
(θ/2)
cos
2
(θ/2)
|α|
2
= |α|
2
1
cos
2
(θ/2)
⇒ α = cos
θ
2
,β= e
iφ
sin
θ
2
,
χ
(r)
+
=
cos(θ/2)
e
iφ
sin(θ/2)
.
Lower sign: Use 1 + cos θ = 2 cos
2
θ
2
,β= −e
iφ
cos(θ/2)
sin(θ/2)
α;1=|α|
2
+
cos
2
(θ/2)
sin
2
(θ/2)
|α|
2
= |α|
2
1
sin
2
(θ/2)
.
Pick α = e
−iφ
sin(θ/2); then β = −cos(θ/2), and χ
(r)
−
=
e
−iφ
sin(θ/2)
−cos(θ/2)
.
Problem 4.31
There are three states: χ
+
=
1
0
0
,χ
0
=
0
1
0
,χ
−
=
0
0
1
.
S
z
χ
+
= χ
+
, S
z
χ
0
=0, S
z
χ
−
= −χ
−
, ⇒ S
z
=
10 0
00 0
00−1
. From Eq. 4.136:
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 107
S
+
χ
+
=0, S
+
χ
0
=
√
2χ
+
, S
+
χ
−
=
√
2χ
0
S
−
χ
+
=
√
2χ
0
, S
−
χ
0
=
√
2χ
−
, S
−
χ
−
=0
⇒ S
+
=
√
2
010
001
000
, S
−
=
√
2
000
100
010
.
S
x
=
1
2
(S
+
+ S
−
)=
√
2
010
101
010
,
S
y
=
1
2i
(S
+
− S
−
)=
i
√
2
0 −10
10−1
01 0
.
Problem 4.32
(a) Using Eqs. 4.151 and 4.163:
c
(x)
+
= χ
(x)†
+
χ =
1
√
2
11
cos
α
2
e
iγB
0
t/2
sin
α
2
e
−iγB
0
t/2
=
1
√
2
cos
α
2
e
iγB
0
t/2
+ sin
α
2
e
−iγB
0
t/2
.
P
(x)
+
(t)=|c
(x)
+
|
2
=
1
2
cos
α
2
e
−iγB
0
t/2
+ sin
α
2
e
iγB
0
t/2
cos
α
2
e
iγB
0
t/2
+ sin
α
2
e
−iγB
0
t/2
=
1
2
cos
2
α
2
+ sin
2
α
2
+ sin
α
2
cos
α
2
e
iγB
0
t
+ e
−iγB
0
t
=
1
2
1+2sin
α
2
cos
α
2
cos(γB
0
t)
=
1
2
[1 + sin α cos(γB
0
t)] .
(b) From Problem 4.29(a): χ
(y)
+
=
1
√
2
1
i
.
c
(y)
+
= χ
(y)†
+
χ =
1
√
2
1 −i
cos
α
2
e
iγB
0
t/2
sin
α
2
e
iγB
0
t/2
=
1
√
2
cos
α
2
e
iγB
0
t/2
− i sin
α
2
e
−iγB
0
t/2
;
P
(y)
+
(t)=|c
(y)
+
|
2
=
1
2
cos
α
2
e
−iγB
0
t/2
+ i sin
α
2
e
iγB
0
t/2
cos
α
2
e
iγB
0
t/2
− i sin
α
2
e
−iγB
0
t/2
=
1
2
cos
2
α
2
+ sin
2
α
2
+ i sin
α
2
cos
α
2
e
iγB
0
t
− e
−iγB
0
t
=
1
2
1 − 2 sin
α
2
cos
α
2
sin(γB
0
t)
=
1
2
[1 − sin α sin(γB
0
t)] .
(c)
χ
(z)
+
=
1
0
; c
(z)
+
=
10
cos
α
2
e
iγB
0
t/2
sin
α
2
e
−iγB
0
t/2
= cos
α
2
e
iγB
0
t/2
; P
(z)
+
(t)=|c
(z)
+
|
2
= cos
2
α
2
.
Problem 4.33
(a)
H = −γB · S = −γB
0
cos ωt S
z
= −
γB
0
2
cos ωt
10
0 −1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
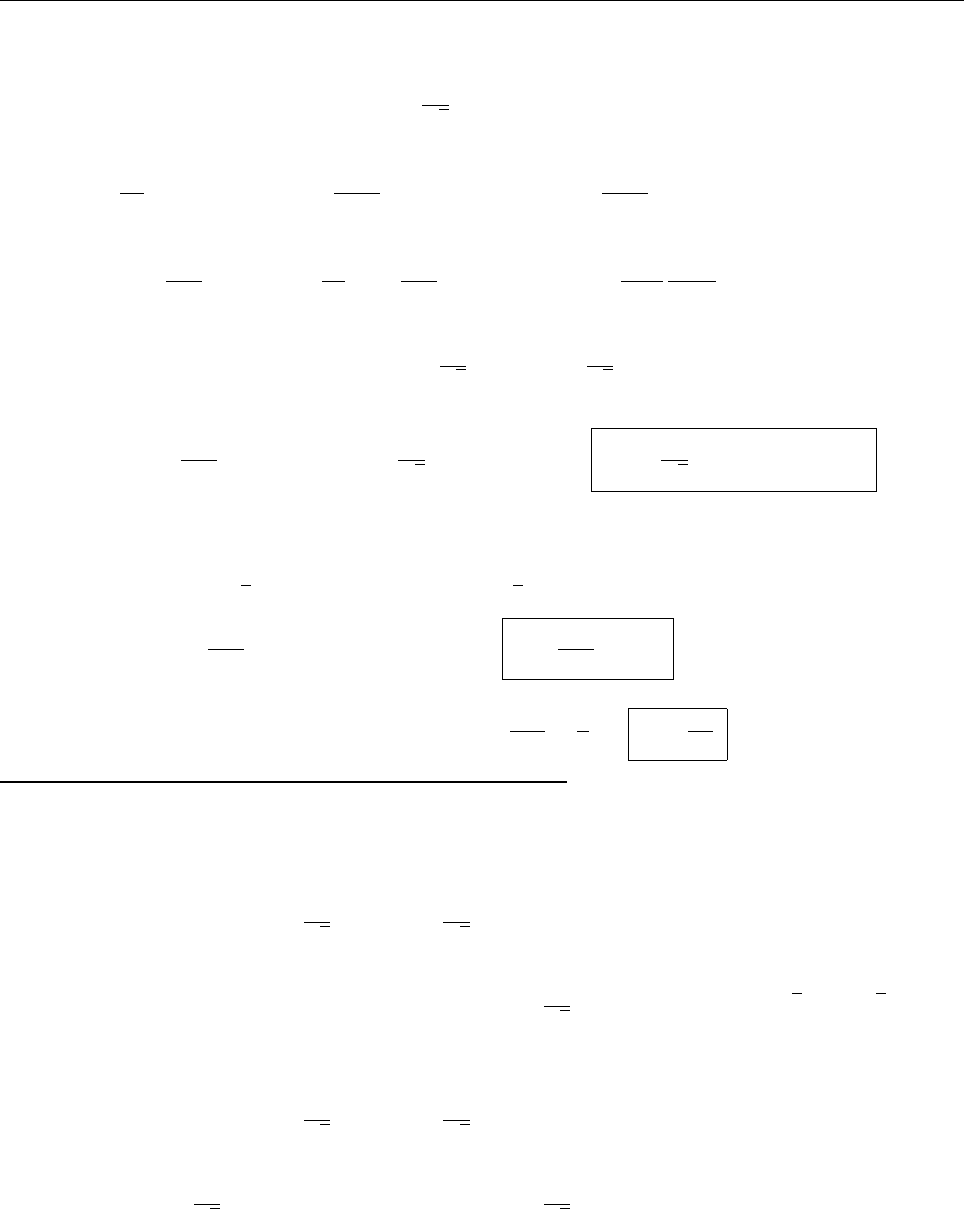
108 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
(b)
χ(t)=
α(t)
β(t)
, with α(0) = β(0) =
1
√
2
.
i
∂χ
∂t
= i
˙α
˙
β
= Hχ = −
γB
0
2
cos ωt
10
0 −1
α
β
= −
γB
0
2
cos ωt
α
−β
.
˙α = i
γB
0
2
cos ωtα ⇒
dα
α
= i
γB
0
2
cos ωtdt ⇒ ln α =
iγB
0
2
sin ωt
ω
+ constant.
α(t)=Ae
i(γB
0
/2ω) sin ωt
; α(0) = A =
1
√
2
, so α(t)=
1
√
2
e
i(γB
0
/2ω) sin ωt
.
˙
β = −i
γB
0
2
cos ωtβ ⇒ β(t)=
1
√
2
e
−i(γB
0
/2ω) sin ωt
. χ(t)=
1
√
2
e
i(γB
0
/2ω) sin ωt
e
−i(γB
0
/2ω) sin ωt
.
(c)
c
(x)
−
= χ
(x)†
−
χ =
1
2
(1 − 1)
e
i(γB
0
/2ω) sin ωt
e
−i(γB
0
/2ω) sin ωt
=
1
2
e
i(γB
0
/2ω) sin ωt
− e
−i(γB
0
/2ω) sin ωt
= i sin
γB
0
2ω
sin ωt
.P
(x)
−
(t)=|c
(x)
−
|
2
= sin
2
γB
0
2ω
sin ωt
.
(d) The argument of sin
2
must reach π/2 (so P =1)⇒
γB
0
2ω
=
π
2
,or
B
0
=
πω
γ
.
Problem 4.34
(a)
S
−
|10 =(S
(1)
−
+ S
(2)
−
)
1
√
2
(↑↓ + ↓↑)=
1
√
2
[(S
−
↑) ↓ +(S
−
↓) ↑ + ↑ (S
−
↓)+ ↓ (S
−
↑)] .
But S
−
↑= ↓,S
−
↓= 0 (Eq. 4.143), so S
−
|10 =
1
√
2
[ ↓↓ +0+0+ ↓↓]=
√
2 ↓↓=
√
2|1 − 1.
(b)
S
±
|00 =(S
(1)
±
+ S
(2)
±
)
1
√
2
(↑↓−↓↑)=
1
√
2
[(S
±
↑) ↓−(S
±
↓) ↑ + ↑ (S
±
↓)−↓(S
±
↑)] .
S
+
|00 =
1
√
2
(0 − ↑↑ + ↑↑ −0) = 0; S
−
|00 =
1
√
2
( ↓↓ −0+0− ↓↓)=0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
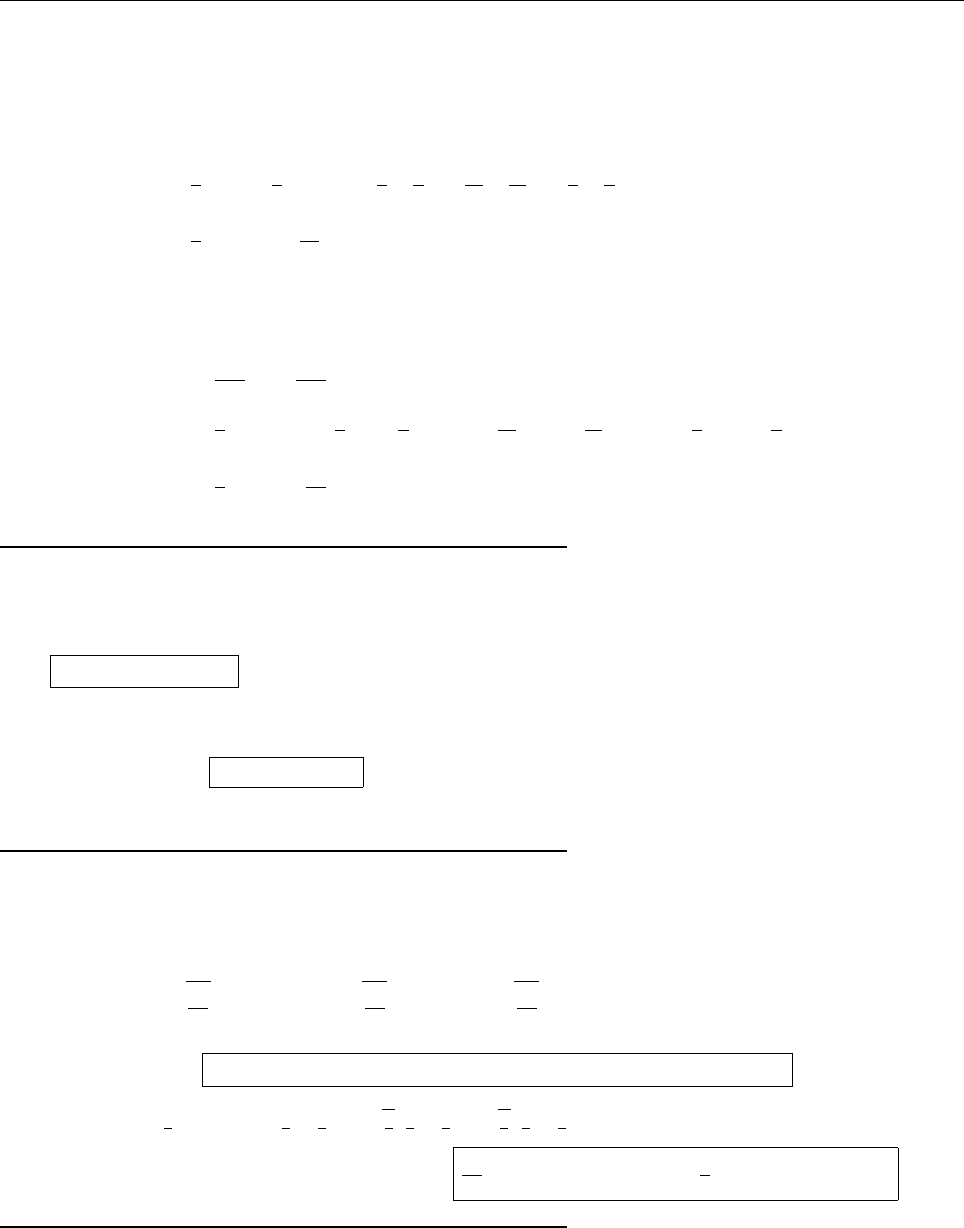
CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 109
(c)
S
2
|11 =
(S
(1)
)
2
+(S
(2)
)
2
+2S
(1)
· S
(2)
↑↑
=(S
2
↑) ↑ + ↑ (S
2
↑)+2[(S
x
↑)(S
x
↑)+(S
y
↑)(S
y
↑)+(S
z
↑)(S
z
↑)]
=
3
4
2
↑↑ +
3
4
2
↑↑ +2
2
↓
2
↓ +
i
2
↓
i
2
↓ +
2
↑
2
↑
=
3
2
2
↑↑ +2
2
4
↑↑
=2
2
↑↑=2
2
|11 = (1)(1 + 1)
2
|11, as it should be.
S
2
|1 − 1 =
(S
(1)
)
2
+(S
(2)
)
2
+2S
(1)
· S
(2)
↓↓
=
3
2
4
↓↓ +
3
2
4
↓↓ +2 [(S
x
↓)(S
x
↓)+(S
y
↓)(S
y
↓)+(S
z
↓)(S
z
↓)]
=
3
2
2
↓↓ +2
2
↑
2
↑
+
−
i
2
↑
−
i
2
↑
+
−
2
↓
−
2
↓
=
3
2
2
↓↓ +2
2
4
↓↓=2
2
↓↓=2
2
|1 − 1.
Problem 4.35
(a) 1/2 and 1/2 gives 1 or zero; 1/2 and 1 gives 3/2 or 1/2; 1/2 and 0 gives 1/2 only. So baryons can have
spin 3/2 or spin 1/2 (and the latter can be acheived in two distinct ways). [Incidentally, the lightest
baryons do carry spin 1/2 (proton, neutron, etc.) or 3/2 (∆, Ω
−
, etc.); heavier baryons can have higher
total spin, but this is because the quarks have orbital angular momentum as well.]
(b) 1/2 and 1/2 gives
spin 1 or spin 0. [Again, these are the observed spins for the lightest mesons: π’s and
K’s have spin 0, ρ’s and ω’s have spin 1.]
Problem 4.36
(a) From the 2 × 1 Clebsch-Gordan table we get
|31 =
1
15
|22|1 − 1 +
8
15
|21|10 +
6
15
|20|11,
so you might get
2 (probability 1/15), (probability 8/15), or (probability 6/15).
(b) From the 1×
1
2
table: |10|
1
2
−
1
2
=
2
3
|
3
2
−
1
2
+
1
3
|
1
2
−
1
2
. So the total is 3/2or1/2, with l(l+1)
2
=
15/4
2
and 3/4
2
, respectively. Thus you get
15
4
2
(probability 2/3), or
3
4
2
(probability 1/3).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
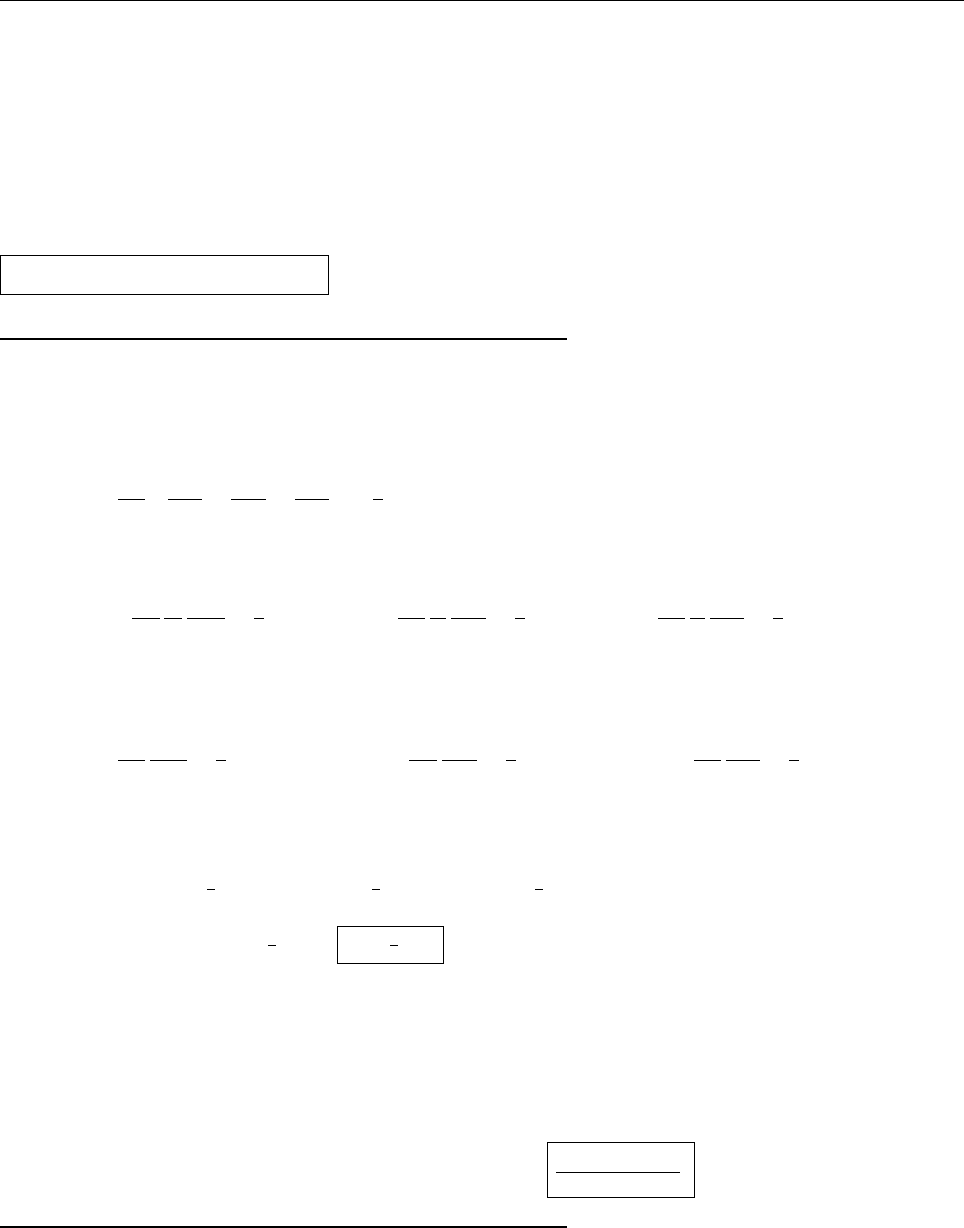
110 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Problem 4.37
Using Eq. 4.179: [S
2
,S
(1)
z
]=[S
(1)
2
,S
(1)
z
]+[S
(2)
2
,S
(1)
z
]+2[S
(1)
· S
(2)
,S
(1)
z
]. But [S
2
,S
z
] = 0 (Eq. 4.102), and
anything with superscript (2) commutes with anything with superscript (1). So
[S
2
,S
(1)
z
]=2
+
S
(2)
x
[S
(1)
x
,S
(1)
z
]+S
(2)
y
[S
(1)
y
,S
(1)
z
]+S
(2)
z
[S
(1)
z
,S
(1)
z
]
,
=2
+
−iS
(1)
y
S
(2)
x
+ iS
(1)
x
S
(2)
y
,
=2i(S
(1)
× S
(2)
)z.
[S
2
,S
(1)
z
]=2i(S
(1)
x
S
(2)
y
− S
(1)
y
S
(2)
x
), and [S
2
, S
(1)
]=2i(S
(1)
×S
(2)
). Note that [S
2
, S
(2)
]=2i(S
(2)
×S
(1)
)=
−2i(S
(1)
× S
(2)
), so [S
2
, (S
(1)
+ S
(2)
)] = 0.]
Problem 4.38
(a)
−
2
2m
∂
2
ψ
∂x
2
+
∂
2
ψ
∂y
2
+
∂
2
ψ
∂z
2
+
1
2
mω
2
x
2
+ y
2
+ z
2
ψ = Eψ.
Let ψ(x, y, z)=X(x)Y (y)Z(z); plug it in, divide by XY Z, and collect terms:
−
2
2m
1
X
d
2
X
dx
2
+
1
2
mω
2
x
2
+
−
2
2m
1
Y
d
2
Y
dy
2
+
1
2
mω
2
y
2
+
−
2
2m
1
Z
d
2
Z
dz
2
+
1
2
mω
2
z
2
= E.
The first term is a function only of x, the second only of y, and the third only of z. So each is a constant
(call the constants E
x
, E
y
, E
z
, with E
x
+ E
y
+ E
z
= E). Thus:
−
2
2m
d
2
X
dx
2
+
1
2
mω
2
x
2
X = E
x
X; −
2
2m
d
2
Y
dy
2
+
1
2
mω
2
y
2
Y = E
y
Y ; −
2
2m
d
2
Z
dz
2
+
1
2
mω
2
z
2
Z = E
z
Z.
Each of these is simply the one-dimensional harmonic oscillator (Eq. 2.44). We know the allowed energies
(Eq. 2.61):
E
x
=(n
x
+
1
2
)ω; E
y
=(n
y
+
1
2
)ω; E
z
=(n
z
+
1
2
)ω; where n
x
,n
y
,n
z
=0, 1, 2, 3,... .
So E =(n
x
+ n
y
+ n
y
+
3
2
)ω = (n +
3
2
)ω, with n ≡ n
x
+ n
y
+ n
z
.
(b) The question is: “How many ways can we add three non-negative integers to get sum n?”
If n
x
= n, then n
y
= n
z
=0; one way.
If n
x
= n − 1, then n
y
=0,n
z
=1, or else n
y
=1,n
z
=0; two ways.
If n
x
= n − 2, then n
y
=0,n
z
=2, or n
y
=1,n
z
=1, or n
y
=2,n
z
=0; three ways.
And so on. Evidently d(n)=1+2+3+···+(n +1)=
(n + 1)(n +2)
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
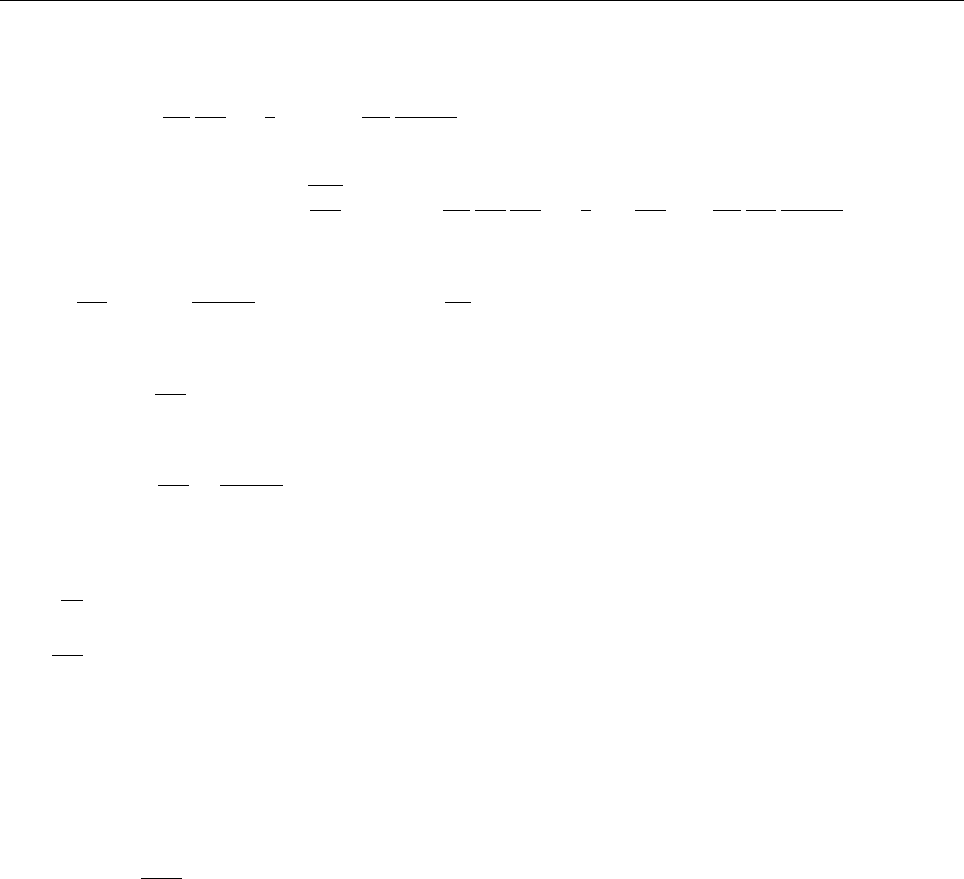
CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 111
Problem 4.39
Eq. 4.37: −
2
2m
d
2
u
dr
2
+
1
2
mω
2
r
2
+
2
2m
l(l +1)
r
2
u = Eu.
Following Eq. 2.71, let ξ ≡
mω
r. Then −
2
2m
mω
d
2
u
dξ
2
+
1
2
mω
2
mω
ξ
2
+
2
2m
mω
l(l +1)
ξ
2
u = Eu,
or
d
2
u
dξ
2
=
ξ
2
+
l(l +1)
ξ
2
− K
u, where K ≡
2E
ω
(as in Eq. 2.73).
At large ξ,
d
2
u
dξ
2
≈ ξ
2
u, and u ∼ ()e
−ξ
2
/2
(see Eq. 2.77).
At small ξ,
d
2
u
dξ
2
≈
l(l +1)
ξ
2
u, and u ∼ ()ξ
l+1
(see Eq. 4.59).
So let u(ξ) ≡ ξ
l+1
e
−ξ
2
/2
v(ξ). [This defines the new function v(ξ).]
du
dξ
=(l +1)ξ
l
e
−ξ
2
/2
v − ξ
l+2
e
−ξ
2
/2
v + ξ
l+1
e
−ξ
2
/2
v
.
d
2
u
dξ
2
= l(l +1)ξ
l−1
e
−ξ
2
/2
v − (l +1)ξ
l+1
e
−ξ
2
/2
v +(l +1)ξ
l
e
−ξ
2
/2
v
− (l +2)ξ
l+1
e
−ξ
2
/2
v
+ ξ
l+3
e
−ξ
2
/2
v − ξ
l+2
e
−ξ
2
/2
v
+(l +1)ξ
l
e
−ξ
2
/2
v
− ξ
l+2
e
−ξ
2
/2
v
+ ξ
l+1
e
−ξ
2
/2
v
=
✭
✭
✭
✭
✭
✭
✭
✭
l(l +1)ξ
l−1
e
−ξ
2
/2
v − (2l +3)ξ
l+1
e
−ξ
2
/2
v +
✘
✘
✘
✘
✘
ξ
l+3
e
−ξ
2
/2
v +2(l +1)ξ
l
e
−ξ
2
/2
v
− 2ξ
l+2
e
−ξ
2
/2
v
+ ξ
l+1
e
−ξ
2
/2
v
=
✘
✘
✘
✘
✘
ξ
l+3
e
−ξ
2
/2
v +
✭
✭
✭
✭
✭
✭
✭
✭
l(l +1)ξ
l−1
e
−ξ
2
/2
v − Kξ
l+1
e
−ξ
2
/2
v.
Cancelling the indicated terms, and dividing off ξ
l+1
e
−ξ
2
/2
, we have:
v
+2v
l +1
ξ
− ξ
+(K − 2l −3) v =0.
Let v(ξ) ≡
∞
j=0
a
j
ξ
j
, so v
=
∞
j=0
ja
j
ξ
j−1
; v
=
∞
j=2
j(j − 1)a
j
ξ
j−2
. Then
∞
j=2
j(j − 1)a
j
ξ
j−2
+2(l +2)
∞
j=1
ja
j
ξ
j−2
− 2
∞
j=1
ja
j
ξ
j
+(K − 2l −3)
∞
j=0
a
j
ξ
j
=0.
In the first two sums, let j → j + 2 (rename the dummy index):
∞
j=0
(j + 2)(j +1)a
j+2
ξ
j
+2(l +1)
∞
j=0
(j +2)a
j+2
ξ
j
− 2
∞
j=0
ja
j
ξ
j
+(K − 2l −3)
∞
j=0
a
j
ξ
j
=0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

112 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Note: the second sum should start at j = −1; to eliminate this term (there is no compensating one in ξ
−1
)we
must take a
1
= 0. Combining the terms:
∞
j=0
[(j + 2)(j +2l +3)a
j+2
+(K − 2j −2l − 3)a
j
]=0, so a
j+2
=
(2j +2l +3− K)
(j + 2)(j +2l +3)
a
j
.
Since a
1
= 0, this gives us a single sequence: a
0
,a
2
,a
4
,.... But the series must terminate (else we get the
wrong behavior as ξ →∞), so there occurs some maximal (even) number j
max
such that a
j
max+2
=0. Thus
K =2j
max
+2l +3. But E =
1
2
ωK, so E =
j
max
+ l +
3
2
ω. Or, letting j
max
+ l ≡ n,
E
n
=(n +
3
2
)ω, and n can be any nonnegative integer.
[Incidentally, we can also determine the degeneracy of E
n
. Suppose n is even; then (since j
max
is even)
l =0, 2, 4,... ,n. For each l there are (2l + 1) values for m.So
d(n)=
n
l=0,2,4,...
(2l +1). Let j = l/2; then d(n)=
n/2
j=0
(4j +1)=4
n/2
j=0
j +
n/2
j=0
1
=4
(
n
2
)(
n
2
+1)
2
+(
n
2
+1)=(
n
2
+ 1)(n +1)=
(n + 1)(n +2)
2
, as before (Problem 4.38(b)).]
Problem 4.40
(a)
d
dt
r · p =
i
[H, r · p].
[H, r · p]=
3
i=1
[H, r
i
p
i
]=
3
i=1
([H, r
i
]p
i
+ r
i
[H, p
i
]) =
3
i=1
1
2m
[p
2
,r
i
]p
i
+ r
i
[V,p
i
]
.
[p
2
,r
i
]=
3
j=1
[p
j
p
j
,r
i
]=
3
j=1
(p
j
[p
j
,r
i
]+[p
j
,r
i
]p
j
)=
3
j=1
[p
j
(−iδ
ij
)+(−iδ
ij
)p
j
]=−2ip
i
.
[V,p
i
]=i
∂V
∂r
i
(Problem 3.13(c)). [H, r · p]=
3
i=1
1
2m
(−2i)p
i
p
i
+ r
i
i
∂V
∂r
i
= i
−
p
2
m
+ r ·∇V
.
d
dt
r · p =
p
2
m
− r ·∇V =2T −r ·∇V .
For stationary states
d
dt
r · p =0, so 2T = r ·∇V . QED
(b)
V (r)=−
e
2
4π9
0
1
r
⇒∇V =
e
2
4π9
0
1
r
2
ˆr ⇒ r ·∇V =
e
2
4π9
0
1
r
= −V. So 2T = −V .
But T = V = E
n
, so T −2T = E
n
, or T = −E
n
; V =2E
n
. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 113
(c)
V =
1
2
mω
2
r
2
⇒∇V = mω
2
r ˆr ⇒ r ·∇V = mω
2
r
2
=2V. So 2T =2V , or T = V .
But T + V = E
n
, so T = V =
1
2
E
n
. QED
Problem 4.41
(a) ∇·J =
i
2m
∇Ψ ·∇Ψ
∗
+Ψ(∇
2
Ψ
∗
) −∇Ψ
∗
·∇Ψ − Ψ
∗
(∇
2
Ψ)
=
i
2m
Ψ(∇
2
Ψ
∗
) − Ψ
∗
(∇
2
Ψ)
.
But the Schr¨odinger equation says i
∂Ψ
∂t
= −
2
2m
∇
2
Ψ+V Ψ, so
∇
2
Ψ=
2m
2
V Ψ − i
∂Ψ
∂t
, ∇
2
Ψ
∗
=
2m
2
V Ψ
∗
+ i
∂Ψ
∗
∂t
. Therefore
∇·J =
i
2m
2m
2
Ψ
V Ψ
∗
+ i
∂Ψ
∗
∂t
− Ψ
∗
V Ψ − i
∂Ψ
∂t
=
i
i
Ψ
∂Ψ
∗
∂t
+Ψ
∗
∂Ψ
∂t
= −
∂
∂t
(Ψ
∗
Ψ) = −
∂
∂t
|Ψ|
2
.
(b) From Problem 4.11(b), Ψ
211
= −
1
√
πa
1
8a
2
re
−r/2a
sin θe
iφ
e
−iE
2
t/
. In spherical coordinates,
∇Ψ=
∂Ψ
∂r
ˆr +
1
r
∂Ψ
∂θ
ˆ
θ +
1
r sin θ
∂Ψ
∂φ
ˆ
φ, so
∇Ψ
211
= −
1
√
πa
1
8a
2
1 −
r
2a
e
−r/2a
sin θe
iφ
e
−iE
2
t/
ˆr +
1
r
re
−r/2a
cos θe
iφ
e
−iE
2
t/
ˆ
θ
+
1
r sin θ
re
−r/2a
sin θie
iφ
e
−iE
2
t/
ˆ
φ
=
1 −
r
2a
ˆr + cot θ
ˆ
θ +
i
sin θ
ˆ
φ
1
r
Ψ
211
.
Therefore
J =
i
2m
1 −
r
2a
ˆr + cot θ
ˆ
θ −
i
sin θ
ˆ
φ −
1 −
r
2a
ˆr −cot θ
ˆ
θ −
i
sin θ
ˆ
φ
1
r
|Ψ
211
|
2
=
i
2m
(−2i)
r sin θ
|Ψ
211
|
2
ˆ
φ =
m
1
πa
1
64a
4
r
2
e
−r/a
sin
2
θ
r sin θ
ˆ
φ =
64πma
5
re
−r/a
sin θ
ˆ
φ.
(c) Now r × J =
64πma
5
r
2
e
−r/a
sin θ
ˆr ×
ˆ
φ
, while
ˆr ×
ˆ
φ
= −
ˆ
θ and ˆz ·
ˆ
θ = −sin θ,so
r × J
z
=
64πma
5
r
2
e
−r/a
sin
2
θ, and hence
L
z
= m
64πma
5
r
2
e
−r/a
sin
2
θ
r
2
sin θdrdθdφ
=
64πa
5
∞
0
r
4
e
−r/a
dr
π
0
sin
3
θdθ
2π
0
dφ =
64πa
5
4!a
5
4
3
(2π)=
,
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

114 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
as it should be, since (Eq. 4.133) L
z
= m, and m = 1 for this state.
Problem 4.42
(a)
ψ =
1
√
πa
3
e
−r/a
⇒ φ(p)=
1
(2π)
3/2
1
√
πa
3
e
−ip·r/
e
−r/a
r
2
sin θdrdθdφ.
With axes as suggested, p · r = pr cos θ. Doing the (trivial) φ integral:
φ(p)=
2π
(2πa)
3/2
1
√
π
∞
0
r
2
e
−r/a
π
0
e
−ipr cos θ/
sin θdθ
dr.
π
0
e
−ipr cos θ/
sin θdθ=
ipr
e
−ipr cos θ/
π
0
=
ipr
e
ipr/
− e
−ipr/
=
2
pr
sin
pr
.
φ(p)=
1
π
√
2
1
(a)
3/2
2
p
∞
0
re
−r/a
sin
pr
dr.
∞
0
re
−r/a
sin
pr
dr =
1
2i
∞
0
re
−r/a
e
ipr/
dr −
∞
0
re
−r/a
e
−ipr/
dr
=
1
2i
1
(1/a − ip/)
2
−
1
(1/a + ip/)
2
=
1
2i
(2ip/a)2
(1/a)
2
+(p/)
2
2
=
(2p/)a
3
[1+(ap/)
2
]
2
.
φ(p)=
2
1
a
3/2
1
πp
2pa
3
1
[1 + (ap/)
2
]
2
=
1
π
2a
3/2
1
[1 + (ap/)
2
]
2
.
(b)
|φ|
2
d
3
p =4π
∞
0
p
2
|φ|
2
dp =4π
1
π
2
2a
3
∞
0
p
2
[1+(ap/)
2
]
4
dp.
From math tables:
∞
0
x
2
(m + x
2
)
4
dx =
π
32
m
−5/2
, so
∞
0
p
2
[1+(ap/)
2
]
4
dp =
a
8
π
32
a
−5
=
π
32
a
3
;
|φ|
2
d
3
p =
32
π
a
3
π
32
a
3
=1.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 115
(c)
p
2
=
p
2
|φ|
2
d
3
p =
1
π
2
2a
3
4π
∞
0
p
4
[1 + (ap/)
2
]
4
dp. From math tables:
∞
0
x
4
[m + x
2
]
4
dx =
π
32
m
−3/2
. So p
2
=
4
π
2a
3
a
8
π
32
a
−3
=
2
a
2
.
(d)
T =
1
2m
p
2
=
1
2m
2
a
2
=
2
2m
m
2
4
e
2
4π9
0
2
=
m
2
2
e
2
4π9
0
2
= −E
1
,
which is consistent with Eq. 4.191.
Problem 4.43
(a) From Tables 4.3 and 4.7,
ψ
321
= R
32
Y
1
2
=
4
81
√
30
1
a
3/2
r
a
2
e
−r/3a
−
15
8π
sin θ cos θe
iφ
=
−
1
√
π
1
81a
7/2
r
2
e
−r/3a
sin θ cos θe
iφ
.
(b)
|ψ|
2
d
3
r =
1
π
1
(81)
2
a
7
r
4
e
−2r/3a
sin
2
θ cos
2
θ
r
2
sin θdrdθdφ
=
1
π(81)
2
a
7
2π
∞
0
r
6
e
−2r/3a
dr
π
0
(1 − cos
2
θ) cos
2
θ sin θdθ
=
2
(81)
2
a
7
6!
3a
2
7
−
cos
3
θ
3
+
cos
5
θ
5
π
0
=
2
3
8
a
7
6 · 5 · 4 · 3 · 2
3
7
a
7
2
7
2
3
−
2
5
=
3 · 5
4
·
4
15
=1.
(c)
r
s
=
∞
0
r
s
|R
32
|
2
r
2
dr =
4
81
2
1
30
1
a
7
∞
0
r
s+6
e
−2r/3a
dr
=
8
15(81)
2
a
7
(s + 6)!
3a
2
s+7
= (s + 6)!
3a
2
5
1
720
=
(s + 6)!
6!
3a
2
3
.
Finite for
s>−7 .
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
116 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Problem 4.44
(a) From Tables 4.3 and 4.7,
ψ
433
= R
43
Y
3
3
=
1
768
√
35
1
a
3/2
r
a
3
e
−r/4a
'
−
35
64π
sin
3
θ cos θe
3iφ
(
=
−
1
6144
√
πa
9/2
r
3
e
−r/4a
sin
3
θe
3iφ
.
(b)
r =
r|ψ|
2
d
3
r =
1
(6144)
2
πa
9
r
r
6
e
−r/2a
sin
6
θ
r
2
sin θdrdθdφ
=
1
(6144)
2
πa
9
∞
0
r
9
e
−r/2a
dr
π
0
sin
7
θdθ
2π
0
dφ
=
1
(6144)
2
πa
9
9!(2a)
10
2
2 · 4 · 6
3 · 5 · 7
(2π)=
18a.
(c) Using Eq. 4.133: L
2
x
+ L
2
y
= L
2
− L
2
z
= 4(5)
2
− (3)
2
= 11
2
, with probability 1.
Problem 4.45
(a)
P =
|ψ|
2
d
3
r =
4π
πa
3
b
0
e
−2r/a
r
2
dr =
4
a
3
−
a
2
r
2
e
−2r/a
+
a
3
4
e
−2r/a
−
2r
a
− 1
b
0
= −
1+
2r
a
+
2r
2
a
2
e
−2r/a
b
0
= 1 −
1+
2b
a
+2
b
2
a
2
e
−2b/a
.
(b)
P =1−
1+9 +
1
2
9
2
e
−5
≈ 1 −
1+9 +
1
2
9
2
1 − 9 +
9
2
2
−
9
3
3!
≈ 1 − 1+9 −
9
2
2
+
9
3
6
− 9 + 9
2
−
9
3
2
−
9
2
2
+
9
3
2
= 9
3
1
6
−
1
2
+
1
2
=
1
6
2b
a
3
=
4
3
b
a
3
.
(c)
|ψ(0)|
2
=
1
πa
3
⇒ P ≈
4
3
πb
3
1
πa
3
=
4
3
b
a
3
.
(d)
P =
4
3
10
−15
0.5 × 10
−10
3
=
4
3
2 × 10
−5
3
=
4
3
· 8 × 10
−15
=
32
3
× 10
−15
= 1.07 × 10
−14
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 117
Problem 4.46
(a) Equation 4.75 ⇒ R
n(n−1)
=
1
r
ρ
n
e
−ρ
v(ρ), where ρ ≡
r
na
; Eq. 4.76 ⇒ c
1
=
2(n − n)
(1)(2n)
c
0
=0.
So v(ρ)=c
0
, and hence R
n(n−1)
= N
n
r
n−1
e
−r/na
, where N
n
≡
c
0
(na)
n
.
1=
∞
0
|R|
2
r
2
dr =(N
n
)
2
∞
0
r
2n
e
−2r/na
dr =(N
n
)
2
(2n)!
na
2
2n+1
; N
n
=
2
na
n
2
na(2n)!
.
(b)
r
l
=
∞
0
|R|
2
r
l+2
dr = N
2
n
∞
0
r
2n+l
e
−2r/na
dr.
r =
2
na
2n+1
1
(2n)!
(2n + 1)!
na
2
2n+2
=
n +
1
2
na.
r
2
=
2
na
2n+1
1
(2n)!
(2n + 2)!
na
2
2n+3
=(2n + 2)(2n +1)
na
2
2
=
n +
1
2
(n + 1)(na)
2
.
(c)
σ
2
r
= r
2
−r
2
=
n +
1
2
(n + 1)(na)
2
−
n +
1
2
2
(na)
2
=
1
2
n +
1
2
(na)
2
=
1
2(n +1/2)
r
2
; σ
r
=
r
√
2n +1
.
r
rr
6a
a
650a
R
10
32
26 25
R
R
Maxima occur at:
dR
n,n−1
dr
=0⇒ (n − 1)r
n−2
e
−r/na
−
1
na
r
n−1
e
−r/na
=0⇒ r = na(n − 1).
Problem 4.47
Here are a couple of examples: {32, 28} and {224,56}; {221, 119} and {119, 91}. For further discussion see
D. Wyss and W. Wyss, Foundations of Physics 23, 465 (1993).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
118 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Problem 4.48
(a) Using Eqs. 3.64 and 4.122: [A, B]=[x
2
,L
z
]=x[x, L
z
]+[x, L
z
]x = x(−iy)+(−iy)x = −2ixy.
Equation 3.62 ⇒ σ
2
A
σ
2
B
≥
1
2i
(−2i)xy
2
=
2
xy
2
⇒ σ
A
σ
B
≥ |xy|.
(b) Equation 4.113 ⇒B = L
z
= m; B
2
= L
2
z
= m
2
2
;soσ
B
= m
2
2
− m
2
2
= 0.
(c) Since the left side of the uncertainty principle is zero, the right side must also be: xy =0, for eigenstates
of L
z
.
Problem 4.49
(a) 1=|A|
2
(1+4+4)=9|A|
2
; A =1/3.
(b)
2
, with probability
5
9
; −
2
, with probability
4
9
.
S
z
=
5
9
2
+
4
9
−
2
=
18
.
(c) From Eq. 4.151,
c
(x)
+
=
χ
(x)
+
†
χ =
1
3
1
√
2
11
1 − 2i
2
=
1
3
√
2
(1 − 2i +2)=
3 − 2i
3
√
2
; |c
(x)
+
|
2
=
9+4
9 · 2
=
13
18
.
c
(x)
−
=
χ
(x)
−
†
χ =
1
3
1
√
2
1 −1
1 − 2i
2
=
1
3
√
2
(1 − 2i − 2) = −
1+2i
3
√
2
; |c
(x)
−
|
2
=
1+4
9 · 2
=
5
18
.
2
, with probability
13
18
; −
2
, with probability
5
18
.
S
x
=
13
18
2
+
5
18
−
2
=
2
9
.
(d) From Problem 4.29(a),
c
(y)
+
=
χ
(y)
+
†
χ =
1
3
1
√
2
1 −i
1 − 2i
2
=
1
3
√
2
(1 − 2i − 2i)=
1 − 4i
3
√
2
; |c
(y)
+
|
2
=
1+16
9 · 2
=
17
18
.
c
(y)
−
=
χ
(y)
−
†
χ =
1
3
1
√
2
1 i
1 − 2i
2
=
1
3
√
2
(1 − 2i +2i)=
1
3
√
2
; |c
(y)
−
|
2
=
1
9 · 2
=
1
18
.
2
, with probability
17
18
; −
2
, with probability
1
18
.
S
y
=
17
18
2
+
1
18
−
2
=
4
9
.
Problem 4.50
We may as well choose axes so that ˆa lies along the z axis and
ˆ
b is in the xz plane. Then S
(1)
a
= S
(1)
z
, and S
(2)
b
=
cos θS
(2)
z
+ sin θS
(2)
x
. 00|S
(1)
a
S
(2)
b
|00 is to be calculated.
S
(1)
a
S
(2)
b
|00 =
1
√
2
S
(1)
z
(cos θS
(2)
z
+ sin θS
(2)
x
)
(↑↓−↓↑)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 119
=
1
√
2
[(S
z
↑)(cos θS
z
↓ + sin θS
x
↓) − (S
z
↓)(cos θS
z
↑ + sin θS
x
↑)]
=
1
√
2
2
↑
cos θ
−
2
↓
+ sin θ
2
↑
−
−
2
↓
cos θ
2
↑
+ sin θ
2
↓
(using Eq. 4.145)
=
2
4
cos θ
1
√
2
(−↑↓+ ↓↑) + sin θ
1
√
2
(↑↑ + ↓↓)
=
2
4
−cos θ|00 + sin θ
1
√
2
(|11 + |1 − 1)
.
so S
(1)
a
S
(2)
b
= 00|S
(1)
a
S
(2)
b
|00 =
2
4
00|
−cos θ|00 + sin θ
1
√
2
(|11 + |1 − 1)
= −
2
4
cos θ00|00
(by orthogonality), and hence S
(1)
a
S
(2)
b
= −
2
4
cos θ. QED
Problem 4.51
(a) First note from Eqs. 4.136 and 4.144 that
S
x
|sm =
1
2
[S
+
|sm + S
−
|sm]
=
2
s(s +1)− m(m +1)|sm+1 +
s(s +1)− m(m − 1)|sm− 1
S
y
|sm =
1
2i
[S
+
|sm−S
−
|sm]
=
2i
s(s +1)− m(m +1)|sm+1−
s(s +1)− m(m − 1)|sm− 1
Now, using Eqs. 4.179 and 4.147:
S
2
|sm =
(S
(1)
)
2
+(S
(2)
)
2
+2(S
(1)
x
S
(2)
x
+ S
(1)
y
S
(2)
y
+ S
(1)
z
S
(2)
z
)
A|
1
2
1
2
|S
2
m −
1
2
+ B|
1
2
−
1
2
|s
2
m +
1
2
= A
S
2
|
1
2
1
2
|s
2
m −
1
2
+ |
1
2
1
2
S
2
|s
2
m −
1
2
+2
S
x
|
1
2
1
2
S
x
|s
2
m −
1
2
+
S
y
|
1
2
1
2
S
y
|s
2
m −
1
2
+
S
z
|
1
2
1
2
S
z
|s
2
m −
1
2
+B
S
2
|
1
2
−
1
2
|s
2
m +
1
2
+ |
1
2
−
1
2
S
2
|s
2
m +
1
2
+2
S
x
|
1
2
−
1
2
S
x
|s
2
m +
1
2
+
S
y
|
1
2
−
1
2
S
y
|s
2
m +
1
2
+
S
z
|
1
2
−
1
2
S
z
|s
2
m +
1
2
= A
3
4
2
|
1
2
1
2
|s
2
m −
1
2
+
2
s
2
(s
2
+1)|
1
2
1
2
|s
2
m −
1
2
+2
2
|
1
2
−
1
2
2
s
2
(s
2
+1)− (m −
1
2
)(m +
1
2
)|s
2
m +
1
2
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

120 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
+
s
2
(s
2
+1)− (m −
1
2
)(m −
3
2
)|s
2
m −
3
2
+
i
2
|
1
2
−
1
2
2i
s
2
(s
2
+1)− (m −
1
2
)(m +
1
2
)|s
2
m +
1
2
−
s
2
(s
2
+1)− (m −
1
2
)(m −
3
2
)|s
2
m −
3
2
+
2
|
1
2
1
2
(m −
1
2
)|s
2
m −
1
2
+B
3
4
2
|
1
2
−
1
2
|s
2
m +
1
2
+
2
s
2
(s
2
+1)|
1
2
−
1
2
|s
2
m +
1
2
+2
2
|
1
2
1
2
2
s
2
(s
2
+1)− (m +
1
2
)(m +
3
2
)|s
2
m +
3
2
+
s
2
(s
2
+1)− (m +
1
2
)(m −
1
2
)|s
2
m −
1
2
+
−i
2
|
1
2
1
2
2i
s
2
(s
2
+1)− (m +
1
2
)(m +
3
2
)|s
2
m +
3
2
−
s
2
(s
2
+1)− (m +
1
2
)(m −
1
2
)|s
2
m −
1
2
+
−
2
|
1
2
−
1
2
(m +
1
2
)|s
2
m +
1
2
=
2
A
3
4
+ s
2
(s
2
+1)+m −
1
2
+ B
s
2
(s
2
+1)− m
2
+
1
4
|
1
2
1
2
|s
2
m −
1
2
+
2
B
3
4
+ s
2
(s
2
+1)− m −
1
2
+ A
s
2
(s
2
+1)− m
2
+
1
4
|
1
2
−
1
2
|s
2
m +
1
2
=
2
s(s +1)|sm =
2
s(s +1)
A|
1
2
1
2
|s
2
m −
1
2
+ B|
1
2
−
1
2
|s
2
m +
1
2
.
A
s
2
(s
2
+1)+
1
4
+ m
+B
s
2
(s
2
+1)− m
2
+
1
4
= s(s +1)A,
B
s
2
(s
2
+1)+
1
4
− m
+A
s
2
(s
2
+1)− m
2
+
1
4
= s(s +1)B,
or
A
s
2
(s
2
+1)− s(s +1)+
1
4
+ m
+B
s
2
(s
2
+1)− m
2
+
1
4
=0,
B
s
2
(s
2
+1)− s(s +1)+
1
4
− m
+A
s
2
(s
2
+1)− m
2
+
1
4
=0,
or
A(a + m)+Bb =0
B(a − m)+Ab =0
,
where a ≡ s
2
(s
2
+1)−s(s +1)+
1
4
,b≡
s
2
(s
2
+1)− m
2
+
1
4
. Multiply by (a −b) and b, then subtract:
A(a
2
− m
2
)+Bb(a − m)=0; Bb(a − m)+Ab
2
=0⇒ A(a
2
− m
2
− b
2
)=0⇒ a
2
− b
2
= m
2
, or:
s
2
(s
2
+1)− s(s +1)+
1
4
2
− s
2
(s
2
+1)+m
2
−
1
4
= m
2
,
s
2
(s
2
+1)− s(s +1)+
1
4
2
= s
2
2
+ s
2
+
1
4
=
s
2
+
1
2
2
,so
s
2
(s
2
+1)− s(s +1)+
1
4
= ±
s
2
+
1
2
; s(s +1)=s
2
(s
2
+1)∓
s
2
+
1
2
+
1
4
.
Add
1
4
to both sides:
s
2
+ s +
1
4
=
s +
1
2
2
= s
2
(s
2
+1)∓
s
2
+
1
2
+
1
2
=
s
2
2
+ s
2
− s
2
−
1
2
+
1
2
= s
2
2
s
2
2
+ s
2
+ s
2
+
1
2
+
1
2
=(s
2
+1)
2
.
So
s +
1
2
= ±s
2
⇒ s = ±s
2
−
1
2
=
s
2
−
1
2
−s
2
−
1
2
s +
1
2
= ±(s
2
+1) ⇒ s = ±(s
2
+1)−
1
2
=
s
2
+
1
2
−s
2
−
3
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 121
But s ≥ 0, so the possibilities are s = s
2
± 1/2. Then:
a = s
2
2
+ s
2
−
s
2
±
1
2
s
2
±
1
2
+1
+
1
4
= s
2
2
+ s
2
− s
2
2
∓
1
2
s
2
− s
2
∓
1
2
s
2
−
1
4
∓
1
2
+
1
4
= ∓s
2
∓
1
2
= ∓
s
2
+
1
2
.
b =
s
2
2
+ s
2
+
1
4
− m
2
=
s
2
+
1
2
2
− m
2
=
s
2
+
1
2
+ m
s
2
+
1
2
− m
.
∴ A
∓
s
2
+
1
2
+ m
= ∓A
s
2
+
1
2
∓ m
= −Bb = −B
s
2
+
1
2
+ m
s
2
+
1
2
− m
⇒ A
s
2
+
1
2
∓ m = ±B
s
2
+
1
2
± m. But |A|
2
+ |B|
2
=1, so
|A|
2
+ |A|
2
s
2
+
1
2
∓ m
s
2
+
1
2
± m
=
|A|
2
(s
2
+
1
2
± m)
s
2
+
1
2
± m + s
2
+
1
2
∓ m
=
(2s
2
+1)
(s
2
+
1
2
± m)
|A|
2
.
⇒
A =
s
2
± m +
1
2
2s
2
+1
.
B = ±A
s
2
+
1
2
∓ m
s
2
+
1
2
± m
=
±
s
2
∓ m +
1
2
2s
2
+1
.
(b) Here are four examples:
(i) From the 1/2 × 1/2 table (s
2
=1/2), pick s = 1 (upper signs), m = 0. Then
A =
1
2
+0+
1
2
1+1
=
1
√
2
; B =
1
2
−0+
1
2
1+1
=
1
√
2
.
(ii) From the 1 × 1/2 table (s
2
= 1), pick s =3/2 (upper signs), m =1/2. Then
A =
1+
1
2
+
1
2
2+1
=
2
3
; B =
1−
1
2
+
1
2
2+1
=
1
√
3
.
(iii) From the 3/2 × 1/2 table (s
2
=3/2), pick s = 1 (lower signs), m = −1. Then
A =
3
2
+1+
1
2
3+1
=
√
3
2
; B = −
3
2
−1+
1
2
3+1
= −
1
2
.
(iv) From the 2 × 1/2 table (s
2
= 2), pick s =3/2 (lower signs), m =1/2. Then
A =
2−
1
2
+
1
2
4+1
=
2
5
; B = −
2+
1
2
+
1
2
4+1
= −
3
5
.
These all check with the values on Table 4.8, except that the signs (which are conventional) are reversed
in (iii) and (iv). Normalization does not determine the sign of A (nor, therefore, of B).
Problem 4.52
|
3
2
3
2
=
1
0
0
0
; |
3
2
1
2
=
0
1
0
0
; |
3
2
−1
2
=
0
0
1
0
; |
3
2
−3
2
=
0
0
0
1
. Equation 4.136 ⇒
S
+
|
3
2
3
2
=0,S
+
|
3
2
1
2
=
√
3|
3
2
3
2
,S
+
|
3
2
−1
2
=2|
3
2
1
2
,S
+
|
3
2
−3
2
=
√
3|
3
2
−1
2
;
S
−
|
3
2
3
2
=
√
3|
3
2
1
2
,S
−
|
3
2
1
2
=2|
3
2
−1
2
,S
−
|
3
2
−1
2
=
√
3|
3
2
−3
2
,S
−
|
3
2
−3
2
=0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

122 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
So: S
+
=
0
√
30 0
0020
000
√
3
0000
; S
−
=
0000
√
30 0 0
0200
00
√
30
; S
x
=
1
2
(S
+
+ S
−
)=
2
0
√
30 0
√
30 2 0
020
√
3
00
√
30
.
−λ
√
30 0
√
3 −λ 20
02−λ
√
3
00
√
3 −λ
= −λ
−λ 20
2 −λ
√
3
0
√
3 −λ
−
√
3
√
32 0
0 −λ
√
3
0
√
3 −λ
= −λ
−λ
3
+3λ +4λ
−
√
3
√
3λ
2
− 3
√
3
= λ
4
− 7λ
2
− 3λ
2
+9=0,
or λ
4
−10λ
2
+9=0; (λ
2
−9)(λ
2
−1) = 0; λ = ±3, ±1. So the eigenvalues of S
x
are
3
2
,
1
2
, −
1
2
, −
3
2
.
Problem 4.53
From Eq. 4.135, S
z
|sm = m|sm. Since s is fixed, here, let’s just identify the states by the value of m (which
runs from −s to +s). The matrix elements of S
z
are
S
nm
= n|S
z
|m = mn|m = mδ
nm
.
It’s a diagonal matrix, with elements m, ranging from m = s in the upper left corner to m = −s in the lower
right corner:
S
z
=
s 00··· 0
0 s − 10··· 0
00s − 2 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0··· −s
.
From Eq. 4.136,
S
±
|sm =
s(s +1)− m(m ± 1) |s (m ±1) =
(s ∓ m)(s ± m +1)|s (m ± 1).
(S
+
)
nm
= n|S
+
|m =
(s − m)(s + m +1)n|m +1 = b
m+1
δ
n (m+1)
= b
n
δ
n (m+1)
.
All nonzero elements have row index (n) one greater than the column index (m), so they are on the diagonal
just above the main diagonal (note that the indices go down, here: s, s − 1, s − 2 ... , −s):
S
+
=
0 b
s
00··· 0
00b
s−1
0 ··· 0
00 0 b
s−2
··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0 0 ··· b
−s+1
00 0 0 ··· 0
.
Similarly
(S
−
)
nm
= n|S
−
|m =
(s + m)(s − m +1)n|m −1 = b
m
δ
n (m−1)
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 123
This time the nonzero elements are on the diagonal just below the main diagonal:
S
−
=
000··· 00
b
s
00··· 00
0 b
s−1
0 ··· 00
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000··· b
−s+1
0
.
To construct S
x
=
1
2
(S
+
+ S
−
) and S
y
=
1
2i
(S
+
− S
−
), simply add and subtract the matrices S
+
and S
−
:
S
x
=
2
0 b
s
00··· 00
b
s
0 b
s−1
0 ··· 00
0 b
s−1
0 b
s−2
··· 00
00b
s−2
0 ··· 00
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0 0··· 0 b
−s+1
00 0 0··· b
−s+1
0
; S
y
=
2i
0 b
s
00··· 00
−b
s
0 b
s−1
0 ··· 00
0 −b
s−1
0 b
s−2
··· 00
00−b
s−2
0 ··· 00
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0 0··· 0 b
−s+1
00 0 0··· −b
−s+1
0
.
Problem 4.54
L
+
Y
m
l
=
l(l +1)− m(m +1)Y
m±1
l
(Eqs. 4.120 and 121). Equation 4.130 ⇒
e
iφ
∂
∂θ
+ i cot θ
∂
∂φ
B
m
l
e
imφ
P
m
l
(cos θ)=
l(l +1)− m(m +1)B
m+1
l
e
i(m+1)φ
P
m+1
l
(cos θ).
B
m
l
d
dθ
− m cot θ
P
m
l
(cos θ)=
l(l +1)− m(m +1)B
m+1
l
P
m+1
l
(cos θ).
Let x ≡ cos θ; cot θ =
cos θ
sin θ
=
x
√
1 − x
2
;
d
dθ
=
dx
dθ
d
dx
= −sin θ
d
dx
= −
1 − x
2
d
dx
.
B
m
l
−
1 − x
2
d
dx
− m
x
√
1 − x
2
P
m
l
(x)=−B
m
l
1
√
1 − x
2
(1 − x
2
)
dP
m
l
dx
+ mxP
m
l
= −B
m
l
P
m+1
l
=
l(l +1)− m(m +1)B
m+1
l
P
m+1
l
(x). ⇒ B
m+1
l
=
−1
l(l +1)− m(m +1)
B
m
l
.
Now l(l +1)− m(m +1)=(l − m)(l + m +1), so
B
m+1
l
=
−1
√
l − m
√
l +1+m
B
m
l
⇒ B
1
l
=
−1
√
l
√
l +1
B
0
l
; B
2
l
=
−1
√
l − 1
√
l +2
B
1
l
=
1
l(l − 1)
(l + 1)(l +2)
B
0
l
;
B
3
l
=
−1
√
l − 2
√
l +3
B
2
l
=
−1
(l + 3)(l + 2)(l +1)l(l − 1)(l −2)
B
0
l
, etc.
Evidently there is an overall sign factor (−1)
m
, and inside the square root the quantity is [(l + m)!/(l − m)!].
Thus:
B
m
l
=(−1)
m
(l − m)!
(l + m)!
C(l)
(where C(l) ≡ B
0
l
), for m ≥ 0. For m<0, we have
B
−1
l
=
−B
0
l
(l +1)l
; B
−2
l
=
−1
(l + 2)(l − 1)
B
−1
l
=
1
(l + 2)(l +1)l(l − 1)
B
0
l
, etc.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
124 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
Thus B
−m
l
= B
m
l
, so in general: B
m
l
=(−1)
m
(l−|m|)!
(l+|m|!
C(l). Now, Problem 4.22 says:
Y
l
l
=
1
2
l
l!
(2l + 1)!
π
(e
iφ
sin θ)
l
= B
l
l
e
ilφ
P
l
l
(cos θ). But
P
l
l
(x)=(1− x
2
)
l/2
d
dx
l
1
2
l
l!
d
dx
l
(x
2
− 1)
l
=
(1 − x
2
)
l/2
2
l
l!
d
dx
2l
(x
2l
− ...)
(2l)!
=
(2l)!
2
l
l!
(1 − x
2
)
l/2
,
so P
l
l
(cos θ)=
(2l)!
2
l
l!
(sin θ)
l
. Therefore
1
2
l
l!
(2l + 1)!
π
(e
iφ
sin θ)
l
= B
l
l
e
ilφ
(2l)!
2
l
l!
(sin θ)
l
⇒ B
l
l
=
1
(2l)!
(2l + 1)!
π
=
(2l +1)
π(2l)!
.
But B
l
l
=(−1)
l
1
(2l)!
C(l), so
C(l)=(−1)
l
2l +1
π
,
and hence B
m
l
=(−1)
l+m
(2l +1)
π
(l −|m|)!
(l + |m|)!
.
This agrees with Eq. 4.32 except for the overall sign, which of course is purely conventional.
Problem 4.55
(a) For both terms, l =1,so
2
(1)(2) = 2
2
,P=1.
(b) 0,P=
1
3
,
or ,P=
2
3
.
(c)
3
4
2
,P=1.
(d)
2
,P=
1
3
,or −
2
,P=
2
3
.
(e) From the 1 ×
1
2
Clebsch-Gordan table (or Problem 4.51):
1
√
3
|
1
2
1
2
|10 +
2
3
|
1
2
−1
2
|11 =
1
√
3
2
3
|
3
2
1
2
−
1
√
3
|
1
2
1
2
+
2
3
1
√
3
|
3
2
1
2
+
2
3
|
1
2
1
2
=
2
√
2
3
|
3
2
1
2
+
1
3
|
1
2
1
2
. So s =
3
2
or
1
2
.
15
4
2
,P=
8
9
,
or
3
4
2
,P=
1
9
.
(f)
1
2
,P=1.
(g)
|ψ|
2
= |R
21
|
2
1
3
|Y
0
1
|
2
(χ
†
+
χ
+
)
1
+
√
2
3
Y
0∗
1
Y
1
1
(χ
†
+
χ
−
)
0
+Y
1∗
1
Y
0
1
(χ
†
−
χ
+
)
0
+
2
3
|Y
1
1
|
2
(χ
†
−
χ
−
)
1
=
1
3
|R
21
|
2
|Y
0
1
|
2
+2|Y
1
1
|
2
=
1
3
·
1
24
·
1
a
3
·
r
2
a
2
e
−r/a
3
4π
cos
2
θ +2
3
8π
sin
2
θ
[Tables 4.3, 4.7]
=
1
3 · 24 · a
5
r
2
e
−r/a
·
3
4π
(cos
2
θ + sin
2
θ)=
1
96πa
5
r
2
e
−r/a
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 125
(h)
1
3
|R
21
|
2
|Y
0
1
|
2
sin
2
θdθdφ=
1
3
|R
21
|
2
=
1
3
·
1
24a
3
r
2
e
−r/a
=
1
72a
5
r
2
e
−r/a
.
Problem 4.56
(a) Equation 4.129 says L
z
=
i
∂
∂φ
, so this problem is identical to Problem 3.39, with ˆp → L
z
and x → φ.
(b) First note that if M is a matrix such that M
2
= 1, then
e
iMφ
=1+iMφ +
1
2
(iMφ)
2
+
1
3!
(iMφ)
3
+ ···=1+iMφ −
1
2
φ
2
− iM
1
3!
φ
3
+ ···
=(1−
1
2
φ
2
+
1
4!
φ
4
−···)+iM(φ −
1
3!
φ
3
+
1
5!
φ
5
−···) = cos φ + iM sin φ.
So R = e
iπσ
x
/2
= cos
π
2
+ iσ
x
sin
π
2
(because σ
2
x
= 1 – see Problem 4.26) = iσ
x
= i
01
10
.
Thus Rχ
+
= i
01
10
1
0
= i
0
1
= iχ
−
; it converts “spin up” into “spin down” (with a factor of i).
(c)
R = e
iπσ
y
/4
= cos
π
4
+ iσ
y
sin
π
4
=
1
√
2
(1 + iσ
y
)=
1
√
2
10
01
+ i
0 −i
i 0
=
1
√
2
11
−11
.
Rχ
+
=
1
√
2
11
−11
1
0
=
1
√
2
1
−1
=
1
√
2
(χ
+
− χ
−
)=χ
(x)
−
(Eq. 4.151).
What had been spin up along z is now spin down along x
(see figure).
y
y'
z
x'
x
z'
(d) R = e
iπσ
z
= cos π + iσ
z
sin π = −1; rotation by 360
◦
changes the sign of the spinor. But since the sign
of χ is arbitrary, it doesn’t matter.
(e)
(σ · ˆn)
2
=(σ
x
n
x
+ σ
y
n
y
+ σ
z
n
z
)(σ
x
n
x
+ σ
y
n
y
+ σ
z
n
z
)
= σ
2
x
n
2
x
+ σ
2
y
n
2
y
+ σ
2
z
n
2
z
+ n
x
n
y
(σ
x
σ
y
+ σ
y
σ
x
)+n
x
n
z
(σ
x
σ
z
+ σ
z
σ
x
)+n
y
n
z
(σ
y
σ
z
− σ
z
σ
y
).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

126 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
But σ
2
x
= σ
2
y
= σ
2
z
=1, and σ
x
σ
y
+ σ
y
σ
x
= σ
x
σ
z
+ σ
z
σ
x
= σ
y
σ
z
+ σ
z
σ
y
= 0 (Problem 4.26), so
(σ · ˆn)
2
= n
2
x
+ n
2
y
+ n
2
z
=1. So e
i(σ·ˆn)φ/2
= cos
φ
2
+ i(σ · ˆn) sin
φ
2
. QED
Problem 4.57
(a)
[q
1
,q
2
]=
1
2
x +
a
2
/
p
y
,x−
a
2
/
p
y
=0, because [x, p
y
]=[x, x]=[p
y
,p
y
]=0.
[p
1
,p
2
]=
1
2
p
x
−
/a
2
y, p
x
+
/a
2
y
=0, because [y, p
x
]=[y, y]=[p
x
,p
x
]=0.
[q
1
,p
1
]=
1
2
x +
a
2
/
p
y
,p
x
−
/a
2
y
=
1
2
([x, p
x
] − [p
y
,y]) =
1
2
[i − (−i)] = i.
[q
2
,p
2
]=
1
2
x −
a
2
/
p
y
,p
x
+
/a
2
y
=
1
2
([x, p
x
] − [p
y
,y]) = i.
[See Eq. 4.10 for the canonical commutators.]
(b)
q
2
1
− q
2
2
=
1
2
x
2
+
a
2
(xp
y
+ p
y
x)+
a
2
2
p
2
y
− x
2
+
a
2
(xp
y
+ p
y
x) −
a
2
2
p
2
y
=
2a
xp
y
.
p
2
1
− p
2
2
=
1
2
p
2
x
−
a
2
(p
x
y + yp
x
)+
a
2
2
y
2
− p
2
x
−
a
2
(p
x
y + yp
x
) −
a
2
2
y
2
= −
2
a
2
yp
x
.
So
2a
2
(q
2
1
− q
2
2
)+
a
2
2
(p
2
1
− p
2
2
)=xp
y
− yp
x
= L
z
.
(c)
H =
1
2m
p
2
+
1
2
mω
2
x
2
=
a
2
2
p
2
+
2a
2
x
2
= H(x, p).
Then H(q
1
,p
1
)=
a
2
2
p
2
1
+
2a
2
q
2
1
≡ H
1
,H(q
2
,p
2
)=
a
2
2
p
2
2
+
2a
2
q
2
2
≡ H
2
; L
z
= H
1
− H
2
.
(d) The eigenvalues of H
1
are (n
1
+
1
2
), and those of H
2
are (n
2
+
1
2
), so the eigenvalues of L
z
are
(n
1
+
1
2
) − (n
2
+
1
2
) =(n
1
− n
2
) = m, and m is an integer, because n
1
and n
2
are.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 127
Problem 4.58
From Problem 4.28 we know that in the generic state χ =
a
b
(with |a|
2
+ |b|
2
= 1),
S
z
=
2
|a|
2
−|b|
2
, S
x
= Re(ab
∗
), S
y
= −Im(ab
∗
); S
2
x
= S
2
y
=
2
4
.
Writing a = |a|e
iφ
a
,b= |b|e
iφ
b
, we have ab
∗
= |a||b|e
i(φ
a
−φ
b
)
= |a||b|e
iθ
, where θ ≡ φ
a
− φ
b
is the phase
difference between a and b. Then
S
x
= Re(|a||b|e
iθ
)=|a||b|cos θ, S
y
= −Im(|a||b|e
iθ
)=−|a||b|sin θ.
σ
2
S
x
= S
2
x
−S
x
2
=
2
4
−
2
|a|
2
|b|
2
cos
2
θ; σ
2
S
y
= S
2
y
−S
y
2
=
2
4
−
2
|a|
2
|b|
2
sin
2
θ.
We want σ
2
S
x
σ
2
S
y
=
2
4
S
z
2
,or
2
4
1 − 4|a|
2
|b|
2
cos
2
θ
2
4
1 − 4|a|
2
|b|
2
sin
2
θ
=
2
4
2
4
|a|
2
−|b|
2
2
.
1 − 4|a|
2
|b|
2
cos
2
θ + sin
2
θ
+16|a|
4
|b|
4
sin
2
θ cos
2
θ = |a|
4
− 2|a|
2
|b|
2
+ |b|
4
.
1+16|a|
4
|b|
4
sin
2
θ cos
2
θ = |a|
4
+2|a|
2
|b|
2
+ |b|
4
=
|a|
2
+ |b|
2
2
=1 ⇒|a|
2
|b|
2
sin θ cos θ =0.
So either θ =0orπ, in which case a and b are relatively real, or else θ = ±π/2, in which case a and b are
relatively imaginary (these two options subsume trivially the solutions a = 0 and b = 0).
Problem 4.59
(a)
Start with Eq. 3.71:
dr
dt
=
i
[H, r].
H =
1
2m
(p − qA) ·(p −qA)+qϕ =
1
2m
p
2
− q(p ·A + A ·p)+q
2
A
2
+ qϕ.
[H, x]=
1
2m
[p
2
,x] −
q
2m
[(p · A + A · p),x].
[p
2
,x]=[(p
2
x
+ p
2
y
+ p
2
z
),x]=[p
2
x
,x]=p
x
[p
x
,x]+[p
x
,x]p
x
= p
x
(−i)+(−i)p
x
= −2ip
x
.
[p · A,x]=[(p
x
A
x
+ p
y
A
y
+ p
z
A
z
),x]=[p
x
A
x
,x]=p
x
[A
x
,x]+[p
x
,x]A
x
= −iA
x
.
[A · p,x]=[(A
x
p
x
+ A
y
p
y
+ A
z
p
z
),x]=[A
x
p
x
,x]=A
x
[p
x
,x]+[A
x
,x]p
x
= −iA
x
.
[H, x]=
1
2m
(−2ip
x
) −
q
2m
(−2iA
x
)=−
i
m
(p
x
− qA
x
); [H, r]=−
i
m
(p − qA).
dr
dt
=
1
m
(p − qA). QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

128 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
(b)
We define the operator v ≡
1
m
(p − qA);
dv
dt
=
i
[H, v] +
∂v
∂t
;
∂v
∂t
= −
q
m
∂A
∂t
.
H =
1
2
mv
2
+ qϕ ⇒ [H, v]=
m
2
[v
2
, v]+q[ϕ, v]; [ϕ, v]=
1
m
[ϕ, p].
[ϕ, p
x
]=i
∂ϕ
∂x
(Eq. 3.65), so [ϕ, p]=i∇ϕ, and [ϕ, v]=
i
m
∇ϕ.
[v
2
,v
x
]=[(v
2
x
+ v
2
y
+ v
2
z
),v
x
]=[v
2
y
,v
x
]+[v
2
z
,v
x
]=v
y
[v
y
,v
x
]+[v
y
,v
x
]v
y
+ v
z
[v
z
,v
x
]+[v
z
,v
x
]v
z
.
[v
y
,v
x
]=
1
m
2
[(p
y
− qA
y
), (p
x
− qA
x
)] = −
q
m
2
([A
y
,p
x
]+[p
y
,A
x
])
= −
q
m
2
i
∂A
y
∂x
− i
∂A
x
∂y
= −
iq
m
2
(∇×A)
z
= −
iq
m
2
B
z
.
[v
z
,v
x
]=
1
m
2
[(p
z
− qA
z
), (p
x
− qA
x
)] = −
q
m
2
([A
z
,p
x
]+[p
z
,A
x
])
= −
q
m
2
i
∂A
z
∂x
− i
∂A
x
∂y
=
iq
m
2
(∇×A)
y
=
iq
m
2
B
y
.
∴ [v
2
,v
x
]=
iq
m
2
(−v
y
B
z
− B
z
v
y
+ v
z
B
y
+ B
y
v
z
)=
iq
m
2
[−(v × B)
x
+(B × v)
x
] .
[v
2
, v]=
iq
m
2
[(B × v) − (v ×B)] . Putting all this together:
dv
dt
=
i
0
m
2
iq
m
2
(B × v − v ×B)+
qi
m
∇ϕ
1
−
q
m
∂A
∂t
.
[] m
dv
dt
=
q
2
(v × B) − (B × v)+ q
0
−∇ϕ −
∂A
dt
1
=
q
2
(v × B − B × v)+ qE. Or, since
v × B − B × v =
1
m
[(p − qA) ×B −B ×(p −qA)] =
1
m
[p × B − B × p] −
q
m
[A × B − B × A] .
[Note: p does not commute with B, so the order does matter in the first term. But A commutes with B,
so B × A = −A × B in the second.]
m
dv
dt
= qE +
q
2m
p × B − B × p−
q
2
m
A × B. QED
(c) Go back to Eq. , and use E = E, v × B = v×B; B × v = B ×v = −v×B. Then
m
dv
dt
= qv×B + qE. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 129
Problem 4.60
(a)
E = −∇ϕ =
−2Kz
ˆ
k. B = ∇×A =
ˆ
i
ˆ
j
ˆ
k
∂/∂x ∂/∂y ∂/∂z
−B
0
y/2 B
0
x/20
=
B
0
ˆ
k.
(b) For time-independent potentials Eq. 4.205 separates in the usual way:
1
2m
i
∇−qA
·
i
∇−qA
ψ + qϕψ = Eψ, or
−
2
2m
∇
2
ψ +
iq
2m
[∇·(Aψ)+A ·(∇ψ)]+
q
2
2m
A
2
+qϕψ = Eψ. But ∇·(Aψ)=(∇·A)ψ +A·(∇ψ), so
−
2
2m
∇
2
ψ +
iq
2m
[2A · (∇ψ)+∇·(Aψ)] +
q
2
2m
A
2
+ qϕ
ψ = Eψ.
This is the time-independent Schr¨odinger equation for electrodynamics. In the present case
∇·A =0, A · (∇ψ)=
B
0
2
x
∂ψ
∂y
− y
∂ψ
∂x
,A
2
=
B
2
0
4
x
2
+ y
2
,ϕ= Kz
2
.
But L
z
=
i
x
∂
∂y
− y
∂
∂x
, so −
2
2m
∇
2
ψ −
qB
0
2m
L
z
ψ +
q
2
B
2
0
8m
x
2
+ y
2
+ qKz
2
ψ = Eψ.
Since L
z
commutes with H, we may as well pick simultaneous eigenfunctions of both: L
z
ψ =¯mψ,
where ¯m =0, ±1, ±2,... (with the overbar to distinguish the magnetic quantum number from the mass).
Then
−
2
2m
∇
2
+
(qB
0
)
2
8m
x
2
+ y
2
+ qKz
2
ψ =
E +
qB
0
2m
¯m
ψ.
Now let ω
1
≡ qB
0
/m, ω
2
≡
2Kq/m, and use cylindrical coordinates (r, φ, z):
−
2
2m
1
r
∂
∂r
r
∂ψ
∂r
+
1
r
2
∂
2
ψ
∂φ
2
+
∂
2
ψ
∂z
2
+
1
8
mω
2
1
x
2
+ y
2
+
1
2
mω
2
2
z
2
ψ =
E +
1
2
¯mω
1
ψ.
But L
z
=
i
∂
∂φ
,so
∂
2
ψ
∂φ
2
= −
1
2
L
2
z
ψ = −
1
2
¯m
2
2
ψ = −¯m
2
ψ. Use separation of variables: ψ(r, φ, z)=
R(r)Φ(φ)Z(z):
−
2
2m
ΦZ
1
r
d
dr
r
dR
dr
−
¯m
2
r
2
RΦZ + RΦ
d
2
Z
dz
2
+
1
8
mω
2
1
r
2
+
1
2
mω
2
2
z
2
RΦZ =
E +
1
2
¯mω
1
RΦZ.
Divide by RΦZ and collect terms:
−
2
2m
1
rR
d
dr
r
dR
dr
−
¯m
2
r
2
+
1
8
mω
2
1
r
2
+
−
2
2m
1
Z
d
2
Z
dz
2
+
1
2
mω
2
2
z
2
=
E +
1
2
¯mω
1
.
The first term depends only on r, the second only on z, so they’re both constants; call them E
r
and E
z
:
−
2
2m
1
r
d
dr
r
dR
dr
−
¯m
2
r
2
R
+
1
8
mω
2
1
r
2
R = E
r
R; −
2
2m
d
2
Z
dz
2
+
1
2
mω
2
2
z
2
Z = E
z
Z; E = E
r
+E
z
−
1
2
¯mω
1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

130 CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS
The z equation is a one-dimensional harmonic oscillator, and we can read off immediately that E
z
=
(n
2
+1/2)ω
2
, with n
2
=0, 1, 2,... . The r equation is actually a two-dimensional harmonic oscillator; to
get E
r
, let u(r) ≡
√
rR, and follow the method of Sections 4.1.3 and 4.2.1:
R =
u
√
r
,
dR
dr
=
u
√
r
−
u
2r
3/2
,r
dR
dr
=
√
ru
−
u
2
√
r
,
d
dr
r
dR
dr
=
√
ru
+
u
4r
3/2
,
1
r
d
dr
r
dR
dr
=
u
√
r
+
u
4r
5/2
; −
2
2m
u
√
r
+
1
4
u
r
2
1
√
r
−
¯m
2
r
2
u
√
r
+
1
8
mω
2
1
r
2
u
√
r
= E
r
u
√
r
−
2
2m
d
2
u
dr
2
+
1
4
− ¯m
2
u
r
2
+
1
8
mω
2
1
r
2
u = E
r
u.
This is identical to the equation we encountered in Problem 4.39 (the three-dimentional harmonic oscil-
lator), only with ω → ω
1
/2,E → E
r
, and l(l +1)→ ¯m
2
− 1/4, which is to say, l
2
+ l +1/4= ¯m
2
,or
(l +1/2)
2
=¯m
2
,orl = |¯m|−1/2. [Our present equation depends only on ¯m
2
, and hence is the same for
either sign, but the solution to Problem 4.39 assumed l +1/2 ≥ 0 (else u is not normalizable), so we need
|m| here.] Quoting 4.39:
E =(j
max
+ l +3/2)ω → E
r
=(j
max
+ |¯m| +1)ω
1
/2, where j
max
=0, 2, 4,... .
E = j
max
+ |¯m| +1)ω
1
/2+(n
2
+1/2)ω
2
− ¯mω
1
/2= (n
1
+
1
2
)ω
1
+(n
2
+
1
2
)ω
2
,
where n
1
=0, 1, 2,... (if ¯m ≥ 0, then n
1
= j
max
/2; if ¯m<0, then n
1
= j
max
/2 − ¯m).
Problem 4.61
(a)
B
= ∇×A
= ∇×A + ∇×(∇λ)=∇×A = B.
[∇×∇λ =0, by equality of cross-derivatives: (∇×∇λ)
x
=
∂
∂y
∂λ
∂z
−
∂
∂z
∂λ
∂y
=0, etc.]
E
= −∇ϕ
−
∂A
∂t
= −∇ϕ + ∇
∂Λ
∂t
−
∂A
∂t
−
∂
∂t
(∇Λ) = −∇ϕ −
∂A
∂t
= E.
[Again: ∇
∂Λ
∂t
=
∂
∂t
(∇Λ) by the equality of cross-derivatives.]
(b)
i
∇−qA −q(∇Λ)
e
iqΛ/
Ψ=q(∇Λ)e
iqΛ/
Ψ+
i
e
iqΛ/
∇Ψ − qAe
iqΛ/
Ψ − q(∇Λ)e
iqΛ/
Ψ
=
i
e
iqΛ/
∇Ψ − qAe
iqΛ/
Ψ.
i
∇−qA −q(∇Λ)
2
e
iqΛ/
Ψ=
i
∇−qA −q(∇Λ)
i
e
iqΛ/
∇Ψ − qAe
iqΛ/
Ψ
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 4. QUANTUM MECHANICS IN THREE DIMENSIONS 131
= −
2
iq
(∇Λ ·∇Ψ)e
iqΛ/
+ e
iqΛ/
∇
2
Ψ
−
q
i
(∇·A)e
iqΛ/
Ψ − q
2
(A ·∇Λ)e
iqΛ/
Ψ
−
q
i
e
iqΛ/
A · (∇Ψ) −
q
i
e
iqΛ/
(A ·∇Ψ) + q
2
A
2
e
iqΛ/
Ψ
−
q
i
e
iqΛ/
(∇Λ ·∇Ψ) + q
2
(A ·∇Λ)e
iqΛ/
Ψ
= e
iqΛ/
-
−
2
∇
2
Ψ+iq(∇·A)Ψ+2iq(A ·∇Ψ) + q
2
A
2
Ψ
−iq(∇Λ) ·(∇Ψ) −q
2
(A ·∇Λ)Ψ + iq(∇Λ) · (∇Ψ) + q
2
(A ·∇Λ)Ψ
.
= e
iqΛ/
i
∇−qA
2
Ψ
.
So:
1
2m
i
∇−qA
2
+ qϕ
Ψ
= e
iqΛ/
1
2m
i
∇−qA
2
+ qϕ − q
∂Λ
∂t
Ψ
[using Eq. 4.205] = e
iqΛ/
i
∂Ψ
∂t
− q
∂Λ
∂t
Ψ
= i
∂
∂t
e
iqΛ/
Ψ
= i
∂Ψ
∂t
. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

132 CHAPTER 5. IDENTICAL PARTICLES
Chapter 5
Identical Particles
Problem 5.1
(a)
(m
1
+ m
2
)R = m
1
r
1
+ m
2
r
2
= m
1
r
1
+ m
2
(r
1
− r)=(m
1
+ m
2
)r
1
− m
2
r ⇒
r
1
= R +
m
2
m
1
+ m
2
r = R +
µ
m
1
r.
(m
1
+ m
2
)R = m
1
(r
2
+ r)+m
2
r
2
=(m
1
+ m
2
)r
2
+ m
1
r ⇒ r
2
= R −
m
1
m
1
+ m
2
r = R −
µ
m
2
r.
Let R =(X, Y, Z), r =(x, y, z).
(∇
1
)
x
=
∂
∂x
1
=
∂X
∂x
1
∂
∂X
+
∂x
∂x
1
∂
∂x
=
m
1
m
1
+ m
2
∂
∂X
+ (1)
∂
∂x
=
µ
m
2
(∇
R
)
x
+(∇
r
)
x
, so ∇
1
=
µ
m
2
∇
R
+ ∇
r
.
(∇
2
)
x
=
∂
∂x
2
=
∂X
∂x
2
∂
∂X
+
∂x
∂x
2
∂
∂x
=
m
2
m
1
+ m
2
∂
∂X
− (1)
∂
∂x
=
µ
m
1
(∇
R
)
x
− (∇
r
)
x
, so ∇
2
=
µ
m
1
∇
R
−∇
r
.
(b)
∇
2
1
ψ = ∇
1
· (∇
1
ψ)=∇
1
·
µ
m
2
∇
R
ψ + ∇
r
ψ
=
µ
m
2
∇
R
·
µ
m
2
∇
R
ψ + ∇
r
ψ
+ ∇
r
·
µ
m
2
∇
R
ψ + ∇
r
ψ
=
µ
m
2
2
∇
2
R
ψ +2
µ
m
2
(∇
r
·∇
R
)ψ + ∇
2
r
ψ.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 5. IDENTICAL PARTICLES 133
Likewise, ∇
2
2
ψ =
µ
m
1
2
∇
2
R
ψ − 2
µ
m
1
(∇
r
·∇
R
)+∇
2
r
ψ.
∴ Hψ = −
2
2m
1
∇
2
1
ψ −
2
2m
2
∇
2
2
ψ + V (r
1
, r
2
)ψ
= −
2
2
µ
2
m
1
m
2
2
∇
2
R
+
2µ
m
1
m
2
∇
r
·∇
R
+
1
m
1
∇
2
r
+
µ
2
m
2
m
2
1
∇
2
R
−
2µ
m
2
m
1
∇
r
·∇
R
+
1
m
2
∇
2
r
ψ
+ V (r)ψ = −
2
2
µ
2
m
1
m
2
1
m
2
+
1
m
1
∇
2
R
+
1
m
1
+
1
m
2
∇
2
r
ψ + V (r)ψ = Eψ.
But
1
m
1
+
1
m
2
=
m
1
+ m
2
m
1
m
2
=
1
µ
, so
µ
2
m
1
m
2
1
m
2
+
1
m
1
=
µ
m
1
m
2
=
m
1
m
2
m
1
m
2
(m
1
+ m
2
)
+
1
m
1
+ m
2
.
−
2
2(m
1
+ m
2
)
∇
2
R
ψ −
2
2µ
∇
2
r
ψ + V (r)ψ = Eψ.
(c) Put in ψ = ψ
r
(r)ψ
R
(R), and divide by ψ
r
ψ
R
:
−
2
2(m
1
+ m
2
)
1
ψ
R
∇
2
R
ψ
R
+
−
2
2µ
1
ψ
r
∇
2
r
ψ
r
+ V (r)
= E.
The first term depends only on R, the second only on r, so each must be a constant; call them E
R
and
E
r
, respectively. Then:
−
2
2(m
1
+ m
2
)
∇
2
ψ
R
= E
R
ψ
R
; −
2
2µ
∇
2
ψ
r
+ V (r)ψ
r
= E
r
ψ
r
, with E
R
+ E
r
= E.
Problem 5.2
(a) From Eq. 4.77, E
1
is proportional to mass, so
∆E
1
E
1
=
∆m
µ
=
m − µ
µ
=
m(m + M)
mM
−
M
M
=
m
M
.
The fractional error is the ratio of the electron mass to the proton mass:
9.109 × 10
−31
kg
1.673 × 10
−27
kg
=5.44 × 10
−4
. The percent error is 0.054% (pretty small).
(b) From Eq. 4.94, R is proportional to m,so
∆(1/λ)
(1/λ)
=
∆R
R
=
∆µ
µ
= −
(1/λ
2
)∆λ
(1/λ)
= −
∆λ
λ
.
So (in magnitude) ∆λ/λ =∆µ/µ. But µ = mM/(m + M), where m = electron mass, and M =
nuclear mass.
∆µ =
m(2m
p
)
m +2m
p
−
mm
p
m + m
p
=
mm
p
(m + m
p
)(m +2m
p
)
(2m +2m
p
− m − 2m
p
)
=
m
2
m
p
(m + m
p
)(m +2m
p
)
=
mµ
m +2m
p
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

134 CHAPTER 5. IDENTICAL PARTICLES
∆λ
λ
=
∆µ
µ
=
m
m +2m
p
≈
m
2m
p
, so ∆λ =
m
2m
p
λ
h
, where λ
h
is the hydrogen wavelength.
1
λ
= R
1
4
−
1
9
5
36
R ⇒ λ =
36
5R
=
36
5(1.097 × 10
7
)
m=6.563 × 10
−7
m.
∴ ∆λ =
9.109 × 10
−31
2(1.673 × 10
−27
)
(6.563 × 10
−7
)m = 1.79 × 10
−10
m.
(c) µ =
mm
m + m
=
m
2
, so the energy is half what it would be for hydrogen: (13.6/2)eV =
6.8 eV.
(d) µ =
m
p
m
µ
m
p
+ m
µ
; R ∝ µ,soR is changed by a factor
m
p
m
µ
m
p
+ m
µ
·
m
p
+ m
e
m
p
m
e
=
m
µ
(m
p
+ m
e
)
m
e
(m
p
+ m
µ
)
, as compared
with hydrogen. For hydrogen, 1/λ = R(1−1/4) =
3
4
R ⇒ λ =4/3R =4/3(1.097×10
7
)m=1.215×10
−7
m,
and λ ∝ 1/R, so for muonic hydrogen the Lyman-alpha line is at
λ =
m
e
(m
p
+ m
µ
)
m
µ
(m
p
+ m
e
)
(1.215 × 10
−7
m) =
1
206.77
(1.673 × 10
−27
+ 206.77 × 9.109 × 10
−31
)
(1.673 × 10
−27
+9.109 × 10
−31
)
(1.215 × 10
−7
m)
=
6.54 × 10
−10
m.
Problem 5.3
The energy of the emitted photon, in a transition from vibrational state n
i
to state n
f
,is
E
p
=(n
i
+
1
2
)ω − (n
f
+
1
2
)ω = nω, (where n ≡ n
i
− n
f
). The frequency of the photon is
ν =
E
p
h
=
nω
2π
=
n
2π
k
µ
. The splitting of this line is given by
∆ν =
n
2π
√
k
−
1
2µ
3/2
∆µ
=
1
2
n
2π
k
µ
∆µ
µ
=
1
2
ν
∆µ
µ
.
Now
µ =
m
h
m
c
m
h
+ m
c
=
1
1
m
c
+
1
m
h
⇒ ∆µ =
−1
1
m
c
+
1
m
h
2
−
1
m
2
c
∆m
c
=
µ
2
m
2
c
∆m
c
.
∆ν =
1
2
ν
µ∆m
c
m
2
c
=
1
2
ν
(∆m
c
/m
c
)
1+
m
c
m
h
.
Using the average value (36) for m
c
, we have ∆m
c
/m
c
=2/36, and m
c
/m
h
=36/1, so
∆ν =
1
2
(1/18)
(1 + 36)
ν =
1
(36)(37)
ν =
7.51 × 10
−4
ν.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 5. IDENTICAL PARTICLES 135
Problem 5.4
(a)
1=
|ψ
±
|
2
d
3
r
1
d
3
r
2
= |A|
2
[ψ
a
(r
1
)ψ
b
(r
2
) ± ψ
b
(r
1
)ψ
a
(r
2
)]
∗
[ψ
a
(r
1
)ψ
b
(r
2
) ± ψ
b
(r
1
)ψ
a
(r
2
)] d
3
r
1
d
3
r
2
= |A|
2
|ψ
a
(r
1
)|
2
d
3
r
1
|ψ
b
(r
2
)|
2
d
3
r
2
±
ψ
a
(r
1
)
∗
ψ
b
(r
1
)d
3
r
1
ψ
b
(r
2
)
∗
ψ
a
(r
2
)d
3
r
2
±
ψ
b
(r
1
)
∗
ψ
a
(r
1
)d
3
r
1
ψ
a
(r
2
)
∗
ψ
b
(r
2
)d
3
r
2
+
|ψ
b
(r
1
)|
2
d
3
r
1
|ψ
a
(r
2
)|
2
d
3
r
2
= |A|
2
(1 · 1 ± 0 · 0 ± 0 · 0+1· 1) = 2|A|
2
=⇒ A =1/
√
2.
(b)
1=|A|
2
[2ψ
a
(r
1
)ψ
a
(r
2
)]
∗
[2ψ
a
(r
1
)ψ
a
(r
2
)] d
3
r
1
d
3
r
2
=4|A|
2
|ψ
a
(r
1
)|
2
d
3
r
1
|ψ
a
(r
2
)|
2
d
3
r
2
=4|A|
2
. A =1/2.
Problem 5.5
(a)
−
2
2m
∂
2
ψ
∂x
2
1
−
2
2m
∂
2
ψ
∂x
2
2
= Eψ (for 0 ≤ x
1
,x
2
≤ a, otherwise ψ =0).
ψ =
√
2
a
sin
πx
1
a
sin
2πx
2
a
− sin
2πx
1
a
sin
πx
2
a
d
2
ψ
dx
2
1
=
√
2
a
−
π
a
2
sin
πx
1
a
sin
2πx
2
a
+
2π
a
2
sin
2πx
1
a
sin
πx
2
a
d
2
ψ
dx
2
2
=
√
2
a
−
2π
a
2
sin
πx
1
a
sin
2πx
2
a
+
π
a
2
sin
2πx
1
a
sin
πx
2
a
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

136 CHAPTER 5. IDENTICAL PARTICLES
d
2
ψ
dx
2
1
+
d
2
ψ
dx
2
2
= −
π
a
2
+
2π
a
2
ψ = −5
π
2
a
2
ψ,
−
2
2m
d
2
ψ
dx
2
1
+
d
2
ψ
dx
2
2
=
5π
2
2
2ma
2
ψ = Eψ, with E =
5π
2
2
2ma
2
=5K.
(b) Distinguishable:
ψ
22
=(2/a) sin (2πx
1
/a) sin (2πx
2
/a) , with E
22
=8K (nondegenerate).
ψ
13
=(2/a) sin (πx
1
/a) sin (3πx
2
/a)
ψ
31
=(2/a) sin (3πx
1
/a) sin (πx
2
/a)
, with E
13
= E
31
=10K (doubly degenerate).
Identical Bosons:
ψ
22
=(2/a) sin (2πx
1
/a) sin (2πx
2
/a), E
22
=8K (nondegenerate).
ψ
13
=(
√
2/a) [sin (πx
1
/a) sin (3πx
2
/a) + sin (3πx
1
/a) sin (πx
2
/a)], E
13
=10K (nondegenerate).
Identical Fermions:
ψ
13
=(
√
2/a)
sin
πx
1
a
sin
3πx
2
a
− sin
3πx
1
a
sin
πx
2
a
, E
13
=10K (nondegenerate).
ψ
23
=(
√
2/a)
sin
2πx
1
a
sin
3πx
2
a
− sin
3πx
1
a
sin
2πx
2
a
, E
23
=13K (nondegenerate).
Problem 5.6
(a) Use Eq. 5.19 and Problem 2.4, with x
n
= a/2 and x
2
n
= a
2
1
3
−
1
2(nπ)
2
.
(x
1
− x
2
)
2
= a
2
1
3
−
1
2(nπ)
2
+ a
2
1
3
−
1
2(mπ)
2
− 2 ·
a
2
·
a
2
= a
2
1
6
−
1
2π
2
1
n
2
+
1
m
2
.
(b) x
mn
=
2
a
a
0
x sin
mπ
a
x
sin
nπ
a
x
dx =
1
a
a
0
x
cos
(m−n)π
a
x
− cos
(m+n)π
a
x
dx
=
1
a
a
(m−n)π
2
cos
(m−n)π
a
x
+
ax
(m−n)π
sin
(m−n)π
a
x
−
a
(m+n)π
2
cos
(m+n)π
a
x
−
ax
(m+n)π
sin
(m+n)π
a
x
a
0
=
1
a
a
(m−n)π
2
(cos[(m − n)π] −1) −
a
(m+n)π
2
(cos[(m + n)π] −1)
.
But cos[(m ± n)π]=(−1)
m+n
, so
x
mn
=
a
π
2
(−1)
m+n
− 1
1
(m − n)
2
−
1
(m + n)
2
=
a(−8mn)
π
2
(m
2
−n
2
)
2
, if m and n have opposite parity,
0, if m and n have same parity.
So Eq. 5.21 ⇒(x
1
− x
2
)
2
= a
2
1
6
−
1
2π
2
1
n
2
+
1
m
2
−
128a
2
m
2
n
2
π
4
(m
2
− n
2
)
4
.
(The last term is present only when m, n have opposite parity.)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 5. IDENTICAL PARTICLES 137
(c) Here Eq. 5.21 ⇒(x
1
− x
2
)
2
= a
2
1
6
−
1
2π
2
1
n
2
+
1
m
2
+
128a
2
m
2
n
2
π
4
(m
2
− n
2
)
4
.
(Again, the last term is present only when m, n have opposite parity.)
Problem 5.7
(a) ψ(x
1
,x
2
,x
3
)=ψ
a
(x
1
)ψ
b
(x
2
)ψ
c
(x
3
).
(b) ψ(x
1
,x
2
,x
3
)=
1
√
6
[ψ
a
(x
1
)ψ
b
(x
2
)ψ
c
(x
3
)+ψ
a
(x
1
)ψ
c
(x
2
)ψ
b
(x
3
)+ψ
b
(x
1
)ψ
a
(x
2
)ψ
c
(x
3
)
+ψ
b
(x
1
)ψ
c
(x
2
)ψ
a
(x
3
)+ψ
c
(x
1
)ψ
b
(x
2
)ψ
a
(x
3
)+ψ
c
(x
1
)ψ
a
(x
2
)ψ
b
(x
3
)]
.
(c) ψ(x
1
,x
2
,x
3
)=
1
√
6
[ψ
a
(x
1
)ψ
b
(x
2
)ψ
c
(x
3
) − ψ
a
(x
1
)ψ
c
(x
2
)ψ
b
(x
3
) − ψ
b
(x
1
)ψ
a
(x
2
)ψ
c
(x
3
)
+ψ
b
(x
1
)ψ
c
(x
2
)ψ
a
(x
3
) − ψ
c
(x
1
)ψ
b
(x
2
)ψ
a
(x
3
)+ψ
c
(x
1
)ψ
a
(x
2
)ψ
b
(x
3
)]
.
Problem 5.8
ψ = A
ψ(r
1
, r
2
, r
3
,... ,r
Z
) ± ψ(r
2
, r
1
, r
3
,... ,r
Z
)+ψ(r
2
, r
3
, r
1
,... ,r
Z
) + etc.
,
where “etc.” runs over all permutations of the arguments r
1
, r
2
,... ,r
Z
, with a + sign for all even permutations
(even number of transpositions r
i
↔ r
j
, starting from r
1
, r
2
,... ,r
Z
), and ± for all odd permutations (+ for
bosons, − for fermions). At the end of the process, normalize the result to determine A. (Typically A =1/
√
Z!,
but this may not be right if the starting function is already symmetric under some interchanges.)
Problem 5.9
(a) The energy of each electron is E = Z
2
E
1
/n
2
=4E
1
/4=E
1
= −13.6eV, so the total initial energy is
2 × (−13.6) eV= −27.2 eV. One electron drops to the ground state Z
2
E
1
/1=4E
1
, so the other is left
with 2E
1
− 4E
1
= −2E
1
= 27.2 eV.
(b) He
+
has one electron; it’s a hydrogenic ion (Problem 4.16) with Z = 2, so the spectrum is
1/λ =4R
1/n
2
f
− 1/n
2
i
,
where R is the hydrogen Rydberg constant, and n
i
,n
f
are the initial and final
quantum numbers (1, 2, 3, ... ).
Problem 5.10
(a) The ground state (Eq. 5.30) is spatially symmetric, so it goes with the symmetric (triplet) spin configura-
tion. Thus the ground state is orthohelium, and it is triply degerate. The excited states (Eq. 5.32) come
in ortho (triplet) and para (singlet) form; since the former go with the symmetric spatial wave function,
the orthohelium states are higher in energy than the corresponding (nondegenerate) para states.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

138 CHAPTER 5. IDENTICAL PARTICLES
(b) The ground state (Eq. 5.30) and all excited states (Eq. 5.32) come in both ortho and para form. All are
quadruply degenerate (or at any rate we have no way a priori of knowing whether ortho or para are higher
in energy, since we don’t know which goes with the symmetric spatial configuration).
Problem 5.11
(a)
0
1
|r
1
− r
2
|
1
=
8
πa
3
2
e
−4(r
1
+r
2
)/a
r
2
1
+ r
2
2
− 2r
1
r
2
cos θ
2
d
3
r
2
d
3
r
1
=2π
∞
0
e
−4(r
1
+r
2
)/a
π
0
sin θ
2
r
2
1
+ r
2
2
− 2r
1
r
2
cos θ
2
dθ
2
r
2
2
dr
2
=
1
r
1
r
2
r
2
1
+ r
2
2
− 2r
1
r
2
cos θ
2
π
0
=
1
r
1
r
2
r
2
1
+ r
2
2
+2r
1
r
2
−
r
2
1
+ r
2
2
− 2r
1
r
2
=
1
r
1
r
2
[(r
1
+ r
2
) −|r
1
− r
2
|]=
2/r
1
(r
2
<r
1
)
2/r
2
(r
2
>r
1
)
=4πe
−4r
1
/a
1
r
1
r
1
0
r
2
2
e
−4r
2
/a
dr
2
+
∞
r
1
r
2
e
−4r
2
/a
dr
2
.
1
r
1
r
1
0
r
2
2
e
−4r
2
/a
dr
2
=
1
r
1
−
a
4
r
2
2
e
−4r
2
/a
+
a
2
a
4
2
e
−4r
2
/a
−
4r
2
a
− 1
r
1
0
= −
a
4r
1
r
2
1
e
−4r
1
/a
+
ar
1
2
e
−4r
1
/a
+
a
2
8
e
−4r
1
/a
−
a
2
8
.
∞
r
1
r
2
e
−4r
2
/a
dr
2
=
a
4
2
e
−4r
2
/a
−
4r
2
a
− 1
∞
r
1
=
ar
1
4
e
−4r
1
/a
+
a
2
16
e
−4r
1
/a
.
=4π
a
3
32r
1
e
−4r
1
/a
+
−
ar
1
a
−
a
2
8
−
a
3
32r
1
+
ar
1
4
+
a
2
16
e
−8r
1
/a
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 5. IDENTICAL PARTICLES 139
=
πa
2
8
a
r
1
e
−4r
1
/a
−
2+
a
r
1
e
−8r
1
/a
.
0
1
|r
1
− r
2
|
1
=
8
πa
4
· 4π
∞
0
a
r
1
e
−4r
1
/a
−
2+
a
r
1
e
−8r
1
/a
r
2
1
dr
1
=
32
a
4
a
∞
0
r
1
e
−4r
1
/a
dr
1
− 2
∞
0
r
2
1
e
−8r
1
/a
dr
1
− a
∞
0
r
1
e
−8r
1
/a
dr
1
=
32
a
4
a ·
a
4
2
− 2 · 2
a
8
3
− a ·
a
8
2
=
32
a
1
16
−
1
128
−
1
64
=
5
4a
.
(b)
V
ee
≈
e
2
4π9
0
0
1
|r
1
− r
2
|
1
=
5
4
e
2
4π9
0
1
a
=
5
4
m
2
e
2
4π9
0
2
=
5
2
(−E
1
)=
5
2
(13.6eV)=
34 eV.
E
0
+ V
ee
=(−109 + 34)eV = −75 eV, which is pretty close to the experimental value (−79 eV).
Problem 5.12
(a) Hydrogen: (1s); helium: (1s)
2
; lithium: (1s)
2
(2s); beryllium: (1s)
2
(2s)
2
;
boron: (1s)
2
(2s)
2
(2p); carbon: (1s)
2
(2s)
2
(2p)
2
; nitrogen: (1s)
2
(2s)
2
(2p)
3
;
oxygen: (1s)
2
(2s)
2
(2p)
4
; fluorine: (1s)
2
(2s)
2
(2p)
5
; neon: (1s)
2
(2s)
2
(2p)
6
.
These values agree with those in Table 5.1—no surprises so far.
(b) Hydrogen:
2
S
1/2
; helium:
1
S
0
; lithium:
2
S
1/2
; beryllium
1
S
0
. (These four are unambiguous,
because the orbital angular momentum is zero in all cases.) For boron, the spin (1/2) and orbital (1)
angular momenta could add to give 3/2 or 1/2, so the possibilities are
2
P
3/2
or
2
P
1/2
. For carbon, the
two p electrons could combine for orbital angular momentum 2, 1, or 0, and the spins could add to 1 or 0:
1
S
0
,
3
S
1
,
1
P
1
,
3
P
2
,
3
P
1
,
3
P
0
,
1
D
2
,
3
D
3
,
3
D
2
,
3
D
1
. For nitrogen, the 3 p electrons can add to orbital angular
momentum 3, 2, 1, or 0, and the spins to 3/2 or 1/2:
2
S
1/2
,
4
S
3/2
,
2
P
1/2
,
2
P
3/2
,
4
P
1/2
,
4
P
3/2
,
4
P
5/2
,
2
D
3/2
,
2
D
5/2
,
4
D
1/2
,
4
D
3/2
,
4
D
5/2
,
4
D
7/2
,
2
F
5/2
,
2
F
3/2
,
4
F
3/2
,
4
F
5/2
,
4
F
7/2
,
4
F
9/2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

140 CHAPTER 5. IDENTICAL PARTICLES
Problem 5.13
(a) Orthohelium should have lower energy than parahelium, for corresponding states (which is true).
(b) Hund’s first rule says S = 1 for the ground state of carbon. But this (the triplet) is symmetric, so the
orbital state will have to be antisymmetric. Hund’s second rule favors L = 2, but this is symmetric, as
you can see most easily by going to the “top of the ladder”: |22 = |11
1
||11
2
. So the ground state of
carbon will be S =1,L= 1. This leaves three possibilities:
3
P
2
,
3
P
1
, and
3
P
0
.
(c) For boron there is only one electron in the 2p subshell (which can accommodate a total of 6), so Hund’s
third rule says the ground state will have J = |L − S|. We found in Problem 5.12(b) that L = 1 and
S =1/2, so J =1/2, and the configuration is
2
P
1/2
.
(d) For carbon we know that S = 1 and L = 1, and there are only two electrons in the outer subshell, so
Hund’s third rule says J = 0, and the ground state configuration must be
3
P
0
.
For nitrogen Hund’s first rule says S =3/2, which is symmetric (the top of the ladder is |
3
2
3
2
=
|
1
2
1
2
1
|
1
2
1
2
2
|
1
2
1
2
3
). Hund’s second rule favors L = 3, but this is also symmetric. In fact, the only
antisymmetric orbital configuration here is L = 0. [You can check this directly by working out the
Clebsch-Gordan coefficients, but it’s easier to reason as follows: Suppose the three outer electrons are in
the “top of the ladder” spin state, so each one has spin up (|
1
2
1
2
); then (since the spin states are all the
same) the orbital states have to be different: |11, |10, and |1−1. In particular, the total z-component of
orbital angular momentum has to be zero. But the only configuration that restricts L
z
to zero is L = 0.]
The outer subshell is exactly half filled (three electrons with n =2,l = 1), so Hund’s third rule says
J = |L − S| = |0 −
3
2
| =3/2. Conclusion: The ground state of nitrogen is
4
S
3/2
. (Table 5.1 confirms
this.)
Problem 5.14
S =2;L =6;J =8. (1s)
2
(2s)
2
(2p)
6
(3s)
2
(3p)
6
(3d)
10
(4s)
2
(4p)
6
definite
(36 electrons)
(4d)
10
(5s)
2
(5p)
6
(4f)
10
(6s)
2
likely
(30 electrons)
.
Problem 5.15
Divide Eq. 5.45 by Eq. 5.43, using Eq. 5.42:
E
tot
/N q
E
F
=
2
(3π
2
Nq)
5/3
10π
2
mV
2/3
1
Nq
2m
2
(3π
2
Nq/V )
2/3
=
3
5
.
Problem 5.16
(a) E
F
=
2
2m
(3ρπ
2
)
2/3
.ρ=
Nq
V
=
N
V
=
atoms
mole
×
moles
gm
×
gm
volume
=
N
A
M
· d, where N
A
is Avogadro’s
number (6.02 ×10
23
), M = atomic mass = 63.5 gm/mol, d = density = 8.96 gm/cm
3
.
ρ =
(6.02 × 10
23
)(8.96 gm/cm
3
)
(63.5gm)
=8.49 × 10
22
/cm
3
=8.49 × 10
28
/m
3
.
E
F
=
(1.055 × 10
−34
J · s)(6.58 × 10
−16
eV · s)
(2)(9.109 × 10
−31
kg)
(3π
2
8.49 × 10
28
/m
3
)
2/3
= 7.04 eV.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 5. IDENTICAL PARTICLES 141
(b)
7.04 eV =
1
2
(0.511 × 10
6
eV/c
2
)v
2
⇒
v
2
c
2
=
14.08
.511 × 10
6
=2.76 × 10
−5
⇒
v
c
=5.25 × 10
−3
,
so it’s
nonrelativistic. v =(5.25 × 10
−3
) × (3 × 10
8
)= 1.57 ×10
6
m/s.
(c)
T =
7.04 eV
8.62 × 10
−5
eV/K
=
8.17 × 10
4
K.
(d)
P =
(3π
2
)
2/3
2
5m
ρ
5/3
=
(3π
2
)
2/3
(1.055 × 10
−34
)
2
5(9.109 × 10
−31
)
(8.49 × 10
28
)
5/3
N/m
2
= 3.84 × 10
10
N/m
2
.
Problem 5.17
P =
(3π
2
)
2/3
2
5m
Nq
V
5/3
= AV
−5/3
⇒ B = −V
dP
dV
= −VA
−5
3
V
−5/3−1
=
5
3
AV
−5/3
=
5
3
P.
For copper, B =
5
3
(3.84 × 10
10
N/m
2
)= 6.4 × 10
10
N/m
2
.
Problem 5.18
(a) Equations 5.59 and 5.63 ⇒ ψ = A sin kx + B cos kx; A sin ka =
e
iKa
− cos ka
B. So
ψ = A sin kx +
A sin ka
(e
iKa
− cos ka)
cos kx =
A
(e
iKa
− cos ka)
e
iKa
sin kx − sin kx cos ka + cos kx sin ka
= C
-
sin kx + e
−iKa
sin[k(a −x)]
.
, where C ≡
Ae
iKa
e
iKa
− cos ka
.
(b) If z = ka = jπ, then sin ka = 0, Eq. 5.64 ⇒ cos Ka = cos ka =(−1)
j
⇒ sin Ka =0,soe
iKa
=
cos Ka + i sin Ka =(−1)
j
, and the constant C involves division by zero. In this case we must go back to
Eq. 5.63, which is a tautology (0=0) yielding no constraint on A or B, Eq. 5.61 holds automatically, and
Eq. 5.62 gives
kA − (−1)
j
k
A(−1)
j
− 0
=
2mα
2
B ⇒ B =0. So ψ = A sin kx.
Here ψ is zero at each delta spike, so the wave function never “feels” the potential at all.
Problem 5.19
We’re looking for a solution to Eq. 5.66 with β = 10 and z π: f(z) = cos z +10
sin z
z
=1.
Mathematica gives z =2.62768. So E =
2
k
2
2m
=
2
z
2
2ma
2
=
z
2
2β
α
a
=
(2.62768)
2
20
eV =
0.345 eV.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

142 CHAPTER 5. IDENTICAL PARTICLES
Problem 5.20
Positive-energy solutions. These are the same as before, except that α (and hence also β) is now a negative
number.
Negative-energy solutions.
On 0 <x<awe have
d
2
ψ
dx
2
= κ
2
ψ, where κ ≡
√
−2mE
⇒ ψ(x)=A sinh kx + B cosh kx.
According to Bloch’s theorem the solution on −a<x<0is
ψ(x)=e
−iKa
[A sinh κ(x + a)+B cosh κ(x + a)] .
Continuity at x =0⇒
B = e
−iKa
[A sinh κa + B cosh κa] , or A sinh κa = B
e
iKa
− cosh κa
. (1)
The discontinuity in ψ
(Eq. 2.125) ⇒
κA−e
−iKa
κ [A cosh κa + B sinh κa]=
2mα
2
B, or A
1 − e
−iKa
cosh κa
= B
2mα
2
κ
+ e
−iKa
sinh κa
. (2)
Plugging (1) into (2) and cancelling B:
e
iKa
− cosh κa
1 − e
−iKa
cosh κa
=
2mα
2
κ
sinh κa + e
−iKa
sinh
2
κa.
e
iKa
− 2 cosh κa + e
−iKa
cosh
2
κa − e
−iKa
sinh
2
κa =
2mα
2
κ
sinh κa.
e
iKa
+ e
−iKa
= 2 cosh κa +
2ma
2
κ
sinh κa,
cos Ka = cosh κa +
mα
2
κ
sinh κa.
This is the analog to Eq. 5.64. As before, we let β ≡ mαa/
2
(but remember it’s now a negative number), and
this time we define z ≡−κa, extending Eq. 5.65 to negative z, where it represents negative-energy solutions.
In this region we define
f(z) = cosh z + β
sinh z
z
. (3)
In the Figure I have plotted f(z) for β = −1.5, using Eq. 5.66 for postive z and (3) for negative z.As
before, allowed energies are restricted to the range −1 ≤ f(z) ≤ 1, and occur at intersections of f(z) with the
N horizontal lines cos Ka = cos(2πn/Na), with n =0, 1, 2 ...N − 1. Evidently the first band (partly negative,
and partly positive) contains N states, as do all the higher bands.
0
1
-1
0 π2π3π4π
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 5. IDENTICAL PARTICLES 143
Problem 5.21
Equation 5.56 says K =
2πn
Na
⇒ Ka =2π
n
N
; at the bottom of page 227 we found that n =0, 1, 2,... ,N − 1.
Each value of n corresponds to a distinct state. To find the allowed energies we draw N horizontal lines on
Figure 5.6, at heights cos Ka = cos(2πn/N), and look for intersections with f(z). The point is that almost all
of these lines come in pairs—two different n’s yielding the same value of cos Ka:
N =1
⇒ n =0⇒ cos Ka =1. Nondegenerate.
N =2
⇒ n =0, 1 ⇒ cos Ka =1, −1. Nondegenerate.
N =3
⇒ n =0, 1, 2 ⇒ cos Ka =1, −
1
2
, −
1
2
. The first is nondegenerate, the other two are degenerate.
N =4
⇒ n =0, 1, 2, 3 ⇒ cos Ka =1, 0, −1, 0. Two are nondegenerate, the others are degenerate.
Evidently they are doubly degenerate (two different n’s give same cos Ka) except when cos Ka = ±1, i.e., at
the
top or bottom of a band. The Bloch factors e
iKa
lie at equal angles in the complex plane, starting with
1 (see Figure, drawn for the case N = 8); by symmetry, there is always one with negative imaginary part
symmetrically opposite each one with positive imaginary part; these two have the same real part (cos Ka).
Only points which fall on the real axis have no twins.
n=0
n=1
n=2
n=3
n=4
n=5
n=6
n=7
cos(Ka)
sin(Ka)
Problem 5.22
(a)
ψ(x
A
,x
B
,x
C
)=
1
√
6
'
2
a
(
3
sin
5πx
A
a
sin
7πx
B
a
sin
17πx
C
a
− sin
5πx
A
a
sin
17πx
B
a
sin
7πx
C
a
+ sin
7πx
A
a
sin
17πx
B
a
sin
5πx
C
a
− sin
7πx
A
a
sin
5πx
B
a
sin
17πx
C
a
+ sin
17πx
A
a
sin
5πx
B
a
sin
7πx
C
a
− sin
17πx
A
a
sin
7πx
B
a
sin
5πx
C
a
.
(b) (i)
ψ =
'
2
a
(
3
sin
11πx
A
a
sin
11πx
B
a
sin
11πx
C
a
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

144 CHAPTER 5. IDENTICAL PARTICLES
(ii)
ψ =
1
√
3
'
2
a
(
3
sin
πx
A
a
sin
πx
B
a
sin
19πx
C
a
+ sin
πx
A
a
sin
19πx
B
a
sin
πx
C
a
+ sin
19πx
A
a
sin
πx
B
a
sin
πx
C
a
.
(iii)
ψ =
1
√
6
'
2
a
(
3
sin
5πx
A
a
sin
7πx
B
a
sin
17πx
C
a
+ sin
5πx
A
a
sin
17πx
B
a
sin
7πx
C
a
+ sin
7πx
A
a
sin
17πx
B
a
sin
5πx
C
a
+ sin
7πx
A
a
sin
5πx
B
a
sin
17πx
C
a
+ sin
17πx
A
a
sin
5πx
B
a
sin
7πx
C
a
+ sin
17πx
A
a
sin
7πx
B
a
sin
5πx
C
a
.
Problem 5.23
(a) E
n
1
n
2
n
3
=(n
1
+ n
2
+ n
3
+
3
2
)ω =
9
2
ω ⇒ n
1
+ n
2
+ n
3
=3. (n
1
,n
2
,n
3
=0, 1, 2, 3 ...).
State Configuration # of States
n
1
n
2
n
3
(N
0
,N
1
,N
2
...)
003
030(2,0,0,1,0,0 ...) 3
300
012
021
102(1,1,1,0,0,0 ...) 6
120
201
210
111 (0,3,0,0,0 ...) 1
Possible single-particle energies:
E
0
= ω/2:P
0
=12/30 = 4/10.
E
1
=3ω/2:P
1
=9/30 = 3/10.
E
2
=5ω/2:P
2
=6/30 = 2/10.
E
3
=7ω/2:P
3
=3/30 = 1/10.
Most probable configuration: (1,1,1,0,0,0 ...).
Most probable single-particle energy: E
0
=
1
2
ω.
(b) For identical fermions the only configuration is (1,1,1,0,0,0 ...) (one state), so this is also the most
probable configuration. The possible one-particle energies are
E
0
(P
0
=1/3),E
1
(P
1
=1/3),E
2
(P
2
=1/3),
and they are all equally likely, so it’s a 3-way tie for the most probable energy.
(c) For identical bosons all three configurations are possible, and there is one state for each. Possible one-
particle energies:
E
0
(P
0
=1/3),E
1
(P
1
=4/9),E
2
(P
2
=1/9),E
3
(P
3
=1/9). Most probable energy: E
1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 5. IDENTICAL PARTICLES 145
Problem 5.24
Here N = 3, and d
n
= 1 for all states, so:
Eq. 5.74 ⇒ Q =6
∞
<
n=1
1
N
n
!
(distinguishable),
Eq. 5.75 ⇒ Q =
∞
<
n=1
1
N
n
!(1 − N
n
)!
(fermions),
Eq. 5.77 ⇒ Q = 1 (bosons).
(In the products, most factors are 1/0! or 1/1!, both of which are 1, so I won’t write them.)
Configuration 1
(N
11
= 3, others 0):
Q =6×
1
3!
=
1 (distinguishable),
Q =
1
3!
×
1
(−2)!
=
0 (fermions),
Q =
1 (bosons).
Configuration 2
(N
5
=1,N
13
= 2):
Q =6×
1
1!
×
1
2!
=
3 (distinguishable),
Q =
1
1!0!
×
1
2!(−1)!
=
0 (fermions),
Q =
1 (bosons).
Configuration 3
(N
1
=2,N
19
= 1):
Q =6×
1
2!
×
1
1!
=
3 (distinguishable),
Q =
1
2!(−1)!
×
1
1!0!
=
0 (fermions),
Q =
1 (bosons).
Configuration 4
(N
5
= N
7
= N
17
= 1):
Q =6×
1
1!
×
1
1!
×
1
1!
=
6 (distinguishable),
Q =
1
1!0!
×
1
1!0!
×
1
1!0!
=
1 (fermions),
Q =
1 (bosons).
All of these agree with what we got “by hand” at the top of page 231.
Problem 5.25
N =1: - can put the ball in any of d baskets, so d ways.
N =2
:
- could put both balls in any of the d baskets : d ways, or
- could put one in one basket (d ways), the other in another(d − 1) ways—but it
doesn’t matter which is which, so divide by 2.
Total
: d +
1
2
d(d − 1) =
1
2
d(2 + d − 1) =
1
2
d(d +1) ways.
N =3
:
- could put all three in one basket : d ways, or
- 2 in one basket, one in another : d(d − 1) ways, or
- 1 each in 3 baskets : d(d − 1)(d − 2)/3! ways.
Total
: d + d(d − 1) + d(d − 1)(d − 2)/6=
1
6
d(6+6d − 6+d
2
− 3d +2)=
1
6
d(d
2
+3d +2)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

146 CHAPTER 5. IDENTICAL PARTICLES
=
d(d + 1)(d +2)
6
ways.
N =4
:
- all in one basket: d ways, or
- 3 in one basket, 1 in another: d(d − 1) ways, or
- 2 in one basket, 2 in another: d(d − 1)/2 ways, or
- 2 in one basket, one each in others: d(d − 1)(d − 2)/2, or
- all in different baskets: d(d − 1)(d − 2)(d − 3)/4!
Total
: d + d(d − 1) + d(d − 1)/2+d(d − 1)(d − 2)/2+d(d − 1)(d − 2)(d − 3)/24
=
1
24
(24+24d − 24+12d − 12+12d
2
− 36d +24+d
3
− 6d
2
+11d − 6)
=
1
24
d(d
3
+6d
2
+11d +6)=
d(d + 1)(d + 2)(d +3)
24
ways.
The general formula seems to be f(N, d)=
d(d + 1)(d +2)···(d + N − 1)
N!
=
(d + N − 1)!
N!(d − 1)!
=
d + N − 1
N
.
Proof: How many ways to put N identical balls in d baskets? Call it f (N, d).
- Could put all of them in the first basket: 1 way.
- Could put all but one in the first basket; there remains 1 ball for d − 1 baskets: f(1,d− 1) ways.
- Could put all but two in the first basket; there remain 2 for d − 1 baskets: f (2,d−1) ways.
.
.
.
- Could put zero in the first basket, leaving N for d − 1 baskets: f(N,d − 1) ways.
Thus: f (N, d)=f(0,d−1)+f(1,d−1)+f(2,d−1)+···+f (N, d−1) =
/
N
j=0
f(j, d−1) (where f(0,d) ≡ 1).
It follows that f (N, d)=
/
N−1
j=0
f(j, d −1) + f (N, d −1) = f(N −1,d)+f(N,d−1). Use this recursion relation
to confirm the conjectured formula by induction:
d + N − 1
N
?
=
d + N − 2
N − 1
+
d + N − 2
N
=
(d + N − 2)!
(N − 1)!(d − 1)!
+
(d + N − 2)!
N!(d − 2)!
=
(d + N − 2)!
N!(d − 1)!
(N + d − 1) =
(d + N − 1)!
N!(d − 1)!
=
d + N − 1
d − 1
.
It works for N =0:
d−1
0
= 1, and for d =1:
N
N
= 1 (which is obviously correct for just one basket). QED
Problem 5.26
A(x, y)=(2x)(2y)=4xy; maximize, subject to the constraint (x/a)
2
+(y/b)
2
=1.
(x,y)
a
b
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 5. IDENTICAL PARTICLES 147
G(x, y, λ) ≡ 4xy + λ
(x/a)
2
+(y/b)
2
− 1
.
∂G
∂x
=4y +
2λx
a
2
=0⇒ y = −
λx
2a
2
.
∂G
∂y
=4x +
2λy
b
2
=0⇒ 4x = −
2λ
b
2
−
λx
2a
2
⇒ 4x =
λ
2
a
2
b
2
x ⇒ x = 0 (minimum), or else λ = ±2ab.
So y = ∓
2abx
2a
2
= ∓
b
a
x. We may as well pick x and y positive, (as in the figure); then y =(b/a)x (and
λ = −2ab).
∂G
∂λ
=0⇒
x
a
2
+
y
b
2
= 1 (of course), so
x
2
a
2
+
b
2
x
2
a
2
b
2
=1,or
2
a
2
x
2
=1,orx = a/
√
2, and hence
y = ba/(a
√
2) ⇒ y = b/
√
2. A =4
a
√
2
b
√
2
=
2ab.
Problem 5.27
(a) ln(10!) = ln(3628800) = 15.1044; 10 ln(10) − 10=23.026 − 10=13.0259; 15.1044 − 13.0259 =
2.0785; 2.0785/15.1044 = 0.1376, or
14% .
(b) The percent error is:
ln(z!) − z ln(z)+z
ln(z!)
× 100.
z %
20 5.7
100 0.89
50 1.9
90 0.996
85 1.06
89 1.009
Since my calculator cannot compute factorials greater than 69! I used Mathematica to construct the table.
Evidently, the smallest integer for which the error is < 1% is
90.
Problem 5.28
Equation 5.108 ⇒ N =
V
2π
2
∞
0
k
2
n(9) dk, where n(9) is given (as T → 0) by Eq. 5.104.
So N =
V
2π
2
k
max
0
k
2
dk =
V
2π
2
k
3
max
3
, where k
max
is given by
2
k
2
max
2m
= µ(0) = E
F
⇒ k
max
=
√
2mE
F
.
N =
V
6π
2
3
(2mE
F
)
3/2
. Compare Eq. 5.43, which says
E
F
=
2
2m
3π
2
Nq
V
2/3
, or
(2mE
F
)
3/2
3
=3π
2
Nq
V
, or N =
V
3π
2
q
3
(2mE
F
)
3/2
.
Here q = 1, and Eq. 5.108 needs an extra factor of 2 on the right, to account for spin, so the two formulas agree.
Equation 5.109 ⇒ E
tot
=
V
2
4π
2
m
k
max
0
k
4
dk =
V
2
4π
2
m
k
5
max
5
⇒ E
tot
=
V
20π
2
m
3
(2mE
F
)
5/2
.
Compare Eq. 5.45, which says E
tot
=
V
2
10π
2
m
k
5
max
. Again, Eq. 5.109 for electrons has an extra factor of 2, so
the two agree.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

148 CHAPTER 5. IDENTICAL PARTICLES
Problem 5.29
(a) Equation 5.103, n(9) > 0 ⇒
1
e
(5−µ)/k
B
T
− 1
> 0 ⇒ e
(5−µ)/k
B
T
> 1 ⇒
(9 − µ)
k
B
T
> 0 ⇒
9>µ(T ), for all
allowed energies 9.
(b) For a free particle gas, E =
2
2m
k
2
→ 0 (as k → 0, in the continuum limit), so µ(T ) is always negative.
(Technically, the lowest energy is
2
π
2
2m
1
l
2
x
+
1
l
2
y
+
1
l
2
z
, but we take the dimensions l
x
l
y
l
z
to be very large
in the continuum limit.) Equation 5.108 ⇒ N/V =
1
2π
2
∞
0
k
2
e
(
2
k
2
/2m−µ)/k
B
T
− 1
dk. The integrand is
always positive, and the only T dependence is in µ(T ) and k
B
T . So, as T decreases, (
2
k
2
/2m) − µ(T )
must also decrease, and hence −µ(T ) decreases, or µ(T ) increases (always negative).
(c)
N
V
=
1
2π
2
∞
0
k
2
e
2
k
2
/2mk
B
T
− 1
dk. Let x ≡
2
k
2
2mk
B
T
, so k =
√
2mk
B
T
x
1/2
; dk =
√
2mk
B
T
1
2
x
−1/2
dx.
N
V
=
1
2π
2
2mk
B
T
2
3/2
1
2
∞
0
x
1/2
e
x
− 1
dx, where
∞
0
x
3/2−1
e
x
− 1
dx = Γ(3/2)ζ(3/2).
Now Γ(3/2) =
√
π/2; ζ(3/2) = 2.61238, so
N
V
=2.612
mk
B
T
2π
2
3/2
; T
c
=
2π
2
mk
B
N
2.612V
2/3
.
(d)
N
V
=
mass/volume
mass/atom
=
0.15 × 10
3
kg/m
3
4(1.67 × 10
−27
kg)
=2.2 × 10
28
/m
3
.
T
c
=
2π(1.05 ×10
−34
J · s)
2
4(1.67 × 10
−27
kg)(1.38 × 10
−23
J/K)
2.2 × 10
28
2.61 m
3
2/3
= 3.1 K.
Problem 5.30
(a)
ω =2πν =
2πc
λ
, so dω = −
2πc
λ
2
dλ, and ρ(ω)=
π
2
c
3
(2πc)
3
λ
3
(e
2πc/k
B
Tλ
− 1)
.
ρ(ω)|dω| =8π
1
λ
3
(e
2πc/k
B
Tλ
− 1)
−
2πc
λ
2
dλ
= ρ(λ) dλ ⇒ ρ(λ)=
16π
2
c
λ
5
(e
2πc/k
B
Tλ
− 1)
.
(For density, we want only the size of the interval, not its sign.)
(b) To maximize, set d
ρ/dλ =0:
0=16π
2
c
−5
λ
6
(e
2πc/k
B
Tλ
− 1)
−
e
2πc/k
B
Tλ
(2πc/k
B
T )
λ
5
(e
2πc/k
B
Tλ
− 1)
2
−
1
λ
2
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 5. IDENTICAL PARTICLES 149
1
2 3
4
5
1
2
3
4
5
5-x
5e
-x
⇒ 5(e
2πc/k
B
Tλ
− 1) = e
2πc/k
B
Tλ
2πc
k
B
Tλ
.
Let x ≡ 2πc/k
B
Tλ; then 5(e
x
− 1) = xe
x
; or 5(1 − e
−x
)=x,or5e
−x
=5− x. From the graph, the
solution occurs slightly below x =5.
Mathematica says x =4.966, so
λ
max
=
2πc
(4.966)k
B
1
T
=
(6.626 × 10
−34
J · s)(2.998 × 10
8
m/s)
(4.966)(1.3807 × 10
−23
J/K)
1
T
=
2.897 × 10
−3
m·K/T.
Problem 5.31
From Eq. 5.113:
E
V
=
∞
0
ρ(ω) dω =
π
2
c
3
∞
0
ω
3
(e
ω/k
B
T
− 1)
dω. Let x ≡
ω
k
B
T
. Then
E
V
=
π
2
c
3
k
B
T
4
∞
0
x
3
e
x
− 1
dx =
(k
B
T )
4
π
2
c
3
3
Γ(4)ζ(4) =
(k
B
T )
4
π
2
c
3
3
· 6 ·
π
4
90
=
π
2
k
4
B
15c
3
3
T
4
=
π
2
(1.3807 × 10
−23
J/K)
4
15(2.998 × 10
8
m/s)
3
(1.0546 × 10
−34
J · s)
3
T
4
=7.566 × 10
−16
J
m
3
K
4
T
4
. QED
Problem 5.32
From Problem 2.11(a),
x
0
= x
1
=0; x
2
0
=
2mω
; x
2
1
=
3
2mω
.
From Eq. 3.98,
x
01
=
∞
−∞
xψ
0
(x)ψ
1
(x) dx = 0|x|1 =
2mω
√
1 δ
00
+
√
0 δ
1 −1
=
2mω
.
(a) Equation 5.19 ⇒(x
1
− x
2
)
2
d
=
2mω
+
3
2mω
− 0=
2
mω
.
(b) Equation 5.21 ⇒(x
1
− x
2
)
2
+
=
2
mω
− 2
2mω
=
mω
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

150 CHAPTER 5. IDENTICAL PARTICLES
(c) Equation 5.21 ⇒(x
1
− x
2
)
2
−
=
2
mω
+2
2mω
=
3
mω
.
Problem 5.33
(a) Each particle has 3 possible states: 3 × 3 × 3= 27.
(b) All in same state: aaa, bbb, ccc ⇒ 3.
2 in one state: aab, aac, bba, bbc, cca, ccb ⇒ 6 (each symmetrized).
3 different states: abc (symmetrized) ⇒ 1.
Total:
10.
(c) Only abc (antisymmetrized) =⇒ 1.
Problem 5.34
Equation 5.39 ⇒ E
n
x
n
y
=
π
2
2
2m
'
n
2
x
l
2
x
+
n
2
y
l
2
y
(
=
2
k
2
2m
, with k =
πn
x
l
x
,
πn
y
l
y
. Each state is represented by an
intersection on a grid in “k-space”—this time a plane—and each state occupies an area π
2
/l
x
l
y
= π
2
/A (where
A ≡ l
x
l
y
is the area of the well). Two electrons per state means
1
4
πk
2
F
=
Nq
2
π
2
A
, or k
F
=
2π
Nq
A
1/2
=(2πσ)
1/2
,
where σ ≡ Nq/A is the number of free electrons per unit area.
∴ E
F
=
2
k
2
F
2m
=
2
2m
2πσ =
π
2
σ
m
.
k
k
y
x
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 5. IDENTICAL PARTICLES 151
Problem 5.35
(a)
V =
4
3
πR
3
, so E =
2
(3π
2
Nq)
5/3
10π
2
m
4
3
πR
3
−2/3
=
2
2
15πmR
2
9
4
πNq
5/3
.
(b) Imagine building up a sphere by layers. When it has reached mass m, and radius r, the work necessary
to bring in the next increment dm is: dW = −(Gm/r) dm. In terms of the mass density ρ, m =
4
3
πr
3
ρ,
and dm =4πr
2
drρ, where dr is the resulting increase in radius. Thus:
dW = −G
4
3
πr
3
ρ 4πr
2
ρ
dr
r
= −
16π
2
3
ρ
2
Gr
4
dr,
and the total energy of a sphere of radius R is therefore
E
grav
= −
16π
2
3
ρ
2
G
R
0
r
4
dr = −
16π
2
ρ
2
R
5
15
G. But ρ =
NM
4/3πR
3
, so
E
grav
= −
16π
2
R
5
15
G
9N
2
M
2
16π
2
R
6
= −
3
5
G
N
2
M
2
R
.
(c)
E
tot
=
A
R
2
−
B
R
, where A ≡
2
2
15πm
9
4
πNq
5/3
and B ≡
3
5
GN
2
M
2
.
dE
tot
dR
= −
2A
R
3
+
B
R
2
=0⇒ 2A = BR, so R =
2A
B
=
4
15πm
9
4
πNq
5/3
5
3GN
2
M
2
.
R =
4
9π
9π
4
5/3
N
5/3
N
2
2
GmM
2
q
5/3
=
9π
4
2/3
2
GmM
2
q
5/3
N
1/3
.
R =
9π
4
2/3
(1.055 × 10
−34
J · s)
2
(1/2)
5/3
(6.673 × 10
−11
Nm
2
/kg
2
)(9.109 × 10
−31
kg)(1.674 × 10
−27
kg)
2
N
−1/3
= (7.58 × 10
25
m)N
−1/3
.
(d) Mass of sun: 1.989 × 10
30
kg, so N =
1.989 × 10
30
1.674 × 10
−27
=1.188 × 10
57
; N
−1/3
=9.44 × 10
−20
.
R =(7.58 ×10
25
)(9.44 × 10
−20
)m = 7.16 × 10
6
m (slightly larger than the earth).
(e)
From Eq. 5.43: E
F
=
2
2m
3π
2
Nq
4/3πR
3
2/3
=
2
2mR
2
9π
4
Nq
2/3
. Numerically:
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

152 CHAPTER 5. IDENTICAL PARTICLES
E
F
=
(1.055 × 10
−34
J · s)
2
2(9.109 × 10
−31
kg)(7.16 × 10
6
m)
2
9π
4
(1.188 × 10
57
)
1
2
2/3
=3.102 × 10
−14
J,
or, in electron volts: E
F
=
3.102 × 10
−14
1.602 × 10
−19
eV = 1.94 × 10
5
eV.
E
rest
= mc
2
=5.11 ×10
5
eV, so the Fermi energy (which is the energy of the most energetic electrons) is
comparable to the rest energy, so they are getting fairly relativistic.
Problem 5.36
(a)
dE =(ck)
V
π
2
k
2
dk ⇒ E
tot
=
cV
π
2
k
F
0
k
3
dk =
cV
4π
2
k
4
F
; k
F
=
3π
2
Nq
V
1/3
.
So E
tot
=
c
4π
2
(3π
2
Nq)
4/3
V
−1/3
.
(b)
V =
4
3
πR
3
⇒ E
deg
=
c
4π
2
R
(3π
2
Nq)
4/3
4π
3
−1/3
=
c
3πR
9
4
πNq
4/3
.
Adding in the gravitational energy, from Problem 5.35(b),
E
tot
=
A
R
−
B
R
, where A ≡
c
3π
9
4
πNq
4/3
and B ≡
3
5
GN
2
M
2
.
dE
tot
dR
= −
(A − B)
R
2
=0⇒ A = B,
but there is no special value of R for which E
tot
is minimal. Critical value: A = B(E
tot
=0)⇒
c
3π
9
4
πNq
4/3
=
3
5
GN
2
M
2
,or
N
c
=
15
16
√
5π
c
G
3/2
q
2
M
3
=
15
16
√
5π
1.055 × 10
−34
J · s × 2.998 × 10
8
m/s
6.673 × 10
−11
N · m
2
/kg
2
3/2
(1/2)
2
(1.674 × 10
−27
kg)
3
= 2.04 × 10
57
. (About twice the value for the sun—Problem 5.35(d).)
(c) Same as Problem 5.35(c), with m → M and q → 1, so multiply old answer by (2)
5/3
m/M :
R =2
5/3
(9.109 × 10
−31
)
(1.674 × 10
−27
)
(7.58 × 10
25
m)N
−1/3
=(1.31 × 10
23
m)N
−1/3
. Using N =1.188 × 10
57
,
R =(1.31 × 10
23
m)(9.44 × 10
−20
)=12.4 km. To get E
F
, use Problem 5.35(e) with q = 1, the new R,
and the neutron mass in place of m:
E
F
=2
2/3
7.16 × 10
6
1.24 × 10
4
2
9.11 × 10
−31
1.67 × 10
−27
(1.94 × 10
5
eV) = 5.60 × 10
7
eV = 56.0 MeV.
The rest energy of a neutron is 940 MeV, so a neutron star is reasonably nonrelativistic.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 5. IDENTICAL PARTICLES 153
Problem 5.37
(a) From Problem 4.38: E
n
=(n +
3
2
)ω, with n =0, 1, 2,...; d
n
=
1
2
(n + 1)(n + 2).
From Eq. 5.103, n(9)=e
−(5−µ)/k
B
T
,soN
n
=
1
2
(n + 1)(n +2)e
(µ−
3
2
ω)/k
B
T
e
−nω/k
B
T
.
N =
∞
n=0
N
n
=
1
2
e
(µ−
3
2
ω)/k
B
T
∞
n=0
(n + 1)(n +2)x
n
, where x ≡ e
−ω/k
B
T
. Now
1
1 − x
=
∞
n=0
x
n
⇒
x
1 − x
=
∞
n=0
x
n+1
⇒
d
dx
x
1 − x
=
∞
n=0
(n +1)x
n
⇒
1
(1 − x)
2
=
∞
n=0
(n +1)x
n
.
x
2
(1 − x)
2
=
∞
n=0
(n +1)x
n+2
, and hence
d
dx
x
2
(1 − x)
2
=
∞
n=0
(n + 1)(n +2)x
n+1
=
2x
(1 − x)
3
.
∞
n=0
(n + 1)(n +2)x
n
=
2
(1 − x)
3
. So N = e
µ/k
B
T
e
−
3
2
ω/k
B
T
1
(1 − e
−ω/k
B
T
)
3
.
e
µ/k
B
T
= N (1 − e
−ω/k
B
T
)
3
e
3
2
ω/k
B
T
; µ = k
B
T
ln N + 3 ln(1 − e
−ω/k
B
T
)+
3
2
ω/k
B
T
.
E =
∞
n=0
N
n
E
n
=
1
2
ωe
(µ−
3
2
ω)/k
B
T
∞
n=0
(n +3/2)(n + 1)(n +2)x
n
. From above,
2x
3/2
(1 − x)
3
=
∞
n=0
(n + 1)(n +2)x
n+3/2
⇒
d
dx
2x
3/2
(1 − x)
3
=
∞
n=0
(n +3/2)(n + 1)(n +2)x
n+1/2
, or
∞
n=0
(n +3/2)(n + 1)(n +2)x
n
=
1
x
1/2
d
dx
2x
3/2
(1 − x)
3
=
2
x
1/2
3
2
x
1/2
(1 − x)
3
+
3x
3/2
(1 − x)
4
=
3(1 + x)
(1 − x)
4
.
E =
1
2
ωe
(µ−
3
2
ω)/k
B
T
3(1 + e
−ω/k
B
T
)
(1 − e
−ω/k
B
T
)
4
. But e
(µ−
3
2
ω)/k
B
T
= N (1 − e
−ω/k
B
T
)
3
, so
E =
3
2
Nω
1+e
−ω/k
B
T
1 − e
−ω/k
B
T
.
(b) k
B
T<<ω (low temperature) ⇒ e
−ω/k
B
T
≈ 0, so E ≈
3
2
Nω (µ ≈
3
2
ω). In this limit, all particles
are in the ground state, E
0
=
3
2
ω.
(c) k
B
T>>ω (high temperature) ⇒ e
−ω/k
B
T
≈ 1 − (ω/k
B
T ), so E ≈ 3Nk
B
T
(µ ≈ k
B
T [ln N + 3 ln (ω/k
B
T )]) . The equipartition theorem says E = N #
1
2
k
B
T , where # is the number
of degrees of freedom for each particle. In this case #/2 = 3, or
#=6 (3 kinetic, 3 potential, for each
particle—one of each for each direction in space).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

154 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Chapter 6
Time-Independent Perturbation
Theory
Problem 6.1
(a)
ψ
0
n
(x)=
2
a
sin
nπ
a
x
, so E
1
n
= ψ
0
n
|H
|ψ
0
n
=
2
a
α
a
0
sin
2
nπ
a
x
δ
x −
a
2
dx.
E
1
n
=
2α
a
sin
2
nπ
a
a
2
=
2α
a
sin
2
nπ
2
=
0, if n is even,
2α/a, if n is odd.
For even n the wave function is zero at the location of the perturbation (x = a/2), so it never “feels” H
.
(b) Here n = 1, so we need
ψ
0
m
|H
|ψ
0
1
=
2α
a
sin
mπ
a
x
δ
x −
a
2
sin
π
a
x
dx =
2α
a
sin
mπ
2
sin
π
2
=
2α
a
sin
mπ
2
.
This is zero for even m, so the first three nonzero terms will be m =3,m = 5, and m = 7. Meanwhile,
E
0
1
− E
0
m
=
π
2
2
2ma
2
(1 − m
2
), so
ψ
1
1
=
m=3,5,7,...
(2α/a) sin(mπ/2)
E
0
1
− E
0
m
ψ
0
m
=
2α
a
2ma
2
π
2
2
−1
1 − 9
ψ
0
3
+
1
1 − 25
ψ
0
5
+
−1
1 − 49
ψ
0
7
+ ...
=
4maα
π
2
2
2
a
1
8
sin
3π
a
x
−
1
24
sin
5π
a
x
+
1
48
sin
7π
a
x
+ ...
=
mα
π
2
2
a
2
sin
3π
a
x
−
1
3
sin
5π
a
x
+
1
6
sin
7π
a
x
+ ...
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 155
Problem 6.2
(a) E
n
=(n +
1
2
)ω
, where ω
≡
k(1 + 9)/m = ω
√
1+9 = ω(1 +
1
2
9 −
1
8
9
2
+
1
16
9
3
···), so
E
n
=(n +
1
2
)ω
√
1+9 =(n +
1
2
)ω(1 +
1
2
9 −
1
8
9
2
+ ···).
(b) H
=
1
2
k
x
2
−
1
2
kx
2
=
1
2
kx
2
(1 + 9 − 1) = 9(
1
2
kx
2
)=9V , where V is the unperturbed potential energy. So
E
1
n
= ψ
0
n
|H
|ψ
0
n
= 9n|V |n, with n|V |n the expectation value of the (unperturbed) potential energy
in the n
th
unperturbed state. This is most easily obtained from the virial theorem (Problem 3.31), but it
can also be derived algebraically. In this case the virial theorem says T = V . But T + V = E
n
.So
V =
1
2
E
0
n
=
1
2
(n +
1
2
)ω; E
1
n
=
5
2
(n +
1
2
)ω, which is precisely the 9
1
term in the power series from
part (a).
Problem 6.3
(a) In terms of the one-particle states (Eq. 2.28) and energies (Eq. 2.27):
Ground state
: ψ
0
1
(x
1
,x
2
)=ψ
1
(x
1
)ψ
1
(x
2
)=
2
a
sin
πx
1
a
sin
πx
2
a
;
E
0
1
=2E
1
=
π
2
2
ma
2
.
First excited state: ψ
0
2
(x
1
,x
2
)=
1
√
2
[ψ
1
(x
1
)ψ
2
(x
2
)+ψ
2
(x
1
)ψ
1
(x
2
)]
=
√
2
a
sin
πx
1
a
sin
2πx
2
a
+ sin
2πx
1
a
sin
πx
2
a
;
E
0
2
= E
1
+ E
2
=
5
2
π
2
2
ma
2
.
(b)
E
1
1
= ψ
0
1
|H
|ψ
0
1
=(−aV
0
)
2
a
2
a
0
a
0
sin
2
πx
1
a
sin
2
πx
2
a
δ(x
2
− x
2
) dx
1
dx
2
= −
4V
0
a
a
0
sin
4
πx
a
dx = −
4V
0
a
a
π
π
0
sin
4
ydy= −
4V
0
π
·
3π
8
=
−
3
2
V
0
.
E
1
2
= ψ
0
2
|H
|ψ
0
2
=(−aV
0
)
2
a
2
a
0
sin
πx
1
a
sin
2πx
2
a
+ sin
2πx
1
a
sin
πx
2
a
2
δ(x
1
− x
2
) dx
1
dx
2
= −
2V
0
a
a
0
sin
πx
a
sin
2πx
a
+ sin
2πx
a
sin
πx
a
2
dx
= −
8V
0
a
a
0
sin
2
πx
a
sin
2
2πx
a
dx = −
8V
0
a
·
a
π
π
0
sin
2
y sin
2
(2y) dy
= −
8V
0
π
· 4
π
0
sin
2
y sin
2
y cos
2
ydy= −
32V
0
π
π
0
(sin
4
y − sin
6
y) dy
= −
32V
0
π
3π
8
−
5π
16
=
−2V
0
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
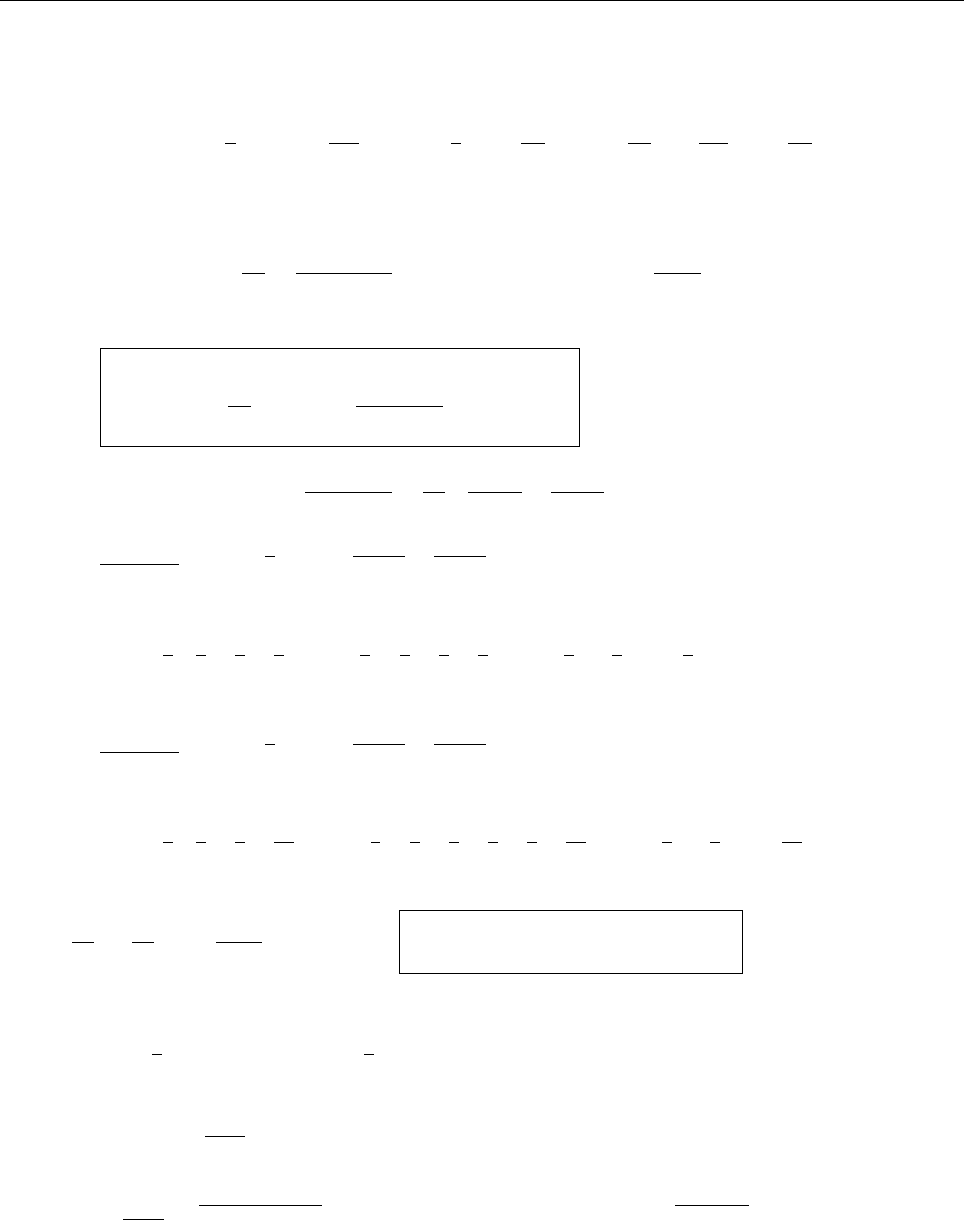
156 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Problem 6.4
(a)
ψ
0
m
|H|ψ
0
n
=
2
a
α
a
0
sin
mπ
a
x
δ
x −
a
2
sin
nπ
a
x
dx =
2α
a
sin
mπ
2
sin
nπ
2
,
which is zero unless both m and n are odd—in which case it is ±2α/a. So Eq. 6.15 says
E
2
n
=
m=n, odd
2α
a
2
1
(E
0
n
− E
0
m
)
. But Eq. 2.27 says E
0
n
=
π
2
2
2ma
2
n
2
, so
E
2
n
=
0, if n is even;
2m
2α
π
2
m=n, odd
1
(n
2
− m
2
)
, if n is odd.
To sum the series, note that
1
(n
2
− m
2
)
=
1
2n
1
m + n
−
1
m − n
. Thus,
for n =1
:
=
1
2
3,5,7,...
1
m +1
−
1
m − 1
=
1
2
1
4
+
1
6
+
1
8
+ ···−
1
2
−
1
4
−
1
6
−
1
8
···
=
1
2
−
1
2
= −
1
4
;
for n =3
:
=
1
6
1,5,7,...
1
m +3
−
1
m − 3
=
1
6
1
4
+
1
8
+
1
10
+ ···+
1
2
−
1
2
−
1
4
−
1
6
−
1
8
−
1
10
···
=
1
6
−
1
6
= −
1
36
.
In general, there is perfect cancellation except for the “missing” term 1/2n in the first sum, so the total
is
1
2n
−
1
2n
= −
1
(2n)
2
. Therefore: E
2
n
=
0, if n is even;
−2m (α/πn)
2
, if n is odd.
(b)
H
=
1
2
9kx
2
; ψ
0
m
|H
|ψ
0
n
=
1
2
9km|x
2
|n. Using Eqs. 2.66 and 2.69:
m|x
2
|n =
2mω
m|(a
2
+
+ a
+
a
−
+ a
−
a
+
+ a
2
−
)|n
=
2mω
(n + 1)(n +2)m|n +2 + nm|n +(n +1)m|n +
n(n − 1)m|n − 2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 157
So, for m = n, ψ
0
m
|H
|ψ
0
n
=
1
2
k9
2mω
(n + 1)(n +2)δ
m,n+2
+
n(n − 1) δ
m,n−2
.
E
2
n
=
9ω
4
2
m=n
(n + 1)(n +2)δ
m,n+2
+
n(n − 1) δ
m,n−2
2
(n +
1
2
)ω − (m +
1
2
)ω
=
9
2
ω
16
m=n
[(n + 1)(n +2)δ
m,n+2
+ n(n − 1) δ
m,n−2
]
(n − m)
=
9
2
ω
16
(n + 1)(n +2)
n − (n +2)
+
n(n − 1)
n − (n − 2)
=
9
2
ω
16
−
1
2
(n + 1)(n +2)+
1
2
n(n − 1)
=
9
2
ω
32
−n
2
− 3n − 2+n
2
− n
=
9
2
ω
32
(−4n − 2) =
−9
2
1
8
ω
n +
1
2
(which agrees with the 9
2
term in the exact solution—Problem 6.2(a)).
Problem 6.5
(a)
E
1
n
= ψ
0
n
|H
|ψ
0
n
= −qEn|x|n = 0 (Problem 2.12).
From Eq. 6.15 and Problem 3.33: E
2
n
=(qE)
2
m=n
|m|x|n|
2
(n − m)ω
=
(qE)
2
ω
2mω
m=n
[
√
n +1δ
m,n+1
+
√
n, δ
m,n−1
]
2
(n − m)
=
(qE)
2
2mω
2
m=n
[(n +1)δ
m,n+1
+ nδ
m,n−1
]
(n − m)
=
(qE)
2
2mω
2
(n +1)
n − (n +1)
+
n
n − (n − 1)
=
(qE)
2
2mω
2
[−(n +1)+n]= −
(qE)
2
2mω
2
.
(b) −
2
2m
d
2
ψ
dx
2
+
1
2
mω
2
x
2
− qEx
ψ = Eψ. With the suggested change of variables,
1
2
mω
2
x
2
− qEx
=
1
2
mω
2
x
+
qE
mω
2
2
− qE
x
+
qE
mω
2
=
1
2
mω
2
x
2
+ mω
2
x
qE
mω
2
+
1
2
mω
2
(qE)
2
m
2
ω
4
− qEx
−
(qE)
2
mω
2
=
1
2
mω
2
x
2
−
1
2
(qE)
2
mω
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

158 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
So the Schr¨odinger equation says
−
2
2m
d
2
ψ
dx
2
+
1
2
mω
2
x
2
ψ =
E +
1
2
(qE)
2
mω
2
ψ,
which is the Schr¨odinger equation for a simple harmonic oscillator, in the variable x
. The constant on
the right must therefore be (n +
1
2
)ω, and we conclude that
E
n
=(n +
1
2
)ω −
1
2
(qE)
2
mω
2
.
The subtracted term is exactly what we got in part (a) using perturbation theory. Evidently all the higher
corrections (like the first-order correction) are zero, in this case.
Problem 6.6
(a)
ψ
0
+
|ψ
0
−
= (α
+
ψ
0
a
+ β
+
ψ
0
b
)|(α
−
ψ
0
a
+ β
−
ψ
0
b
)
= α
∗
+
α
−
ψ
0
a
|ψ
0
a
+ α
∗
+
β
−
ψ
0
a
|ψ
0
b
+ β
∗
+
α
−
ψ
0
b
|ψ
0
a
+ β
∗
+
β
−
ψ
0
b
|ψ
0
b
= α
∗
+
α
−
+ β
∗
+
β
−
. But Eq. 6.22 ⇒ β
±
= α
±
(E
1
±
− W
aa
)/W
ab
, so
ψ
0
+
|ψ
0
−
= α
∗
+
α
−
1+
(E
1
+
− W
aa
)(E
1
−
− W
aa
)
W
ab
∗
W
ab
=
α
∗
+
α
−
|W
ab
|
2
|W
ab
|
2
+(E
1
+
− W
aa
)(E
1
−
− W
aa
)
.
The term in square brackets is:
[]=E
1
+
E
1
−
− W
aa
(E
1
+
+ E
1
−
)+|W
ab
|
2
+ W
2
aa
. But Eq. 6.27 ⇒ E
1
±
=
1
2
[(W
aa
+ W
bb
) ±
√
], where
√
is
shorthand for the square root term. So E
1
+
+ E
1
−
= W
aa
+ W
bb
, and
E
1
+
E
1
−
=
1
4
(W
aa
+ W
bb
)
2
− (
√
)
2
=
1
4
(W
aa
+ W
bb
)
2
− (W
aa
− W
bb
)
2
− 4|W
ab
|
2
= W
aa
W
bb
−|W
ab
|
2
.
Thus [ ] = W
aa
W
bb
−|W
ab
|
2
− W
aa
(W
aa
+ W
bb
)+|W
ab
|
2
+ W
2
aa
=0, so ψ
0
+
|ψ
0
−
=0. QED
(b)
ψ
0
+
|H
|ψ
0
−
= α
∗
+
α
−
ψ
0
a
|H
|ψ
0
a
+ α
∗
+
β
−
ψ
0
a
|H
|ψ
0
b
+ β
∗
+
α
−
ψ
0
b
|H
|ψ
0
a
+ β
∗
+
β
−
ψ
0
b
|H
|ψ
0
b
= α
∗
+
α
−
W
aa
+ α
∗
+
β
−
W
ab
+ β
∗
+
α
−
W
ba
+ β
∗
+
β
−
W
bb
= α
∗
+
α
−
W
aa
+ W
ab
(E
1
−
− W
aa
)
W
ab
+ W
ba
(E
1
+
− W
aa
)
W
∗
ab
+ W
bb
(E
1
+
− W
aa
)
W
∗
ab
(E
1
−
− W
aa
)
W
ab
= α
∗
+
α
−
W
aa
+ E
1
−
− W
aa
+ E
1
+
− W
aa
+ W
bb
(E
1
+
− W
aa
)(E
1
−
− W
aa
)
|W
ab
|
2
.
But we know from (a) that
(E
1
+
− W
aa
)(E
1
−
− W
aa
)
|W
ab
|
2
= −1, so
ψ
0
+
|H
|ψ
0
−
= α
∗
+
α
−
[E
1
−
+ E
1
+
− W
aa
− W
bb
]=0. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
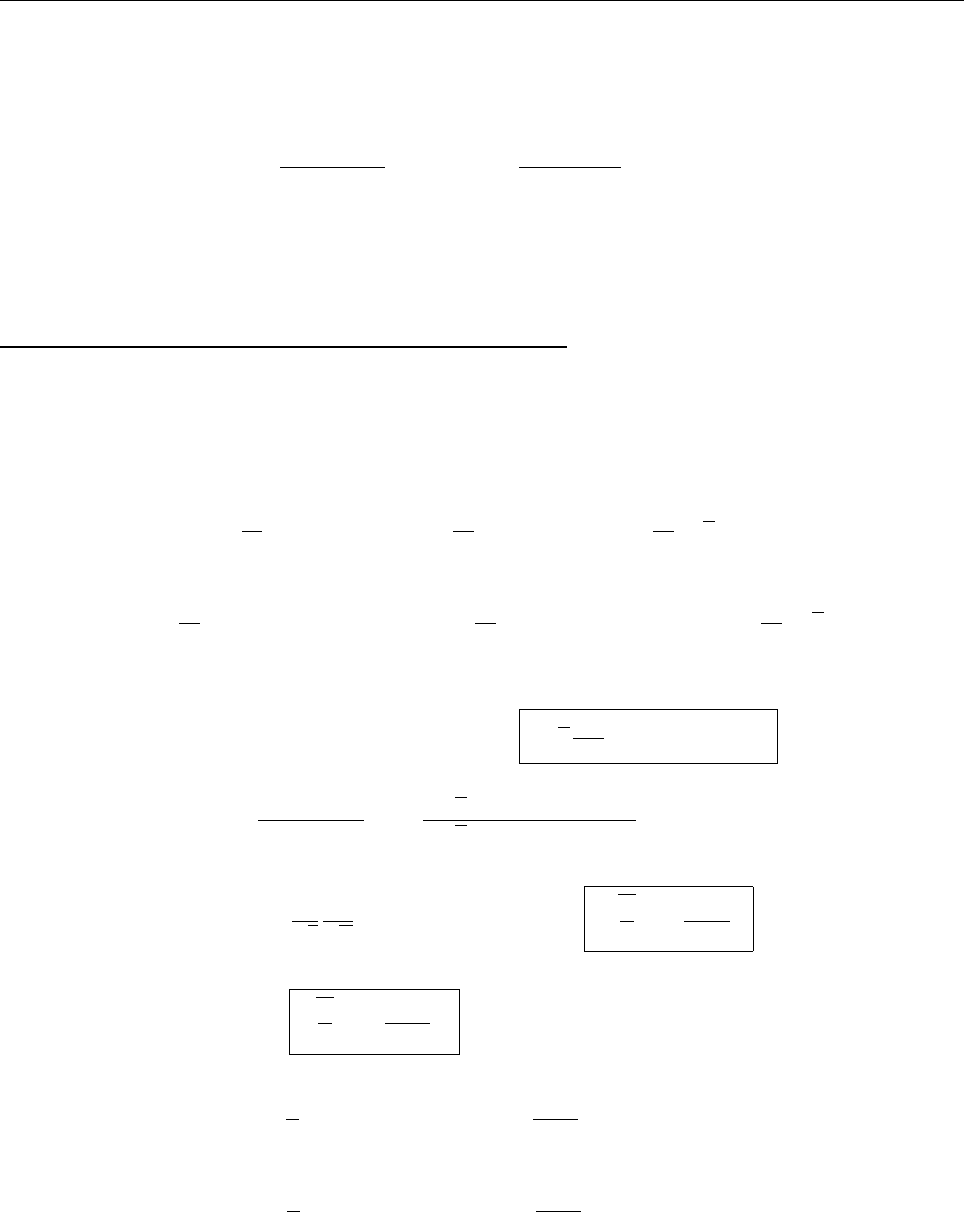
CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 159
(c)
ψ
0
±
|H
|ψ
0
±
= α
∗
±
α
±
ψ
0
a
|H
|ψ
0
a
+ α
∗
±
β
±
ψ
0
a
|H
|ψ
0
b
+ β
∗
±
α
±
ψ
0
b
|H
|ψ
0
a
+ β
∗
±
β
±
ψ
0
b
|H
|ψ
0
b
= |α
±
|
2
W
aa
+ W
ab
(E
1
±
− W
aa
)
W
ab
+ |β
±
|
2
W
ba
(E
1
±
− W
bb
)
W
ba
+ W
bb
(this time I used Eq. 6.24 to express α in terms of β, in the third term).
∴ ψ
0
±
|H
|ψ
0
±
= |α
±
|
2
(E
1
±
)+|β
±
|
2
(E
1
±
)=
|α
±
|
2
+ |β
±
|
2
E
1
±
= E
1
±
. QED
Problem 6.7
(a) See Problem 2.46.
(b) With a → n, b →−n, we have:
W
aa
= W
bb
= −
V
0
L
L/2
−L/2
e
−x
2
/a
2
dx ≈−
V
0
L
∞
−∞
e
−x
2
/a
2
dx = −
V
0
L
a
√
π.
W
ab
= −
V
0
L
L/2
−L/2
e
−x
2
/a
2
e
−4πnix/L
dx ≈−
V
0
L
∞
−∞
e
−(x
2
/a
2
+4πnix/L)
dx = −
V
0
L
a
√
πe
−(2πna/L)
2
.
(We did this integral in Problem 2.22.) In this case W
aa
= W
bb
, and W
ab
is real, so Eq. 6.26 ⇒
E
1
±
= W
aa
±|W
ab
|, or E
1
±
= −
√
π
V
0
a
L
1 ∓ e
−(2πna/L)
2
.
(c) Equation 6.22 ⇒ β = α
(E
1
−
− W
aa
)
W
ab
= α
±
√
π(V
0
a/L)e
−(2πna/L)
2
−
√
π(V
0
a/L)e
−(2πna/L)
2
= ∓α. Evidently, the “good” linear
combinations are:
ψ
+
= αψ
n
− αψ
−n
=
1
√
2
1
√
L
e
i2πnx/L
− e
−i2πnx/L
=
i
2
L
sin
2πnx
L
and
ψ
−
= αψ
n
+ αψ
−n
=
2
L
cos
2πnx
L
.
Using Eq. 6.9, we have :
E
1
+
= ψ
+
|H
|ψ
+
=
2
L
(−V
0
)
L/2
−L/2
e
−x
2
/a
2
sin
2
2πnx
L
dx,
E
1
−
= ψ
−
|H
|ψ
−
=
2
L
(−V
0
)
L/2
−L/2
e
−x
2
/a
2
cos
2
2πnx
L
dx.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

160 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
But sin
2
θ =(1−cos 2θ)/2, and cos
2
θ = (1 + cos 2θ)/2, so
E
1
±
≈−
V
0
L
∞
−∞
e
−x
2
/a
2
1 ∓ cos
4πnx
L
dx = −
V
0
L
∞
−∞
e
−x
2
/a
2
dx ∓
∞
−∞
e
−x
2
/a
2
cos
4πnx
L
dx
= −
V
0
L
√
πa∓ a
√
πe
−(2πna/L)
2
= −
√
π
V
0
a
L
1 ∓ e
−(2πna/L)
2
, same as (b).
(d) Af(x)=f(−x) (the parity operator). The eigenstates are even functions (with eigenvalue +1) and odd
functions (with eigenvalue −1). The linear combinations we found in (c) are precisely the odd and even
linear combinations of ψ
n
and ψ
−n
.
Problem 6.8
Ground state is nondegenerate; Eqs. 6.9 and 6.31 ⇒
E
1
=
2
a
3
a
3
V
0
a
0
sin
2
π
a
x
sin
2
π
a
y
sin
2
π
a
z
δ(x −
a
4
)δ(y −
a
2
)δ(z −
3a
4
) dx dy dz
=8V
0
sin
2
π
4
sin
2
π
2
sin
2
3π
4
=8V
0
1
2
(1)
1
2
=
2V
0
.
First excited states (Eq. 6.34):
W
aa
=8V
0
sin
2
π
a
x
sin
2
π
a
y
sin
2
2π
a
z
δ(x −
a
4
)δ(y −
a
2
)δ(z −
3a
4
) dx dy dz
=8V
0
1
2
(1)(1) = 4V
0
.
W
bb
=8V
0
sin
2
π
a
x
sin
2
2π
a
y
sin
2
π
a
z
δ(x −
a
4
)δ(y −
a
2
)δ(z −
3a
4
) dx dy dz
=8V
0
1
2
(0)
1
2
=0.
W
cc
=8V
0
sin
2
2π
a
x
sin
2
π
a
y
sin
2
π
a
z
δ(x −
a
4
)δ(y −
a
2
)δ(z −
3a
4
) dx dy dz
=8V
0
(1)(1)
1
2
=4V
0
.
W
ab
=8V
0
sin
2
π
4
sin
π
2
sin(π) sin
3π
2
sin
3π
4
=0.
W
ac
=8V
0
sin
π
4
sin
π
2
sin
2
π
2
sin
3π
2
sin
3π
4
=8V
0
1
√
2
(1)(1)(−1)
1
√
2
= −4V
0
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
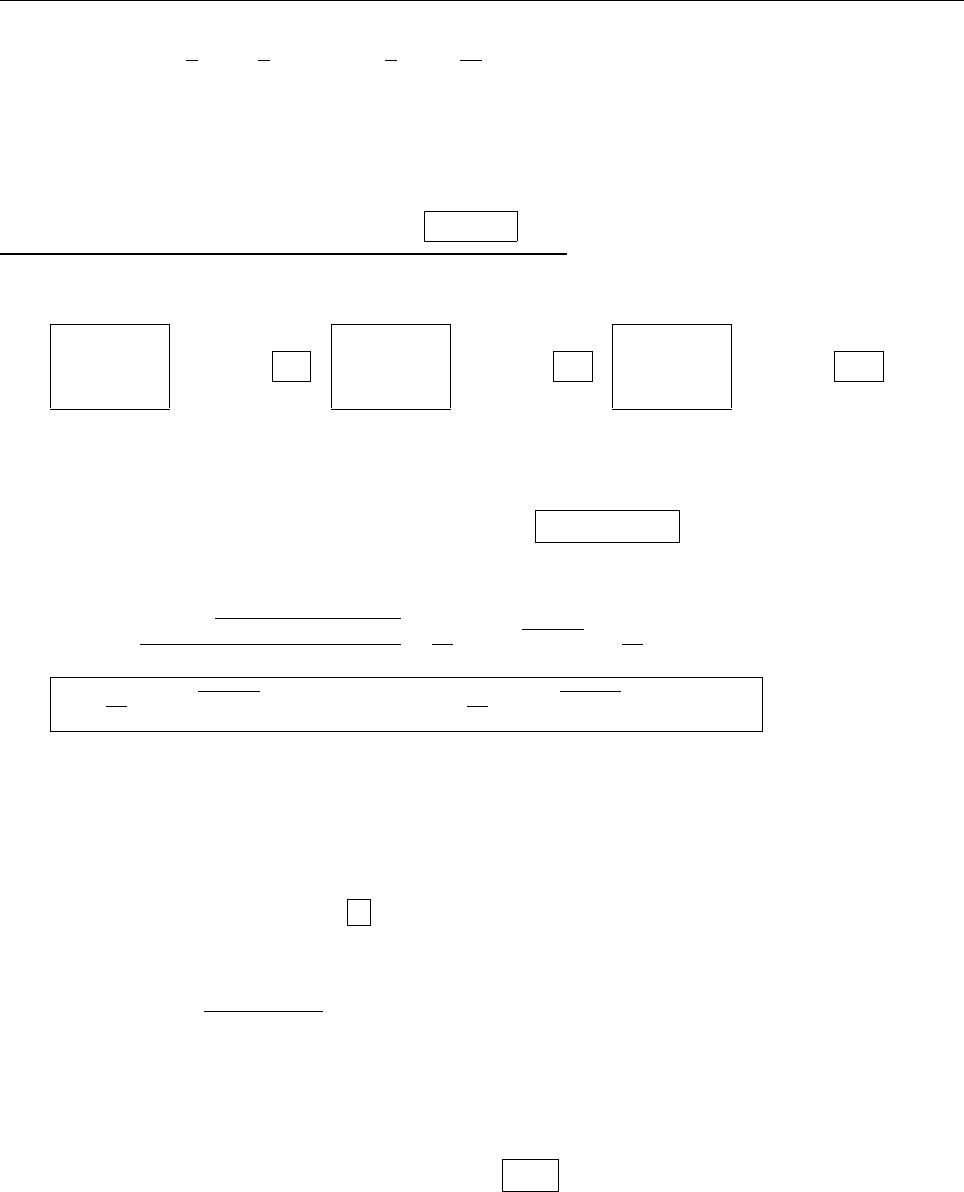
CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 161
W
bc
=8V
0
sin
π
4
sin
π
2
sin(π) sin
π
2
sin
3π
4
=0.
W =4V
0
10−1
000
−10 1
=4V
0
D; det(D − λ)=
(1 − λ)0 −1
0 −λ 0
−10(1− λ)
= −λ(1 − λ)
2
+ λ =0 ⇒
λ =0, or (1 − λ)
2
=1⇒ 1 − λ = ±1 ⇒ λ =0 or λ =2.
So the first-order corrections to the energies are
0, 0, 8V
0
.
Problem 6.9
(a) χ
1
=
1
0
0
, eigenvalue V
0
; χ
2
=
0
1
0
, eigenvalue V
0
; χ
3
=
0
0
1
, eigenvalue 2V
0
.
(b) Characteristic equation: det(H − λ)=
[V
0
(1 − 9) − λ]0 0
0[V
0
− λ] 9V
0
0 9V
0
[2V
0
− λ]
=0;
[V
0
(1 − 9) − λ][(V
0
− λ)(2V
0
− λ) − (9V
0
)
2
]=0⇒ λ
1
= V
0
(1 − 9).
(V
0
− λ)(2V
0
− λ) − (9V
0
)
2
=0⇒ λ
2
− 3V
0
λ +(2V
2
0
− 9
2
V
2
0
)=0⇒
λ =
3V
0
±
9V
2
0
− 4(2V
2
0
− 9
2
V
2
0
)
2
=
V
0
2
3 ±
1+49
2
≈
V
0
2
3 ± (1+29
2
)
.
λ
2
=
V
0
2
3 −
1+49
2
≈ V
0
(1 − 9
2
); λ
3
=
V
0
2
3+
1+49
2
≈ V
0
(2 + 9
2
).
(c)
H
= 9V
0
−100
001
010
; E
1
3
= χ
3
|H
|χ
3
= 9V
0
001
−100
001
010
0
0
1
= 9V
0
001
0
1
0
=
0 (no first-order correction).
E
2
3
=
m=1,2
|χ
m
|H
|χ
3
|
2
E
0
3
− E
0
m
; χ
1
|H
|χ
3
= 9V
0
100
−100
001
010
0
0
1
= 9V
0
100
0
1
0
=0,
χ
2
|H
|χ
3
= 9V
0
010
0
0
1
= 9V
0
.
E
0
3
− E
0
2
=2V
0
− V
0
= V
0
.SoE
2
3
=(9V
0
)
2
/V
0
= 9
2
V
0
. Through second-order, then,
E
3
= E
0
3
+ E
1
3
+ E
2
3
=2V
0
+0+9
2
V
0
= V
0
(2 + 9
2
) (same as we got for λ
3
in (b)).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

162 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
(d)
W
aa
= χ
1
|H
|χ
1
= 9V
0
100
−100
001
010
1
0
0
= 9V
0
100
−1
0
0
= −9V
0
.
W
bb
= χ
2
|H
|χ
2
= 9V
0
010
−100
001
010
0
1
0
= 9V
0
010
0
0
1
=0.
W
ab
= χ
1
|H
|χ
2
= 9V
0
100
−100
001
010
0
1
0
= 9V
0
100
0
0
1
=0.
Plug the expressions for W
aa
, W
bb
, and W
ab
into Eq. 6.27:
E
1
±
=
1
2
−9V
0
+0±
9
2
V
2
0
+0
=
1
2
(−9V
0
± 9V
0
)={0, −9V
0
}.
To first-order, then,
E
1
= V
0
− 9V
0
,E
2
= V
0
, and these are consistent (to first order in 9) with what
we got in (b).
Problem 6.10
Given a set of orthonornal states {ψ
0
j
} that are degenerate eigenfunctions of the unperturbed Hamiltonian:
Hψ
0
j
= E
0
ψ
0
j
, ψ
0
j
|ψ
0
l
= δ
jl
,
construct the general linear combination,
ψ
0
=
n
j=1
α
j
ψ
0
j
.
It too is an eigenfunction of the unperturbed Hamiltonian, with the same eigenvalue:
H
0
ψ
0
=
n
j=1
α
j
H
0
ψ
0
j
= E
0
n
j=1
α
j
ψ
0
j
= E
0
ψ
0
.
We want to solve the Schr¨odinger equation Hψ = Eψ for the perturbed Hamiltonian H = H
0
+ λH
.
Expand the eigenvalues and eigenfunctions as power series in λ:
E = E
0
+ λE
1
+ λ
2
E
2
+ ... , ψ = ψ
0
+ λψ
1
+ λ
2
ψ
2
+ ... .
Plug these into the Schr¨odinger equation and collect like powers:
(H
0
+ λH
)(ψ
0
+ λψ
1
+ λ
2
ψ
2
+ ...)=(E
0
+ λE
1
+ λ
2
E
2
+ ...)(ψ
0
+ λψ
1
+ λ
2
ψ
2
+ ...) ⇒
H
0
ψ
0
+ λ(H
0
ψ
1
+ H
ψ
0
)+...= E
0
ψ
0
+ λ(E
0
ψ
1
+ E
1
ψ
0
)+...
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
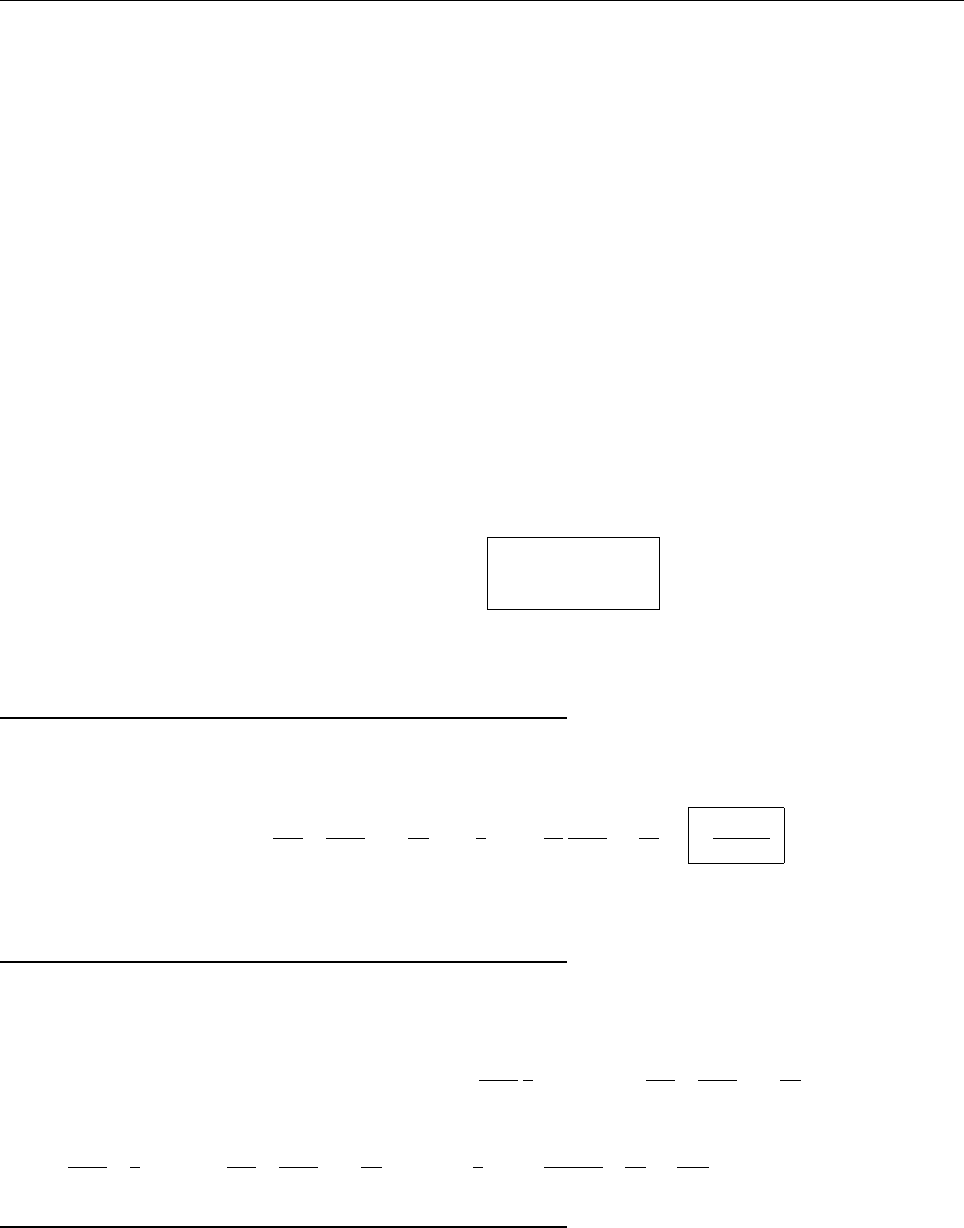
CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 163
The zeroth-order terms cancel; to first order
H
0
ψ
1
+ H
ψ
0
= E
0
ψ
1
+ E
1
ψ
0
.
Take the inner product with ψ
0
j
:
ψ
0
j
|H
0
ψ
1
+ ψ
0
j
|H
ψ
0
= E
0
ψ
0
j
|ψ
1
+ E
1
ψ
0
j
|ψ
0
.
But ψ
0
j
|H
0
ψ
1
= H
0
ψ
0
j
|ψ
1
= E
0
ψ
0
j
|ψ
1
, so the first terms cancel, leaving
ψ
0
j
|H
ψ
0
= E
1
ψ
0
j
|ψ
0
.
Now use ψ
0
=
n
l=1
α
l
ψ
0
l
, and exploit the orthonormality of {ψ
0
l
}:
n
l=1
α
l
ψ
0
j
|H
|ψ
0
l
= E
1
n
l=1
α
l
ψ
0
j
|ψ
0
l
= E
1
α
j
,
or, defining
W
jl
≡ψ
0
j
|H
|ψ
0
l
,
n
l=1
W
jl
α
l
= E
1
α
l
.
This (the generalization of Eq. 6.22 for the case of n-fold degeneracy) is the eigenvalue equation for the matrix
W (whose jl
th
element, in the {ψ
0
j
} basis, is W
jl
); E
1
is the eigenvalue, and the eigenvector (in the {ψ
0
j
} basis)
is χ
j
= α
j
. Conclusion: The first-order corrections to the energy are the eigenvalues of W. QED
Problem 6.11
(a) From Eq. 4.70: E
n
= −
m
2
2
e
2
4π9
0
2
1
n
2
= −
1
2
mc
2
1
c
e
2
4π9
0
2
1
n
2
= −
α
2
mc
2
2n
2
.
(b) I have found a wonderful solution—unfortunately, there isn’t enough room on this page for the proof.
Problem 6.12
Equation 4.191 ⇒V =2E
n
, for hydrogen. V = −
e
2
4π9
0
1
r
; E
n
= −
m
2
2
e
2
4π9
0
2
1
n
2
.So
−
e
2
4π9
0
0
1
r
1
= −2
m
2
2
e
2
4π9
0
2
1
n
2
⇒
0
1
r
1
=
me
2
4π9
0
2
1
n
2
=
1
an
2
(Eq. 4.72). QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

164 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Problem 6.13
In Problem 4.43 we found (for n =3,l =2,m = 1) that r
s
=
(s + 6)!
6!
3a
2
s
.
s =0
: 1 =
6!
6!
(1) =
1 (of course).
s = −1
:
0
1
r
1
=
5!
6!
3a
2
−1
=
1
6
·
2
3a
=
1
9a
Eq. 6.55 says
1
3
2
a
=
1
9a
.
s = −2
:
0
1
r
2
1
=
4!
6!
3a
2
−2
=
1
6 · 5
·
4
9a
2
=
2
135a
2
Eq. 6.56 says
1
(5/2) · 27 · a
2
=
2
135a
2
.
s = −3
:
0
1
r
3
1
=
3!
6!
3a
2
−3
=
1
6 · 5 · 4
·
8
27a
3
=
1
405a
3
Eq. 6.64 says
1
2(5/2)3 · 27 · a
3
=
1
405a
3
.
For s = −7 (or smaller) the integral does not converge: 1/r
7
= ∞ in this state; this is reflected in the fact
that (−1)! = ∞.
Problem 6.14
Equation 6.53 ⇒ E
1
r
= −
1
2mc
2
E
2
− 2EV + V
2
. Here E =(n +
1
2
)ω, V =
1
2
mω
2
x
2
⇒
E
1
r
= −
1
2mc
2
n +
1
2
2
2
ω
2
− 2
n +
1
2
ω
1
2
mω
2
x
2
+
1
4
m
2
ω
4
x
4
.
But Problem 2.12 ⇒x
2
=(n +
1
2
)
mω
, so
E
1
r
= −
1
2mc
2
n +
1
2
2
2
ω
2
−
n +
1
2
2
2
ω
2
+
1
4
m
2
ω
4
x
4
= −
mω
4
8c
2
x
4
.
From Eq. 2.69: x
4
=
2
4m
2
ω
2
a
2
+
+ a
+
a
−
+ a
−
a
+
+ a
2
−
a
2
+
+ a
+
a
−
+ a
−
a
+
+ a
2
−
,
x
4
=
2
4m
2
ω
2
n|
a
2
+
a
2
−
+ a
+
a
−
a
+
a
−
+ a
+
a
−
a
−
a
+
+ a
−
a
+
a
+
a
−
+ a
−
a
+
a
−
a
+
+ a
2
−
a
2
+
|n.
(Note that only terms with equal numbers of raising and lowering operators will survive). Using Eq. 2.66,
x
4
=
2
4m
2
ω
2
n|
a
2
+
n(n − 1) |n −2
+ a
+
a
−
(n |n)+a
+
a
−
(n +1)|n
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 165
+a
−
a
+
(n |n)+a
−
a
+
(n +1)|n
+ a
2
−
(n + 1)(n +2)|n +2
=
2
4m
2
ω
2
n|
n(n − 1)
n(n − 1) |n
+ n (n |n)+(n +1)(n |n)
+n
(n +1)|n
+(n +1)
(n +1)|n
+
(n + 1)(n +2)
(n + 1)(n +2)|n
=
2
4m
2
ω
2
n(n − 1) + n
2
+(n +1)n + n(n +1)+(n +1)
2
+(n + 1)(n +2)
=
2mω
2
(n
2
− n + n
2
+ n
2
+ n + n
2
+ n + n
2
+2n +1+n
2
+3n +2)=
2mω
2
(6n
2
+6n +3).
E
1
r
= −
mω
4
8c
2
·
2
4m
2
ω
2
· 3(3n
2
+2n +1)= −
3
32
2
ω
2
mc
2
(2n
2
+2n + 1).
Problem 6.15
Quoting the Laplacian in spherical coordinates (Eq. 4.13), we have, for states with no dependence on θ or φ:
p
2
= −
2
∇
2
= −
2
r
2
d
dr
r
2
d
dr
.
Question: Is it Hermitian?
Using integration by parts (twice), and test functions f(r) and g(r):
f|p
2
g = −
2
∞
0
f
1
r
2
d
dr
r
2
dg
dr
4πr
2
dr = −4π
2
∞
0
f
d
dr
r
2
dg
dr
dr
= −4π
2
r
2
f
dg
dr
∞
0
−
∞
0
r
2
df
dr
dg
dr
dr
= −4π
2
r
2
f
dg
dr
∞
0
− r
2
g
df
dr
∞
0
+
∞
0
d
dr
r
2
df
dr
gdr
= −4π
2
r
2
f
dg
dr
− r
2
g
df
dr
∞
0
+ p
2
f|g.
The boundary term at infinity vanishes for functions f(r) and g(r) that go to zero exponentially; the boundary
term at zero is killed by the factor r
2
, as long as the functions (and their derivatives) are finite. So
f|p
2
g = p
2
f|g,
and hence p
2
is Hermitian.
Now we apply the same argument to
p
4
=
4
r
2
d
dr
r
2
d
dr
1
r
2
d
dr
r
2
d
dr
,
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
166 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
integrating by parts four times:
f|p
4
g =4π
4
∞
0
f
d
dr
r
2
d
dr
1
r
2
d
dr
r
2
dg
dr
dr
=4π
4
r
2
f
d
dr
1
r
2
d
dr
r
2
dg
dr
∞
0
−
∞
0
r
2
df
dr
d
dr
1
r
2
d
dr
r
2
dg
dr
dr
=4π
4
r
2
f
d
dr
1
r
2
d
dr
r
2
dg
dr
−
df
dr
d
dr
r
2
dg
dr
∞
0
+
∞
0
1
r
2
d
dr
r
2
df
dr
d
dr
r
2
dg
dr
dr
=4π
4
r
2
f
d
dr
1
r
2
d
dr
r
2
dg
dr
−
df
dr
d
dr
r
2
dg
dr
+
d
dr
r
2
df
dr
dg
dr
∞
0
−
∞
0
r
2
d
dr
1
r
2
d
dr
r
2
df
dr
dg
dr
dr
=4π
4
r
2
f
d
dr
1
r
2
d
dr
r
2
dg
dr
−
df
dr
d
dr
r
2
dg
dr
+
d
dr
r
2
df
dr
dg
dr
− r
2
g
d
dr
1
r
2
d
dr
r
2
df
dr
∞
0
+
∞
0
d
dr
r
2
d
dr
1
r
2
d
dr
r
2
df
dr
gdr
=4π
4
r
2
f
d
dr
1
r
2
d
dr
r
2
dg
dr
− r
2
g
d
dr
1
r
2
d
dr
r
2
df
dr
∞
0
− 4π
4
df
dr
d
dr
r
2
dg
dr
−
d
dr
r
2
df
dr
dg
dr
∞
0
+ p
4
f|g
This time there are four boundary terms to worry about. Infinity is no problem; the trouble comes at r =0.
If the functions f and g went to zero at the origin (as they do for states with l>0) we’d be OK, but states
with l = 0 go like exp(−r/na). So let’s test the boundary terms using
f(r)=e
−r/na
,g(r)=e
−r/ma
.
In this case
r
2
dg
dr
= −
1
ma
r
2
e
−r/ma
d
dr
r
2
dg
dr
=
1
(ma)
2
r
2
− 2mar
e
−r/ma
df
dr
d
dr
r
2
dg
dr
= −
1
na
e
−r/na
1
(ma)
2
r
2
− 2mar
e
−r/ma
.
This goes to zero as r → 0, so the second pair of boundary terms vanishes—but not the first pair:
1
r
2
d
dr
r
2
dg
dr
=
1
(ma)
2
1 −
2ma
r
e
−r/ma
d
dr
1
r
2
d
dr
r
2
dg
dr
=
1
(ma)
3
r
2
2(ma)
2
+2mar − r
2
e
−r/ma
r
2
f
d
dr
1
r
2
d
dr
r
2
dg
dr
=
1
(ma)
3
2(ma)
2
+2mar − r
2
e
−r/ma
e
−r/na
This does not vanish as r → 0; rather, it goes to 2/ma. For these particular states, then,
f|p
4
g =
8π
4
a
1
m
−
1
n
+ p
4
f|g,
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 167
or, tacking on the normalization factor,
ψn00 =
1
√
π (na)
3/2
e
−r/na
, ψ
n00
|p
4
ψ
m00
=
8
4
a
4
(n − m)
(nm)
5/2
+ p
4
ψ
n00
|ψ
m00
,
and hence p
4
is not Hermitian, for such states.
Problem 6.16
(a)
[L · S,L
x
]=[L
x
S
x
+ L
y
S
y
+ L
z
S
z
,L
x
]=S
x
[L
x
,L
x
]+S
y
[L
y
,L
x
]+S
z
[L
z
,L
x
]
= S
x
(0) + S
y
(−iL
z
)+S
z
(iL
y
)=i(L
y
S
z
− L
z
S
y
)=i(L × S)
x
.
Same goes for the other two components, so
[L · S, L]=i(L ×S).
(b) [L · S, S] is identical, only with L ↔ S: [L · S, S]=i(S ×L).
(c) [L · S, J]=[L ·S, L]+[L ·S, S]=i(L × S + S × L)= 0.
(d) L
2
commutes with all components of L (and S),so
L · S,L
2
=0.
(e) Likewise,
L · S,S
2
=0.
(f)
L · S,J
2
=
L · S,L
2
+
L · S,S
2
+2[L · S, L · S]=0+0+0=⇒
L · S,J
2
=0.
Problem 6.17
With the plus sign, j = l +1/2(l = j − 1/2) : Eq. 6.57 ⇒ E
1
r
= −
(E
n
)
2
2mc
2
4n
j
− 3
.
Equation 6.65 ⇒ E
1
so
=
(E
n
)
2
mc
2
n
j(j +1)− (j −
1
2
)(j +
1
2
) −
3
4
(j −
1
2
)j(j +
1
2
)
=
(E
n
)
2
mc
2
n(j
2
+ j − j
2
+
1
4
−
3
4
)
(j −
1
2
)j(j +
1
2
)
=
(E
n
)
2
mc
2
n
j(j +
1
2
)
.
E
1
fs
= E
1
r
+ E
1
so
=
(E
n
)
2
2mc
2
−
4n
j
+3+
2n
j(j +
1
2
)
=
(E
n
)
2
2mc
2
3+
2n
j(j +
1
2
)
1 − 2
j +
1
2
=
(E
n
)
2
2mc
2
3 −
4n
j +
1
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

168 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
With the minus sign, j = l − 1/2(l = j +1/2) : Eq. 6.57 ⇒ E
1
r
= −
(E
n
)
2
2mc
2
4n
j +1
− 3
.
Equation 6.65 ⇒ E
1
so
=
(E
n
)
2
mc
2
n
j(j +1)− (j +
1
2
)(j +
3
2
) −
3
4
(j +
1
2
)(j + 1)(j +
3
2
)
=
(E
n
)
2
mc
2
n(j
2
+ j − j
2
− 2j −
3
4
−
3
4
)
(j +
1
2
)(j + 1)(j +
3
2
)
=
(E
n
)
2
mc
2
−n
(j + 1)(j +
1
2
)
.
E
1
fs
=
(E
n
)
2
2mc
2
−
4n
j +1
− 3+
2n
(j + 1)(j +
1
2
)
=
(E
n
)
2
2mc
2
3 −
2n
(j + 1)(j +
1
2
)
1+2
j +
1
2
=
(E
n
)
2
2mc
2
3 −
4n
j +
1
2
. For both signs, then, E
1
fs
=
(E
n
)
2
2mc
2
3 −
4n
j +
1
2
. QED
Problem 6.18
E
0
3
− E
0
2
= hν =
2πc
λ
= E
1
1
9
−
1
4
= −
5
36
E
1
⇒ λ = −
36
5
2πc
E
1
; E
1
= −13.6eV;
c =1.97 × 10
−11
MeV·cm; λ =
36
5
(2π)(1.97 ×10
−11
× 10
6
eV · cm)
(13.6 eV)
=6.55 × 10
−5
cm= 655 nm.
ν =
c
λ
=
3.00 × 10
8
m/s
6.55 × 10
−7
m
=
4.58 × 10
14
Hz. Equation 6.66 ⇒ E
1
fs
=
(E
n
)
2
2mc
2
3 −
4n
j +
1
2
:
For n =2
: l =0orl =1, so j =1/2or3/2. Thus n = 2 splits into two levels :
j =1/2
: E
1
2
=
(E
2
)
2
2mc
2
3 −
8
1
= −
5
2
(E
2
)
2
mc
2
= −
5
2
1
4
2
(E
1
)
2
mc
2
= −
5
32
(13.6 eV)
2
(.511 × 10
6
eV)
= −5.66 × 10
−5
eV.
j =3/2
: E
1
2
=
(E
2
)
2
2mc
2
3 −
8
2
= −
1
2
(E
2
)
2
mc
2
= −
1
32
(3.62 × 10
−4
eV) = −1.13 × 10
−5
eV.
For n =3
: l =0, 1or2, so j =1/2, 3/2or5/2. Thus n = 3 splits into three levels :
j =1/2
: E
1
3
=
(E
3
)
2
2mc
2
3 −
12
1
= −9
(E
3
)
2
mc
2
= −
9
2
1
9
2
(E
1
)
2
mc
2
= −
1
18
(3.62 × 10
−4
eV) = −2.01 × 10
−5
eV.
j =3/2
: E
1
3
=
(E
3
)
2
2mc
2
3 −
12
2
= −
3
2
(E
3
)
2
mc
2
= −
1
54
(3.62 × 10
−4
eV) = −0.67 × 10
−5
eV.
j =5/2
: E
1
3
=
(E
3
)
2
2mc
2
3 −
12
3
= −
1
2
(E
3
)
2
mc
2
= −
1
162
(3.62 × 10
−4
eV) = −0.22 × 10
−5
eV.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 169
E
E
0
0
3
2
12
3
4
5
6
5/2
3/2
1/2
3/2
1/2
j=
j=
j=
j=
j=
There are six transitions here; their energies are (E
0
3
+ E
1
3
) − (E
0
2
+ E
1
2
)=(E
0
3
− E
0
2
)+∆E, where
∆E ≡ E
1
3
− E
1
2
. Let β ≡ (E
1
)
2
/mc
2
=3.62 × 10
−4
eV. Then:
(
1
2
→
3
2
)
:∆E =
−
1
18
−
−
1
32
β = −
7
288
β = −8.80 × 10
−6
eV.
(
3
2
→
3
2
)
:∆E =
−
1
54
−
−
1
32
β =
11
864
β =4.61 × 10
−6
eV.
(
5
2
→
3
2
)
:∆E =
−
1
162
+
1
32
β =
65
2592
β =9.08 × 10
−6
eV.
(
1
2
→
1
2
)
:∆E =
5
32
−
1
18
β =
29
288
β =36.45 × 10
−6
eV.
(
3
2
→
1
2
)
:∆E =
−
1
54
+
5
32
β =
119
864
β =49.86 × 10
−6
eV.
(
5
2
→
1
2
)
:∆E =
−
1
162
+
5
32
β =
389
2592
β =54.33 × 10
−6
eV.
Conclusion: There are six lines; one of them (
1
2
→
3
2
) has a frequency less than the unperturbed line, the
other five have (slightly) higher frequencies. In order they are:
3
2
→
3
2
;
5
2
→
3
2
;
1
2
→
1
2
;
3
2
→
1
2
;
5
2
→
1
2
. The
frequency spacings are:
ν
2
− ν
1
=(∆E
2
− ∆E
1
)/2π =3.23 × 10
9
Hz
ν
3
− ν
3
=(∆E
3
− ∆E
2
)/2π =1.08 × 10
9
Hz
ν
4
− ν
3
=(∆E
4
− ∆E
3
)/2π =6.60 × 10
9
Hz
ν
5
− ν
4
=(∆E
5
− ∆E
4
)/2π =3.23 × 10
9
Hz
ν
6
− ν
5
=(∆E
6
− ∆E
5
)/2π =1.08 × 10
9
Hz
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

170 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Problem 6.19
j +
1
2
2
− α
2
=
j +
1
2
1 −
α
j +
1
2
2
≈
j +
1
2
1 −
1
2
α
j +
1
2
2
=(j +
1
2
) −
α
2
2(j +
1
2
)
.
α
n − (j +
1
2
)+
j +
1
2
2
− α
2
≈
α
n −
j +
1
2
+
j +
1
2
−
α
2
2(j+
1
2
)
=
α
n −
α
2
2(j+
1
2
)
=
α
n
1 −
α
2
2n(j+
1
2
)
≈
α
n
1+
α
2
2n(j +
1
2
)
.
1+
α
n − (j +
1
2
)+
j +
1
2
2
− α
2
2
−1/2
≈
1+
α
2
n
2
1+
α
2
n(j +
1
2
)
−1/2
≈ 1 −
1
2
α
2
n
2
1+
α
2
n(j +
1
2
)
+
3
8
α
4
n
4
=1−
α
2
2n
2
+
α
4
2n
4
−n
j +
1
2
+
3
4
.
E
nj
≈ mc
2
1 −
α
2
2n
2
+
α
4
2n
4
−n
j +
1
2
+
3
4
− 1
= −
α
2
mc
2
2n
2
1+
α
2
n
2
n
j +
1
2
−
3
4
= −
13.6eV
n
2
1+
α
2
n
2
n
j +
1
2
−
3
4
, confirming Eq. 6.67.
Problem 6.20
Equation 6.59 ⇒ B =
1
4π9
0
e
mc
2
r
3
L.SayL = , r = a; then
B =
1
4π9
0
e
mc
2
a
3
=
(1.60 × 10
−19
C)(1.05 × 10
−34
J · s)
4π
8.9 × 10
−12
C
2
/N · m
2
(9.1 × 10
−31
kg) (3 ×10
8
m/s)
2
(0.53 × 10
−10
m)
3
= 12 T.
So a “strong” Zeeman field is B
ext
10 T, and a “weak” one is B
ext
10 T. Incidentally, the earth’s field
(10
−4
T) is definitely weak.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 171
Problem 6.21
For n =2,l =0(j =1/2) or l =1(j =1/2or3/2). The eight states are:
|1 = |20
1
2
1
2
|2 = |20
1
2
−
1
2
g
J
=
1+
(1/2)(3/2)+(3/4)
2(1/2)(3/2)
=1+
3/2
3/2
=2.
|3 = |21
1
2
1
2
|4 = |21
1
2
−
1
2
g
J
=
1+
(1/2)(3/2) − (1)(2) + (3/4)
2(1/2)(3/2)
=1+
−1/2
3/2
=2/3.
In these four cases, E
nj
= −
13.6eV
4
1+
α
2
4
2
1
−
3
4
= −3.4eV
1+
5
16
α
2
.
|5 = |21
3
2
3
2
|6 = |21
3
2
1
2
|7 = |21
3
2
−
1
2
|8 = |21
3
2
−
3
2
g
J
=
1+
(3/2)(5/2) − (1)(2) + (3/4)
2(3/2)(5/2)
=1+
5/2
15/2
=4/3.
In these four cases, E
nj
= −3.4eV
1+
α
2
4
2
2
−
3
4
= −3.4eV
1+
1
16
α
2
.
The energies are:
E
1
= −3.4eV
1+
5
16
α
2
+ µ
B
B
ext
.
E
2
= −3.4eV
1+
5
16
α
2
− µ
B
B
ext
.
E
3
= −3.4eV
1+
5
16
α
2
+
1
3
µ
B
B
ext
.
E
4
= −3.4eV
1+
5
16
α
2
−
1
3
µ
B
B
ext
.
E
5
= −3.4eV
1+
1
16
α
2
+2µ
B
B
ext
.
E
6
= −3.4eV
1+
1
16
α
2
+
2
3
µ
B
B
ext
.
E
7
= −3.4eV
1+
1
16
α
2
−
2
3
µ
B
B
ext
.
E
8
= −3.4eV
1+
1
16
α
2
− 2µ
B
B
ext
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
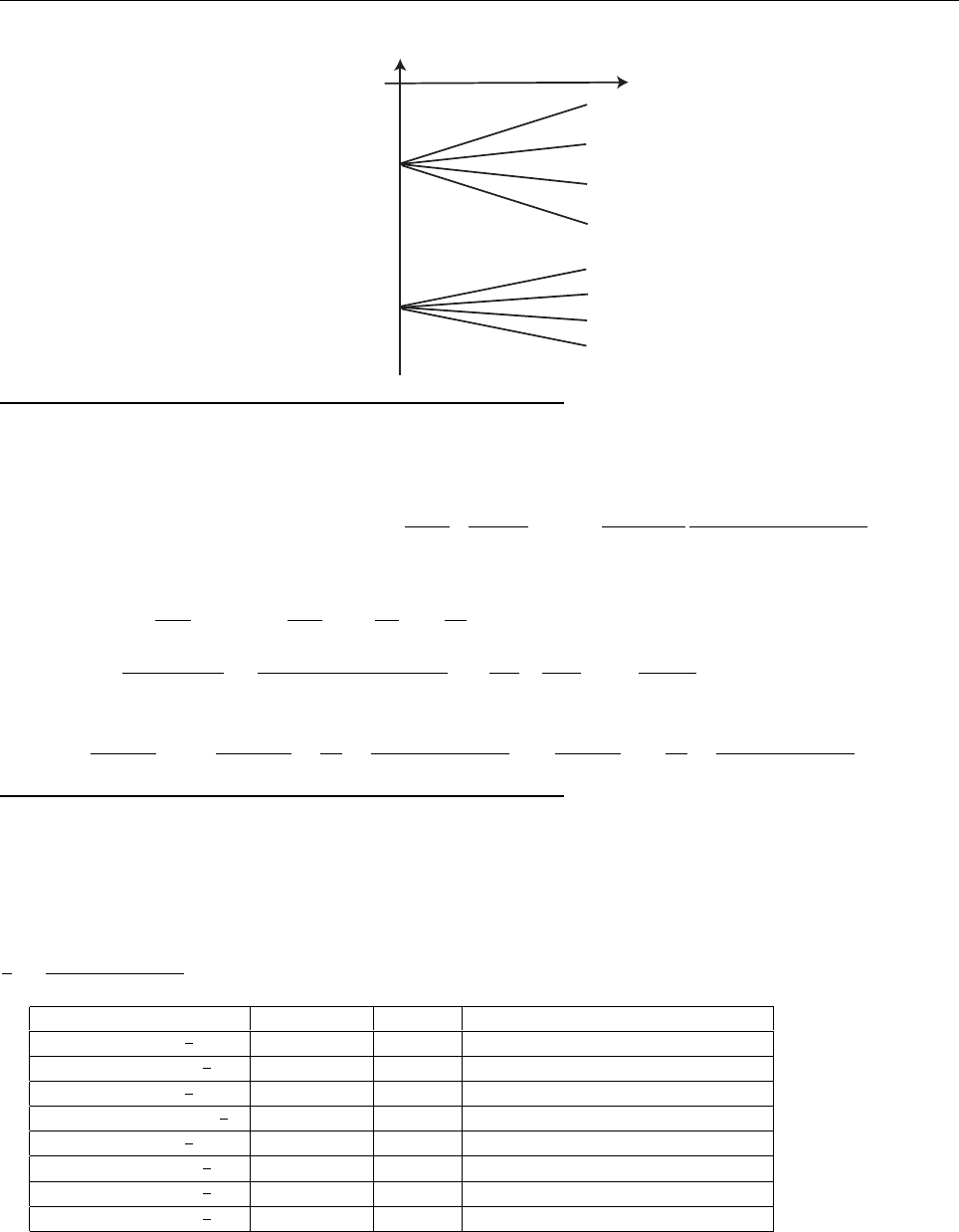
172 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
E
B
ext
B
µ
2 (slope -1)
4 (slope -1/3)
3 (slope 1/3)
1 (slope 1)
8 (slope -2)
7 (slope -2/3)
6 (slope 2/3)
5 (slope 2)
-3.4 (1+α /16) eV
2
-3.4 (1+5α /16) eV
2
Problem 6.22
E
1
fs
= nlm
l
m
s
|(H
r
+ H
so
)|nlm
l
m
s
= −
E
2
n
2mc
2
4n
l +1/2
− 3
+
e
2
8π9
0
m
2
c
2
2
m
l
m
s
l(l +1/2)(l +1)n
3
a
3
.
Now
2E
2
n
mc
2
=
−
2E
1
mc
2
−
E
1
n
4
=
α
2
n
4
(13.6 eV). (Problem 6.11.)
e
2
2
8π9
0
m
2
c
2
a
3
=
e
2
2
(me
2
)
3
2 · 4π9
0
m
2
c
2
(4π9
0
2
)
3
=
m
2
2
e
2
4π9
0
2
e
2
4π9
0
c
2
= α
2
(13.6 eV).
E
1
fs
=
13.6eV
n
3
α
2
−
1
(l +1/2)
+
3
4n
+
m
l
m
s
l(l +1/2)(l +1)
=
13.6eV
n
3
α
2
3
4n
−
l(l +1)− m
l
m
s
l(l +1/2)(l +1)
. QED
Problem 6.23
The Bohr energy is the same for all of them: E
2
= −13.6eV/2
2
= −3.4eV. The Zeeman contribution is the
second term in Eq. 6.79: µ
B
B
ext
(m
l
+2m
s
). The fine structure is given by Eq. 6.82: E
1
fs
= (13.6eV/8)α
2
{···}=
(1.7 eV)α
2
{···}. In the table below I record the 8 states, the value of (m
l
+2m
s
), the value of {···} ≡
3
8
−
l(l +1)− m
l
m
s
l(l +1/2)(l +1)
, and (in the last column) the total energy, −3.4eV[1−(α
2
/2){···}]+(m
l
+2m
s
)µ
B
B
ext
.
State = |nlm
l
m
s
(m
l
+2m
s
) {···} Total Energy
|1 = |200
1
2
1 −5/8 -3.4 eV [1 + (5/16)α
2
]+µ
B
B
ext
|2 = |200−
1
2
−1 −5/8 -3.4 eV [1 + (5/16)α
2
] − µ
B
B
ext
|3 = |211
1
2
2 −1/8 -3.4 eV [1 + (1/16)α
2
]+2µ
B
B
ext
|4 = |21− 1 −
1
2
−2 −1/8 -3.4 eV [1 + (1/16)α
2
] − 2µ
B
B
ext
|5 = |210
1
2
1 −7/24 -3.4 eV [1 + (7/48)α
2
]+µ
B
B
ext
|6 = |210−
1
2
−1 −7/24 -3.4 eV [1 + (7/48)α
2
] − µ
B
B
ext
|7 = |211−
1
2
0 −11/24 -3.4 eV [1 + (11/48)α
2
]
|8 = |21− 1
1
2
0 −11/24 -3.4 eV [1 + (11/48)α
2
]
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 173
Ignoring fine structure there are five distinct levels—corresponding to the possible values of (m
l
+2m
s
):
2(d = 1); 1 (d = 2); 0 (d = 2); −1(d = 2); −2(d = 1).
Problem 6.24
Equation 6.72 ⇒ E
1
z
=
e
2m
B
ext
·L +2S =
e
2m
B
ext
2m
s
=2m
s
µ
B
B
ext
(same as the Zeeman term in Eq. 6.79,
with m
l
= 0). Equation 6.67 ⇒ E
nj
= −
13.6eV
n
2
1+
α
2
n
2
n −
3
4
(since j =1/2). So the total energy is
E = −
13.6eV
n
2
1+
α
2
n
2
n −
3
4
+2m
s
µ
B
B
ext
.
Fine structure is the α
2
term: E
1
fs
= −
13.6eV
n
4
α
2
n −
3
4
=
13.6eV
n
3
α
2
3
4n
− 1
, which is the same as
Eq. 6.82, with the term in square brackets set equal to 1. QED
Problem 6.25
Equation 6.66 ⇒ E
1
fs
=
E
2
2
2mc
2
3 −
8
j +1/2
=
E
2
1
32mc
2
3 −
8
j +1/2
;
E
1
mc
2
= −
α
2
2
(Problem 6.11), so
E
1
fs
= −
E
1
32
α
2
2
3 −
8
j +1/2
=
13.6eV
64
α
2
3 −
8
j +1/2
= γ
3 −
8
j +1/2
.
For j =1/2(ψ
1
,ψ
2
,ψ
6
,ψ
8
),H
1
fs
= γ(3 −8) = −5γ. For j =3/2(ψ
3
,ψ
4
,ψ
5
,ψ
7
),H
1
fs
= γ(3 −
8
2
)=−γ.
This confirms all the γ terms in −W (p. 281). Meanwhile, H
z
=(e/2m)B
ext
(L
z
+2S
z
) (Eq. 6.71); ψ
1
,ψ
2
,ψ
3
,ψ
4
are eigenstates of L
z
and S
z
; for these there are only diagonal elements:
H
z
=
e
2m
B
ext
(m
l
+2m
s
)=(m
l
+2m
s
)β; H
z
11
= β; H
z
22
= −β; H
z
33
=2β; H
z
44
= −2β.
This confirms the upper left corner of −W. Finally:
(L
z
+2S
z
)|ψ
5
=+
2
3
|10|
1
2
1
2
(L
z
+2S
z
)|ψ
6
= −
1
3
|10|
1
2
1
2
(L
z
+2S
z
)|ψ
7
= −
2
3
|10|
1
2
−
1
2
(L
z
+2S
z
)|ψ
8
= −
1
3
|10|
1
2
−
1
2
so
H
z
55
=(2/3)β,
H
z
66
=(1/3)β,
H
z
77
= −(2/3)β,
H
z
88
= −(1/3)β,
H
z
56
= H
z
65
= −(
√
2/3)β,
H
z
78
= H
z
87
= −(
√
2/3)β,
which confirms the remaining elements.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

174 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Problem 6.26
There are eighteen n = 3 states (in general, 2n
2
).
WEAK FIELD
Equation 6.67 ⇒ E
3j
= −
13.6eV
9
1+
α
2
9
3
j +1/2
−
3
4
= −1.51 eV
1+
α
2
3
1
j +1/2
−
1
4
.
Equation 6.76 ⇒ E
1
z
= g
J
m
j
µ
B
B
ext
.
State |3 ljm
j
g
J
(Eq. 6.75)
1
3
1
j+1/2
−
1
4
Total Energy
l =0,j=1/2 |30
1
2
1
2
2 1/4 −1.51 eV
1+
α
2
4
+ µ
B
B
ext
l =0,j=1/2 |30
1
2
−
1
2
2 1/4 −1.51 eV
1+
α
2
4
− µ
B
B
ext
l =1,j=1/2 |31
1
2
1
2
2/3 1/4 −1.51 eV
1+
α
2
4
+
1
3
µ
B
B
ext
l =1,j=1/2 |31
1
2
−
1
2
2/3 1/4 −1.51 eV
1+
α
2
4
−
1
3
µ
B
B
ext
l =1,j=3/2 |31
3
2
3
2
4/3 1/12 −1.51 eV
1+
α
2
12
+2µ
B
B
ext
l =1,j=3/2 |31
3
2
1
2
4/3 1/12 −1.51 eV
1+
α
2
12
+
2
3
µ
B
B
ext
l =1,j=3/2 |31
3
2
−
1
2
4/3 1/12 −1.51 eV
1+
α
2
12
−
2
3
µ
B
B
ext
l =1,j=3/2 |31
3
2
−
3
2
4/3 1/12 −1.51 eV
1+
α
2
12
− 2µ
B
B
ext
l =2,j=3/2 |32
3
2
3
2
4/5 1/12 −1.51 eV
1+
α
2
12
+
6
5
µ
B
B
ext
l =2,j=3/2 |32
3
2
1
2
4/5 1/12 −1.51 eV
1+
α
2
12
+
2
5
µ
B
B
ext
l =2,j=3/2 |32
3
2
−
1
2
4/5 1/12 −1.51 eV
1+
α
2
12
−
2
5
µ
B
B
ext
l =2,j=3/2 |32
3
2
−
3
2
4/5 1/12 −1.51 eV
1+
α
2
12
−
6
5
µ
B
B
ext
l =2,j=5/2 |32
5
2
5
2
6/5 1/36 −1.51 eV
1+
α
2
36
+3µ
B
B
ext
l =2,j=5/2 |32
5
2
3
2
6/5 1/36 −1.51 eV
1+
α
2
36
+
9
5
µ
B
B
ext
l =2,j=5/2 |32
5
2
1
2
6/5 1/36 −1.51 eV
1+
α
2
36
+
3
5
µ
B
B
ext
l =2,j=5/2 |32
5
2
−
1
2
6/5 1/36 −1.51 eV
1+
α
2
36
−
3
5
µ
B
B
ext
l =2,j=5/2 |32
5
2
−
3
2
6/5 1/36 −1.51 eV
1+
α
2
36
−
9
5
µ
B
B
ext
l =2,j=5/2 |32
5
2
−
5
2
6/5 1/36 −1.51 eV
1+
α
2
36
− 3µ
B
B
ext
STRONG FIELD
Equation 6.79 ⇒−1.51 eV + (m
l
+2m
s
)µ
B
B
ext
;
Equation 6.82 ⇒
13.6eV
27
α
2
1
4
−
l(l +1)− m
l
m
s
l(l +1/2)(l +1)
= −1.51 eV
α
2
3
l(l +1)− m
l
m
s
l(l +1/2)(l +1)
−
1
4
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 175
E
tot
= −1.51 eV(1 + α
2
A)+(m
l
+2m
s
)µ
B
B
ext
, where A ≡
1
3
l(l +1)− m
l
m
s
l(l +1/2)(l +1)
−
1
4
.
These terms are given in the table below:
State |nlm
l
m
s
(m
l
+2m
s
) A Total Energy
l =0 |300
1
2
1 1/4 −1.51 eV
1+
α
2
4
+ µ
B
B
ext
l =0 |300−
1
2
−1 1/4 −1.51 eV
1+
α
2
4
− µ
B
B
ext
l =1 |311
1
2
2 1/12 −1.51 eV
1+
α
2
12
+2µ
B
B
ext
l =1 |31− 1 −
1
2
−2 1/12 −1.51 eV
1+
α
2
12
− 2µ
B
B
ext
l =1 |310
1
2
1 5/36 −1.51 eV
1+
5α
2
36
+ µ
B
B
ext
l =1 |310−
1
2
−1 5/36 −1.51 eV
1+
5α
2
36
− µ
B
B
ext
l =1 |31− 1
1
2
0 7/36 −1.51 eV
1+
7α
2
36
l =1 |311−
1
2
0 7/36 −1.51 eV
1+
7α
2
36
l =2 |322
1
2
3 1/36 −1.51 eV
1+
α
2
36
+3µ
B
B
ext
l =2 |32− 2 −
1
2
−3 1/36 −1.51 eV
1+
α
2
36
− 3µ
B
B
ext
l =2 |321
1
2
2 7/180 −1.51 eV
1+
7α
2
180
+2µ
B
B
ext
l =2 |32− 1 −
1
2
−2 7/180 −1.51 eV
1+
7α
2
180
− 2µ
B
B
ext
l =2 |320
1
2
1 1/20 −1.51 eV
1+
α
2
20
+ µ
B
B
ext
l =2 |320−
1
2
−1 1/20 −1.51 eV
1+
α
2
20
− µ
B
B
ext
l =2 |32− 1
1
2
0 11/180 −1.51 eV
1+
11α
2
180
l =2 |321−
1
2
0 11/180 −1.51 eV
1+
11α
2
180
l =2 |32− 2
1
2
−1 13/180 −1.51 eV
1+
13α
2
180
− µ
B
B
ext
l =2 |322−
1
2
1 13/180 −1.51 eV
1+
13α
2
180
+ µ
B
B
ext
INTERMEDIATE FIELD
As in the book, I’ll use the basis |nljm
j
(same as for weak field); then the fine structure matrix elements
are diagonal: Eq. 6.66 ⇒
E
1
fs
=
E
2
3
2mc
2
3 −
12
j +1/2
=
E
2
1
54mc
2
1 −
4
j +1/2
= −
E
1
α
2
108
1 −
4
j +1/2
=3γ
1 −
4
j +1/2
,
γ ≡
13.6eV
324
α
2
. For j =1/2,E
1
fs
= −9γ; for j =3/2,E
1
fs
= −3γ; for j =5/2,E
1
fs
= −γ.
The Zeeman Hamiltonian is Eq. 6.71: H
z
=
1
(L
z
+2S
z
)µ
B
B
ext
. The first eight states (l = 0 and l = 1) are
the same as before (p. 281), so the β terms in W are unchanged; recording just the non-zero blocks of −W:
(9γ − β), (9γ + β), (3γ − 2β), (3γ +2β),
'
(3γ −
2
3
β)
√
2
3
β
√
2
3
β (9γ −
1
3
β)
(
,
'
(3γ +
2
3
β)
√
2
3
β
√
2
3
β (9γ +
1
3
β)
(
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
176 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
The other 10 states (l = 2) must first be decomposed into eigenstates of L
z
and S
z
:
|
5
2
5
2
= |22|
1
2
1
2
=⇒ (γ − 3β)
|
5
2
−
5
2
= |2 −2|
1
2
−
1
2
=⇒ (γ +3β)
|
5
2
3
2
=
1
5
|22|
1
2
−
1
2
+
4
5
|21|
1
2
1
2
|
3
2
3
2
=
4
5
|22|
1
2
−
1
2
−
1
5
|21|
1
2
1
2
=⇒
(γ −
9
5
β)
2
5
β
2
5
β (3γ −
6
5
β)
|
5
2
1
2
=
2
5
|21|
1
2
−
1
2
+
3
5
|20|
1
2
1
2
|
3
2
1
2
=
3
5
|21|
1
2
−
1
2
−
2
5
|20|
1
2
1
2
=⇒
'
(γ −
3
5
β)
√
6
5
β
√
6
5
β (3γ −
2
5
β)
(
|
5
2
−
1
2
=
3
5
|20|
1
2
−
1
2
+
2
5
|2 − 1|
1
2
1
2
|
3
2
−
1
2
=
2
5
|20|
1
2
−
1
2
−
3
5
|2 − 1|
1
2
1
2
=⇒
'
(γ +
3
5
β)
√
6
5
β
√
6
5
β (3γ +
2
5
β)
(
|
5
2
−
3
2
=
4
5
|2 − 1|
1
2
−
1
2
+
1
5
|2 − 2|
1
2
1
2
|
3
2
−
3
2
=
1
5
|2 − 1|
1
2
−
1
2
−
4
5
|2 − 2|
1
2
1
2
=⇒
(γ +
9
5
β)
2
5
β
2
5
β (3γ +
6
5
β)
[Sample Calculation: For the last two, letting Q ≡
1
(L
z
+2S
z
), we have
Q|
5
2
−
3
2
= −2
4
5
|2 − 1|
1
2
−
1
2
−
1
5
|2 − 2|
1
2
1
2
;
Q|
3
2
−
3
2
= −2
1
5
|2 − 1|
1
2
−
1
2
+
4
5
|2 − 2|
1
2
1
2
.
5
2
−
3
2
|Q|
5
2
−
3
2
=(−2)
4
5
−
1
5
= −
9
5
;
3
2
−
3
2
|Q|
3
2
−
3
2
=(−2)
1
5
−
4
5
= −
6
5
;
5
2
−
3
2
|Q|
3
2
−
3
2
= −2
4
5
1
5
+
1
5
4
5
= −
4
5
+
2
5
= −
2
5
=
3
2
−
3
2
|Q|
5
2
−
3
2
.]
So the 18 × 18 matrix −W splits into six 1 × 1 blocks and six 2 × 2 blocks. We need the eigenvalues of the
2 × 2 blocks. This means solving 3 characteristic equations (the other 3 are obtained trivially by changing the
sign of β):
3γ −
2
3
β − λ
9γ −
1
3
β − λ
−
2
9
β
2
=0=⇒ λ
2
+ λ(β − 12γ)+γ(27γ − 7β)=0.
γ −
9
5
β − λ
3γ −
6
5
β − λ
−
4
25
β
2
=0=⇒ λ
2
+ λ(3β − 4γ)+γ
3γ
2
−
33
5
γβ +2β
2
=0.
γ −
3
5
β − λ
3γ −
2
5
β − λ
−
6
25
β
2
=0=⇒ λ
2
+ λ(β − 4γ)+γ
3γ −
11
5
β
=0.
The solutions are:
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 177
λ = −β/2+6γ ±
(β/2)
2
+ βγ +9γ
2
λ = −3β/2+2γ ±
(β/2)
2
+
3
5
βγ + γ
2
λ = −β/2+2γ ±
(β/2)
2
+
1
5
βγ + γ
2
⇒
9
1
= E
3
− 9γ + β
9
2
= E
3
− 3γ +2β
9
3
= E
3
− γ +3β
9
4
= E
3
− 6γ + β/2+
9γ
2
+ βγ + β
2
/4
9
5
= E
3
− 6γ + β/2 −
9γ
2
+ βγ + β
2
/4
9
6
= E
3
− 2γ +3β/2+
γ
2
+
3
5
βγ + β
2
/4
9
7
= E
3
− 2γ +3β/2 −
γ
2
+
3
5
βγ + β
2
/4
9
8
= E
3
− 2γ + β/2+
γ
2
+
1
5
βγ + β
2
/4
9
9
= E
3
− 2γ + β/2 −
γ
2
+
1
5
βγ + β
2
/4
(The other 9 9’s are the same, but with β →−β.) Here γ =
13.6eV
324
α
2
, and β = µ
B
B
ext
.
In the weak-field limit (β γ)
:
9
4
≈ E
3
− 6γ + β/2+3γ
1+β/9γ ≈ E
3
− 6γ + β/2+3γ(1 + β/18γ)=E
3
− 3γ +
2
3
β.
9
5
≈ E
3
− 6γ + β/2 −3γ(1 + β/18γ)=E
3
− 9γ +
1
3
β.
9
6
≈ E
3
− 2γ +3β/2+γ(1+3β/10γ)=E
3
− γ +
9
5
β.
9
7
≈ E
3
− 2γ +3β/2 − γ(1+3β/10γ)=E
3
− 3γ +
6
5
β.
9
8
≈ E
3
− 2γ + β/2+γ(1 + β/10γ)=E
3
− γ +
3
5
β.
9
9
≈ E
3
− 2γ + β/2 −γ(1 + β/10γ)=E
3
− 3γ +
2
5
β.
Noting that γ = −(E
3
/36)α
2
=
1.51 eV
36
α
2
, we see that the weak field energies are recovered as in the first table.
In the strong-field limit (β γ)
:
9
4
≈ E
3
− 6γ + β/2+β/2
1+4γ/β ≈ E
3
− 6γ + β/2+β/2(1+2γ/β)=E
3
− 5γ + β.
9
5
≈ E
3
− 6γ + β/2 −β/2(1+2γ/β)=E
3
− 7γ.
9
6
≈ E
3
− 2γ +3β/2+β/2(1+6γ/5β)=E
3
−
7
5
γ +2β.
9
7
≈ E
3
− 2γ +3β/2 − β/2(1+6γ/5β)=E
3
−
13
5
γ + β.
9
8
≈ E
3
− 2γ + β/2+β/2(1+2γ/5β)=E
3
−
9
5
γ + β.
9
9
≈ E
3
− 2γ + β/2 −β/2(1+2γ/5β)=E
3
−
11
5
γ.
Again, these reproduce the strong-field results in the second table.
In the figure below each line is labeled by the level number and (in parentheses) the starting and ending
slope; for each line there is a corresponding one starting from the same point but sloping down.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
178 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
E
Ε
3
Ε
3
Ε
3
−3γ
−γ
Ε
3
−9γ
3(3)
6(9/5−> 2)
8(3/5−>1)
2(2)
7(6/5−>1)
4(2/5−>1)
9(2/5−>0)
1(1)
5(1/3−>0)
Problem 6.27
I ≡
(a · ˆr)(b · ˆr) sin θdθdφ
=
(a
x
sin θ cos φ + a
y
sin θ sin φ + a
z
cos θ)(b
x
sin θ cos φ + b
y
sin θ sin φ + b
z
cos θ) sin θ dθ dφ.
But
2π
0
sin φdφ =
2π
0
cos φdφ =
2π
0
sin φ cos φdφ=0, so only three terms survive :
I =
(a
x
b
x
sin
2
θ cos
2
φ + a
y
b
y
sin
2
θ sin
2
φ + a
z
b
z
cos
2
θ) sin θdθdφ.
But
2π
0
sin
2
φdφ=
2π
0
cos
2
φdφ= π,
2π
0
dφ =2π, so
I =
π
0
π(a
x
b
x
+ a
y
b
y
) sin
2
θ +2πa
z
b
z
cos
2
θ
sin θdθ. But
π
0
sin
3
θdθ=
4
3
,
π
0
cos
2
θ sin θdθ =
2
3
,
so I = π(a
x
b
x
+ a
y
b
y
)
4
3
+2πa
z
b
z
2
3
=
4π
3
(a
x
b
x
+ a
y
b
y
+ a
z
b
z
)=
4π
3
(a · b). QED
[Alternatively, noting that I has to be a scalar bilinear in a and b, we know immediately that I = A(a·b), where
A is some constant (same for all a and b). To determine A, pick a = b =
ˆ
k; then I = A =
cos
2
θ sin θdθdφ=
4π/3.]
For states with l = 0, the wave function is independent of θ and φ (Y
0
0
=1/
√
4π), so
0
3(S
p
· ˆr)(S
e
· ˆr) −S
p
· S
e
r
3
1
=
∞
0
1
r
3
|ψ(r)|
2
r
2
dr
[3(S
p
· ˆr)(S
e
· ˆr)] sin θ dθ dφ.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 179
The first angular integral is 3(4π/3)(S
p
· S
e
)=4π(S
p
· S
e
), while the second is −(S
p
· S
e
)
sin θdθdφ =
−4π(S
p
· S
e
), so the two cancel, and the result is zero. QED [Actually, there is a little sleight-of-hand here,
since for l =0,ψ → constant as r → 0, and hence the radial integral diverges logarithmically at the origin.
Technically, the first term in Eq. 6.86 is the field outside an infinitesimal sphere; the delta-function gives the
field inside. For this reason it is correct to do the angular integral first (getting zero) and not worry about the
radial integral.]
Problem 6.28
From Eq. 6.89 we see that ∆E ∝
g
m
p
m
e
a
3
; we want reduced mass in a, but not in m
p
m
e
(which come from
Eq. 6.85); the notation in Eq. 6.93 obscures this point.
(a) g and m
p
are unchanged; m
e
→ m
µ
= 207m
e
, and a → a
µ
. From Eq. 4.72, a ∝ 1/m,so
a
a
µ
=
m
µ
(reduced)
m
e
=
m
µ
m
p
m
µ
+ m
p
·
1
m
e
=
207
1 + 207(m
e
/m
p
)
=
207
1 + 207
(9.11×10
−31
)
1.67×10
−27
)
=
207
1.11
= 186.
∆E =(5.88 × 10
−6
eV) (1/207) (186)
3
= 0.183 eV.
(b) g :5.59 → 2; m
p
→ m
e
;
a
a
p
=
m
p
(reduced)
m
e
=
m
2
e
m
e
+ m
e
·
1
m
e
=
1
2
.
∆E =(5.88 × 10
−6
eV)
2
5.59
1.67 × 10
−27
9.11 × 10
−31
1
2
3
= 4.82 ×10
−4
eV.
(c) g :5.59 → 2; m
p
→ m
µ
;
a
a
m
=
m
m
(reduced)
m
e
=
m
e
m
µ
m
e
+ m
µ
·
1
m
e
=
207
208
.
∆E =(5.88 × 10
−6
)
2
5.59
1.67 × 10
−27
(207)(9.11 × 10
−31
)
207
208
3
= 1.84×10
−5
eV.
Problem 6.29
Use perturbation theory:
H
= −
e
2
4π9
0
1
b
−
1
r
, for 0 <r<b. ∆E = ψ|H
|ψ, with ψ ≡
1
√
πa
3
e
−r/a
.
∆E = −
e
2
4π9
0
1
πa
3
4π
b
0
1
b
−
1
r
e
−2r/a
r
2
dr = −
e
2
π9
0
a
3
1
b
b
0
r
2
e
−2r/a
dr −
b
0
re
−2r/a
dr
= −
e
2
π9
0
a
3
1
b
−
a
2
r
2
e
−2r/a
+ a
a
2
2
e
−2r/a
−
2r
a
− 1
−
a
2
2
e
−2r/a
−
2r
a
− 1
b
0
= −
e
2
π9
0
a
3
−
a
2b
b
2
e
−2b/a
+
a
3
4b
e
−2b/a
−
2b
a
− 1
−
a
2
4
e
−2b/a
−
2b
a
− 1
+
a
3
4b
−
a
2
4
= −
e
2
π9
0
a
3
e
−2b/a
−
ab
2
−
a
2
2
−
a
3
4b
+
ab
2
+
a
2
4
+
a
2
4
a
b
− 1
= −
e
2
π9
0
a
3
e
−2b/a
−
a
2
4
a
b
+1
+
a
2
4
a
b
− 1
=
e
2
4π9
0
a
1 −
a
b
+
1+
a
b
e
−2b/a
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

180 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Let +2b/a = 9 (very small). Then the term in square brackets is:
1 −
2
9
+
1+
2
9
1 − 9 +
9
2
2
−
9
3
6
+ ···
=
✁
1 −
✄
✄
✄
2
9
+
✁
1+
✄
✄
✄
2
9
−
✁
9 −
✁
2+
9
2
2
+
✁
9 −
9
3
6
−
9
2
3
+()9
3
+ ···=
9
2
6
+()9
3
+()9
4
···
To leading order, then, ∆E =
e
2
4π9
0
1
a
4b
2
6a
2
.
E = E
1
= −
me
4
2(4π9
0
)
2
2
; a =
4π9
0
2
me
2
;soEa = −
e
2
2(4π9
0
)
.
∆E
E
=
e
2
4π9
0
−
2(4π9
0
)
e
2
2b
2
3a
2
= −
4
3
b
a
2
.
Putting in a =5× 10
−11
m:
∆E
E
= −
4
3
10
−15
5 × 10
−11
= −
16
3
× 10
−10
≈ −5 × 10
−10
.
By contrast,
fine structure: ∆E/E ≈ α
2
=(1/137)
2
=5× 10
−5
,
hyperfine structure: ∆E/E ≈ (m
e
/m
p
)α
2
=(1/1800)(1/137)
2
=3× 10
−8
.
So the correction for the finite size of the nucleus is much smaller (about 1% of hyperfine).
Problem 6.30
(a) In terms of the one-dimensional harmonic oscillator states {ψ
n
(x)}, the unperturbed ground state is
|0 = ψ
0
(x)ψ
0
(y)ψ
0
(z).
E
1
0
= 0|H
|0 = ψ
0
(x)ψ
0
(y)ψ
0
(z)|λx
2
yz|ψ
0
(x)ψ
0
(y)ψ
0
(z) = λx
2
0
y
0
z
0
.
But y
0
= z
0
= 0. So there is no change, in first order.
(b) The (triply degenerate) first excited states are
|1 = ψ
0
(x)ψ
0
(y)ψ
1
(z)
|2 = ψ
0
(x)ψ
1
(y)ψ
0
(z)
|3 = ψ
1
(x)ψ
0
(y)ψ
0
(z)
In this basis the perturbation matrix is W
ij
= i|H
|j,i=1, 2, 3.
1|H
|1 = ψ
0
(x)ψ
0
(y)ψ
1
(z)|λx
2
yz|ψ
0
(x)ψ
0
(y)ψ
1
(z) = λx
2
0
y
0
z
1
=0,
2|H
|2 = ψ
0
(x)ψ
1
(y)ψ
0
(z)|λx
2
yz|ψ
0
(x)ψ
1
(y)ψ
0
(z) = λx
2
0
y
1
z
0
=0,
3|H
|3 = ψ
1
(x)ψ
0
(y)ψ
0
(z)|λx
2
yz|ψ
1
(x)ψ
0
(y)ψ
0
(z) = λx
2
1
y
0
z
0
=0,
1|H
|2 = ψ
0
(x)ψ
0
(y)ψ
1
(z)|λx
2
yz|ψ
0
(x)ψ
1
(y)ψ
0
(z) = λx
2
0
0|y|11|z|0
= λ
2mω
|0|x|1|
2
= λ
2mω
2
[using Problems 2.11 and 3.33].
1|H
|3 = ψ
0
(x)ψ
0
(y)ψ
1
(z)|λx
2
yz|ψ
1
(x)ψ
0
(y)ψ
0
(z) = λ0|x
2
|1y
0
1|z|0 =0,
2|H
|3 = ψ
0
(x)ψ
1
(y)ψ
0
(z)|λx
2
yz|ψ
1
(x)ψ
0
(y)ψ
0
(z) = λ0|x
2
|11|y|0
0
z
0
=0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 181
W =
0 a 0
a 00
000
, where a ≡ λ
2mω
2
.
Eigenvalues of W :
−Ea 0
a −E 0
00−E
= −E
3
+ Ea
2
=0⇒ E = {0, ±a} = 0, ±λ
2mω
2
.
Problem 6.31
(a) The first term is the nucleus/nucleus interaction, the second is the interaction between the nucleus of
atom 2 and the electron in atom 1, the third is between nucleus 1 and electron 2, and the last term is the
interaction between the electrons.
1
R − x
=
1
R
1 −
x
R
−1
=
1
R
1+
x
R
+
x
R
2
+ ...
,
so
H
∼
=
1
4π9
0
e
2
R
1 −
1+
x
1
R
+
x
1
R
2
−
1 −
x
2
R
+
x
2
R
2
+
1+
x
1
− x
2
R
+
x
1
− x
2
R
2
≈
1
4π9
0
e
2
R
−
2x
1
x2
R
2
= −
e
2
x
1
x
2
2π9
0
R
3
.
(b) Expanding Eq. 6.99:
H =
1
2m
p
2
+
+ p
2
−
+
1
2
k
x
2
+
+ x
2
−
−
e
2
4π9
0
R
3
x
2
+
− x
2
−
=
1
2m
p
2
1
+ p
2
2
+
1
2
k
x
2
1
+ x
2
2
−
e
2
4π9
0
R
3
(2x
1
x
2
)=H
0
+ H
(Eqs. 6.96 and 6.98).
(c)
ω
±
=
k
m
1 ∓
e
2
2π9
0
R
3
k
1/2
∼
=
ω
0
1 ∓
1
2
e
2
2π9
0
R
3
mω
2
0
−
1
8
e
2
2π9
0
R
3
mω
2
0
2
+ ...
.
∆V
∼
=
1
2
ω
0
1 −
1
2
e
2
2π9
0
R
3
mω
2
0
−
1
8
e
2
2π9
0
R
3
mω
2
0
2
+
1+
1
2
e
2
2π9
0
R
3
mω
2
0
−
1
8
e
2
2π9
0
R
3
mω
2
0
2
− ω
0
=
1
2ω
0
−
1
4
e
2
2π9
0
R
3
mω
2
0
2
= −
1
8
m
2
ω
3
0
e
2
2π9
0
2
1
R
6
.
(d) In first order:
E
1
0
= 0|H
|0 = −
e
2
2π9
0
R
3
ψ
0
(x
1
)ψ
0
(x
2
)|x
1
x
2
|ψ
0
(x
1
)ψ
0
(x
2
) = −
e
2
2π9
0
R
3
x
0
x
0
=0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

182 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
In second order:
E
2
0
=
∞
n=1
|ψ
n
|H
|ψ
0
|
2
E
0
− E
n
. Here |ψ
0
= |0|0, |ψ
n
= |n
1
|n
2
, so
=
e
2
2π9
0
R
3
2
∞
n
1
=1
∞
n
2
=1
|n
1
|x
1
|0|
2
|n
2
|x
2
|0|
2
E
0,0
− E
n
1
,n
2
[use Problem 3.33]
=
e
2
2π9
0
R
3
2
|1|x|0|
2
|1|x|0|
2
(
1
2
ω
0
+
1
2
ω
0
) − (
3
2
ω
0
+
3
2
ω
0
)
[zero unless n
1
= n
2
=1]
=
e
2
2π9
0
R
3
2
−
1
2ω
0
2mω
0
2
= −
8m
2
ω
3
0
e
2
2π9
0
2
1
R
6
.
Problem 6.32
(a) Let the unperturbed Hamiltonian be H(λ
0
), for some fixed value λ
0
. Now tweak λ to λ
0
+ dλ. The
perturbing Hamiltonian is H
= H(λ
0
+ dλ) − H(λ
0
)=(∂H/∂λ) dλ (derivative evaluated at λ
0
).
The change in energy is given by Eq. 6.9:
dE
n
= E
1
n
= ψ
0
n
|H
|ψ
0
n
= ψ
n
|
∂H
∂λ
|ψ
n
dλ (all evaluated at λ
0
); so
∂E
n
∂λ
= ψ
n
|
∂H
∂λ
|ψ
n
.
[Note: Even though we used perturbation theory, the result is exact, since all we needed (to calculate the
derivative) was the infinitesimal change in E
n
.]
(b) E
n
=(n +
1
2
)ω; H = −
2
2m
d
2
dx
2
+
1
2
mω
2
x
2
.
(i)
∂E
n
∂ω
=(n +
1
2
);
∂H
∂ω
= mωx
2
; so F-H ⇒ (n +
1
2
) = n|mωx
2
|n. But
V =
1
2
mω
2
x
2
, so V = n|
1
2
mω
2
x
2
|n =
1
2
ω(n +
1
2
);
V =
1
2
(n +
1
2
)ω.
(ii)
∂E
n
∂
=(n +
1
2
)ω;
∂H
∂
= −
m
d
2
dx
2
=
2
−
2
2m
d
2
dx
2
=
2
T ;
so F-H ⇒ (n +
1
2
)ω =
2
n|T |n, or
T =
1
2
(n +
1
2
)ω.
(iii)
∂E
n
∂
m
=0;
∂H
∂m
=
2
2m
2
d
2
dx
2
+
1
2
ω
2
x
2
= −
1
m
−
2
2m
d
2
dx
2
+
1
m
1
2
mω
2
x
2
= −
1
m
T +
1
m
V.
So F-H ⇒ 0=−
1
m
T +
1
m
V ,or
T = V . These results are consistent with what we found in
Problems 2.12 and 3.31.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
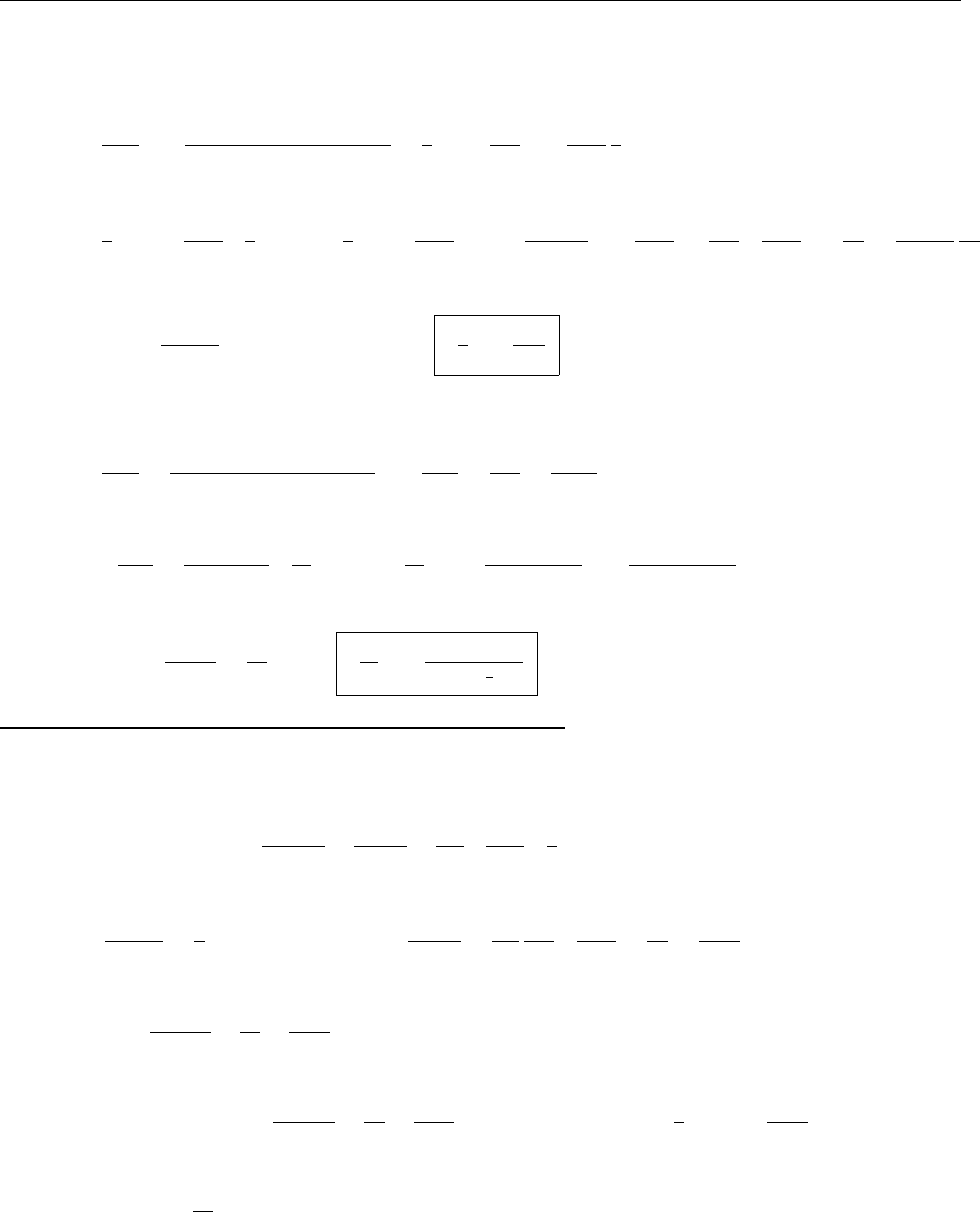
CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 183
Problem 6.33
(a)
∂E
n
∂e
= −
4me
3
32π
2
9
2
0
2
(j
max
+ l +1)
2
=
4
e
E
n
;
∂H
∂e
= −
2e
4π9
0
1
r
. So the F-H theorem says:
4
e
E
n
= −
e
2π9
0
0
1
r
1
, or
0
1
r
1
= −
8π9
0
e
2
E
n
= −
8π9
0
E
1
e
2
n
2
= −
8π9
0
e
2
−
m
2
2
e
2
4π9
0
2
1
n
2
=
e
2
m
4π9
0
2
1
n
2
.
But
4π9
0
2
me
2
= a (by Eq. 4.72), so
0
1
r
1
=
1
n
2
a
.
(Agrees with Eq. 6.55.)
(b)
∂E
n
∂l
=
2me
4
32π
2
9
2
0
2
(j
max
+ l +1)
3
= −
2E
n
n
;
∂H
∂l
=
2
2mr
2
(2l + 1); so F-H says
−
2E
n
n
=
2
(2l +1)
2m
0
1
r
2
1
, or
0
1
r
2
1
= −
4mE
n
n(2l +1)
2
= −
4mE
1
n
3
(2l +1)
2
.
But −
4mE
1
2
=
2
a
2
, so
0
1
r
2
1
=
1
n
3
(l +
1
2
)a
2
. (Agrees with Eq. 6.56.)
Problem 6.34
Equation 4.53 ⇒ u
=
l(l +1)
r
2
−
2mE
n
2
−
2m
2
e
2
4π9
0
1
r
u.
But
me
2
4π9
0
2
=
1
a
(Eq. 4.72), and −
2mE
n
2
=
2m
2
m
2
2
e
2
4π9
0
2
1
n
2
=
1
a
2
n
2
. So
u
=
l(l +1)
r
2
−
2
ar
+
1
n
2
a
2
u.
∴
(ur
s
u
) dr =
ur
s
l(l +1)
r
2
−
2
ar
+
1
n
2
a
2
udr = l(l +1)r
s−2
−
2
a
r
s−1
+
1
n
2
a
2
r
s
= −
d
dr
(ur
s
)u
dr = −
(u
r
s
u
) dr − s
(ur
s−1
u
) dr.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
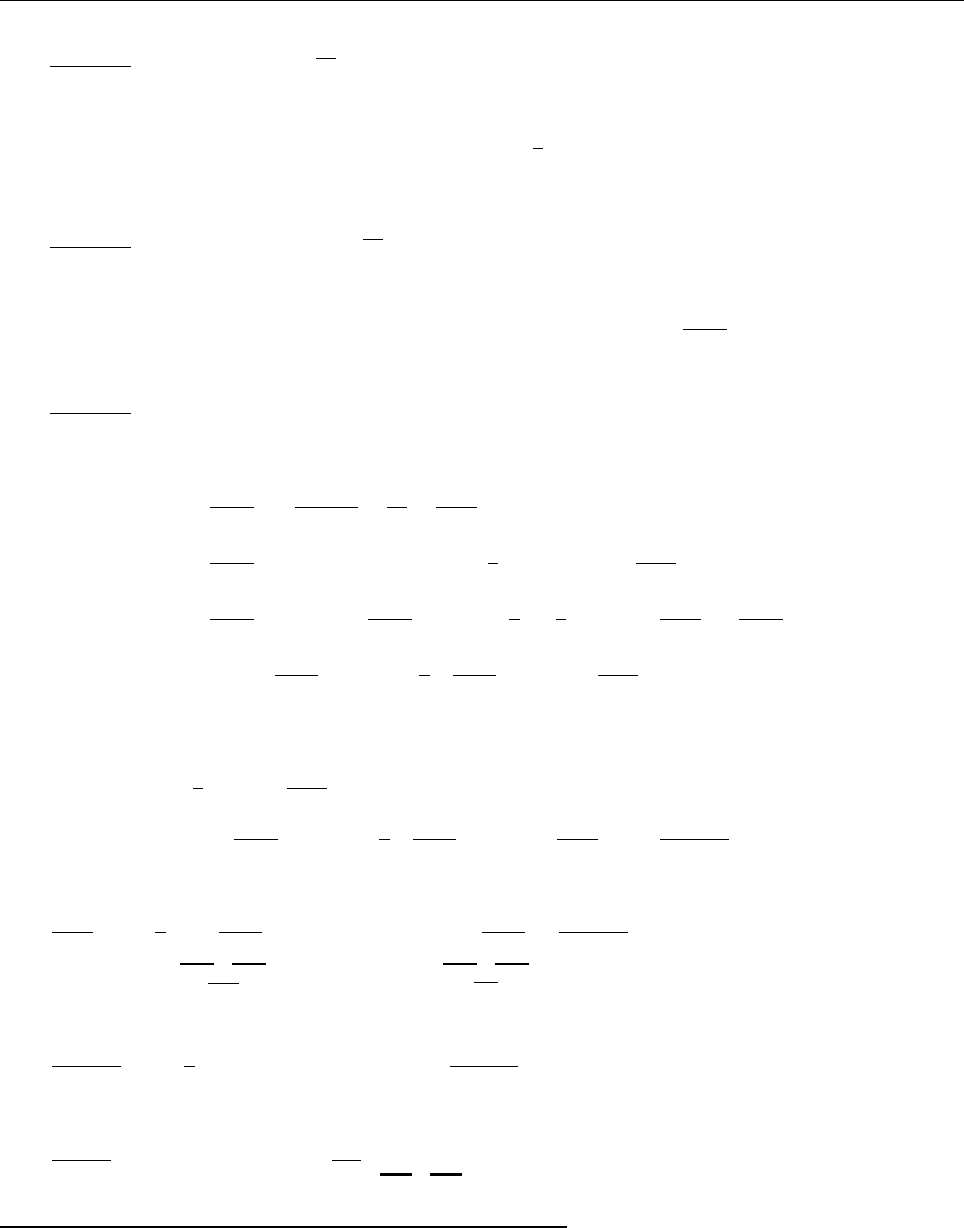
184 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Lemma 1:
(ur
s
u
) dr = −
d
dr
(ur
s
)udr = −
(u
r
s
u) dr − s
ur
s−1
udr ⇒
2
(ur
s
u
) dr = −sr
s−1
, or
(ur
s
u
) dr = −
s
2
r
s−1
.
Lemma 2
:
(u
r
s+1
u
) dr = −
u
d
dr
(r
s+1
u
) dr = −(s +1)
(u
r
s
u
) dr −
(u
r
s+1
u
) dr.
2
(u
r
s+1
u
) dr = −(s +1)
(u
r
s
u
) dr, or:
(u
r
s
u
) dr = −
2
s +1
(u
r
s+1
u
) dr.
Lemma 3
: Use in Lemma 2, and exploit Lemma 1:
(u
r
s
u
) dr = −
2
s +1
l(l +1)
r
2
−
2
ar
+
1
n
2
a
2
(ur
s+1
u
) dr
= −
2
s +1
l(l +1)
(ur
s−1
u
) dr −
2
a
(ur
s
u
) dr +
1
n
2
a
2
(ur
s+1
u
) dr
= −
2
s +1
l(l +1)
−
s − 1
2
r
s−2
−
2
a
−
s
2
r
s−1
+
1
n
2
a
2
−
s +1
2
r
s
= l(l +1)
s − 1
s +1
r
s−2
−
2
a
s
s +1
r
s−1
+
1
n
2
a
2
r
s
.
Plug Lemmas 1 and 3 into :
l(l +1)r
s−2
−
2
a
r
s−1
+
1
n
2
a
2
r
s
= −l(l +1)
s − 1
s +1
r
s−2
+
2
a
s
s +1
r
s−1
−
1
n
2
a
2
r
s
+
s(s − 1)
2
r
s−2
.
2
n
2
a
2
r
s
−
2
a
1+
s
s +1
2s+1
s+1
r
s−1
+
l(l +1)
1+
s − 1
s +1
2s
s+1
−
s(s − 1)
2
r
s−2
=0.
2(s +1)
n
2
a
2
r
s
−
2
a
(2s +1)r
s−1
+2s
l
2
+ l −
(s
2
− 1)
4
r
s−2
=0, or, finally,
(s +1)
n
2
r
s
−a(2s +1)r
s−1
+
sa
2
4
(4l
2
+4l +1
(2l+1)
2
−s
2
)r
s−2
=0. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 185
Problem 6.35
(a)
1
n
2
1−a
0
1
r
1
+0=0⇒
0
1
r
1
=
1
n
2
a
.
2
n
2
r−3a1+
1
4
(2l +1)
2
− 1
a
2
0
1
r
1
=0⇒
2
n
2
r =3a − l(l +1)a
2
1
n
2
a
=
a
n
2
3n
2
− l(l +1)
.
r =
a
2
3n
2
− l(l +1)
.
3
n
2
r
2
−5ar+
1
2
(2l +1)
2
− 4
a
2
=0⇒
3
n
2
r
2
=5a
a
2
3n
2
− l(l +1)
−
a
2
2
(2l +1)
2
− 4
3
n
2
r
2
=
a
2
2
15n
2
− 5l(l +1)− 4l(l +1)− 1+4
=
a
2
2
15n
2
− 9l(l +1)+3
=
3a
2
2
5n
2
− 3l(l +1)+1
; r
2
=
n
2
a
2
2
5n
2
− 3l(l +1)+1
.
4
n
2
r
3
−7ar
2
+
3
4
(2l +1)
2
− 9
a
2
r =0=⇒
4
n
2
r
3
=7a
n
2
a
2
2
5n
2
− 3l(l +1)+1
−
3
4
[4l(l +1)− 8] a
2
a
2
3n
2
− l(l +1)
=
a
3
2
-
35n
4
− 21l(l +1)n
2
+7n
2
− [3l(l +1)− 6]
3n
2
− l(l +1)
.
=
a
3
2
35n
4
− 21l(l +1)n
2
+7n
2
− 9l(l +1)n
2
+3l
2
(l +1)
2
+18n
2
− 6l(l +1)
=
a
3
2
35n
4
+25n
2
− 30l(l +1)n
2
+3l
2
(l +1)
2
− 6l(l +1)
.
r
3
=
n
2
a
3
8
35n
4
+25n
2
− 30l(l +1)n
2
+3l
2
(l +1)
2
− 6l(l +1)
.
(b)
0+a
0
1
r
2
1
−
1
4
(2l +1)
2
− 1
a
2
0
1
r
3
1
=0⇒
0
1
r
2
1
= al(l +1)
0
1
r
3
1
.
(c)
al(l +1)
0
1
r
3
1
=
1
(l +1/2)n
3
a
2
⇒
0
1
r
3
1
=
1
l(l +1/2)(l +1)n
3
a
3
. Agrees with Eq. 6.64.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

186 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Problem 6.36
(a)
|100 =
1
√
πa
3
e
−r/a
(Eq. 4.80),E
1
s
= 100|H
|100 = eE
ext
1
πa
3
e
−2r/a
(r cos θ)r
2
sin θdrdθdφ.
But the θ integral is zero:
π
0
cos θ sin θdθ=
sin
2
θ
2
π
0
=0. So E
1
s
=0. QED
(b) From Problem 4.11:
|1 = ψ
200
=
1
√
2πa
1
2a
1 −
r
2a
e
−r/2a
|2 = ψ
211
= −
1
√
πa
1
8a
2
re
−r/2a
sin θe
iφ
|3 = ψ
210
=
1
√
2πa
1
4a
2
re
−r/2a
cos θ
|4 = ψ
21−1
=
1
√
πa
1
8a
2
re
−r/2a
sin θe
−iφ
1|H
s
|1 = {...}
π
0
cos θ sin θdθ=0
2|H
s
|2 = {...}
π
0
sin
2
θ cos θ sin θdθ =0
3|H
s
|3 = {...}
π
0
cos
2
θ cos θ sin θdθ =0
4|H
s
|4 = {...}
π
0
sin
2
θ cos θ sin θdθ =0
1|H
s
|2 = {...}
2π
0
e
iφ
dφ =0
1|H
s
|4 = {...}
2π
0
e
−iφ
dφ =0
2|H
s
|3 = {...}
2π
0
e
−iφ
dφ =0
2|H
s
|4 = {...}
2π
0
e
−2iφ
dφ =0
3|H
s
|4 = {...}
2π
0
e
−iφ
dφ =0
All matrix elements of H
s
are zero
except 1|H
s
|3 and 3|H
s
|1
(which are complex conjugates,
so only one needs to be evaluated).
1|H
s
|3 = eE
ext
1
√
2πa
1
2a
1
√
2πa
1
4a
2
1 −
r
2a
e
−r/2a
re
−r/2a
cos θ(r cos θ)r
2
sin θdrdθdφ
=
eE
ext
2πa8a
3
(2π)
π
0
cos
2
θ sin θdθ
∞
0
1 −
r
2a
e
−r/a
r
4
dr
=
eE
ext
8a
4
2
3
∞
0
r
4
e
−r/a
dr −
1
2a
∞
0
r
5
e
−r/a
dr
=
eE
ext
12a
4
4!a
5
−
1
2a
5!a
6
=
eE
ext
12a
4
24a
5
1 −
5
2
= eaE
ext
(−3) = −3aeE
ext
.
W = −3aeE
ext
0010
0000
1000
0000
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 187
We need the eigenvalues of this matrix. The characteristic equation is:
−λ 010
0 −λ 00
10−λ 0
000−λ
= −λ
−λ 00
0 −λ 0
00−λ
+
0 −λ 0
10 0
00−λ
= −λ(−λ)
3
+(−λ
2
)=λ
2
(λ
2
− 1) = 0.
The eigenvalues are 0, 0, 1, and −1, so the perturbed energies are
E
2
,E
2
,E
2
+3aeE
ext
,E
2
− 3aeE
ext
. Three levels.
(c) The eigenvectors with eigenvalue 0 are |2 =
0
1
0
0
and |4 =
0
0
0
1
; the eigenvectors with eigenvalues ±1
are |± ≡
1
√
2
1
0
±1
0
. So the “good” states are
ψ
211
,ψ
21−1
,
1
√
2
(ψ
200
+ ψ
210
),
1
√
2
(ψ
200
− ψ
210
).
p
e
4
= −e
1
πa
1
64a
4
r
2
e
−r/a
sin
2
θ
r sin θ cos φ
ˆ
i + r sin θ sin φ
ˆ
j + r cos θ
ˆ
k
r
2
sin θdrdθdφ.
But
2π
0
cos φdφ =
2π
0
sin φdφ =0,
π
0
sin
3
θ cos θdθ =
sin
4
θ
4
π
0
=0, so
p
e
4
= 0. Likewise p
e
2
=0.
p
e
±
= −
1
2
e
(ψ
1
± ψ
3
)
2
(r)r
2
sin θdrdθdφ
= −
1
2
e
1
2πa
1
4a
2
1 −
r
2a
±
r
2a
cos θ
2
e
−r/a
r(sin θ cos φ
ˆ
i + sin θ sin φ
ˆ
j + cos θ
ˆ
k)r
2
sin θdrdθdφ
= −
e
2
ˆ
k
2πa
1
4a
2
2π
1 −
r
2a
±
r
2a
cos θ
2
r
3
e
−r/a
cos θ sin θdrdθ.
But
π
0
cos θ sin θdθ=
π
0
cos
3
θ sin θdθ = 0, so only the cross-term survives:
p
e
±
= −
e
8a
3
ˆ
k
±
1
a
1 −
r
2a
r cos θr
3
e
−r/a
cos θ sin θdrdθ
= ∓
e
8a
4
ˆ
k
π
0
cos
2
θ sin θdθ
∞
0
1 −
r
2a
r
4
e
−r/a
dr = ∓
e
8a
4
ˆ
k
2
3
4!a
5
−
1
2a
5!a
6
= ∓e
ˆ
k
1
12a
4
24a
5
1 −
5
2
=
±3ae
ˆ
k.
Problem 6.37
(a) The nine states are:
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

188 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
l =0
: |300 = R
30
Y
0
0
l =1: |311 = R
31
Y
1
1
|310 = R
31
Y
0
1
|31− 1 = R
31
Y
−1
1
l =2: |322 = R
32
Y
2
2
|321 = R
32
Y
1
2
|320 = R
32
Y
0
2
|32− 1 = R
32
Y
−1
2
|32− 2 = R
32
Y
−2
2
H
s
contains no φ dependence, so the φ integral will be:
nlm|H
s
|n
l
m
= {···}
2π
0
e
−imφ
e
im
φ
dφ, which is zero unless m
= m.
For diagonal elements: nlm|H
s
|nlm = {···}
π
0
[P
m
l
(cos θ)]
2
cos θ sin θdθ. But (p. 137 in the text)
P
m
l
is a polynomial (even or odd) in cos θ, multiplied (if m is odd) by sin θ. Since sin
2
θ =1− cos
2
θ,
[P
m
l
(cos θ)]
2
is a polynomial in even powers of cos θ. So the θ integral is of the form
π
0
(cos θ)
2j+1
sin θdθ= −
(cos θ)
2j+2
(2j +2)
π
0
=0. All diagonal elements are zero.
There remain just 4 elements to calculate:
m = m
=0: 300|H
s
|310, 300|H
s
|320, 310|H
s
|320; m = m
= ±1: 31 ± 1|H
s
|32 ± 1.
300|H
s
|310 = eE
ext
R
30
R
31
r
3
dr
Y
0
0
Y
0
1
cos θ sin θdθdφ. From Table 4.7 :
R
30
R
31
r
3
dr =
2
√
27
1
a
3/2
8
27
√
6
1
a
3/2
1
a
1 −
2r
3a
+
2r
2
27a
2
e
−r/3a
1 −
r
6a
re
−r/3a
r
3
dr.
Let x ≡ 2r/3a:
R
30
R
31
r
3
dr =
2
4
3
5
√
2a
4
3a
2
5
∞
0
1 − x +
x
2
6
1 −
x
4
x
4
e
−x
dx
=
a
2
√
2
∞
0
1 −
5
4
x +
5
12
x
2
−
1
24
x
3
x
4
e
−x
dx =
a
2
√
2
4! −
5
4
5! +
5
12
6! −
1
24
7!
= −9
√
2a.
Y
0
0
Y
0
1
cos θ sin θdθdφ=
1
√
4π
3
4π
cos θ cos θ sin θdθdφ=
√
3
4π
2π
π
0
cos
3
θ sin θdθ =
√
3
2
2
3
=
√
3
3
.
300|H
s
|310 = eE
ext
(−9
√
2a)
'
√
3
3
(
=
−3
√
6aeE
ext
.
300|H
s
|320 = eE
ext
R
30
R
31
r
3
dr
Y
0
0
Y
0
2
cos θ sin θ dθ dφ.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 189
Y
0
0
Y
0
2
cos θ sin θdθdφ=
1
√
4π
5
16π
(3 cos
2
θ −1) cos θ sin θdθdφ=0. 300 |H
s
|320 =0.
310|H
s
|320 = eE
ext
R
31
R
32
r
3
dr
Y
0
1
Y
0
2
cos θ sin θ dθ dφ.
R
31
R
32
r
3
dr =
8
27
√
6
1
a
3/2
1
a
4
81
√
30
1
a
3/2
1
a
2
1 −
r
6a
re
−r/3a
r
2
e
−r/3a
r
3
dr
=
2
4
3
8
√
5a
6
3a
2
7
∞
0
1 −
x
4
x
6
e
−x
dx =
a
24
√
5
6! −
1
4
7!
= −
9
√
5
2
a.
Y
0
1
Y
0
2
sin θ cos θdθdφ =
3
4π
5
16π
cos θ(3 cos
2
θ −1) cos θ sin θdθdφ
=
√
15
8π
2π
π
0
(3 cos
4
θ −cos
2
θ) sin θdθ=
√
15
4
−
3
5
cos
5
θ +
1
3
cos
3
θ
π
0
=
2
√
15
.
310|H
s
|320 = eE
ext
'
−
9
√
5
2
a
(
2
√
15
=
−3
√
3aeE
ext
.
31 ± 1|H
s
|32 ± 1 = eE
ext
R
31
R
32
r
3
dr
Y
±1
1
∗
Y
±1
2
cos θ sin θdθdφ.
Y
±1
1
∗
Y
±1
2
cos θ sin θdθdφ =
'
∓
3
8π
('
∓
15
8π
(
sin θe
∓iφ
sin θ cos θe
±iφ
cos θ sin θdθdφ
=
3
√
5
8π
2π
π
0
cos
2
θ(1 −cos
2
θ) sin θdθ=
3
4
√
5
−
cos
3
θ
3
+
cos
5
θ
5
π
0
=
1
√
5
.
31 ± 1|H
s
|32 ± 1 = eE
ext
'
−9
√
5
2
a
(
1
√
5
=
−
9
2
aeE
ext
.
Thus the matrix representing H
s
is (all empty boxes are zero; all numbers multiplied by −aeE
ext
):
(b) The perturbing matrix (below) breaks into a 3×3 block, two 2 ×2 blocks, and two 1 ×1 blocks, so we can
work out the eigenvalues in each block separately.
3 × 3
:3
√
3
0
√
20
√
201
010
;
−λ
√
20
√
2 −λ 1
01−λ
= −λ
3
+ λ +2λ = −λ(λ
2
− 3) = 0;
λ =0, ±
√
3 ⇒ E
1
1
=0,E
1
2
=9aeE
ext
,E
1
3
= −9aeE
ext
.
2 × 2
:
9
2
01
10
;
−λ 1
1 −λ
= λ
2
− 1=0⇒ λ = ±1.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

190 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
300
310 320 311
321 31-1 32-1 322 32-2
300
310
320
311
321
31-1
32-1
322
32-2
3√6
3√6
3√3
3√3
9/2
9/2
9/2
9/2
E
1
4
=
9
2
aeE
ext
,E
1
5
= −
9
2
aeE
ext
. From the other 2×2 we get E
1
6
= E
1
4
,E
1
7
= E
1
5
, and from the 1×1’s we
get E
1
8
= E
1
9
= 0. Thus the perturbations to the energy (E
3
) are:
0 (degeneracy 3)
(9/2)aeE
ext
(degeneracy 2)
−(9/2)aeE
ext
(degeneracy 2)
9aeE
ext
(degeneracy 1)
−9aeE
ext
(degeneracy 1)
Problem 6.38
Equation 6.89 ⇒ E
1
hf
=
µ
0
g
d
e
2
3πm
d
m
e
a
3
S
d
· S
e
;Eq. 6.91 ⇒ S
d
· S
e
=
1
2
(S
2
− S
2
e
− S
2
d
).
Electron has spin
1
2
,soS
2
e
=
1
2
3
2
2
=
3
4
2
; deuteron has spin 1, so S
2
d
= 1(2)
2
=2
2
.
Total spin could be
3
2
[in which case S
2
=
3
2
5
2
2
=
15
4
2
]or
1
2
[in which case S
2
=
3
4
2
]. Thus
S
d
· S
e
=
1
2
15
4
2
−
3
4
2
− 2
2
=
1
2
2
1
2
3
4
2
−
3
4
2
− 2
2
= −
2
; the difference is
3
2
2
, so ∆E =
µ
0
g
d
e
2
2
2πm
d
m
e
a
3
.
But µ
0
9
0
=
1
c
2
⇒ µ
0
=
1
9
0
c
2
, so ∆E =
2g
d
e
2
2
4π9
0
m
d
m
e
c
2
a
3
=
2g
d
4
m
d
m
2
e
c
2
a
4
=
3
2
g
d
g
p
m
p
m
d
∆E
hydrogen
(Eq. 6.98).
Now, λ =
c
ν
=
ch
∆E
, so λ
d
=
2
3
g
p
g
d
m
d
m
p
λ
h
, and since m
d
=2m
p
,λ
d
=
4
3
5.59
1.71
(21 cm) =
92 cm.
Problem 6.39
(a) The potential energy of the electron (charge −e)at(x, y, z) due to q’s at x = ±d alone is:
V = −
eq
4π9
0
1
(x + d)
2
+ y
2
+ z
2
+
1
(x − d)
2
+ y
2
+ z
2
. Expanding (with d x, y, z):
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 191
1
(x ± d)
2
+ y
2
+ z
2
=(x
2
± 2dx + d
2
+ y
2
+ z
2
)
−1/2
=(d
2
± 2dx + r
2
)
−1/2
=
1
d
1 ±
2x
d
+
r
2
d
2
−1/2
≈
1
d
1 ∓
x
d
−
r
2
2d
2
+
3
8
4x
2
d
2
=
1
d
1 ∓
x
d
+
1
2d
2
(3x
2
− r
2
)
.
V = −
eq
4π9
0
d
1 −
x
d
+
1
2d
2
(3x
2
− r
2
)+1+
x
d
+
1
2d
2
(3x
2
− r
2
)
= −
2eq
4π9
0
d
−
eq
4π9
0
d
3
(3x
2
− r
2
)
=2βd
2
+3βx
2
− βr
2
, where β ≡−
e
4π9
0
q
d
3
.
Thus with all six charges in place
H
=2(β
1
d
2
1
+ β
2
d
2
2
+ β
3
d
2
3
)+3(β
1
x
2
+ β
2
y
2
+ β
3
z
2
) − r
2
(β
1
+ β
2
+ β
3
). QED
(b) 100|H
|100 =
1
πa
3
e
−2r/a
H
r
2
sin θdrdθdφ
= V
0
+
3
πa
3
e
−2r/a
(β
1
x
2
+ β
2
y
2
+ β
3
z
2
)r
2
sin θdr dθ dφ −
(β
1
+ β
2
+ β
3
)
πa
3
r
2
e
−2r/a
r
2
sin θdrdθdφ.
I
1
≡
r
2
e
−2r/a
r
2
sin θdrdθdφ=4π
∞
0
r
4
e
−2r/a
dr =4π4!(
a
2
)
5
=3πa
5
.
I
2
≡
e
−2r/a
(β
1
x
2
+ β
2
y
2
+ β
3
z
2
)r
2
sin θdrdθdφ
=
r
4
e
−2r/a
(β
1
sin
2
θ cos
2
φ + β
2
sin
2
θ sin
2
φ + β
3
cos
2
θ) sin θdrdθdφ.
But
2π
0
cos
2
φdφ=
2π
0
sin
2
φdφ= π,
2π
0
dφ =2π. So
=
∞
0
r
4
e
−2r/a
dr
π
0
π(β
1
+ β
2
) sin
2
θ +2πβ
3
cos
2
θ
sin θdθ.
But
π
0
sin
3
θdθ=
4
3
,
π
0
cos
2
θ sin θdθ =
2
3
. So
=4!
a
2
5
4π
3
(β
1
+ β
2
)+
4π
3
β
3
= πa
5
(β
1
+ β
2
+ β
3
).
100|H
|100 = V
0
+
3
πa
3
πa
5
(β
1
+ β
2
+ β
3
) −
(β
1
+ β
2
+ β
3
)
πa
3
3πa
5
= V
0
.
(c) The four states are
|200 = R
20
Y
0
0
|211 = R
21
Y
1
1
|21− 1 = R
21
Y
−1
1
|210 = R
21
Y
0
1
(functional forms in Problem 4.11).
Diagonal elements
: nlm|H
|nlm = V
0
+3
β
1
x
2
+ β
2
y
2
+ β
3
z
2
− (β
1
+ β
2
+ β
3
)r
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

192 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
For |200, x
2
= y
2
= z
2
=
1
3
r
2
(Y
0
0
does not depend on φ, θ; this state has spherical symmetry),
so
200|H
|200 = V
0
. (I could have used the same argument in (b).)
From Problem 6.35(a), r
2
=
n
2
a
2
2
5n
2
− 3l(l +1)+1
, so for n =2,l =1: r
2
=30a
2
. Moreover,
since x
2
= {...}
2π
0
cos
2
φdφ = {...}
2π
0
sin
2
φdφ = y
2
, and x
2
+ y
2
+ z
2
= r
2
, it follows
that x
2
= y
2
=
1
2
(r
2
−z
2
)=15a
2
−
1
2
z
2
. So all we need to calculate is z
2
.
210|z
2
|210 =
1
2πa
1
16a
4
r
2
e
−r/a
cos
2
θ(r
2
cos
2
θ)r
2
sin θdrdθdφ
=
1
16a
5
∞
0
r
6
e
−r/a
dr
π
0
cos
4
θ sin θdθ =
1
16a
5
6!a
7
2
5
=18a
2
; x
2
= y
2
=15a
2
− 9a
2
=6a
2
.
210|H
|210 = V
0
+ 3(6a
2
β
1
+6a
2
β
2
+18a
2
β
3
) − 30a
2
(β
1
+ β
2
+ β
3
)
=
V
0
− 12a
2
(β
1
+ β
2
+ β
3
)+36a
2
β
3
.
21 ± 1|z
2
|21 ± 1 =
1
πa
1
64a
4
r
2
e
−r/a
sin
2
θ(r
2
cos
2
θ)r
2
sin θdrdθdφ
=
1
32a
5
∞
0
r
6
e
−r/a
dr
π
0
(1 − cos
2
θ) cos
2
θ sin θdθ =
1
32a
5
6!a
7
2
3
−
2
5
=6a
2
;
x
2
= y
2
=15a
2
− 3a
2
=12a
2
.
21 ± 1|H
|21 ± 1 = V
0
+ 3(12a
2
β
1
+12a
2
β
2
+6a
2
β
3
) − 30a
2
(β
1
+ β
2
+ β
3
)
=
V
0
+6a
2
(β
1
+ β
2
+ β
3
) − 18a
2
β
3
.
Off-diagonal elements: We need 200|H
|210, 200|H
|21±1, 210|H
|21±1, and 21−1|H
|211.
Now nlm|V
0
|n
l
m
= 0, by orthogonality, and nlm|r
2
|n
l
m
= 0, by orthogonality of Y
m
l
,so
all we need are the matrix elements of x
2
and y
2
(|z
2
| = −|x
2
|−|y
2
). For 200|x
2
|21± 1 and
210|x
2
|21± 1 the φ integral is
2π
0
cos
2
φe
±iφ
dφ =
2π
0
cos
3
φdφ± i
2π
0
cos
2
φ sin φdφ = 0, and the
same goes for y
2
.So 200|H
|21± 1 = 210|H
|21± 1 =0.
For 200|x
2
|210 and 200|y
2
|210 the θ integral is
π
0
cos θ(sin
2
θ) sin θdθ = sin
4
θ/4
π
0
=0, so
200|H
|210 =0. Finally:
21− 1|x
2
|211 = −
1
πa
1
64a
4
r
2
e
−r/a
sin
2
θe
2iφ
(r
2
sin
2
θ cos
2
φ)r
2
sin θdrdθdφ
= −
1
64πa
5
∞
0
r
6
e
−r/a
dr
6!a
7
π
0
sin
5
θdθ
16/15
2π
0
e
2iφ
cos
2
φdφ
π/2
= −
1
64πa
5
6!a
7
16
15
π
2
= −6a
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 193
For y
2
, the φ integral is
2π
0
e
2iφ
sin
2
φdφ= −π/2, so 21 − 1|y
2
|211 =6a
2
, and 21− 1|z
2
|211 =0.
21− 1|H
|211 =3
β
1
(−6a
2
)+β
2
(6a
2
)
= −18a
2
(β
1
− β
2
).
The perturbation matrix is:
200 210 211 21-1
200 V
0
0 0 0
210 0 V
0
− 12a
2
(β
1
+ β
2
)+24a
2
β
3
0 0
211 0 0 V
0
+6a
2
(β
1
+ β
2
) − 12a
2
β
3
−18a
2
(β
1
− β
2
)
21-1 0 0 −18a
2
(β
1
− β
2
) V
0
+6a
2
(β
1
+ β
2
) − 12a
2
β
3
The 2×2 block has the form
AB
BA
; its characteristic equation is (A−λ)
2
−B
2
=0,soA−λ = ±B,
or
λ = A ∓ B = V
0
+6a
2
(β
1
+ β
2
) − 12a
2
β
3
± 18a
2
(β
1
− β
2
)=
V
0
+24a
2
β
1
− 12a
2
β
2
− 12a
2
β
3
,
V
0
− 12a
2
β
1
+24a
2
β
2
− 12a
2
β
3
.
The first-order corrections to the energy (E
2
) are therefore:
9
1
= V
0
9
2
= V
0
− 12a
2
(β
1
+ β
2
− 2β
3
)
9
3
= V
0
− 12a
2
(−2β
1
+ β
2
+ β
3
)
9
4
= V
0
− 12a
2
(β
1
− 2β
2
+ β
3
)
(i) If β
1
= β
2
= β
3
, then 9
1
= 9
2
= 9
3
= 9
4
= V
0
: one level (still 4-fold degenerate).
(ii) If β
1
= β
2
= β
3
, then 9
1
= V
0
,9
2
= V
0
− 24a
2
(β
1
− β
3
),9
3
= 9
4
= V
0
+12a
2
(β
1
− β
3
): three levels
(one remains doubly degenerate).
(iii) If all three β’s are different, there are
four levels (no remaining degeneracy).
Problem 6.40
(a) (i) Equation 6.10: (H
0
− E
0
0
)ψ
1
0
= −(H
− E
1
0
)ψ
0
0
.
H
0
= −
2
2m
∇
2
−
e
2
4π9
0
1
r
= −
2
2m
∇
2
+
2
ar
, since a =
4π9
0
2
me
2
.
E
0
0
= −
2
2ma
2
.
H
= eE
ext
r cos θ; E
1
0
= 0 (Problem6.36(a)).
ψ
0
0
=
1
√
πa
3
e
−r/a
; ψ
1
0
= f(r)e
−r/a
cos θ.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

194 CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY
Equation 4.13 ⇒
∇
2
ψ
1
0
=
cos θ
r
2
d
dr
r
2
d
dr
fe
−r/a
+
fe
−r/a
r
2
sin θ
d
dθ
sin θ
d
dθ
(cos θ)
=
cos θ
r
2
d
dr
r
2
f
−
1
a
f
e
−r/a
+
fe
−r/a
r
2
sin θ
d
dθ
−sin
2
θ
=
cos θ
r
2
2r
f
−
1
a
f
e
−r/a
+ r
2
f
−
2
a
f
+
1
a
2
f
e
−r/a
−
2 cos θ
r
2
fe
−r/a
= cos θe
−r/a
f
−
2
a
f
+
1
a
2
f
+2
f
−
1
a
f
1
r
− 2f
1
r
2
.
Plug this into Eq. 6.10:
−
2
2m
cos θe
−r/a
f
−
2
a
f
+
1
a
2
f
+2
f
−
1
a
f
1
r
− 2f
1
r
2
+2f
1
a
1
r
− f
1
a
2
= −eE
ext
r cos θ
1
√
πa
3
e
−r/a
,
f
−
2
a
f
+2f
1
r
− 2f
1
r
2
=
2meE
ext
2
√
πa
3
r =
4γ
a
r, where
γ ≡
meE
ext
2
2
√
πa
.
Now let f (r)=A + Br + Cr
2
,sof
= B +2Cr and f
=2C. Then
2C −
2
a
(B +2Cr)+
2
r
(B +2Cr) −
2
r
2
(A + Br + Cr
2
)=
4γ
a
r.
Collecting like powers of r:
r
−2
: A =0.
r
−1
:2B − 2B = 0 (automatic).
r
0
:2C − 2B/a +4C −2C =0⇒ B =2aC.
r
1
: −4C/a =4γ/a ⇒ C = −γ.
Evidently the function suggested does satisfy Eq. 6.10, with the coefficients A =0,B= −2aγ, C = −γ;
the second-order correction to the wave function is
ψ
1
0
= −γr(r +2a)e
−r/a
cos θ.
(ii) Equation 6.11 says, in this case:
E
2
0
= ψ
0
0
|H
|ψ
1
0
= −
1
√
πa
3
meE
ext
2
2
√
πa
eE
ext
e
−r/a
(r cos θ)r(r +2a)e
−r/a
cos θr
2
sin θdrdθdφ
= −
m(eE
ext
)
2
2πa
2
2
2π
∞
0
r
4
(r +2a)e
−2r/a
dr
π
0
cos
2
θ sin θdθ
= −m
eE
ext
a
2
5!
a
2
6
+2a 4!
a
2
5
−
cos
3
θ
3
π
0
= −m
eE
ext
a
2
27
8
a
6
2
3
=
−m
3eE
ext
a
2
2
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 6. TIME-INDEPENDENT PERTURBATION THEORY 195
(b) (i) This is the same as (a) [note that E
1
0
= 0, as before, since ψ
0
0
is spherically symmetric, so cos θ =0]
except for the r-dependence of H
. So Eq. ⇒
f
+2f
1
r
−
1
a
− 2f
1
r
2
= −
2mep
4π9
0
2
√
πa
3
1
r
2
= −
2β
r
2
, where β ≡
mep
4π9
0
2
√
πa
3
.
The solution this time it obvious: f (r)=β (constant). [For the general solution we would add the general
solution to the homogeneous equation (right side set equal to zero), but this would simply reproduce the
unperturbed ground state, ψ
0
0
, which we exclude—see p. 253.] So
ψ
1
0
= βe
−r/a
cos θ.
(ii) The electric dipole moment of the electron is
p
e
= −er cos θ = −eψ
0
0
+ψ
1
0
|r cos θ|ψ
0
0
+ψ
1
0
= −e
ψ
0
0
|r cos θ|ψ
0
0
+2ψ
0
0
|r cos θ|ψ
1
0
+ ψ
1
0
|r cos θ|ψ
1
0
.
But the first term is zero, and the third is higher order, so
p
e
= −2e
1
√
πa
3
β
e
−r/a
(r cos θ)e
−r/a
cos θr
2
sin θdrdθdφ
= −2e
mep
4π9
0
2
πa
3
2π
∞
0
r
3
e
−2r/a
dr
π
0
cos
2
θ sin θdθ = −
me
2
p
9
0
2
πa
3
3!
a
2
4
2
3
= −
me
2
p
9
0
2
πa
3
3a
4
8
2
3
= −
me
2
pa
4π9
0
2
=
−p.
Evidently the dipole moment associated with the perturbation of the electron cloud cancels the dipole
moment of the nucleus, and the total dipole moment of the atom is zero.
(iii) The first-order correction is zero (as noted in (i)). The second-order correction is
E
2
0
= ψ
0
0
|H
|ψ
1
0
=
1
√
πa
3
−
ep
4π9
0
mep
4π9
0
2
√
πa
3
e
−r/a
cos θ
r
2
e
−r/a
cos θr
2
sin θdrdθdφ
= −m
(ep)
2
(4π9
0
)
2
2
πa
3
2π
∞
0
e
−2r/a
dr
π
0
cos
2
θ sin θdθ = −2m
(ep)
2
(4π9
0
)
2
2
a
3
a
2
2
3
=
4
3
−
me
4
2(4π9
0
)
2
2
p
2
e
2
a
2
=
4
3
p
ea
2
E
1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
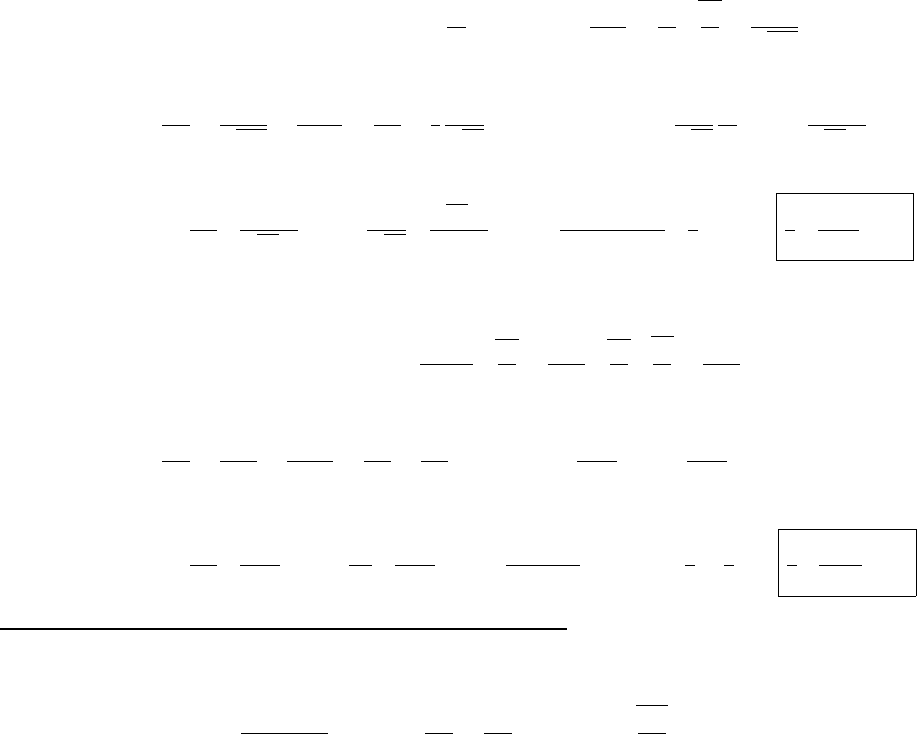
196 CHAPTER 7. THE VARIATIONAL PRINCIPLE
Chapter 7
The Variational Principle
Problem 7.1
(a)
V =2αA
2
∞
0
xe
−2bx
2
dx =2αA
2
−
1
4b
e
−2bx
2
∞
0
=
αA
2
2b
=
α
2b
2b
π
=
α
√
2bπ
.
H =
2
b
2m
+
α
√
2πb
.
∂H
∂b
=
2
2m
−
1
2
α
√
2π
b
−3/2
=0=⇒ b
3/2
=
α
√
2π
m
2
; b =
mα
√
2π
2
2/3
.
H
min
=
2
2m
mα
√
2π
2
2/3
+
α
√
2π
'
√
2π
2
mα
(
1/3
=
α
2/3
2/3
m
1/3
(2π)
1/3
1
2
+1
=
3
2
α
2
2
2πm
1/3
.
(b)
V =2αA
2
∞
0
x
4
e
−2bx
2
dx =2αA
2
3
8(2b)
2
π
2b
=
3α
16b
2
π
2b
2b
π
=
3α
16b
2
.
H =
2
b
2m
+
3α
16b
2
.
∂H
∂b
=
2
2m
−
3α
8b
3
=0=⇒ b
3
=
3αm
4
2
; b =
3αm
4
2
1/3
.
H
min
=
2
2m
3αm
4
2
1/3
+
3α
16
4
2
3αm
2/3
=
α
1/3
4/3
m
2/3
3
1/3
4
−1/3
1
2
+
1
4
=
3
4
3α
4
4m
2
1/3
.
Problem 7.2
Normalize: 1 = 2|A|
2
∞
0
1
(x
2
+ b
2
)
2
dx =2|A|
2
π
4b
3
=
π
2b
3
|A|
2
.A=
2b
3
π
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 7. THE VARIATIONAL PRINCIPLE 197
Kinetic Energy: T = −
2
2m
|A|
2
∞
−∞
1
(x
2
+ b
2
)
d
2
dx
2
1
(x
2
+ b
2
)
dx.
But
d
2
dx
2
1
(x
2
+ b
2
)
=
d
dx
−2x
(x
2
+ b
2
)
2
=
−2
(x
2
+ b
2
)
2
+2x
4x
(x
2
+ b
2
)
3
=
2(3x
2
− b
2
)
(x
2
+ b
2
)
3
, so
T = −
2
2m
2b
3
π
∞
0
(3x
2
− b
2
)
(x
2
+ b
2
)
4
dx = −
4
2
b
3
πm
3
∞
0
1
(x
2
+ b
2
)
3
dx − 4b
2
∞
0
1
(x
2
+ b
2
)
4
dx
= −
4
2
b
3
πm
3
3π
16b
5
− 4b
2
5π
32b
7
=
2
4mb
2
.
Potential Energy: V =
1
2
mω
2
|A|
2
2
∞
0
x
2
(x
2
+ b
2
)
2
dx = mω
2
2b
3
π
π
4b
=
1
2
mω
2
b
2
.
H =
2
4mb
2
+
1
2
mω
2
b
2
.
∂H
∂b
= −
2
2mb
3
+ mω
2
b =0=⇒ b
4
=
2
2m
2
ω
2
=⇒ b
2
=
1
√
2
mω
.
H
min
=
2
4m
√
2mω
+
1
2
mω
2
1
√
2
mω
= ω
'
√
2
4
+
1
2
√
2
(
=
√
2
2
ω
=0.707 ω>
1
2
ω.
Problem 7.3
ψ(x)=
A(x + a/2), (−a/2 <x<0),
A(a/2 − x), (0 <x<a/2),
0, (otherwise).
1=|A|
2
2
a/2
0
a
2
− x
2
dx = −2|A|
2
1
3
a
2
− x
3
a/2
0
=
2
3
|A|
2
a
3
3
=
a
3
12
|A|
2
; A =
12
a
3
(as before).
dψ
dx
=
A, (−a/2 <x<0),
−A, (0 <x<a/2),
0, (otherwise).
d
2
ψ
dx
2
= Aδ
x +
a
2
− 2Aδ(x)+Aδ
x −
a
2
.
T = −
2
2m
ψ
Aδ
x +
a
2
− 2Aδ(x)+Aδ
x −
a
2
dx =
2
2m
2Aψ(0) =
2
m
A
2
a
2
=
2
a
2m
12
a
3
=6
2
ma
2
(as before).
V = −α
|ψ|
2
δ(x) dx = −α|ψ(0)|
2
= −αA
2
a
2
2
= −3
α
a
. H = T + V =6
2
ma
2
− 3
α
a
.
∂
∂a
H = −12
2
ma
3
+3
α
a
2
=0⇒ a =4
2
mα
.
H
min
=6
2
m
mα
4
2
2
− 3α
mα
4
2
=
mα
2
2
3
8
−
3
4
=
−
3mα
2
8
2
> −
mα
2
2
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

198 CHAPTER 7. THE VARIATIONAL PRINCIPLE
Problem 7.4
(a) Follow the proof in §7.1: ψ =
∞
n=1
c
n
ψ
n
, where ψ
1
is the ground state. Since ψ
1
|ψ = 0, we have:
∞
n=1
c
n
ψ
1
|ψ = c
1
= 0; the coefficient of the ground state is zero. So
H =
∞
n=2
E
n
|c
n
|
2
≥ E
fe
∞
n=2
|c
n
|
2
= E
fe
, since E
n
≥ E
fe
for all n except 1.
(b)
1=|A|
2
∞
−∞
x
2
e
−2bx
2
dx = |A|
2
2
1
8b
π
2b
=⇒|A|
2
=4b
2b
π
.
T = −
2
2m
|A|
2
∞
−∞
xe
−bx
2
d
2
dx
2
xe
−bx
2
dx
d
2
dx
2
xe
−bx
2
=
d
dx
e
−bx
2
− 2bx
2
e
−bx
2
= −2bxe
−bx
2
− 4bxe
−bx
2
+4b
2
x
3
e
−bx
2
T = −
2
2m
4b
2b
π
2
∞
0
−6bx
2
+4b
2
x
4
e
−2bx
2
dx = −
2
2
b
m
2b
π
2
−6b
1
8b
π
2b
+4b
2
3
32b
2
π
2b
= −
4
2
b
m
−
3
4
+
3
8
=
3
2
b
2m
.
V =
1
2
mω
2
|A|
2
∞
−∞
x
2
e
−2bx
2
x
2
dx =
1
2
mω
2
4b
2b
π
2
3
32b
2
π
2b
=
3mω
2
8b
.
H =
3
2
b
2m
+
3mω
8b
;
∂H
∂b
=
3
2
2m
−
3mω
2
8b
2
=0=⇒ b
2
=
m
2
ω
2
4
2
=⇒ b =
mω
2
.
H
min
=
3
2
2m
mω
2
+
3mω
2
8
2
mω
= ω
3
4
+
3
4
=
3
2
ω.
This is exact, since the trial wave function is in the form of the true first excited state.
Problem 7.5
(a) Use the unperturbed ground state (ψ
0
gs
) as the trial wave function. The variational principle says
ψ
0
gs
|H|ψ
0
gs
≥E
0
gs
. But H = H
0
+ H
,soψ
0
gs
|H|ψ
0
gs
= ψ
0
gs
|H
0
|ψ
0
gs
+ ψ
0
gs
|H
|ψ
0
gs
. But ψ
0
gs
|H
0
|ψ
0
gs
=
E
0
gs
(the unperturbed ground state energy), and ψ
0
gs
|H
|ψ
0
gs
is precisely the first order correction to the
ground state energy (Eq. 6.9), so E
0
gs
+ E
1
gs
≥ E
gs
. QED
(b) The second order correction (E
2
gs
)isE
2
gs
=
m=gs
|ψ
0
m
|H
|ψ
gs
|
2
E
0
gs
− E
0
m
. But the numerator is clearly positive,
and the denominator is always negative (since E
0
gs
<E
0
m
for all m), so E
2
gs
is negative.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 7. THE VARIATIONAL PRINCIPLE 199
Problem 7.6
He
+
is a hydrogenic ion (see Problem 4.16); its ground state energy is (2)
2
(−13.6 eV), or −54.4 eV. It takes
79.0 − 54.4=
24.6 eV to remove one electron.
Problem 7.7
I’ll do the general case of a nucleus with Z
0
protons. Ignoring electron-electron repulsion altogether gives
ψ
0
=
Z
3
0
πa
3
e
−Z
0
(r
1
+r
2
)/a
, (generalizing Eq. 7.17)
and the energy is 2Z
2
0
E
1
. V
ee
goes like 1/a (Eqs. 7.20 and 7.25), so the generalization of Eq. 7.25 is V
ee
=
−
5
4
Z
0
E
1
, and the generalization of Eq. 7.26 is H =(2Z
2
0
−
5
4
Z
0
)E
1
.
If we include shielding, the only change is that (Z −2) in Eqs. 7.28, 7.29, and 7.32 is replaced by (Z − Z
0
).
Thus Eq. 7.32 generalizes to
H =
2Z
2
− 4Z(Z −Z
0
) −
5
4
Z
E
1
=
−2Z
2
+4ZZ
0
−
5
4
Z
E
1
.
∂H
∂Z
=
−4Z +4Z
0
−
5
4
E
1
=0=⇒ Z = Z
0
−
5
16
.
H
min
=
−2
Z
0
−
5
16
2
+4
Z
0
−
5
16
Z
0
−
5
4
Z
0
−
5
16
E
1
=
−2Z
2
0
+
5
4
Z
0
−
25
128
+4Z
2
0
−
5
4
Z
0
−
5
4
Z
0
+
25
64
E
1
=
2Z
2
0
−
5
4
Z
0
+
25
128
E
1
=
(16Z
0
− 5)
2
128
E
1
,
generalizing Eq. 7.34. The first term is the naive estimate ignoring electron-electron repulsion altogether; the
second term is V
ee
in the unscreened state, and the third term is the effect of screening.
Z
0
=1(H
−
): Z =1−
5
16
=
11
16
=0.688.
The effective nuclear charge is less than 1, as expected.
H
min
=
11
2
128
E
1
=
121
128
E
1
= −12.9 eV.
Z
0
= 2 (He): Z =2−
5
16
=
27
16
=1.69 (as before); H
min
=
27
2
128
E
1
=
729
128
E
1
= −77.5 eV.
Z
0
= 3 (Li
+
): Z =3−
5
16
=
43
16
=2.69
(somewhat less than 3); H
min
=
43
2
128
E
1
=
1849
128
E
1
= −196 eV.
Problem 7.8
D = aψ
0
(r
1
)
1
r
2
ψ
0
(r
1
) = aψ
0
(r
2
)
1
r
1
ψ
0
(r
2
) = a
1
πa
3
e
−2r
2
/a
1
r
1
d
3
r
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

200 CHAPTER 7. THE VARIATIONAL PRINCIPLE
=
1
πa
3
e
−
2
a
√
r
2
+R
2
−2rR cos θ
1
r
r
2
sin θdrdθdφ=
2π
πa
3
∞
0
r
π
0
e
−
2
a
√
r
2
+R
2
−2rR cos θ
sin θdθ
dr.
[...]=
1
rR
r+R
|r−R|
e
−2y/a
ydy= −
a
2rR
e
−2(r+R)/a
r + R +
a
2
− e
−2|r−R|/a
|r −R| +
a
2
D =
2
a
2
−
a
2R
e
−2R/a
∞
0
e
−2r/a
r + R +
a
2
dr
−e
−2R/a
R
0
e
2R/a
R − r +
a
2
dr −e
2R/a
∞
R
e
−2r/a
r −R +
a
2
dr
= −
1
aR
e
−2R/a
a
2
2
+
R +
a
2
a
2
− e
−2R/a
R +
a
2
a
2
e
2r/a
R
0
+e
−2R/a
a
2
2
e
2r/a
2r
a
− 1
R
0
− e
2R/a
−R +
a
2
−
a
2
e
−2r/a
∞
R
− e
2R/a
a
2
2
e
−2r/a
−
2r
a
− 1
∞
R
= −
1
aR
e
−2R/a
a
2
4
+
aR
2
+
a
2
4
+
aR
2
+
a
2
4
+
a
2
4
+
−
aR
2
−
a
2
4
+
a
2
4
2R
a
−
a
2
4
+
aR
2
−
a
2
4
−
a
2
4
2R
a
−
a
2
4
= −
1
aR
e
−2R/a
a
2
+ aR
+
−a
2
=⇒
D =
a
R
−
1+
a
R
e
−2R/a
(confirms Eq. 7.47).
X = aψ
0
(r
1
)
1
r
1
ψ
0
(r
2
) = a
1
πa
3
e
−r
1
/a
e
−r
2
/a
1
r
1
d
3
r
=
1
πa
2
e
−r/a
e
−
√
r
2
+R
2
−2rR cos θ/a
1
r
r
2
sin θdrdθdφ=
2π
πa
2
∞
0
re
−r/a
π
0
e
−
√
r
2
+R
2
−2rR cos θ/a
sin θdθ
dr.
[...]=−
a
rR
e
−(r+R)/a
(r + R + a) − e
−|r−R| /a
(|r −R| + a)
X =
2
a
2
−
a
R
e
−R/a
∞
0
e
−2r/a
(r + R + a)dr
−e
−R/a
R
0
(R − r + a)dr −e
R/a
∞
R
e
−2r/a
(r −R + a)dr
= −
2
aR
e
−R/a
a
2
2
+(R + a)
a
2
− e
−R/a
(R + a)R −
R
2
2
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
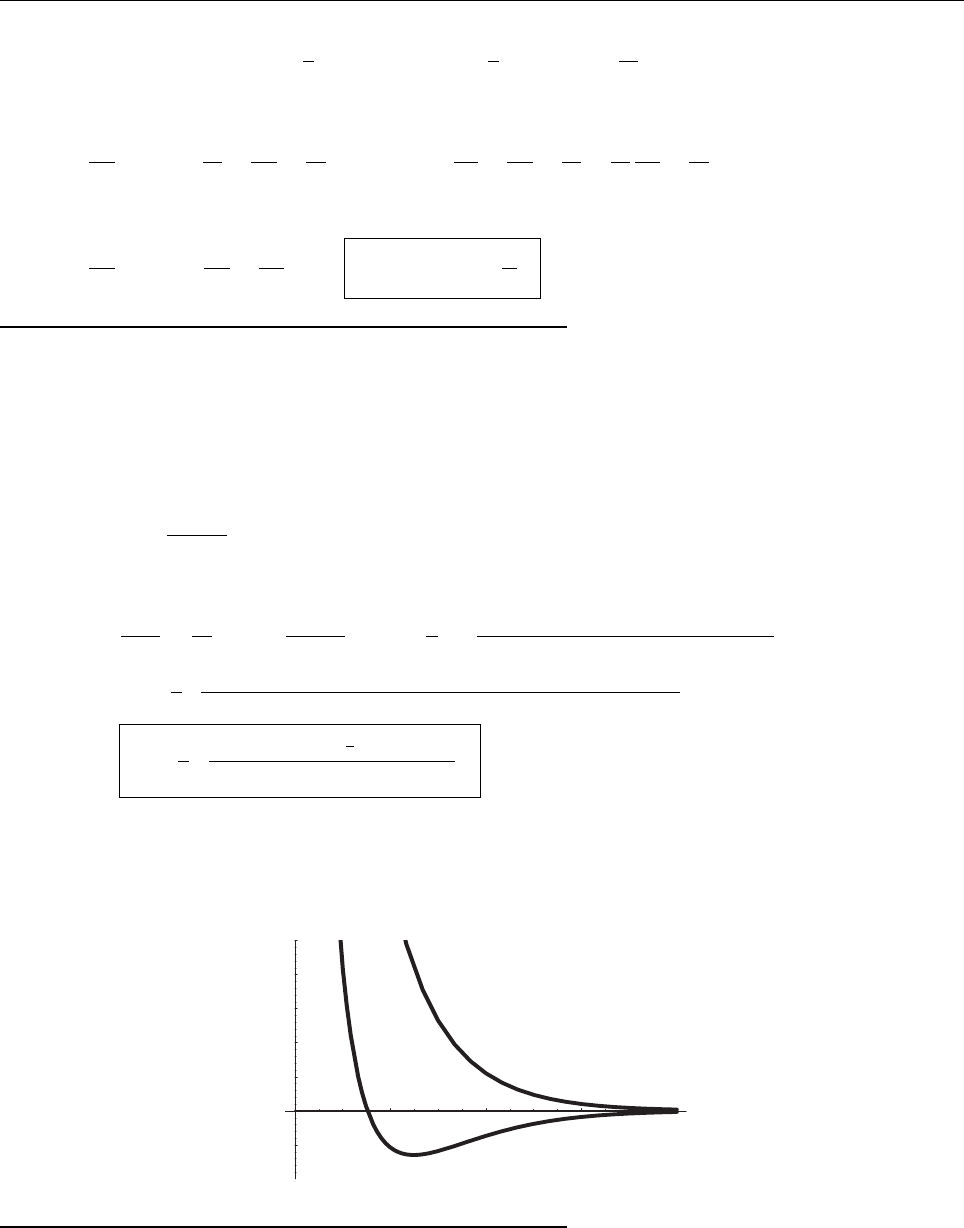
CHAPTER 7. THE VARIATIONAL PRINCIPLE 201
−e
R/a
(−R + a)
−
a
2
e
−2r/a
∞
R
− e
R/a
a
2
2
e
−2r/a
−
2r
a
− 1
∞
R
= −
2
aR
e
−R/a
a
2
4
+
aR
2
+
a
2
2
− R
2
− aR +
R
2
2
+
aR
2
−
a
2
2
−
a
2
4
2R
a
−
a
2
4
= −
2
aR
e
−R/a
−
aR
2
−
R
2
2
=⇒
X = e
−R/a
1+
R
a
(confirms Eq. 7.48).
Problem 7.9
There are two changes: (1) the 2 in Eq. 7.38 changes sign ... which amounts to changing the sign of I in
Eq. 7.43; (2) the last term in Eq. 7.44 changes sign ... which amounts to reversing the sign of X. Thus Eq. 7.49
becomes
H =
1+2
D −X
1 − I
E
1
, and hence Eq. 7.51 becomes
F (x)=
E
tot
−E
1
=
2a
R
− 1 − 2
D −X
1 − I
= −1+
2
x
− 2
1/x − (1+1/x) e
−2x
− (1 + x)e
−x
1 − (1 + x + x
2
/3)e
−x
= −1+
2
x
1 − (1 + x + x
2
/3)e
−x
− 1+(x +1)e
−2x
+(x + x
2
)e
−x
1 − (1 + x + x
2
/3)e
−x
=
−1+
2
x
(1 + x)e
−2x
+
2
3
x
2
− 1
e
−x
1 − (1 + x + x
2
/3)e
−x
.
The graph (with plus sign for comparison) has no minimum, and remains above −1, indicating that the energy
is greater than for the proton and atom dissociated. Hence, no evidence of bonding here.
2
4
6 8
-1.1
-0.9
-0.8
-0.7
-0.6
-0.5
x
F(x)
(−)
(+)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

202 CHAPTER 7. THE VARIATIONAL PRINCIPLE
Problem 7.10
According to Mathematica, the minimum occurs at x =2.493, and at this point F
=0.1257.
mω
2
= V
= −
E
1
a
2
F
, so ω =
1
a
−(0.1257)E
1
m
.
Here m is the reduced mass of the proton: m =
m
p
m
p
m
p
+ m
p
=
1
2
m
p
.
ω =
3 × 10
8
m/s
(0.529 × 10
−10
m)
(0.1257)(13.6 eV)
(938 × 10
6
eV)/2
=3.42 × 10
14
/s.
1
2
ω =
1
2
(6.58 × 10
−16
eV · s)(3.42 × 10
14
/s) = 0.113 eV (ground state vibrational energy).
Mathematica says that at the minimum F = −1.1297, so the binding energy is (0.1297)(13.6 eV) = 1.76 eV.
Since this is substantially greater than the vibrational energy, it stays bound. The highest vibrational energy is
given by (n +
1
2
)ω =1.76 eV, so n =
1.76
0.226
−
1
2
=7.29. I estimate
eight bound vibrational states (including
n = 0).
Problem 7.11
(a)
1=
|ψ|
2
dx = |A|
2
a/2
−a/2
cos
2
πx
a
dx = |A|
2
a
2
⇒ A =
2
a
.
T = −
2
2m
ψ
d
2
ψ
dx
2
dx =
2
2m
π
a
2
ψ
2
dx =
π
2
2
2ma
2
.
V =
1
2
mω
2
x
2
ψ
2
dx =
1
2
mω
2
2
a
a/2
−a/2
x
2
cos
2
πx
a
dx =
mω
2
a
a
π
3
π/2
−π/2
y
2
cos
2
ydy
=
mω
2
a
2
π
3
y
3
6
+
y
2
4
−
1
8
sin 2y +
y cos 2y
4
π/2
−π/2
=
mω
2
a
2
4π
2
π
2
6
− 1
.
H =
π
2
2
2ma
2
+
mω
2
a
2
4π
2
π
2
6
− 1
;
∂H
∂a
= −
π
2
2
ma
3
+
mω
2
a
2π
2
π
2
6
− 1
=0 ⇒
a = π
mω
2
π
2
/6 − 1
1/4
.
H
min
=
π
2
2
2mπ
2
mω
π
2
/6 − 1
2
+
mω
2
4π
2
π
2
6
− 1
π
2
mω
2
π
2
/6 − 1
=
1
2
ω
π
2
3
− 2
=
1
2
ω(1.136) >
1
2
ω.
[We do not need to worry about the kink at ±a/2. It is true that d
2
ψ/dx
2
has delta functions there, but
since ψ(±a/2) = 0 no “extra” contribution to T comes from these points.]
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 7. THE VARIATIONAL PRINCIPLE 203
(b) Because this trial function is odd, it is orthogonal to the ground state, so by Problem 7.4 H will give
an upper bound to the first excited state.
1=
|ψ|
2
dx = |B|
2
a
−a
sin
2
πx
a
dx = |B|
2
a ⇒ B =
1
√
a
.
T = −
2
2m
ψ
d
2
ψ
dx
2
dx =
2
2m
π
a
2
ψ
2
dx =
π
2
2
2ma
2
.
V =
1
2
mω
2
x
2
ψ
2
dx =
1
2
mω
2
1
a
a
−a
x
2
sin
2
πx
a
dx =
mω
2
2a
a
π
3
π
−π
y
2
sin
2
ydy
=
mω
2
a
2
2π
3
y
3
6
−
y
2
4
−
1
8
sin 2y −
y cos 2y
4
π
−π
=
mω
2
a
2
4π
2
2π
2
3
− 1
.
H =
π
2
2
2ma
2
+
mω
2
a
2
4π
2
2π
2
3
− 1
;
∂H
∂a
= −
π
2
2
ma
3
+
mω
2
a
2π
2
2π
2
3
− 1
=0 ⇒
a = π
mω
2
2π
2
/3 − 1
1/4
.
H
min
=
π
2
2
2mπ
2
mω
2π
2
/3 − 1
2
+
mω
2
4π
2
2π
2
3
− 1
π
2
mω
2
2π
2
/3 − 1
=
1
2
ω
4π
2
3
− 2
=
1
2
ω(3.341) >
3
2
ω.
Problem 7.12
We will need the following integral repeatedly:
∞
0
x
k
(x
2
+ b
2
)
l
dx =
1
2b
2l−k−1
Γ
k+1
2
Γ
2l−k−1
2
Γ(l)
.
(a)
1=
∞
−∞
|ψ|
2
dx =2|A|
2
∞
0
1
(x
2
+ b
2
)
2n
dx =
|A|
2
b
4n−1
Γ
1
2
Γ
4n−1
2
Γ(2n)
⇒ A =
b
4n−1
Γ(2n)
Γ
1
2
Γ
4n−1
2
.
T = −
2
2m
∞
−∞
ψ
d
2
ψ
dx
2
dx = −
2
2m
A
2
∞
−∞
1
(x
2
+ b
2
)
n
d
dx
−2nx
(x
2
+ b
2
)
n+1
dx
=
n
2
m
A
2
∞
−∞
1
(x
2
+ b
2
)
n
1
(x
2
+ b
2
)
n+1
−
2(n +1)x
2
(x
2
+ b
2
)
n+2
dx
=
2n
2
m
A
2
∞
0
1
(x
2
+ b
2
)
2n+1
dx − 2(n +1)
∞
0
x
2
(x
2
+ b
2
)
2n+2
dx
=
2n
2
m
b
4n−1
Γ(2n)
Γ
1
2
Γ
4n−1
2
1
2b
4n−1
Γ
1
2
Γ
4n−1
2
Γ(2n +1)
−
2(n +1)
2b
4n−1
Γ
3
2
Γ
4n+1
2
Γ(2n +2)
=
2
4mb
2
n(4n − 1)
(2n +1)
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

204 CHAPTER 7. THE VARIATIONAL PRINCIPLE
V =
1
2
mω
2
∞
−∞
ψ
2
x
2
dx =
1
2
mω
2
2A
2
∞
0
x
2
(x
2
+ b
2
)
2n
dx
= mω
2
b
4n−1
Γ(2n)
Γ
1
2
Γ
4n−1
2
1
2b
4n−3
Γ
3
2
Γ
4n−3
2
Γ(2n)
=
mω
2
b
2
2(4n − 3)
.
H =
2
4mb
2
n(4n − 1)
(2n +1)
+
mω
2
b
2
(4n − 3)
;
∂H
∂b
= −
2
2mb
3
n(4n − 1)
(2n +1)
+
mω
2
b
(4n − 3)
=0 ⇒
b =
mω
n(4n − 1)(4n − 3)
2(2n +1)
1/4
.
H
min
=
2
4m
n(4n − 1)
(2n +1)
mω
2(2n +1)
n(4n − 1)(4n − 3)
+
mω
2
2(4n − 3)
mω
n(4n − 1)(4n − 3)
2(2n +1)
=
1
2
ω
2n(4n − 1)
(2n + 1)(4n − 3)
=
1
2
ω
8n
2
− 2n
8n
2
− 2n − 3
>
1
2
ω.
(b)
1=2|B|
2
∞
0
x
2
(x
2
+ b
2
)
2n
dx =
|B|
2
b
4n−3
Γ
3
2
Γ
4n−3
2
Γ(2n)
⇒ B =
b
4n−3
Γ(2n)
Γ
3
2
Γ
4n−3
2
.
T = −
2
2m
B
2
∞
−∞
x
(x
2
+ b
2
)
n
d
dx
1
(x
2
+ b
2
)
n
−
2nx
2
(x
2
+ b
2
)
n+1
dx
= −
2
B
2
2m
∞
−∞
x
(x
2
+ b
2
)
n
−2nx
(x
2
+ b
2
)
n+1
−
4nx
(x
2
+ b
2
)
n+1
+
4n(n +1)x
3
(x
2
+ b
2
)
n+2
dx
=
4n
2
B
2
2m
3
∞
0
x
2
(x
2
+ b
2
)
2n+1
dx − 2(n +1)
∞
0
x
4
(x
2
+ b
2
)
2n+2
dx
=
2n
2
m
b
4n−3
Γ(2n)
Γ
3
2
Γ
4n−3
2
3
2b
4n−1
Γ
3
2
Γ
4n−1
2
Γ(2n +1)
−
2(n +1)
2b
4n−1
Γ
5
2
Γ
4n−1
2
Γ(2n +2)
=
3
2
4mb
2
n(4n − 3)
(2n +1)
.
V =
1
2
mω
2
2B
2
∞
0
x
4
(x
2
+ b
2
)
2n
dx =
1
2
mω
2
b
4n−3
Γ(2n)
Γ
3
2
Γ
4n−3
2
2
2b
4n−5
Γ
5
2
Γ
4n−5
2
Γ(2n)
=
3
2
mω
2
b
2
(4n − 5)
.
H =
3
2
4mb
2
n(4n − 3)
(2n +1)
+
3
2
mω
2
b
2
(4n − 5)
;
∂H
∂b
= −
3
2
2mb
3
n(4n − 3)
(2n +1)
+
3mω
2
b
(4n − 5)
=0 ⇒
b =
mω
n(4n − 3)(4n − 5)
2(2n +1)
1/4
.
H
min
=
3
2
4m
n(4n − 3)
(2n +1)
mω
2(2n +1)
n(4n − 3)(4n − 5)
+
3
2
mω
2
(4n − 5)
mω
n(4n − 3)(4n − 5)
2(2n +1)
=
3
2
ω
2n(4n − 3)
(2n + 1)(4n − 5)
=
3
2
ω
8n
2
− 6n
8n
2
− 6n − 5
>
3
2
ω.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 7. THE VARIATIONAL PRINCIPLE 205
(c) As n →∞, ψ becomes more and more “gaussian”. In the figures I have plotted the trial wave functions
for n =2,n = 3, and n = 4, as well as the exact states (heavy line). Even for n = 2 the fit is pretty good,
so it is hard to see the improvement, but the successive curves do move perceptably toward the correct
result.
1
2 3
4
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
1
2 3
4
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Analytically, for large n, b ≈
mω
n · 4n · 4n
2 · 2n
1/4
=
2n
mω
, so
x
2
+ b
2
n
= b
2n
1+
x
2
b
2
n
≈ b
2n
1+
mωx
2
2n
n
→ b
2n
e
mωx
2
/2
.
Meanwhile, using Stirling’s approximation (Eq. 5.84), in the form Γ(z +1)≈ z
z
e
−z
:
A
2
=
b
4n−1
Γ(2n)
Γ
1
2
Γ
2n −
1
2
≈
b
4n−1
√
π
(2n − 1)
2n−1
e
−(2n−1)
2n −
3
2
2n−3/2
e
−(2n−3/2)
≈
b
4n−1
√
π
1
√
e
2n − 1
2n −
3
2
2n−1
2n − 3/2.
But
1 −
1
2n
1 −
3
4n
≈
1 −
1
2n
1+
3
4n
≈ 1+
3
4n
−
1
2n
=1+
1
4n
;
so
2n − 1
2n −
3
2
2n−1
≈
1+
1
4n
n
2
1
1+1/4n
→
e
1/4
2
=
√
e.
=
b
4n−1
√
πe
√
e
√
2n =
2n
π
b
4n−1
⇒ A ≈
2n
π
1/4
b
2n−1/2
. So
ψ ≈
2n
π
1/4
b
2n−1/2
1
b
2n
e
−mωx
2
/2
=
2n
π
1/4
mω
2n
1/4
e
−mωx
2
/2
=
mω
π
1/4
e
−mωx
2
/2
,
which is precisely the ground state of the harmonic oscillator (Eq. 2.59). So it’s no accident that we get
the exact energies, in the limit n →∞.
Problem 7.13
1=|A|
2
e
−2br
2
r
2
sin θdrdθdφ=4π|A|
2
∞
0
r
2
e
−2br
2
dr = |A|
2
π
2b
3/2
⇒ A =
2b
π
3/4
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

206 CHAPTER 7. THE VARIATIONAL PRINCIPLE
V = −
e
2
4π9
0
|A|
2
4π
∞
0
e
−2br
2
1
r
r
2
dr = −
e
2
4π9
0
2b
π
3/2
4π
1
4b
= −
e
2
4π9
0
2
2b
π
.
T = −
2
2m
|A|
2
e
−br
2
(∇
2
e
−br
2
) r
2
sin θdrdθdφ
But (∇
2
e
−br
2
)=
1
r
2
d
dr
r
2
d
dr
e
−br
2
=
1
r
2
d
dr
−2br
3
e
−br
2
=
−2b
r
2
3r
2
− 2br
4
e
−br
2
.
=
−
2
2m
2b
π
3/2
(4π)(−2b)
∞
0
(3r
2
− 2br
4
)e
−2br
2
dr =
2
m
πb4
2b
π
3/2
3
1
8b
π
2b
− 2b
3
32b
2
π
2b
=
2
m
4πb
2b
π
3
8b
−
3
16b
=
3
2
b
2m
.
H =
3
2
b
2m
−
e
2
4π9
0
2
2b
π
;
∂H
∂b
=
3
2
2m
−
e
2
4π9
0
2
π
1
√
b
=0 ⇒
√
b =
e
2
4π9
0
2
π
2m
3
2
.
H
min
=
3
2
2m
e
2
4π9
0
2
2
π
4m
2
9
4
−
e
2
4π9
0
2
2
π
e
2
4π9
0
2
π
2m
3
2
=
e
2
4π9
0
2
m
2
4
3π
−
8
3π
= −
m
2
2
e
2
4π9
0
2
8
3π
=
8
3π
E
1
= −11.5 eV.
Problem 7.14
Let ψ =
1
√
πb
3
e
−r/b
(same as hydrogen, but with a → b adjustable). From Eq. 4.191, we have T = −E
1
=
2
2ma
2
for hydrogen, so in this case T =
2
2mb
2
.
V = −
e
2
4π9
0
4π
πb
3
∞
0
e
−2r/b
e
−µr
r
r
2
dr = −
e
2
4π9
0
4
b
3
∞
0
e
−(µ+2/b)r
rdr= −
e
2
4π9
0
4
b
3
1
(µ +2/b)
2
= −
e
2
4π9
0
1
b(1 +
µb
2
)
2
.
H =
2
2mb
2
−
e
2
4π9
0
1
b(1 +
µb
2
)
2
.
∂H
∂b
= −
2
mb
3
+
e
2
4π9
0
1
b
2
(1 + µb/2)
2
+
µ
b(1 + µb/2)
3
= −
2
mb
3
+
e
2
4π9
0
(1+3µb/2)
b
2
(1 + µb/2)
3
=0 ⇒
2
m
4π9
0
e
2
= b
(1+3µb/2)
(1 + µb/2)
3
, or b
(1+3µb/2)
(1 + µb/2)
3
= a.
This determines b, but unfortunately it’s a cubic equation. So we use the fact that µ is small to obtain a suitable
approximate solution. If µ = 0, then b = a (of course), so µa 1=⇒ µb 1 too. We’ll expand in powers of
µb:
a ≈ b
1+
3µb
2
1 −
3µb
2
+6
µb
2
2
≈ b
1 −
9
4
(µb)
2
+
6
4
(µb)
2
= b
1 −
3
4
(µb)
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 7. THE VARIATIONAL PRINCIPLE 207
Since the
3
4
(µb)
2
term is already a second-order correction, we can replace b by a:
b ≈
a
1 −
3
4
(µb)
2
≈ a
1+
3
4
(µa)
2
.
H
min
=
2
2ma
2
1+
3
4
(µa)
2
2
−
e
2
4π9
0
1
a
1+
3
4
(µa)
2
1+
1
2
(µa)
2
≈
2
2ma
2
1 − 2
3
4
(µa)
2
−
e
2
4π9
0
1
a
1 −
3
4
(µa)
2
1 − 2
µa
2
+3
µa
2
2
= −E
1
1 −
3
2
(µa)
2
+2E
1
1 − µa +
3
4
(µa)
2
−
3
4
(µa)
2
=
E
1
1 − 2(µa)+
3
2
(µa)
2
.
Problem 7.15
(a)
H =
E
a
h
hE
b
; det(H − λ)=(E
a
− λ)(E
b
− λ) − h
2
=0=⇒ λ
2
− λ(E
a
+ E
b
)+E
a
E
b
− h
2
=0.
λ =
1
2
E
a
+ E
b
±
E
2
a
+2E
a
E
b
+ E
2
b
− 4E
a
E
b
+4h
2
⇒
E
±
=
1
2
E
a
+ E
b
±
(E
a
− E
b
)
2
+4h
2
.
(b) Zeroth order: E
0
a
= E
a
,E
0
b
= E
b
. First order: E
1
a
= ψ
a
|H
|ψ
a
=0,E
1
b
= ψ
b
|H
|ψ
b
= 0. Second
order:
E
2
a
=
|ψ
b
|H
|ψ
a
|
2
E
a
− E
b
= −
h
2
E
b
− E
a
; E
2
b
=
|ψ
a
|H
|ψ
b
|
2
E
b
− E
a
=
h
2
E
b
− E
a
;
E
−
≈ E
a
−
h
2
(E
b
− E
a
)
; E
+
≈ E
b
+
h
2
(E
b
− E
a
)
.
(c)
H = cos φψ
a
+ sin φψ
b
|(H
0
+ H
)|cos φψ
a
+ sin φψ
b
= cos
2
φ ψ
a
|H
0
|ψ
a
+ sin
2
φ ψ
b
|H
0
|ψ
b
+ sin φ cos φ ψ
b
|H
|ψ
a
+ sin φ cos φ ψ
a
|H
|ψ
b
= E
a
cos
2
φ + E
b
sin
2
φ +2h sin φ cos φ.
∂H
∂φ
= −E
a
2 cos φ sin φ + E
b
2 sin φ cos φ +2h(cos
2
φ − sin
2
φ)=(E
b
− E
a
) sin 2φ +2h cos 2φ =0.
tan 2φ = −
2h
E
b
− E
a
= −9 where 9 ≡
2h
E
b
− E
a
.
sin 2φ
1 − sin
2
2φ
= −9; sin
2
2φ = 9
2
(1 − sin
2
2φ);
or sin
2
2φ(1 + 9
2
)=9
2
; sin 2φ =
±9
√
1+9
2
; cos
2
2φ =1−sin
2
2φ =1−
9
2
1+9
2
=
1
1+9
2
;
cos 2φ =
∓1
√
1+9
2
(sign dictated by tan 2φ =
sin 2φ
cos 2φ
= −9).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

208 CHAPTER 7. THE VARIATIONAL PRINCIPLE
cos
2
φ =
1
2
(1 + cos 2φ)=
1
2
1 ∓
1
√
1+9
2
; sin
2
φ =
1
2
(1 − cos 2φ)=
1
2
1 ±
1
√
1+9
2
.
H
min
=
1
2
E
a
1 ∓
1
√
1+9
2
+
1
2
E
b
1 ±
1
√
1+9
2
± h
9
√
1+9
2
=
1
2
E
a
+ E
b
±
(E
b
− E
a
+2h9)
√
1+9
2
But
(E
b
− E
a
+2h9)
√
1+9
2
=
(E
b
− E
a
)+2h
2h
(E
b
−E
a
)
1+
4h
2
(E
b
−E
a
)
2
=
(E
b
− E
a
)
2
+4h
2
(E
b
− E
a
)
2
+4h
2
=
(E
b
− E
a
)
2
+4h
2
, So
H
min
=
1
2
E
a
+ E
b
±
(E
b
− E
a
)
2
+4h
2
we want the minus sign (+ is maximum)
=
1
2
E
a
+ E
b
−
(E
b
− E
a
)
2
+4h
2
.
(d) If h is small, the exact result (a) can be expanded: E
±
=
1
2
(E
a
+ E
b
) ± (E
b
− E
a
)
1+
4h
2
(E
b
−E
a
)
2
.
=⇒ E
±
≈
1
2
E
a
+ E
b
± (E
b
− E
a
)
1+
2h
2
(E
b
− E
a
)
2
=
1
2
E
a
+ E
b
± (E
b
− E
a
) ±
2h
2
(E
b
− E
a
)
,
so E
+
≈ E
b
+
h
2
(E
b
− E
a
)
,E
−
≈ E
a
−
h
2
(E
b
− E
a
)
,
confirming the perturbation theory results in (b). The variational principle (c) gets the ground state (E
−
)
exactly right—not too surprising since the trial wave function Eq. 7.56 is almost the most general state
(there could be a relative phase factor e
iθ
).
Problem 7.16
For the electron, γ = −e/m,soE
±
= ±eB
z
/2m (Eq. 4.161). For consistency with Problem 7.15, E
b
>E
a
,
so χ
b
= χ
+
=
1
0
,χ
a
= χ
−
=
0
1
,E
b
= E
+
=
eB
z
2m
,E
a
= E
−
= −
eB
z
2m
.
(a)
χ
a
|H
|χ
a
=
eB
x
m
2
01
01
10
0
1
=
eB
x
2m
01
1
0
=0;
χ
b
|H
|χ
b
=
eB
x
2m
10
01
10
1
0
=0; χ
b
|H
|χ
a
=
eB
x
2m
10
01
10
0
1
=
eB
x
2m
;
χ
a
|H
|χ
b
=
eB
x
2m
01
01
10
1
0
=
eB
x
2m
01
0
1
=
eB
x
2m
. So
h =
eB
x
2m
,
and the conditions of Problem 7.15 are met.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 7. THE VARIATIONAL PRINCIPLE 209
(b) From Problem 7.15(b),
E
gs
≈ E
a
−
h
2
(E
b
− E
a
)
= −
eB
z
2m
−
(eB
x
/2m)
2
(eB
z
/m)
=
−
e
2m
B
z
+
B
2
x
2B
z
.
(c) From Problem 7.15(c), E
gs
=
1
2
E
a
+ E
b
−
(E
b
− E
a
)
2
+4h
2
(it’s actually the exact ground state).
E
gs
= −
1
2
eB
z
m
2
+4
eB
x
2m
2
= −
e
2m
B
2
z
+ B
2
x
(which was obvious from the start, since the square root is simply the magnitude of the total field).
Problem 7.17
(a)
r
1
=
1
√
2
(u + v); r
2
=
1
√
2
(u − v); r
2
1
+ r
2
2
=
1
2
(u
2
+2u · v + v
2
+ u
2
− 2u · v + v
2
)=u
2
+ v
2
.
(∇
2
1
+ ∇
2
2
)f(r
1
, r
2
)=
∂
2
f
∂x
2
1
+
∂
2
f
∂y
2
1
+
∂
2
f
∂z
2
1
+
∂
2
f
∂x
2
2
+
∂
2
f
∂y
2
2
+
∂
2
f
∂z
2
2
.
∂f
∂x
1
=
∂f
∂u
x
∂u
x
∂x
1
+
∂f
∂v
x
∂v
x
∂x
1
=
1
√
2
∂f
∂u
x
+
∂f
∂v
x
;
∂f
∂x
2
=
∂f
∂u
x
∂u
x
∂x
2
+
∂f
∂v
x
∂v
x
∂x
2
=
1
√
2
∂f
∂u
x
−
∂f
∂v
x
.
∂
2
f
∂x
2
1
=
1
√
2
∂
∂x
1
∂f
∂u
x
+
∂f
∂v
x
=
1
√
2
∂
2
f
∂u
2
x
∂u
x
∂x
1
+
∂
2
f
∂u
x
∂v
x
∂v
x
∂x
1
+
∂
2
f
∂v
x
∂u
x
∂u
x
∂x
1
+
∂
2
f
∂v
2
x
∂v
x
∂x
1
=
1
2
∂
2
f
∂u
2
x
+2
∂
2
f
∂u
x
∂v
x
+
∂
2
f
∂v
2
x
;
∂
2
f
∂x
2
2
=
1
√
2
∂
∂x
2
∂f
∂u
x
−
∂f
∂v
x
=
1
√
2
∂
2
f
∂u
2
x
∂u
x
∂x
2
+
∂
2
f
∂u
x
∂v
x
∂v
x
∂x
2
−
∂
2
f
∂v
x
∂u
x
∂u
x
∂x
2
−
∂
2
f
∂v
2
x
∂v
x
∂x
2
=
1
2
∂
2
f
∂u
2
x
− 2
∂
2
f
∂u
x
∂v
x
+
∂
2
f
∂v
2
x
.
So
∂
2
f
∂x
2
1
+
∂
2
f
∂x
2
2
=
∂
2
f
∂u
2
x
+
∂
2
f
∂v
2
x
, and likewise for y and z: ∇
2
1
+ ∇
2
2
= ∇
2
u
+ ∇
2
v
.
H = −
2
2m
(∇
2
u
+ ∇
2
v
)+
1
2
mω
2
(u
2
+ v
2
) −
λ
4
mω
2
2v
2
=
−
2
2m
∇
2
u
+
1
2
mω
2
u
2
+
−
2
2m
∇
2
v
+
1
2
mω
2
v
2
−
1
2
λmω
2
v
2
. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

210 CHAPTER 7. THE VARIATIONAL PRINCIPLE
(b) The energy is
3
2
ω (for the u part) and
3
2
ω
√
1 − λ (for the v part): E
gs
=
3
2
ω
1+
√
1 − λ
.
(c) The ground state for a one-dimensional oscillator is
ψ
0
(x)=
mω
π
1/4
e
−mωx
2
/2
(Eq. 2.59).
So, for a 3-D oscillator, the ground state is ψ
0
(r)=
mω
π
3/4
e
−mωr
2
/2
, and for two particles
ψ(r
1
, r
2
)=
mω
π
3/2
e
−
mω
2
(r
2
1
+r
2
2
)
. (This is the analog to Eq. 7.17.)
H =
3
2
ω +
3
2
ω + V
ee
=3ω + V
ee
(the analog to Eq. 7.19).
V
ee
= −
λ
4
mω
2
mω
π
3
e
−
mω
(r
2
1
+r
2
2
)
(r
1
− r
2
)
2
r
2
1
−2r
1
·r
2
+r
2
2
d
3
r
1
d
3
r
2
(the analog to Eq. 7.20).
The r
1
· r
2
term integrates to zero, by symmetry, and the r
2
2
term is the same as the r
2
1
term, so
V
ee
= −
λ
4
mω
2
mω
π
3
2
e
−
mω
(r
2
1
+r
2
2
)
r
2
1
d
3
r
1
d
3
r
2
= −
λ
2
mω
2
mω
π
3
(4π)
2
∞
0
e
−mωr
2
2
/
r
2
2
dr
2
∞
0
e
−mωr
2
1
/
r
4
1
dr
1
= −λ
8m
4
ω
5
π
3
1
4
mω
π
mω
3
8
mω
2
π
mω
= −
3
4
λω.
H =3ω −
3
4
λω =
3ω
1 −
λ
4
.
The variational principle says this must exceed the exact ground-state energy (b); let’s check it:
3ω
1 −
λ
4
>
3
2
ω
1+
√
1 − λ
⇔ 2 −
λ
2
> 1+
√
1 − λ ⇔ 1 −
λ
2
>
√
1 − λ ⇔ 1 −λ +
λ
2
4
> 1 −λ.
It checks. In fact, expanding the exact answer in powers of λ, E
gs
≈
3
2
ω(1 + 1 −
1
2
λ)=3ω
1 −
λ
4
,
we recover the variational result.
Problem 7.18
1==
|ψ|
2
d
3
r
1
d
3
r
2
= |A|
2
ψ
2
1
d
3
r
1
ψ
2
2
d
3
r
2
+2
ψ
1
ψ
2
d
3
r
1
ψ
1
ψ
2
d
3
r
2
+
ψ
2
2
d
3
r
1
ψ
2
1
d
3
r
2
= |A|
2
(1+2S
2
+1),
where
S ≡
ψ
1
(r)ψ
2
(r) d
3
r =
(Z
1
Z
2
)
3
πa
3
e
−(Z
1
+Z
2
)r/a
4πr
2
dr =
4
a
3
y
2
3
2a
3
(Z
1
+ Z
2
)
3
=
y
x
3
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 7. THE VARIATIONAL PRINCIPLE 211
A
2
=
1
2
1+(y/x)
6
.
H = −
2
2m
(∇
2
1
+ ∇
2
2
) −
e
2
4π9
0
1
r
1
+
1
r
2
+
e
2
4π9
0
1
|r
1
− r
2
|
,
Hψ = A
−
2
2m
(∇
2
1
+ ∇
2
2
) −
e
2
4π9
0
Z
1
r
1
+
Z
2
r
2
ψ
1
(r
1
)ψ
2
(r
2
)
+
−
2
2m
(∇
2
1
+ ∇
2
2
) −
e
2
4π9
0
Z
1
r
1
+
Z
2
r
2
ψ
2
(r
1
)ψ
1
(r
2
)
+ A
e
2
4π9
0
Z
1
− 1
r
1
+
Z
2
− 1
r
2
ψ
1
(r
1
)ψ
2
(r
2
)+
Z
2
− 1
r
1
+
Z
1
− 1
r
2
ψ
2
(r
1
)ψ
1
(r
2
)
+ V
ee
ψ,
where V
ee
≡
e
2
4π9
0
1
|r
1
− r
2
|
.
The term in first curly brackets is (Z
2
1
+ Z
2
2
)E
1
ψ
1
(r
1
)ψ
2
(r
2
)+(Z
2
2
+ Z
2
1
)ψ
2
(r
1
)ψ
1
(r
2
), so
Hψ =(Z
2
1
+ Z
2
2
)E
1
ψ
+ A
e
2
4π9
0
Z
1
− 1
r
1
+
Z
2
− 1
r
2
ψ
1
(r
1
)ψ
2
(r
2
)+
Z
2
− 1
r
1
+
Z
1
− 1
r
2
ψ
2
(r
1
)ψ
1
(r
2
)
+ V
ee
ψ
H =(Z
2
1
+ Z
2
2
)E
1
+ V
ee
+ A
2
e
2
4π9
0
×
ψ
1
(r
1
)ψ
2
(r
2
)+ψ
2
(r
1
)ψ
1
(r
2
)
Z
1
− 1
r
1
+
Z
2
− 1
r
2
ψ
1
(r
1
)ψ
2
(r
2
) +
Z
2
− 1
r
1
+
Z
1
− 1
r
2
ψ
2
(r
1
)ψ
1
(r
2
)
.
=(Z
1
− 1)ψ
1
(r
1
)
1
r
1
ψ
1
(r
1
) +(Z
2
− 1)ψ
2
(r
2
)
1
r
2
ψ
2
(r
2
)
+(Z
2
− 1)ψ
1
(r
1
)
1
r
1
ψ
2
(r
1
)ψ
2
(r
2
)|ψ
1
(r
2
)
+(Z
1
− 1)ψ
1
(r
1
)|ψ
2
(r
1
)ψ
2
(r
2
)
1
r
2
ψ
1
(r
2
) +(Z
1
− 1)ψ
2
(r
1
)
1
r
1
ψ
1
(r
1
)ψ
1
(r
2
)|ψ
2
(r
2
)
+(Z
2
− 1)ψ
2
(r
1
)|ψ
1
(r
1
)ψ
1
(r
2
)
1
r
2
ψ
2
(r
2
) +(Z
2
− 1)ψ
2
(r
1
)
1
r
1
ψ
2
(r
1
)
+(Z
1
− 1)ψ
1
(r
2
)
1
r
2
ψ
1
(r
2
)
=2(Z
1
− 1)
0
1
r
1
1
+2(Z
1
− 1)
0
1
r
1
2
+2(Z
1
− 1)ψ
1
|ψ
2
ψ
1
1
r
ψ
2
+2(Z
2
− 1)ψ
1
|ψ
2
ψ
1
1
r
ψ
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

212 CHAPTER 7. THE VARIATIONAL PRINCIPLE
But
0
1
r
1
1
= ψ
1
(r)
1
r
ψ
1
(r) =
Z
1
a
;
0
1
r
1
2
=
Z
2
a
, so H =(Z
2
1
+ Z
2
2
)E
1
+ A
2
e
2
4π9
0
2
1
a
(Z
1
− 1)Z
1
+
1
a
(Z
2
− 1)Z
2
+(Z
1
+ Z
2
− 2)ψ
1
|ψ
2
ψ
1
1
r
ψ
2
+ V
ee
.
And ψ
1
|ψ
2
= S =(y/x)
3
, so
ψ
1
1
r
ψ
2
=
(Z
1
Z
2
)
3
πa
3
4π
e
−(Z
1
+Z
2
)r/a
rdr=
y
3
2a
3
a
Z
1
+ Z
2
2
=
y
3
2ax
2
.
H =(x
2
−
1
2
y
2
)E
1
+ A
2
e
2
4π9
0
2
a
Z
2
1
+ Z
2
2
− (Z
1
+ Z
2
)
+(x − 2)
y
x
3
y
3
2x
2
+ V
ee
=(x
2
−
1
2
y
2
)E
1
+4E
1
A
2
x
2
−
1
2
y
2
− x +
1
2
(x − 2)
y
6
x
5
+ V
ee
.
V
ee
=
e
2
4π9
0
ψ
1
|r
1
− r
2
|
ψ
=
e
4π9
0
A
2
ψ
1
(r
1
)ψ
2
(r
2
)+ψ
2
(r
1
)+ψ
1
(r
2
)
1
|r
1
− r
2
|
ψ
1
(r
1
)ψ
2
(r
2
)+ψ
2
(r
1
)ψ
1
(r
2
)
=
e
4π9
0
A
2
2ψ
1
(r
1
)ψ
2
(r
2
)
1
|r
1
− r
2
|
ψ
1
(r
1
)ψ
2
(r
2
) +2ψ
1
(r
1
)ψ
2
(r
2
)
1
|r
1
− r
2
|
ψ
2
(r
1
)ψ
1
(r
2
)
=2
e
4π9
0
A
2
(B + C), where
B ≡ψ
1
(r
1
)ψ
2
(r
2
)
1
|r
1
− r
2
|
ψ
1
(r
1
)ψ
2
(r
2
); C ≡ψ
1
(r
1
)ψ
2
(r
2
)
1
|r
1
− r
2
|
ψ
2
(r
1
)ψ
1
(r
2
).
B =
Z
3
1
Z
3
2
(πa
3
)
2
e
−2Z
1
r
1
/a
e
−2Z
2
r
2
/a
1
|r
1
− r
2
|
d
3
r
1
d
3
r
2
. As on pp 300-301, the r
2
integral is
e
−2Z
2
r
2
/a
1
r
2
1
+ r
2
2
− 2r
1
r
2
cos θ
2
d
3
r
2
=
πa
3
Z
3
2
r
1
1 −
1+
Z
2
r
1
a
e
−2Z
2
r
1
/a
(Eq. 7.24, but with a →
2
Z
2
a).
B =
Z
3
1
Z
3
2
(πa
3
)
2
(πa
3
)
Z
3
2
4π
∞
0
e
−2Z
1
r
1
/a
1
r
1
1 −
1+
Z
2
r
1
a
e
−2Z
2
r
1
/a
r
2
1
dr
1
=
4Z
3
1
a
3
∞
0
r
1
e
−2Z
1
r
1
/a
− r
1
e
−2(Z
1
+Z
2
)r
1
/a
−
Z
2
a
r
2
1
e
−2(Z
1
+Z
2
)r
1
/a
dr
1
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 7. THE VARIATIONAL PRINCIPLE 213
=
4Z
3
1
a
3
a
2Z
1
2
−
a
2(Z
1
+ Z
2
)
2
−
Z
2
a
2
a
2(Z
1
+ Z
2
)
3
=
Z
3
1
a
1
Z
2
1
−
1
(Z
1
+ Z
2
)
2
−
Z
2
(Z
1
+ Z
2
)
3
=
Z
1
Z
2
a(Z
1
+ Z
2
)
1+
Z
1
Z
2
(Z
1
+ Z
2
)
2
=
y
2
4ax
1+
y
2
4x
2
.
C =
Z
3
1
Z
3
2
(πa
3
)
2
e
−Z
1
r
1
/a
e
−Z
2
r
2
/a
e
−Z
2
r
1
/a
e
−Z
1
r
2
/a
1
|r
1
− r
2
|
d
3
r
1
d
3
r
2
=
(Z
1
Z
2
)
3
(πa
3
)
2
e
−(Z
1
+Z
2
)(r
1
+r
2
)/a
1
|r
1
− r
2
|
d
3
r
1
d
3
r
2
.
The integral is the same as in Eq. 7.20, only with a →
4
Z
1
+Z
2
a. Comparing Eqs. 7.20 and 7.25, we see that the
integral itself was
5
4a
πa
3
8
2
=
5
256
π
2
a
5
. So C =
(Z
1
Z
2
)
3
(πa
3
)
2
5π
2
256
4
5
a
5
(Z
1
+ Z
2
)
5
=
20
a
(Z
1
Z
2
)
3
(Z
1
+ Z
2
)
5
=
5
16a
y
6
x
5
.
V
ee
=2
e
4π9
0
A
2
y
2
4ax
1+
y
2
4x
2
+
5
16a
y
6
x
5
=2A
2
(−2E
1
)
y
2
4x
1+
y
2
4x
2
+
5y
4
4x
4
.
H = E
1
x
2
−
1
2
y
2
−
2
[1+(y/x)
6
]
x
2
−
1
2
y
2
− x +
1
2
(x − 2)
y
6
x
5
−
2
[1+(y/x)
6
]
y
2
4x
1+
y
2
4x
2
+
5y
4
4x
4
=
E
1
(x
6
+ y
6
)
(x
2
−
1
2
y
2
)(x
6
+ y
6
) − 2x
6
x
2
−
1
2
y
2
− x +
1
2
y
6
x
4
−
y
6
x
5
+
y
2
4x
+
y
4
16x
3
+
5y
6
16x
5
=
E
1
(x
6
+ y
6
)
x
8
+ x
2
y
6
−
1
2
x
6
y
2
−
1
2
y
8
− 2x
8
+ x
6
y
2
+2x
7
− x
2
y
6
+2xy
6
−
1
2
x
5
y
2
−
1
8
x
3
y
4
−
5
8
xy
6
=
E
1
(x
6
+ y
6
)
−x
8
+2x
7
+
1
2
x
6
y
2
−
1
2
x
5
y
2
−
1
8
x
3
y
4
+
11
8
xy
6
−
1
2
y
8
.
Mathematica finds the minimum of H at x =1.32245,y=1.08505, corresponding to Z
1
=1.0392,Z
2
=
0.2832. At this point,
H
min
=1.0266E
1
= −13.962 eV, which is less than −13.6 eV—but not by much!
Problem 7.19
The calculation is the same as before, but with m
e
→ m
µ
(reduced), where
m
µ
(reduced) =
m
µ
m
d
m
µ
+ m
d
=
m
µ
2m
p
m
µ
+2m
p
=
m
µ
1+m
µ
/2m
p
. From Problem 6.28, m
µ
= 207m
e
, so
1+
m
µ
2m
p
=1+
207
2
(9.11 × 10
−31
)
(1.67 × 10
−27
)
=1.056; m
µ
(reduced) =
207 m
e
1.056
= 196 m
e
.
This shrinks the whole molecule down by a factor of almost 200, bringing the deuterons much closer together,
as desired. The equilibrium separation for the electron case was 2.493 a (Problem 7.10), so for muons, R =
2.493
196
(0.529 × 10
−10
m) = 6.73 × 10
−13
m.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
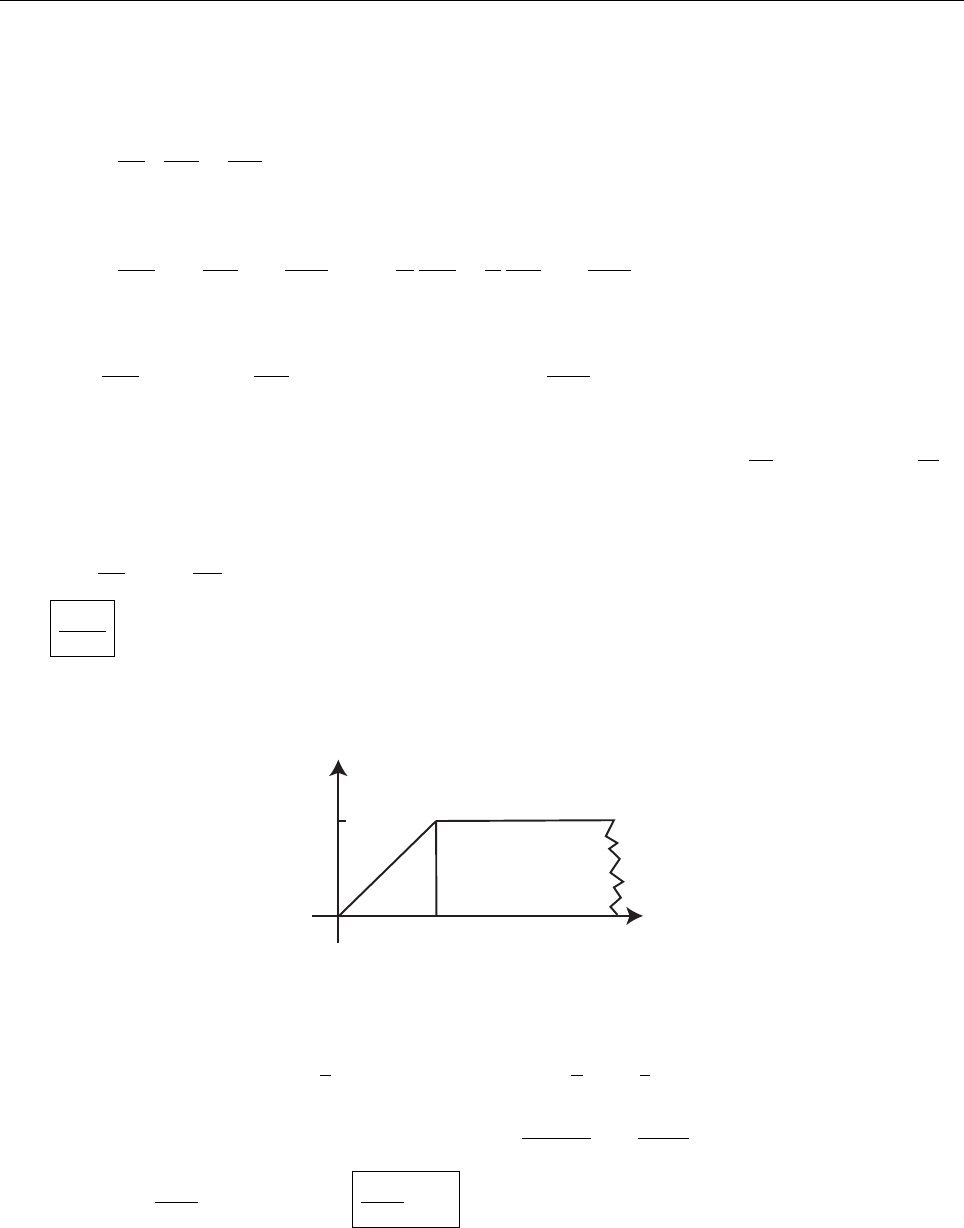
214 CHAPTER 7. THE VARIATIONAL PRINCIPLE
Problem 7.20
(a)
−
2
2m
∂
2
ψ
∂x
2
+
∂
2
ψ
∂y
2
= Eψ. Let ψ(x, y)=X(x)Y (y).
Y
d
2
X
dx
2
+ X
d
2
Y
dy
2
= −
2mE
2
XY ;
1
X
d
2
X
dx
2
+
1
Y
d
2
Y
dy
2
= −
2mE
2
.
d
2
X
dx
2
= −k
2
x
X;
d
2
Y
dy
2
= −k
2
y
Y, with k
2
x
+ k
2
y
=
2mE
2
. The general solution to the y equation is
Y (y)=A cos k
y
y + B sin k
y
y; the boundary conditions Y (±a) = 0 yield k
y
=
nπ
2a
with minimum
π
2a
.
[Note that k
2
y
has to be positive, or you cannot meet the boundary conditions at all.] So
E ≥
2
2m
k
2
x
+
π
2
4a
2
. For a traveling wave k
2
x
has to be positive. Conclusion: Any solution with E<
π
2
2
8ma
2
will be a bound state.
(b)
a
a
x
y
II
I
Integrate over regions I and II (in the figure), and multiply by 8.
I
II
= A
2
∞
x=a
a
y=0
1 −
y
a
2
e
−2αx/a
dx dy. Let u ≡
x
a
,v≡
y
a
,dx= a du, dy = adv.
= A
2
a
2
∞
1
1
0
(1 − v)
2
e
−2αu
du dv = A
2
a
2
(1 − v)
3
3
1
0
×
e
−2αu
2α
∞
1
=
A
2
a
2
6α
(−1)
− e
−2α
=
A
2
a
2
6α
e
−2α
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 7. THE VARIATIONAL PRINCIPLE 215
I
I
=
1
2
A
2
a
x=0
a
y=0
1 −
xy
a
2
2
e
−2α
dx dy
=
1
2
A
2
a
2
1
0
1
0
(1 − uv)
2
e
−2α
du dv =
1
2
A
2
a
2
e
−2α
1
0
(1 − uv)
3
−3v
1
0
dv
= −
1
2
A
2
a
2
e
−2α
1
3
1
0
(1 − v)
3
− 1
v
dv =
1
6
A
2
a
2
e
−2α
1
0
(v
2
− 3v +3)dv,
=
1
6
A
2
a
2
e
−2α
v
3
3
− 3
v
2
2
+3v
1
0
=
11
36
A
2
a
2
e
−2α
.
Normalizing: 8
A
2
a
2
6α
e
−2α
+
11
36
A
2
a
2
e
−2α
=1 ⇒
A
2
=
9α
2a
2
e
2α
(6+11α)
.
H = −
2
2m
ψ|
∂
2
∂x
2
+
∂
2
∂y
2
|ψ = −8
2
2m
(J
I
+ J
II
). [Ignore roof-lines for the moment.]
J
II
= A
2
∞
x=a
a
y=0
1 −
y
a
e
−αx/a
∂
2
∂x
2
+
✼
0
∂
2
∂y
2
1 −
y
a
e
−αx/a
dx dy
= A
2
∞
x=a
a
y=0
1 −
y
a
2
α
a
2
e
−2αx/a
dx dy =
α
a
2
I
II
=
α
✁
a
✄
2
A
2
a
2
6
✚
α
e
−2α
=
1
6
A
2
αe
−2α
.
J
I
=
1
2
A
2
a
0
a
0
1 −
xy
a
2
e
−α
∂
2
∂x
2
+
∂
2
∂y
2
1 −
xy
a
2
e
−α
dx dy = 0.
[Note that
∂
2
∂x
2
1 −
xy
a
2
=
∂
∂x
−
y
a
2
=0, and likewise for ∂
2
/∂y
2
.]
H
so far
= −
2
3
A
2
2
α
m
e
−2α
.
Now the roof-lines; label them as follows:
I. Right arm: at y =0:K
I
.
II. Central square: at x = 0 and at y =0:K
II
.
III. Boundaries: at x = ±a and at y = ±a : K
III
.
K
I
=4
−
2
2m
A
2
∞
x=a
a
y=−a
1 −
|y|
a
e
−αx/a
∂
2
∂x
2
+
∂
2
∂y
2
1 −
|y|
a
e
−αx/a
dx dy.
|y| = y
θ(y) − θ(−y)
,
∂
∂y
1 −
|y|
a
= −
1
a
θ(y) − θ(−y)+
✟
✟
✟
yδ(y)+
✟
✟
✟
yδ(y)
,
∂
2
∂y
2
1 −
|y|
a
= −
1
a
δ(y) −δ(−y)(−1)
= −
2
a
δ(y).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

216 CHAPTER 7. THE VARIATIONAL PRINCIPLE
K
I
= −
2
2
m
A
2
∞
x=a
e
−2αx/a
dx
♣
a
y=−a
1 −
|y|
a
−
2
a
δ(y)
dy
♠
♣ =
e
−2αx/a
(−2α/a)
∞
a
= −
e
−2α
(−2α/a)
=
a
2α
e
−2α
; ♠ = −
2
a
,
=
−
2
2
A
2
m
✁
a
✁
2α
e
−2α
−
2
✁
a
; K
I
=
2
2
mα
e
−2α
A
2
.
K
II
=4A
2
−
2
2m
a
x=0
a
y=−a
1 −
x|y|
a
2
e
−α
∂
2
∂x
2
+
∂
2
∂y
2
1 −
x|y|
a
2
e
−α
dx dy
= −
2
2
m
A
2
e
−2α
a
x=0
a
y=−a
1 −
x|y|
a
2
−
2x
a
2
δ(y)
dx dy
=
−
2
2
A
2
m
e
−2α
−
✁
✁
✁
2
a
2
a
0
xdx
a
2
2
; K
II
=
2
2
m
e
−2α
A
2
.
K
III
=8
−
2
2m
a
y=0
a+5
x=a−5
ψ
∂
2
∂x
2
+
∂
2
∂y
2
ψdxdy.
In this region (x, y both positive) ψ = A
1 − xy/a
2
e
−α
(x<a)
1 − y/a
e
−αx/a
(x>a)
, or
ψ = A
1 −
y
a
θ(x −a)+
x
a
θ(a −x)
e
−α
[
θ(a−x)+
x
a
θ(x−a)
]
.
∂ψ
∂x
= A
−
y
a
✘
✘
✘
✘
δ(x − a)+
1
a
θ(a −x) −
✟
✟
✟
✟
✟
x
a
δ(a − x)
e
−α
[
θ(a−x)+
x
a
θ(x−a)
]
+
1 −
y
a
θ(x −a)+
x
a
θ(a −x)
e
−α
[
θ(a−x)+
x
a
θ(x−a)
]
α
✘
✘
✘
✘
δ(a − x) −
α
a
θ(x −a) −
✘
✘
✘
✘
✘
✘
αx
a
δ(x − a)
[Note: f(x)=xδ(x) should be zero—but perhaps we should check that this is still safe when we’re
planning to take it’s derivative: df/dx = δ(x)+x dδ/dx :
g
df
dx
dx =
g
δ(x)+x
dδ
dx
dx = g(0) +
gx
dδ
dx
dx
= g(0) +
✘
✘
✘
✘
✘
✘✿
0
gxδ(x)|
x=0
−
d
dx
(gx)δ(x)dx = g(0) −
g + x
dg
dx
δ(x)dx
= g(0) − g(0) − (xg
)|
x=0
=0.
This confirms that f(x) can be taken to be zero even when differentiated.]
So δ(x − a) −
x
a
δ(a − x)=
1
a
(a − x)δ(a −x)=0. Hence the cancellations above, leaving
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 7. THE VARIATIONAL PRINCIPLE 217
∂ψ
∂x
= A
−
y
a
2
θ(a −x)e
−α
[
θ(a−x)+
x
a
θ(x−a)
]
−
α
a
θ(x −a)
1 −
y
a
θ(x −a)+
x
a
θ(a −x)
e
−α
[
θ(a−x)+
x
a
θ(x−a)
]
= Ae
−α
[
θ(a−x)+
x
a
θ(x−a)
]
−
y
a
2
θ(a −x) −
α
a
θ(x −a)
1 −
y
a
θ(x −a)+
x
a
θ(a −x)
= −
A
a
e
−α
[
θ(a−x)+
x
a
θ(x−a)
]
y
a
θ(a −x)+αθ(x − a)
1 −
y
a
.
∂
2
ψ
∂x
2
= −
A
a
e
−α
[
θ(a−x)+
x
a
θ(x−a)
]
−
y
a
δ(a − x)+αδ(x −a)
1 −
y
a
− α
−
✘
✘
✘
✘
δ(a − x)+
1
a
θ(x −a)
integral 0
+
✟
✟
✟
✟
✟
x
a
δ(x − a)
= −
A
a
e
−α
δ(x − a)
α −
αy
a
−
y
a
.
K
III
= −
4
2
m
a
y=0
a+5
x=a−5
ψ(x, y)
−
A
a
e
−α
δ(x − a)
α −
αy
a
−
y
a
dx dy
=
4
2
A
ma
e
−α
a
y=0
ψ(a, y)
A(1−y/a)e
−α
α −
αy
a
−
y
a
dy =
4
2
A
2
ma
e
−2α
a
0
α − 2
αy
a
−
y
a
+
αy
2
a
2
+
y
2
a
2
dy
=
4
2
A
2
ma
e
−2α
αa −
✁
2
α
✁
a
a
✄
2
✁
2
−
1
a
a
2
2
+
α
a
2
a
3
3
+
1
a
2
a
3
3
=
4
2
A
2
m
e
−2α
✟
✟
αa −
✟
✟
αa −
✁
a
2
+
α
✁
a
3
+
✁
a
3
α
3
−
1
6
=
1
6
(2α−1)
=
4
2
A
2
6m
(2α − 1)e
−2α
; K
III
=
2
2
A
2
3m
(2α − 1)e
−2α
.
H = −
2
3
A
2
2
α
m
e
−2α
+
2
2
mα
e
−2α
A
2
+
2
2
m
e
−2α
A
2
+
2
2
3m
A
2
(2α − 1)e
−2α
=
A
2
e
−2α
2
m
−
2
3
α +
2
α
+2+
2
3
(2α − 1)
=
2A
2
e
−2α
2
3m
− α +
3
α
+3+2α − 1
=
2A
2
e
−2α
2
3m
α +2+
3
α
=
2A
2
e
−2α
2
3mα
α
2
+2α +3
=
✁
2
3
✘
✘
✘
e
−2α
2
m
✚
α
α
2
+2α +3
9
✁
2
✚
α
a
2
✟
✟
e
2α
(6+11α)
=
3
2
ma
2
(α
2
+2α +3)
(6+11α)
.
dH
dα
=
3
2
ma
2
(6+11α)(2α +2)− (α
2
+2α + 3)(11)
(6+11α)
2
=0 ⇒ (6+11α)(2α + 2) = 11(α
2
+2α +3).
12α +12+22α
2
+22α =11α
2
+22α +33⇒ 11α
2
+12α −21 = 0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

218 CHAPTER 7. THE VARIATIONAL PRINCIPLE
α =
−12 ± 2
(12)
2
+4· 11 · 21
22
=
−6 ±
√
36 + 231
11
=
−6 ± 16.34
11
=
10.34
11
[α has to be positive]=
0.940012239.
H
min
=
3
2
ma
2
2(α +1)
11
=
6
11
2
ma
2
(α +1) = 1.058
2
ma
2
.
But E
threshold
=
π
2
8
2
ma
2
= 1.2337
2
ma
2
,
so E
0
is definitely less than E
threshold
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 8. THE WKB APPROXIMATION 219
Chapter 8
The WKB Approximation
Problem 8.1
a
0
p(x) dx = nπ, with n =1, 2, 3,... and p(x)=
2m[E − V (x)] (Eq. 8.16).
Here
a
0
p(x) dx =
√
2mE
a
2
+
2m(E − V
0
)
a
2
=
√
2m
a
2
√
E +
E − V
0
= nπ
⇒ E + E − V
0
+2
E(E − V
0
)=
4
2m
nπ
a
2
=4E
0
n
;2
E(E − V
0
)=(4E
0
n
− 2E + V
0
).
Square again: 4E(E − V
0
)=4E
2
− 4EV
0
=16E
0
n
2
+4E
2
+ V
2
0
− 16EE
0
n
+8E
0
n
V
0
− 4EV
0
⇒ 16EE
0
n
=16E
0
n
2
+8E
0
n
V
0
+ V
2
0
⇒ E
n
= E
0
n
+
V
0
2
+
V
2
0
16E
0
n
.
Perturbation theory gave E
n
= E
0
n
+
V
0
2
; the extra term goes to zero for very small V
0
(or, since E
0
n
∼ n
2
), for
large n.
Problem 8.2
(a)
dψ
dx
=
i
f
e
if/
;
d
2
ψ
dx
2
=
i
f
e
if/
+
i
(f
)
2
e
if/
=
i
f
−
1
2
(f
)
2
e
if/
.
d
2
ψ
dx
2
= −
p
2
2
ψ =⇒
i
f
−
1
2
(f
)
2
e
if/
= −
p
2
2
e
if/
=⇒ if
− (f
)
2
+ p
2
=0. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

220 CHAPTER 8. THE WKB APPROXIMATION
(b) f
= f
0
+ f
1
+
2
f
2
+ ···=⇒ (f
)
2
=(f
0
+ f
1
+
2
f
2
+ ···)
2
=(f
0
)
2
+2f
0
f
1
+
2
[2f
0
f
2
+(f
1
)
2
]+···
f
= f
0
+ f
1
+
2
f
2
+ ···.i(f
0
+ f
1
+
2
f
2
) − (f
0
)
2
− 2f
0
f
1
−
2
[2f
0
f
2
+(f
1
)
2
]+p
2
+ ···=0.
0
:(f
0
)
2
= p
2
;
1
: if
0
=2f
0
f
1
;
2
: if
1
=2f
0
f
2
+(f
1
)
2
; ...
(c)
df
0
dx
= ±p =⇒ f
0
= ±
p(x)dx + constant ;
df
1
dx
=
i
2
f
0
f
0
=
i
2
±p
±p
=
i
2
d
dx
ln p =⇒ f
1
=
i
2
ln p + const.
ψ = exp
if
= exp
i
±
p(x) dx +
i
2
ln p + K
= exp
±
i
pdx
p
−1/2
e
iK/
=
C
√
p
exp
±
i
pdx
. QED
Problem 8.3
γ =
1
|p(x)|dx =
1
2a
0
2m(V
0
− E) dx =
2a
2m(V
0
− E). T ≈ e
−4a
√
2m(V
0
−E)/
.
From Problem 2.33, the exact answer is
T =
1
1+
V
2
0
4E(V
0
−E)
sinh
2
γ
.
Now, the WKB approximation assumes the tunneling probability is small (p. 322)—which is to say that γ is
large. In this case, sinh γ =
1
2
(e
γ
− e
−γ
) ≈
1
2
e
γ
, and sinh
2
γ ≈
1
4
e
2γ
, and the exact result reduces to
T ≈
1
1+
V
2
0
16E(V
0
−E)
e
2γ
≈
16E(V
0
− E)
V
2
0
e
−2γ
.
The coefficient in {}is of order 1; the dominant dependence on E is in the exponential factor. In this sense
T ≈ e
−2γ
(the WKB result).
Problem 8.4
I take the masses from Thornton and Rex, Modern Physics, Appendix 8. They are all atomic masses, but the
electron masses subtract out in the calculation of E. All masses are in atomic units (u): 1 u = 931 MeV/c
2
.
The mass of He
4
is 4.002602 u, and that of the α-particle is 3727 MeV/c
2
.
U
238
: Z =92,A= 238,m= 238.050784 u → Th
234
: m = 234.043593 u.
r
1
=(1.07 × 10
−15
m)(238)
1/3
=6.63 × 10
−15
m.
E = (238.050784 −234.043593 −4.002602)(931) MeV = 4.27 MeV.
V =
2E
m
=
(2)(4.27)
3727
× 3 × 10
8
m/s=1.44 × 10
7
m/s.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 8. THE WKB APPROXIMATION 221
γ =1.980
90
√
4.27
− 1.485
90(6.63) = 86.19 − 36.28 = 49.9.
τ =
(2)(6.63 × 10
−15
)
1.44 × 10
7
e
98.8
s=7.46 × 10
21
s=
7.46 × 10
21
3.15 × 10
7
yr = 2.4 × 10
14
yrs.
Po
212
: Z =84,A= 212,m= 211.988842 u → Pb
208
: m = 207.976627 u.
r
1
=(1.07 × 10
−15
m)(212)
1/3
=6.38 × 10
−15
m.
E = (211.988842 −207.976627 −4.002602)(931) MeV = 8.95 MeV.
V =
2E
m
=
(2)(8.95)
3727
× 3 × 10
8
m/s=2.08 × 10
7
m/s.
γ =1.980
82
√
8.95
− 1.485
82(6.38) = 54.37 − 33.97 = 20.4.
τ =
(2)(6.38 × 10
−15
)
2.08 × 10
7
e
40.8
s= 3.2 × 10
−4
s.
These results are way off—but note the extraordinary sensitivity to nuclear masses: a tiny change in E produces
enormous changes in τ.
Much more impressive results are obtained when you plot the logarithm of lifetimes against 1/
√
E,asin
Figure 8.6. Thanks to David Rubin for pointing this out. Some experimental values are listed below (all energies
in MeV):
Uranium
(Z = 92):
A E τ
238 4.198 4.468 × 10
9
yr
236 4.494 2.342 × 10
7
yr
234 4.775 2.455 × 10
5
yr
232 5.320 68.9yr
230 5.888 20.8day
228 6.680 9.1 min
226 7.570 0.35 s
Protactinium (Z = 91):
A E τ
224 7.488 0.79 s
222 8.540 2.9ms
220 9.650 0.78 µs
218 9.614 0.12 ms
Thorium (Z = 90):
A E τ
232 4.012 1.405 × 10
10
yr
230 4.687 7.538 × 10
4
yr
228 5.423 1.912 yr
226 6.337 30.57 min
Radium (Z = 88):
A E τ
226 4.784 1600 yr
224 5.685 3.66 day
222 6.559 38 s
220 7.455 18 ms
218 8.389 25.6 µs
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

222 CHAPTER 8. THE WKB APPROXIMATION
Problem 8.5
(a) V (x)=mgx.
(b)
−
2
2m
d
2
ψ
dx
2
+ mgxψ = Eψ =⇒
d
2
ψ
dx
2
=
2m
2
g
2
x −
E
mg
. Let y ≡ x −
E
mg
, and α ≡
2m
2
g
2
1/3
.
Then
d
2
ψ
dy
2
= α
3
yψ. Let z ≡ αy = α(x −
E
mg
), so
d
2
ψ
dz
2
= zψ. This is the Airy equation (Eq. 8.36), and
the general solution is ψ = aAi(z)+bBi(z). However, Bi(z) blows up for large z,sob = 0 (to make ψ
normalizable). Hence
ψ(x)=aAi
α(x −
E
mg
)
.
(c) Since V (x)=∞ for x<0, we require ψ(0) = 0; hence Ai [α(−E/mg)] = 0. Now, the zeros of Ai are
a
n
(n =1, 2, 3,...). Abramowitz and Stegun list a
1
= −2.338,a
2
= −4.088,a
3
= −5.521,a
4
= −6.787,
etc. Here −
αE
n
mg
= a
n
,orE
n
= −
mg
α
a
n
= −mg
2
2m
2
g
1/3
a
n
,or E
n
= −(
1
2
mg
2
2
)
1/3
a
n
. In this case
1
2
mg
2
2
=
1
2
(0.1 kg)(9.8 m/s
2
)
2
(1.055 × 10
−34
J·s)
2
=5.34 × 10
−68
J
3
;(
1
2
mg
2
2
)
1/3
=3.77 × 10
−23
J.
E
1
=8.81 × 10
−23
J,E
2
=1.54 × 10
−22
J,E
3
=2.08 × 10
−22
J,E
4
=2.56 × 10
−22
J.
(d)
2T = x
dV
dX
(Eq. 3.97); here
dV
dx
= mg, so x
dV
dx
= mgx = V , so T =
1
2
V .
But T + V = H = E
n
, so
3
2
V = E
n
, or V =
2
3
E
n
. But V = mgx, so x =
2E
n
3mg
.
For the electron,
1
2
mg
2
2
1/3
=
1
2
(9.11 × 10
−31
)(9.8)
2
(1.055 × 10
−34
)
2
1/3
=7.87 × 10
−33
J.
E
1
=1.84 × 10
−32
J= 1.15 × 10
−13
eV. x =
2(1.84 × 10
−32
)
3(9.11 × 10
−31
)(9.8)
=1.37 × 10
−3
= 1.37 mm.
Problem 8.6
(a)
Eq. 8.47 =⇒
x
2
0
p(x) dx =(n −
1
4
)π, where p(x)=
2m(E − mgx) and E = mgx
2
=⇒ x
2
= E/mg.
x
2
0
p(x) dx =
√
2m
x
2
0
E − mgx dx =
√
2m
−
2
3mg
(E − mgx)
3/2
x
2
0
= −
2
3
2
m
1
g
(E − mgx
2
)
3/2
− E
3/2
=
2
3
2
m
1
g
E
3/2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
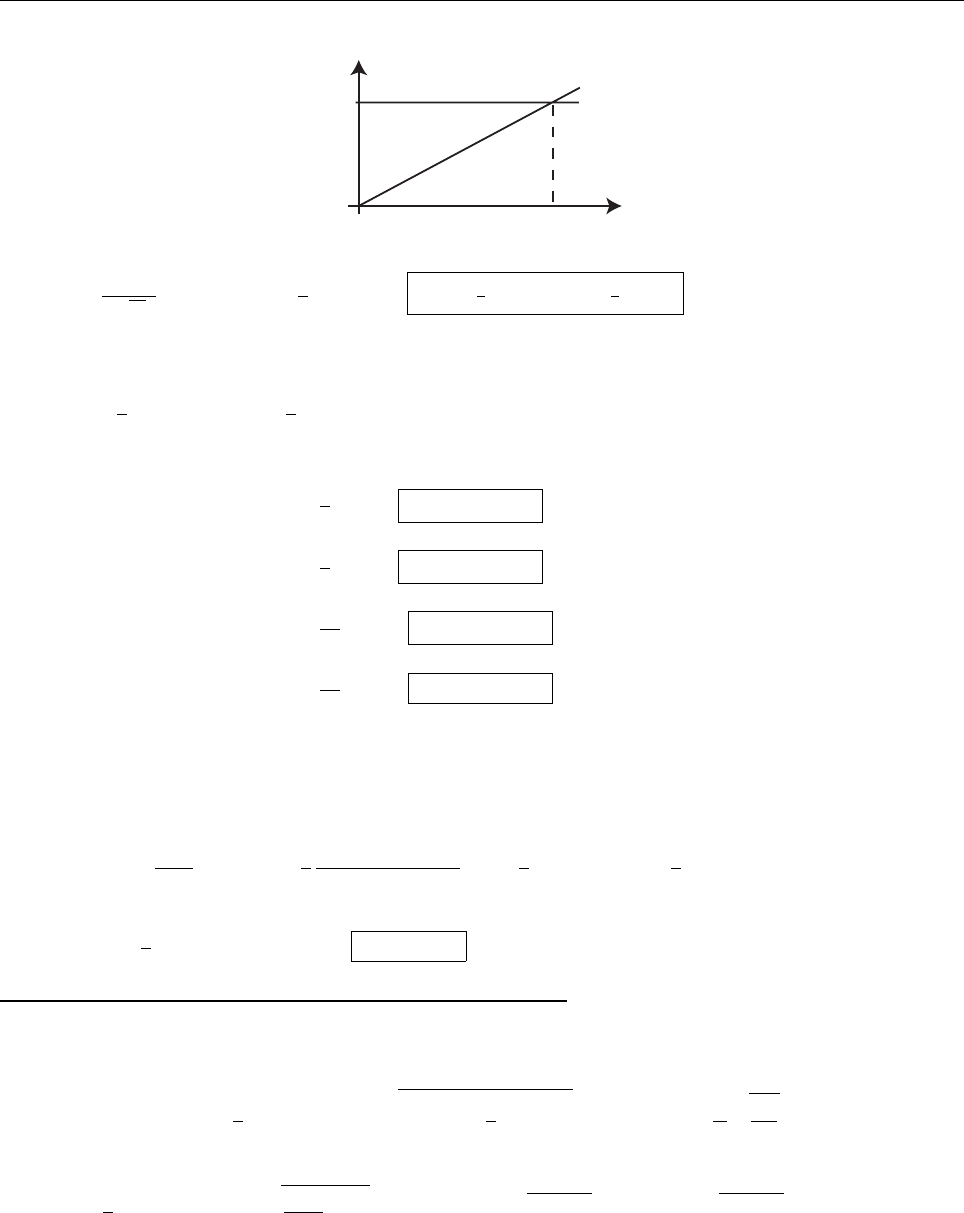
CHAPTER 8. THE WKB APPROXIMATION 223
E
V(x)
x
x
mgx
2
1
3
√
mg
(2E)
3/2
=(n −
1
4
)π, or
E
n
=
9
8
π
2
mg
2
2
(n −
1
4
)
2
1/3
.
(b)
9
8
π
2
mg
2
2
1/3
=
9
8
π
2
(0.1)(9.8)
2
(1.055 × 10
−34
)
2
1/3
=1.0588 × 10
−22
J.
E
1
=(1.0588 × 10
−22
)
3
4
2/3
= 8.74 × 10
−23
J,
E
2
=(1.0588 × 10
−22
)
7
4
2/3
= 1.54 × 10
−22
J,
E
3
=(1.0588 × 10
−22
)
11
4
2/3
= 2.08 × 10
−22
J,
E
4
=(1.0588 × 10
−22
)
15
4
2/3
= 2.56 × 10
−22
J.
These are in very close agreement with the exact results (Problem 8.5(c)). In fact, they agree precisely
(to 3 significant digits), except for E
1
(for which the exact result was 8.81 × 10
−23
J).
(c) From Problem 8.5(d),
x =
2E
n
3mg
, so 1 =
2
3
(1.0588 × 10
−22
)
(0.1)(9.8)
n −
1
4
2/3
, or
n −
1
4
2/3
=1.388 × 10
22
.
n =
1
4
+(1.388 × 10
22
)
3/2
= 1.64 × 10
33
.
Problem 8.7
x
2
x
1
p(x) dx =
n −
1
2
π; p(x)=
2m
E −
1
2
mω
2
x
2
; x
2
= −x
1
=
1
ω
2E
m
.
n −
1
2
π = mω
x
2
−x
2
2E
mω
2
− x
2
dx =2mω
x
2
0
x
2
2
− x
2
dx = mω
x
x
2
2
− x
2
+ x
2
2
sin
−1
(x/x
2
)
x
2
0
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
224 CHAPTER 8. THE WKB APPROXIMATION
= mωx
2
2
sin
−1
(1) =
π
2
mωx
2
2
=
π
2
mω
2E
mω
2
=
πE
ω
.
E
n
=
n −
1
2
ω
(n =1, 2, 3,...)
Since the WKB numbering starts with n = 1, whereas for oscillator states we traditionally start with n =0,
letting n → n + 1 converts this to the usual formula E
n
=(n +
1
2
)ω. In this case the WKB approximation
yields the exact results.
Problem 8.8
(a)
1
2
mω
2
x
2
2
= E
n
=
n +
1
2
ω (counting n =0, 1, 2,...);
x
2
=
(2n +1)
mω
.
(b)
V
lin
(x)=
1
2
mω
2
x
2
2
+(mω
2
x
2
)(x − x
2
)=⇒ V
lin
(x
2
+ d)=
1
2
mω
2
x
2
2
+ mω
2
x
2
d.
V (x
2
+ d) − V
lin
(x
2
+ d)
V (x
2
)
=
1
2
mω
2
(x
2
+ d)
2
−
1
2
mω
2
x
2
2
− mω
2
x
2
d
1
2
mω
2
x
2
2
=
x
2
2
+2x
2
d + d
2
− x
2
2
− 2x
2
d
x
2
2
=
d
x
2
2
=0.01. d =0.1 x
2
.
(c)
α =
2m
2
mω
2
x
2
1/3
(Eq. 8.34), so 0.1 x
2
2m
2
ω
2
2
x
2
1/3
≥ 5=⇒
2m
2
ω
2
2
x
4
2
1/3
≥ 50.
2m
2
ω
2
2
(2n +1)
2
2
m
2
ω
2
≥ (50)
3
;or(2n +1)
2
≥
(50)
3
2
= 62500; 2n +1≥ 250; n ≥
249
2
= 124.5.
n
min
= 125. However, as we saw in Problems 8.6 and 8.7, WKB may be valid at much smaller n.
Problem 8.9
Shift origin to the turning point.
ψ
WKB
=
1
|p(x)|
De
−
1
0
x
|p(x
)|dx
(x<0)
1
|p(x)|
Be
i
x
0
p(x
) dx
+ Ce
−
i
x
0
p(x
) dx
(x>0)
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 8. THE WKB APPROXIMATION 225
x
0
Nonclassical Classical
overlap 2
overlap 1
WKB
P
ψ
ψ
WKB
ψ
patching region
E
Linearized potential in the patching region:
V (x) ≈ E +V
(0)x. Note : V
(0) is negative.
d
2
ψ
p
dx
2
=
2mV
(0)
2
xψ
p
= −α
3
xψ
p
, whereα ≡
2m|V
(0)|
2
1/3
.
ψ
p
(x)=aAi(−αx)+bBi(−αx). (Note change of sign, as compared with Eq. 8.37).
p(x)=
2m[E − E − V
(0)x]=
−2mV
(0)x =
2m|V
(0)|x =
√
α
3
2
x = α
3/2
√
x.
Overlap region 1 (x<0)
:
0
x
|p(x
)|dx
= α
3/2
0
x
√
−x
dx
= α
3/2
−
2
3
(−x
)
3/2
0
x
=
2
3
α
3/2
(−x)
3/2
=
2
3
(−αx)
3/2
.
ψ
WKB
≈
1
1/2
α
3/2
(−x)
1/4
De
−
2
3
(−αx)
3/2
. For large positive argument (−αx 1) :
ψ
p
≈ a
1
2
√
π(−αx)
1/4
e
−
2
3
(−αx)
3/2
+ b
1
√
π(−αx)
1/4
e
2
3
(−αx)
3/2
. Comparing ⇒ a =2D
π
α
; b =0.
Overlap region 2 (x>0)
:
x
0
|p(x
)|dx
= α
3/2
x
0
√
x
dx
= α
3/2
2
3
(x
)
3/2
x
0
=
2
3
(αx)
3/2
.
ψ
WKB
≈
1
1/2
α
3/4
x
1/4
Be
i
2
3
(αx)
3/2
+ Ce
−i
2
3
(αx)
3/2
. For large negative argument (−αx −1) :
ψ
p
(x) ≈ a
1
√
π(αx)
1/4
sin
2
3
(αx)
3/2
+
π
4
=
a
√
π(αx)
1/4
1
2i
e
iπ/4
e
i
2
3
(αx)
3/2
− e
−iπ/4
e
−i
2
3
(αx)
3/2
(remember : b =0).
Comparing the two: B =
a
2i
α
π
e
iπ/4
,C= −
a
2i
α
π
e
−iπ/4
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

226 CHAPTER 8. THE WKB APPROXIMATION
Inserting the expression for a from overlap region 1 : B = −ie
iπ/4
D; C = ie
−iπ/4
D. For x>0, then,
ψ
WKB
=
−iD
p(x)
e
i
x
0
p(x
) dx
+i
π
4
− e
−
i
x
0
p(x
) dx
−i
π
4
=
2D
p(x)
sin
1
x
0
p(x
) dx
+
π
4
.
Finally, switching the origin back to x
1
:
ψ
WKB
(x)=
D
|p(x)|
e
−
1
x
1
x
|p(x
)|dx
, (x<x
1
);
2D
p(x)
sin
1
x
x
1
p(x
)dx
+
π
4
, (x>x
1
).
QED
Problem 8.10
At x
1
, we have an upward-sloping turning point. Follow the method in the book. Shifting origin to x
1
:
ψ
WKB
(x)=
1
p(x)
Ae
i
0
x
p(x
) dx
+ B
−
i
0
x
p(x
) dx
(x<0)
1
p(x)
Ce
1
x
0
|p(x
)|dx
+ D
−
1
x
0
|p(x
)|dx
(x>0)
In overlap region 2
, Eq. 8.39 becomes ψ
WKB
≈
1
1/2
α
3/4
x
1/4
Ce
2
3
(αx)
3/2
+ De
−
2
3
(αx)
3/2
,
whereas Eq. 8.40 is unchanged. Comparing them =⇒ a =2D
π
α
,b= C
π
α
.
In overlap region 1
, Eq. 8.43 becomes ψ
WKB
≈
1
1/2
α
3/4
(−x)
1/4
Ae
i
2
3
(−αx)
3/2
+ Be
−i
2
3
(−αx)
3/2
,
and Eq. 8.44 (with b = 0) generalizes to
ψ
p
(x) ≈
a
√
π(−αx)
1/4
sin
2
3
(−αx)
3/2
+
π
4
+
b
√
π(−αx)
1/4
cos
2
3
(−αx)
3/2
+
π
4
=
1
2
√
π(−αx)
1/4
)
(−ia + b)e
i
2
3
(−αx)
3/2
e
iπ/4
+(ia + b)e
−i
2
3
(−αx)
3/2
e
−iπ/4
. Comparing them =⇒
A =
α
π
−ia + b
2
e
iπ/4
; B =
α
π
ia + b
2
e
−iπ/4
. Putting in the expressions above for a and b :
A =
C
2
− iD
e
iπ/4
; B =
C
2
+ iD
e
−iπ/4
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 8. THE WKB APPROXIMATION 227
These are the connection formulas relating A, B, C, and D,atx
1
.
At x
2
, we have a downward-sloping turning point, and follow the method of Problem 8.9. First rewrite the
middle expression in Eq. 8.52:
ψ
WKB
=
1
|p(x)|
Ce
1
x
2
x
1
|p(x
)|dx
+
1
x
x
2
|p(x
)|dx
+ De
−
1
x
2
x
1
|p(x
)|dx
−
1
x
x
2
|p(x
)|dx
.
Let γ ≡
x
2
x
1
|p(x)|dx, as before (Eq. 8.22), and let C
≡ De
−γ
, D
≡ Ce
γ
. Then (shifting the origin to x
2
):
ψ
WKB
=
1
|p(x)|
C
e
1
0
x
|p(x
)|dx
+ D
e
−
1
0
x
|p(x
)|dx
, (x<0);
1
p(x)
Fe
i
x
0
p(x
) dx
, (x>0).
In the patching region ψ
p
(x)=aAi(−αx)+bBi(−αx), where α ≡
2m|V
(0)|
2
1/3
; p(x)=α
3/2
√
x.
In overlap region 1
(x<0):
0
x
|p(x
)|dx
=
2
3
(−αx)
3/2
, so
ψ
WKB
≈
1
1/2
α
3/4
(−x)
1/4
C
e
2
3
(−αx)
3/2
+ D
e
−
2
3
(−αx)
3/2
ψ
p
≈
a
2
√
π(−αx)
1/4
e
−
2
3
(−αx)
3/2
+
b
√
π(−αx)
1/4
e
2
3
(−αx)
3/2
Comparing =⇒
a =2
π
α
D
b =
π
α
C
In overlap region 2 (x>0):
x
0
p(x
) dx
=
2
3
(αx)
3/2
=⇒ ψ
WKB
≈
1
1/2
α
3/4
x
1/4
Fe
i
2
3
(αx)
3/2
.
ψ
p
≈
a
√
π(αx)
1/4
sin
2
3
(αx)
3/2
+
π
4
+
b
√
π(αx)
1/4
cos
2
3
(αx)
3/2
+
π
4
=
1
2
√
π(αx)
1/4
(−ia + b)e
i
π
4
e
i
2
3
(αx)
3/2
+(ia + b)e
−i
π
4
e
−i
2
3
(αx)
3/2
. Comparing =⇒ (ia + b)=0;
F =
α
π
−ia + b
2
e
iπ/4
= b
α
π
e
iπ/4
.b=
π
α
e
−iπ/4
F ; a = i
π
α
e
−iπ/4
F.
C
=
α
π
b = e
−iπ/4
F, D
=
1
2
α
π
a =
i
2
e
−iπ/4
F. D = e
γ
e
−iπ/4
F ; C =
i
2
e
−γ
e
−iπ/4
F.
These are the connection formulas at x
2
. Putting them into the equation for A:
A =
C
2
− iD
e
iπ/4
=
i
4
e
−γ
e
−iπ/4
F − ie
γ
e
−iπ/4
F
e
iπ/4
= i
e
−γ
4
− e
γ
F.
T =
F
A
2
=
1
(e
γ
−
e
−γ
4
)
2
=
e
−2γ
1 − (e
−γ/2
)
2
2
.
If γ 1, the denominator is essentially 1, and we recover T = e
−2γ
(Eq. 8.22).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

228 CHAPTER 8. THE WKB APPROXIMATION
Problem 8.11
Equation 8.51 ⇒
n −
1
2
π =2
x
2
0
2m(E − αx
ν
) dx =2
√
2mE
x
2
0
1 −
α
E
x
ν
dx; E = αx
ν
2
. Let
z ≡
α
E
x
ν
, so x =
zE
α
1/ν
; dx =
E
α
1/ν
1
ν
z
1
ν
−1
dz. Then
n −
1
2
π =2
√
2mE
E
α
1/ν
1
ν
1
0
z
1
ν
−1
√
1 − zdz =2
√
2mE
E
α
1/ν
1
ν
Γ(1/ν)Γ(3/2)
Γ(
1
ν
+
3
2
)
=2
√
2mE
E
α
1/ν
Γ(
1
ν
+1)
1
2
√
π
Γ(
1
ν
+
3
2
)
=
√
2πmE
E
α
1/ν
Γ(
1
ν
+1)
Γ(
1
ν
+
3
2
)
.
E
1
ν
+
1
2
=
(n −
1
2
)π
√
2πm
α
1/ν
Γ(
1
ν
+
3
2
)
Γ(
1
ν
+1)
;
E
n
=
n −
1
2
π
2mα
Γ(
1
ν
+
3
2
)
Γ(
1
ν
+1)
(
2ν
ν+2
)
α.
For ν =2: E
n
=
n −
1
2
π
2mα
Γ(2)
Γ(3/2)
α =(n −
1
2
)
2α
m
.
For a harmonic oscillator, with α =
1
2
mω
2
,E
n
=
n −
1
2
ω (n =1, 2, 3,...).
Problem 8.12
V (x)=−
2
a
2
m
sech
2
(ax). Eq. 8.51 =⇒
n −
1
2
π =2
x
2
0
2m
E +
2
a
2
m
sech
2
(ax)
dx
=2
√
2a
x
2
0
sech
2
(ax)+
mE
2
a
2
dx.
E = −
2
a
2
m
sech
2
(ax
2
) defines x
2
. Let b ≡−
mE
2
a
2
,z≡ sech
2
(ax), so that x =
1
a
sech
−1
√
z, and hence
dx =
1
a
−1
√
z
√
1 − z
1
2
√
z
dz = −
1
2a
1
z
√
1 − z
dz. Then
n −
1
2
π =2
√
2 a
−
1
2a
z
2
z
1
√
z − b
z
√
1 − z
dz.
Limits :
x =0 =⇒ z = sech
2
(0) = 1
x = x
2
=⇒ z = sech
2
(ax
2
)=−
mE
2
a
2
= b
.
n −
1
2
π =
√
2
1
b
1
z
z − b
1 − z
dz.
1
z
z − b
1 − z
=
1
z
(z − b)
(1 − z)(z − b)
=
1
(1 − z)(z − b)
−
b
z
(1 − z)(z − b)
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 8. THE WKB APPROXIMATION 229
n −
1
2
π =
√
2
1
b
1
(1 − z)(z − b)
dz − b
1
b
1
z
−b +(1+b)z − z
2
dz
=
√
2
−2 tan
−1
1 − z
z − b
−
√
b sin
−1
(1 + b)z − 2b
z(1 − b)
1
b
=
√
2
−2 tan
−1
(0) + 2 tan
−1
(∞) −
√
b sin
−1
(1) +
√
b sin
−1
(−1)
=
√
2
0+2
π
2
−
√
b
π
2
−
√
b
π
2
=
√
2π(1 −
√
b);
(n −
1
2
)
√
2
=1−
√
b;
√
b =1−
1
√
2
n −
1
2
.
Since the left side is positive, the right side must also be: (n −
1
2
) <
√
2,n<
1
2
+
√
2=0.5+1.414=1.914.
So the only possible n is 1; there is only one bound state (which is correct—see Problem 2.51).
For n =1,
√
b =1−
1
2
√
2
; b =1−
1
√
2
+
1
8
=
9
8
−
1
√
2
;
E
1
= −
2
a
2
m
9
8
−
1
√
2
= −0.418
2
a
2
m
.
The exact answer (Problem 2.51(c)) is −0.5
2
a
2
m
. Not bad.
Problem 8.13
n −
1
4
π =
r
0
0
2m [E − V
0
ln(r/a)] dr; E = V
0
ln(r
0
/a) defines r
0
.
=
√
2m
r
0
0
V
0
ln(r
0
/a) − V
0
ln(r/a) dr =
2mV
0
r
0
0
ln(r
0
/r) dr.
Let x ≡ ln(r
0
/r), so e
x
= r
0
/r, or r = r
0
e
−x
=⇒ dr = −r
0
e
−x
dx.
n −
1
4
π =
2mV
0
(−r
0
)
x
2
x
1
√
xe
−e
dx. Limits :
r =0=⇒ x
1
= ∞
r = r
0
=⇒ x
2
=0
.
n −
1
4
π =
2mV
0
r
0
∞
0
√
xe
−x
dx =
2mV
0
r
0
Γ(3/2) =
2mV
0
r
0
√
π
2
.
r
0
=
2π
mV
0
n −
1
4
⇒
E
n
= V
0
ln
a
2π
mV
0
n −
1
4
= V
0
ln
n −
1
4
+ V
0
ln
a
2π
mV
0
.
E
n+1
− E
n
= V
0
ln
n +
3
4
− V
0
ln
n −
1
4
= V
0
ln
n +3/4
n − 1/4
, which is indeed independent of m (and a).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

230 CHAPTER 8. THE WKB APPROXIMATION
Problem 8.14
n −
1
2
π =
r
2
r
1
2m
E +
e
2
4π9
0
1
r
−
2
2m
l(l +1)
r
2
dr =
√
−2mE
r
2
r
1
−1+
A
r
−
B
r
2
dr,
where A ≡−
e
2
4π9
0
1
E
and B ≡−
2
2m
l(l +1)
E
are positive constants, since E is negative.
n −
1
2
π =
√
−2mE
r
2
r
1
√
−r
2
+ Ar −B
r
dr.
Let r
1
and r
2
be the roots of the polynomial in the numerator: − r
2
+ Ar −B =(r − r
1
)(r
2
− r).
n −
1
2
π =
√
−2mE
r
2
r
1
(r −r
1
)(r
2
− r)
r
dr =
√
−2mE
π
2
(
√
r
2
−
√
r
1
)
2
.
2
n −
1
2
=
√
−2mE (r
2
+ r
1
− 2
√
r
1
r
2
) . But −r
2
+ Ar −B = −r
2
+(r
1
+ r
2
)r −r
1
r
2
=⇒ r
1
+ r
2
= A; r
1
r
2
= B. Therefore
2
n −
1
2
=
√
−2mE
A − 2
√
B
=
√
−2mE
'
−
e
2
4π9
0
1
E
− 2
−
2
2m
l(l +1)
E
(
=
e
2
4π9
0
−
2m
E
− 2
l(l +1).
e
2
4π9
0
−
2m
E
=2
n −
1
2
+
l(l +1)
; −
E
2m
=
(e
2
/4π9
0
)
2
4
2
n −
1
2
+
l(l +1)
2
.
E =
−(m/2
2
)(e
2
/4π9
0
)
2
n −
1
2
+
l(l +1)
2
=
−13.6eV
n −
1
2
+
l(l +1)
2
.
Problem 8.15
(a) (i) ψ
WKB
(x)=
D
|p(x)|
e
−
1
x
x
2
|p(x
)|dx
(x>x
2
);
(ii) ψ
WKB
(x)=
1
p(x)
Be
i
x
2
x
p(x
) dx
+ Ce
−
i
x
2
x
p(x
) dx
(x
1
<x<x
2
);
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 8. THE WKB APPROXIMATION 231
(iii) ψ
WKB
(x)=
1
|p(x)|
Fe
1
x
1
x
|p(x
)|dx
+ Ge
−
1
x
1
x
|p(x
)|dx
(0 <x<x
1
).
Equation 8.46 =⇒
(ii) ψ
WKB
=
2D
p(x)
sin
1
x
2
x
p(x
)dx
+
π
4
(x
1
<x<x
2
).
To effect the join at x
1
, first rewrite (ii):
(ii) ψ
WKB
=
2D
p(x)
sin
1
x
2
x
1
p(x
) dx
−
1
x
x
1
p(x
) dx
+
π
4
= −
2D
p(x)
sin
1
x
x
1
p(x
) dx
− θ −
π
4
,
where θ is defined in Eq. 8.58. Now shift the origin to x
1
:
ψ
WKB
=
1
|p(x)|
Fe
1
0
x
|p(x
)|dx
+ Ge
−
1
0
x
|p(x
)|dx
(x<0)
−
2D
p(x)
sin
1
x
0
p(x
) dx
− θ −
π
4
(x>0)
.
Following Problem 8.9: ψ
p
(x)=aAi(−αx)+bBi(−αx), with α ≡
2m|V
(0)|
2
1/3
; p(x)=α
3/2
√
x.
Overlap region 1 (x<0)
:
0
x
|p(x
)|dx
=
2
3
(−αx)
3/2
.
ψ
WKB
≈
1
1/2
α
3/4
(−x)
1/4
Fe
2
3
(−αx)
3/2
+ Ge
−
2
3
(−αx)
3/2
ψ
p
≈
a
2
√
π(−αx)
1/4
e
−
2
3
(−αx)
3/2
+
b
√
π(−αx)
1/4
e
2
3
(−αx)
3/2
=⇒ a =2G
π
α
; b = F
π
α
.
Overlap region 2 (x>0)
:
x
0
p(x
) dx
=
2
3
(αx)
3/2
.
=⇒ ψ
WKB
≈−
2D
1/2
α
3/4
x
1/4
sin
2
3
(αx)
3/2
− θ −
π
4
,
ψ
p
≈
a
√
π(αx)
1/4
sin
2
3
(αx)
3/2
+
π
4
+
b
√
π(αx)
1/4
cos
2
3
(αx)
3/2
+
π
4
.
Equating the two expressions:
−2D
1/2
α
3/4
1
2i
e
i
2
3
(αx)
3/2
e
−iθ
e
−iπ/4
− e
−i
2
3
(αx)
3/2
e
iθ
e
iπ/4
=
1
√
πα
1/4
a
2i
e
i
2
3
(αx)
3/2
e
iπ/4
− e
−i
2
3
(αx)
3/2
e
−iπ/4
+
b
2
e
i
2
3
(αx)
3/2
e
iπ/4
+ e
−i
2
3
(αx)
3/2
e
−iπ/4
=⇒
−2D
π
α
e
−iθ
e
−iπ/4
=(a + ib)e
iπ/4
, or (a + ib)=2D
π
α
ie
−iθ
2D
π
α
e
iθ
e
iπ/4
=(−a + ib)e
−iπ/4
, or (a − ib)=−2D
π
α
ie
iθ
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

232 CHAPTER 8. THE WKB APPROXIMATION
=⇒
2a =2D
π
α
i(e
−iθ
− e
iθ
) ⇒ a =2D
π
α
sin θ,
2ib =2D
π
α
i(e
−iθ
+ e
iθ
) ⇒ b =2D
π
α
cos θ.
Combining these with the results from overlap region 1 =⇒
2G
π
α
=2D
π
α
sin θ, or G = D sin θ; F
π
α
=2D
π
α
cos θ, or F =2D cos θ.
Putting these into (iii) :
ψ
WKB
(x)=
D
|p(x)|
2 cos θe
1
x
1
x
|p(x
)|dx
+ sin θe
−
1
x
1
x
|p(x
)|dx
(0 <x<x
1
).
(b)
Odd(−) case: (iii) =⇒ ψ(0) = 0 ⇒ 2 cos θe
1
x
1
0
|p(x
)|dx
+ sin θe
−
1
x
1
0
|p(x
)|dx
=0.
1
x
1
0
|p(x
)|dx
=
1
2
φ, with φ defined by Eq. 8.60. So sin θe
−φ/2
= −2 cos θe
φ/2
, or tan θ = −2e
φ
.
Even(+) case: (iii) =⇒ ψ
(0) = 0 ⇒−
1
2
D
(|p(x)|)
3/2
d|p(x)|
dx
0
2 cos θe
φ/2
+ sin θe
−φ/2
+
D
|p(x)|
2 cos θe
1
x
1
0
|p(x
)|dx
−
1
|p(0)|
+ sin θe
−
1
x
1
0
|p(x
)|dx
1
|p(0)|
=0.
Now
d|p(x)|
dx
=
d
dx
2m[V (x) − E]=
√
2m
1
2
1
√
V − E
dV
dx
, and
dV
dx
0
=0, so
d|p(x)|
dx
0
=0.
2 cos θe
φ/2
= sin θe
−φ/2
, or tan θ =2e
φ
. Combining the two results: tan θ = ±2e
φ
. QED
(c)
tan θ = tan
n +
1
2
π + 9
=
sin
n +
1
2
π + 9
cos
n +
1
2
π + 9
=
(−1)
n
cos 9
(−1)
n+1
sin 9
= −
cos 9
sin 9
≈−
1
9
.
So −
1
9
≈±2e
φ
, or 9 ≈∓
1
2
e
−φ
, or θ −
n +
1
2
π ≈∓
1
2
e
−φ
, so θ ≈
n +
1
2
π ∓
1
2
e
−φ
. QED
[Note
: Since θ (Eq. 8.58) is positive, n must be a non-negative integer: n =0, 1, 2,.... This is like
harmonic oscillator (conventional) numbering, since it starts with n = 0.]
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 8. THE WKB APPROXIMATION 233
a
-a
xx
x
V(x)
1
2
(d)
θ =
1
x
2
x
1
2m
E −
1
2
mω
2
(x − a)
2
dx. Let z = x −a (shifts the origin to a).
=
2
z
2
0
2m
E −
1
2
mω
2
z
2
dz, where E =
1
2
mω
2
z
2
2
.
=
2
mω
z
2
0
z
2
2
− z
2
dz =
mω
z
z
2
2
− z
2
+ z
2
2
sin
−1
(z/z
2
)
z
2
0
=
mω
z
2
2
sin
−1
(1) =
π
2
mω
z
2
2
,
=
π
2
mω
2E
mω
2
=
πE
ω
.
Putting this into Eq. 8.61 yields
πE
ω
≈
n +
1
2
π ∓
1
2
e
−φ
, or E
±
n
≈
n +
1
2
ω ∓
ω
2π
e
−φ
. QED
(e)
Ψ(x, t)=
1
√
2
ψ
+
n
e
−iE
+
n
t/
+ ψ
−
n
e
−iE
−
n
t/
=⇒
|Ψ(x, t)|
2
=
1
2
|ψ
+
n
|
2
+ |ψ
−
n
|
2
+ ψ
+
n
ψ
−
n
e
i(E
−
n
−E
+
n
)t/
+ e
−i(E
−
n
−E
+
n
)t/
.
(Note that the wave functions (i), (ii), (iii) are real ). But
E
−
n
− E
+
n
≈
1
2
ω
2π
e
−φ
=
ω
π
e
−φ
,so
|Ψ(x, t)|
2
=
1
2
ψ
+
n
(x)
2
+ ψ
−
n
(x)
2
+ ψ
+
n
(x)ψ
−
n
(x) cos
ω
π
e
−φ
t
.
It oscillates back and forth, with period τ =
2π
(ω/π) e
−φ
=
2π
2
ω
e
φ
. QED
(f)
φ =2
1
x
1
0
2m
1
2
mω
2
(x − a)
2
− E
dx =
2
√
2mE
x
1
0
mω
2
2E
(x − a)
2
− 1 dx.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
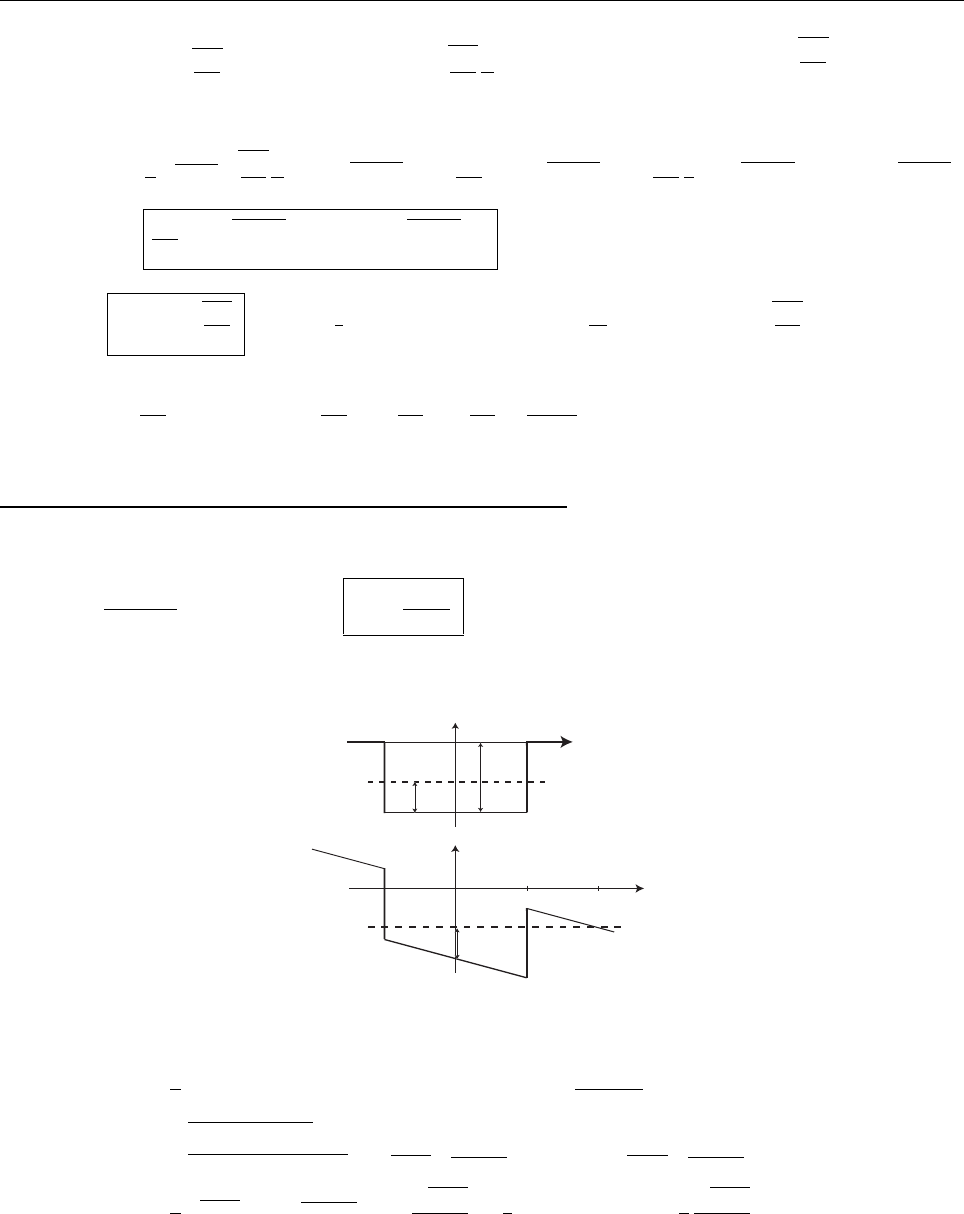
234 CHAPTER 8. THE WKB APPROXIMATION
Let z ≡
m
2E
ω(a −x), so dx = −
2E
m
1
ω
dz. Limits:
x =0 =⇒ z =
m
2E
ωa ≡ z
0
x = x
1
=⇒ radicand = 0 =⇒ z =1
.
φ =
2
√
2mE
2E
m
1
ω
z
0
1
z
2
− 1 dz =
4E
ω
z
0
1
z
2
− 1 dz =
4E
ω
1
2
z
z
2
− 1 − ln(z +
z
2
− 1)
z
0
1
=
2E
ω
z
0
z
2
0
− 1 − ln
z
0
+
z
2
0
− 1
,
where z
0
= aω
m
2E
.
V (0) =
1
2
mω
2
a
2
,soV (0) E ⇒
m
2
ω
2
a
2
E ⇒ aω
m
2E
1, or z
0
1.
In that case
φ ≈
2E
ω
z
2
0
− ln(2z
0
)
≈
2E
ω
z
2
0
=
2E
ω
a
2
ω
2
m
2E
=
mωa
2
.
This, together with Eq. 8.64, gives us the period of oscillation in a double well.
Problem 8.16
(a) E
n
≈
n
2
π
2
2
2m(2a)
2
. With n =1, E
1
=
π
2
2
8ma
2
.
(b)
V(x)
x
V
0
E
1
a
-a
V(x)
x
E
1
a
-a
x
0
E
tunneling
(c)
γ =
1
x
0
a
|p(x)|dx. αx
0
= V
0
− E
1
⇒ x
0
=
V
0
− E
1
α
.
p(x)=
2m [E − V (x)]; V (x)=−αx, E = E
1
− V
0
.
=
2m(E
1
− V
0
+ αx)=
√
2mα
√
x − x
0
; |p(x)| =
√
2mα
√
x
0
− x.
γ =
1
√
2mα
x
0
a
√
x
0
− xdx=
√
2mα
−
2
3
(x
0
− x)
3/2
x
0
a
=
2
3
√
2mα
(x
0
− a)
3/2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 8. THE WKB APPROXIMATION 235
Now x
0
− a =(V
0
− E
1
− aα)/α, and αa
2
/ma
2
≈ E
1
V
0
, so we can drop E
1
and αa. Then
γ ≈
2
3
√
2mα
V
0
α
3/2
=
8mV
3
0
3α
.
Equation 8.28 ⇒ τ =
4a
v
e
2γ
, where
1
2
mv
2
≈
π
2
2
8ma
2
⇒ v
2
=
π
2
2
4m
2
a
2
,orv =
π
2ma
. So
τ =
4a
π
2ma e
2γ
=
8ma
2
π
e
2γ
.
(d)
τ =
(8)
9.1 × 10
−31
10
−10
2
π (1.05 ×10
−34
)
e
2γ
=
2 × 10
−19
e
2γ
;
γ =
(8) (9.1 ×10
−31
) (20 ×1.6 ×10
−19
)
3
(3) (1.6 ×10
−19
)(7× 10
6
)(1.05 × 10
−34
)
=4.4 × 10
4
; e
2γ
= e
8.8×10
4
=
10
log e
8.8×10
4
=10
38,000
.
τ =
2 × 10
−19
× 10
38,000
s= 10
38,000
yr.
Seconds, years ... it hardly matters; nor is the factor out front significant. This is a huge number—the
age of the universe is about 10
10
years. In any event, this is clearly not something to worry about.
Problem 8.17
Equation 8.22 ⇒ the tunneling probability: T = e
−2γ
, where
γ =
1
x
0
0
2m(V − E) dx. Here V (x)=mgx, E =0,x
0
=
R
2
+(h/2)
2
− h/2 (half the diagonal).
=
√
2m
√
mg
x
0
0
x
1/2
dx =
m
2g
2
3
x
3/2
x
0
0
=
2m
3
2gx
3/2
0
.
I estimate: h = 10 cm, R = 3 cm, m = 300 gm; let g =9.8 m/s
2
. Then x
0
=
√
9+25− 5=0.83 cm, and
γ =
(2)(0.3)
(3)(1.05 × 10
−34
)
(2)(9.8) (0.0083)
3/2
=6.4 × 10
30
.
Frequency of “attempts”: say f = v/2R. We want the product of the number of attempts (ft) and the
probability of toppling at each attempt (T ), to be 1:
t
v
2R
e
−2γ
=1 ⇒ t =
2R
v
e
2γ
.
Estimating the thermal velocity:
1
2
mv
2
=
1
2
k
B
T (I’m done with the tunneling probability; from now on T
is the temperature, 300 K) ⇒ v =
k
B
T/m.
t =2R
m
k
B
T
e
2γ
= 2(0.03)
0.3
(1.4 × 10
−23
)(300)
e
12.8×10
30
=5× 10
8
10
log e
13×10
30
=(5× 10
8
) × 10
5.6×10
30
s
=
16 × 10
5.6×10
30
yr.
Don’t hold your breath.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

236 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
Chapter 9
Time-Dependent Perturbation Theory
Problem 9.1
ψ
nlm
= R
nl
Y
m
l
. From Tables 4.3 and 4.7:
ψ
100
=
1
√
πa
3
e
−r/a
; ψ
200
=
1
√
8πa
3
1 −
r
2a
e
−r/2a
;
ψ
210
=
1
√
32πa
3
r
a
e
−r/2a
cos θ; ψ
21±1
= ∓
1
√
64πa
3
r
a
e
r/2a
sin θe
±iφ
.
But r cos θ = z and r sin θe
±iφ
= r sin θ(cos φ ± i sin φ)=r sin θ cos φ ± ir sin θ sin φ = x ± iy. So |ψ|
2
is an
even function of z in all cases, and hence
z|ψ|
2
dx dy dz =0,so H
ii
=0. Moreover, ψ
100
is even in z, and
so are ψ
200
, ψ
211
, and ψ
21−1
,so H
ij
=0 for all except
H
100,210
= −eE
1
√
πa
3
1
√
32πa
3
1
a
e
−r/a
e
−r/2a
z
2
d
3
r = −
eE
4
√
2πa
4
e
−3r/2a
r
2
cos
2
θr
2
sin θdrdθdφ
= −
eE
4
√
2πa
4
∞
0
r
4
e
−3r/2a
dr
π
0
cos
2
θ sin θdθ
2π
0
dφ = −
eE
4
√
2πa
4
4!
2a
3
5
2
3
2π =
−
2
8
3
5
√
2
eEa,
or −0.7449 eEa.
Problem 9.2
˙c
a
= −
i
H
ab
e
−iω
0
t
c
b
;˙c
b
= −
i
H
ba
e
iω
0
t
c
a
. Differentiating with respect to t :
¨c
b
= −
i
H
ba
iω
0
e
iω
0
t
c
a
+ e
iω
0
t
˙c
a
= iω
0
−
i
H
ba
e
iω
0
t
c
a
−
i
H
ba
e
iω
o
t
−
i
H
ab
e
−iω
0
t
c
b
, or
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 237
¨c
b
= iω
0
˙c
b
−
1
2
|H
ab
|
2
c
b
. Let α
2
≡
1
2
|H
ab
|
2
. Then ¨c
b
− iω
0
˙c
b
+ α
2
c
b
=0.
This is a linear differential equation with constant coefficients, so it can be solved by a function of the form
c
b
= e
λt
:
λ
2
− iω
0
λ + α
2
=0=⇒ λ =
1
2
iω
0
±
−ω
2
0
− 4α
2
=
i
2
(ω
0
± ω) , where ω ≡
ω
2
0
+4α
2
.
The general solution is therefore
c
b
(t)=Ae
i(ω
0
+ω)/2
+ Be
i(ω
0
−ω)/2
= e
iω
0
t/2
Ae
iωt/2
+ Be
−iωt/2
, or
c
b
(t)=e
iω
0
t/2
[C cos (ωt/2) + D sin (ωt/2)] . But c
b
(0) = 0, so C =0, and hence
c
b
(t)=De
iω
0
t/2
sin (ωt/2) . Then
˙c
b
= D
iω
0
2
e
iω
0
t/2
sin (ωt/2) +
ω
2
e
iω
0
t/2
cos (ωt/2)
=
ω
2
De
iω
0
t/2
cos (ωt/2) + i
ω
0
ω
sin (ωt/2)
= −
i
H
ba
e
iω
0
t
c
a
.
c
a
=
i
H
ba
ω
2
e
−iω
0
t/2
D
cos (ωt/2) + i
ω
0
ω
sin (ωt/2)
. But c
a
(0) = 1, so
i
H
ba
ω
2
D =1. Conclusion:
c
a
(t)=e
−iω
0
t/2
cos (ωt/2) + i
ω
0
ω
sin (ωt/2)
,
c
b
(t)=
2H
ba
iω
e
iω
0
t/2
sin (ωt/2) ,
where ω ≡
ω
2
0
+4
|H
ab
|
2
2
.
|c
a
|
2
+ |c
b
|
2
= cos
2
(ωt/2) +
ω
2
0
ω
2
sin
2
(ωt/2) +
4|H
ab
|
2
2
ω
2
sin
2
(ωt/2)
= cos
2
(ωt/2) +
1
ω
2
ω
2
0
+4
|H
ab
|
2
2
sin
2
(ωt/2) = cos
2
(ωt/2) + sin
2
(ωt/2) = 1.
Problem 9.3
This is a tricky problem, and I thank Prof. Onuttom Narayan for showing me the correct solution. The safest
approach is to represent the delta function as a sequence of rectangles:
δ
5
(t)=
(1/29), −9<t<9,
0, otherwise.
Then Eq. 9.13 ⇒
t<−9 : c
a
(t)=1,c
b
(t)=0,
t>9: c
a
(t)=a, c
b
(t)=b,
−9<t<9:
˙c
a
= −
iα
25
e
−iω
0
t
c
b
,
˙c
b
= −
iα
∗
25
e
iω
0
t
c
a
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

238 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
In the interval −9<t<9,
d
2
c
b
dt
2
= −
iα
∗
29
iω
0
e
iω
0
t
c
a
+ e
iω
0
t
−iα
29
e
−iω
0
t
c
b
= −
iα
∗
29
iω
0
i29
α
∗
dc
b
dt
−
iα
29
c
b
= iω
0
dc
b
dt
−
|α|
2
(29)
2
c
b
.
Thus c
b
satisfies a homogeneous linear differential equation with constant coefficients:
d
2
c
b
dt
2
− iω
0
dc
b
dt
+
|α|
2
(29)
2
c
b
=0.
Try a solution of the form c
b
(t)=e
λt
:
λ
2
− iω
0
λ +
|α|
2
(29)
2
=0⇒ λ =
iω
0
±
−ω
2
0
−|α|
2
/(9)
2
2
,
or
λ =
iω
0
2
±
iω
2
, where ω ≡
ω
2
0
+ |α|
2
/(9)
2
.
The general solution is
c
b
(t)=e
iω
0
t/2
Ae
iωt/2
+ Be
−iωt/2
.
But
c
b
(−9)=0⇒ Ae
−iω5/2
+ Be
iω5/2
=0⇒ B = −Ae
−iω5
,
so
c
b
(t)=Ae
iω
0
t/2
e
iωt/2
− e
−iω(5+t/2)
.
Meanwhile
c
a
(t)=
2i9
α
∗
e
−iω
0
t
˙c
b
=
2i9
α
∗
e
−iω
0
t/2
A
iω
0
2
e
iωt/2
− e
−iω(5+t/2)
+
iω
2
e
iωt/2
+ e
−iω(5+t/2)
= −
9
α
∗
e
−iω
0
t/2
A
(ω + ω
0
)e
iωt/2
+(ω − ω
0
)e
−iω(5+t/2)
.
But c
a
(−9)=1=−
9
α
∗
e
i(ω
0
−ω)5/2
A [(ω + ω
0
)+(ω − ω
0
)] = −
29ω
α
∗
e
i(ω
0
−ω)5/2
A, so A = −
α
∗
29ω
e
i(ω−ω
0
)5/2
.
c
a
(t)=
1
2ω
e
−iω
0
(t+5)/2
(ω + ω
0
)e
iω(t+5)/2
+(ω − ω
0
)e
−iω(t+5)/2
= e
−iω
0
(t+5)/2
cos
ω(t + 9)
2
+ i
ω
0
ω
sin
ω(t + 9)
2
;
c
b
(t)=−
iα
∗
29ω
e
iω
0
(t−5)/2
e
iω(t+5)/2
− e
−iω(t+5)/2
= −
iα
∗
9ω
e
iω
0
(t−5)/2
sin
ω(t + 9)
2
.
Thus
a = c
a
(9)=e
−iω
0
5
cos(ω9)+i
ω
0
ω
sin(ω9)
,b= c
b
(9)=−
iα
∗
9ω
sin(ω9).
This is for the rectangular pulse; it remains to take the limit 9 → 0: ω →|α|/9,so
a → cos
|α|
+ i
ω
0
9
|α|
sin
|α|
→ cos
|α|
,b→−
iα
∗
|α|
sin
|α|
,
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 239
and we conclude that for the delta function
c
a
(t)=
1,t<0,
cos(|α|/),t>0;
c
b
(t)=
0,t<0,
−i
α
∗
α
sin(|α|/),t>0.
Obviously, |c
a
(t)|
2
+ |c
b
(t)|
2
= 1 in both time periods. Finally,
P
a→b
= |b|
2
= sin
2
(|α|/).
Problem 9.4
(a)
Eq. 9.10 =⇒ ˙c
a
= −
i
c
a
H
aa
+ c
b
H
ab
e
−iω
0
t
Eq. 9.11 =⇒ ˙c
b
= −
i
c
b
H
bb
+ c
a
H
ba
e
iω
0
t
(these are exact, and replace Eq. 9.13).
Initial conditions
: c
a
(0) = 1,c
b
(0) = 0.
Zeroth order
: c
a
(t)=1,c
b
(t)=0.
First order
:
˙c
a
= −
i
H
aa
=⇒
˙c
b
= −
i
H
ba
e
iω
0
t
=⇒
c
a
(t)=1−
i
t
0
H
aa
(t
) dt
c
b
(t)=−
i
t
0
H
ba
(t
)e
iω
0
t
dt
|c
a
|
2
=
1 −
i
t
0
H
aa
(t
) dt
1+
i
t
0
H
aa
(t
) dt
=1+
1
t
0
H
aa
(t
) dt
2
= 1 (to first order in H
).
|c
b
|
2
=
−
i
t
0
H
ba
(t
)e
iω
0
t
dt
i
t
0
H
ab
(t
)e
−iω
0
t
dt
= 0 (to first order in H
).
So |c
a
|
2
+ |c
b
|
2
= 1 (to first order).
(b)
˙
d
a
= e
i
t
0
H
aa
(t
) dt
i
H
aa
c
a
+ e
i
t
0
H
aa
(t
) dt
˙c
a
. But ˙c
a
= −
i
c
a
H
aa
+ c
b
H
ab
e
−iω
0
t
Two terms cancel, leaving
˙
d
a
= −
i
e
i
t
0
H
aa
(t
) dt
c
b
H
ab
e
−iω
0
t
. But c
b
= e
−
i
t
0
H
bb
(t
) dt
d
b
.
= −
i
e
i
t
0
[
H
aa
(t
)−H
bb
(t
)
]
dt
H
ab
e
−iω
0
t
d
b
, or
˙
d
a
= −
i
e
iφ
H
ab
e
−iω
0
t
d
b
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

240 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
Similarly,
˙
d
b
= e
i
t
0
H
bb
(t
) dt
i
H
bb
c
b
+ e
i
t
0
H
bb
(t
) dt
˙c
b
. But ˙c
b
= −
i
c
b
H
bb
+ c
a
H
ba
e
iω
0
t
.
= −
i
e
i
t
0
H
bb
(t
) dt
c
a
H
ba
e
iω
0
t
. But c
a
= e
−
i
t
0
H
aa
(t
) dt
d
a
.
= −
i
e
i
t
0
[
H
bb
(t
)−H
aa
(t
)
]
dt
H
ba
e
iω
0
t
d
a
= −
i
e
−iφ
H
ba
e
iω
0
t
d
a
. QED
(c)
Initial conditions
: c
a
(0) = 1 =⇒ d
a
(0) = 1; c
b
(0) = 0 =⇒ d
b
(0) = 0.
Zeroth order
: d
a
(t)=1,d
b
(t)=0.
First order
:
˙
d
a
=0=⇒ d
a
(t)=1=⇒ c
a
(t)=e
−
i
t
0
H
aa
(t
) dt
.
˙
d
b
= −
i
e
−iφ
H
ba
e
iω
0
t
=⇒ d
b
= −
i
t
0
e
−iφ(t
)
H
ba
(t
)e
iω
0
t
dt
=⇒
c
b
(t)=−
i
e
−
i
t
0
H
bb
(t
)dt
t
0
e
−iφ(t
)
H
ba
(t
)e
iω
0
t
dt
.
These don’t look much like the results in (a), but remember, we’re only working to first order in H
,
so c
a
(t) ≈ 1 −
i
t
0
H
aa
(t
) dt
(to this order), while for c
b
, the factor H
ba
in the integral means it is
already first order and hence both the exponential factor in front and e
−iφ
should be replaced by 1. Then
c
b
(t) ≈−
i
t
0
H
ba
(t
)e
iω
0
t
dt
, and we recover the results in (a).
Problem 9.5
Zeroth order: c
(0)
a
(t)=a, c
(0)
b
(t)=b.
First order
:
˙c
a
= −
i
H
ab
e
−iω
0
t
b =⇒ c
(1)
a
(t)=a −
ib
t
0
H
ab
(t
)e
−iω
0
t
dt
.
˙c
b
= −
i
H
ba
e
iω
0
t
a =⇒ c
(1)
b
(t)=b −
ia
t
0
H
ba
(t
)e
iω
0
t
dt
.
Second order
:˙c
a
= −
i
H
ab
e
−iω
0
t
b −
ia
t
0
H
ba
(t
)e
iω
0
t
dt
=⇒
c
(2)
a
(t)=a −
ib
t
0
H
ab
(t
)e
−iω
0
t
dt
−
a
2
t
0
H
ab
(t
)e
−iω
0
t
t
0
H
ba
(t
)e
iω
0
t
dt
dt
.
To get c
b
, just switch a ↔ b (which entails also changing the sign of ω
0
):
c
(2)
b
(t)=b −
ia
t
0
H
ba
(t
)e
iω
0
t
dt
−
b
2
t
0
H
ba
(t
)e
iω
0
t
t
0
H
ab
(t
)e
−iω
0
t
dt
dt
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 241
Problem 9.6
For H
independent of t, Eq. 9.17 =⇒ c
(2)
b
(t)=c
(1)
b
(t)=−
i
H
ba
t
0
e
iω
0
t
dt
=⇒
c
(2)
b
(t)=−
i
H
ba
e
iω
0
t
iω
0
t
0
= −
H
ba
ω
0
e
iω
0
t
− 1
. Meanwhile Eq. 9.18 =⇒
c
(2)
a
(t)=1−
1
2
|H
ab
|
2
t
0
e
−iω
0
t
t
0
e
iω
0
t
dt
dt
=1−
1
2
|H
ab
|
2
1
iω
0
t
0
1 − e
−iω
0
t
dt
=1+
i
ω
0
2
|H
ab
|
2
'
t
+
e
−iω
0
t
iω
0
(
t
0
= 1+
i
ω
0
2
|H
ab
|
2
t +
1
iω
0
e
−iω
0
t
− 1
.
For comparison with the exact answers (Problem 9.2), note first that c
b
(t) is already first order (because of
the H
ba
in front), whereas ω differs from ω
0
only in second order, so it suffices to replace ω → ω
0
in the exact
formula to get the second-order result:
c
b
(t) ≈
2H
ba
iω
0
e
iω
0
t/2
sin (ω
0
t/2) =
2H
ba
iω
0
e
iω
0
t/2
1
2i
e
iω
0
t/2
− e
−iω
0
t/2
= −
H
ba
ω
0
e
iω
0
t
− 1
,
in agreement with the result above. Checking c
a
is more difficult. Note that
ω = ω
0
1+
4|H
ab
|
2
ω
2
0
2
≈ ω
0
1+2
|H
ab
|
2
ω
2
0
2
= ω
0
+2
|H
ab
|
2
ω
0
2
;
ω
0
ω
≈ 1 − 2
|H
ab
|
2
ω
2
0
2
.
Taylor expansion:
cos(x + 9) = cos x −9 sin x =⇒ cos (ωt/2) = cos
ω
0
t
2
+
|H
ab
|
2
t
ω
0
2
≈ cos (ω
0
t/2) −
|H
ab
|
2
t
ω
0
2
sin (ω
0
t/2)
sin(x + 9) = sin x + 9 cos x =⇒ sin (ωt/2) = sin
ω
0
t
2
+
|H
ab
|
2
t
ω
0
2
≈ sin (ω
0
t/2) +
|H
ab
|
2
t
ω
0
2
cos (ω
0
t/2)
c
a
(t) ≈ e
−iω
0
t/2
cos
ω
0
t
2
−
|H
ab
|
2
t
ω
0
2
sin
ω
0
t
2
+ i
1 − 2
|H
ab
|
2
ω
2
0
2
sin
ω
0
t
2
+
|H
ab
|
2
t
ω
0
2
cos
ω
0
t
2
= e
−iω
0
t/2
cos
ω
0
t
2
+ i sin
ω
0
t
2
−
|H
ab
|
2
ω
0
2
t
sin
ω
0
t
2
− i cos
ω
0
t
2
+
2i
ω
0
sin
ω
0
t
2
= e
−iω
0
t/2
e
iω
0
t/2
−
|H
ab
|
2
ω
0
2
−ite
iω
0
t/2
+
2i
ω
1
2i
e
iω
0
t/2
− e
−iω
0
t/2
=1−
|H
ab
|
2
ω
0
2
−it +
1
ω
0
1 − e
−iω
0
t
=1+
i
ω
0
2
|H
ab
|
2
t +
1
iω
0
e
−iω
0
t
− 1
, as above.
Problem 9.7
(a)
˙c
a
= −
i
2
V
ab
e
iωt
e
−iω
0
t
c
b
;˙c
b
= −
i
2
V
ba
e
−iωt
e
iω
0
t
c
a
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

242 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
Differentiate the latter, and substitute in the former:
¨c
b
= −i
V
ba
2
i(ω
0
− ω)e
i(ω
0
−ω)t
c
a
+ e
i(ω
0
−ω)t
˙c
a
= i(ω
0
− ω)
−i
V
ba
2
e
i(ω
0
−ω)t
c
a
− i
V
ba
2
e
i(ω
0
−ω)t
−i
V
ab
2
e
−i(ω
0
−ω)t
c
b
= i(ω
0
− ω)˙c
b
−
|V
ab
|
2
(2)
2
c
b
.
d
2
c
b
dt
2
+ i(ω − ω
0
)
dc
b
dt
+
|V
ab
|
2
4
2
c
b
=0. Solution is of the form c
b
= e
λt
: λ
2
+ i(ω − ω
0
)λ +
|V
ab
|
2
4
2
=0.
λ =
1
2
−i(ω − ω
0
) ±
−(ω − ω
0
)
2
−
|V
ab
|
2
2
= i
−
(ω − ω
0
)
2
± ω
r
, with ω
r
defined in Eq. 9.30.
General solution: c
b
(t)=Ae
i
−
(ω−ω
0
)
2
+ω
r
t
+ Be
i
−
(ω−ω
0
)
2
+ω
r
t
= e
−i(ω−ω
0
)t/2
Ae
iω
r
t
+ Be
−iω
r
t
,
or, more conveniently: c
b
(t)=e
−i(ω−ω
0
)t/2
[C cos(ω
r
t)+D sin(ω
r
t)] . But c
b
(0) = 0, so C =0:
c
b
(t)=De
i(ω
0
−ω)t/2
sin(ω
r
t). ˙c
b
= D
i
ω
0
− ω
2
e
i(ω
0
−ω)t/2
sin(ω
r
t)+ω
r
e
i(ω
0
−ω)t/2
cos(ω
r
t)
;
c
a
(t)=i
2
V
ba
e
i(ω−ω
0
)t
˙c
b
= i
2
V
ba
e
i(ω−ω
0
)t/2
D
i
ω
0
− ω
2
sin(ω
r
t)+ω
r
cos(ω
r
t)
. But c
a
(0) = 1 :
1=i
2
V
ba
Dω
r
, or D =
−iV
ba
2ω
r
.
c
b
(t)=−
i
2ω
r
V
ba
e
i(ω
0
−ω)t/2
sin(ω
r
t),c
a
(t)=e
i(ω−ω
0
)t/2
cos(ω
r
t)+i
ω
0
− ω
2ω
r
sin(ω
r
t)
.
(b)
P
a→b
(t)=|c
b
(t)|
2
=
|V
ab
|
2ω
r
2
sin
2
(ω
r
t). The largest this gets (when sin
2
=1)is
|V
ab
|
2
/
2
4ω
2
r
,
and the denominator, 4ω
2
r
=(ω − ω
0
)
2
+ |V
ab
|
2
/
2
, exceeds the numerator, so P ≤ 1 (and 1 only if ω = ω
0
).
|c
a
|
2
+ |c
b
|
2
= cos
2
(ω
r
t)+
ω
0
− ω
2ω
r
2
sin
2
(ω
r
t)+
|V
ab
|
2ω
r
2
sin
2
(ω
r
t)
= cos
2
(ω
r
t)+
(ω − ω
0
)
2
+(|V
ab
|/)
2
4ω
2
r
sin
2
(ω
r
t) = cos
2
(ω
r
t) + sin
2
(ω
r
t)=1.
(c) If
|V
ab
|
2
2
(ω − ω
0
)
2
, then ω
r
≈
1
2
|ω − ω
0
|, and P
a→b
≈
|V
ab
|
2
2
sin
2
ω−ω
0
2
t
(ω − ω
0
)
2
, confirming
Eq. 9.28.
(d) ω
r
t = π =⇒ t = π/ω
r
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 243
Problem 9.8
Spontaneous emission rate (Eq. 9.56): A =
ω
3
|℘|
2
3π9
0
c
3
. Thermally stimulated emission rate (Eq. 9.47):
R =
π
39
0
2
|℘|
2
ρ(ω), with ρ(ω)=
π
2
c
3
ω
3
(e
ω/k
B
T
− 1)
(Eq. 9.52).
So the ratio is
A
R
=
ω
3
|℘|
2
3π9
0
c
3
·
39
0
2
π|℘|
2
·
π
2
c
3
e
ω/k
B
T
− 1
ω
3
= e
ω/k
B
T
− 1.
The ratio is a monotonically increasing function of ω, and is 1 when
e
ω/k
b
t
=2, or
ω
k
B
T
=ln2,ω=
k
B
T
ln 2, or ν =
ω
2π
=
k
B
T
h
ln 2. For T = 300 K,
ν =
(1.38 × 10
−23
J/K)(300 K)
(6.63 × 10
−34
J · s)
ln 2 = 4.35 ×10
12
Hz.
For higher frequencies, (including light, at 10
14
Hz), spontaneous emission dominates.
Problem 9.9
(a) Simply remove the factor
e
ω/k
B
T
− 1
in the denominator of Eq. 5.113: ρ
0
(ω)=
ω
3
π
2
c
3
.
(b) Plug this into Eq. 9.47:
R
b→a
=
π
39
0
2
|℘|
2
ω
3
π
2
c
3
=
ω
3
|℘|
2
3π9
0
c
3
,
reproducing Eq. 9.56.
Problem 9.10
N(t)=e
−t/τ
N(0) (Eqs. 9.58 and 9.59). After one half-life, N (t)=
1
2
N(0), so
1
2
= e
−t/τ
,or2=e
t/τ
,
so t/τ =ln2, or
t
1/2
= τ ln 2.
Problem 9.11
In Problem 9.1 we calculated the matrix elements of z; all of them are zero except 100|z|210 =
2
8
3
5
√
2
a.As
for x and y, we noted that |100, |200, and |210 are even (in x, y), whereas |21 ± 1 is odd. So the only
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

244 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
non-zero matrix elements are 100|x|21± 1 and 100|y|21± 1. Using the wave functions in Problem 9.1:
100|x|21± 1 =
1
√
πa
3
∓1
8
√
πa
3
1
a
e
−r/a
re
−r/2a
sin θe
±iφ
(r sin θ cos φ)r
2
sin θdrdθdφ
= ∓
1
8πa
4
∞
0
r
4
e
−3r/2a
dr
π
0
sin
3
θdθ
2π
0
(cos φ ±i sin φ) cos φdφ
=
∓1
8πa
4
4!
2a
3
5
4
3
(π)=∓
2
7
3
5
a.
100|y|21± 1 =
∓1
8πa
4
4!
2a
3
5
4
3
2π
0
(cos φ ±i sin φ) sin φdφ
=
∓1
8πa
4
4!
2a
3
5
4
3
(±iπ)=−i
2
7
3
5
a.
100|r|200 =0; 100|r|210 =
2
7
√
2
3
5
a
ˆ
k; 100|r|21±1 =
2
7
3
5
a
∓
ˆ
i − i
ˆ
j
, and hence
℘
2
= 0 (for |200→|100), and |℘|
2
=(qa)
2
2
15
3
10
(for |210→100 and |21± 1→|100).
Meanwhile, ω =
E
2
− E
1
=
1
E
1
4
− E
1
= −
3E
1
4
, so for the three l = 1 states:
A = −
3
3
E
3
1
2
6
3
(ea)
2
2
15
3
10
1
3π9
0
c
3
= −
2
9
3
8
π
E
3
1
e
2
a
2
9
0
4
c
3
=
2
10
3
8
E
1
mc
2
2
c
a
=
2
10
3
8
13.6
0.511 × 10
6
2
(3.00 × 10
8
m/s)
(0.529 × 10
−10
m)
=6.27 × 10
8
/s; τ =
1
A
=
1.60 × 10
−9
s
for the three l = 1 states (all have the same lifetime); τ = ∞ for the l = 0 state.
Problem 9.12
[L
2
,z]=[L
2
x
,z]+[L
2
y
,z]+[L
2
z
,z]=L
x
[L
x
,z]+[L
x
,z]L
x
+ L
y
[L
y
,z]+[L
y
,z]L
y
+ L
z
[L
z
,z]+[L
z
,z]L
z
But
[L
x
,z]= [yp
z
− zp
y
,z]= [yp
z
,z] − [zp
y
,z]= y[p
z
,z]=−iy,
[L
y
,z]= [zp
x
− xp
z
,z]= [zp
x
,z] − [xp
z
,z]= −x[p
z
,z]=ix,
[L
z
,z]= [xp
y
− yp
x
,z]= [xp
y
,z] − [yp
x
,z]= 0.
So: [L
2
,z]=L
x
(−iy)+(−iy)L
x
+ L
y
(ix)+(ix)L
y
= i(−L
x
y − yL
x
+ L
y
x + xL
y
).
But
L
x
y = L
x
y − yL
x
+ yL
x
=[L
x
,y]+yL
x
= iz + yL
x
,
L
y
x = L
y
x − xL
y
+ xL
y
=[L
y
,x]+xL
y
= −iz + xL
y
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 245
So: [L
2
,z]=i(2xL
y
− iz − 2yL
x
− iz)=⇒ [L
2
,z]=2i(xL
y
− yL
x
− iz).
L
2
, [L
2
,z]
=2i
-
[L
2
,xL
y
] − [L
2
,yL
x
] − i[L
2
,z]
.
=2i
-
[L
2
,x]L
y
+ x[L
2
,L
y
] − [L
2
,y]L
x
− y[L
2
,L
x
] − i(L
2
z − zL
2
)
.
.
But [L
2
,L
y
]=[L
2
,L
x
] = 0 (Eq. 4.102), so
L
2
, [L
2
,z]
=2i
-
(yL
z
− zL
y
− ix) L
y
− 2i(zL
x
− xL
z
− iy) L
x
− i
L
2
z − zL
2
.
, or
L
2
, [L
2
,z]
= −2
2
2yL
z
L
y
−2zL
2
y
− 2zL
2
x
−2z(L
2
x
+L
2
y
+L
2
z
)+2zL
2
z
−2ixL
y
+2xL
z
L
x
+2iyL
x
− L
2
z + zL
2
= −2
2
2yL
z
L
y
− 2ixL
y
+2xL
z
L
x
+2iyL
x
+2zL
2
z
− 2zL
2
− L
2
z + zL
2
= −2
2
zL
2
+ L
2
z
− 4
2
(yL
z
− ix)
L
z
y
L
y
+(xL
z
+ iy)
L
z
x
L
x
+ zL
z
L
z
=2
2
zL
2
+ L
2
z
− 4
2
(L
z
yL
y
+ L
z
xL
x
+ L
z
zL
z
)
L
z
(r·L)=0
=2
2
(zL
2
+ L
2
z). QED
Problem 9.13
|n 00 = R
n0
(r)Y
0
0
(θ, φ)=
1
√
4π
R
n0
(r), so n
00|r|n 00 =
1
4π
R
n
0
(r)R
n0
(r)(x
ˆ
i + y
ˆ
j + z
ˆ
k) dx dy dz.
But the integrand is odd in x, y,orz, so the integral is zero.
Problem 9.14
(a)
|300→
|210
|211
|21−1
→|100. (|300→|200 and |300→|100 violate ∆l = ±1 rule.)
(b)
From Eq. 9.72: 210|r|300 = 210|z|300
ˆ
k.
From Eq. 9.69: 21± 1|r|300 = 21±1|x|300
ˆ
i + 21± 1|y|300
ˆ
j.
From Eq. 9.70: ±21±1|x|300 = i21± 1|y|300.
Thus |210|r|300|
2
= |210|z|300|
2
and |21± 1|r|300|
2
=2|21± 1|x|300|
2
,
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

246 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
so there are really just two matrix elements to calculate.
ψ
21m
= R
21
Y
m
1
,ψ
300
= R
30
Y
0
0
. From Table 4.3:
Y
0
1
Y
0
0
cos θ sin θdθdφ=
3
4π
1
4π
π
0
cos
2
θ sin θdθ
2π
0
dφ =
√
3
4π
−
cos
3
θ
3
π
0
(2π)=
√
3
2
2
3
=
1
√
3
.
Y
±1
1
∗
Y
0
0
sin
2
θ cos φdθdφ= ∓
3
8π
1
4π
π
0
sin
3
θdθ
2π
0
cos φe
∓iφ
dφ
= ∓
1
4π
3
2
4
3
2π
0
cos
2
φdφ∓ i
2π
0
cos φ sin φdφ
= ∓
1
π
√
6
(π ∓ 0) = ∓
1
√
6
.
From Table 4.7:
K ≡
∞
0
R
21
R
30
r
3
dr =
1
√
24a
3/2
2
√
27a
3/2
∞
0
r
a
e
−r/2a
1 −
2
3
r
a
+
2
27
r
a
2
e
−r/3a
r
3
dr
=
1
9
√
2a
3
a
4
∞
0
1 −
2
3
u +
2
27
u
2
u
4
e
−5u/6
du =
a
9
√
2
4!
6
5
5
−
2
3
5!
6
5
6
+
2
27
6!
6
5
7
=
a
9
√
2
4! 6
5
5
6
5 −
2
3
6 · 5+
2
27
6
3
=
a
9
√
2
4! 6
5
5
6
=
2
7
3
4
5
6
√
2 a.
So:
21± 1|x|300 =
R
21
(Y
±1
1
)
∗
(r sin θ cos φ)R
30
Y
0
0
r
2
sin θdrdθdφ= K
∓
1
√
6
.
210|z|300 =
R
21
Y
0
1
(r cos θ)R
30
Y
0
0
r
2
sin θdrdθdφ= K
1
√
3
.
|210|r|300|
2
= |210|z|300|
2
= K
2
/3;
|21± 1|r|300 |
2
=2|21± 1|x|300 |
2
= K
2
/3.
Evidently the three transition rates are equal, and hence
1/3 go by each route.
(c) For each mode, A =
ω
3
e
2
|r|
2
3π9
0
c
3
; here ω =
E
3
− E
2
=
1
E
1
9
−
E
1
4
= −
5
36
E
1
, so the total
decay rate is
R =3
−
5
36
E
1
3
e
2
3π9
0
c
3
1
3
2
7
3
4
5
6
√
2a
2
=6
2
5
9
E
1
mc
2
2
c
a
=6
2
5
9
13.6
0.511 × 10
6
2
3 × 10
8
0.529 × 10
−10
/s=6.32 × 10
6
/s.τ=
1
R
=
1.58 × 10
−7
s.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 247
Problem 9.15
(a)
Ψ(t)=
c
n
(t)e
−iE
n
t/
ψ
n
.HΨ=i
∂Ψ
∂t
; H = H
0
+ H
(t); H
0
ψ
n
= E
n
ψ
n
. So
c
n
e
−iE
n
t/
E
n
ψ
n
+
c
n
e
−iE
n
t/
H
ψ
n
= i
˙c
n
e
−iE
n
t/
ψ
n
+ i
−
i
c
n
E
n
e
−iE
n
t/
ψ
n
.
The first and last terms cancel, so
c
n
e
−iE
n
t/
H
ψ
n
= i
˙c
n
e
−iE
n
t/
ψ
n
. Take the inner product with ψ
m
:
c
n
e
−iE
n
t/
ψ
m
|H
|ψ
n
= i
˙c
n
e
−iE
n
t/
ψ
m
|ψ
n
.
Assume orthonormality of the unperturbed states, ψ
m
|ψ
n
= δ
mn
, and define H
mn
≡ψ
m
|H
|ψ
n
.
c
n
e
−iE
n
t/
H
mn
= i ˙c
m
e
−iE
m
t/
, or ˙c
m
= −
i
n
c
n
H
mn
e
i(E
m
−E
n
)t/
.
(b) Zeroth order: c
N
(t)=1,c
m
(t) = 0 for m = N. Then in first order:
˙c
N
= −
i
H
NN
,or c
N
(t)=1−
i
t
0
H
NN
(t
) dt
, whereas for m = N :
˙c
m
= −
i
H
mN
e
i(E
m
−E
N
)t/
,or c
m
(t)=−
i
t
0
H
mN
(t
)e
i(E
m
−E
N
)t
/
dt
.
(c)
c
M
(t)=−
i
H
MN
t
0
e
i(E
M
−E
N
)t
/
dt
= −
i
H
MN
e
i(E
M
−E
N
)t
/
i(E
M
− E
N
)/
t
0
= −H
MN
e
i(E
M
−E
N
)t/
− 1
E
M
− E
N
= −
H
MN
(E
M
− E
N
)
e
i(E
M
−E
N
)t/2
2i sin
E
M
− E
N
2
t
.
P
N→M
= |c
M
|
2
=
4|H
MN
|
2
(E
M
− E
N
)
2
sin
2
E
M
− E
N
2
t
.
(d)
c
M
(t)=−
i
V
MN
1
2
t
0
e
iωt
+ e
−iωt
e
i(E
M
−E
N
)t
/
dt
= −
iV
MN
2
e
i(ω+E
M
−E
N
)t
/
i(ω + E
M
− E
N
)/
+
e
i(−ω+E
M
−E
N
)t
/
i(−ω + E
M
− E
N
)/
t
0
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

248 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
If E
M
>E
N
, the second term dominates, and transitions occur only for ω ≈ (E
M
− E
N
)/:
c
M
(t) ≈−
iV
MN
2
1
(i/)(E
M
− E
N
− ω)
e
i(E
M
−E
N
−ω)t/2
2i sin
E
M
− E
N
− ω
2
t
, so
P
N→M
= |c
M
|
2
=
|V
MN
|
2
(E
M
− E
N
− ω)
2
sin
2
E
M
− E
N
− ω
2
t
.
If E
M
<E
N
the first term dominates, and transitions occur only for ω ≈ (E
N
− E
M
)/:
c
M
(t) ≈−
iV
MN
2
1
(i/)(E
M
− E
N
+ ω)
e
i(E
M
−E
N
+ω)t/2
2i sin
E
M
− E
N
+ ω
2
t
, and hence
P
N→M
=
|V
MN
|
2
(E
M
− E
N
+ ω)
2
sin
2
E
M
− E
N
+ ω
2
t
.
Combining the two results, we conclude that transitions occur to states with energy E
M
≈ E
N
±ω, and
P
N→M
=
|V
MN
|
2
(E
M
− E
N
± ω)
2
sin
2
E
M
− E
N
± ω
2
t
.
(e) For light, V
ba
= −℘E
0
(Eq. 9.34). The rest is as before (Section 9.2.3), leading to Eq. 9.47:
R
N→M
=
π
39
0
2
|℘|
2
ρ(ω), with ω = ±(E
M
− E
N
)/ (+ sign ⇒ absorption, − sign ⇒ stimulated emission).
Problem 9.16
For example (c):
c
N
(t)=1−
i
H
NN
t; c
m
(t)=−2i
H
mN
(E
m
− E
N
)
e
i(E
m
−E
N
)t/2
sin
E
m
− E
N
2
t
(m = N).
|c
N
|
2
=1+
1
2
|H
NN
|
2
t
2
, |c
m
|
2
=4
|H
mN
|
2
(E
m
− E
N
)
2
sin
2
E
m
− E
N
2
t
, so
m
|c
m
|
2
=1+
t
2
2
|H
NN
|
2
+4
m=N
|H
mN
|
2
(E
m
− E
N
)
2
sin
2
E
m
− E
N
2
t
.
This is plainly greater than 1! But remember: The c’s are accurate only to first order in H
; to this order the
|H
|
2
terms do not belong. Only if terms of first order appeared in the sum would there be a genuine problem
with normalization.
For example (d):
c
N
=1−
i
V
NN
t
0
cos(ωt
) dt
=1−
i
V
NN
sin(ωt
)
ω
t
0
=⇒ c
N
(t)=1−
i
ω
V
NN
sin(ωt).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 249
c
m
(t)=−
V
mN
2
e
i(E
m
−E
N
+ω)t/
− 1
(E
m
− E
N
+ ω)
+
e
i(E
m
−E
N
−ω)t/
− 1
(E
m
− E
N
− ω)
(m = N).
So
|c
N
|
2
=1+
|V
NN
|
2
(ω)
2
sin
2
(ωt); and in the rotating wave approximation
|c
m
|
2
=
|V
mN
|
2
(E
m
− E
N
± ω)
2
sin
2
E
m
− E
N
± ω
2
t
(m = N).
Again, ostensibly
/
|c
m
|
2
> 1, but the “extra” terms are of second order in H
, and hence do not belong (to
first order).
You would do
better to use 1 −
/
m=N
|c
m
|
2
. Schematically: c
m
= a
1
H + a
2
H
2
+ ···,so|c
m
|
2
=
a
2
1
H
2
+2a
1
a
2
H
3
+ ···, whereas c
N
=1+b
1
H + b
2
H
2
+ ···,so|c
N
|
2
=1+2b
1
H +(2b
2
+ b
2
1
)H
2
+ ···.
Thus knowing c
m
to first order (i.e., knowing a
1
) gets you |c
m
|
2
to second order, but knowing c
N
to first order
(i.e., b
1
)doesnot get you |c
N
|
2
to second order (you’d also need b
2
). It is precisely this b
2
term that would
cancel the “extra” (second-order) terms in the calculations of
/
|c
m
|
2
above.
Problem 9.17
(a)
Equation 9.82 ⇒ ˙c
m
= −
i
n
c
n
H
mn
e
i(E
m
−E
n
)t/
. Here H
mn
= ψ
m
|V
0
(t)|ψ
n
= δ
mn
V
0
(t).
˙c
m
= −
i
c
m
V
0
(t);
dc
m
c
m
= −
i
V
0
(t) dt ⇒ ln c
m
= −
i
V
0
(t
) dt
+ constant.
c
m
(t)=c
m
(0)e
−
i
t
0
V
0
(t
) dt
. Let Φ(t) ≡−
1
t
0
V
0
(t
) dt
; c
m
(t)=e
iΦ
c
m
(0). Hence
|c
m
(t)|
2
= |c
m
(0)|
2
, and there are no transitions. Φ(T )=−
1
T
0
V
0
(t) dt.
(b)
Eq. 9.84 ⇒ c
N
(t) ≈ 1 −
i
t
0
V
0
(t
) dt =1+iΦ.
Eq. 9.85 ⇒ c
m
(t)=−
i
t
0
δ
mN
V
0
(t
)e
i(E
m
−E
N
)t
/
dt
=0(m = N).
c
N
(t)=1+iΦ(t),
c
m
(t)=0(m = N).
The exact answer is c
N
(t)=e
iΦ(t)
, c
m
(t) = 0, and they are consistent, since e
iΦ
≈ 1+iΦ, to first order.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

250 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
Problem 9.18
Use result of Problem 9.15(c). Here E
n
=
n
2
π
2
2
2ma
2
, so E
2
− E
1
=
3π
2
2
2ma
2
.
H
12
=
2
a
a/2
0
sin
π
a
x
V
0
sin
2π
a
x
dx
=
2V
0
a
sin
π
a
x
2(π/a)
−
sin
3π
a
x
2(3π/a)
a/2
0
=
V
0
π
sin
π
2
−
1
3
sin
3π
2
=
4V
0
3π
.
Eq. 9.86 =⇒ P
1→2
=4
4V
0
3π
2ma
2
3π
2
2
2
sin
2
3π
2
4ma
2
t
=
16ma
2
V
0
9π
3
2
sin
3π
2
T
4ma
2
2
.
[Actually, in this case H
11
and H
22
are nonzero:
H
11
= ψ
1
|H
|ψ
1
=
2
a
V
0
a/2
0
sin
2
π
a
x
dx =
V
0
2
,H
22
= ψ
2
|H
|ψ
2
=
2
a
V
0
a/2
0
sin
2
2π
a
x
dx =
V
0
2
.
However, this does not affect the answer, for according to Problem 9.4, c
1
(t) picks up an innocuous phase factor,
while c
2
(t) is not affected at all, in first order (formally, this is because H
bb
is multiplied by c
b
, in Eq. 9.11, and
in zeroth order c
b
(t) = 0).]
Problem 9.19
Spontaneous absorption would involve taking energy (a photon) from the ground state of the electromagnetic
field. But you can’t do that, because the gound state already has the lowest allowed energy.
Problem 9.20
(a)
H = −γB ·S = −γ (B
x
S
x
+ B
y
S
y
+ B
z
S
z
);
H = −γ
2
(B
x
σ
x
+ B
y
σ
y
+ B
z
σ
z
)=−
γ
2
B
x
01
10
+ B
y
0 −i
i 0
+ B
z
10
0 −1
= −
γ
2
B
z
B
x
− iB
y
B
x
+ iB
y
−B
z
= −
γ
2
B
0
B
rf
(cos ωt + i sin ωt)
B
rf
(cos ωt − i sin ωt) −B
0
=
−
γ
2
B
0
B
rf
e
iωt
B
rf
e
−iωt
−B
0
.
(b) i ˙χ = Hχ ⇒
i
˙a
˙
b
= −
γ
2
B
0
B
rf
e
iωt
B
rf
e
−iωt
−B
0
a
b
= −
γ
2
B
0
aB
rf
e
iωt
b
B
rf
e
−iωt
a −B
0
b
⇒
˙a = i
γ
2
B
0
a + B
rf
e
iωt
b
=
i
2
Ωe
iωt
b + ω
0
a
,
˙
b = −i
γ
2
B
0
b − B
rf
e
−iωt
a
=
i
2
Ωe
−iωt
a − ω
0
b
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 251
(c) You can decouple the equations by differentiating with respect to t, but it is simpler just to check the quoted
results. First of all, they clearly satisfy the initial conditions: a(0) = a
0
and b(0) = b
0
. Differentiating a:
˙a =
iω
2
a +
−a
0
ω
2
sin(ω
t/2) +
i
ω
[a
0
(ω
0
− ω)+b
0
Ω]
ω
2
cos(ω
t/2)
e
iωt/2
=
i
2
e
iωt/2
ωa
0
cos(ω
t/2) + i
ω
ω
[a
0
(ω
0
− ω)+b
0
Ω] sin(ω
t/2)
+ iω
a
0
sin(ω
t/2)+[a
0
(ω
0
− ω)+b
0
Ω] cos(ω
t/2)
Equation 9.90 says this should be equal to
i
2
Ωe
iωt
b + ω
0
a
=
i
2
e
iωt/2
Ωb
0
cos(ω
t/2) + i
Ω
ω
[b
0
(ω − ω
0
)+a
0
Ω] sin(ω
t/2)
+ ω
0
a
0
cos(ω
t/2) + i
ω
0
ω
[a
0
(ω
0
− ω)+b
0
Ω] sin(ω
t/2)
.
By inspection the cos(ω
t/2) terms in the two expressions are equal; it remains to check that
i
ω
ω
[a
0
(ω
0
− ω)+b
0
Ω] + iω
a
0
= i
Ω
ω
[b
0
(ω − ω
0
)+a
0
Ω] + i
ω
0
ω
[a
0
(ω
0
− ω)+b
0
Ω] ,
which is to say
a
0
ω(ω
0
− ω)+b
0
ωΩ+a
0
(ω
)
2
= b
0
Ω(ω − ω
0
)+a
0
Ω
2
+ a
0
ω
0
(ω
0
− ω)+b
0
ω
0
Ω,
or
a
0
ωω
0
− ω
2
+(ω
)
2
− Ω
2
− ω
2
0
+ ω
0
ω
= b
0
[Ωω − ω
0
Ω+ω
0
Ω − ωΩ] = 0.
Substituting Eq. 9.91 for ω
, the coefficient of a
0
on the left becomes
2ωω
0
− ω
2
+(ω − ω
0
)
2
+Ω
2
− Ω
2
− ω
2
0
=0.
The check of b(t) is identical, with a ↔ b, ω
0
→−ω
0
, and ω →−ω.
(d)
b(t)=i
Ω
ω
sin(ω
t/2)e
−iωt/2
; P (t)=|b(t)|
2
=
Ω
ω
2
sin
2
(ω
t/2).
(e)
P(ω)
ω
1
1/2
ω
0
∆ω
The maximum (P
max
= 1) occurs (obviously) at ω = ω
0
.
P =
1
2
⇒ (ω − ω
0
)
2
=Ω
2
⇒ ω = ω
0
± Ω, so ∆ω = ω
+
− ω
−
= 2Ω.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
252 CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY
(f) B
0
=10, 000 gauss = 1 T; B
rf
=0.01 gauss = 1 × 10
−6
T.ω
0
= γB
0
. Comparing Eqs. 4.156 and
6.85, γ =
g
p
e
2m
p
, where g
p
=5.59. So
ν
res
=
ω
0
2π
=
g
p
e
4πm
p
B
0
=
(5.59)(1.6 × 10
−19
)
4π(1.67 ×10
−27
)
(1) =
4.26 × 10
7
Hz.
∆ν =
∆ω
2π
=
Ω
π
=
γ
2π
2B
rf
= ν
res
2B
rf
B
0
=(4.26 × 10
7
)(2 × 10
−6
)= 85.2Hz.
Problem 9.21
(a)
H
= −qE · r = −q(E
0
· r)(k · r) sin(ωt). Write E
0
= E
0
ˆn, k =
ω
c
ˆ
k. Then
H
= −q
E
0
ω
c
(ˆn ·r)(
ˆ
k ·r) sin(ωt).H
ba
= −
qE
0
ω
c
b|(ˆn ·r)(
ˆ
k ·r)|asin(ωt).
This is the analog to Eq. 9.33: H
ba
= −qE
0
b|ˆn · r|acos ωt. The rest of the analysis is identical to the
dipole case (except that it is sin(ωt) instead of cos(ωt), but this amounts to resetting the clock, and clearly
has no effect on the transition rate). We can skip therefore to Eq. 9.56, except for the factor of 1/3, which
came from the averaging in Eq. 9.46:
A =
ω
3
π9
0
c
3
q
2
ω
2
c
2
|b|(ˆn ·r)(
ˆ
k ·r)|a|
2
=
q
2
ω
5
π9
0
c
5
|b|(ˆn ·r)(
ˆ
k ·r)|a|
2
.
(b) Let the oscillator lie along the x direction, so (ˆn ·r)=ˆn
x
x and
ˆ
k ·r =
ˆ
k
x
x. For a transition from n to n
,
we have
A =
q
2
ω
5
π9
0
c
5
ˆ
k
x
ˆn
x
2
|n
|x
2
|n|
2
. From Example 2.5, n
|x
2
|n =
2m¯ω
n
|(a
2
+
+a
+
a
−
+a
−
a
+
+a
2
−
)|n,
where ¯ω is the frequency of the oscillator, not to be confused with ω, the frequency of the electromagnetic
wave. Now, for spontaneous emission the final state must be lower in energy, so n
<n, and hence the
only surviving term is a
2
−
. Using Eq. 2.66:
n
|x
2
|n =
2m¯ω
n
|
n(n − 1)|n − 2 =
2m¯ω
n(n − 1) δ
n
,n−2
.
Evidently transitions only go from |n to |n − 2, and hence
ω =
E
n
− E
n−2
=
1
(n +
1
2
)¯ω − (n − 2+
1
2
)¯ω
=2¯ω.
n
|x
2
|n =
mω
n(n − 1) δ
n
,n−2
; R
n→n−2
=
q
2
ω
5
π9
0
c
5
(
ˆ
k
x
ˆn
x
)
2
2
m
2
ω
2
n(n − 1).
It remains to calculate the average of (
ˆ
k
x
ˆn
x
)
2
. It’s easiest to reorient the oscillator along a direction ˆr,
making angle θ with the z axis, and let the radiation be incident from the z direction (so
ˆ
k
x
→
ˆ
k
r
= cos θ).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 9. TIME-DEPENDENT PERTURBATION THEORY 253
Averaging over the two polarizations (
ˆ
i and
ˆ
j): ˆn
2
r
=
1
2
ˆ
i
2
r
+
ˆ
j
2
r
=
1
2
sin
2
θ cos
2
φ + sin
2
θ sin
2
φ
=
1
2
sin
2
θ. Now average overall directions:
ˆ
k
2
r
ˆn
2
r
=
1
4π
1
2
sin
2
θ cos
2
θ sin θdθdφ=
1
8π
2π
π
0
(1 − cos
2
θ) cos
2
θ sin θdθ
=
1
4
−
cos
3
θ
3
+
cos
5
θ
5
π
0
=
1
4
2
3
−
2
5
=
1
15
.
R =
1
15
q
2
ω
3
π9
0
m
2
c
5
n(n − 1). Comparing Eq. 9.63:
R(forbidden)
R(allowed)
=
2
5
(n − 1)
ω
mc
2
.
For a nonrelativistic system, ω mc
2
; hence the term “forbidden”.
(c) If both the initial state and the final state have l = 0, the wave function is independent of angle (Y
0
0
=
1/
√
4π), and the angular part of the integral is:
a|(ˆn ·r)(
ˆ
k ·r)|b = ···
(ˆn ·r)(
ˆ
k ·r) sin θdθdφ= ···
4π
3
(ˆn ·
ˆ
k) (Eq. 6.95).
But ˆn ·
ˆ
k = 0, since electromagnetic waves are transverse. So R = 0 in this case, both for allowed and
for forbidden transitions.
Problem 9.22
[This is done in Fermi’s Notes on Quantum Mechanics (Chicago, 1995), Section 24, but I am looking for a more
accessible treatment.]
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
254 CHAPTER 10. THE ADIABATIC APPROXIMATION
Chapter 10
The Adiabatic Approximation
Problem 10.1
(a)
Let (mvx
2
− 2E
i
n
at)/2w = φ(x, t). Φ
n
=
2
w
sin
nπ
w
x
e
iφ
, so
∂Φ
n
∂t
=
√
2
−
1
2
1
w
3/2
v
sin
nπ
w
x
e
iφ
+
2
w
−
nπx
w
2
v cos
nπ
w
x
e
iφ
+
2
w
sin
nπ
w
x
i
∂φ
∂t
e
iφ
=
−
v
2w
−
nπxv
w
2
cot
nπ
w
x
+ i
∂φ
∂t
Φ
n
.
∂φ
∂t
=
1
2
−
2E
i
n
a
w
−
v
w
2
mvx
2
− 2E
i
n
at
= −
E
i
n
a
w
−
v
w
φ.
i
∂Φ
n
∂t
= −i
v
2w
+
nπxv
w
2
cot
nπ
w
x
+ i
E
i
n
a
w
+ i
v
w
φ
Φ
n
.
HΦ
n
= −
2
2m
∂
2
Φ
n
∂x
2
.
∂Φ
n
∂x
=
2
w
nπ
w
cos
nπ
w
x
e
iφ
+
2
w
sin
nπ
w
x
e
iφ
i
∂φ
∂x
.
∂φ
∂x
=
mvx
w
.
∂Φ
n
∂x
=
nπ
w
cot
nπ
w
x
+ i
mvx
w
Φ
n
.
∂
2
Φ
n
∂x
2
=
−
nπ
w
2
csc
2
nπ
w
x
+
imb
w
Φ
n
+
nπ
w
cot
nπ
w
x
+ i
mvx
w
2
Φ
n
.
So the Schr¨odinger equation (i∂Φ
n
/∂t = HΦ
n
) is satisfied ⇔
−i
v
2w
+
nπxv
w
2
cot
nπ
w
x
+ i
E
i
n
a
w
+ i
v
w
φ
= −
2
2m
−
nπ
w
2
csc
2
nπ
w
x
+
imv
w
+
nπ
w
cot
nπ
w
x
+ i
mvx
w
2
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 10. THE ADIABATIC APPROXIMATION 255
Cotangent terms: − i
nπxv
w
2
?
= −
2
2m
2
nπ
w
i
mvx
w
= −i
nπvx
w
2
.
Remaining trig terms on right
:
−
nπ
w
2
csc
2
nπ
w
x
+
nπ
w
2
cot
2
nπ
w
x
= −
nπ
w
2
1 − cos
2
(nπx/w)
sin
2
(nπx/w)
= −
nπ
w
2
.
This leaves:
i
v
2w
+ i
E
i
n
a
w
+ i
v
w
mvx
2
− 2E
i
n
at
2w
?
=
2m
−
nπ
w
2
+
imv
w
−
m
2
v
2
x
2
2
w
2
✁
✁
✁
iv
2
−
E
i
n
a
−
✚
✚
✚
✚
mv
2
x
2
2w
+
vE
i
n
at
w
?
= −
n
2
π
2
2mw
+
✁
✁
✁
iv
2
−
✚
✚
✚
✚
mv
2
x
2
2w
−
E
i
n
a
w
(w −vt)=−
E
i
n
a
2
w
?
= −
n
2
π
2
2mw
⇔−
n
2
π
2
2
2ma
2
a
2
w
= −
n
2
π
2
2mw
= r.h.s.
So Φ
n
does satisfy the Schr¨odinger equation, and since Φ
n
(x, t)=(···) sin (nπx/w), it fits the boundary
conditions: Φ
n
(0,t)=Φ
n
(w, t)=0.
(b)
Equation 10.4 =⇒ Ψ(x, 0) =
c
n
Φ
n
(x, 0) =
c
n
2
a
sin
nπ
a
x
e
imvx
2
/2a
.
Multiply by
2
a
sin
n
π
a
x
e
−imvx
2
/2a
and integrate:
2
a
a
0
Ψ(x, 0) sin
n
π
a
x
e
−imvx
2
/2a
dx =
c
n
2
a
π
0
sin
nπ
a
x
sin
n
π
a
x
dx
δ
nn
= c
n
.
So, in general: c
n
=
2
a
a
0
e
−imvx
2
/2a
sin
nπ
a
x
Ψ(x, 0)dx. In this particular case,
c
n
=
2
a
a
0
e
−imvx
2
/2a
sin
nπ
a
sin
π
a
x
dx. Let
π
a
x ≡ z; dx =
a
π
dz;
mvx
2
2a
=
mvz
2
2a
a
2
π
2
=
mva
2π
2
z
2
.
c
n
=
2
π
π
0
e
−iαz
2
sin(nz) sin(z) dz. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
256 CHAPTER 10. THE ADIABATIC APPROXIMATION
(c)
w(T
e
)=2a ⇒ a + vT
e
=2a ⇒ vT
e
= a ⇒ T
e
a/v; e
−iE
1
t/
⇒ ω =
E
1
⇒ T
i
=
2π
ω
=2π
E
1
, or
T
i
=
2π
π
2
2
2ma
2
=
4
π
ma
2
.
T
i
=
4ma
2
π
.
Adiabatic ⇒ T
e
T
i
⇒
a
v
4ma
2
π
⇒
4
π
mav
1, or
8π
mav
2π
2
=8πα 1, so α 1. Then c
n
=
2
π
π
0
sin(nz) sin(z)dz = δ
n1
. Therefore
Ψ(x, t)=
2
w
sin
πx
w
e
i(mvx
2
−2E
i
1
at)/2w
,
which (apart from a phase factor) is the ground state of the instantaneous well, of width w, as required
by the adiabatic theorem. (Actually, the first term in the exponent, which is at most
mva
2
2a
=
mva
2
1
and could be dropped, in the adiabatic regime.)
(d)
θ(t)=−
1
π
2
2
2m
t
0
1
(a + vt
)
2
dt
= −
π
2
2m
−
1
v
1
a + vt
t
0
= −
π
2
2mv
1
a
−
1
w
= −
π
2
2mv
vt
aw
= −
π
2
t
2maw
.
So (dropping the
mvx
2
2w
term, as explained in (c)) Ψ(x, t)=
2
w
sin
πx
w
e
−iE
i
1
at/w
can be written
(since −
E
i
1
at
w
= −
π
2
2
2ma
2
at
w
= −
π
2
t
2maw
= θ):
Ψ(x, t)=
2
w
sin
πx
w
e
iθ
.
This is exactly what one would naively expect: For a fixed well (of width a) we’d have Ψ(x, t)=
Ψ
1
(x)e
−iE
1
t/
; for the (adiabatically) expanding well, simply replace a by the (time-dependent) width
w, and integrate to get the accumulated phase factor, noting that E
1
is now a function of t.
Problem 10.2
To show: i
∂χ
∂t
= Hχ, where χ is given by Eq. 10.31 and H is given by Eq. 10.25.
∂χ
∂t
=
λ
2
−sin
λt
2
− i
(ω
1
−ω)
λ
cos
λt
2
cos
α
2
e
−iωt/2
−
iω
2
cos
λt
2
−
i(ω
1
−ω)
λ
sin
λt
2
cos
α
2
e
−iωt/2
λ
2
−sin
λt
2
− i
(ω
1
+ω)
λ
cos
λt
2
sin
α
2
e
iωt/2
+
iω
2
cos
λt
2
−
i(ω
1
+ω)
λ
sin
λt
2
sin
α
2
e
iωt/2
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 10. THE ADIABATIC APPROXIMATION 257
Hχ =
ω
1
2
cos α
cos(
λt
2
) − i
(ω
1
−ω)
λ
sin(
λt
2
)
cos
α
2
e
−iωt/2
+ e
−iωt
sin α
cos(
λt
2
) −
i(ω
1
+ω)
λ
sin(
λt
2
)
sin
α
2
e
iωt/2
e
iωt
cos α
cos(
λt
2
) − i
(ω
1
−ω)
λ
sin(
λt
2
)
cos
α
2
e
−iωt/2
− cos α
cos(
λt
2
) −
i(ω
1
+ω)
λ
sin(
λt
2
)
sin
α
2
e
iωt/2
(1) Upper elements:
i
✁
λ
✁
2
−sin
λt
2
− i
(ω
1
− ω)
λ
cos
λt
2
✚
✚
✚
cos
α
2
−
iω
✁
2
cos
λt
2
−
i(ω
1
− ω)
λ
sin
λt
2
✚
✚
✚
cos
α
2
?
=
✁
ω
1
✁
2
cos
λt
2
− i
(ω
1
− ω)
λ
sin
λt
2
cos α
✚
✚
✚
cos
α
2
+
cos
λt
2
− i
(ω
1
+ ω)
λ
sin
λt
2
sin α
sin
α
2
,
where = 2 sin
α
2
✚
✚
✚
cos
α
2
The sine terms:
sin
λt
2
−iλ −
iω(ω
1
− ω)
λ
+
ω
1
(ω
1
− ω)
λ
cos α +
iω
1
(ω
1
+ ω)
λ
2 sin
2
α
2
?
=0.
i
λ
sin
λt
2
✟
✟
✟
−ω
2
− ω
2
1
+2ωω
1
cos α −ωω
1
+
✚
✚
ω
2
+(ω
2
1
− ωω
1
) cos α +(ω
2
1
+ ωω
1
)(1 − cos α)
= −
i
λ
sin
λt
2
✟
✟
✟
−ω
2
1
+2ωω
1
cos α −
✘
✘
ωω
1
+
✘
✘
✘
✘
ω
2
1
cos α −ωω
1
cos α +
ω
2
1
+
✘
✘
ωω
1
−
✘
✘
✘
✘
ω
2
1
cos α −ωω
1
cos α
=0.
The cosine terms:
cos
λt
2
(ω
1
−
✚
ω)+
✚
ω − ω
1
cos α −ω
1
2 sin
2
α
2
= −ω
1
cos
λt
2
[−1 + cos α +(1− cos α)] = 0.
(2) Lower elements:
i
✁
λ
✁
2
−sin
λt
2
− i
(ω
1
+ ω)
λ
cos
λt
2
✟
✟
✟
✟
sin
α
2
+
iω
✁
2
cos
λt
2
−
i(ω
1
+ ω)
λ
sin
λt
2
✟
✟
✟
✟
sin
α
2
?
=
✁
ω
1
✁
2
cos
λt
2
− i
(ω
1
− ω)
λ
sin
λt
2
2
✚
✚
✚
sin
α
2
cos
2
α
2
−
cos
λt
2
−
i(ω
1
+ ω)
λ
sin
λt
2
cos α
✚
✚
✚
sin
α
2
.
The sine terms:
sin
λt
2
−iλ +
iω(ω
1
+ ω)
λ
+
iω
1
(ω
1
− ω)
λ
2 cos
2
α
2
−
iω
1
(ω
1
+ ω)
λ
cos α
?
=0.
i
λ
sin
λt
2
−
✚
✚
ω
2
− ω
2
1
+2ωω
1
cos α + ωω
1
+
✚
✚
ω
2
+(ω
2
1
− ωω
1
)(1 + cos α) −(ω
2
1
+ ωω
1
) cos α
=
i
λ
sin
λt
2
−
ω
2
1
+2ωω
1
cos α +
✘
✘
ωω
1
+
ω
2
1
−
✘
✘
ωω
1
+
✘
✘
✘
✘
ω
2
1
cos α −ωω
1
cos α −
✘
✘
✘
✘
ω
2
1
cos α −ωω
1
cos α
=0.
The cosine terms:
cos
λt
2
(ω
1
+
✚
ω) −
✚
ω − ω
1
2 cos
2
α
2
+ ω
1
cos α
= cos
λt
2
[ω
1
− ω
1
(1 + cos α)+ω
1
cos α]=0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

258 CHAPTER 10. THE ADIABATIC APPROXIMATION
As for Eq. 10.33:
cos
λt
2
− i
(ω
1
− ω cos α)
λ
sin
λt
2
e
−iωt/2
cos
α
2
e
iωt
sin
α
2
+ i
ω
λ
sin α sin
λt
2
e
−iωt/2
sin
α
2
−e
iωt
cos
α
2
=
α
β
, with
α =
cos
λt
2
−
iω
1
λ
sin
λt
2
cos
α
2
+
iω
λ
cos α cos
α
2
+ sin α sin
α
2
cos(α−
α
2
)=cos
α
2
sin
λt
2
e
−iωt/2
=
cos
λt
2
−
i(ω
1
− ω)
λ
sin
λt
2
cos
α
2
e
−iωt/2
(confirming the top entry).
β =
cos
λt
2
−
iω
1
λ
sin
λt
2
sin
α
2
+
iω
λ
cos α sin
α
2
− sin α cos
α
2
sin(
α
2
−α)=−sin
α
2
sin
λt
2
e
iωt/2
=
cos
λt
2
−
i(ω
1
+ ω)
λ
sin
λt
2
sin
α
2
e
iωt/2
(confirming the bottom entry).
|c
+
|
2
+ |c
−
|
2
= cos
2
λt
2
+
(ω
1
− ω cos α)
2
λ
2
sin
2
λt
2
+
ω
2
λ
2
sin
2
α sin
2
λt
2
= cos
2
λt
2
+
1
λ
2
ω
2
1
− 2ωω
1
cos α + ω
2
cos
2
α + ω
2
sin
2
α
ω
2
+ω
2
1
−2ωω
1
cos α=λ
2
sin
2
λt
2
= cos
2
λt
2
+ sin
2
λt
2
=1.
Problem 10.3
(a)
ψ
n
(x)=
2
w
sin
nπ
w
x
. In this case R = w.
∂ψ
n
∂R
=
√
2
−
1
2
1
w
3/2
sin
nπ
w
x
+
2
w
−
nπ
w
2
x
cos
nπ
w
x
;
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 10. THE ADIABATIC APPROXIMATION 259
0
ψ
n
∂ψ
n
∂R
1
=
w
0
ψ
n
∂ψ
n
∂R
dx
= −
1
w
2
w
0
sin
2
nπ
w
x
dx −
2nπ
w
3
w
0
x sin
nπ
w
x
cos
nπ
w
x
1
2
sin
(
2nπ
w
x
)
dx
= −
1
w
2
w
2
−
nπ
w
3
w
0
x sin
2nπ
w
x
dx
= −
1
2w
−
nπ
w
3
w
2nπ
2
sin
2nπ
w
x
−
wx
2nπ
cos
2nπ
w
x
w
0
= −
1
2w
−
nπ
w
3
−
w
2
2nπ
cos(2nπ)
= −
1
2w
+
1
2w
=0.
So Eq. 10.42 =⇒
γ
n
(t)=0. (If the eigenfunctions are real, the geometric phase vanishes.)
(b)
Equation 10.39 =⇒ θ
n
(t)=
1
t
0
n
2
π
2
2
2mw
2
dt
= −
n
2
π
2
2m
1
w
2
dt
dw
dw;
θ
n
= −
n
2
π
2
2mv
w
2
w
1
1
w
2
dw =
n
2
π
2
2mv
1
w
w
2
w
1
=
n
2
π
2
2mv
1
w
2
−
1
w
1
.
(c) Zero.
Problem 10.4
ψ =
√
mα
e
−mα|x|/
2
. Here R = α, so
∂ψ
∂R
=
√
m
1
2
1
√
α
e
−mα|x|/
2
+
√
mα
−
m|x|
2
e
−mα|x|/
2
.
ψ
∂ψ
∂R
=
√
mα
1
2
m
α
−
m
√
mα
3
|x|
e
−2mα|x|/
2
=
m
2
2
−
m
2
α
4
|x|
e
−2mα|x|/
2
.
0
ψ
∂ψ
∂R
1
=2
m
2
2
∞
0
e
−2mαx/
2
dx −
m
2
α
4
∞
0
xe
−2mαx/
2
dx
=
m
2
2
2mα
−
2m
2
α
4
2
2mα
2
=
1
2α
−
1
2α
=0. So Eq. 10.42 =⇒
γ(t)=0.
E = −
mα
2
2
2
, so θ(t)=−
1
T
0
−
mα
2
2
2
dt
=
m
2
3
α
2
α
1
α
2
dt
dα
dα =
m
2
3
c
α
2
α
1
α
2
dα =
m
6
2
c
α
3
2
− α
3
1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

260 CHAPTER 10. THE ADIABATIC APPROXIMATION
Problem 10.5
According to Eq. 10.44 the geometric phase is
γ
n
(t)=i
R
f
R
i
ψ
n
|∇
R
ψ
n
·dR.
Now ψ
n
|ψ
n
=1, so
∇
R
ψ
n
|ψ
n
= ∇
R
ψ
n
|ψ
n
+ ψ
n
|∇
R
ψ
n
= ψ
n
|∇
R
ψ
n
∗
+ ψ
n
|∇
R
ψ
n
=0,
and hence ψ
n
|∇
R
ψ
n
is pure imaginary.Ifψ
n
is real, then, ψ
n
|∇
R
ψ
n
must in fact be zero.
Suppose we introduce a phase factor to make the (originally real) wave function complex:
ψ
n
= e
iφ
n
(R)
ψ
n
, where ψ
n
is real. Then ∇
R
ψ
n
= e
iφ
n
∇
R
ψ
n
+ i(∇
R
φ
n
)e
iφ
n
ψ
n
. So
ψ
n
|∇
R
ψ
n
= e
−iφ
n
e
iφ
n
ψ
n
|∇
R
ψ
n
+ ie
−iφ
n
(∇
R
φ
n
)e
iφ
n
ψ
n
|ψ
n
. But ψ
n
|ψ
n
=1, and
ψ
n
|∇
R
ψ
n
= 0 (as we just found), so ψ
n
|∇
R
ψ
n
= i∇
R
φ
n
, and Eq. 10.44 =⇒
γ
n
(t)=i
R
f
R
i
i∇
R
(φ
n
) · dR = −[φ
n
(R
f
) − φ
n
(R
i
)] , so Eq. 10.38 gives:
Ψ
n
(x, t)=ψ
n
(x, t)e
−
i
t
0
E
n
(t
)dt
e
−i[φ
n
(R
f
)−φ
n
(R
i
)]
.
The wave function picks up a (trivial) phase factor, whose only function is precisely to kill the phase factor we
put in “by hand”:
Ψ
n
(x, t)=
ψ
n
(x, t)e
−
i
t
0
E
n
(t
)dt
e
iφ
n
(R
i
)
=Ψ
n
(x, t)e
iφ
n
(R
i
)
.
In particular, for a closed loop φ
n
(R
f
)=φ
n
(R
i
), so γ
n
(T )=0.
Problem 10.6
H =
e
m
B · S. Here B = B
0
sin θ cos φ
ˆ
i + sin θ sin φ
ˆ
j + cos θ
ˆ
k
; take spin matrices from Problem 4.31.
H =
eB
0
m
√
2
sin θ cos φ
010
101
010
+ sin θ sin φ
0 −i 0
i 0 −i
0 i 0
+ cos θ
√
20 0
00 0
00−
√
2
=
eB
0
√
2 m
√
2 cos θe
−iφ
sin θ 0
e
iφ
sin θ 0 e
−iφ
sin θ
0 e
iφ
sin θ −
√
2 cos θ
.
We need the “spin up” eigenvector: Hχ
+
=
eB
0
m
χ
+
.
√
2 cos θe
−iφ
sin θ 0
e
iφ
sin θ 0 e
−iφ
sin θ
0 e
iφ
sin θ −
√
2 cos θ
a
b
c
=
√
2
a
b
c
=⇒
(i)
√
2 cos θa + e
−iφ
sin θb =
√
2a.
(ii) e
iφ
sin θa + e
−iφ
sin θc =
√
2b.
(iii) e
iφ
sin θb −
√
2 cos θc =
√
2c.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 10. THE ADIABATIC APPROXIMATION 261
(i) ⇒ b =
√
2e
iφ
1 − cos θ
sin θ
a =
√
2e
iφ
tan (θ/2) a; (iii) ⇒ b =
√
2e
−iφ
1 + cos θ
sin θ
c =
√
2e
−iφ
cot (θ/2) c.
Thus c = e
2iφ
tan
2
(θ/2) a; (ii) is redundant. Normalize: |a|
2
+ 2 tan
2
(θ/2)|a|
2
+ tan
4
(θ/2)|a|
2
=1⇒
|a|
2
1 + tan
2
(θ/2)
2
= |a|
2
1
cos(θ/2)
4
=1⇒|a|
2
= cos
4
(θ/2) .
Pick a = e
−iφ
cos
2
(θ/2); then b =
√
2 sin(θ/2) cos(θ/2) and c = e
iφ
sin
2
(θ/2), and
χ
+
=
e
−iφ
cos
2
(θ/2)
√
2 sin (θ/2) cos (θ/2)
e
iφ
sin
2
(θ/2)
.
This is the spin-1 analog to Eq. 10.57.
∇χ
+
=
∂χ
+
∂r
ˆr +
1
r
∂χ
+
∂θ
ˆ
θ +
1
r sin θ
∂χ
+
∂φ
ˆ
φ
=
1
r
−e
−iφ
cos (θ/2) sin (θ/2)
√
2
cos
2
(θ/2) − sin
2
(θ/2)
/2
e
iφ
sin (θ/2) cos (θ/2)
ˆ
θ +
1
r sin θ
−ie
−iφ
cos
2
(θ/2)
0
ie
iφ
sin
2
(θ/2)
ˆ
φ.
χ
+
|∇χ
+
=
1
r
-
−cos
2
(θ/2) [cos (θ/2) sin (θ/2)] + sin (θ/2) cos (θ/2)
cos
2
(θ/2) − sin
2
(θ/2)
+ sin
2
(θ/2) [sin (θ/2) cos (θ/2)]
.
ˆ
θ
+
1
r sin θ
-
cos
2
(θ/2)
−i cos
2
(θ/2)
+ sin
2
(θ/2)
i sin
2
(θ/2)
.
ˆ
φ
=
i
r sin θ
sin
4
(θ/2) − cos
4
(θ/2)
ˆ
φ
=
i
r sin θ
sin
2
(θ/2) + cos
2
(θ/2)
sin
2
(θ/2) − cos
2
(θ/2)
ˆ
φ
=
i
r sin θ
(1)(−cos θ)
ˆ
φ = −
i
r
cot θ
ˆ
φ.
∇×χ
+
|∇χ
+
=
1
r sin θ
∂
∂θ
sin θ
−
i
r
cot θ
ˆr =
−i
r
2
sin θ
∂
∂θ
(cos θ)ˆr =
i sin θ
r
2
sin θ
ˆr =
i
r
2
ˆr.
Equation 10.51 =⇒ γ
+
(T )=i
i
r
2
r
2
dΩ= −Ω.
Problem 10.7
(a) Giving H a test function f to act upon:
Hf =
1
2m
i
∇−qA
·
i
∇f − qAf
+ qϕf
=
1
2m
−
2
∇·(∇f) −
q
i
∇·(Af)
(∇·A)f+A·(∇f)
−
q
i
A · (∇f)+q
2
A · Af
+ qϕf.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

262 CHAPTER 10. THE ADIABATIC APPROXIMATION
But ∇·A = 0 and ϕ = 0 (see comments after Eq. 10.66), so
Hf =
1
2m
−
2
∇
2
f +2iqA ·∇f + q
2
A
2
f
, or H =
1
2m
−
2
∇
2
+ q
2
A
2
+2iqA ·∇
. QED
(b) Apply
i
∇−qA
· to both sides of Eq. 10.78:
i
∇−qA
2
Ψ=
i
∇−qA
·
i
e
ig
∇Ψ
= −
2
∇·(e
ig
∇Ψ
) −
q
i
e
ig
A ·∇Ψ
.
But ∇·(e
ig
∇Ψ
)=ie
ig
(∇g) ·(∇Ψ
)+e
ig
∇·(∇Ψ
) and ∇g =
q
A, so the right side is
−i
2
q
e
ig
A ·∇Ψ
−
2
e
ig
∇
2
Ψ
+ iqe
ig
A ·∇Ψ
= −
2
e
ig
∇
2
Ψ
. QED
Problem 10.8
(a) Schr¨odinger equation:
−
2
2m
d
2
ψ
dx
2
= Eψ, or
d
2
ψ
dx
2
= −k
2
ψ (k ≡
√
2mE/)
0 <x<
1
2
a + 9,
1
2
a + 9<x<a.
Boundary conditions: ψ(0) = ψ(
1
2
a + 9)=ψ(a)=0.
Solution:
(1) 0 <x<
1
2
a + 9 : ψ(x)=A sin kx + B cos kx. But ψ(0) = 0 ⇒ B =0, and
ψ(
1
2
a + 9)=0⇒
k(
1
2
a + 9)=nπ (n =1, 2, 3,...) ⇒ E
n
= n
2
π
2
2
/2m(a/2+9)
2
,
or else A =0.
(2)
1
2
a + 9<x<a: ψ(x)=F sin k(a − x)+G cos k(a − x). But ψ(a)=0⇒ G =0, and
ψ(
1
2
a + 9)=0⇒
k(
1
2
a − 9)=n
π (n
=1, 2, 3,...) ⇒ E
n
=(n
)
2
π
2
2
/2m(a/2 − 9)
2
,
or else F =0.
The ground state energy is
either E
1
=
π
2
2
2m(
1
2
a + 9)
2
(n =1), with F =0,
or else E
1
=
π
2
2
2m(
1
2
a − 9)
2
(n
=1), with A =0.
Both are allowed energies, but E
1
is (slightly) lower (assuming 9 is positive), so the ground state is
ψ(x)=
2
1
2
a+5
sin
πx
1
2
a+5
, 0 ≤ x ≤
1
2
a + 9;
0,
1
2
a + 9 ≤ x ≤ a.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
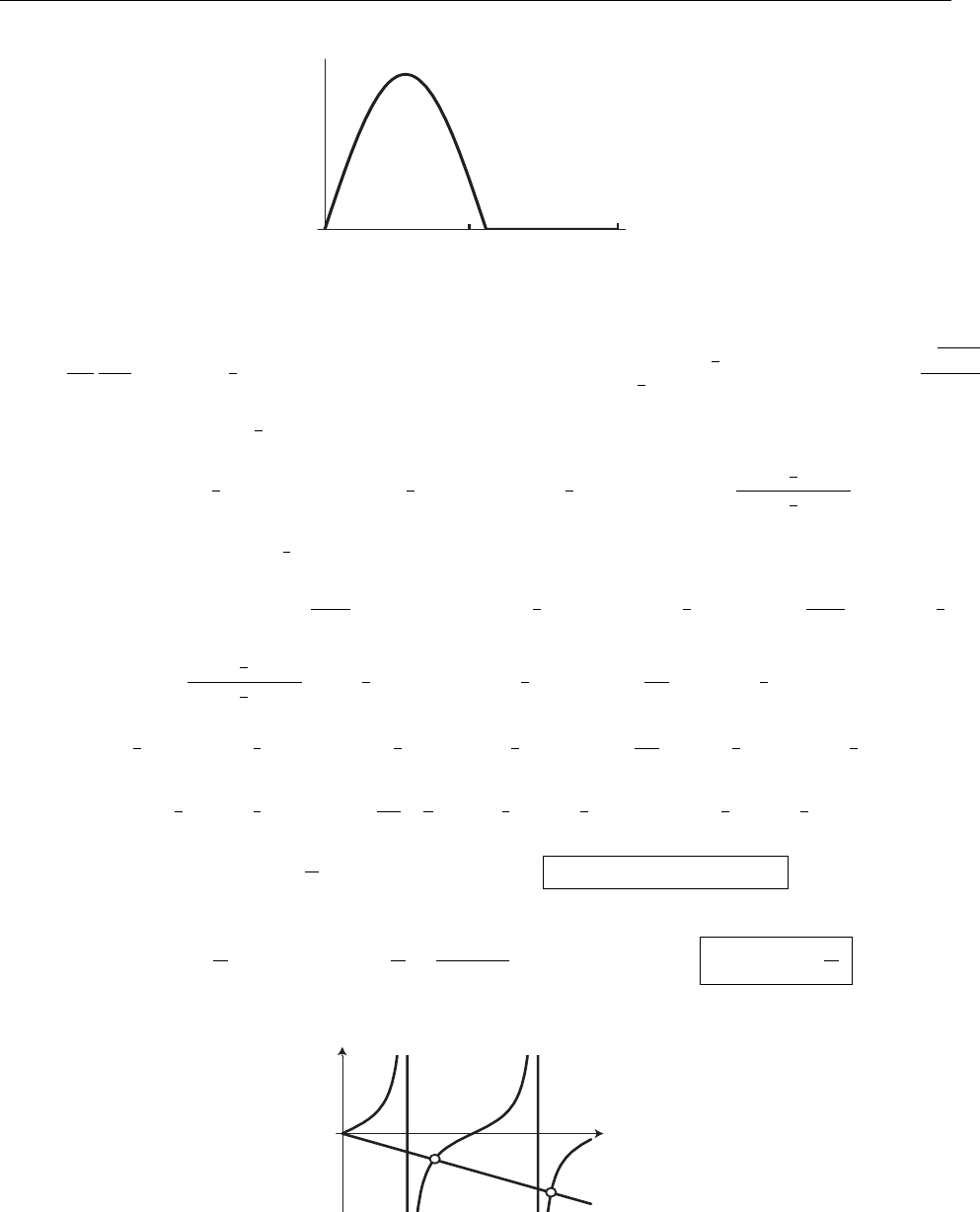
CHAPTER 10. THE ADIABATIC APPROXIMATION 263
x
ψ(x)
aa
_
2
_
2
a
+ε
(b)
−
2
2m
d
2
ψ
dx
2
+f(t)δ(x−
1
2
a−9)ψ = Eψ ⇒ ψ(x)=
A sin kx, 0 ≤ x<
1
2
a + 9,
F sin k(a −x),
1
2
a + 9<x≤ a,
where k ≡
√
2mE
.
Continuity in ψ at x =
1
2
a + 9 :
A sin k
1
2
a + 9
= F sin k
a −
1
2
a − 9
= F sin k
1
2
a − 9
⇒ F = A
sin k
1
2
a + 9
sin k
1
2
a − 9
.
Discontinuity in ψ
at x =
1
2
a + 9 (Eq. 2.125):
−Fkcos k(a−x)−Ak cos kx =
2mf
2
A sin kx ⇒ F cos k
1
2
a − 9
+A cos k
1
2
a + 9
= −
2mf
2
k
A sin k
1
2
a + 9
.
A
sin k
1
2
a + 9
sin k
1
2
a − 9
cos k
1
2
a − 9
+ A cos k
1
2
a + 9
= −
2T
z
A sin k
1
2
a + 9
.
sin k
1
2
a + 9
cos k
1
2
a − 9
+ cos k
1
2
a + 9
sin k
1
2
a − 9
= −
2T
z
sin k
1
2
a + 9
sin k
1
2
a − 9
.
sin k
1
2
a + 9 +
1
2
a − 9
= −
2T
z
1
2
cos k
1
2
a + 9 −
1
2
a + 9
− cos k
1
2
a + 9 +
1
2
a − 9
.
sin ka = −
T
z
(cos 2k9 − cos ka) ⇒
z sin z = T [cos z − cos(zδ)].
(c)
sin z =
T
z
(cos z − 1) ⇒
z
T
=
cos z − 1
sin z
= −tan(z/2) ⇒
tan(z/2) = −
z
T
.
Plot tan(z/2) and −z/T on the same graph, and look for intersections:
tan(z/2)
π
z
2π
3π
-z/T
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
264 CHAPTER 10. THE ADIABATIC APPROXIMATION
As t :0→∞, T :0→∞, and the straight line rotates counterclockwise from 6 o’clock to 3 o’clock,
so the smallest z goes from π to 2π, and the ground state energy goes from ka = π ⇒ E(0) =
2
π
2
2ma
2
(appropriate to a well of width a)toka =2π ⇒ E(∞)=
2
π
2
2m(a/2)
2
(appropriate for a well of width a/2.
(d) Mathematica yields the following table:
T 0 1 5 20 100 1000
z 3.14159 3.67303 4.76031 5.72036 6.13523 6.21452
(e) P
r
=
I
r
I
r
+ I
l
=
1
1+(I
l
/I
r
)
, where
I
l
=
a/2+5
0
A
2
sin
2
kx dx = A
2
1
2
x −
1
4k
sin(2kx)
a/2+5
0
= A
2
1
2
a
2
+ 9
−
1
4k
sin
2k
a
2
+ 9
=
a
4
A
2
1+
29
a
−
1
ka
sin
ka +
29
a
ka
=
a
4
A
2
1+δ −
1
z
sin(z + zδ)
.
I
r
=
a
a/2+5
F
2
sin
2
k(a −x) dx. Let u ≡ a − x, du = −dx.
= −F
2
0
a/2−5
sin
2
ku du = F
2
a/2−5
0
sin
2
ku du =
a
4
F
2
1 − δ −
1
z
sin(z − zδ)
.
I
l
I
r
=
A
2
[1 + δ − (1/z) sin(z + zδ)]
F
2
[1 − δ − (1/z) sin(z − zδ)]
. But (from (b))
A
2
F
2
=
sin
2
k(a/2 −9)
sin
2
k(a/2+9)
=
sin
2
[z(1 − δ)/2]
sin
2
[z(1 + δ)/2]
.
=
I
+
I
−
, where I
±
≡
1 ± δ −
1
z
sin z(1 ±δ)
sin
2
[z(1 ∓ δ)/2]. P
r
=
1
1+(I
+
/I
−
)
.
Using δ =0.01 and the z’s from (d), Mathematica gives
T 0 1 5 20 100 1000
P
r
0.490001 0.486822 0.471116 0.401313 0.146529 0.00248443
As t :0→∞(so T :0→∞), the probability of being in the right half drops from almost 1/2 to zero—the
particle gets sucked out of the slightly smaller side, as it heads for the ground state in (a).
(f)
T=0
T=1
T=5
T=20
T=100 T=1000
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 10. THE ADIABATIC APPROXIMATION 265
Problem 10.9
(a) Check the answer given: x
c
= ω
t
0
f(t
) sin [ω(t − t
)] dt
=⇒ x
c
(0) = 0.
˙x
c
= ωf(t) sin [ω(t −t)] + ω
2
t
0
f(t
) cos [ω(t − t
)] dt
= ω
2
t
0
f(t
) cos [ω(t − t
)] dt
⇒ ˙x
c
(0) = 0.
¨x
c
= ω
2
f(t) cos [ω(t − t)] − ω
3
t
0
f(t
) sin [ω(t − t
)] dt
= ω
2
f(t) − ω
2
x
c
.
Now the classical equation of motion is m(d
2
x/dt
2
)=−mω
2
x + mω
2
f. For the proposed solution,
m(d
2
x
c
/dt
2
)=mω
2
f −mω
2
x
c
,soitdoes satisfy the equation of motion, with the appropriate boundary
conditions.
(b) Let z ≡ x − x
c
(so ψ
n
(x − x
c
)=ψ
n
(z), and z depends on t as well as x).
∂Ψ
∂t
=
dψ
n
dz
(−˙x
c
)e
i{}
+ ψ
n
e
i{}
i
− (n +
1
2
)ω + m¨x
c
(x −
x
c
2
) −
m
2
˙x
2
c
+
mω
2
2
fx
c
[]=−(n +
1
2
)ω +
mω
2
2
2x(f − x
c
)+x
2
c
−
˙x
2
c
ω
2
.
∂Ψ
∂t
= −˙x
c
dψ
n
dz
e
i{}
+ iΨ
−(n +
1
2
)ω +
mω
2
2
2x(f − x
c
)+x
2
c
−
˙x
2
c
ω
2
.
∂Ψ
∂x
=
dψ
n
dz
e
i{}
+ ψ
n
e
i{}
i
(m ˙x
c
);
∂
2
Ψ
∂x
2
=
d
2
ψ
n
dz
2
e
i{}
+2
dψ
n
dz
e
i{}
i
(m ˙x
c
) −
m ˙x
c
2
ψ
n
e
i{}
.
HΨ=−
2
2m
∂
2
Ψ
∂x
2
+
1
2
mω
2
x
2
Ψ − mω
2
fxΨ
= −
2
2m
d
2
ψ
n
dz
2
e
i{}
−
2
2m
2
dψ
n
dz
e
i{}
im ˙x
c
+
2
2m
m ˙x
c
2
Ψ+
1
2
mω
2
x
2
Ψ − mω
2
fxΨ.
But −
2
2m
d
2
ψ
n
dz
2
+
1
2
mω
2
z
2
ψ
n
=(n +
1
2
)ωψ
n
,so
HΨ=
✟
✟
✟
✟
✟
(n +
1
2
)ωΨ −
1
2
mω
2
z
2
Ψ −
✟
✟
✟
✟
✟
i ˙x
c
dΨ
n
dz
e
i{}
+
m
2
˙x
2
c
Ψ+
1
2
mω
2
x
2
Ψ − mω
2
fxΨ
?
= i
∂Ψ
∂t
=
✟
✟
✟
✟
✟
−i ˙x
c
dψ
n
dz
e
i{}
− Ψ
✟
✟
✟
✟
✟
−(n +
1
2
)ω +
mω
2
2
(2xf − 2xx
c
+ x
2
c
−
1
ω
2
˙x
2
c
)
−
1
2
mω
2
z
2
+
m
2
˙x
2
c
+
1
2
mω
2
x
2
−
✘
✘
✘
✘
mω
2
fx
?
= −
mω
2
2
'
✟
✟
2xf − 2xx
c
+ x
2
c
−
1
ω
2
˙x
2
c
(
z
2
− x
2
?
= −2xx
c
+ x
2
c
; z
2
?
=(x
2
− 2xx
c
+ x
2
c
)=(x − x
c
)
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

266 CHAPTER 10. THE ADIABATIC APPROXIMATION
(c)
Eq. 10.90 ⇒ H = −
2
2m
∂
2
∂x
2
+
1
2
mω
2
x
2
− 2xf + f
2
−
1
2
mω
2
f
2
. Shift origin: u ≡ x − f.
H =
−
2
2m
∂
2
∂u
2
+
1
2
mω
2
u
2
−
1
2
mω
2
f
2
.
The first term is a simple harmonic oscillator in the variable u; the second is a constant (with respect
to position). So the eigenfunctions are ψ
n
(u), and the eigenvalues are harmonic oscillator ones, (n +
1
2
)ω, less the constant: E
n
=(n +
1
2
)ω −
1
2
mω
2
f
2
.
(d) Note that sin [ω(t − t
)] =
1
ω
d
dt
cos [ω(t −t
)], so x
c
(t)=
t
0
f(t
)
d
dt
cos [ω(t −t
)] dt
,or
x
c
(t)=f(t
) cos [ω(t − t
)]
t
0
−
t
0
df
dt
cos [ω(t −t
)] dt
= f(t) −
t
0
df
dt
cos [ω(t −t
)] dt
(since f(0) = 0). Now, for an adiabatic process we want df /dt very small; specifically:
df
dt
ωf(t)
(0 <t
≤ t). Then the integral is negligible compared to f (t), and we have x
c
(t) ≈ f(t). (Physically,
this says that if you pull on the spring very gently, no fancy oscillations will occur; the mass just moves
along as though attached to a string of fixed length.)
(e) Put x
c
≈ f into Eq. 10.92, using Eq. 10.93:
Ψ(x, t)=ψ
n
(x, t)e
i
−(n+
1
2
)ωt+m
˙
f(x−f/2)+
mω
2
2
t
0
f
2
(t
)dt
.
The dynamic phase (Eq. 10.39) is
θ
n
(t)=−
1
t
0
E
n
(t
) dt
= −(n +
1
2
)ωt +
mω
2
2
t
0
f
2
(t
) dt
, so Ψ(x, t)=ψ
n
(x, t)e
iθ
n
(t)
e
iγ
n
(t)
,
confirming Eq. 10.94, with the geometric phase given (ostensibly) by γ
n
(t)=
m
˙
f(x − f/2). But the
eigenfunctions here are real, and hence(Problem 10.5) the geometric phase should be zero. The point is that
(in the adiabatic approximation)
˙
f is extremely small (see above), and hence in this limit
m
˙
f(x−f/2) ≈ 0
(at least, in the only region of x where ψ
n
(x, t) is nonzero).
Problem 10.10
(a)
˙c
m
= −
j
δ
jn
e
iγ
n
ψ
m
|
˙
ψ
j
e
i(θ
j
−θ
m
)
= −ψ
m
|
∂ψ
n
∂t
e
iγ
n
e
i(θ
n
−θ
m
)
⇒
c
m
(t)=c
m
(0) −
t
0
ψ
m
|
∂ψ
n
∂t
e
iγ
n
e
i(θ
n
−θ
m
)
dt
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 10. THE ADIABATIC APPROXIMATION 267
(b) From Problem 10.9:
ψ
n
(x, t)=ψ
n
(x − f)=ψ
n
(u), where u ≡ x − f,
and ψ
n
(u) is the nth state of the ordinary harmonic oscillator;
∂ψ
n
∂t
=
∂ψ
n
∂u
∂u
∂t
= −
˙
f
∂ψ
n
∂u
.
But ˆp =
i
∂
∂u
, so ψ
m
|
∂ψ
n
∂t
= −
i
˙
fm|p|n, where (from Problem 3.33):
m|p|n = i
mω
2
√
mδ
n,m−1
−
√
nδ
m,n−1
. Thus:
ψ
m
|
∂ψ
n
∂t
=
˙
f
mω
2
√
mδ
n,m−1
−
√
nδ
m,n−1
.
Evidently transitions occur only to the immediately adjacent states, n ± 1, and
(1) m = n +1:
c
n+1
= −
t
0
˙
f
mω
2
√
n +1
e
iγ
n
e
i(θ
n
−θ
n+1
)
dt
.
But γ
n
=0, because the eigenfunctions are real (Problem 10.5), and (Eq. 10.39)
θ
n
= −
1
(n +
1
2
)ωt =⇒ θ
n
− θ
n+1
=
−(n +
1
2
)+(n +1+
1
2
)
ωt = ωt.
So
c
n+1
= −
mω
2
√
n +1
t
0
˙
fe
iωt
dt
.
(2) m = n −1:
c
n−1
= −
t
0
−
˙
f
mω
2
√
n
e
iγ
n
e
i(θ
n
−θ
n−1
)
dt
;
θ
n
− θ
n−1
=
−(n +
1
2
)+(n − 1+
1
2
)
ωt = −ωt.
c
n−1
=
mω
2
√
n
t
0
˙
fe
−iωt
dt
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

268 CHAPTER 11. SCATTERING
Chapter 11
Scattering
Problem 11.1
(a)
q
q
b
r
1
2
φ
θ
Conservation of energy: E =
1
2
m(˙r + r
2
˙
φ
2
)+V (r), where V (r)=
q
1
q
2
4π9
1
r
.
Conservation of angular momentum: J = mr
2
˙
φ. So
˙
φ =
J
mr
2
.
˙r
2
+
J
2
m
2
r
2
=
2
m
(E − V ). We want r as a function of φ (not t). Also, let u ≡ 1/r. Then
˙r =
dr
dt
=
dr
du
du
dφ
dφ
dt
=
−
1
u
2
du
dφ
J
m
u
2
= −
J
m
du
dφ
. Then:
−
J
m
du
dφ
2
+
J
2
m
2
u
2
=
2
m
(E − V ), or
du
dφ
2
=
2m
J
2
(E − V ) − u
2
;
du
dφ
=
2m
J
2
(E − V ) − u
2
; dφ =
du
2m
J
2
(E − V ) − u
2
=
du
I(u)
, where
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 11. SCATTERING 269
I(u) ≡
2m
J
2
(E − V ) − u
2
. Now, the particle q
1
starts out at r = ∞ (u = 0), φ = 0, and the point
of closest approach is r
min
(u
max
), Φ: Φ=
u
max
0
du
√
I
. It now swings through an equal angle Φ
on the way out,so Φ+Φ+θ = π, or θ = π − 2Φ.θ= π − 2
u
max
0
du
I(u)
.
So far this is general; now we put in the specific potential:
I(u)=
2mE
J
2
−
2m
J
2
q
1
q
2
4π9
0
u − u
2
=(u
2
− u)(u − u
1
), where u
1
and u
2
are the two roots.
(Since du/dφ =
I(u),u
max
is one of the roots; setting u
2
>u
1
, u
max
= u
2
.)
θ = π −2
u
2
0
du
(u
2
− u)(u − u
1
)
= π + 2 sin
−1
−2u + u
1
+ u
2
u
2
− u
1
u
2
0
= π +2
sin
−1
(−1) − sin
−1
u
1
+ u
2
u
2
− u
1
= π +2
−
π
2
− sin
−1
u
1
+ u
2
u
2
− u
1
= −2 sin
−1
u
1
+ u
2
u
2
− u
1
.
Now J = mvb, E =
1
2
mv
2
, where v is the incoming velocity, so J
2
= m
2
b
2
(2E/m)=2mb
2
E, and hence
2m/J
2
=1/b
2
E.So
I(u)=
1
b
2
−
1
b
2
1
E
q
1
q
2
4π9
0
u − u
2
. Let A ≡
q
1
q
2
4π9
0
E
, so − I(u)=u
2
+
A
b
2
u −
1
b
2
.
To get the roots: u
2
+
A
b
2
u −
1
b
2
=0=⇒ u =
1
2
−
A
b
2
±
A
2
b
4
+
4
b
2
=
A
2b
2
−1 ±
1+
2b
A
2
.
Thus u
2
=
A
2b
2
−1+
1+
2b
A
2
,u
1
=
A
2b
2
−1 −
1+
2b
A
2
;
u
1
+ u
2
u
2
− u
1
=
−1
1+(2b/A)
2
.
θ = 2 sin
−1
1
1+(2b/A)
2
, or
1
1+(2b/A)
2
= sin
θ
2
;1+
2b
A
2
=
1
sin
2
(θ/2)
;
2b
A
2
=
1 − sin
2
(θ/2)
sin
2
(θ/2)
=
cos
2
(θ/2)
sin
2
(θ/2)
;
2b
A
= cot(θ/2), or
b =
q
1
q
2
8π9
0
E
cot(θ/2).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

270 CHAPTER 11. SCATTERING
(b)
D(θ)=
b
sin θ
db
dθ
. Here
db
dθ
=
q
1
q
2
8π9
0
E
−
1
2 sin
2
(θ/2)
.
=
1
2 sin(θ/2) cos(θ/2)
q
1
q
2
8π9
0
E
cos(θ/2)
sin(θ/2)
q
1
q
2
8π9
0
E
1
2 sin
2
(θ/2)
=
q
1
q
2
16π9
0
E sin
2
(θ/2)
2
.
(c)
σ =
D(θ) sin θdθdφ=2π
q
1
q
2
8π9
0
E
2
π
0
sin θ
sin
4
(θ/2)
dθ.
This integral does not converge, for near θ = 0 (and again near π) we have sin θ ≈ θ, sin(θ/2) ≈ θ/2, so
the integral goes like 16
5
0
θ
−3
dθ = − 8θ
−2
5
0
→∞.
Problem 11.2
x
r
θ
Two dimensions: ψ(r, θ) ≈ A
e
ikx
+ f(θ)
e
ikr
√
r
.
One dimension: ψ(x) ≈ A
e
ikx
+ f(x/|x|)e
−ikx
.
Problem 11.3
Multiply Eq. 11.32 by P
l
(cos θ) sin θdθ and integrate from 0 to π, exploiting the orthogonality of the Leg-
endre polynomials (Eq. 4.34)—which, with the change of variables x ≡ cos θ,says
π
0
P
l
(cos θ)P
l
(cos θ) sin θdθ=
2
2l +1
δ
ll
.
The delta function collapses the sum, and we get
2i
l
j
l
(ka)+ika
l
h
(1)
l
(ka)
=0,
and hence (dropping the primes)
a
l
= −
j
l
(ka)
ikh
(1)
l
(ka)
. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 11. SCATTERING 271
Problem 11.4
Keeping only the l = 0 terms, Eq. 11.29 says that in the exterior region:
ψ ≈ A
j
0
(kr)+ika
0
h
(1)
0
(kr)
P
0
(cos θ)=A
sin(kr)
kr
+ ika
0
−i
e
ikr
kr
= A
sin(kr)
kr
+ a
0
e
ikr
r
(r>a).
In the internal region Eq. 11.18 (with n
l
eliminated because it blows up at the origin) yields
ψ(r) ≈ bj
0
(kr)=b
sin(kr)
kr
(r<a).
The boundary conditions hold independently for each l, as you can check by keeping the summation over l and
exploiting the orthogonality of the Legendre polynomials:
(1) ψ continuous at r = a: A
sinka
ka
+ a
0
e
ika
a
= b
sin ka
ka
.
(2) ψ
discontinuous at r = a: Integrating the radial equation across the delta function gives
−
2
2m
d
2
u
dr
2
dr +
αδ(r − a)+
2
2m
l(l +1)
r
2
udr ⇒−
2
2m
∆u
+ αu(a)=0, or ∆u
=
2mα
2
u(a).
Now u = rR, so u
= R+rR
;∆u
=∆R+a∆R
= a∆R
=
2mα
2
aR(a), or ∆ψ
=
2mα
2
ψ(a)=
β
a
ψ(a).
A
ka
k cos(ka)+a
0
ik
2
e
ika
−
A
ka
2
✭
✭
✭
✭
✭
✭
✭
✭
✭
sin(ka)+a
0
ke
ika
−
b
ka
k cos(ka)+
✟
✟
✟
✟
✟
b
ka
2
sin ka =
β
a
b
sin(ka)
ka
.
The indicated terms cancel (by (1)), leaving A
cos(ka)+ia
0
ke
ika
= b
cos(ka)+
β
ka
sin(ka)
.
Using (1) to eliminate b: A
cos(ka)+ia
0
ke
ika
=
cot(ka)+
β
ka
sin(ka)+a
0
ke
ika
A.
✘
✘
✘
✘
cos(ka)+ia
0
ke
ika
=
✘
✘
✘
✘
cos(ka)+
β
ka
sin(ka)+a
0
k cot(ka)e
ika
+ β
a
0
a
e
ika
.
ia
0
ke
ika
1+i cot(ka)+i
β
ka
=
β
ka
sin(ka). But ka 1, so sin(ka) ≈ ka, and cot(ka)=
cos(ka)
sin(ka)
≈
1
ka
.
ia
0
k(1 + ika)
1+
i
ka
(1 + β)
= β; ia
0
k
1+
i
ka
(1 + β)+ika − 1 − β
≈ ia
0
k
i
ka
(1 + β)
= β.
a
0
= −
aβ
1+β
.
Equation 11.25 ⇒ f (θ) ≈ a
0
= −
aβ
1+β
.
Equation 11.14 ⇒ D = |f|
2
=
aβ
1+β
2
.
Equation 11.27 ⇒ σ =4πD = 4π
aβ
1+β
2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

272 CHAPTER 11. SCATTERING
Problem 11.5
(a) In the region to the left
ψ(x)=Ae
ikx
+ B
−ikx
(x ≤−a).
In the region −a<x<0, the Schr¨odinger equation gives
−
h
2
2m
d
2
ψ
dx
2
− V
0
ψ = Eψ ⇒
d
2
ψ
dx
2
= −k
ψ
where k
=
2m(E + V
0
)/. The general solution is
ψ = C sin(k
x)+D cos(k
x)
But ψ(0) = 0 implies D =0,so
ψ(x)=C sin(k
x)(−a ≤ x ≤ 0).
The continuity of ψ(x) and ψ
(x)atx = −a says
Ae
−ika
+ Be
ika
= −C sin(k
a),ikAe
−ika
− ikB
ika
= k
C cos(k
a).
Divide and solve for B:
ikAe
−ika
− ikBe
ika
Ae
−ika
+ Be
ika
= −k
cot(k
a),
ikAe
−ika
− ikBe
ika
= −Ae
−ika
k
cot(k
a) − Be
ika
k
cot(k
a),
Be
ika
[−ik + k
cot(k
a)] = Ae
−ika
[−ik −k
cot(k
a)] .
B = Ae
−2ika
k −ik
cot(k
a)
k + ik
cot(k
a)
.
(b)
|B|
2
= |A|
2
k −ik
cot(k
a)
k + ik
cot(k
a)
·
k + ik
cot(k
a)
k −ik
cot(k
a)
= |A|
2
.
(c) From part (a) the wave function for x<−a is
ψ(x)=Ae
ikx
+ Ae
−2ika
k −ik
cot(k
a)
k + ik
cot(k
a)
e
−ikx
.
But by definition of the phase shift (Eq. 11.40)
ψ(x)=A
e
ikx
− e
i(2δ−kx)
.
so
e
−2ika
k −ik
cot(k
a)
k + ik
cot(k
a)
= −e
2iδ
.
This is exact. For a very deep well, E V
0
, k =
√
2mE/
2m(E + V
0
)/ = k
,so
e
−2ika
−ik
cot(k
a)
ik
cot(k
a)
= −e
2iδ
; e
−2ika
= e
2iδ
; δ = −ka.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 11. SCATTERING 273
Problem 11.6
From Eq. 11.46, a
l
=
1
k
e
iδ
l
sin δ
l
, and Eq. 11.33, a
l
= i
j
l
(ka)
kh
(1)
l
(ka)
, it follows that e
iδ
l
sin δ
l
= i
j
l
(ka)
h
(1)
l
(ka)
.
But (Eq. 11.19) h
(1)
l
(x)=j
l
(x)+in
l
(x), so
e
iδ
l
sin δ
l
= i
j
l
(ka)
j
l
(x)+in
l
(x)
= i
1
1+i(n/j)
= i
1 − i(n/j)
1+(n/j)
2
=
(n/j)+i
1+(n/j)
2
,
(writing (n/j) as shorthand for n
l
(ka)/j
l
(ka)). Equating the real and imaginary parts:
cos δ
l
sin δ
l
=
(n/j)
1+(n/j)
2
; sin
2
δ
l
=
1
1+(n/j)
2
.
Dividing the second by the first, I conclude that
tan δ
l
=
1
(n/j)
, or
δ
l
= tan
−1
j
l
(ka)
n
l
(ka)
.
Problem 11.7
r>a: u(r)=A sin(kr + δ);
r<a: u(r)=B sin kr + D cos kr = B sin kr, because u(0) = 0 =⇒ D =0.
Continuity at r = a =⇒ B sin(ka)=A sin(ka + δ)=⇒ B = A
sin(ka + δ)
sin(ka)
. So u(r)=A
sin(ka + δ)
sin(ka)
sin kr.
From Problem 11.4,
∆
du
dr
r=a
=
β
a
u(a) ⇒ Ak cos(ka + δ) −A
sin(ka + δ)
sin(ka)
k cos(ka)=
β
a
A sin(ka + δ).
cos(ka + δ) −
sin(ka + δ)
sin(ka)
cos(ka)=
β
ka
sin(ka + δ),
sin(ka) cos(ka + δ) −sin(ka + δ) cos(ka)=
β
ka
sin(ka + δ) sin(ka),
sin(ka − ka −δ)=
β
ka
sin(ka) [sin(ka) cos δ + cos(ka) sin δ] ,
−sin δ = β
sin
2
(ka)
ka
[cos δ + cot(ka) sin δ]; −1=β
sin
2
(ka)
ka
[cot δ + cot(ka)] .
cot δ = −cot(ka) −
ka
β sin
2
(ka)
;
cot δ = −
cot(ka)+
ka
β sin
2
(ka)
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

274 CHAPTER 11. SCATTERING
Problem 11.8
G = −
e
ikr
4πr
=⇒∇G = −
1
4π
1
r
∇e
ikr
+ e
ikr
∇
1
r
=⇒
∇
2
G = ∇·(∇G)=−
1
4π
2
∇
1
r
· (∇e
ikr
)+
1
r
∇
2
(e
ikr
)+e
ikr
∇
2
1
r
.
But ∇
1
r
= −
1
r
2
ˆr; ∇(e
ikr
)=ike
ikr
ˆr; ∇
2
e
ikr
= ik∇·(e
ikr
ˆr)=ik
1
r
2
d
dr
(r
2
e
ikr
)
(see reference in footnote 12) =⇒∇
2
e
ikr
=
ik
r
2
(2re
ikr
+ ikr
2
e
ikr
)=ike
ikr
2
r
+ ik
;
∇
2
1
r
= −4πδ
3
(r). So ∇
2
G = −
1
4π
2
−
1
r
2
ˆr
·
ike
ikr
ˆr
+
1
r
ike
ikr
2
r
+ ik
− 4πe
ikr
δ
3
(r)
.
But e
ikr
δ
3
(r)=δ
3
(r), so
∇
2
G = δ
3
(r) −
1
4π
e
ikr
−
2ik
r
2
+
2ik
r
2
−
k
2
r
= δ
3
(r)+k
2
e
ikr
4πr
= δ
3
(r) − k
2
G.
Therefore (∇
2
+ k
2
)G = δ
3
(r). QED
Problem 11.9
ψ =
1
√
πa
3
e
−r/a
; V = −
e
2
4π9
0
r
= −
2
ma
1
r
(Eq. 4.72); k = i
√
−2mE
=
i
a
.
In this case there is no “incoming” wave, and ψ
0
(r) = 0. Our problem is to show that
−
m
2π
2
e
ik|r−r
0
|
|r − r
0
|
V (r
0
)ψ(r
0
) d
3
r
0
= ψ(r).
We proceed to evaluate the left side (call it I):
I =
−
m
2π
2
−
2
ma
1
√
πa
3
e
−|r−r
0
|/a
|r − r
0
|
1
r
0
e
−r
0
/a
d
3
r
0
=
1
2πa
1
√
πa
3
e
−
√
r
2
+r
2
0
−2rr
0
cos θ/a
e
−r
0
/a
r
2
+ r
2
0
− 2rr
0
cos θr
0
r
2
0
sin θdr
0
dθ dφ.
(I have set the z
0
axis along the—fixed—direction r, for convenience.) Doing the φ integral (2π):
I =
1
a
√
πa
3
∞
0
r
0
e
−r
0
/a
π
0
e
−
√
r
2
+r
2
0
−2rr
0
cos θ/a
r
2
+ r
2
0
− 2rr
0
cos θ
sin θdθ
dr
0
. The θ integral is
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 11. SCATTERING 275
π
0
e
−
√
r
2
+r
2
0
−2rr
0
cos θ/a
r
2
+ r
2
0
− 2rr
0
cos θ
sin θdθ= −
a
rr
0
e
−
√
r
2
+r
2
0
−2rr
0
cos θ/a
π
0
= −
a
rr
0
e
−(r+r
0
)/a
− e
−|r−r
0
|/a
.
I = −
1
r
√
πa
3
∞
0
e
−r
0
/a
e
−(r
0
+r)/a
− e
−|r
0
−r|/a
dr
0
= −
1
r
√
πa
3
e
−r/a
∞
0
e
−2r
0
/a
dr
0
− e
−r/a
r
0
dr −e
r/a
∞
r
e
−2r
0
/a
dr
0
= −
1
r
√
πa
3
e
−r/a
a
2
− e
−r/a
(r) −e
r/a
−
a
2
e
−2r
0
/a
∞
r
= −
1
r
√
πa
3
a
2
e
−r/a
− re
−r/a
−
a
2
e
r/a
e
−2r/a
=
1
√
πa
3
e
−r/a
= ψ(r). QED
Problem 11.10
For the potential in Eq. 11.81, Eq. 11.88 =⇒
f(θ)=−
2m
2
κ
V
0
a
0
r sin(κr) dr = −
2mV
0
2
κ
1
κ
2
sin(κr) −
r
κ
cos(κr)
a
0
= −
2mV
0
2
κ
3
[sin(κa) − κa cos(κa)] ,
where (Eq. 11.89) κ =2k sin(θ/2). For low-energy scattering (ka 1):
sin(κa) ≈ κa −
1
3!
(κa)
3
; cos(κa)=1−
1
2
(κa)
2
;so
f(θ) ≈−
2mV
0
2
κ
3
κa −
1
6
(κa)
3
− κa +
1
2
(κa)
3
=
−
2
3
mV
0
a
3
2
, in agreement with Eq. 11.82.
Problem 11.11
sin(κr)=
1
2i
e
iκr
− e
−iκr
, so
∞
0
e
−µr
sin(κr) dr =
1
2i
∞
0
e
−(µ−iκ)r
− e
−(µ+iκ)r
dr
=
1
2i
e
−(µ−iκ)r
−(µ − iκ)
−
e
−(µ+iκ)r
−(µ + iκ)
∞
0
=
1
2i
1
µ − iκ
−
1
µ + iκ
=
1
2i
µ + iκ − µ + iκ
µ
2
+ κ
2
=
κ
µ
2
+ κ
2
.
So f(θ)=−
2mβ
2
κ
κ
µ
2
+ κ
2
= −
2mβ
2
(µ
2
+ κ
2
)
. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
276 CHAPTER 11. SCATTERING
Problem 11.12
Equation 11.91 =⇒ D(θ)=|f(θ)|
2
=
2mβ
2
2
1
(µ
2
+ κ
2
)
2
, where Eq. 11.89 ⇒ κ =2k sin(θ/2).
σ =
D(θ) sin θdθdφ=2π
2mβ
2
2
1
µ
4
π
0
1
1+(2k/µ)
2
sin
2
(θ/2)
2
2 sin(θ/2) cos(θ/2) dθ.
Let
2k
µ
sin(θ/2) ≡ x, so 2 sin(θ/2) =
µ
k
x, and cos(θ/2) dθ =
µ
k
dx. Then
σ =2π
2mβ
2
2
1
µ
4
µ
k
2
x
1
x
0
x
(1 + x
2
)
2
dx. The limits are
θ =0=⇒ x = x
0
=0,
θ = π =⇒ x = x
1
=2k/µ.
So
σ =2π
2mβ
2
2
1
(µk)
2
−
1
2
1
(1 + x
2
)
2k/µ
0
= π
2mβ
2
2
1
(µk)
2
1 −
1
1+(2k/µ)
2
= π
2mβ
2
2
1
(µk)
2
4(k/µ)
2
1+4k
2
/µ
2
= π
4mβ
2
2
1
µ
2
1
µ
2
+4k
2
. But k
2
=
2mE
2
, so
σ = π
4mβ
µ
2
1
(µk)
2
+8mE
.
Problem 11.13
(a)
V (r)=αδ(r − a). Eq. 11.80 =⇒ f = −
m
2π
2
V (r) d
3
r = −
m
2π
2
α4π
∞
0
δ(r − a)r
2
dr.
f = −
2mα
2
a
2
; D = |f|
2
=
2mα
2
a
2
2
; σ =4πD = π
4mα
2
a
2
2
.
(b)
Eq. 11.88 =⇒ f = −
2m
2
κ
α
∞
0
rδ(r − a) sin(κr) dr = −
2mα
2
κ
a sin(κa)
(κ =2k sin(θ/2)).
(c) Note first that (b) reduces to (a) in the low-energy regime (ka 1=⇒ κa 1). Since Problem 11.4
was also for low energy, what we must confirm is that Problem 11.4 reproduces (a) in the regime for
which the Born approximation holds. Inspection shows that the answer to Problem 11.4 does reduce to
f = −2mαa
2
/
2
when β 1, which is to say when f/a 1. This is the appropriate condition, since
(Eq. 11.12) f/a is a measure of the relative size of the scattered wave, in the interaction region.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
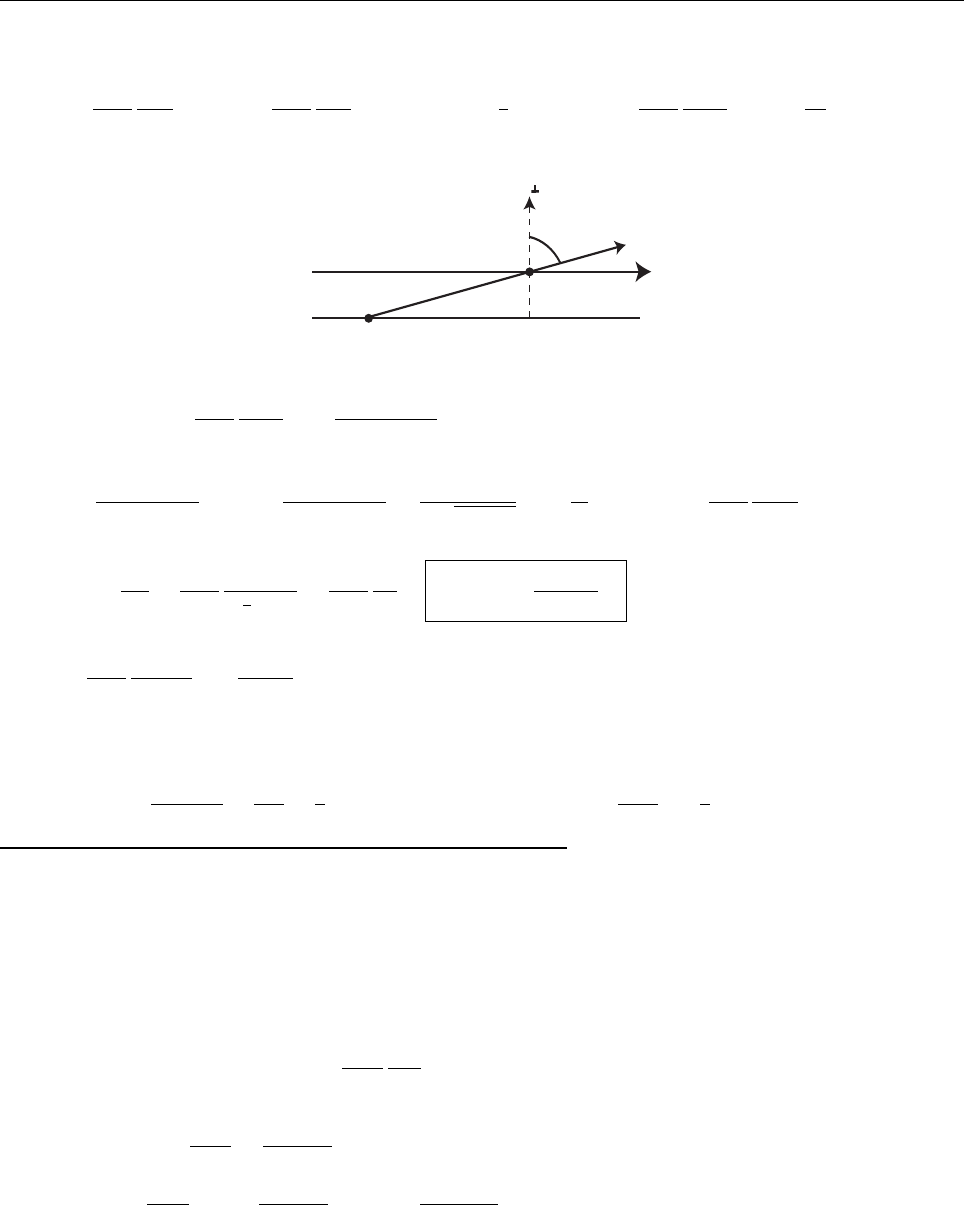
CHAPTER 11. SCATTERING 277
Problem 11.14
F =
1
4π9
0
q
1
q
2
r
2
ˆr; F
⊥
=
1
4π9
0
q
1
q
2
r
2
cos φ; cos φ =
b
r
, so F
⊥
=
1
4π9
0
q
1
q
2
b
r
3
; dt =
dx
v
.
b
q
q
F
r
r
x
φ
1
2
I
⊥
=
F
⊥
dt =
1
4π9
0
q
1
q
2
b
v
∞
−∞
dx
(x
2
+ b
2
)
3/2
. But
∞
−∞
dx
(x
2
+ b
2
)
3/2
=2
∞
0
dx
(x
2
+ b
2
)
3/2
=
2x
b
2
√
x
2
+ b
2
∞
0
=
2
b
2
, so I
⊥
=
1
4π9
0
2q
1
q
2
bv
.
tan θ =
I
⊥
mv
=
q
1
q
2
4π9
0
1
b(
1
2
mv
2
)
=
q
1
q
2
4π9
0
1
bE
.
θ = tan
−1
q
1
q
2
4π9
0
bE
.
b =
q
1
q
2
4π9
0
1
E tan θ
=
q
1
q
2
8π9
0
E
(2 cot θ).
The exact answer is the same, only with cot(θ/2) in place of 2 cot θ. So I must show that cot(θ/2) ≈ 2 cot θ,
for small θ (that’s the regime in which the impulse approximation should work). Well:
cot(θ/2) =
cos(θ/2)
sin(θ/2)
≈
1
θ/2
=
2
θ
, for small θ, while 2 cot θ =2
cos θ
sin θ
≈ 2
1
θ
. So it works.
Problem 11.15
First let’s set up the general formalism. From Eq. 11.101:
ψ(r)=ψ
0
(r)+
g(r −r
0
)V (r
0
)ψ
0
(r
0
) d
3
r
0
+
g(r −r
0
)V (r
0
)
g(r
0
− r
1
)V (r
1
)ψ
0
(r
1
) d
3
r
1
d
3
r
0
+ ···
Put in ψ
0
(r)=Ae
ikz
,g(r)=−
m
2π
2
e
ikr
r
:
ψ(r)=Ae
ikz
−
mA
2π
2
e
ik|r−r
0
|
|r − r
0
|
V (r
0
)e
ikz
0
d
3
r
0
+
m
2π
2
2
A
e
ik|r−r
0
|
|r − r
0
|
V (r
0
)
e
ik|r
0
−r
1
|
|r
0
− r
1
|
V (r
1
)e
ikz
1
d
3
r
1
d
3
r
0
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

278 CHAPTER 11. SCATTERING
In the scattering region r r
0
, Eq. 11.73 =⇒
e
ik|r−r
0
|
|r − r
0
|
≈
e
ikr
r
e
−ik·r
0
, with k ≡ kˆr, so
ψ(r)=A
e
ikz
−
m
2π
2
e
ikr
r
e
−ik·r
0
V (r
0
)e
ikz
0
d
3
r
0
m
2π
2
2
e
ikr
r
e
−ik·r
0
V (r
0
)
e
ik|r
0
−r
1
|
|r
0
− r
1
|
V (r
1
)e
ikz
1
d
3
r
1
d
3
r
0
f(θ, φ)=−
m
2π
2
e
i(k
−k)·r
V (r) d
3
r +
m
2π
2
2
e
−ik·r
V (r)
e
ik|r−r
0
|
|r − r
0
|
V (r
0
)e
ikz
0
d
3
r
0
d
3
r.
I simplified the subscripts, since there is no longer any possible ambiguity. For low-energy scattering we drop
the exponentials (see p. 414):
f(θ, φ) ≈−
m
2π
2
V (r) d
3
r +
m
2π
2
2
V (r)
1
|r − r
0
|
V (r
0
) d
3
r
0
d
3
r.
Now apply this to the potential in Eq. 11.81:
1
|r − r
0
|
V (r
0
) d
3
r
0
= V
0
a
0
1
|r − r
0
|
r
2
0
sin θ
0
dr
0
dθ
0
dφ
0
.
Orient the z
0
axis along r,so|r − r
0
| = r
2
+ r
2
0
− 2rr
0
cos θ
0
.
1
|r − r
0
|
V (r
0
) d
3
r
0
= V
0
2π
a
0
r
2
0
π
0
1
r
2
+ r
2
0
− 2rr
0
cos θ
0
sin θ
0
dθ
0
dr
0
. But
π
0
1
r
2
+ r
2
0
− 2rr
0
cos θ
0
sin θ
0
dθ
0
=
1
rr
0
r
2
+ r
2
0
− 2rr
0
cos θ
0
π
0
=
1
rr
0
[(r
0
+ r) −|r
0
− r|]=
2/r, r
0
<r;
2/r
0
,r
0
>r.
Here r<a(from the “outer” integral), so
1
|r − r
0
|
V (r
0
) d
3
r
0
=4πV
0
1
r
r
0
r
2
0
dr
0
+
a
r
r
0
dr
0
=4πV
0
1
r
r
3
3
+
1
2
(a
2
− r
2
)
=2πV
0
a
2
−
1
3
r
2
.
V (r)
1
|r − r
0
|
V (r
0
) d
3
r
0
d
3
r = V
0
(2πV
0
)4π
a
0
a
2
−
1
3
r
2
r
2
dr =8π
2
V
2
0
a
2
a
3
3
−
1
3
a
5
5
=
32
15
π
2
V
2
0
a
5
.
f(θ)=−
m
2π
2
V
0
4
3
πa
3
+
m
2π
2
2
32
15
π
2
V
2
0
a
5
= −
2mV
0
a
3
3
2
1 −
4
5
mV
0
a
2
2
.
Problem 11.16
d
2
dx
2
+ k
2
G(x)=δ(x) (analog to Eq. 11.52).G(x)=
1
√
2π
e
isx
g(s) ds (analog to Eq. 11.54).
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
CHAPTER 11. SCATTERING 279
d
2
dx
2
+ k
2
G =
1
√
2π
(−s
2
+ k
2
)g(s)e
isx
ds = δ(x)=
1
2π
e
isx
ds =⇒ g(s)=
1
√
2π(k
2
− s
2
)
.
G(x)=
1
2π
∞
−∞
e
isx
k
2
− s
2
ds. Skirt the poles as in Fig. 11.10. For x>0, close above:
G(x)=−
1
2π
?
e
isx
s + k
1
s − k
ds = −
1
2π
2πi
e
isx
s + k
s=k
= −i
e
ikx
2k
. For x<0, close below:
G(x)=+
1
2π
?
e
isx
s − k
1
s + k
ds =
1
2π
2πi
e
isx
s − k
s=−k
= −i
e
−ikx
2k
.
In either case, then,
G(x)=−
i
2k
e
ik|x|
. (Analog to Eq. 11.65.)
ψ(x)=G(x −x
0
)
2m
2
V (x
0
)ψ(x
0
) dx
0
= −
i
2k
2m
2
e
ik|x−x
0
|
V (x
0
)ψ(x
0
) dx
0
,
plus any solution ψ
0
(x) to the homogeneous Schr¨odinger equation:
d
2
dx
2
+ k
2
ψ
0
(x)=0. So:
ψ(x)=ψ
0
(x) −
im
2
k
∞
−∞
e
ik|x−x
0
|
V (x
0
)ψ(x
0
) dx
0
.
Problem 11.17
For the Born approximation let ψ
0
(x)=Ae
ikx
, and ψ(x) ≈ Ae
ikx
.
ψ(x) ≈ A
e
ikx
−
im
2
k
∞
−∞
e
ik|x−x
0
|
V (x
0
)e
ikx
0
dx
0
= A
e
ikx
−
im
2
k
x
−∞
e
ik(x−x
0
)
V (x
0
)e
ikx
0
dx
0
−
im
2
k
∞
x
e
ik(x
0
−x)
V (x
0
)e
ikx
0
dx
0
.
ψ(x)=A
e
ikx
−
im
2
k
e
ikx
x
−∞
V (x
0
) dx
0
−
im
2
k
e
−ikx
∞
x
e
2ikx
0
V (x
0
) dx
0
.
Now assume V (x) is localized; for large positive x, the third term is zero, and
ψ(x)=Ae
ikx
1 −
im
2
k
∞
−∞
V (x
0
) dx
0
. This is the transmitted wave.
For large negative x the middle term is zero:
ψ(x)=A
e
ikx
−
im
2
k
e
−ikx
∞
−∞
e
2ikx
0
V (x
0
)dx
0
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
280 CHAPTER 11. SCATTERING
Evidently the first term is the incident wave and the second the reflected wave:
R =
m
2
k
2
∞
−∞
e
2ikx
V (x) dx
2
.
If you try in the same spirit to calculate the transmission coefficient, you get
T =
1 −
im
2
k
∞
−∞
V (x)dx
2
=1+
m
2
k
2
∞
−∞
V (x)dx
2
,
which is nonsense (greater than 1). The first Born approximation gets R right, but all you can say to this order
is T ≈ 1 (you would do better using T =1− R).
Problem 11.18
Delta function: V (x)=−αδ(x).
∞
−∞
e
2ikx
V (x) dx = −α, so R =
mα
2
k
2
,
or, in terms of energy (k
2
=2mE/
2
):
R =
m
2
α
2
2mE
2
=
mα
2
2
2
E
; T =1− R =
1 −
mα
2
2
2
E
.
The exact answer (Eq. 2.141) is
1
1+
mα
2
2
2
E
≈ 1 −
mα
2
2
2
E
, so they agree provided E
mα
2
2
.
Finite square well
: V (x)=
−V
0
(−a<x<a)
0 (otherwise)
.
∞
−∞
e
2ikx
V (x) dx = −V
0
a
−a
e
2ikx
dx = −V
0
e
2ikx
2ik
a
−a
= −
V
0
k
e
2ika
− e
−2ika
2i
= −
V
0
k
sin(2ka).
So R =
m
2
k
2
V
0
k
sin(2ka)
2
. T =1−
V
0
2E
sin
2a
√
2mE
2
.
If E V
0
, the exact answer (Eq. 2.169) becomes
T
−1
≈ 1+
V
0
2E
sin
2a
√
2mE
2
=⇒ T ≈ 1 −
V
0
2E
sin
2a
√
2mE
2
,
so they agree provided E V
0
.
Problem 11.19
The Legendre polynomials satisfy P
l
(1) = 1 (see footnote 30, p. 124), so Eq. 11.47 ⇒
f(0) =
1
k
∞
l=0
(2l +1)e
iδ
l
sin δ
l
. Therefore Im[f(0)] =
1
k
∞
l=0
(2l + 1) sin
2
δ
l
,
and hence (Eq. 11.48):
σ =
4π
k
Im[f(0)]. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

CHAPTER 11. SCATTERING 281
Problem 11.20
Using Eq. 11.88 and integration by parts:
f(θ)=−
2m
2
κ
∞
0
rAe
−µr
2
sin(κr) dr = −
2mA
2
κ
∞
0
d
dr
−
1
2µ
e
−µr
2
sin(κr) dr
=
2mA
2µ
2
κ
e
−µr
2
sin(κr)
∞
0
−
∞
0
e
−µr
2
d
dr
[sin(κr)] dr
=
mA
µ
2
κ
0 − κ
∞
0
e
−µr
2
cos(κr) dr
= −
mA
µ
2
√
π
2
√
µ
e
−κ
2
/4µ
= −
mA
√
π
2
2
µ
3/2
e
−κ
2
/4µ
, where κ =2k sin(θ/2) (Eq. 11.89).
From Eq. 11.14, then,
dσ
dΩ
=
πm
2
A
2
4
4
µ
3
e
−κ
2
/2µ
,
and hence
σ =
dσ
dΩ
dΩ=
πm
2
A
2
4
4
µ
3
e
−4k
2
sin
2
(θ/2)/2µ
sin θdθdφ
=
π
2
m
2
A
2
2
4
µ
3
π
0
e
−2k
2
sin
2
(θ/2)/µ
sin θdθ; write sin θ = 2 sin(θ/2) cos(θ/2) and let x ≡ sin(θ/2)
=
π
2
m
2
A
2
2
4
µ
3
1
0
e
−2k
2
x
2
/µ
2x 2 dx =
2π
2
m
2
A
2
4
µ
3
1
0
xe
−2k
2
x
2
/µ
dx
=
2π
2
m
2
A
2
4
µ
3
−
µ
4k
2
e
−2k
2
x
2
/µ
1
0
= −
π
2
m
2
A
2
2
4
µ
2
k
2
e
−2k
2
/µ
− 1
=
π
2
m
2
A
2
2
4
µ
2
k
2
1 − e
−2k
2
/µ
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

282 CHAPTER 12. AFTERWORD
Chapter 12
Afterword
Problem 12.1
Suppose, on the contrary, that
α|φ
a
(1)|φ
b
(2) + β|φ
b
(1)|φ
a
(2) = |ψ
r
(1)|ψ
s
(2),
for some one-particle states |ψ
r
and |ψ
s
. Because |φ
a
and |φ
b
constitute a complete set of one-particle states
(this is a two-level system), any other one-particle state can be expressed as a linear combination of them. In
particular,
|ψ
r
= A|φ
a
+ B|φ
b
, and |ψ
s
= C|φ
a
+ D|φ
b
,
for some complex numbers A, B, C, and D.Thus
α|φ
a
(1)|φ
b
(2) + β|φ
b
(1)|φ
a
(2) =
A|φ
a
(1) + B|φ
b
(1)
C|φ
a
(2) + D|φ
b
(2)
= AC|φ
a
(1)|φ
a
(2) + AD|φ
a
(1)|φ
b
(2) + BC|φ
b
(1)|φ
a
(2) + BD|φ
b
(1)|φ
b
(2).
(i) Take the inner product with φ
a
(1)|φ
b
(2)|: α = AD.
(ii) Take the inner product with φ
a
(1)|φ
a
(2)|:0=AC.
(iii) Take the inner product with φ
b
(1)|φ
a
(2)|: β = BC.
(iv) Take the inner product with φ
b
(1)|φ
b
(2)|:0=BD.
(ii) ⇒ either A =0orC = 0. But if A = 0, then (i) ⇒ α = 0, which is excluded by assumption, whereas if
C = 0, then (iii) ⇒ β = 0, which is likewise excluded. Conclusion: It is impossible to express this state as a
product of one-particle states. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

APPENDIX. LINEAR ALGEBRA 283
Appendix A
Linear Algebra
Problem A.1
(a) Yes; two-dimensional.
(b) No; the sum of two such vectors has a
z
= 2, and is not in the subset. Also, the null vector (0,0,0) is not
in the subset.
(c)
Yes; one-dimensional.
Problem A.2
(a) Yes; 1,x,x
2
,... ,x
N−1
is a convenient basis. Dimension: N.
(b) Yes; 1,x
2
,x
4
,.... Dimension N/2 (if N is even) or (N +1)/2 (if N is odd).
(c)
No. The sum of two such “vectors” is not in the space.
(d)
Yes; (x − 1), (x − 1)
2
, (x −1)
3
,... ,(x −1)
N−1
. Dimension: N − 1.
(e) No. The sum of two such “vectors” would have value 2 at x =0.
Problem A.3
Suppose |α = a
1
|e
1
+ a
2
|e
2
+ ···a
n
|e
n
and |α = b
1
|e
1
+ b
2
|e
2
+ ···+ b
n
|e
n
. Subtract: 0 = (a
1
−b
1
)|e
1
+
(a
2
− b
2
)|e
2
+ ···+(a
n
− b
n
)|e
n
. Suppose a
j
= b
j
for some j; then we can divide by (a
j
− b
j
) to get:
|e
j
= −
(a
1
− b
1
)
(a
j
− b
j
)
|e
1
−
(a
2
− b
2
)
(a
j
− b
j
)
|e
2
−···−0|e
j
−···−
(a
n
− b
n
)
(a
j
− b
j
)
|e
n
,
so |e
j
is linearly dependent on the others, and hence {|e
j
} is not a basis. If {|e
j
} is a basis, therefore, the
components must all be equal (a
1
= b
1
,a
2
= b
2
,... ,a
n
= b
n
). QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

284 APPENDIX. LINEAR ALGEBRA
Problem A.4
(i)
e
1
|e
1
= |1+i|
2
+1+|i|
2
=(1+i)(1 −i)+1+(i)(−i)=1+1+1+1=4. "e
1
" =2.
|e
1
=
1
2
(1 + i)
ˆ
i +
1
2
ˆ
j +
i
2
ˆ
k.
(ii)
e
1
|e
2
=
1
2
(1 − i)(i)+
1
2
(3) +
−i
2
1=
1
2
(i +1+3− i)=2.
|e
2
≡|e
2
−e
1
|e
2
|e
1
=(i − 1 − i)
ˆ
i +(3− 1)
ˆ
j +(1− i)
ˆ
k =(−1)
ˆ
i + (2)
ˆ
j +(1− i)
ˆ
k.
e
2
|e
2
=1+4+2=7. |e
2
=
1
√
7
[−
ˆ
i +2
ˆ
j +(1− i)
ˆ
k].
(iii)
e
1
|e
3
=
1
2
28 = 14; e
2
|e
3
=
2
√
7
28=8
√
7.
|e
3
= |e
3
−e
1
|e
3
|e
1
−e
2
|e
3
|e
2
= |e
3
−7|e
1
−8|e
2
=(0− 7 − 7i +8)
ˆ
i + (28 − 7 − 16)
ˆ
j +(0− 7i − 8+8i)
ˆ
k =(1−7i)
ˆ
i +5
ˆ
j +(−8+i)
ˆ
k.
"e
3
"
2
=1+49+25+64+1=140. |e
3
=
1
2
√
35
[(1 − 7i)
ˆ
i +5
ˆ
j +(−8+i)
ˆ
k].
Problem A.5
From Eq. A.21: γ|γ = γ|
|β−
α|β
α|α
|α
= γ|β−
α|β
α|α
γ|α. From Eq. A.19:
γ|β
∗
= β|γ = β|
|β−
α|β
α|α
|α
= β|β−
α|β
α|α
β|α = β|β−
|α|β|
2
α|α
, which is real.
γ|α
∗
= α|γ = α|
|β−
α|β
α|α
|α
= α|β−
α|β
α|α
α|α =0. γ|α =0. So (Eq. A.20) :
γ|γ = β|β−
|α|β|
2
α|α
≥ 0, and hence |α|β|
2
≤α|αβ|β. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

APPENDIX. LINEAR ALGEBRA 285
Problem A.6
α|β =(1− i)(4 − i) + (1)(0) + (−i)(2 − 2i)=4− 5i − 1 − 2i − 2=1−7i; β|α =1+7i;
α|α =1+1+1+1=4; β|β =16+1+4+4=25; cosθ =
1+49
4 · 25
=
1
√
2
;
θ =45
◦
.
Problem A.7
Let |γ≡|α+ |β; γ|γ = γ|α + γ|β.
γ|α
∗
= α|γ = α|α + α|β =⇒γ|α = α|α + β|α.
γ|β
∗
= β|γ = β|α + β|β =⇒γ|β = α|β + β|β.
"(|α + |β)"
2
= γ|γ = α|α + β|β+ α|β + β|α.
But α|β + β|α = 2Re(α|β) ≤ 2|α|β| ≤ 2
α|αβ|β (by Schwarz inequality), so
"(|α + |β)"
2
≤"α"
2
+ "β"
2
+2"α""β" =("α" + "β")
2
, and hence "(|α + |β)"≤"α"+ "β". QED
Problem A.8
(a)
110
213
3i (3 − 2i)4
.
(b)
(−2+0− 1) (0+1+3i)(i +0+2i)
(4+0+3i) (0+0+9) (−2i +0+6)
(4i +0+2i)(0− 2i +6) (2+0+4)
=
−3 (1+3i)3i
(4+3i)9(6− 2i)
6i (6 − 2i)6
.
(c) BA =
(−2+0+2) (2+0− 2) (2i +0−2i)
(0+2+0) (0+0+0) (0+3+0)
(−i +6+4i)(i +0−4i)(−1+9+4)
=
000
203
(6+3i) −3i 12
.
[A, B]=AB −BA =
−3 (1+3i)3i
(2+3i)9(3− 2i)
(−6+3i)(6+i) −6
.
(d)
−12 2i
10−2i
i 32
.
(e)
−11−i
203
−2i 2i 2
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

286 APPENDIX. LINEAR ALGEBRA
(f)
−12−2i
102i
−i 32
.
(g) 4+0+0− 1 − 0 − 0= 3.
(h)
B
−1
=
1
3
˜
C; C =
|
10
32
|−|
00
i 2
||
01
i 3
|
−
0 −i
32
2 −i
i 2
−|
20
i 3
|
0 −i
10
−
2 −i
00
|
20
01
|
=
20−i
−3i 3 −6
i 02
.
B
−1
=
1
3
2 −3ii
030
−i −62
.
BB
−1
=
1
3
(4+0− 1) (−6i +0+6i)(2i +0− 2i)
(0+0+0) (0+3+0) (0+0+0)
(2i +0− 2i) (3+9−12) (−1+0+4)
=
1
3
300
030
003
=
100
010
001
.
det A =0+6i +4− 0 − 6i − 4=0.
No; A does not have an inverse.
Problem A.9
(a)
−i +2i +2i
2i +0+6
−2+4+4
=
3i
6+2i
6
.
(b)
−i −2i 2
2
1 − i
0
= −2i − 2i(1 − i)+0=
−2 − 4i.
(c)
i 2i 2
20−i
01 0
i 32
2
1 − i
0
=
i 2i 2
4
1 − i
3 − i
=4i +2i(1 − i) + 2(3 − i)=
8+4i.
(d)
i
2i
2
2(1+i)0
=
2i (−1+i)0
4i (−2+2i)0
4 (2+2i)0
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
APPENDIX. LINEAR ALGEBRA 287
Problem A.10
(a) S =
1
2
(T +
˜
T);
A =
1
2
(T −
˜
T).
(b) R =
1
2
(T + T
∗
); M =
1
2
(T − T
∗
).
(c) H =
1
2
(T + T
†
); K =
1
2
(T − T
†
).
Problem A.11
(
@
ST)
ki
=(ST)
ik
=
n
j=1
S
ij
T
jk
=
n
j=1
˜
T
kj
˜
S
ji
=(
˜
T
˜
S)
ki
⇒
@
ST =
˜
T
˜
S. QED
(ST)
†
=(
@
ST)
∗
=(
˜
T
˜
S)
∗
=
˜
T
∗
˜
S
∗
= T
†
S
†
. QED
(T
−1
S
−1
)(ST)=T
−1
(S
−1
S)T = T
−1
T = I ⇒ (ST)
−1
= T
−1
S
−1
. QED
U
†
= U
−1
, W
†
= W
−1
⇒ (WU)
†
= U
†
W
†
= U
−1
W
−1
=(WU)
−1
⇒ WU is unitary.
H = H
†
, J = J
†
⇒ (HJ)
†
= J
†
H
†
= JH;
the product is hermitian ⇔ this is HJ, i.e. ⇔
[H, J]=0 (they commute).
(U + W)
†
= U
†
+ W
†
= U
−1
+ W
−1
?
=(U + W)
−1
. No; the sum of two unitary matrices is not unitary.
(H + J)
†
= H
†
+ J
†
= H + J. Yes; the sum of two hermitian matrices is hermitian.
Problem A.12
U
†
U = I =⇒ (U
†
U)
ik
= δ
ik
=⇒
n
j=1
U
†
ij
U
jk
=
n
j=1
U
∗
ji
U
jk
= δ
ik
.
Construct the set of n vectors a
(j)
i
≡ U
ij
(a
(j)
is the j-th column of U; its i-th component is U
ij
). Then
a
(i)†
a
(k)
=
n
j=1
a
(i)
∗
j
a
(k)
j
=
n
j=1
U
∗
ji
U
jk
= δ
ik
,
so these vectors are orthonormal. Similarly,
UU
†
= I =⇒ (UU
†
)
ik
= δ
ik
=⇒
n
j=1
U
ij
U
†
jk
=
n
j=1
U
∗
kj
U
ij
= δ
ki
.
This time let the vectors b
(j)
be the rows of U: b
(j)
i
≡ U
ji
. Then
b
(k)†
b
(i)
=
n
j=1
b
(k)
∗
j
b
(i)
j
=
n
j=1
U
∗
kj
U
ij
= δ
ki
,
so the rows are also orthonormal.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
288 APPENDIX. LINEAR ALGEBRA
Problem A.13
H
†
= H (hermitian) ⇒ det H = det(H
†
) = det(
˜
H
∗
) = (det
˜
H)
∗
= (det H)
∗
⇒ det H is real.
U
†
= U
−1
(unitary) ⇒ det(UU
†
) = (det U)(det U
†
) = (det U)(det
˜
U)
∗
= |det U|
2
= det I =1, so det U =1.
˜
S = S
−1
(orthogonal) ⇒ det(S
˜
S) = (det S)(det
˜
S) = (det S)
2
=1, so det S = ±1.
Problem A.14
(a)
ˆ
i
= cos θ
ˆ
i + sin θ
ˆ
j;
ˆ
j
= −sin θ
ˆ
i + cos θ
ˆ
j;
ˆ
k
=
ˆ
k. T
a
=
cos θ −sin θ 0
sin θ cos θ 0
001
.
x
z, z'
x'
y
y'
θ
θ
(b)
ˆ
i
=
ˆ
j;
ˆ
j
=
ˆ
k;
ˆ
k
=
ˆ
i. T
b
=
001
100
010
.
x, z'
z, y'
y, x'
(c)
ˆ
i
=
ˆ
i;
ˆ
j
=
ˆ
j;
ˆ
k
= −
ˆ
k. T
c
=
10 0
01 0
00−1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
APPENDIX. LINEAR ALGEBRA 289
(d)
˜
T
a
T
a
=
cos θ sin θ 0
−sin θ cos θ 0
001
cos θ −sin θ 0
sin θ cos θ 0
001
=
100
010
001
.
˜
T
b
T
b
=
010
001
100
001
100
010
=
100
010
001
.
˜
T
c
T
c
=
10 0
01 0
00−1
10 0
01 0
00−1
=
100
010
001
.
det T
a
= cos
2
θ + sin
2
θ = 1. det T
b
= 1. det T
c
= -1.
Problem A.15
x, x'
z
y
θ
θ
z'
y'
ˆ
i
=
ˆ
i;
ˆ
j
= cos θ
ˆ
j + sin θ
ˆ
k;
ˆ
k
= cos θ
ˆ
k −sin θ
ˆ
j. T
x
(θ)=
10 0
0 cos θ −sin θ
0 sin θ cos θ
.
x
z
x'
y, y'
θ
θ
z'
ˆ
i
= cos θ
ˆ
i − sin θ
ˆ
k;
ˆ
j
=
ˆ
j;
ˆ
k
= cos θ
ˆ
k + sin θ
ˆ
i. T
y
(θ)=
cos θ 0 sin θ
010
−sin θ 0 cos θ
.
ˆ
i
=
ˆ
j;
ˆ
j
= −
ˆ
i;
ˆ
k
=
ˆ
k. S =
0 −10
100
001
. S
−1
=
010
−100
001
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

290 APPENDIX. LINEAR ALGEBRA
ST
x
S
−1
=
0 −10
100
001
10 0
0 cos θ −sin θ
0 sin θ cos θ
010
−100
001
=
0 −10
100
001
010
−cos θ 0 −sin θ
−sin θ 0 cos θ
=
cos θ 0 sin θ
010
−sin θ 0 cos θ
= T
y
(θ).
ST
y
S
−1
=
0 −10
100
001
cos θ 0 sin θ
010
−sin θ 0 cos θ
010
−100
001
=
0 −10
100
001
0 cos θ sin θ
−10 0
0 −sin θ cos θ
=
10 0
0 cos θ sin θ
0 −sin θ cos θ
= T
x
(−θ).
Is this what we would expect? Yes, for rotation about the x axis now means rotation about the y axis, and
rotation about the y axis has become rotation about the −x axis—which is to say, rotation in the opposite
direction about the +x axis.
Problem A.16
From Eq. A.64 we have
A
f
B
f
= SA
e
S
−1
SB
e
S
−1
= S(A
e
B
e
)S
−1
= SC
e
S
−1
= C
f
.
Suppose S
†
= S
−1
and H
e
= H
e†
(S unitary, H
e
hermitian). Then
H
f†
=(SH
e
S
−1
)
†
=(S
−1
)
†
H
e†
S
†
= SH
e
S
−1
= H
f
, so H
f
is hermitian.
In an orthonormal basis, α|β = a
†
b (Eq. A.50). So if {|f
i
} is orthonormal, α|β = a
f†
b
f
. But b
f
= Sb
e
(Eq. A.63), and also a
f†
= a
e†
S
†
.Soα|β = a
e†
S
†
Sb
e
. This is equal to a
e†
b
e
(and hence {|e
i
} is also
orthonormal), for all vectors |α and |β⇔S
†
S = I, i.e. S is unitary.
Problem A.17
Tr(T
1
T
2
)=
n
i=1
(T
1
T
2
)
ii
=
n
i=1
n
j=1
(T
1
)
ij
(T
2
)
ji
=
n
j=1
n
i=1
(T
2
)
ji
(T
1
)
ij
=
n
j=1
(T
2
T
1
)
jj
=Tr(T
2
T
1
).
Is Tr(T
1
T
2
T
3
)=Tr(T
2
T
1
T
3
)? No. Counterexample:
T
1
=
01
00
, T
2
=
00
10
, T
3
=
10
00
.
T
1
T
2
T
3
=
01
00
00
10
10
00
=
01
00
00
10
=
10
00
=⇒ Tr(T
1
T
2
T
3
)=1.
T
2
T
1
T
3
=
00
10
01
00
10
00
=
00
10
00
00
=
00
00
=⇒ Tr(T
2
T
1
T
3
)=0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
APPENDIX. LINEAR ALGEBRA 291
Problem A.18
Eigenvalues:
(cos θ − λ) −sin θ
sin θ (cos θ − λ)
= (cos θ − λ)
2
+ sin
2
θ = cos
2
θ −2λ cos θ + λ
2
+ sin
2
θ =0, or λ
2
− 2λ cos θ +1=0.
λ =
2 cos θ ±
√
4 cos
2
θ −4
2
= cos θ ±
−sin
2
θ = cos θ ± i sin θ = e
±iθ
.
So there are two eigenvalues, both of them complex. Only if sin θ = 0 does this matrix possess real eigenvalues,
i.e., only if θ =0orπ.
Eigenvectors:
cos θ −sin θ
sin θ cos θ
α
β
= e
±iθ
α
β
=⇒ cos θα− sin θβ= (cos θ ± i sin θ)α ⇒ β = ∓iα. Normalizing:
a
(1)
=
1
√
2
1
−i
; a
(2)
=
1
√
2
1
i
.
Diagonalization:
(S
−1
)
11
= a
(1)
1
=
1
√
2
;(S
−1
)
12
= a
(2)
1
=
1
√
2
;(S
−1
)
21
= a
(1)
2
=
−i
√
2
;(S
−1
)
22
= a
(2)
2
=
i
√
2
.
S
−1
=
1
√
2
11
−ii
; inverting: S =
1
√
2
1 i
1 −i
.
STS
−1
=
1
2
1 i
1 −i
cos θ −sin θ
sin θ cos θ
11
−ii
=
1
2
1 i
1 −i
(cos θ + i sin θ) (cos θ − i sin θ)
(sin θ − i cos θ) (sin θ + i cos θ)
=
1
2
1 i
1 −i
e
iθ
e
−iθ
−ie
iθ
ie
−iθ
=
1
2
2e
iθ
0
02e
−iθ
=
e
iθ
0
0 e
−iθ
.
Problem A.19
(1 − λ)1
0(1− λ)
=(1− λ)
2
=0=⇒ λ =1 (only one eigenvalue).
11
01
α
β
=
α
β
=⇒ α + β = α =⇒ β =0;
a =
1
0
(only one eigenvector—up to an arbitrary constant factor). Since the eigenvectors do not span the space, this
matrix
cannot be diagonalized. [If it could be diagonalized, the diagonal form would have to be
10
01
, since
the only eigenvalue is 1. But in that case I = SMS
−1
. Multiplying from the left by S
−1
and on the right by
S : S
−1
IS = S
−1
SMS
−1
S = M. But S
−1
IS = S
−1
S = I. So M = I, which is false.]
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

292 APPENDIX. LINEAR ALGEBRA
Problem A.20
Expand the determinant (Eq. A.72) by minors, using the first column:
det(T − λ1)=(T
11
− λ)
(T
22
− λ) ... ...
.
.
.
.
.
.
.
.
.(T
nn
− λ)
+
n
j=2
T
j1
cofactor(T
j1
).
But the cofactor of T
j1
(for j>1) is missing two of the original diagonal elements: (T
11
− λ) (from the first
column), and (T
jj
− λ) (from the j-th row). So its highest power of λ will be (n − 2). Thus terms in λ
n
and
λ
n−1
come exclusively from the first term above. Indeed, the same argument applied now to the cofactor of
(T
11
−λ) – and repeated as we expand that determinant – shows that only the product of the diagonal elements
contributes to λ
n
and λ
n−1
:
(T
11
− λ)(T
22
− λ) ···(T
nn
− λ)=(−λ)
n
+(−λ)
n−1
(T
11
+ T
22
+ ···+ T
nn
)+···
Evidently then, C
n
=(−1)
n
, and C
n−1
=(−1)
n−1
Tr(T). To get C
0
– the term with no factors of λ – we simply
set λ =0. ThusC
0
= det(T).Fora3× 3 matrix:
(T
11
− λ) T
12
T
13
T
21
(T
22
− λ) T
23
T
31
T
32
(T
33
− λ)
=(T
11
− λ)(T
22
− λ)(T
33
− λ)+T
12
T
23
T
31
+ T
13
T
21
T
32
− T
31
T
13
(T
22
− λ) − T
32
T
23
(T
11
− λ) − T
12
T
21
(T
33
− λ)
= −λ
3
+ λ
2
(T
11
+ T
22
+ T
33
) − λ(T
11
T
22
+ T
11
T
33
+ T
22
T
33
)+λ(T
13
T
31
+ T
23
T
32
+ T
12
T
21
)
+ T
11
T
22
T
33
+ T
12
T
23
T
31
+ T
13
T
21
T
32
− T
31
T
13
T
22
− T
32
T
23
T
11
− T
12
T
21
T
33
= −λ
3
+ λ
2
Tr(T)+λC
1
+ det(T), with
C
1
=(T
13
T
31
+ T
23
T
32
+ T
12
T
21
) − (T
11
T
22
+ T
11
T
33
+ T
22
T
33
).
Problem A.21
The characteristic equation is an n-th order polynomial, which can be factored in terms of its n (complex) roots:
(λ
1
− λ)(λ
2
− λ) ···(λ
n
− λ)=(−λ)
n
+(−λ)
n−1
(λ
1
+ λ
2
+ ···+ λ
n
)+···+(λ
1
λ
2
···λ
n
)=0.
Comparing Eq. A.84, it follows that Tr(T)=λ
1
+ λ
2
+ ···λ
n
and det(T)=λ
1
λ
2
···λ
n
. QED
Problem A.22
(a)
[T
f
1
, T
f
2
]=T
f
1
T
f
2
−T
f
2
T
f
1
= ST
e
1
S
−1
ST
e
2
S
−1
−ST
e
2
S
−1
ST
e
1
S
−1
= ST
e
1
T
e
2
S
−1
−ST
e
2
T
e
1
S
−1
= S[T
e
1
, T
e
2
]S
−1
= 0.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
APPENDIX. LINEAR ALGEBRA 293
(b) Suppose SAS
−1
= D and SBS
−1
= E, where D and E are diagonal:
D =
d
1
0 ··· 0
0 d
2
··· 0
.
.
.
.
.
.
.
.
.
00··· d
n
, E =
e
1
0 ··· 0
0 e
2
··· 0
.
.
.
.
.
.
.
.
.
00··· e
n
.
Then
[A, B]=AB −BA =(S
−1
DS)(S
−1
ES) − (S
−1
ES)(S
−1
DS)=S
−1
DES − S
−1
EDS = S
−1
[D, E]S.
But diagonal matrices always commute:
DE =
d
1
e
1
0 ··· 0
0 d
2
e
2
··· 0
.
.
.
.
.
.
.
.
.
00··· d
n
e
n
= ED,
so [A, B]=0. QED
Problem A.23
(a)
M
†
=
11
1 −i
; MM
†
=
2(1− i)
(1 + i)2
, M
†
M =
2(1+i)
(1 − i)2
;[M, M
†
]=
0 −2i
2i 0
= 0. No.
(b) Find the eigenvalues:
(1 − λ)1
1(i −λ)
=(1− λ)(i − λ) − 1=i − λ(1 + i)+λ
2
− 1=0;
λ =
(1 + i) ±
(1 + i)
2
− 4(i − 1)
2
=
(1 + i) ±
√
4 − 2i
2
.
Since there are two distinct eigenvalues, there must be two linearly independent eigenvectors, and that’s
enough to span the space. So
this matrix is diagonalizable, even though it is not normal.
Problem A.24
Let |γ = |α + c|β, for some complex number c. Then
γ|
ˆ
Tγ = α|
ˆ
Tα+ cα|
ˆ
Tβ + c
∗
β|
ˆ
Tα+ |c|
2
β|
ˆ
Tβ, and
ˆ
Tγ|γ =
ˆ
Tα|α + c
∗
ˆ
Tβ|α + c
ˆ
Tα|β + |c|
2
ˆ
Tβ|β.
Suppose
ˆ
Tγ|γ = γ|
ˆ
Tγ for all vectors. For instance,
ˆ
Tα|α = α|
ˆ
Tα and
ˆ
Tβ|β = β|
ˆ
Tβ), so
cα|
ˆ
Tβ + c
∗
β|
ˆ
Tα = c
ˆ
Tα|β + c
∗
ˆ
Tβ|α, and this holds for any complex number c.
In particular, for c =1:α|
ˆ
Tβ+β|
ˆ
Tα =
ˆ
Tα|β+
ˆ
Tβ|α, while for c = i: α|
ˆ
Tβ−β|
ˆ
Tα =
ˆ
Tα|β−
ˆ
Tβ|α.
(I canceled the i’s). Adding: α|
ˆ
Tβ =
ˆ
Tα|β. QED
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
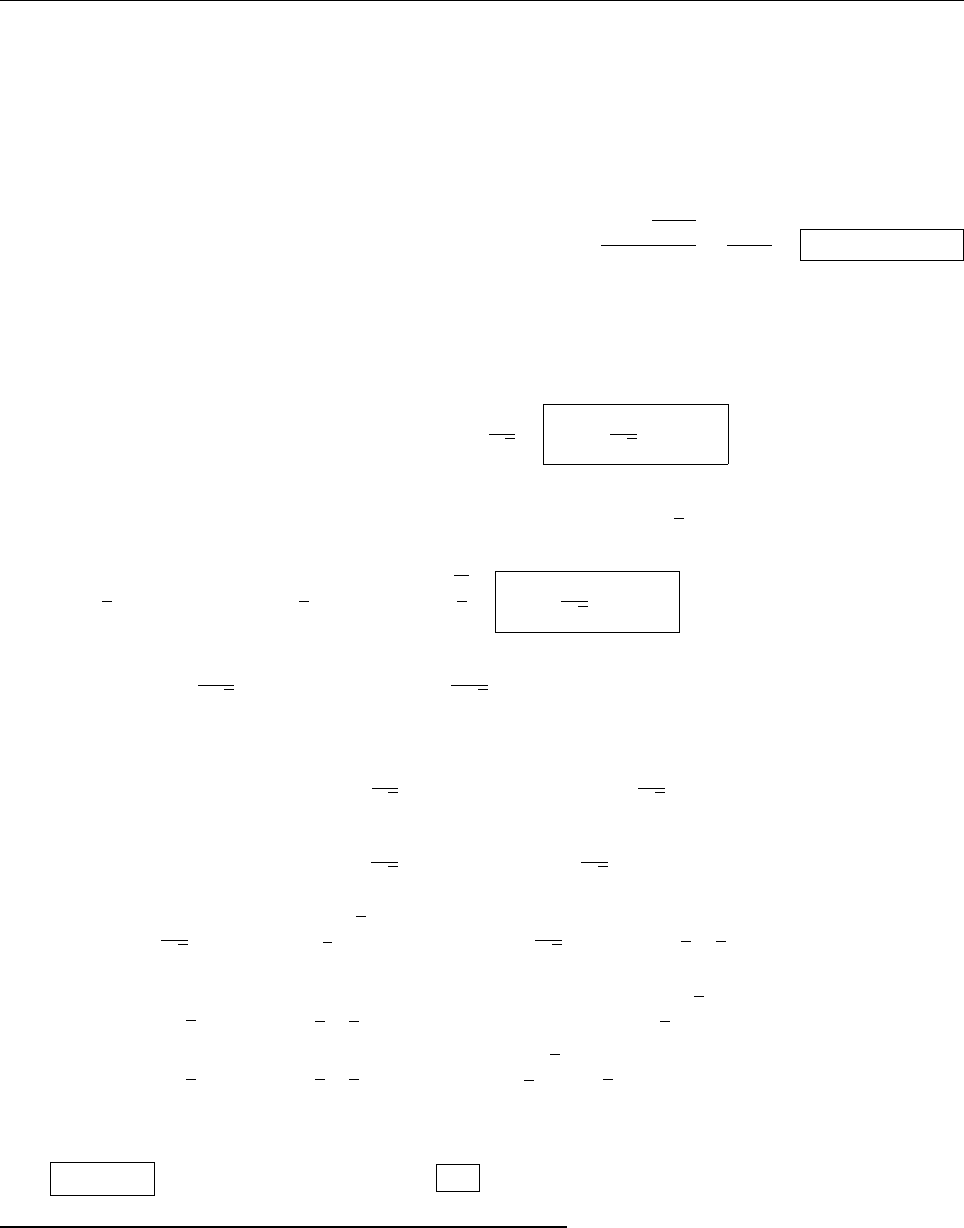
294 APPENDIX. LINEAR ALGEBRA
Problem A.25
(a)
T
†
=
˜
T
∗
=
11− i
1+i 0
= T.
(b)
(1 − λ)(1− i)
(1 + i)(0− λ)
= −(1 −λ)λ −1 −1=0; λ
2
−λ −2=0; λ =
1 ±
√
1+8
2
=
1 ± 3
2
.
λ
1
=2,λ
2
= −1.
(c)
1(1− i)
(1 + i)0
α
β
=2
α
β
=⇒ α +(1− i)β =2α =⇒ α =(1− i)β.
|α|
2
+ |β|
2
=1=⇒ 2|β|
2
+ |β|
2
=1=⇒ β =
1
√
3
.
a
(1)
=
1
√
3
1 − i
1
.
1(1− i)
(1 + i)0
α
β
= −
α
β
=⇒ α +(1− i)β = −α; α = −
1
2
(1 − i)β.
1
4
2|β|
2
+ |β|
2
=1=⇒
3
2
|β|
2
=1; β =
2
3
.
a
(2)
=
1
√
6
i − 1
2
.
a
(1)†
a
(2)
=
1
3
√
2
(1 + i)1
(i − 1)
2
=
1
3
√
2
(i − 1 − 1 − i +2)=0.
(d)
Eq. A.81 =⇒ (S
−1
)
11
= a
(1)
1
=
1
√
3
(1 − i); (S
−1
)
12
= a
(2)
1
=
1
√
6
(i − 1);
(S
−1
)
21
= a
(1)
2
=
1
√
3
;(S
−1
)
22
= a
(2)
2
=
2
√
6
.
S
−1
=
1
√
3
(1 − i)(i − 1)/
√
2
1
√
2
; S =(S
−1
)
†
=
1
√
3
(1 + i)1
(−i − 1)/
√
2
√
2
.
STS
−1
=
1
3
(1 + i)1
−(1 + i)/
√
2
√
2
1(1− i)
(1 + i)0
(1 − i)(i − 1)/
√
2
1
√
2
=
1
3
(1 + i)1
−(1 + i)/
√
2
√
2
2(1 − i)(1− i)/
√
2
2 −
√
2
=
1
3
60
0 −3
=
20
0 −1
.
(e)
Tr(T)=1; det(T)=0− (1 + i)(1 − i)= −2. Tr(STS
−1
)=2− 1=1. det(STS
−1
)=−2.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.
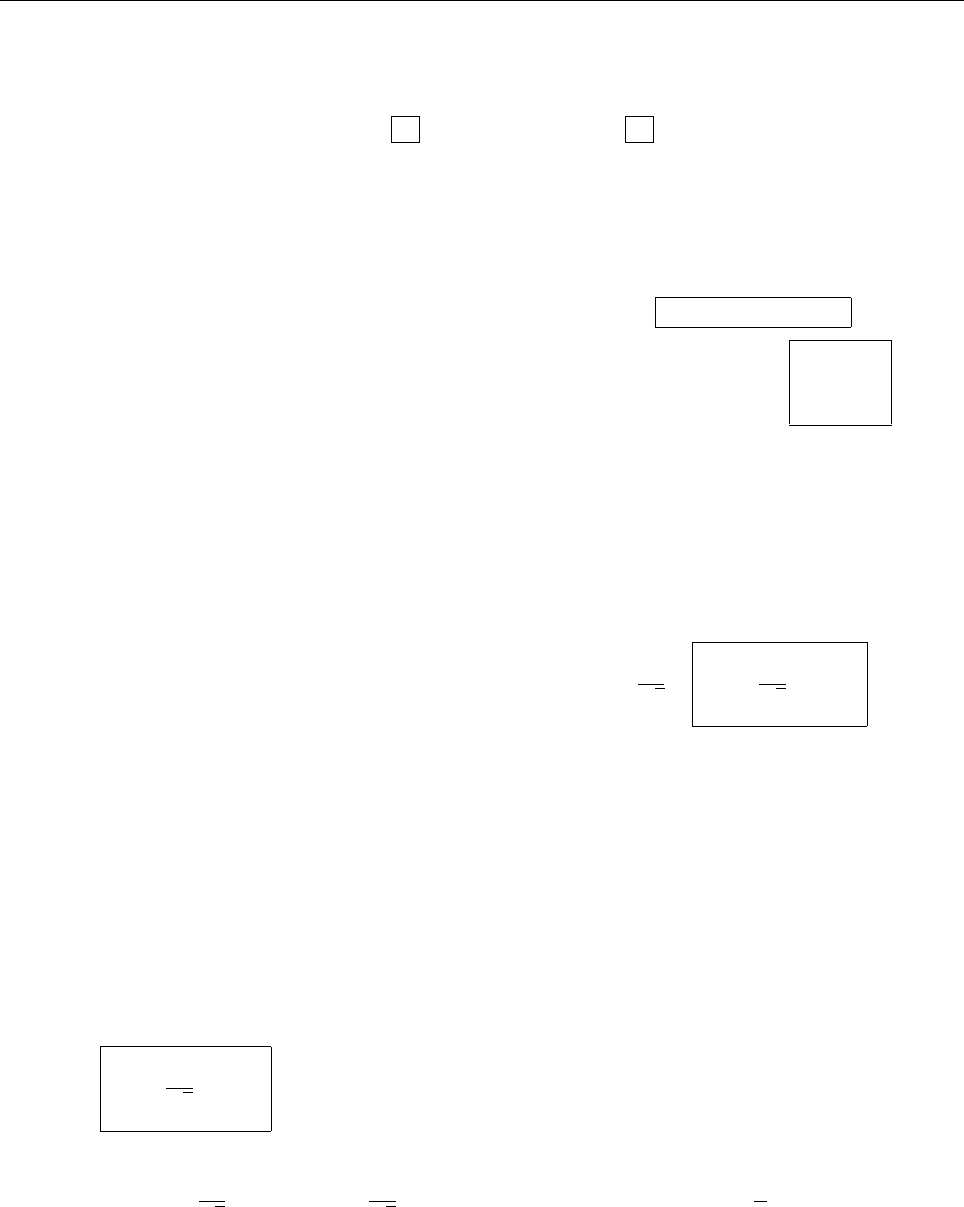
APPENDIX. LINEAR ALGEBRA 295
Problem A.26
(a)
det(T)=8− 1 − 1 − 2 − 2 − 2=
0. Tr(T)=2+2+2= 6.
(b)
(2 − λ) i 1
−i (2 − λ) i
1 −i (2 − λ)
=(2−λ)
3
−1 −1 −(2 −λ) −(2 −λ) −(2 −λ)=8−12λ +6λ
2
−λ
3
−8+3λ =0.
−λ
3
+6λ
2
− 9λ = −λ(λ
2
− 6λ +9)=−λ(λ − 3)
2
=0. λ
1
=0,λ
2
= λ
3
=3.
λ
1
+ λ
2
+ λ
3
=6=Tr(T). λ
1
λ
2
λ
3
= 0 = det(T). Diagonal form:
000
030
003
.
(c)
2 i 1
−i 2 i
1 −i 2
α
β
γ
=0=⇒
2α + iβ + γ =0
−iα +2β + iγ =0=⇒ α +2iβ − γ =0
.
Add the two equations: 3α +3iβ =0=⇒ β = iα;2α − α + γ =0=⇒ γ = −α.
a
(1)
=
α
iα
−α
. Normalizing: |α|
2
+ |α|
2
+ |α|
2
=1=⇒ α =
1
√
3
.
a
(1)
=
1
√
3
1
i
−1
.
2 i 1
−i 2 i
1 −i 2
α
β
γ
=3
α
β
γ
=⇒
2α + iβ + γ =3α =⇒−α + iβ + γ =0,
−iα +2β + iγ =3β =⇒ α − iβ − γ =0,
α − iβ +2γ =3γ =⇒ α − iβ − γ =0.
The three equations are redundant – there is only one condition here: α − iβ − γ =0. We could pick
γ =0,β= −iα, or β =0,γ= α. Then
a
(2)
0
=
α
−iα
0
; a
(3)
0
=
α
0
α
.
But these are not orthogonal, so we use the Gram-Schmidt procedure (Problem A.4); first normalize a
(2)
0
:
a
(2)
=
1
√
2
1
−i
0
.
a
(2)
†
a
(3)
0
=
α
√
2
1 i 0
1
0
1
=
α
√
2
. So a
(3)
0
− (a
(2)
†
a
(3)
0
) a
(2)
= α
1
0
1
−
α
2
1
−i
0
= α
1/2
i/2
1
.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

296 APPENDIX. LINEAR ALGEBRA
Normalize: |α|
2
1
4
+
1
4
+1
=
3
2
|α|
2
=1 =⇒ α =
2
3
.
a
(3)
=
1
√
6
1
i
2
.
Check orthogonality:
a
(1)
†
a
(2)
=
1
√
6
1 −i −1
1
−i
0
=
1
√
6
(1 − 1+0)=0.
a
(1)
†
a
(3)
=
1
3
√
2
1 −i −1
1
i
2
=
1
3
√
2
(1+1− 2)=0.
(d) S
−1
is the matrix whose columns are the eigenvectors of T (Eq. A.81):
S
−1
=
1
√
6
√
2
√
31
√
2 i −
√
3 ii
−
√
202
; S =(S
−1
)
†
=
1
√
6
√
2 −
√
2 i −
√
2
√
3
√
3 i 0
1 −i 2
.
STS
−1
=
1
6
√
2 −
√
2 i −
√
2
√
3
√
3 i 0
1 −i 2
2 i 1
−i 2 i
1 −i 2
√
2
√
31
√
2 i −
√
3 ii
−
√
202
03
√
33
0 −3
√
3 i 3i
00 6
=
1
6
00 0
018 0
0018
=
000
030
003
.
Problem A.27
(a)
ˆ
Uα|
ˆ
Uβ =
ˆ
U
†
ˆ
Uα|β = α|β.
(b)
ˆ
U|α = λ|α =⇒
ˆ
Uα|
ˆ
Uα = |λ|
2
α|α. But from (a) this is also α|α.So|λ| =1.
(c)
ˆ
U|α = λ|α,
ˆ
U|β = µ|β =⇒|β = µ
ˆ
U
−1
|β,so
ˆ
U
†
|β =
1
µ
|β = µ
∗
|β (from (b)).
β|
ˆ
Uα = λβ|α =
ˆ
U
†
β|α = µβ|α,or(λ − µ)β|α =0. So if λ = µ, then β|α =0. QED
Problem A.28
(a) (i)
M
2
=
004
000
000
; M
3
=
000
000
000
, so
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

APPENDIX. LINEAR ALGEBRA 297
e
M
=
100
010
001
+
013
004
000
+
1
2
004
000
000
=
115
014
001
.
(ii)
M
2
=
−θ
2
0
0 −θ
2
= −θ
2
I; M
3
= −θ
3
M; M
4
= θ
4
I; etc.
e
M
= I + θ
01
−10
−
1
2
θ
2
I −
θ
3
3!
01
−10
+
θ
4
4!
I + ···
=
1 −
θ
2
2
+
θ
4
4!
−···
I +
θ −
θ
3
3!
+
θ
5
5!
−···
01
−10
= cos θ
10
01
+ sin θ
01
−10
=
cos θ sin θ
−sin θ cos θ
.
(b)
SMS
−1
= D =
d
1
0
.
.
.
0 d
n
for some S.
Se
M
S
−1
= S
I + M +
1
2
M
2
+
1
3!
M
3
+ ···
S
−1
. Insert SS
−1
= I :
Se
M
S
−1
= I + SMS
−1
+
1
2
SMS
−1
SMS
−1
+
1
3!
SMS
−1
SMS
−1
SMS
−1
+ ···
= I + D +
1
2
D
2
+
1
3!
D
3
+ ···= e
D
. Evidently
det(e
D
) = det(Se
M
S
−1
) = det(S) det(e
M
) det(S
−1
) = det(e
M
). But
D
2
=
d
2
1
0
.
.
.
0 d
2
n
, D
3
=
d
3
1
0
.
.
.
0 d
3
n
, D
k
=
d
k
1
0
.
.
.
0 d
k
n
, so
e
D
= I +
d
1
0
.
.
.
0 d
n
+
1
2
d
2
1
0
.
.
.
0 d
2
n
+
1
3!
d
3
1
0
.
.
.
0 d
3
n
+ ···=
e
d
1
0
.
.
.
0 e
d
n
.
det(e
D
)=e
d
1
e
d
2
···e
d
n
= e
(d
1
+d
2
+···d
n
)
= e
Tr D
= e
Tr M
(Eq. A.68), so det(e
M
)=e
Tr M
. QED
(c) Matrices that commute obey the same algebraic rules as ordinary numbers, so the standard proofs of
e
x+y
= e
x
e
y
will do the job. Here are two:
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

298 APPENDIX. LINEAR ALGEBRA
n
m
(i) Combinatorial Method: Use the binomial theorem (valid if multiplication is commutative):
e
M+N
=
∞
n=0
1
n!
(M + N)
n
=
∞
n=0
1
n!
n
m=0
n
m
M
m
N
n−m
=
∞
n=0
n
m=0
1
m!(n − m)!
M
m
N
n−m
.
Instead of summing vertically first, for fixed n (m :0→ n), sum horizontally first, for fixed m (n :
m →∞,ork ≡ n − m :0→∞)—see diagram (each dot represents a term in the double sum).
e
M+N
=
∞
m=0
1
m!
M
m
∞
k=0
1
k!
N
k
= e
M
e
N
. QED
(ii) Analytic Method:
Let
S(λ) ≡ e
λM
e
λN
;
dS
dλ
= Me
λM
e
λN
+ e
λM
Ne
λN
=(M + N)e
λM
e
λN
=(M + N)S.
(The second equality, in which we pull N through e
λM
, would not hold if M and N did not commute.)
Solving the differential equation: S(λ)=Ae
(M+N)λ
, for some constant A. But S(0) = I,soA =1,
and hence e
λM
e
λN
= e
λ(M+N)
, and (setting λ = 1) we conclude that e
M
e
N
= e
(M+N)
. [This method
generalizes most easily when M and N do not commute—leading to the famous Baker-Campbell-
Hausdorf lemma.]
As a counterexample when [M, N] = 0, let M =
01
00
, N =
00
−10
. Then M
2
= N
2
= 0,so
e
M
= I + M =
11
01
,e
N
= I + N =
10
−11
; e
M
e
N
=
11
01
10
−11
=
01
−11
.
But (M + N)=
01
−10
, so (from a(ii)): e
M+N
=
cos(1) sin(1)
−sin(1) cos(1)
.
The two are clearly not equal.
(d)
e
iH
=
∞
n=0
1
n!
i
n
H
n
=⇒ (e
iH
)
†
=
∞
n=0
1
n!
(−i)
n
(H
†
)
n
=
∞
n=0
1
n!
(−i)
n
H
n
= e
−iH
(for H hermitian).
(e
iH
)
†
(e
iH
)=e
−iH
e
iH
= e
i(H−H)
= I, using (c). So e
iH
is unitary.
c
2005 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the
publisher.

299
2
nd
Edition – 1
st
Edition Problem Correlation Grid
N = New
M = 1/e problem number (modified for 2/e)
X = 2/e problem number (unchanged from 1/e)
Chapter 1
2/e 1/e
1 1
2N
3 6
4 7
5 8
6 11
7 12
8 13
9 14
10 2
11 3
12 4
13 5
14 9M
15 10
16N
17N
18N
Chapter 2
2/e 1/e
1 1
2 2
3 3
4 5
5 6M
6 7
7N
8N
9N
10 13M
11 14
12 37
13 17M
14N
15 15
16 16
17 18
18 19M
19N
20 20
21N
22 22
23 23
24 24
25N
26 25
27 26
28 27
29 28
30 29
31 30
32 31
33 32
34 33
35 41M
36 4M
37 36
38 3.48
39N
40N
41N
42 38
43 40
44 39
Chapter 2 (cont.)
2/e 1/e
45 42
46 43
47 44
48N
49 45
50 47
51 48M
52 34M, 35M
53 49
54N
55N
56N

300
2
nd
Edition – 1
st
Edition Problem Correlation Grid
N = New
M = 1/e problem number (modified for 2/e)
(M) = 1/e problem number (distant model for 2/e)
X = 2/e problem number (unchanged from 1/e)
Chapter 3
2/e 1/e
1N
2N (33M)
3N (21M)
4N (12M)
5N
6N
7N
8N
9N
10N
11 38
12 51
13 41M
14 39
15N
16 42
17 43
18 44
19 45
20 46
21 57M
22N
23N
24 57M
25 25M
26N
27N
28 52M
29N
30N
31 53
32 56
33 50
34 49M
35N
36N
37N
38N
39 55
40N
Chapter 4
2/e 1/e
1 1
2 2
3 3
4 4
5 5
6 6
7 7M
8 8
9 9M
10 10
11 11
12 12
13 13
14N
15N
16 17
17 16
18 19
19 20
20 21
21N
22 22
23 23
24 25
25 26
26 27
27 28
28 29
29 30
30 31M
31 32
32 33
33 34
34 35
35 36
36 37
37 38
38 39
39 40
40 41
41N
42 42
Chapter 4 (cont.)
2/e 1/e
43 43
44N
45 14
46 15
47N
48N
49N
50 44
51 45M
52 46
53N
54 47
55 48
56 49
57 50
58N
59 51
60 52M
61 53
301
2
nd
Edition – 1
st
Edition Problem Correlation Grid
N = New
M = 1/e problem number (modified for 2/e)
X = 2/e problem number (unchanged from 1/e)
Chapter 5
2/e 1/e
1 1
2 2
3N
4 3
5 4
6 5
7 6
8 7
9 8
10 9
11 10
12 11M
13 11M
14 12
15N
16 13
17 14
18 15M
19 16M
20 17M
21 18
22 19M
23 20
24 21M
25 22
26 23
27 24
28 25
29 26
30 27M
31 28
32N
33 29
34 30
35 31
36 32
37 33
Chapter 6
2/e 1/e
1 1M
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10N
11 10
12 11
13 12
14 13
15N
16 14
17 15
18 16
19 17
20 18
21 19
22 20
23 21
24 22
25 23
26 24
27 25
28 26
29N
30N
31N
32 27
33 28
34 29
35 30
36 31
37 32
38 33
39 34
40N
Chapter 7
2/e 1/e
1 1
2 2M
3 3M
4 4
5 5
6 6
7 7
8 8
9 9
10 10
11N
12N
13 11
14 12
15 13
16 14
17 15
18 16
19 17
20N

302
2
nd
Edition – 1
st
Edition Problem Correlation Grid
N = New
M = 1/e problem number (modified for 2/e)
X = 2/e problem number (unchanged from 1/e)
Chapter 8
2/e 1/e
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10 10
11 11
12 12
13 13
14 14
15 15
16N
17N
Chapter 9
2/e 1/e
1 1
2 2
3 3M
4 4
5 5
6 6
7 7
8 8
9N
10 9
11 10
12 11
13 12
14 13
15 14
16 15
17 16
18 17
19 21
20 19M
21 20
22N
Chapter 10
2/e 1/e
1 1
2 3M
3 4
4 5
5 6
6 8
7 9
8N
9 10
10 11M
303
2
nd
Edition – 1
st
Edition Problem Correlation Grid
N = New
M = 1/e problem number (modified for 2/e)
X = 2/e problem number (unchanged from 1/e)
Chapter 11
2/e 1/e
1 1
2 2
3 3
4 4
5N
6N
7N
8 5
9 6
10 7
11 8
12 9
13 10
14 11
15 12
16 13
17 14
18 15
19N
20N
Chapter 12
2/e 1/e
1N
Appendix
2/e 1/e
1 3.1
2 3.2
3 3.3
4 3.4
5 3.5
6 3.6
7 3.7
8 3.9
9 3.10.
10 3.11
11 3.12
12 3.16
13N
14N
15 3.13
16 3.14
17 3.15
18 3.17
19 3.18
20 3.19
21 3.20.
22 3.40M
23N
24 3.21M
25 3.22
26 3.23
27 3.24
28 3.47
