
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
Note: For the benefit of the students, specially the aspiring ones, the question of JEE(advanced), 2022 are also
given in this booklet. Keeping the interest of students studying in class XI, the questions based on topics
from class XI have been marked with ‘*’, which can be attempted as a test. For this test the time
allocated in Physics, Chemistry & Mathematics are 25 minutes, 25 minutes and 25 minutes respectively.
FIITJEE
SOLUTIONS TO JEE (ADVANCED) – 2022
(Paper1)
MATHEMATICS
SECTION 1 (Maximum Marks: 24)
This section contains EIGHT (08) questions.
The answer to each question is a NUMERCAL VALUE.
For each question, enter the correct numerical values of the answer using the mouse and the onscreen
virtual numerical keypad in the place designated to enter the answer. If the numerical value has more than
two decimal places, truncate/roundoff the value to TWO decimal places.
Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +3 ONLY if the correct numerical values is entered;
Zero Marks : 0 In all other cases.
*Q.1. Considering only the principal values of the inverse trigonometric functions, the value of
1 1 1
2 2
3 2 1 2 2 2
cos sin tan
2 4
2 2
is __________.
Q.2. Let be a positive real number. Let :
f R R
and
: ,
g R
be the functions defined by
sin
12
x
f x and
2log
log
e
x
e
x
g x
e e
.
Then the value of
lim
x
f g x
is __________.
Q.3. In a study about a pandemic, data of 900 persons was collected. It was found that
190 persons had symptom of fever,
220 persons had symptom of cough,
220 persons had symptom of breathing problem,
330 persons had symptom of fever or cough or both,
350 persons had symptom of cough or breathing problem or both,
340 persons had symptom of fever or breathing problem or both,
30 persons had all three symptoms (fever, cough and breathing problem).
If a person is chosen randomly from these 900 persons, then the probability that the person has at most one
symptom is __________.
*Q.4. Let z be a complex number with nonzero imaginary part. If
2
2
2 3 4
2 3 4
z z
z z
is a real number, then the value
of
2
z
is __________.
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
2
*Q.5. Let
z
denote the complex conjugate of a complex number z and let
1
i . In the set of complex
numbers, the number of distinct roots of the equation
2 2
z z i z z
is __________.
*Q.6. Let
1 2 100
, , .....,
l l l
be consecutive terms of an arithmetic with common difference
1
d
, and let
1 2 100
, , .....,
w w w
be consecutive terms of another arithmetic progression with common difference
2
d
,
where
1 2
10
d d . For each i = 1, 2, ....., 100, let R
i
be a rectangle with length l
i
, width
i
w
and area
i
A
. If
51 50
1000
A A , then the value of
100 90
A A
is __________.
*Q.7. The number of 4digit integers in the closed interval [2022, 4482] formed by using the digits 0, 2, 3, 4, 6, 7
is __________.
*Q.8. Let ABC be the triangle with AB = 1, AC = 3 and
2
BAC . If a circle of radius r > 0 touches the sides
AB, AC and also touches internally the Circumcircle of the triangle ABC, then the value of r is __________.
SECTION 2 (Maximum Marks: 24)
This section contains SIX (06) questions.
Each questions has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four option(s)
is(are) correct answer(s).
For each question, choose the option(s) corresponding to (all) the correct answer(s).
Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +4 ONLY if (all) the correct option(s) is(are) chosen;
Partial Marks : +3 If all the four options are correct but ONLY three options are chosen;
Partial Marks : +2 If three or more options are correct but ONLY two options are chosen, both of which
are correct;
Partial Marks : +1 If two or more options are correct but ONLY one option is chosen and it is a correct
option;
Zero Marks : 0 If none of these of the options is chosen (i.e. the question is unanswered);
Negative Marks : –2 In all other cases.
Q.9. Consider the equation
1
2
2
3
1
2
log
1
log
e
e
e
x
dx
x a x
,
, 0 1,
a .
Which of the following statements is/are TRUE?
(A) No a satisfies the above equation
(B) An integer a satisfies the above equation
(C) An irrational number a satisfies the above equation
(D) More than one a satisfy the above equation
*Q.10. Let
1 2 3
, , , .....
a a a be an arithmetic progression with
1
7
a and common difference 8. Let
1 2 3
, , , .....
T T T
be such that
1
3
T and
1
n n n
T T a
for n 1. Then, which of the following is/are TRUE?
(A)
20
1604
T (B)
20
1
10510
k
k
T
(C)
30
3454
T (D)
30
1
35610
k
k
T
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
3
Q.11. Let
1
P
and
2
P
be two planes given by
1
:10 15 12 60 0
P x y z ,
2
: 2 5 4 20 0
P x y z . Which of
the following straight lines can be an edge of some tetrahedron whose two faces lie on
1
P
and
2
P
?
(A)
1 1 1
0 0 5
x y z
(B)
6
5 2 3
x y z
(C)
4
2 5 4
x y z
(D)
4
1 2 3
x y z
Q.12. Let S be the reflection of a point Q with respect to the plane given by
ˆ
ˆ ˆ
1
r t p i t j p k
where t,
p are real parameters and
ˆ
ˆ ˆ
, ,
i j k
are the unit vectors along the three positive coordinate axes. If the position
vectors of Q and S are
ˆ
ˆ ˆ
10 15 20
i j k
and
ˆ
ˆ ˆ
i j k
respectively, then which of the following is/are
TRUE?
(A)
3 101
(B)
3 71
(C)
3 86
(D)
3 121
*Q.13. Consider the parabola
2
4
y x
. Let S be the focus of the parabola. A pair of tangents drawn to the parabola
from the point
2, 1
P meet the parabola at
1
P
and
2
P
. Let
1
Q
and
2
Q
be points on the lines
1
SP
and
2
SP
respectively such that
1
PQ
is perpendicular to
1
SP
and
2
PQ
is perpendicular to
2
SP
. Then, which of
the following is/are TRUE?
(A)
1
2
SQ (B)
1 2
3 10
5
Q Q
(C)
1
3
PQ (D)
2
1
SQ
Q.14. Let
M
denote the determinant of a square matrix M. Let : 0,
2
g R
be the function defined by
1 1
2
g f f
where
sin cos tan
4 4
1 sin 1
1 4
sin 1 sin sin cos log
2 4 2
1 sin 1
cot log tan
4 4
e
e
f .
Let p(x) be a quadratic polynomial whose roots are the maximum and minimum values of the function
g and
2 2 2
p . Then, which of the following is/are TRUE?
(A)
3 2
0
4
p (B)
1 3 2
0
4
p
(C)
5 2 1
0
4
p (D)
5 2
0
4
p

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
4
SECTION 3 (Maximum Marks: 12)
This section contains FOUR (04) Matching List Sets.
Each set has ONE Multiple Choice Question.
Each set has TWO lists: ListI and ListII.
ListI has Four entries (I), (II), (III) and (IV) and ListII has Five entries (P), (Q), (R), (S) and (T).
FOUR options are given in each Multiple Choice Question based on ListI and ListII and ONLY ONE of
these four options satisfies the condition asked in the Multiple Choice Question.
Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +3 ONLY if the option corresponding to the correct combination is chosen;
Zero Marks : 0 If none of these of the options is chosen (i.e. the question is unanswered);
Negative Marks : –1 In all other cases.
*Q.15. Consider the following lists:
ListI ListII
(I)
2 2
, : cos sin 1
3 3
x x x
(P) has two elements
(II)
5 5
, : 3 tan 3 1
18 18
x x
(Q) has three elements
(III)
6 6
, : 2 cos 2 3
5 5
x x
(R) has four elements
(IV)
7 7
, : sin cos 1
4 4
x x x
(S) has five elements
(T) has six elements
The correct option is:
(A) (I) (P); (II) (S); (III) (P); (IV) (S)
(B) (I) (P); (II) (P); (III) (T); (IV) (R)
(C) (I) (Q); (II) (P); (III) (T); (IV) (S)
(D) (I) (Q); (II) (S); (III) (P); (IV) (R)
Q.16. Two players,
1
P
and
2
P
, play a game against each other. In every round of the game, each player rolls a
fair die once, where the six faces of the die have six distinct numbers. Let x and y denote the readings on
the die rolled by
1
P
and
2
P
, respectively. If x > y, then
1
P
scores 5 points and
2
P
scores 0 points. If x = y,
then each player scores 2 points. If x < y, then
1
P
scores 0 point and
2
P
scores 5 points. Let X
i
and Y
i
be the
total scores of P
1
and P
2
, respectively, after playing the i
th
round.
ListI ListII
(I)
Probability of
2 2
X Y
is
(P)
3
8
(II)
Probability of
2 2
X Y
is
(Q)
11
16
(III)
Probability of
3 3
X Y
is
(R)
5
16
(IV)
Probability of
3 3
X Y
is
(S)
355
864
(T)
77
432
The correct option is:
(A) (I) (Q; (II) (R); (III) (T); (IV) (S) (B) (I) (Q; (II) (R); (III) (T); (IV) (T)
(C) (I) (P); (II) (R); (III) (Q); (IV) (S) (D) (I) (P); (II) (R); (III) (Q); (IV) (T)

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
5
Q.17. Let p, q, r be nonzero real numbers that are, respectively, the 10
th
, 100
th
and 1000
th
terms of a harmonic
progression. Consider the system of linear equation
x + y + z = 1
10x + 100y + 1000z = 0
qrx + pry + pqz = 0
ListI ListII
(I)
If
10
q
r
, then the system of linear equations
has
(P)
x = 0,
10
9
y ,
1
9
z
(II)
If
100
p
r
, then the system of linear
equations has
(Q)
10 1
, , 0
9 9
x y z as a solution
(III)
If
10
p
q
, then the system of linear equation
has
(R) infinitely many solutions
(IV)
If
10
p
q
, then the system of linear equations
has
(S) no solution
(T) at least one solution
The correct option is:
(A) (I) (T); (II) (R); (III) (S); (IV) (T)
(B) (I) (Q); (II) (S); (III) (S); (IV) (R)
(C) (I) (Q); (II) (R); (III) (P); (IV) (R)
(D) (I) (T); (II) (S); (III) (P); (IV) (T)
*Q.18 Consider the ellipse
2 2
1
4 3
x y
. Let
, 0
H , 0 < < 2, be a point. A straight line drawn through H
parallel to yaxis crosses the ellipse and its auxiliary circle at points E and F respectively, in the first
quadrant. The tangents to the ellipse at the point E intersects the positive xaxis at a point G. Suppose the
straight line joining F and the origin makes an angle
with the positive xaxis.
ListI ListII
(I)
If
4
, then the area of the triangle FGH is
(P)
4
3 1
8
(II)
If
3
, then the area of the triangle FGH is
(Q) 1
(III) If
6
, then the area of the triangle FGH is (R)
3
4
(IV)
If
12
, then the area of the triangle FGH is
(S)
1
2 3
(T)
3 3
2
The correct option is:
(A) (I) (R); (II) (S); (III) (Q); (IV) (P)
(B) (I) (R); (II) (T); (III) (S); (IV) (P)
(C) (I) (Q); (II) (T); (III) (S); (IV) (P)
(D) (I) (Q); (II) (S); (III) (Q); (IV) (P)

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
6
PART II: PHYSICS
SECTION 1 (Maximum Marks: 24)
This section contains EIGHT (08) questions.
The answer to each question is a NUMERCAL VALUE.
For each question, enter the correct numerical values of the answer using the mouse and the onscreen
virtual numerical keypad in the place designated to enter the answer. If the numerical value has more than
two decimal places, truncate/roundoff the value to TWO decimal places.
Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +3 ONLY if the correct numerical values is entered;
Zero Marks : 0 In all other cases.
*Q.1 Two spherical stars A and B have densities ρ
A
and ρ
B
, respectively. A and B have the same radius, and their
masses M
A
and M
B
are related by M
B
= 2 M
A
. Due to an interaction process, star A loses some of its mass,
so that its radius is halved, while its spherical shape is retained, and its density remains ρ
A
. The entire mass
lost by A is deposited as a thick spherical shell on B with the density of the shell being ρ
A
. If
A
and
B
are
the escape velocities from A and B after the interaction process, the ratio
1/3
10
15
B
A
n
. The value of n is
______
Q.2 The minimum kinetic energy needed by an alpha particle to cause the nuclear reaction
16 4 1 19
7 2 1 8
N He H O
in a laboratory frame is n (in MeV). Assume that
16
7
N
is at rest in the
laboratory frame. The masses of
16 4 1 19
7 2 1 8
, ,
N He H and O
can be taken to be 16.006 u, 4.003 u, 1.008
u and 19.003 u, respectively, where 1 u = 930 MeVc
−2
. The value of n is _________.
Q3. In the following circuit C
1
= 12 F, C
2
= C
3
= 4 F and C
4
= C
5
= 2
F. The charge stored in C
3
is ______ C.
6V
C
2
C
1
C
3
C
5
2V
C
4
Q.4 A rod of length 2 cm makes an angle
2
3
rad with the
principal axis of a thin convex lens. The lens has a focal
length of 10 cm and is placed at a distance of
40
3
cm from the object as shown in the figure, The
height of the image is
30 3
13
and the angle made by it
with respect to the principal axis is rad. The value of
α is
rad
n
, where n is __________
3
2
40
3
cm
30 3
13
cm
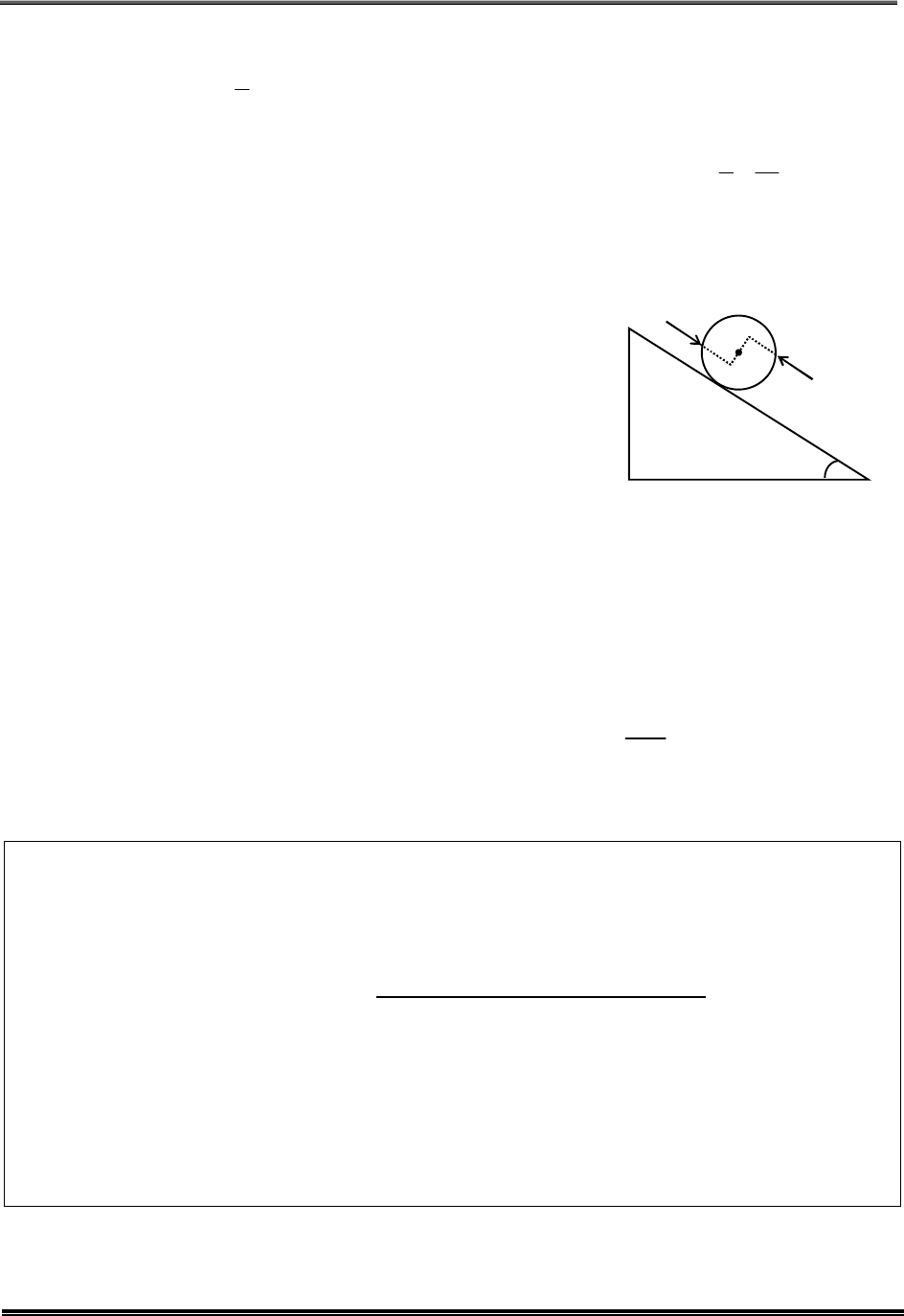
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
7
*Q.5 At time t=0, a disk of radius 1 m starts to roll without slipping on a horizontal plane with an angular
acceleration of
2
2
3
rad s
. A small stone is stuck to the disk. At t = 0, it is at the contact point of the
disk and the plane. Later, at time t = s, the stone detaches itself and flies off tangentially from the disk.
The maximum height (in m) reached by the stone measured from the plane is
1
.
2 10
x
The value of
x is______ [Take g = 10ms
−2
.]
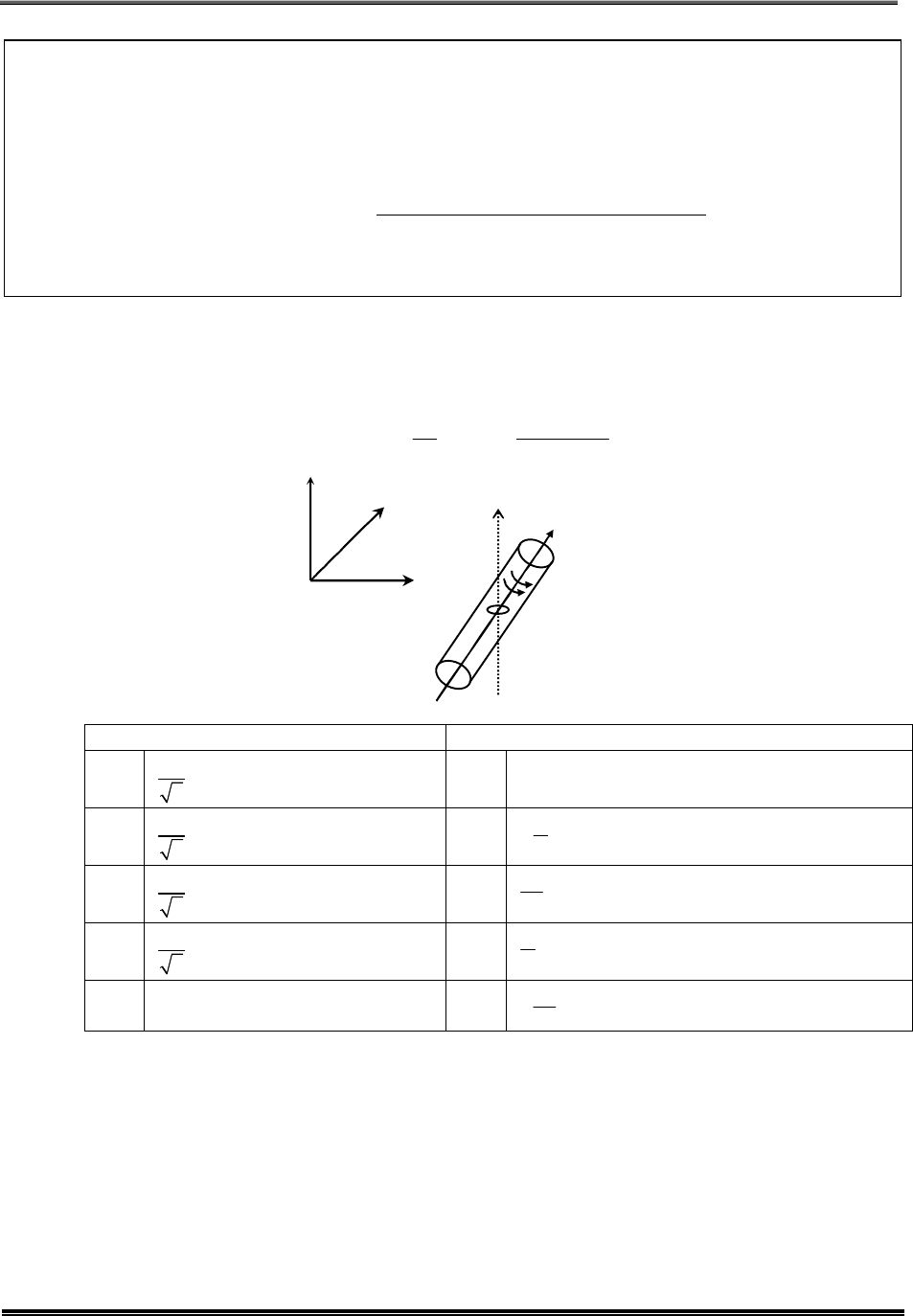
*Q.6 A solid sphere of mass 1 kg and radius 1 m rolls without slipping
on a fixed inclined plane with an angle of inclination θ=30 from the
horizontal. Two forces of magnitude 1N each, parallel to the incline,
act on the sphere, both at distance r = 0.5 m from the center of the
sphere, as shown in the figure. The acceleration of the sphere down
the plane is _______ ms
2
. (Take g = 10 ms
2
.)
r
r
Q.7 Consider an LC circuit, with inductance L=0.1 H and capacitance C = 10
−3
F, kept on a plane. The area of
the circuit is 1 m
2
. It is placed in a constant magnetic field of strength B
0
which is perpendicular to the
plane of the circuit. At time t = 0, the magnetic field strength starts increasing linearly as B=B
0
+ βt with
β=0.04Ts
−1
. The maximum magnitude of the current in the circuit is__________ mA .
*Q.8 A projectile is fired from horizontal ground with speed v and projection angle θ. When the acceleration due
to gravity is g, the range of the projectile is d. If at the highest point in its trajectory, the projectile enters a
different region where the effective acceleration due to gravity is '
0.81
g
g , then the new range is d′ = nd.
The value of n is _________.
SECTION 2 (Maximum Marks: 24)
This section contains SIX (06) questions.
Each questions has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four option(s)
is(are) correct answer(s).
For each question, choose the option(s) corresponding to (all) the correct answer(s).
Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +4 ONLY if (all) the correct option(s) is(are) chosen;
Partial Marks : +3 If all the four options are correct but ONLY three options are chosen;
Partial Marks : +2 If three or more options are correct but ONLY two options are chosen, both of which
are correct;
Partial Marks : +1 If two or more options are correct but ONLY one option is chosen and it is a correct
option;
Zero Marks : 0 If none of the options is chosen (i.e. the question is unanswered);
Negative Marks : –2 In all other cases.
Q.9 A medium having dielectric constant K > 1 fills the space between the plates of a parallel plate capacitor.
The plates have large area, and the distance between them is d. The capacitor is connected to a battery of

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
8
voltage V, as shown in Figure (a). Now, both the plates are moved by a distance d/2 of from their original
positions, as shown in Figure (b).
Figure(a)
Figure(b)
V
V
d
d
d/2
d/2
In the process of going from the configuration depicted in Figure (a) to that in Figure (b), which of the
following statement(s) is(are) correct?
(A) The electric field inside the dielectric material is reduced by a factor of 2K.
(B) The capacitance is decreased by a factor of
1
1
K
.
(C) The voltage between the capacitor plates is increased by a factor of (K+1).
(D) The work done in the process DOES NOT depend on the presence of the dielectric material.
Q.10 The figure shows a circuit having eight resistances of 1 each, labelled R
1
to R
8
, and two ideal batteries
with voltages
1
=12 V and
2
= 6 V.
1
R
6
R
2
R
7
R
1
R
3
R
5
R
8
R
4
2
Which of the following statement(s) is(are) correct?
(A) The magnitude of current flowing through R
1
is 7.2 A.
(B) The magnitude of current flowing through R
2
is 1.2 A.
(C) The magnitude of current flowing through R
3
is 4.8 A.
(D) The magnitude of current flowing through R
5
is 2.4 A.
*Q.11 An ideal gas of density = 0.2 kg m
3
enters a chimney of height h at the rate of = 0.8 kg s
1
from its
lower end, and escapes through the upper end as shown in the figure. The cross-sectional area of the lower
end is A
1
= 0.1 m
2
and the upper end is A
2
= 0.4 m
2
. The pressure and the temperature of the gas at the
lower end are 600 Pa and 300 K, respectively, while its temperature at the upper end is 150 K. The chimney
is heat insulated so that the gas undergoes adiabatic expansion. Take g = 10 ms
2
and the ratio of specific
heats of the gas = 2. Ignore atmospheric pressure.
h
A
2
A
1

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
9
Which of the following statement(s) is(are) correct?
(A) The pressure of the gas at the upper end of the chimney is 300 Pa.
(B) The velocity of the gas at the lower end of the chimney is 40 ms
1
and at the upper end is 20 ms
1
.
(C) The height of the chimney is 590m.
(D) The density of the gas at the upper end is 0.05 kg m
3
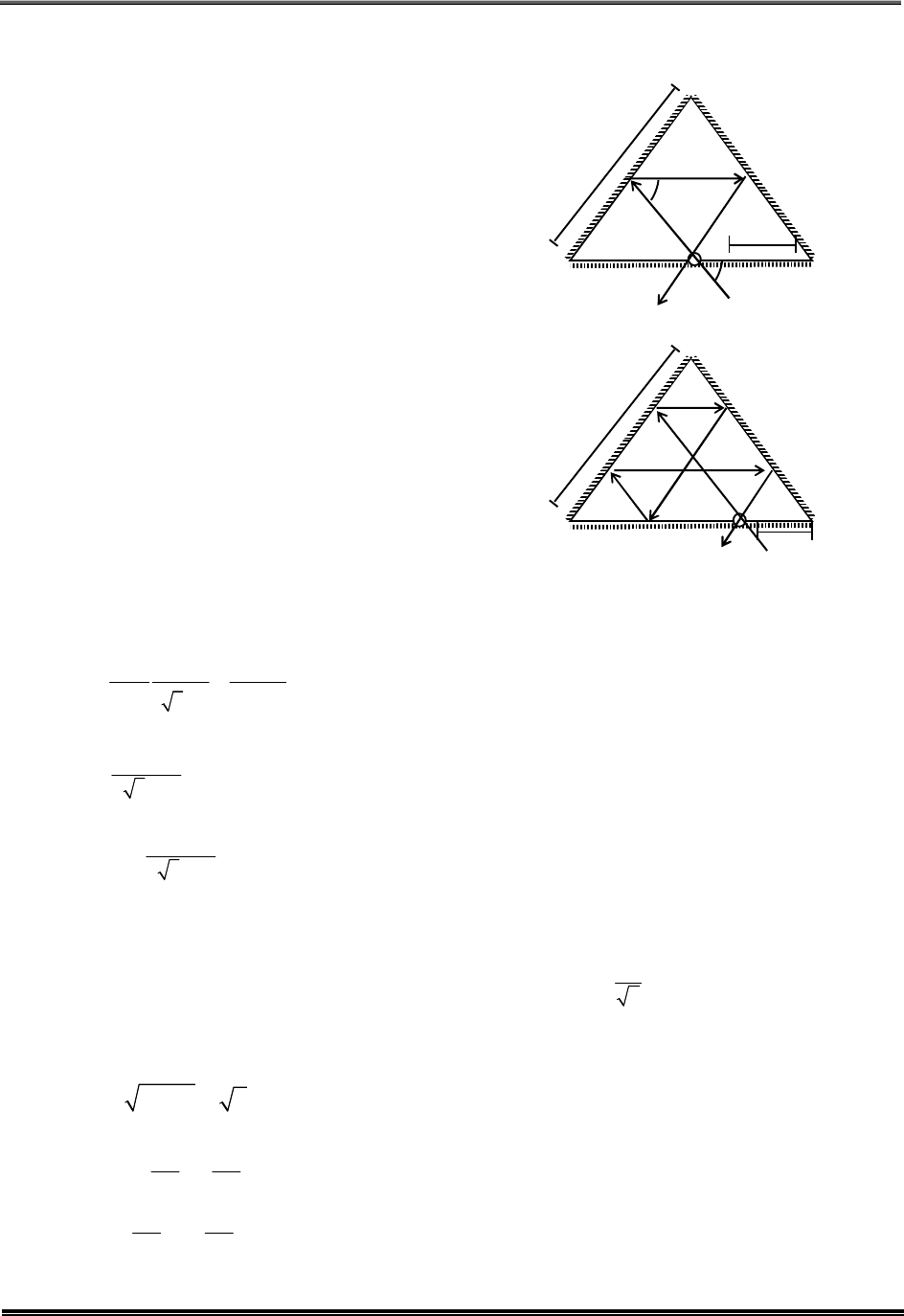
Q.12 Three plane mirrors form an equilateral triangle with each side of length L. There is a small hole at a
distance l > 0 from one of the corners as shown in the figure. A ray of light is passed through the hole at an
angle and can only come out through the same hole. The cross section of the mirror configuration and the
ray of light lie on the same plane.
l
L
Which of the following statement(s) is(are) correct?
(A) The ray of light will come out for = 30, for 0 < l < L.
(B) There is an angle for
2
L
l
at which the ray of light will come out after two reflections.
(C) The ray of light will NEVER come out for = 60, and
3
L
l
(D) The ray of light will come out for = 60, and 0 <
2
L
l
after six reflections.
Q.13 Six charges are placed around a regular hexagon of side length a as shown in the figure. Five of them have
charge q , and the remaining one has charge x . The perpendicular from each charge to the nearest hexagon
side passes through the center O of the hexagon and is bisected by the side.
q
90
q
q
q
q
a
O
x
Which of the following statement(s) is(are) correct in SI units?

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
10
(A) When x = q , the magnitude of the electric field at O is zero.
(B) When x = −q , the magnitude of the electric field at O is
2
0
6
q
a
(C) When x = 2q, the potential at O is
0
7
4 3
q
a
.
(D) When x = − 3q , the potential at O is
0
3
4 3
q
a
Q.14 The binding energy of nucleons in a nucleus can be affected by the pairwise Coulomb repulsion. Assume
that all nucleons are uniformly distributed inside the nucleus. Let the binding energy of a proton be
p
b
E
and
the binding energy of a neutron be
n
b
E
in the nucleus.
Which of the following statement(s) is(are) correct?
(A)
p
b
E
−
n
b
E
is proportional to Z(Z−1) where Z is the atomic number of the nucleus.
(B)
p
b
E
−
n
b
E
is proportional to
1
3
A
where A is the mass number of the nucleus.
(C)
p
b
E
−
n
b
E
is positive.
(D)
p
b
E
increases if the nucleus undergoes a beta decay emitting a positron.
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
11
SECTION 3 (Maximum Marks: 12)
This section contains FOUR (04) Matching List Sets.
Each set has ONE Multiple Choice Question.
Each set has TWO lists: List-I and List-II.
List-I has Four entries (I), (II), (III) and (IV) and List-II has Five entries (P), (Q), (R), (S) and (T).
FOUR options are given in each Multiple Choice Question based on List-I and List-II and ONLY ONE of
these four options satisfies the condition asked in the Multiple Choice Question.
Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +3 ONLY if the option corresponding to the correct combination is chosen;
Zero Marks : 0 If none of the options is chosen (i.e. the question is unanswered);
Negative Marks : –1 In all other cases.
Q.15 A smaller circular loop of area A and resistance R is fixed on a horizontal xy-plane with the center of the
loop always on the axis
n
of a long solenoid. The solenoid has m turns per unit length and carries current I
counterclockwise as shown in the figure. The magnetic field due to the solenoid is in
n
direction. List-I
gives time dependences of
n
in terms of a constant angular frequency . List-II gives the torques
experienced by the circular loop at time
t .
6
Let
2 2 2 2
0
A m I
.
2R
List –I List -II
(I)
1
ˆ ˆ
sin t j cos t k
2
(P) 0
(II)
1
ˆ ˆ
sin t i cos t j
2
(Q)
ˆ
i
4
(III)
1
ˆ ˆ
sin t i cos t k
2
(R)
3
ˆ
i
4
(IV)
1
ˆ ˆ
cos t j sin t k
2
(S)
ˆ
j
4
(T)
3
ˆ
i
4
Which one of the following options is correct ?
(A) I Q, II P, III S, IV T (B) I S, II T, III Q, IV P
(C) I Q, II P, III S, IV R (D) I T, II Q, III P, IV R
z
y
x
z
I
ˆ
n

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
12
*Q.16 List I describes four systems, each with two particles A and B in relative motion as shown in figures. List II
gives possible magnitudes of their relative velocities (in m s
–1
) at time
t s.
3
List –I List -II
(I)
A and B are moving on a horizontal circle of radius 1 m with
uniform angular speed = 1 rad s
–1
. The initial angular
positions of A and B at time t = 0 are = 0 and
,
2
respectively.
(P)
3 1
2
(II) Projectiles A and B are fired (in the same vertical plane) at t
= 0 and t = 0.1 s respectively, with the same speed
5
v
2
m s
–1
and at 45° from the horizontal plane. The initial
separation between A and B is large enough so that they do
not collide. (g = 10 m s
–2
).
(Q)
3 1
2
(III) Two harmonic oscillators A and B moving in the x direction
according to
A 0
0
t
x x sin
t
and
B 0
0
t
x x sin
t 2
respectively, starting from t = 0. Take x
0
= 1 m, t
0
= 1 s.
(R)
10
B
x
A
B 0
0
t
x x sin
t 2
A 0
0
t
x x sin
t
45°
A
45°
B
t = 0.1s
t = 0
y
B
A
x
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
13
(IV) Particle A is rotating in a horizontal circular path of radius 1
m on the xy plane, with constant angular speed = 1 rad s
–1
.
Particle B is moving up at a constant speed 3 m s
–1
in the
vertical direction as shown in the figure. (Ignore gravity.)
(S)
2
(T)
2
25 1
Which one of the following options is correct ?
(A) I R, II T, III P, IV S
(B) I S, II P, III Q, IV R
(C) I S, II T, III P, IV R
(D) I T, II P, III R, IV S
*Q.17 List I describes thermodynamic processes in four different systems. List II gives the magnitudes (either
exactly or as a close approximation) of possible changes in the internal energy of the system due to the
process.
List –I List -II
(I) 10
–3
kg of water at 100°C is converted to steam at the same
temperature, at a pressure of 10
5
Pa. The volume of the system
changes from 10
–6
m
3
to 10
–3
m
3
in the process. Latent heat of
water = 2250 kJ/kg.
(P) 2 kJ
(II)
0.2 moles of a rigid diatomic ideal gas with volume V at
temperature 500 K undergoes an isobaric expansion to volume 3
V. Assume R = 8.0 J mol
–1
K
–1
.
(Q) 7 kJ
(III)
One mole of a monatomic ideal gas is compressed adiabatically
from volume
3
1
V m
3
and pressure 2 kPa to volume
v
.
8
(R) 4 kJ
(IV)
Three moles of a diatomic ideal gas whose molecules can
vibrate, is given 9 kJ of heat and undergoes isobaric expansion.
(S) 5 kJ
(T) 3 kJ
Which one of the following options is correct ?
(A) I T, II R, III S, IV Q (B) I S, II P, III T, IV P
(C) I P, II R, III T, IV Q (D) I Q, II R, III S, IV T
A
z
x
y
3 m s
–
1

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
14
Q.18 List I contains four combinations of two lenses (1 and 2) whose focal lengths (in cm) are indicated in the
figures. In all cases, the object is placed 20 cm from the first lens on the left, and the distance between the
two lenses is 5 cm. List II contains the positions of the final images.
List –I List -II
(I)
(P)
Final image is formed at 7.5 cm on the
right side of lens 2.
(II)
(Q)
Final image is formed at 60.0 cm on the
right side of lens 2.
(III)
(R)
Final image is formed at 30.0 cm on the
left side of lens 2.
(IV)
(S)
Final image is formed at 6.0 cm on the
right side of lens 2.
(T) Final image is formed at 30.0 cm on the
right side of lens 2.
Which one of the following options is correct?
(A) (I) P; (II) R; (III) Q; (IV) T (B) (I) Q; (II) P; (III) T; (IV) S
(C) (I) P; (II) T; (III) R; (IV) Q (D) (I) T; (II) S; (III) Q; (IV) R
+10
O
1
2
f = –20
20 cm
5 cm
–20
O
20 cm
1
2
5 cm
f = +10
+10
O
20 cm
1
2
5 cm
f = +10
+15
O
20 cm
1
2
5 cm
f = +10

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
15
PART III: CHEMISTRY
SECTION 1 (Maximum Marks: 24)
• This section contains EIGHT (08) questions.
• The answer to each question is a NUMERICAL VALUE.
• For each question, enter the correct numerical value of the answer using the mouse and the onscreen
virtual numeric keypad in the place designated to enter the answer. If the numerical value has more than
two decimal places, truncate/round off the value to TWO decimal places.
• Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +3 ONLY if the correct numerical value is entered;
Zero Marks : 0 In all other cases.
*Q1. 2 mol of Hg(g) is combusted in a fixed volume bomb calorimeter with excess of O
2
at 298 K and 1 atm into
HgO(s). During the reaction, temperature increases from 298.0 K to 312.8 K. If heat capacity of the bomb
calorimeter and enthalpy of formation of Hg(g) are 20.00 kJ K
-1
and 61.32 kJ mol
-1
at 298 K, respectively,
the calculated standard molar enthalpy of formation of HgO(s) at 298 K is X kJ mol
-1
. The value of |X| is
_______.
[Given: Gas constant R = 8.3 J K
-1
mol
-1
]
Q2. The reduction potential
0
4
E , in V of MnO aq / Mn s is
2 2
4 2 2
0 0 0
MnO aq / MnO s MnO s /Mn aq Mn aq /Mn s
Given : E 1.68V; E 1.21V; E 1.03V
*Q3. A solution is prepared by mixing 0.01 mol each of H
2
CO
3
, NaHCO
3
, Na
2
CO
3
, and NaOH in 100 mL of
water. pH of the resulting solution is _______.
[Given: pKa
1
and pKa
2
of H
2
CO
3
are 6.37 and 10.32, respectively; log 2 = 0.30]
*Q4. The treatment of an aqueous solution of 3.74 g of Cu(NO
3
)
2
with excess KI results in a brown solution
along with the formation of a precipitate. Passing H
2
S through this brown solution gives another precipitate
X. The amount of X (in g) is ________.
[Given: Atomic mass of H = 1, N = 14, O = 16, S = 32, K = 39, Cu = 63, I = 127]
*Q5 Dissolving 1.24 g of white phosphorous in boiling NaOH solution in an inert atmosphere gives a gas Q.
The amount of CuSO
4
(in g) required to completely consume the gas Q is _______.
[Given: Atomic mass of H = 1, O = 16, Na = 23, P = 31, S = 32, Cu = 63]
Q6. Consider the following reaction.
On estimation of bromine in 1.00 g of R using Carius method, the amount of AgBr formed (in g) is
________.
[Given: Atomic mass of H = 1, C = 12, O = 16, P = 31, Br = 80, Ag = 108].

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
16
Q7. The weight percentage of hydrogen in Q, formed in the following reaction sequence, is ________.
[Given: Atomic mass of H = 1, C = 12, N = 14, O = 16, S = 32, Cl = 35]
Q8. If the reaction sequence given below is carried out with 15 moles of acetylene, the amount of the product D
formed (in g) is ________.
The yields of A, B, C and D are given in parentheses.
[Given: Atomic mass of H = 1, C = 12, O = 16, Cl = 35]
SECTION 2 (Maximum Marks: 24)
This section contains SIX (06) questions.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MOER THAN ONE of these four option(s) is
(are) correct answer(s).
For each question, choose the option(s) corresponding to (all) the correct answer(s).
Answer to each question will be evaluated according to the following marking scheme:
Full Mark : +4 If only (all) the correct option(s) is(are) chosen;
Partial Marks : +3 If all the four options are correct but ONLY three options are chosen;
Partial Marks : +2 If three or more options are correct but ONLY two options are chosen, both of
which are correct;
Partial Marks : +1 If two or more options are correct but ONLY one option is chosen and it is a
correct option;
Zero Marks : 0 If unanswered;
Negative Marks : 2 In all other cases.
*Q9 For diatomic molecules, the correct statement(s) about the molecular orbitals formed by the overlap of two
2p
z
orbitals is(are)
(A) orbital has a total of two nodal planes
(B) * orbital has one node in the xz-plane containing the molecular axis.
(C) orbital has one node in the plane which is perpendicular to the molecular axis and goes through the
center of the molecule.
(D) * orbital has one node in the xy-plane containing the molecular axis.
Q10. The correct opion(s) related to adsorption process is (are)
(A) Chemisorption results in unimolecular layer.
(B) The enthalpy change during physisorption is in the range of 100 to 140 kJ mol
–1
(C) Chemisorption is an endothermic process
(D) Lowering the temperature favours physisorption process
Q11. The electrochemical extraction of aluminum from bauxite ore involves
(A) the reaction of Al
2
O
3
with coke (C) at a temperature > 2500 ºC.
(B) the neutralization of aluminate solution by passing CO
2
gas to precipitate hydrated alumina
(Al
2
O
3
·3H
2
O).
(C) the dissolution of Al
2
O
3
in hot aqueous NaOH.
(D) the electrolysis of Al
2
O
3
mixed with Na
3
AlF
6
to give Al and CO
2
.

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
17
Q12. The treatment of galena with HNO
3
produces a gas that is
(A) paramagnetic (B) bent in geometry
(C) an acidic oxide (D) colorless
Q13. Considering the reaction sequence given below, the correct statement(s) is(are)
(A) P can be reduced to a primary alcohol using NaBH
4
.
(B) Treating P with conc. NH
4
OH solution followed by acidification gives Q.
(C) Treating Q with a solution of NaNO
2
in aq. HCl liberates N
2
.
(D) P is more acidic than CH
3
CH
2
COOH.
Q14. Considering the following reaction sequence,
the correct option(s) is(are)
(A)
2 2 3 2
4
P H / Pd,ethanol R NaNO / HCl U 1.H PO
2.KMnO .KOH,heat
(B)
(C)
(D)
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
18
SECTION 3 (Maximum Marks: 12)
• This section contains FOUR (04) Matching List Sets.
• Each set has ONE Multiple Choice Question.
• Each set has TWO lists: List I and List II.
• List I has Four entries (I), (II), (III) and (IV) and List II has Five entries (P), (Q), (R), (S) and (T).
• FOUR options are given in each Multiple Choice Question based on List I and List II and ONLY ONE of
these four options satisfies the condition asked in the Multiple Choice Question.
• Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +3 ONLY if the option corresponding to the correct combination is chosen;
Zero Marks : 0 If none of the options is chosen (i.e. the question is unanswered);
Negative Marks : −1 In all other cases.
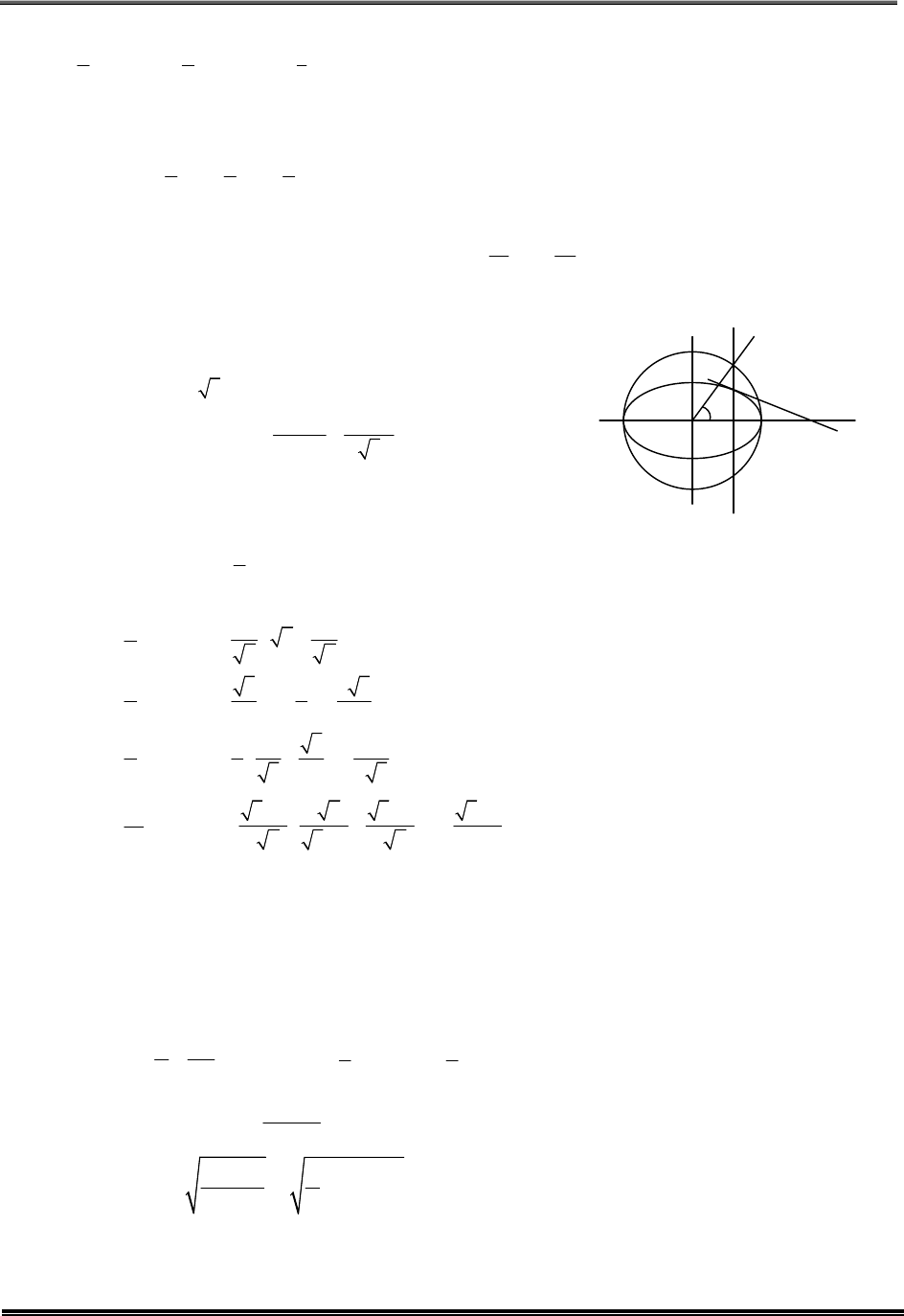
*Q15. Match the rate expressions in LIST-I for the decomposition of X with the corresponding profiles provided
in LIST-II. X
s
and k are constants having appropriate units.
LIST- I LIST-II
(I)
s
k X
rate
X X
under all possible initial concentrations of X
(P)
(II)
s
k X
rate
X X
where initial concentrations of X are
much less than X
s
(Q)
(III)
s
k X
rate
X X
where initial concentrations of X are
much higher than X
s
(R)
(IV)
2
s
k X
rate
X X
where initial concentration of X is
much higher than X
s
(S)
(T)
(A) I→ P; II→ Q; III → S; IV → T (B) I→ R; II→ S; III → S; IV → T
(C) I→ P; II→ Q; III → Q; IV → R (D) I→ R; II→ S; III → Q; IV → R

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
19
*Q16. LIST-I contains compounds and LIST-II contains reactions.
LIST- I LIST-II
(I) H
2
O
2
(P)
3
2 2
Mg HCO Ca OH
(II) Mg(OH)
2
(Q)
2 2 4
BaO H SO
(III) BaCl
2
(R)
2
2
Ca OH MgCl
(IV) CaCO
3
(S)
2
BaO HCl
(T)
3
2 2
Ca HCO Ca OH
Match each compound in LIST-I with its formation reaction(s) in LIST-II, and choose the correct option
(A) I → Q; II → P; III → S; IV → R
(B) I → T; II → P; III → Q; IV → R
(C) I → T; II → R; III → Q; IV → P
(D) I → Q; II → R; III → S; IV → P
Q17. LIST-I contains metal species and LIST-II contains their properties.
LIST- I LIST-II
(I)
4
6
Cr CN
(P)
2g
t
orbitals contain 4 electrons
(II)
2
6
RuCl
(Q)
spin only 4.9BM
(III)
2
2 6
Cr H O
(R) Low spin complex ion
(IV)
2
2
6
Fe H O
(S) Metal ion in 4+ oxidation state
(T) d
4
species
[Given: Atomic number of Cr = 24, Ru = 44, Fe = 26]
Match each metal species in LIST-I with their properties in LIST-II, and choose the correct option
(A) I → R, T; II → P, S; III → Q, T; IV → P, Q
(B) I → R, S; II → P, T; III → P, Q; IV → Q, T
(C) I → P, R; II → R, S; III → R, T; IV → P, T
(D) I → Q, T; II → S, T; III → P, T; IV → Q, R
Q18. Match the compounds in LIST-I with the observations in LIST-II, and choose the correct option.
LIST- I LIST-II
(I) Aniline (P) Sodium fusion extract of the compound on boiling
with FeSO
4
, followed by acidification with conc.
H
2
SO
4
, gives Prussian blue color.
(II) o-Cresol (Q) Sodium fusion extract of the compound on
treatment with sodium nitroprusside gives blood red
color.
(III) Cysteine (R) Addition of the compound to a saturated solution of
NaHCO
3
results in effervescence.
(IV) Caprolactam (S) The compound reacts with bromine water to give a
white precipitate.
(T) Treating the compound with neutral FeCl
3
solution
produces violet color.
(A) I→P,Q; II→S; III→Q,R; IV→P
(B) I→P; II→R,S; III→R; IV→Q,S
(C) I→Q,S; II→P,T; III→P; IV→S
(D) I→P,S; II→T; III→Q,R; IV→P

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
20
FIITJEE JEE (Advanced Paper)
(PAPER-1)
ANSWER KEY
MATHEMATICS
1. 2.35 or 2.36 2. 0.5 3. 0.80 4. 0.50
5. 4 6. 18900 7. 569 8. 0.83 or 0.84
9. C, D 10. B, C 11. A, B, D 12. A, B, C
13. B, C, D 14. A, C 15. B 16. A
17. B 18. C
PHYSICS
1. 2.30 2. 2.32 3. 8.00 4. 6.00
5. 0.52 6. 2.85 7. 4.00 8. 0.95
9. B 10. A, B, C, D 11. B 12. A, B
13. A, B, C 14. A, B, D 15. None 16. C
17. C 18. A
CHEMISTRY
1. 90.39 2. 0.77 3. 10.02 4. 0.32
5. 2.38 6. 1.50 7. 1.31 8. 136.00
9. A, D 10. A, D 11. B, C, D 12. A, D
13. B, C, D 14. A,B,C 15. A 16. D
17. A 18. D

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
21
HINTS AND SOLUTIONS
MATHEMATICS
1. 2.35 or 2.36
Let tan =
2
4 2
2 tan
1 1 1
2 2
3 2 1 2 2 2 tan 2
cos sin tan
2 4
2 2 tan 2 2 tan
2 tan
=
1 1 1
3 1
cos cos sin sin 2 tan cot
2 4
3 1 3
2
2 4 2 4 2 4
2. 0.5
x x
lim f g x f lim g x
Now
x
x x
2ln x
lim g x lim
ln e e
Apply D'L Hospital
x
x
x
1 1
2
2 x
x
lim
1 1
e
2 x
e e
x
x
x
2 e e
lim
e x
x
x
x
2e e 1
lim 2
e x
Now f(x) =
x
sin
12
given
f(2) =
2
1
sin sin
12 6 2
= 0.5
3. 0.80
Let A denote the persons having symptoms of fever.
B denote the persons having symptoms of cough
C denote the persons having symptoms of breathing
problem
Given that
n(A) = 190 n(B) = 220 n(C) = 220
n(A B C) = 30
n(A B) = 330 n(B C) = 350 n(C A) = 340
n(A B) = n(A) + b(B) n(A B)
330 = 190 + 220 n(A B) n(A B) = 80
Similarly n(B C) = 90 and n(C A) = 70
If we make the Venn diagram
A
B
C
80
70
30
50
40
60
90
480

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
22
n(A B C) = n(A) + n(B) + n(C) n(A B) n(B C) n(C A) + n(A B C)
= 190 + 220 + 220 80 90 70 + 30 = 420
Number of person having atmost one symptom
= 480 + 70 + 80 + 90 = 720
Probability =
720 4
900 5
= 0.80
4. 0.50
2
2
2 3z 4z
2 3z 4z
is a real number
6
1 R
2
3 4z
z
1
2z R
z
1 1
2z 2z
z z
2zz 1 z z 0
|z|
2
=
1
2
= 0.50
5. 4
Let z = x + iy
x iy x
2
+ y
2
2ixy = i(x iy + x
2
y
2
+ 2ixy)
(x x
2
+ y
2
) i(y + 2xy) = (y 2xy) + i(x + x
2
y
2
)
x x
2
+ y
2
= y 2xy …(1)
x + x
2
y
2
= y 2xy …(2)
(1) + (2) 2x = 4xy
x = 2xy x(1 + 2y) = 0 x = 0 or y =
1
2
Put x = 0 in (1) or (2) we get
y
2
= y y = 0, 1
2 complex numbers are possible 0 + 0i and 0 + i
put y =
1
2
in (1) or (2) x x
2
+
1 1
x
4 2
x
2
=
3
4
x =
3
2
3 i
2 2
and
3 i
2 2
are possible
4 solutions are possible.
6. 18900
A
51
A
50
= 1000
l
51
w
51
l
50
w
50
= 100
(l
1
+ 50d
1
) (w
1
+ 50d
2
) (l
1
+ 49d
1
) (w
1
+ 49d
2
) = 1000
l
1
w
1
+ 50l
1
d
2
+ 50d
1
w
1
+ 2500d
1
d
2
l
1
w
1
49l
1
d
2
49d
1
w
1
240d
1
d
2
= 1000
l
1
d
2
+ d
1
w
1
+ 99d
1
d
2
= 1000
l
1
d
2
+ d
1
w
1
= 10
A
100
A
90
= (l
100
w
100
) (l
90
w
90
)
= (l
1
+ 99d
1
) (w
1
+ 99d
2
) (l
1
+ 89d
1
) (w
1
+ 89d
2
)
= 10d
1
w
1
+ 10l
1
d
2
+ 1880d
1
d
2
= 10 10 + 18800 = 18900

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
23
7. 569
Number of numbers whose digits are
2 0
6 6 7 = 209
2
5 6 6 = 180
3
6 6 6 = 216
4
4 6 6 = 144
Total number are (36 7) + (5 6 6) + (6 6 6) + 4 6 6 = 569
8. 0.83 or 0.84
Let A be (0, 0), B(1, 0) and C(0, 3)
AB lies on x-axis and AC lies on y-axis
equation of circle touching both x and y-axis is of the form
(x h)
2
+ (y h)
2
= h
2
(
h = k = r)
It touches the circle
2 2
1 3 5
x y
2 2 2
c
1
c
2
= |r
1
r
2
|
2 2
1 3 5
h h h
2 2
2
2 2 2
1 9 5
h h h 3h h 10h
4 4 2
2
h 10 4 h 0
h =
4 10
r =
4 10 0.8377
C(0, 3)
A(0, 0)
B(1, 0)
9. C, D
1/ 2
e
2
3/ 2
1
ln x
dx 1
x a ln x
a (ln x)
3/2
= t
1/ 2
3 1
ln x dx dt
2 x
a 1
2
a
2
dt
3
1
t
a 1
2 1
1
3 t
2 1 1
1
3 a 1 a
a a 1 3
a a 1 2
3(a
2
a) = 2
3a
2
3a 2 = 0
3 9 24 3 33
a
6 6

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
24
10. B, C
n
n 1 n n
n 1
T T a
n 1 1 n
n
T T a 2 7 n 1 8
2
T
n+1
= n(4n + 3) + T
1
T
n+1
= 4n
2
+ 3n + 3
(A) T
20
= 4 19
2
+ 3 9 + 3
= 1444 + 27 + 3 = 1474
(B)
19 19
n 1
k 0 k 0
T k 4k 3 3
=
19
2
k 0
4k 3k 3
= 10510
(C) T
30
= 29(4 29 + 3) + 3 = 3454
(D)
30 29 29
k n 1
k 1 n 0 n 0
T T n 4n 3 3
=
3 29 30
29 30 59
4 90 35615
6 2
11. A, B, D
The line should be either coincident on P
1
or on P
2
or intersect on P
1
and P
2
on different points.
(D)
x y 4 z
1 2 3
(, 2 + 4, 3) lie on P
2
(A)
x 1 y 1 z 1
0 0 5
intersects P
1
and P
2
on different points.
(B)
x 6 y z
5 2 3
also intersects P
1
and P
2
on different points.
12. A, B, C
Clearly plane is given by x + y + z = 1
using mirror image formula
2 2 2
2 10 15 20 1
10 15 20 88
1 1 1 3
1 1 1
58 43 28
; and
3 3 3
13. B, C, D
Let P
1
and P
2
be
2 2
1 1 2 2
t , 2t and t , 2t
P (t
1
t
2
, t
1
+ t
2
) (2, 1)
t
1
= 2, t
2
= 1 or t
1
= 1, t
2
= 2
P
1
(4, 4) and P
2
(1, 2)
Slope of SP
1
=
4
3
slope of SP
2
=
Equation of SP
1
y 0 =
4
3
(x 1) 4x 3y 4 = 0
Equation of PQ
1
P
1
Q
1
P
S(1, 0)
Q
2
P
2

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
25
y 1 =
4
3
(x + 2) 3x + 4y + 2 = 0
1
2 4
Q ,
5 5
Equation of SP
2
x = 1
Equation of PQ
2
y = 1 Q
2
(1, 1)
SQ
1
= 1, Q
1
Q
2
=
3 10
5
PQ
1
=
2 2
2 4 144 81
2 1 3
5 5 25 25
and SQ
2
=
2 2
1 1 1 0 1
14. A, C
f() =
e
e
sin cos tan
4 4
0 0 2
1 4
sin 1 sin sin cos log
2 4 2
1 sin 1
cot log tan
4 4
As second determinant is skew symmetric its value is 0.
f() = (1 + sin
2
)
g() = |sin| + |cos|
1, 2
p(x) = a(x 1)
x 2
as p(2) =
2 2
a = 1
p(x) = (x 1)
x 2
and hence
3 2
p 0
4
and
5 2 1
p 0
4
15. B
(I) cosx + sinx = 1
2 cos x 1
4
1
cos x
4
2
x 2n
4 4
for n = 0, x =
2
, 0
for n = 1, 2, 3, ….. no solution in
2 2
,
3 3
I P
(II) tan3x =
1
3
3x = n +
6
x =
n
3 18
for n = 0 x =
18
for n = 1, x =
5
18
for n = 1, 2, 3, …. no solution II P

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
26
(III) cos2x =
3
2
2x = 2n
6
x = n
12
for n = 1 x =
13 11
,
12 12
III T
(IV)
1
cos x
4
2
3
x 2n
4 4
for n = 0 x =
2
,
for n = 1 x = for n = 1 x =
3
2
IV R
16. A
Let A
1
; P
1
won the round P(A
1
) =
6
2
2
C
6 5
2 6 6
6
P(A
1
) =
5
12
A
2
; P
2
won the round P(A
2
) =
5
12
D ; round ends in draw P(D) =
2
6 1
6
6
(i) P(X
2
Y
2
) = P(A
1
A
1
) + 2P(A
1
A
1
) + P(D
D) + 2P(A
1
D)
=
5 5 5 5 1 1 5 1
2 2
12 12 12 12 6 6 12 6
=
11
16
(1) (Q)
(ii) P(X
2
> Y
2
) = P(A
1
A
1
) + 2P(A
1
D)
=
5 5 5 1 25 5
2
12 12 12 6 144 36
=
45 5
144 16
(ii) R
(iii) P(X
3
= Y
3
) = 3P(A
1
D
A
2
) + P(D
D
D)
=
5 5 1 1 1 1
6
12 12 6 6 6 6
=
25 1 75 2 77
144 216 432 432
(iii) T
(iv) P(X
3
> Y
3
) = P(A
1
A
1
A
1
) +3P(A
1
A
1
A
2
) + 3P((A
1
A
1
D) + 3P(A
1
D
D)
=
5 5 5 5 5 5 5 5 1 5 1 1
3 3 3
12 12 12 12 12 12 12 12 6 12 6 6
=
3
710 355 355
144 6 864
12
IV S
17. B
x + y + z = 1 ..... (1)
10x + 100y + 1000z = 0 ..... (2)
x y z
0
p q r
..... (3)
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
27
1
A 9d
p
;
1
A 99d
q
;
1
A 999d
r
From equation (2) and (3), we get
A d x A d y A d z 0
If A d, then no solution
If A = d
p q p
10, 10, 100
q r r
then the equations have infinite solutions
Now, equation (2) and (3) both are same
So, (1) and (2) both equation are satisfying x = 0,
10
y
9
,
1
z
9
18. C
Equation of auxiliary circle x
2
+ y
2
= 4
Let F be (2 cos , 2 sin )
E is
2cos , 3 sin
Equation of tangent at E,
x cos ysin
1
2
3
It cuts x-axis at (2 sec , 0)
G is (2 sec , 0)
G
F
E
H
H is (2 cos , 0) and F(2 cos , 2 sin )
Area of FGH is
1
2sin 2 sec 2 cos
2
= 2 sin (sec – cos )
If
4
, area =
1 1
2 2 1
2 2
If
3
, area =
3 1 3 3
2 2
2 2 2
If
6
, area =
1 2 3 1
2
2 2
3 2 3
If
12
, area =
4
3 1 2 2 3 1 3 1
2
8
2 2 3 1 2 2
.
PHYSICS
1. 2.30
M
B
= 2M
A
B
= 2
A
Now after the mass transfer,
M’
A
=
A
3
4
3 8
R
and M’
B
=
3 3
A A
4 7
G 2 R R
3 8
and outer radius R’ =
1/3
(15)
2
R
So, v
A
=
2
2 2
3
A
A
GM
G R
R

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
28
v
B
=
3 3
7
2 (4 / 3) (2 )
8
A A
G R R
R
1/3 1/3
23 (2.3)(10)
(15) (15)
B
A
v
v
So, n = 2.30
2. 2.32
14 4 1 19
7 2 1 8
N He H O
Q = [16.006 + 4.003 – 1.008 – 19.003] 930
= - 1.86 MeV
E
th
=
4
1 1 1.86 2.32
16
m
Q MeV
M
3. 8.00
In the loop 1234, + 6 -
3
48
0
12 4
q
, q
1
= 12 (6 – 2) = 48 C
q
3
= 8 C
2V
6V
C
1
+
q
1
C
2
C
3
+q
3
C
5
C
4
+
-
3
2
1
4
4. 6.00
1
40
u
3
f = 10
1
1 1 3 1
V 40 10
V
1
= 40
2
43
u
3
2
1 1 3 43 30
V 10 43 430
2
430
V
13
2 1 2
430 90
x V V 40
13 13
30 3 30 3 13 1
tan
13 x 13 90
3
3
2
40
3
cm
30 3
13
cm
V
1
V
2
x
2

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
29
6 n
n = 6
5. 0.52
2
1
t
2
1 2
60
2 3 3
cm
v t
Net velocity of point P is V = t at an angle 60°
with horizontal
y
u t sin 60
V
net
=
V
v
v
60°
2
2 2
y
max
u
1 1 t 3
y
2 2g 2 20 4
=
1
2 60
x = 0.52
6. 2.85
P
R 3R
mgsin R 1 1 I
2 2
2
10 1 3 7
1 mR
2 2 2 5
7
5 1
3
20
7
cm
20
a R
7
r
r
P
7. 4.00
= (B
0
+ t)A
ind
d
A
dt
Applying kVL in the equivalent circuit diagram of the loop.
A
Ldi q
dt C
= 0 … (i)
Also, i =
dq
dt
. . . (ii)
From (i) and (ii)
2
2
d i i
L
dt c
i = i
m
sin t =
1
LC
0 0
sin( )
q
t
m
dq i t dt
q =
m
i
(1 cos t)
+
i
–
C
+
–
q
L
V =
A
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
30
when i = i
m
sin t = 1 cost = 0
q =
m
i
AC
I
m
= AC = A
C
L
= 4mA
8. 0.95
d =
2 2
d 2H d 2 v sin
v cos v cos
2 g 2 g 2g
2
d V sin cos d d 9 19d
d
2 2 2 10 20
g
g
0.81
d = 0.95d
n = 0.95
V
d
2
2V sin cos
d
g
v
d
vcos
g
g =
H
9. B
Refer to figure (a)
V = E
1
d
0
1
k A
C
d
Figure(a)
V
d
E
1
Refer to figure (b)
3 2 3
d d d
V E E E
2 2 2
Also E
3
= E
2
K
V = E
2
d + KE
2
d
V = (K + 1) E
2
d
0 0
2
A A
K
C
d
K 1 d
d
K
Now
1
2
E
K 1
E
1
2
C
K 1
C
W
ext
+ W
battery
= U
W
ext
+
2
2
2 1 2 1
V
C C V C C
2
Figure(
b
)
V
d
d/2
d/2
E
2
E
3
E
3

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
31
W
ext
=
2 2
2 2
0 0
1 2
K A K AV
V 1 V
C C 1
2 d K 1 2 2d K 1
10. A, B, C, D
1 1 1
1 1
i i 6 i i i 0
2 2
1
1
i3
i i 6 0
2 2
2
1
i3 3
i i 6 0
2 2 2
1
3
i 2i 6 0
2
1
i i
i 12 0
2 2
1
i 3
i 12 0
2 2
1
5
i 6 0
2
1
6 2 12
i 2.4
5 5
1.2 1.5i 12 0
1.5i 10.8
10.8
i
1.5
i = 7.2
1
1/2
2
1/2
1/2
1
1
i
i–i
1
i
1
11. B
1
P T Const.
P
2
= 150 Pa …(1)
1 1 1
dm
A v
dt
v
1
= 40 m/s …(2)
PM
RT
2
= 0.1 Kg/m
3
…(3)
1 1 1 2 2 2
A v A v
v
2
= 20 m/s …(4)
From work energy theorem,
P
1
A
1
v
1
dt –
2
A
2
v
2
dt +
1
A
1
v
1
dt g(0) –
2
A
2
v
2
dt g(h)
=
2 2
2 2 2 2 1 1 1 1
1 1 1
A v dt v A v dt v
2 2 1
2 2 2 1 1 1
P A v dt P A v dt
h = 360 m.
h
A
2
A
1
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
32
12. A, B
For option ‘A’ there will be normal incidence
and ray retrace its path. For option ‘B’
60
L/2
L
60
1
L/3
L
2
5
4
3
13. A, B, C
When x = q, electric field at O is zero.
When x = –q, electric field at O is,
2 2
0
0
1 2q q
E
4
6 a
3a
When x = 2q, potential at O is,
0
7q
V
4 3 a
When x = – 3q, potential at O is,
0
2q
V
4 3 a
14. A, B, D
15. None
The magnitude of
ˆ
n
mentioned in List-I of the question is not 1, it is
1
2
16. C
is same, therefore angle between velocity vectors remain same.
V
rel
=
2 2
1 1 2 /
m s
1
5 5
ˆ ˆ
2 3
v i j
1
5 5
ˆ ˆ
1
2 3
v i j

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
33
v
rel
= |
2
2 1
| | 25 1
v v
17. C
W = PV = 0.1 kJ
Q = mL = 2.25 kJ
U = Q – W = 2.15 kJ
3
500
V V
T
T = 1500
U = nC
v
T = 4kJ
W =
PV (32P)(V / 8)
1 5 / 3
= 3 [PV = P (V/8)
; P= 32 P ]
1
v
P
nC T
U
Q nC T v
( f = 6 – vibration included )
U = 9 (3/4) 7
18. A
1 1 1
( )
concavelens
v f u
v = - 10
1 1 1
( )
convexlens
v f u
1 1 1
10 15
v
v = + 30
CHEMISTRY
1. T = 312.8 – 298 = 14.8
Molar heat capacity of calorimeter = 20 kJ K
1
Heat released by combustion of 2 moles of Hg(g)
= 20 14.8
= 296 kJ
1
combustion
296
U 148 kJ mol
2
2
1
Hg g O g HgO s
2
g
1 3
n 0 1
2 2
combustion combustion g
H U n RT
3
3
148 8.3 10 298
2
= 148 3.710
=
1
151.710 kJ mol

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
34
2
1
Hg O g HgO s
2
combustion f f 2
Hg Hg g
1
H H HgO H H O
2
151.710 = H
f
(HgO) 61.32 + 0
H
f
(HgO) = 151.710 + 61.32 = 90.39
H
f
= 90.39
2. (i)
4 2 1 1
MnO aq 8H 7e Mn s 4H O ; G 7 F E
(ii)
4 2 2 2
MnO 4H 3e MnO s 2H O ; G 3 F 1.68
(iii)
2
2 2 3
MnO s 4H 2e Mn aq 2H O ; G 2 F 1.21
(iv)
2
4
Mn aq 2e Mn s ; G 2 F 1.03
Now,
(i) = (ii) + (iii) + (iv)
1 2 3 4
G G G G
1
7 F E 3 F 1.68 2 F 1.21 2 F 1.03
1
7E 3 1.68 2 1.21 2 1.03
1
3 1.68 2 1.21 2 1.03
E
7
1
5.04 2.42 2.06
E
7
= 0.7714
= 0.77 V
3.
2 3 3 2
H CO NaOH NaHCO H O
Initial mol 0.01 0.01 0.01
After neutralization 0 0 0.01 0.01
0.02
Now, mixture contains 0.01 mole Na
2
CO
3
and 0.02 mol of NaHCO
3
so it is a buffer.
2
2
3
a
3
CO
pH pK log
HCO
0.01
pH 10.32 log
0.02
= 10.32 + log
1
2
= 10.32 – 0.30
= 10.02
4.
3 2 3
2
2Cu NO 4KI 2CuI I 4KNO
2 3
I KI KI
3 3 3
2
2Cu NO 5KI 2CuI KI 4KNO
Mole =
3.74
0.02
187
0.02
0.01
2
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
35
3 2
KI H S S 2HI KI
0.01 mol 0.01 mol
X
Mass of ‘S’ = 0.01 32= 0.32
5.
Mole of P
4
=
1.24
0.01
124
4 2 2 2 3
Q
P 3NaOH 3H O 3NaH PO PH
mole 0.01 0.01
3 4 3 2 2 4
Q
2PH 3CuSO Cu P 3H SO
3
mole0.01 0.01
2
Mole of CuSO
4
required =
3
0.01
2
Weight of CuSO
4
=
3
0.01 159 2.385 g
2
6.
OH
Br
2
Re d P
Br
Br
Br
(R)
(C
7
H
6
Br
2
)
Molecular weight of (R) = 7 12 + 1 6 + 80 2= 250 g/mol
Mole of AgBr formed = 2 mole of (R)
=
1
2 188
250
= 8 10
3
188 = 1.504 g
7.
Cl
NaOH, 623 K, 300 atm
O Na
2 4 3
conc. H SO then conc.HNO
OH
O
2
N NO
2
NO
2
Picric acid
C
6
H
3
O
7
N
3
Molecular weight = 12 6 + 1 3 + 16 7 + 14 3
= 72 + 3 + 112 + 42 = 229 gm/mole
Weight percentage of H =
3
100 1.3100 %
229

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
36
8.
Re d hot
Fe
CH CH
15 mole
(A)
3
AlCl
Cl
(B)
2
3
i O
ii H O
OH
(C)
O
CH
3
C
O
Cl
Pyridine
O C
O
CH
3
(D)
3
4 mole 2 mole
1 mole
1 mole
Molecular weight = C
8
H
8
O
2
= 12 8 + 1 8 + 16 2 = 96 + 8 + 32 = 136
Moles of product (D) formed
=
15 3
0.8 0.5 0.5 1
3 3
Weight of product (D) = 1 136 = 136 g
9.

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
37
10. Chemisorption is unimolecular layer and exothermic.
The enthalpy change in physiorption is 20 – 40 kJ/mol.
Physiorption decreases with increase of temperature.
11.
2 2 2 2 3
3
2NaAlO CO 3H O 2Al OH Na CO
2 3 2
3
2Al OH Al O 3H O
2 3 2 2
Al O 2NaOH 2NaAlO H O
During electrolysis of alumina, cryolite (Na
3
AlF
6
) and fluorspar (CaF
2
) are added to decrease the
melting point of alumina.
Al metal is obtained at cathode while CO
2
releases at anode.
12.
3 3 2
2
3PbS 8HNO 3Pb NO 3S 2NO 4H O
NO paramagnetic, neutral oxide and colourless gas
13.
CH
3
COOH
2
2
i Br / Re d P
ii H O
COOH
Br
(P)
3
i
ii NaOH
iii H O
N K
O
O
COOH
COOH
H
2
N
H
CH
3
COOH
Alanine
Q
COOH
NH
2
3
NH aq
COOH
Br
(P)
Q
COOH
Br
COOH <
(Acidic strength)
14.
(A)
NO
2
CH
3
2
H / Pd
ethanol
(P)
NH
2
CH
3
(Q)
2
NaNO / HCl
(R)
N
2
Cl
CH
3
(S)
3 2
4
i H PO
ii KMnO KOH, heat
COOH
(U)
(B)
NO
2
CH
3
Sn / HCl
(P)
NH
2
CH
3
(Q)
2
HNO
(R)
N
2
Cl
CH
3
(S)
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
38
(C)
OH
CH
3
3 2
4
i CH CH OH
ii KMnO KOH / heat
N
2
Cl
CH
3
(S)
(T)
(U)
COOH
2
H O
15.
s
k X
I Rate
X X
If [X] is low, then it follows first order kinetic ie. t
1/2
is constant (OA part in graph)
If [X] is high, then it follows zero order kinetics. So half life (t
1/2
) varies linearly with [X] as shown in
graph.
O
Initial conc.of X
1/2
cons tant t
1/2
half life( t )
A
I → P
s
k X
II Rate
X X
If [X] is less than X
s
, then reaction follows I
st
order kinetics as shown by the graph Q and T
II → Q, T
s
k X
III Rate
X X
If [X] >> X
s
, then reaction follows zero order kinetics, as show by the graph (S)
III → S
2
s
k X
IV Rate
X X
If [X] >> [X
s
], then reaction follows first order kinetics, as show by the graph (Q), (T)
IV → Q, T
16.
3 3 2
2 2 2
Mg HCO 2Ca OH Mg OH 2CaCO 2H O
2 2 4 4 2 2
BaO H SO BaSO H O
2 2
2 2
Ca OH MgCl Mg OH CaCl
2 2 2 2
BaO 2HCl BaCl H O
JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
39
3 3 2
2 2
Ca HCO Ca OH 2CaCO H O
I → Q,S; II → P,R; III → S; IV → P,T
17.
4
6
Cr CN
Cr
2+
4s
0
3d
4
(Configuration)
I P, T, R
4 0
2g g
t e
Low spin
n = 2
2 2 2
=
8 B.M
[RuCl
6
]
2
Ru
4+
4s
0
3d
4
II P, R, S,
T
4 0
2g g
t e
Low spin
8 B.M
2
2
6
Cr H O
2 0 4
Cr 4s 3d
III Q, T
3 1
2g g
t e
High spin
24 B.M
2
2
6
Fe H O
2 0 6
Cr 4s 3d
IV P, T
4 2
2g g
t e
High spin
4 4 2 24 B.M
18. (I) since aniline contains C and N so its sodium extract will give Prussian Blue colour with
FeSO
4
/Conc.H
2
SO
4
NH
2
2 2
Br / H O
NH
2
Br
Br
Br
white ppt
(II) Produces violet colour with neutral FeCl
3
CH
3
OH
(III) It contains –COOH, so it give effervescence with NaHCO
3
It also contains C, N, S, so its Na-extract will give blood red colour with FeCl
3
/H
2
SO
4
.
H
2
N COOH
H
SH

JEE (ADVANCED)-2022-Paper-1-MPC
FIITJEE Ltd., FIITJEE House, 29-A, Kalu Sarai, Sarvapriya Vihar, New Delhi -110016, Ph 46106000, 26569493, Fax 26513942
website: www.fiitjee.com
40
(IV) Caprolectum, it contains C and N, so its sodium extract will give Prussian blue colour
NH
O
